Progressive Collapse Analysis of Intact and Damaged Ships under Unsymmetrical Bending
Abstract
:1. Introduction
2. Method of Analysis
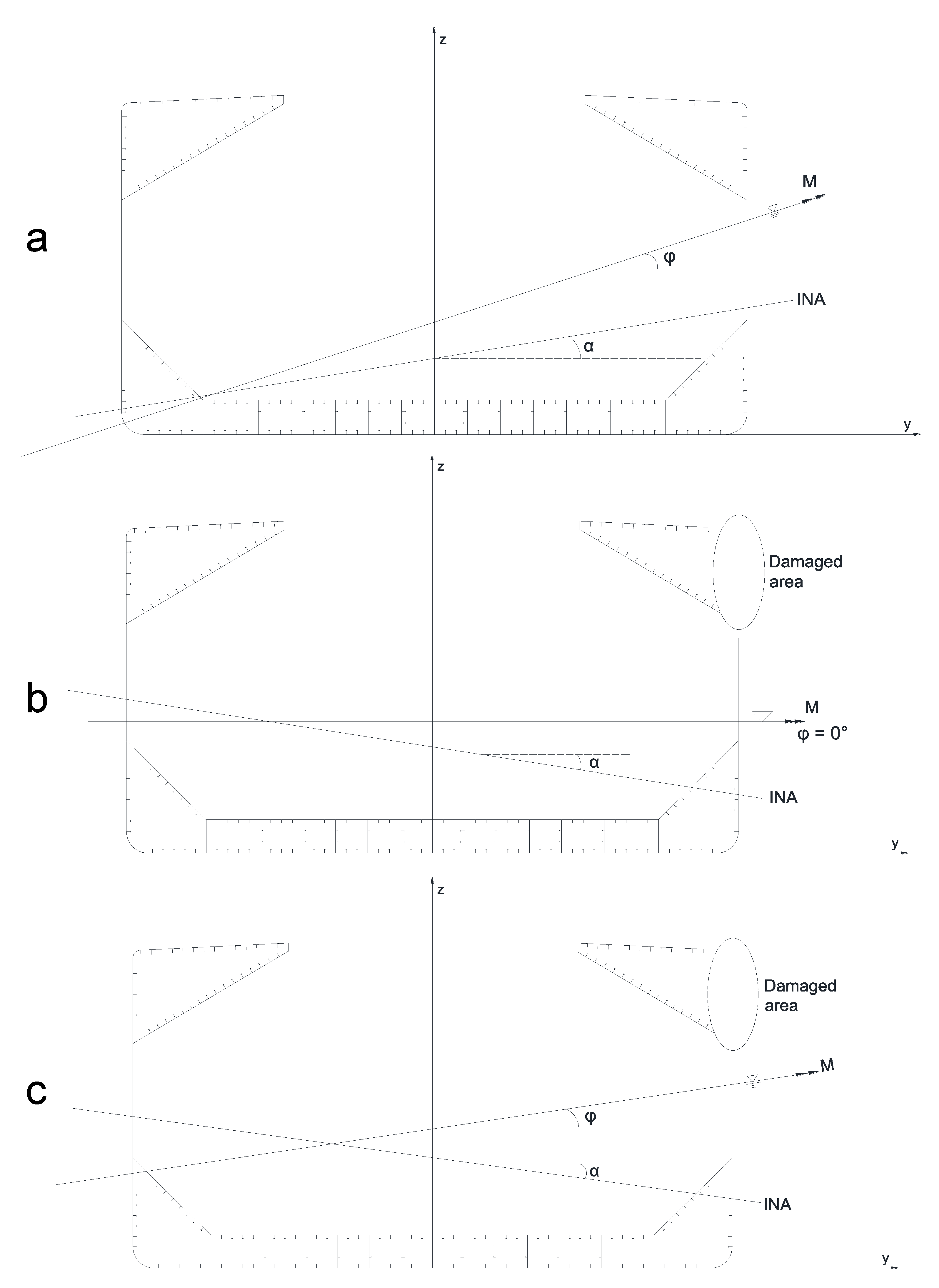
2.1. Elastic Response under Unsymmetrical Bending
2.2. Progressive Collapse under Unsymmetrical Bending
- The cross-sections remain in the plane (Navier’s hypothesis);
- The hull girder collapses between two transverse frames (interframe collapse);
- The structural units act independently.
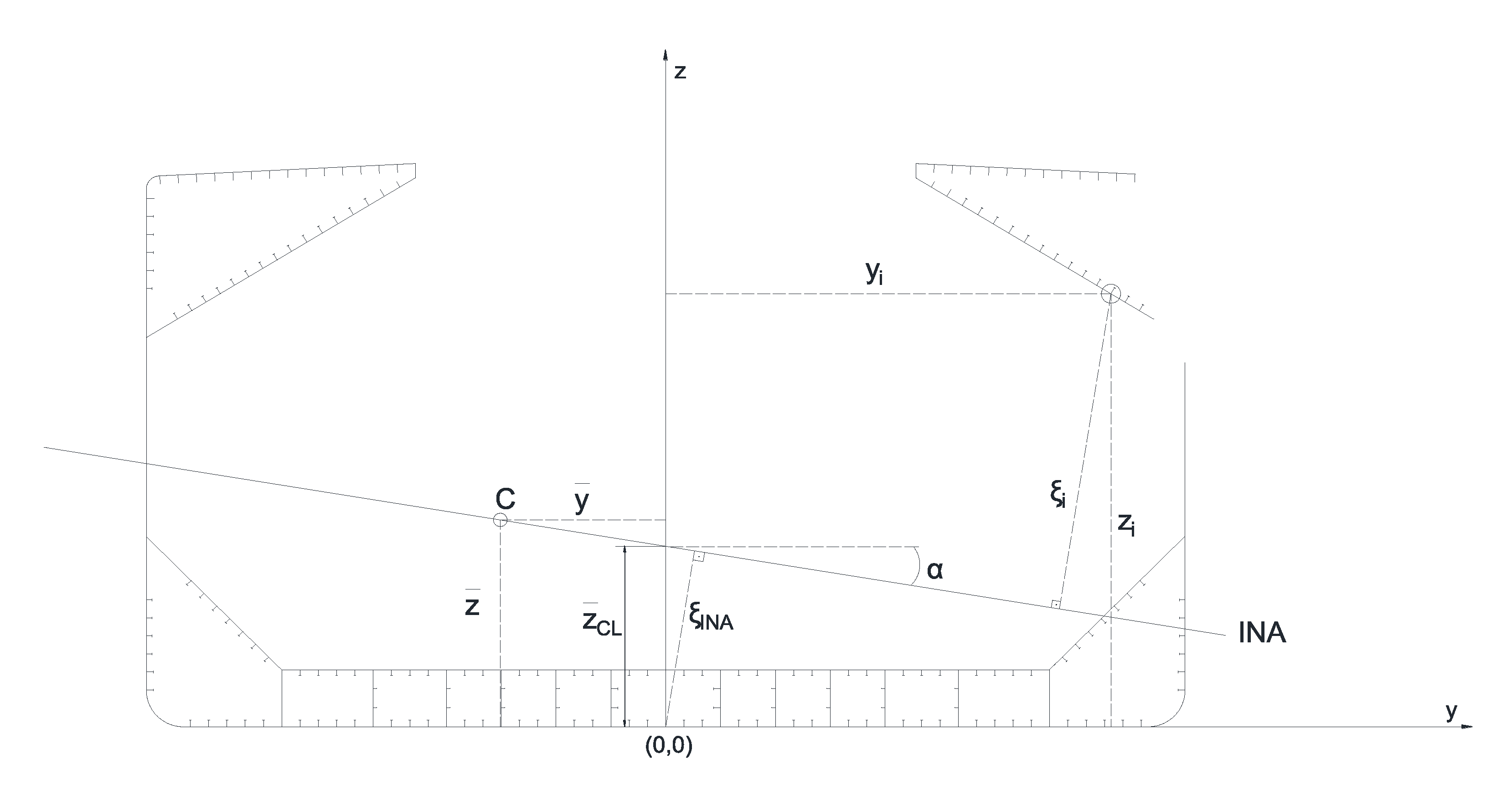
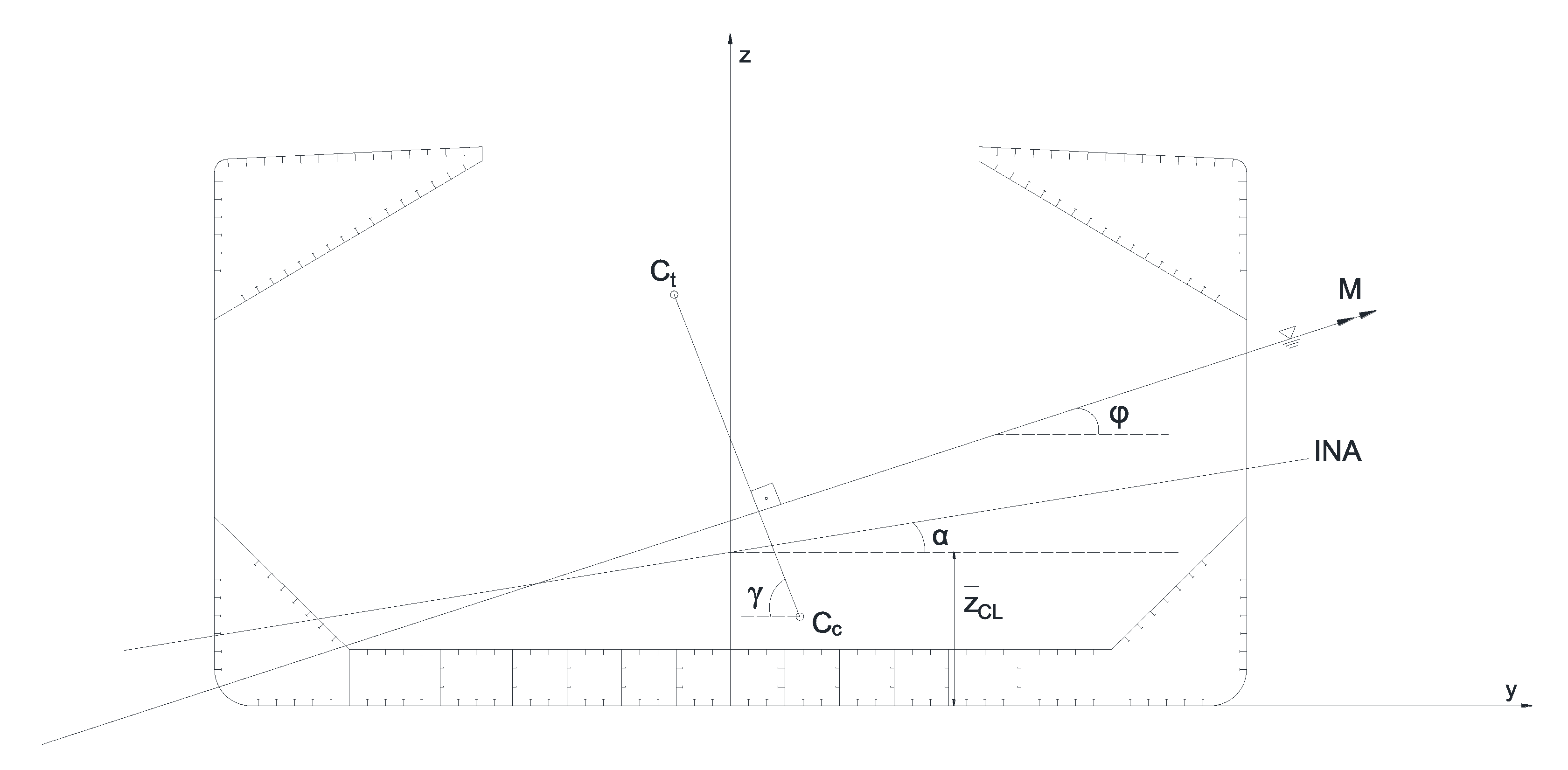
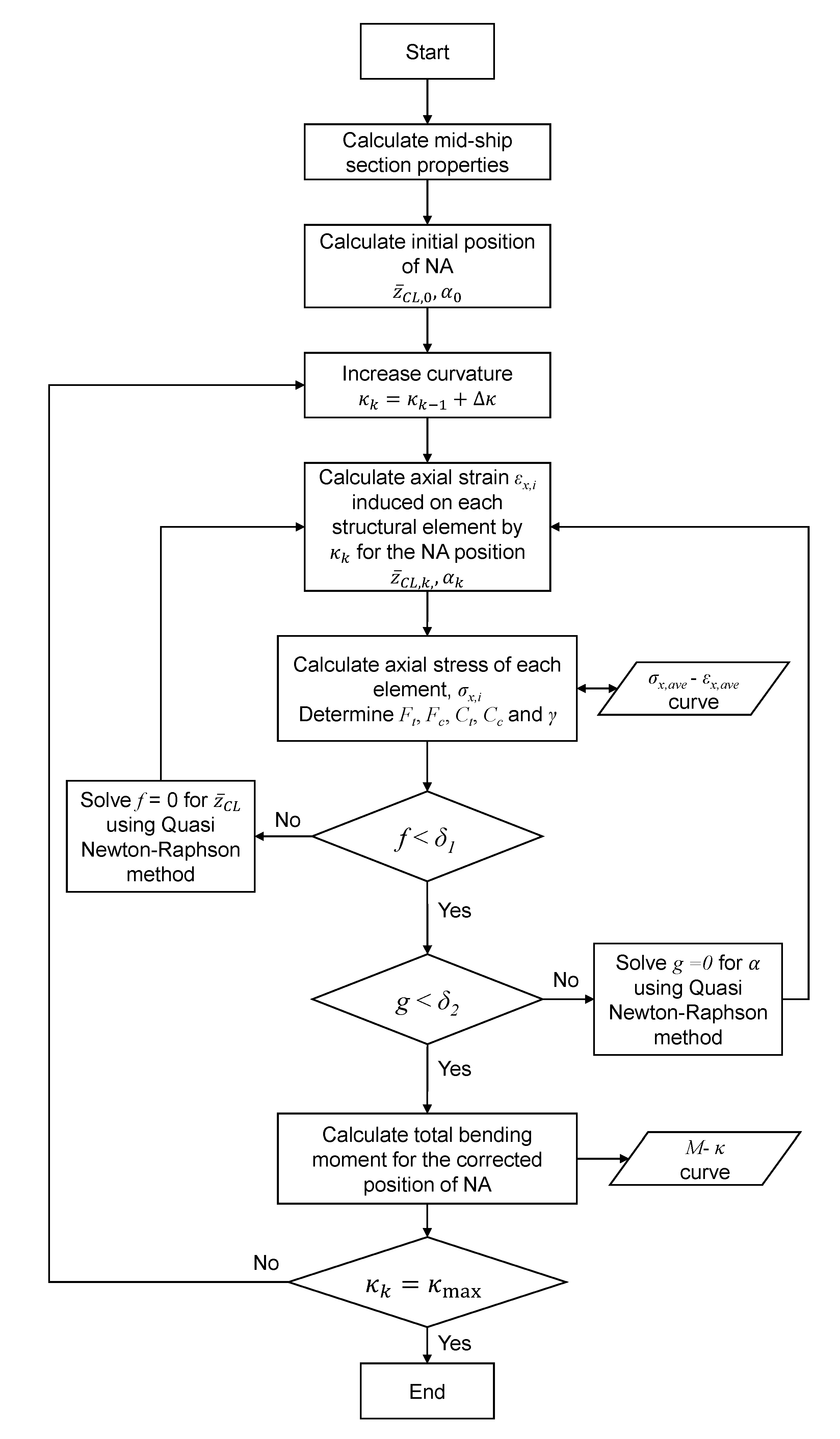
- Calculate the initial position of the neutral axis and apply incremental curvature about this instantaneous neutral axis (INA).
- Following the first fundamental assumption of Smith’s method, calculate the strain for each structural unit with respect to its vertical position and obtain the axial strain using the provided average stress-strain data.
- Integrate the axial stresses over the entire cross-section to obtain the bending moment.
- In each increment of curvature, find the position instantaneous neutral axis, and follow the above steps until the target curvature, is reached.
3. Applications
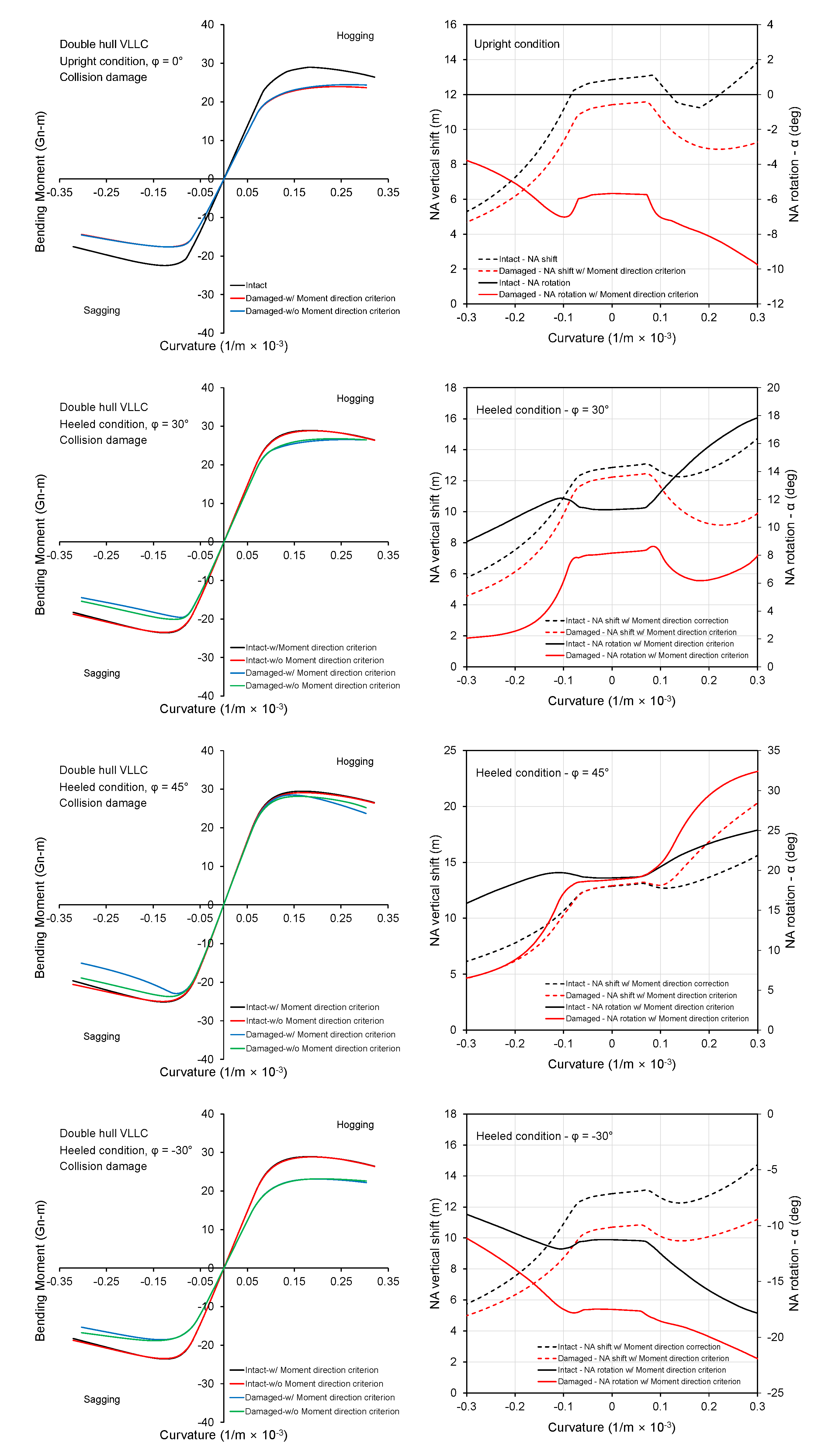
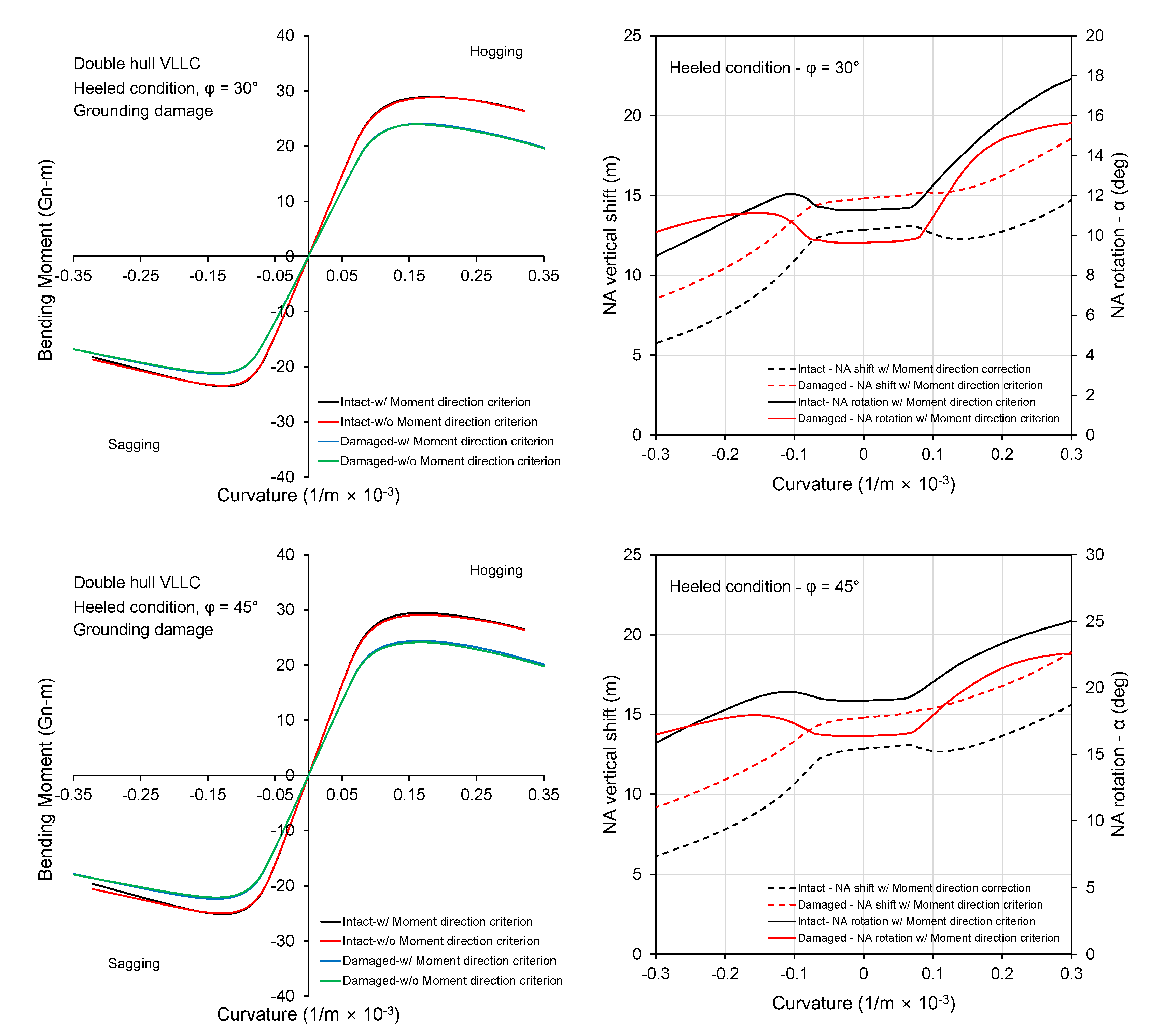
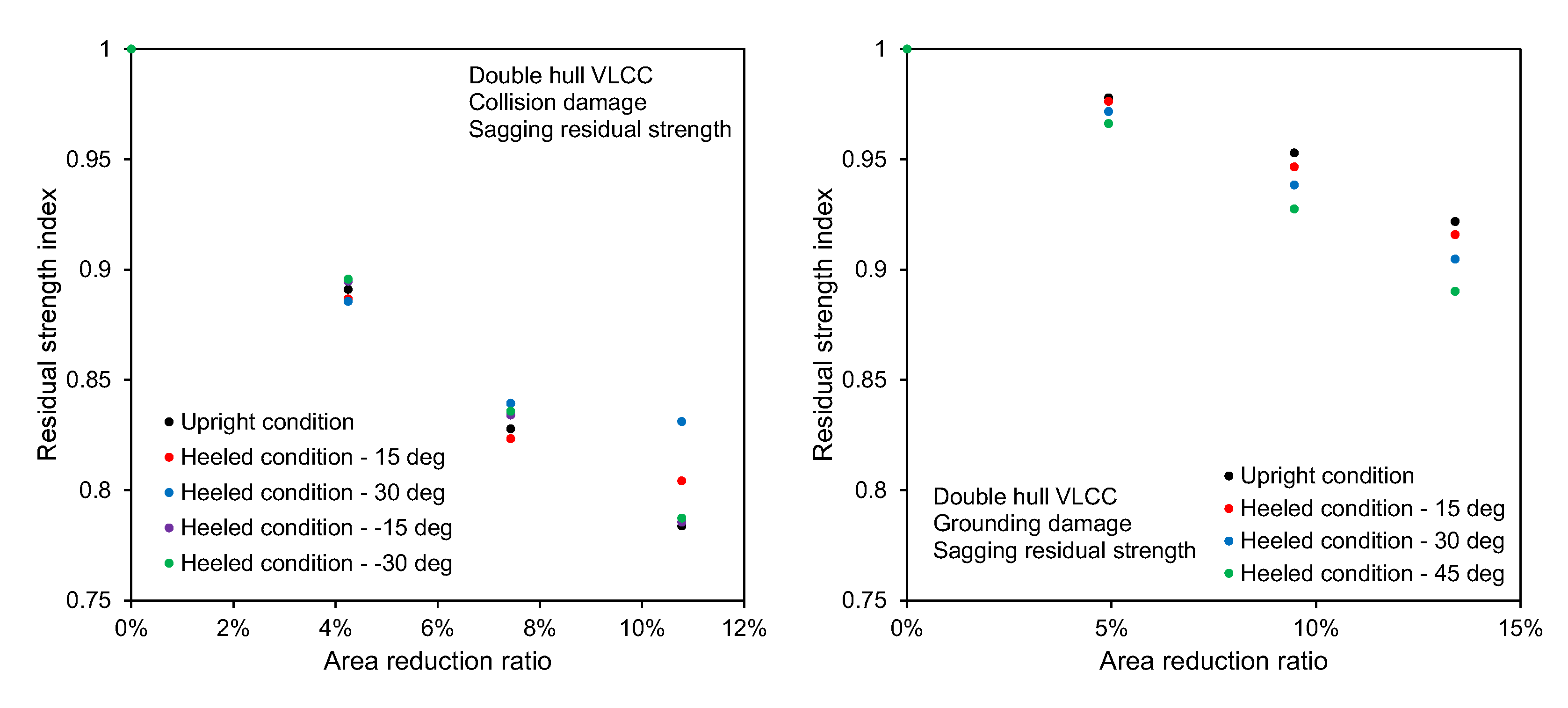
3.1. Double Hull VLCC
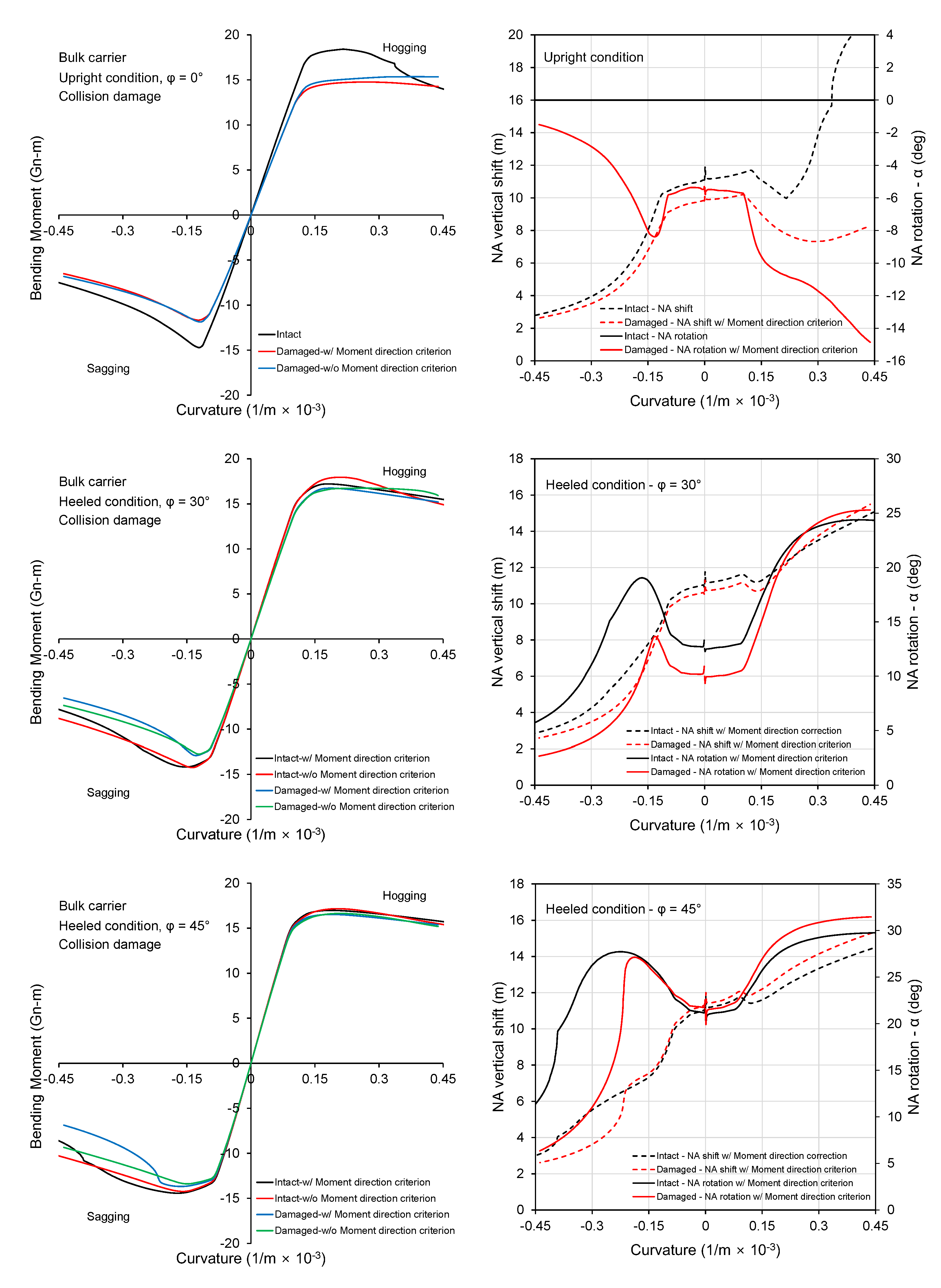
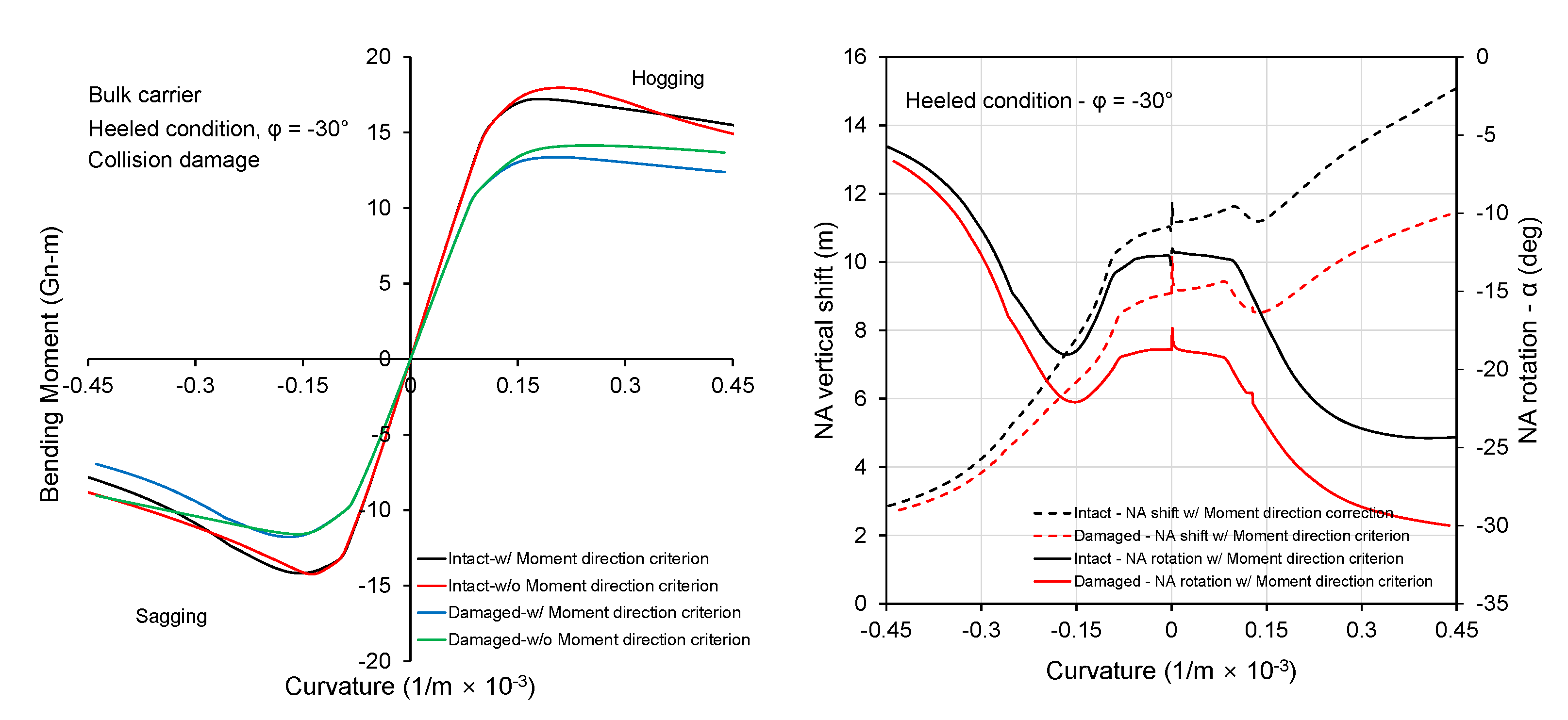
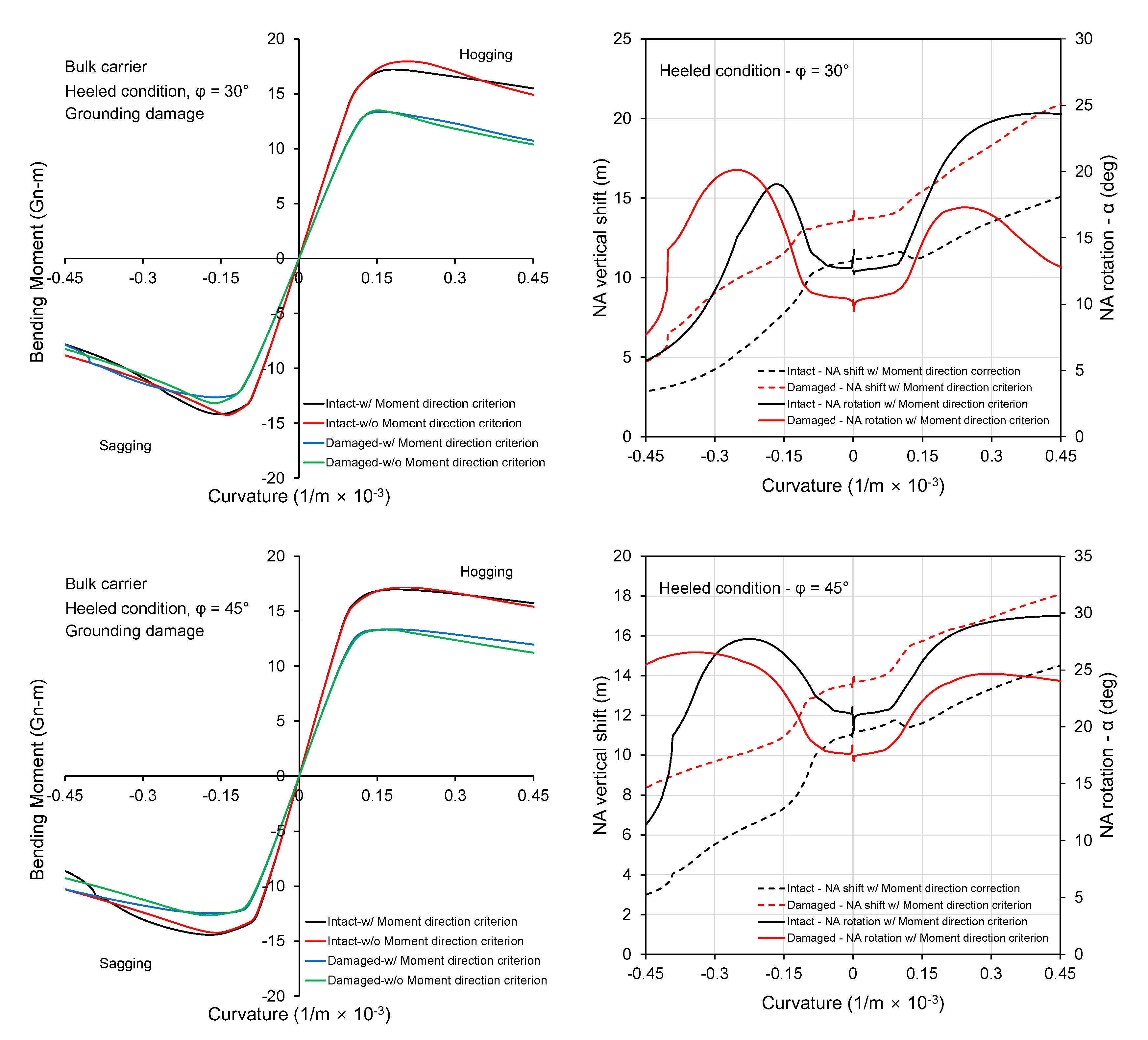
3.2. Bulk Carrier
3.3. Discussions
4. Conclusions
- The moment direction criterion can be implemented in the analysis procedure of Smith’s method by adopting a nested iteration algorithm when determining the INA position. A quasi-Newton-Raphson method is appropriate for solving the iterative part of the progressive collapse analysis, yielding a fast and robust solution.
- The influence of rotation of NA on the structural response is particularly important for the post-collapse regime. The relative importance of this phenomenon depends strongly on the structural configuration of the ship, loading condition (heeling angle), and damage location among others. A double hull VLCC showed less sensitivity to the inclusion of moment direction criterion compared to the bulk carrier.
- The reduced strength of a bulk carrier caused by collision and grounding damage is sensitive to the heeling angle. This was attributed to side and deck structure construction type.
- Overall, the proposed methodology, which adopts the moment direction criterion of a ship hull girder, can address the particular differences observed for each structural response of a ship under unsymmetrical loading.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BL | Baseline |
| CL | Centerline |
| CSR | Common Structural Rules |
| IACS | International Association of Classification Societies |
| INA | Instantaneous neutral axis |
| NA | Neutral axis |
| VLCC | Very large crude carrier |
Appendix A
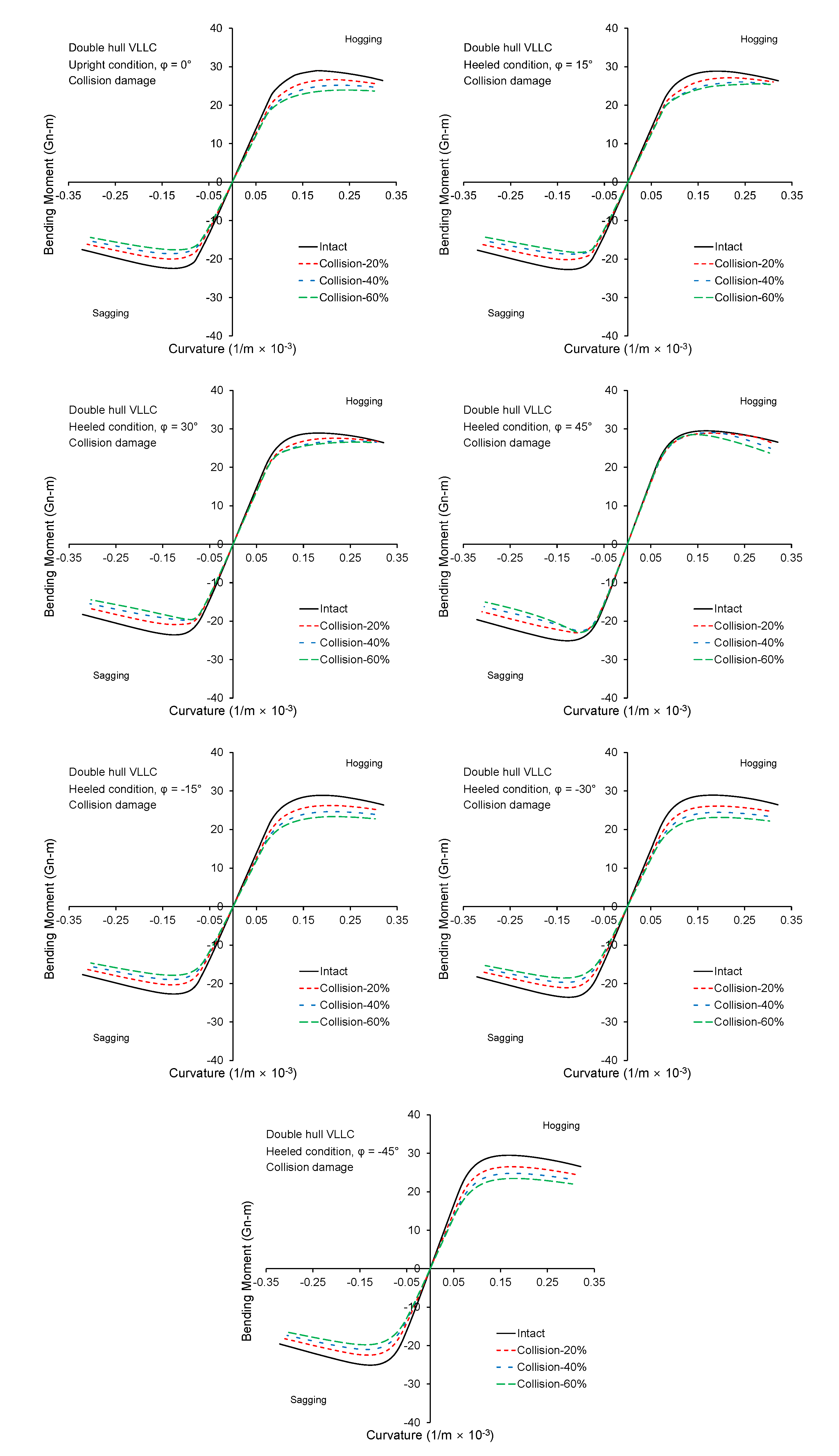
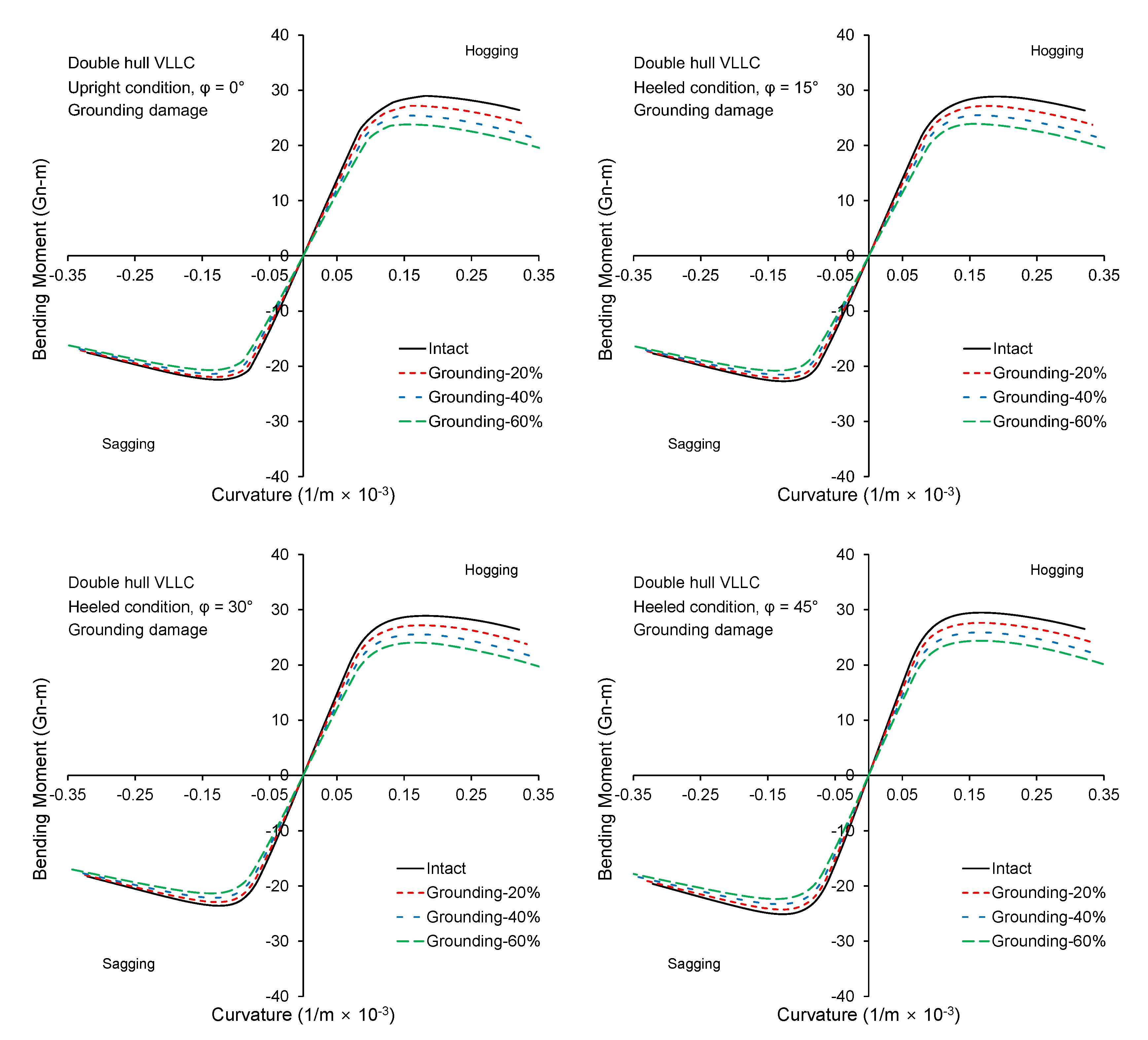
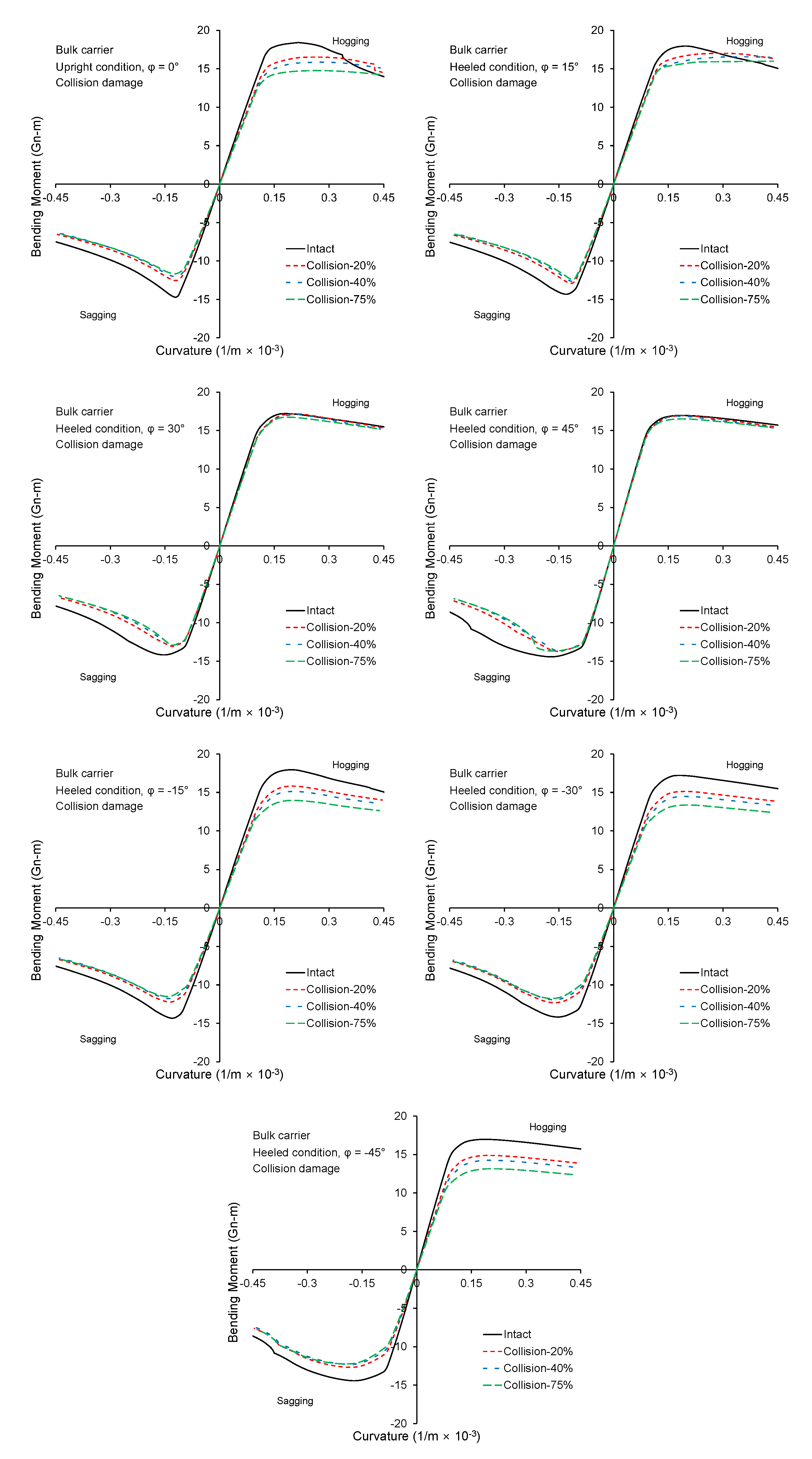
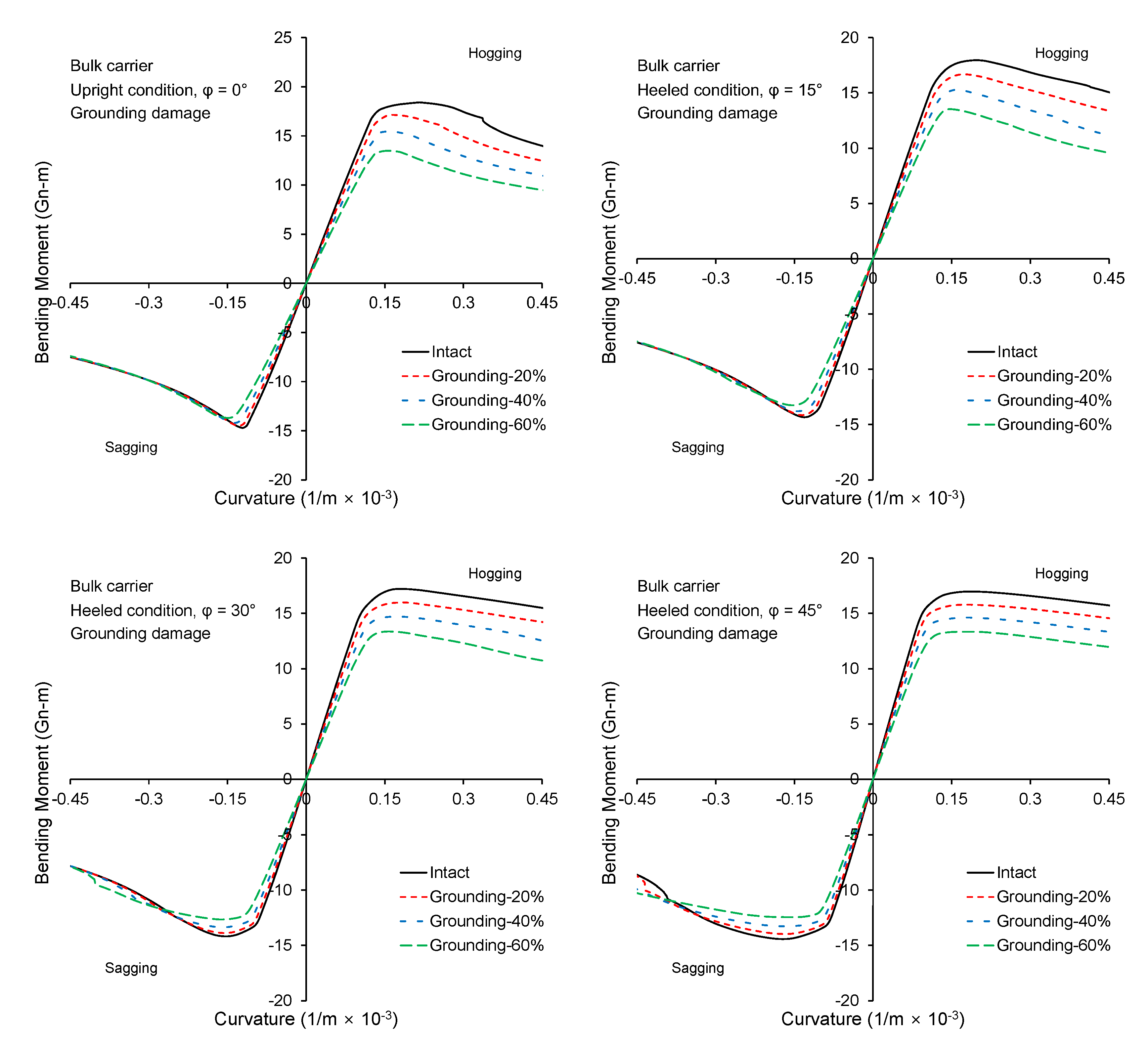
References
- Smith, C.S. Influence of local compressive failure on ultimate longitudinal strength of a ship’s hull. In Proceedings of the International Symposium on Practical Design in Shipbuilding, Tokyo, Japan, 18–20 October 1977; pp. 73–79. [Google Scholar]
- Dow, R.S.; Hugill, R.C.; Clark, J.D.; Smith, C.S. Evaluation of ultimate ship hull strength. In Proceedings of the Extreme Loads Response Symposium, Arlington, VA, USA, 19–20 October 1981; pp. 133–148. [Google Scholar]
- Smith, C.S. Structural redundancy and damage tolerance in relation to ultimate ship hull strength. In Proceedings of the International Symposium on Role of Design, Inspection and Redundancy in Marine Structural Reliability, Williamsburg, VA, USA, 14–16 November 1983; pp. 133–148. [Google Scholar]
- Smith, M.J.; Pegg, N.G. Automated assessment of ultimate hull girder strength. J. Offshore Mech. Arct. Eng. 2003, 125, 211–218. [Google Scholar] [CrossRef]
- Fujikubo, M.; Zubair Muis Alie, M.; Takemura, K.; Iijima, K.; Oka, S. Residual hull girder strength of asymmetrically damaged ships. J. Jpn. Soc. Nav. Archit. Ocean Eng. 2012, 16, 131–140. [Google Scholar] [CrossRef] [Green Version]
- IACS. Common Structural Rules for Bulk Carriers and Oil Tankers; International Association of Classification Societies: London, UK, 2020. [Google Scholar]
- Gordo, J.M.; Guedes Soares, C. Approximate method to evaluate the hull girder collapse strength. Mar. Struct. 1996, 9, 449–470. [Google Scholar] [CrossRef]
- Gordo, J.M.; Guedes Soares, C. Interaction equation for the collapse of tankers and containerships under combined bending moments. J. Ship Res. 1997, 41, 230–240. [Google Scholar]
- Gordo, J.M.; Guedes Soares, C. Residual strength of damaged ship hulls. In Proceedings of the IX International Maritime Association of Mediterranean Congress (IMAM 2000), Ischia, Italy, 2–6 April 2000; pp. 79–86. [Google Scholar]
- Fang, C.; Das, P.K. Survivability and reliability of damaged ships after collision and grounding. Ocean Eng. 2005, 32, 293–307. [Google Scholar] [CrossRef]
- Khan, I.A.; Das, P.K. Reliability analysis of intact and damaged ships considering combined vertical and horizontal bending moments. Ships Offshore Struct. 2008, 3, 371–384. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Luís, R.M.; Nikolov, P.; Downes, J.; Taczala, M.; Modiga, M.; Quesnel, T.; Toderan, C.; Samuelides, M. Benchmark study on the use of simplified structural codes to predict the ultimate strength of a damaged ship hull. Int. Shipbuild. Prog. 2008, 55, 87–107. [Google Scholar] [CrossRef]
- Hussein, A.; Guedes Soares, C. Reliability and residual strength of double hull tankers designed according to the new IACS common structural rules. Ocean Eng. 2009, 36, 1446–1459. [Google Scholar] [CrossRef]
- Luís, R.; Teixeira, A.; Guedes Soares, C. Longitudinal strength reliability of a tanker hull accidentally grounded. Struct. Saf. 2009, 31, 224–233. [Google Scholar] [CrossRef]
- Choung, J.; Nam, J.M.; Ha, T.B. Assessment of residual ultimate strength of an asymmetrically damaged tanker considering rotational and translational shifts of neutral axis plane. Mar. Struct. 2012, 25, 71–84. [Google Scholar] [CrossRef]
- Choung, J.; Nam, J.M.; Tayyar, G.T. Residual ultimate strength of a very large crude carrier considering probabilistic damage extents. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Campanile, A.; Piscopo, V.; Scamardella, A. Statistical properties of bulk carrier residual strength. Ocean Eng. 2015, 106, 47–67. [Google Scholar] [CrossRef]
- Campanile, A.; Piscopo, V.; Scamardella, A. Comparative analysis among deterministic and stochastic collision damage models for oil tanker and bulk carrier reliability. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 21–36. [Google Scholar] [CrossRef]
- Tekgoz, M.; Garbatov, Y.; Guedes Soares, C. Strength assessment of an intact and damaged container ship subjected to asymmetrical bending loadings. Mar. Struct. 2018, 58, 172–198. [Google Scholar] [CrossRef]
- Zhu, Z.; Ren, H.; Li, C.; Zhou, X. Ultimate limit state function and its fitting method of damaged ship under combined loads. J. Mar. Sci. Eng. 2020, 8, 117. [Google Scholar] [CrossRef] [Green Version]
- Makouei, S.H.; Teixeira, A.P.; Guedes Soares, C. A study on the progressive collapse behavior of a damaged hull girder. In Maritime Technology and Engineering; Guedes Soares, C., Santos, T.A., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 405–416. [Google Scholar]
- Kuznecovs, A.; Ringsberg, J.W.; Johnson, E.; Yamada, Y. Ultimate limit state analysis of a double-hull tanker subjected to biaxial bending in intact and collision-damaged conditions. Ocean Eng. 2020, 209, 107519. [Google Scholar] [CrossRef]
- Parunov, J.; Rudan, S.; Bužančić Primorac, B. Residual ultimate strength assessment of double hull oil tanker after collision. Eng. Struct. 2017, 148, 704–717. [Google Scholar] [CrossRef]
- Nielsen, L. Structural Capacity of the Hull Girder. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 1998. [Google Scholar]
- Yao, T.; Astrup, O.; Caridis, P.; Chen, Y.N.; Cho, S.R.; Dow, R.S.; Niho, O.; Rigo, P. Report of Special Task Committee VI.2 Ultimate Hull Girder Strength. In Proceedings of the 14th International Ship and Offshore Structures Congress (ISSC 2000), Nagasaki, Japan, 2–6 October 2000; pp. 321–397. [Google Scholar]
- Paik, J.K.; Amlashi, H.; Boon, B.; Branner, K.; Caridis, P.; Das, P.; Fujikubo, M.; Huang, C.H.; Josefson, L.; Kaeding, P.; et al. Report of Committee III.1 Ultimate Strength. In Proceedings of the 18th International Ship and Offshore Structures Congress (ISSC 2012), Rostock, Germany, 10–13 September 2012; pp. 285–363. [Google Scholar]
- Cerik, B.C.; Ringsberg, J.W.; Choung, J. Revisiting MARSTRUCT benchmark study on side-shell collision with a combined localized necking and stress-state dependent ductile fracture model. Ocean Eng. 2019, 187, 106173. [Google Scholar] [CrossRef]
- Cerik, B.C.; Lee, K.; Park, S.J.; Choung, J. Simulation of ship collision and grounding damage using Hosford-Coulomb fracture model for shell elements. Ocean Eng. 2019, 173, 415–432. [Google Scholar] [CrossRef]
- Cerik, B.C.; Park, S.J.; Choung, J. Use of localized necking and fracture as a failure criterion in ship collision analysis. Mar. Struct. 2020, 73, 102787. [Google Scholar] [CrossRef]
- Cerik, B.C.; Choung, J. Rate-dependent combined necking and fracture model for predicting ductile fracture with shell elements at high strain rates. Int. J. Impact Eng. 2020, 146, 103697. [Google Scholar] [CrossRef]
- Cerik, B.C. Ultimate longitudinal compressive strength of steel plates with lateral patch load induced plastic deformation. Thin-Walled Struct. 2018, 122, 416–424. [Google Scholar] [CrossRef]
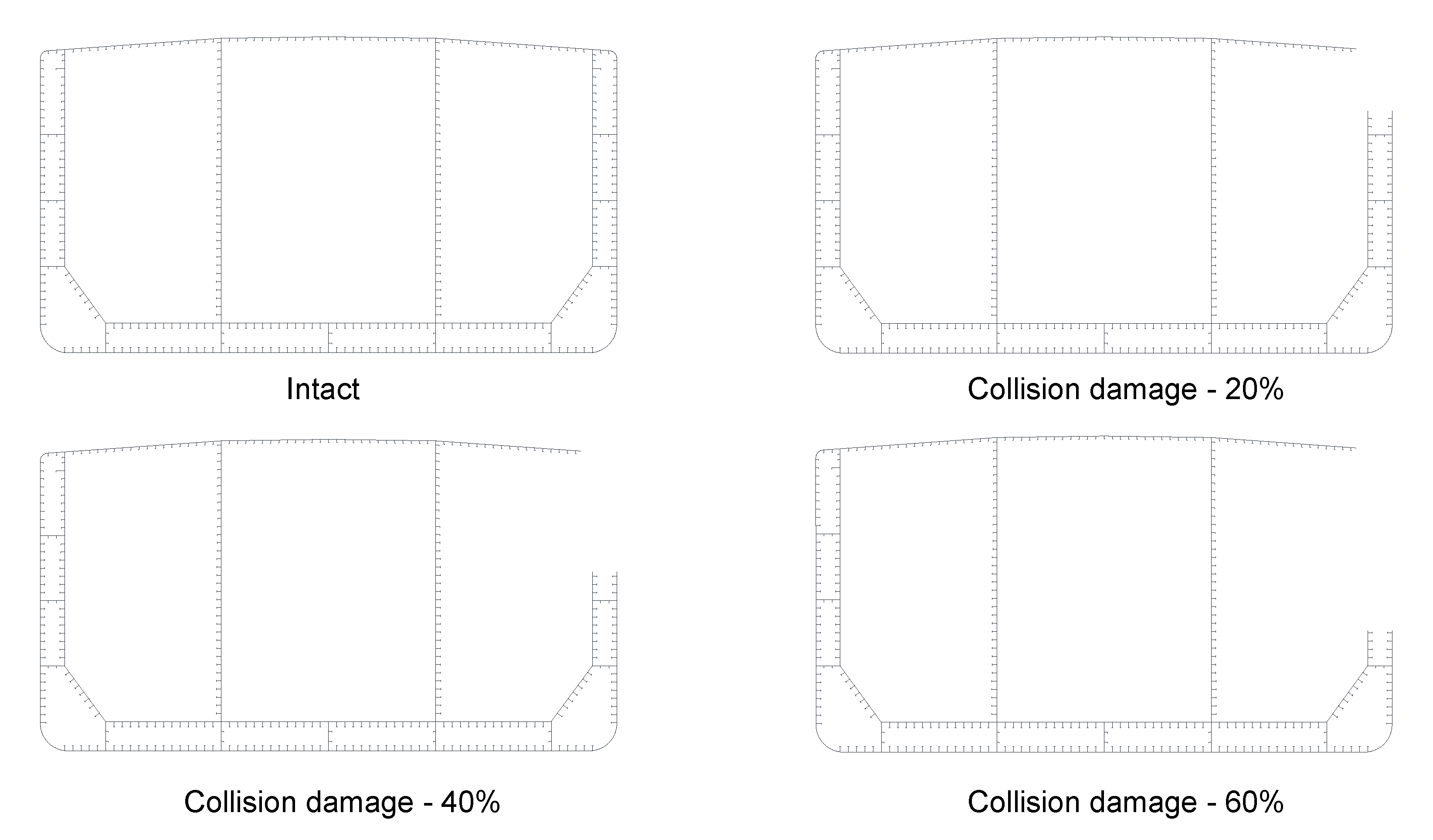
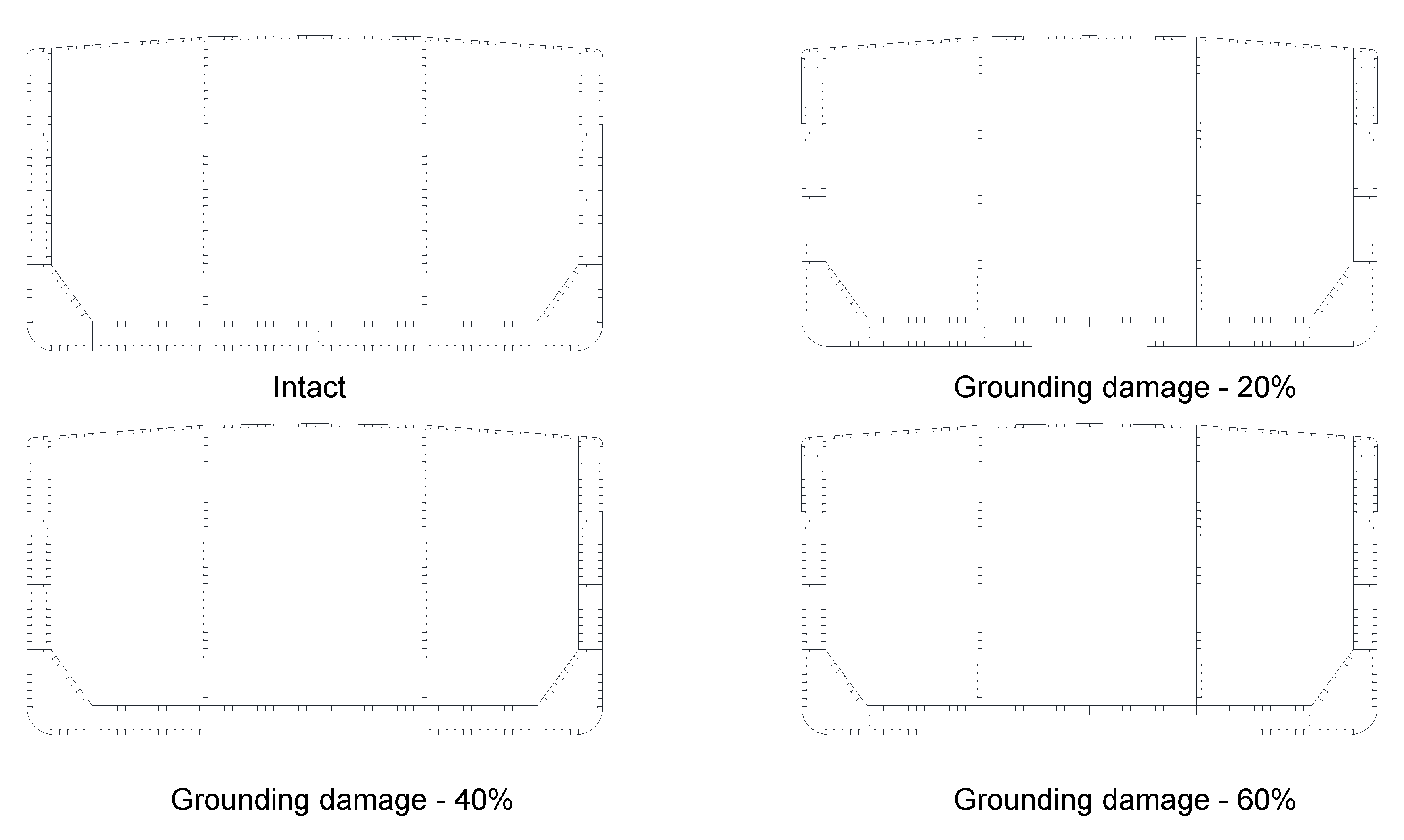
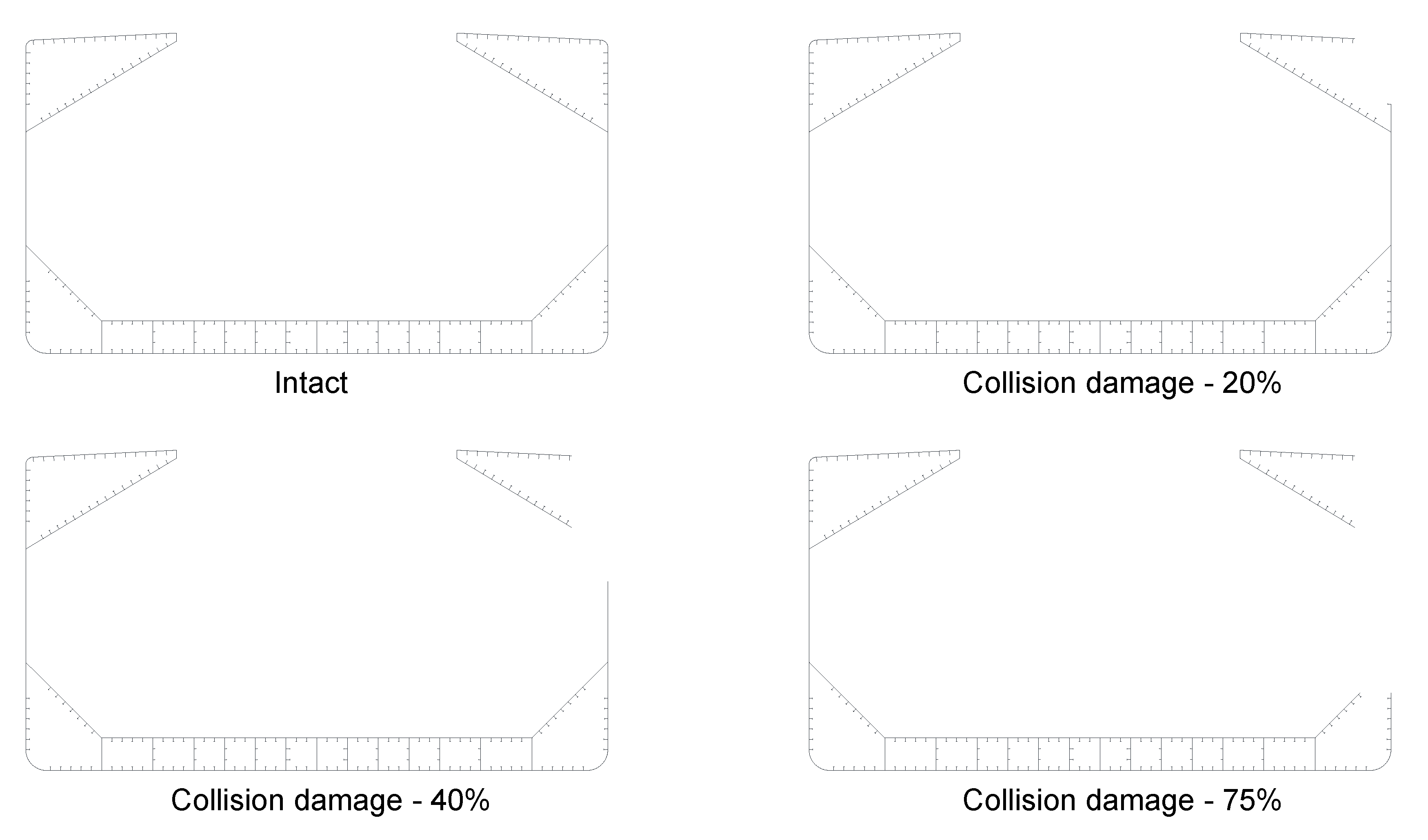


| Particular | Double Hull VLCC | Bulk Carrier |
|---|---|---|
| Length (m) | 315 | 285 |
| Breadth (m) | 58 | 50 |
| Depth (m) | 30.3 | 26.7 |
| Block coefficient | 0.82 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerik, B.C.; Choung, J. Progressive Collapse Analysis of Intact and Damaged Ships under Unsymmetrical Bending. J. Mar. Sci. Eng. 2020, 8, 988. https://doi.org/10.3390/jmse8120988
Cerik BC, Choung J. Progressive Collapse Analysis of Intact and Damaged Ships under Unsymmetrical Bending. Journal of Marine Science and Engineering. 2020; 8(12):988. https://doi.org/10.3390/jmse8120988
Chicago/Turabian StyleCerik, Burak Can, and Joonmo Choung. 2020. "Progressive Collapse Analysis of Intact and Damaged Ships under Unsymmetrical Bending" Journal of Marine Science and Engineering 8, no. 12: 988. https://doi.org/10.3390/jmse8120988
APA StyleCerik, B. C., & Choung, J. (2020). Progressive Collapse Analysis of Intact and Damaged Ships under Unsymmetrical Bending. Journal of Marine Science and Engineering, 8(12), 988. https://doi.org/10.3390/jmse8120988






