On the Separation Period Discriminating Gravity and Infragravity Waves off Gyeongpo Beach, Korea
Abstract
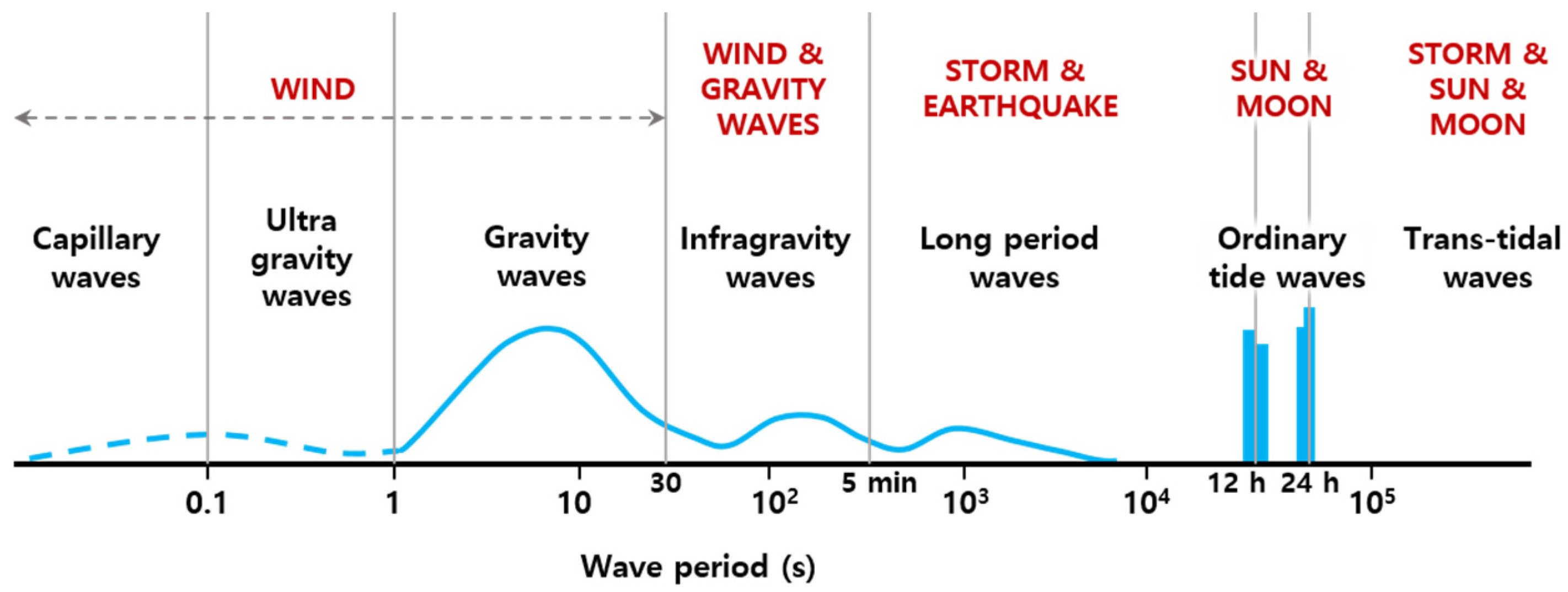
:1. Introduction
2. Materials and Methods
2.1. Long-Term Wave Monitoring Data off Gyeongpo Beach
2.2. Methods of Wave Analysis
3. Results and Discussion
3.1. Separation Period of Infragravity Waves
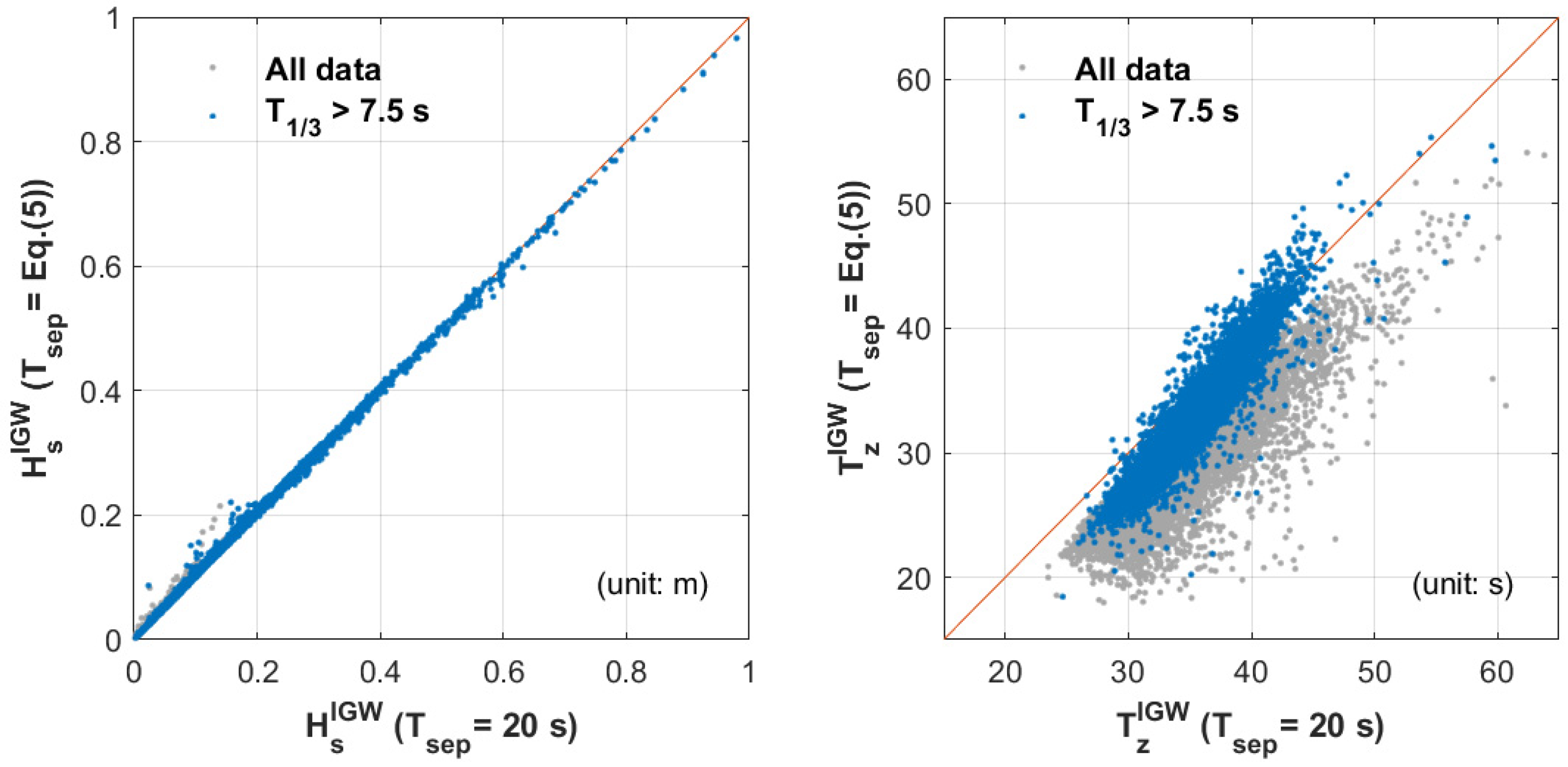
3.2. A Formula for Evaluating the Separation Frequency
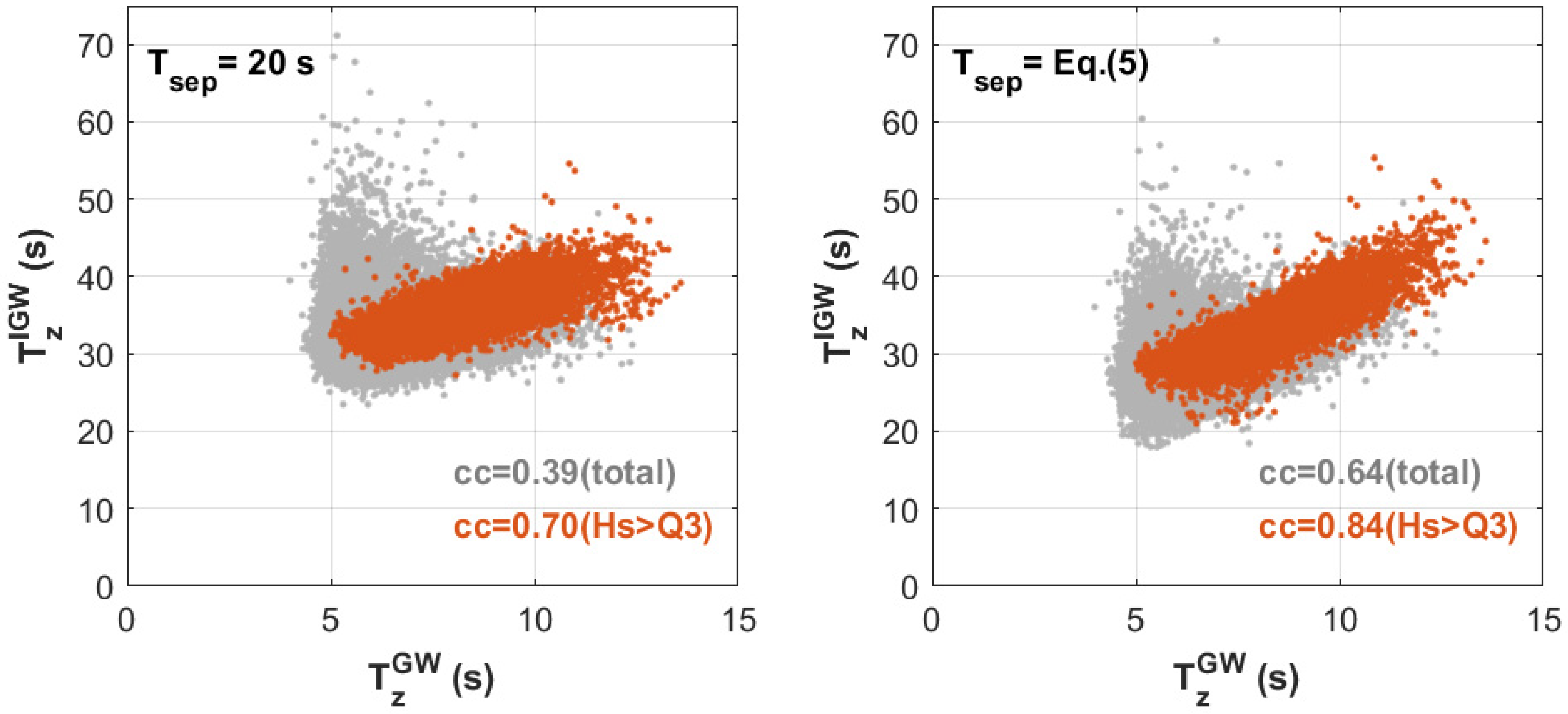
3.3. Influence of Applying Different Methods of Determining the Separation Period
3.4. Relationship between the Significant Wave Heights of Gravity and Infragravity Waves
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Munk, W.H. Origin and generation of waves. In Proceedings of the 1st International Conference on Coastal Engineering, Long Beach, CA, USA, 1 October 1950; pp. 1–4. [Google Scholar]
- Hathaway, K.K.; Oltman-Shay, J.; Howd, P.; Holman, R.A. Infragravity Waves in the Nearshore Zone; US Army Engineers, Waterways Experiment Station: Washington, DC, USA, 1998. [Google Scholar]
- Guza, R.T.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. Ocean. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Elgar, S.; Herbers, T.H.C.; Okihiro, M.; Oltman-Shay, J.; Guza, R.T. Observations of infragravity waves. J. Geophys. Res. Ocean. 1992, 97, 15573–15577. [Google Scholar] [CrossRef]
- De Bakker, A.T.M.; Brinkkemper, J.A.; Van der Steen, F.; Tissier, M.F.S.; Ruessink, B.G. Cross-shore sand transport by infragravity waves as a function of beach steepness. J. Geophys. Res. Earth Surf. 2016, 121, 1786–1799. [Google Scholar] [CrossRef]
- Okihiro, M.; Guza, R.T.; Seymour, R.J. Excitation of seiche observed in a small harbor. J. Geophys. Res. Ocean. 1993, 98, 18201–18211. [Google Scholar] [CrossRef] [Green Version]
- Cho, H.Y.; Jeong, W.M.; Oh, S.H. Analysis on the characteristics of the infragravity waves inside and outside Pohang new harbor using a transfer function model. J. Korean Soc. Coast. Ocean. Eng. 2014, 26, 131–139. [Google Scholar] [CrossRef]
- Jeong, W.M.; Back, J.D.; Choi, H.; Kim, S.I. Analysis on the reduction effects of the gravity waves and infragravity waves of detached submerged breakwater by field monitoring. J. Korean Soc. Coast. Ocean. Eng. 2018, 30, 51–60. [Google Scholar] [CrossRef]
- Son, D.; Yoo, J.; Shin, H. Effect of infragravity waves on nearshore morphodynamics in the east coast: Case study-Ilsan beach. Ocean. Polar Res. 2018, 40, 87–98. [Google Scholar]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Gallagher, B. Generation of surf beat by non-linear wave interactions. J. Fluid Mech. 1971, 49, 1–20. [Google Scholar] [CrossRef]
- Van Dongeren, A.R.J.A.; Battjes, J.; Janssen, T.; Van Noorloos, J.; Steenhauer, K.; Steenbergen, G.; Reniers, A.J.H.M. Shoaling and shoreline dissipation of low-frequency waves. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Henderson, S.M.; Guza, R.T.; Elgar, S.; Herbers, T.H.C.; Bowen, A.J. Nonlinear generation and loss of infragravity wave energy. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- De Bakker, A.T.M.; Herbers, T.H.C.; Smit, P.B.; Tissier, M.F.S.; Ruessink, B.G. Nonlinear infragravity-wave interactions on a gently sloping laboratory beach. J. Phys. Oceanogr. 2015, 45, 589–605. [Google Scholar] [CrossRef] [Green Version]
- De Bakker, A.T.M.; Tissier, M.F.S.; Ruessink, B.G. Shoreline dissipation of infragravity waves. Cont. Shelf Res. 2014, 72, 73–82. [Google Scholar] [CrossRef]
- Bowen, A.J.; Guza, R.T. Edge waves and surf beat. J. Geophys. Res. Ocean. 1978, 83, 1913–1920. [Google Scholar] [CrossRef]
- Herbers, T.H.C.; Elgar, S.; Guza, R.T. Infragravity-frequency (0.005–0.05 Hz) motions on the shelf. Part I: Forced waves. J. Phys. Oceanogr. 1994, 24, 917–927. [Google Scholar] [CrossRef]
- Herbers, T.H.C.; Elgar, S.; Guza, R.T. Generation and propagation of infragravity waves. J. Geophys. Res. Ocean. 1995, 100, 24863–24872. [Google Scholar] [CrossRef]
- Fiedler, J.W.; Brodie, K.L.; McNinch, J.E.; Guza, R.T. Observations of runup and energy flux on a low-slope beach with high-energy, long-period ocean swell. Geophys. Res. Lett. 2015, 42, 9933–9941. [Google Scholar] [CrossRef] [Green Version]
- Ruessink, B.G.; Kleinhans, M.G.; Van den Beukel, P.G.L. Observations of swash under highly dissipative conditions. J. Geophys. Res. Ocean. 1998, 103, 3111–3118. [Google Scholar] [CrossRef]
- Jeong, W.M.; Ryu, K.H.; Baek, W.D.; Choi, H.J. Downtime analysis for Pohang new harbor through long-term investigation of waves and winds. J. Korean Soc. Coast. Ocean. Eng. 2011, 23, 226–235. [Google Scholar] [CrossRef] [Green Version]
- Jeong, W.M.; Park, W.S.; Kim, K.H.; Kim, J.H. Correlations between long-and short-period waves in shallow water region around Sokcho harbor. J. Korean Soc. Civil. Eng. 2002, 22, 711–721. [Google Scholar]
- Jeong, W.M.; Chae, J.W.; Park, W.-S.; Lee, K.S.; Suh, K.-D. Correlation between storm waves and far-infra-gravity waves observed in Okkye harbor. J. Korean Soc. Coast. Ocean. Eng. 2001, 13, 209–229. [Google Scholar]
- United States Army Corps of Engineers (USACE). Shore Protection Manual, 3rd ed.; US Government Printing Office: Washington, DC, USA, 1977.
- Paroscientific, Inc. User’s Manual for Digiquartz ® Broadband Intelligent Instruments with Dual RS-232 and RS-485 Interfaces; Paroscientific, Inc.: Redmond, WA, USA, 2009. [Google Scholar]
- Polster, A.; Fabian, M.; Villinger, H. Effective resolution and drift of Paroscientific pressure sensors derived from long-term seafloor measurements. Geochem. Geophys. Geosyst. 2009, 10, Q08008. [Google Scholar] [CrossRef]
- DiMarco, S.F.; Kelly, F.J.; Zhang, J.; Guinasso, N.L., Jr. Directional wave spectra on the Louisiana-Texas shelf during Hurricane Andrew. J. Coast. Res. 1995, SI 21, 217–233. [Google Scholar]
- Kennedy, A.B.; Gravois, U.; Zachry, B.; Luettich, R.; Whipple, T.; Weaver, R.; Reynolds-Fleming, J.; Chen, Q.J.; Avissar, R. Rapidly installed temporary gauging for hurricane waves and surge, and application to Hurricane Gustav. Cont. Shelf Res. 2010, 30, 1743–1752. [Google Scholar] [CrossRef]
- Chun, H.; Suh, K.D. Estimation of significant wave period from wave spectrum. Ocean. Eng. 2018, 163, 609–616. [Google Scholar] [CrossRef]
- Suh, K.D.; Kwon, H.D.; Lee, D.Y. Some statistical characteristics of large deepwater waves around the Korean Peninsula. Coast. Eng. 2010, 57, 375–384. [Google Scholar] [CrossRef] [Green Version]
- Goda, Y. Revisiting Wilson’s formulas for simplified wind-wave prediction. J. Waterw. Port Coast. 2003, 129, 93–95. [Google Scholar] [CrossRef]

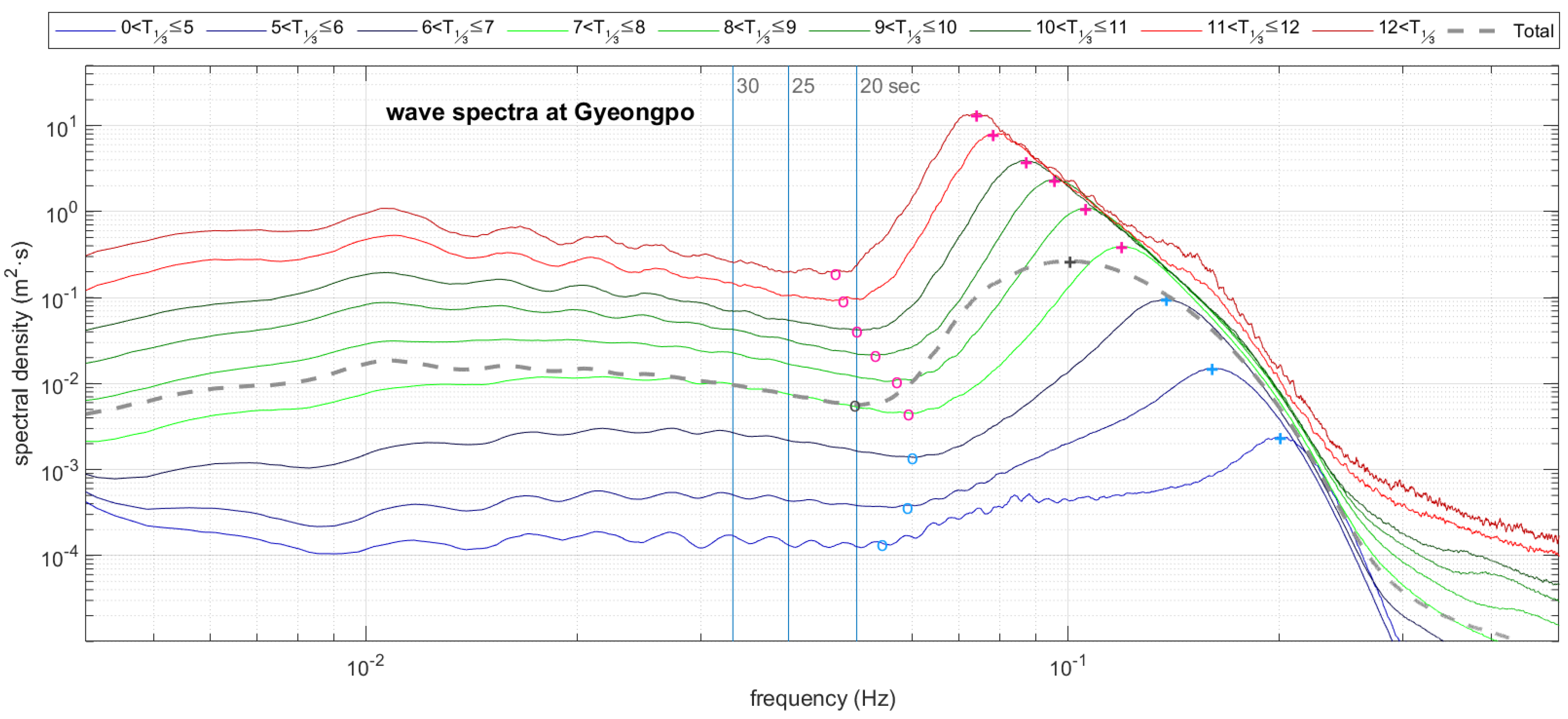
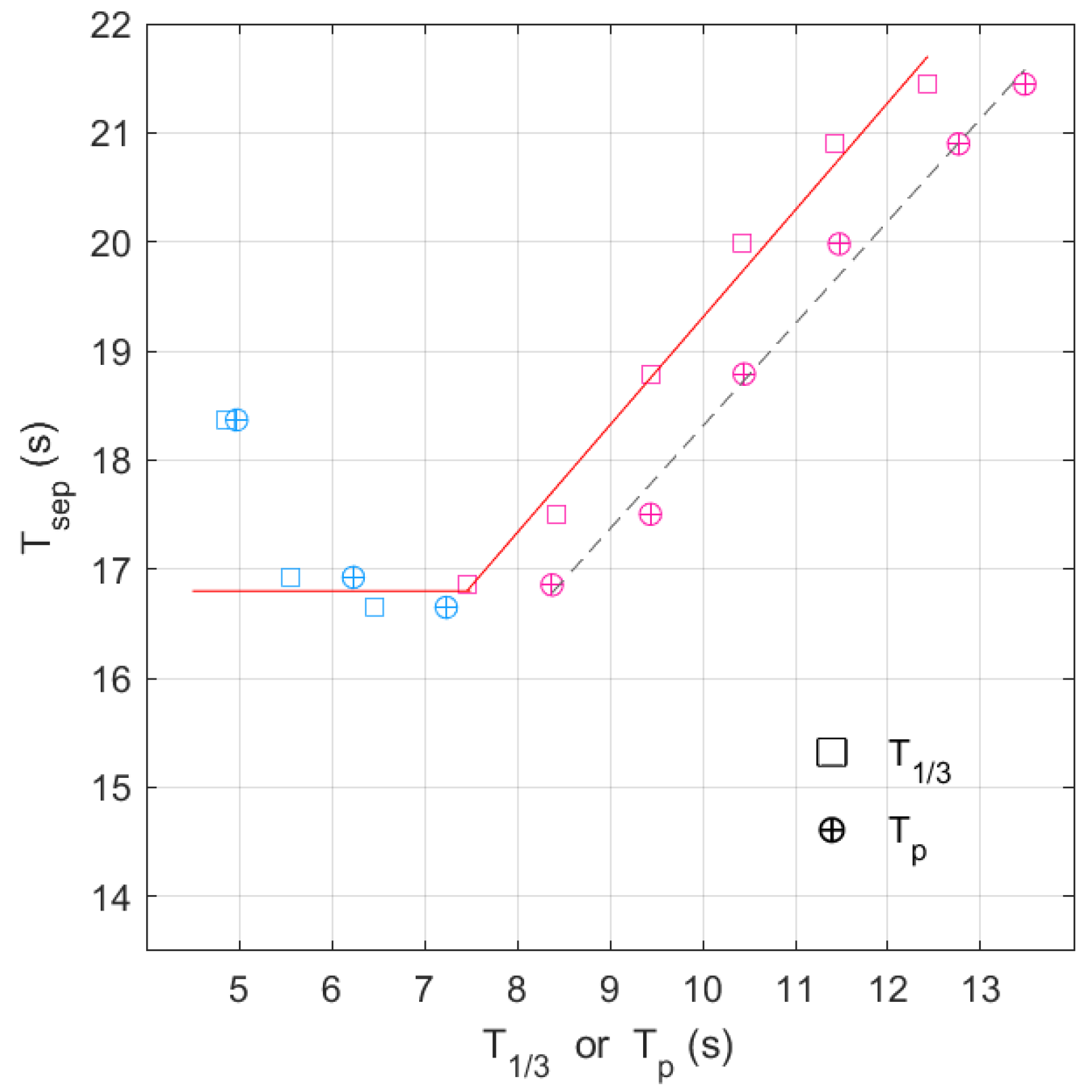

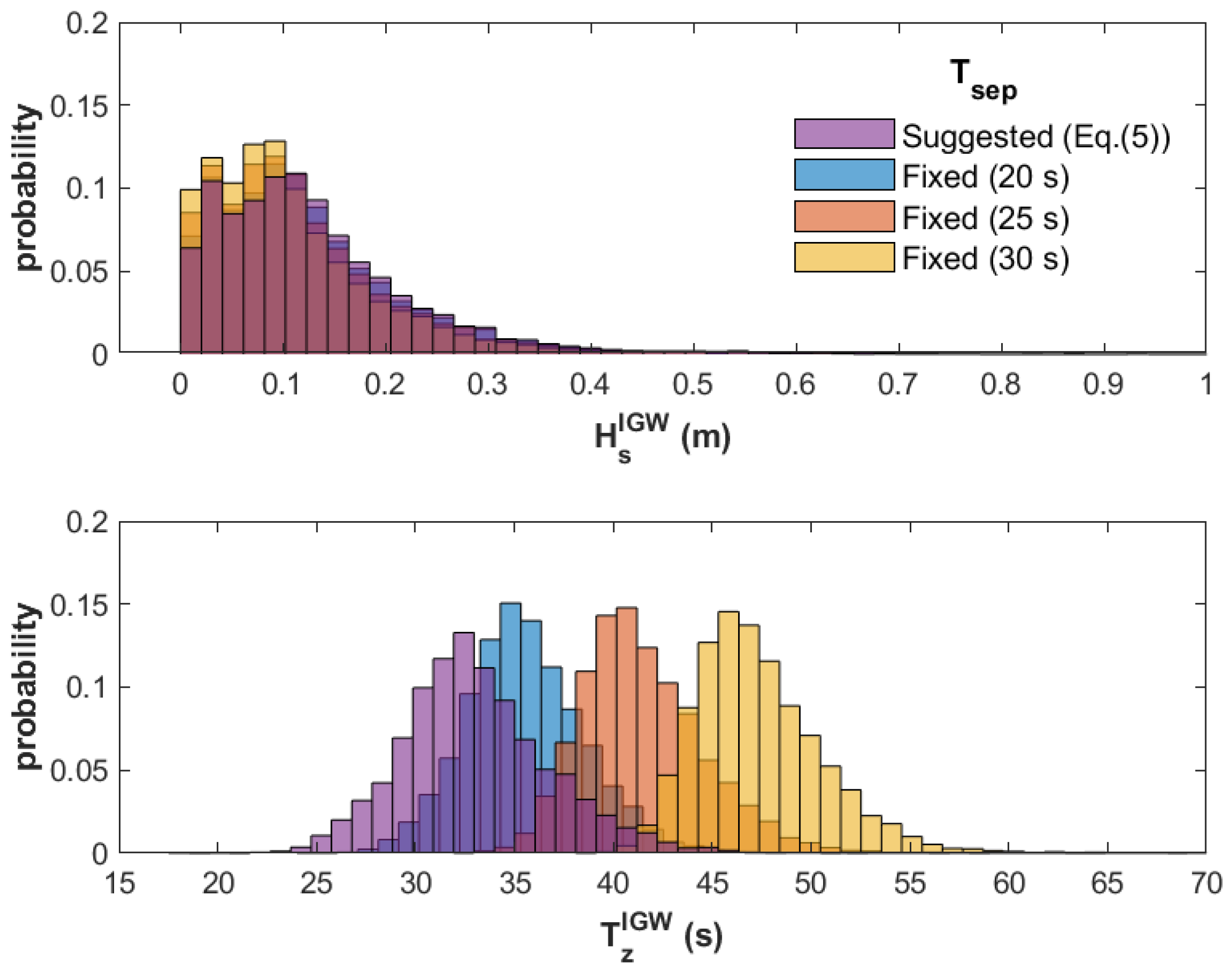


| Class | No. of Spectra | Data Ratio (%) | Energy Ratio (%) | |||
|---|---|---|---|---|---|---|
| 0 < ≤ 5 | 1377 | 3.0 | 0.0 | 4.9 | 18.4 | 5.0 |
| 5 < ≤ 6 | 14,136 | 30.4 | 1.9 | 5.6 | 16.9 | 6.2 |
| 6 < ≤ 7 | 14,464 | 31.1 | 9.3 | 6.5 | 16.7 | 7.2 |
| 7 < ≤ 8 | 8789 | 18.9 | 19.2 | 7.5 | 16.9 | 8.4 |
| 8 < ≤ 9 | 4351 | 9.4 | 22.7 | 8.4 | 17.5 | 9.4 |
| 9 < ≤ 10 | 2041 | 4.4 | 19.9 | 9.4 | 18.8 | 10.5 |
| 10 < ≤ 11 | 963 | 2.1 | 15.0 | 10.4 | 20.0 | 11.5 |
| 11 < ≤ 12 | 284 | 0.6 | 7.8 | 11.4 | 20.9 | 12.8 |
| 12 < | 95 | 0.2 | 4.2 | 12.4 | 21.4 | 13.5 |
| total | 46,500 | 100.0 | 100.0 | |||
| mean | 20.1 | 9.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, J.-E.; Jeong, W.-M.; Chang, Y.S.; Oh, S.-H. On the Separation Period Discriminating Gravity and Infragravity Waves off Gyeongpo Beach, Korea. J. Mar. Sci. Eng. 2020, 8, 167. https://doi.org/10.3390/jmse8030167
Oh J-E, Jeong W-M, Chang YS, Oh S-H. On the Separation Period Discriminating Gravity and Infragravity Waves off Gyeongpo Beach, Korea. Journal of Marine Science and Engineering. 2020; 8(3):167. https://doi.org/10.3390/jmse8030167
Chicago/Turabian StyleOh, Jung-Eun, Weon-Mu Jeong, Yeon S. Chang, and Sang-Ho Oh. 2020. "On the Separation Period Discriminating Gravity and Infragravity Waves off Gyeongpo Beach, Korea" Journal of Marine Science and Engineering 8, no. 3: 167. https://doi.org/10.3390/jmse8030167
APA StyleOh, J.-E., Jeong, W.-M., Chang, Y. S., & Oh, S.-H. (2020). On the Separation Period Discriminating Gravity and Infragravity Waves off Gyeongpo Beach, Korea. Journal of Marine Science and Engineering, 8(3), 167. https://doi.org/10.3390/jmse8030167







