A Probabilistic Model of Coastal Bluff-Top Erosion in High Latitudes Due to Thermoabrasion: A Case Study from Baydaratskaya Bay in the Kara Sea
Abstract
:1. Introduction
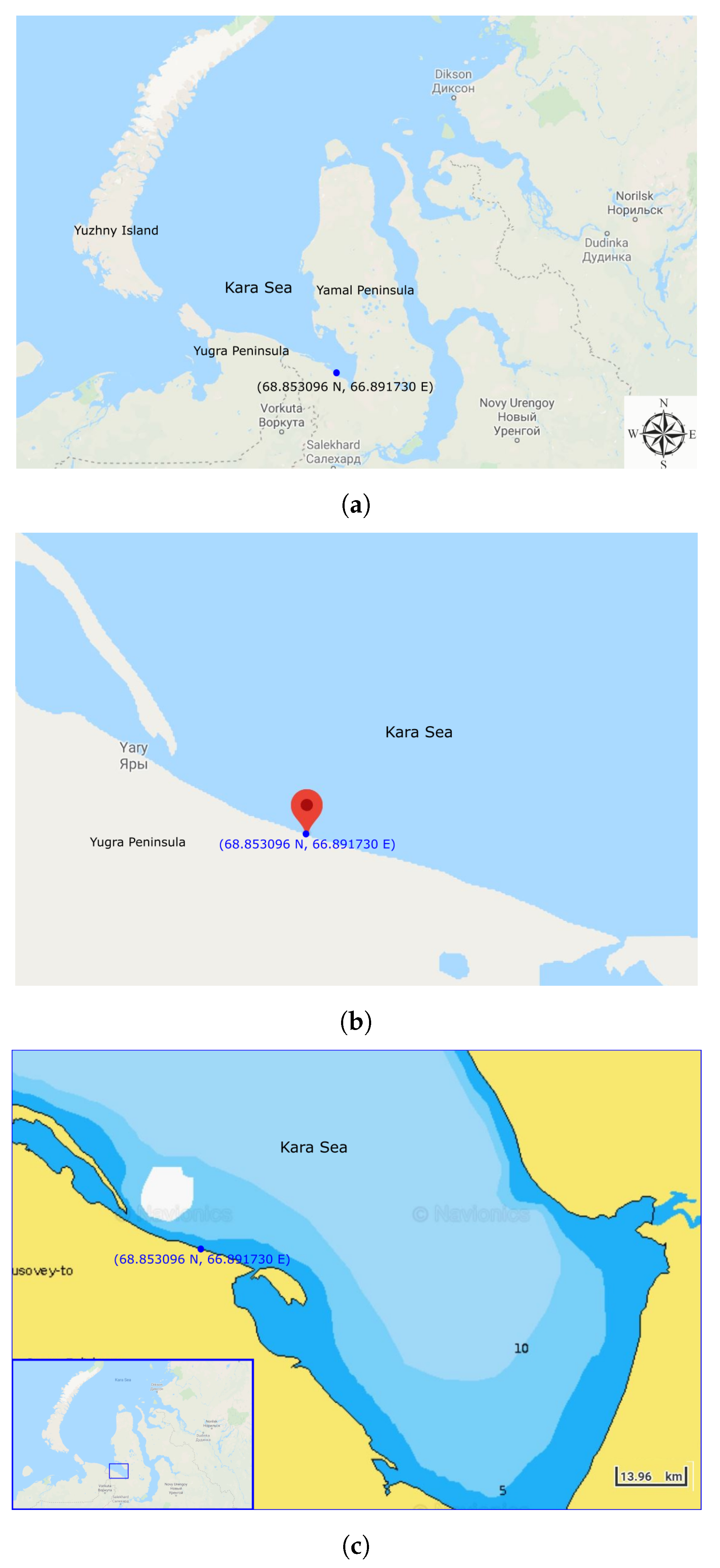
2. Field Measurements of Arctic Coastal Erosion in the Kara Sea, Russia
2.1. Geomorphology and Cryology of the Study Area
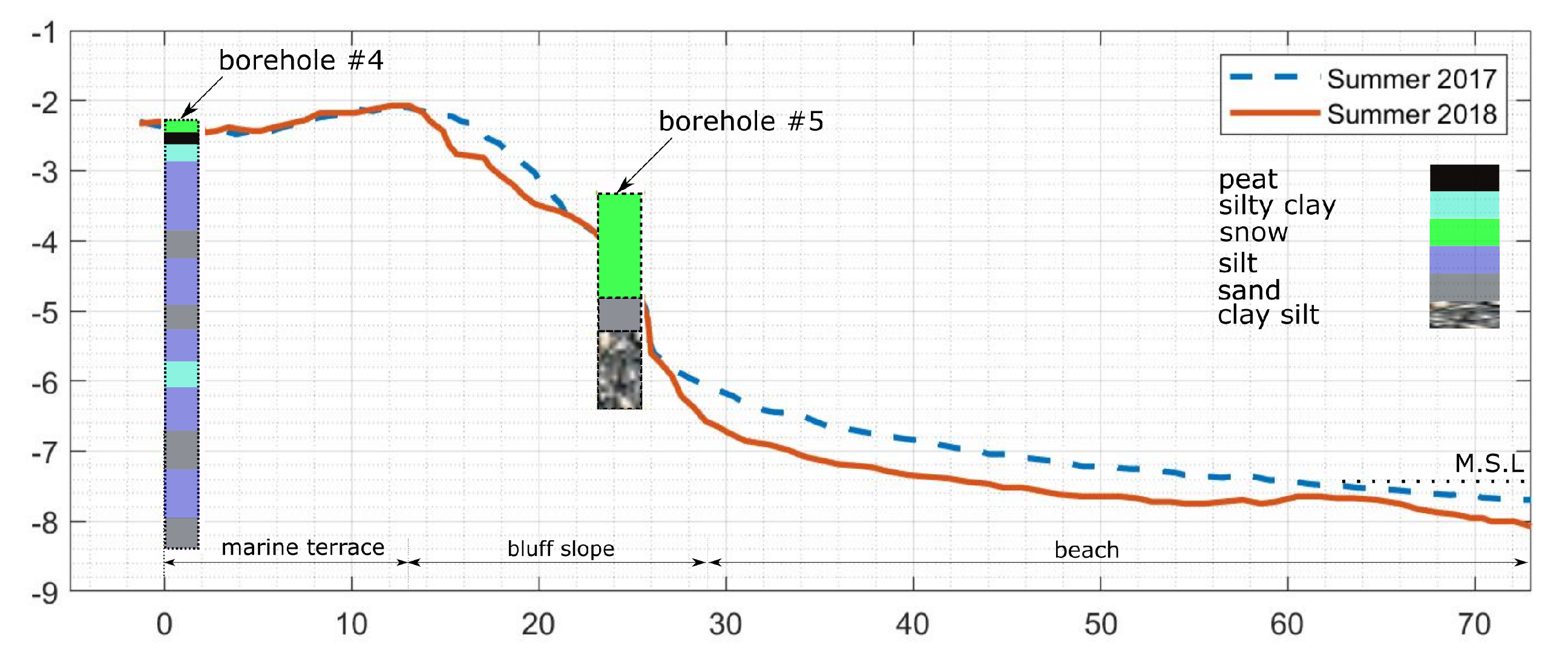
2.2. Physical Parameters and Environmental Forcing
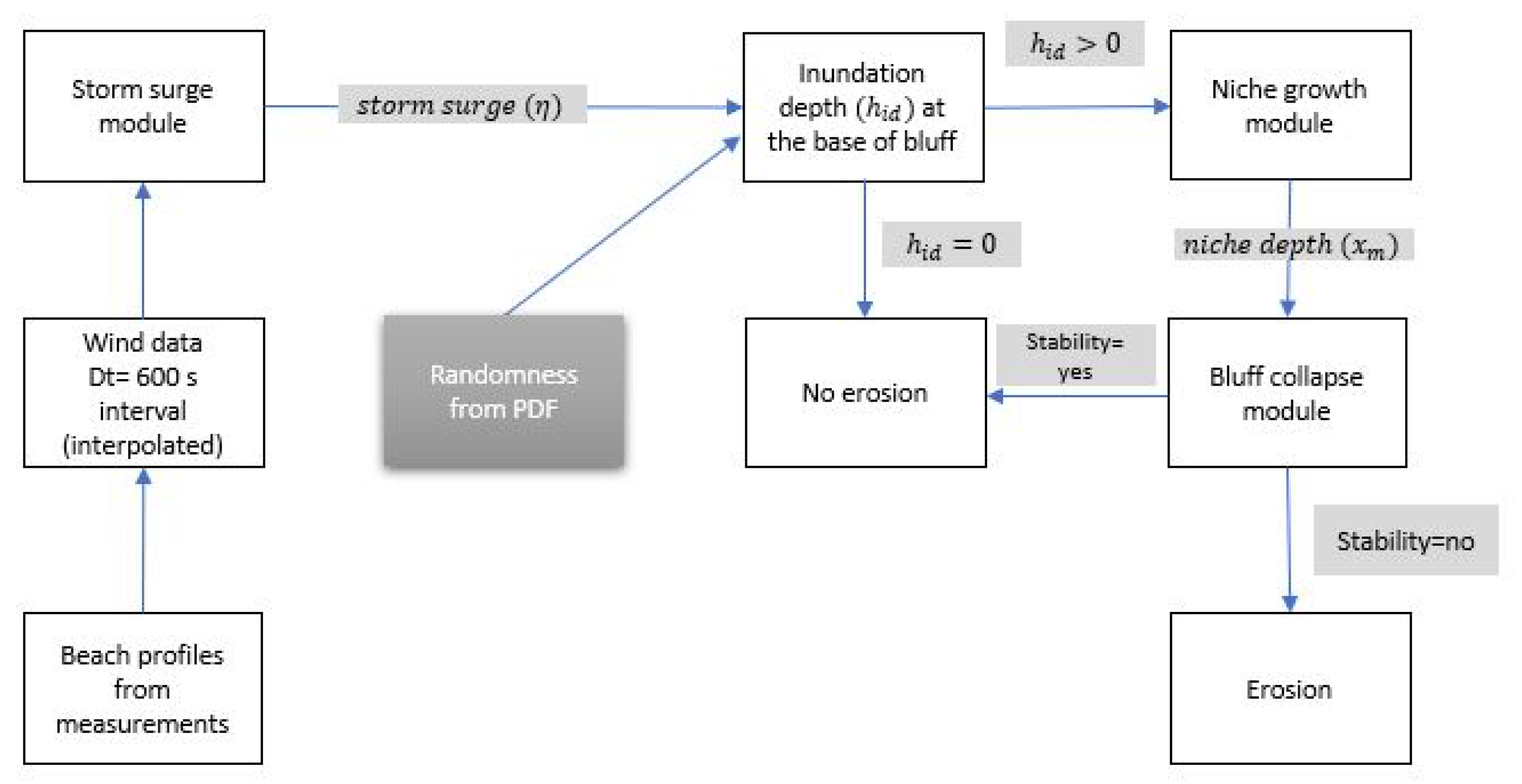
3. Conceptual Model of Thermoabrasion
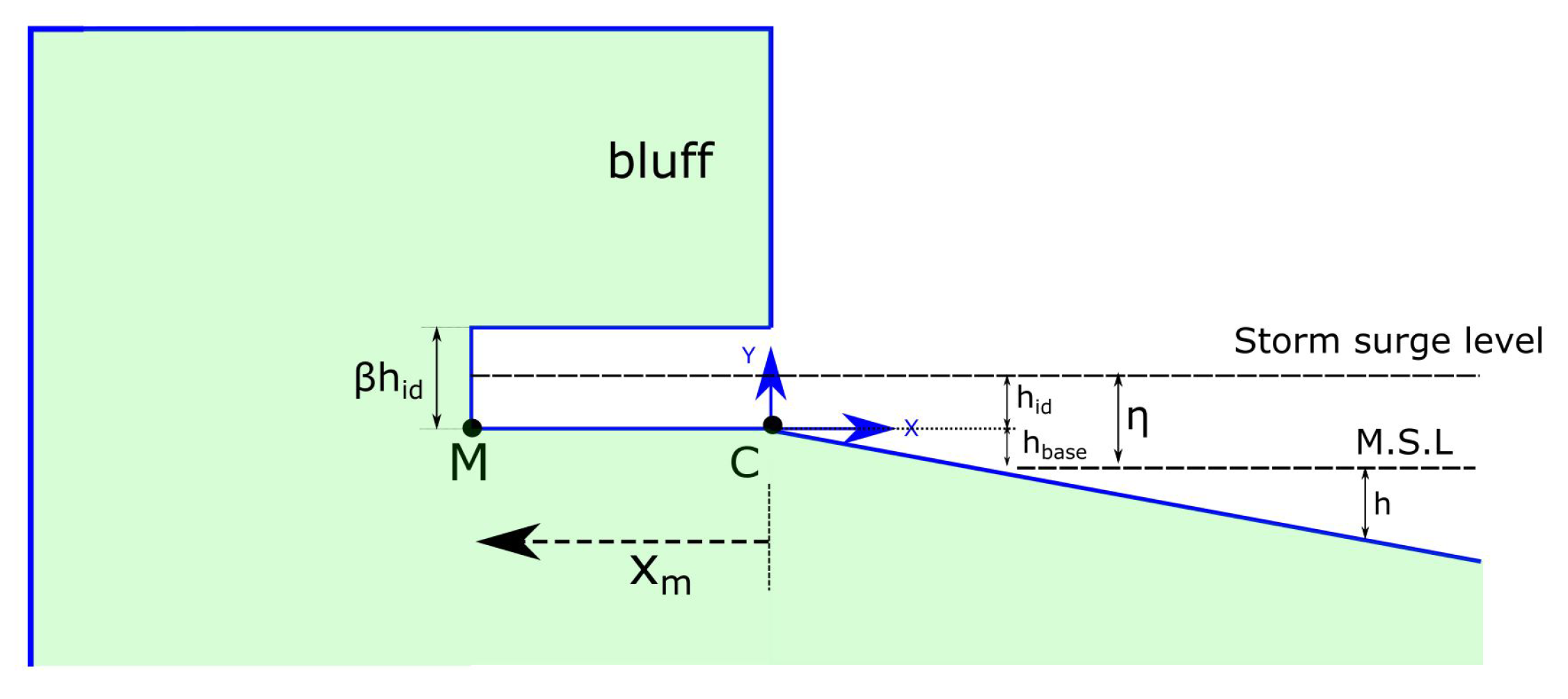
3.1. Storm Surge Module
3.2. Niche Growth Module
3.3. Bluff Collapse Module
- the resisting moments, i.e., the self-weight,
- the moment from the force acting at the vertical failure line,
- the moment from the force acting at the horizontal failure line,
- the moment from the weight of the overhanging bluff,
3.4. Numerical Scheme
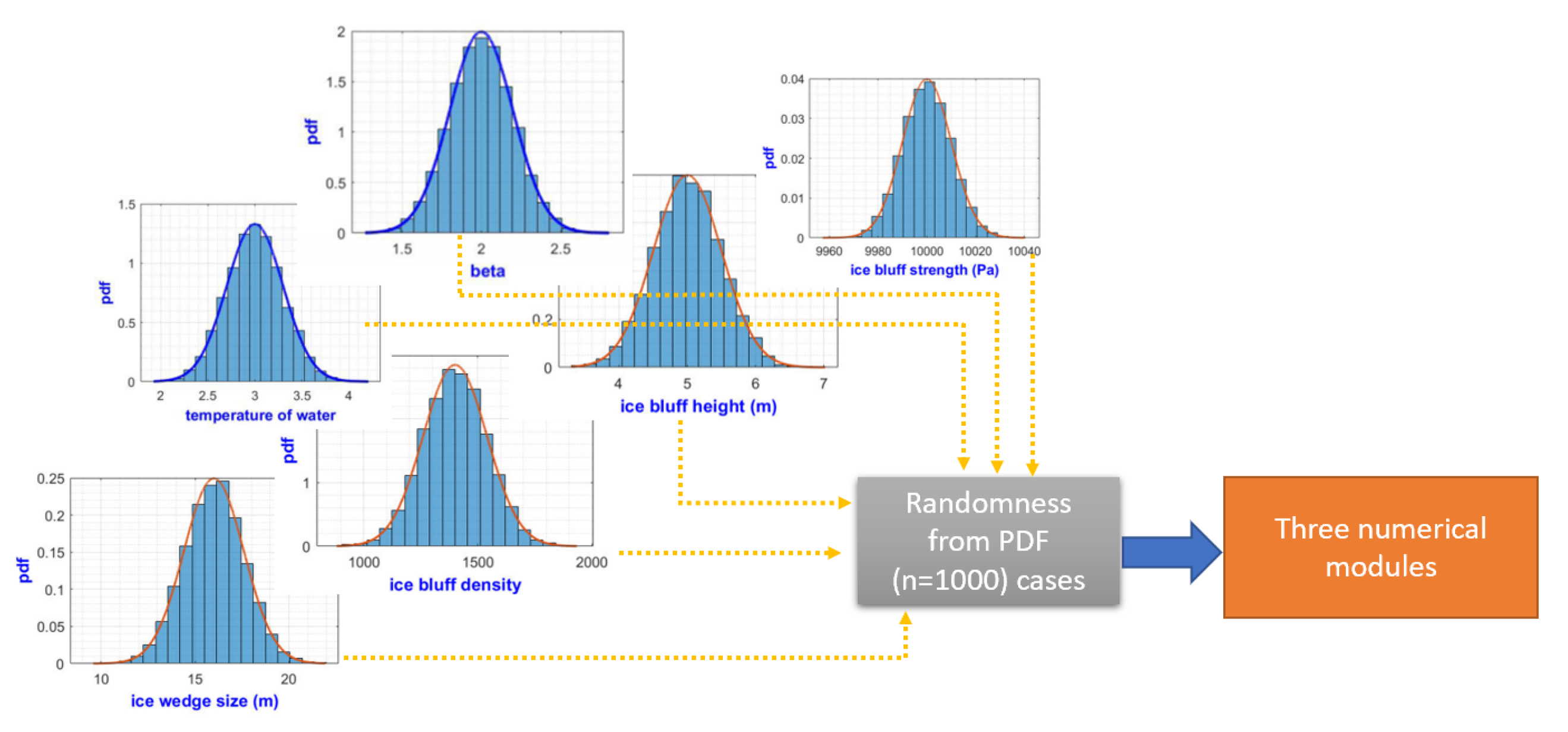
3.5. Probabilistic Model of Arctic Coastal Erosion
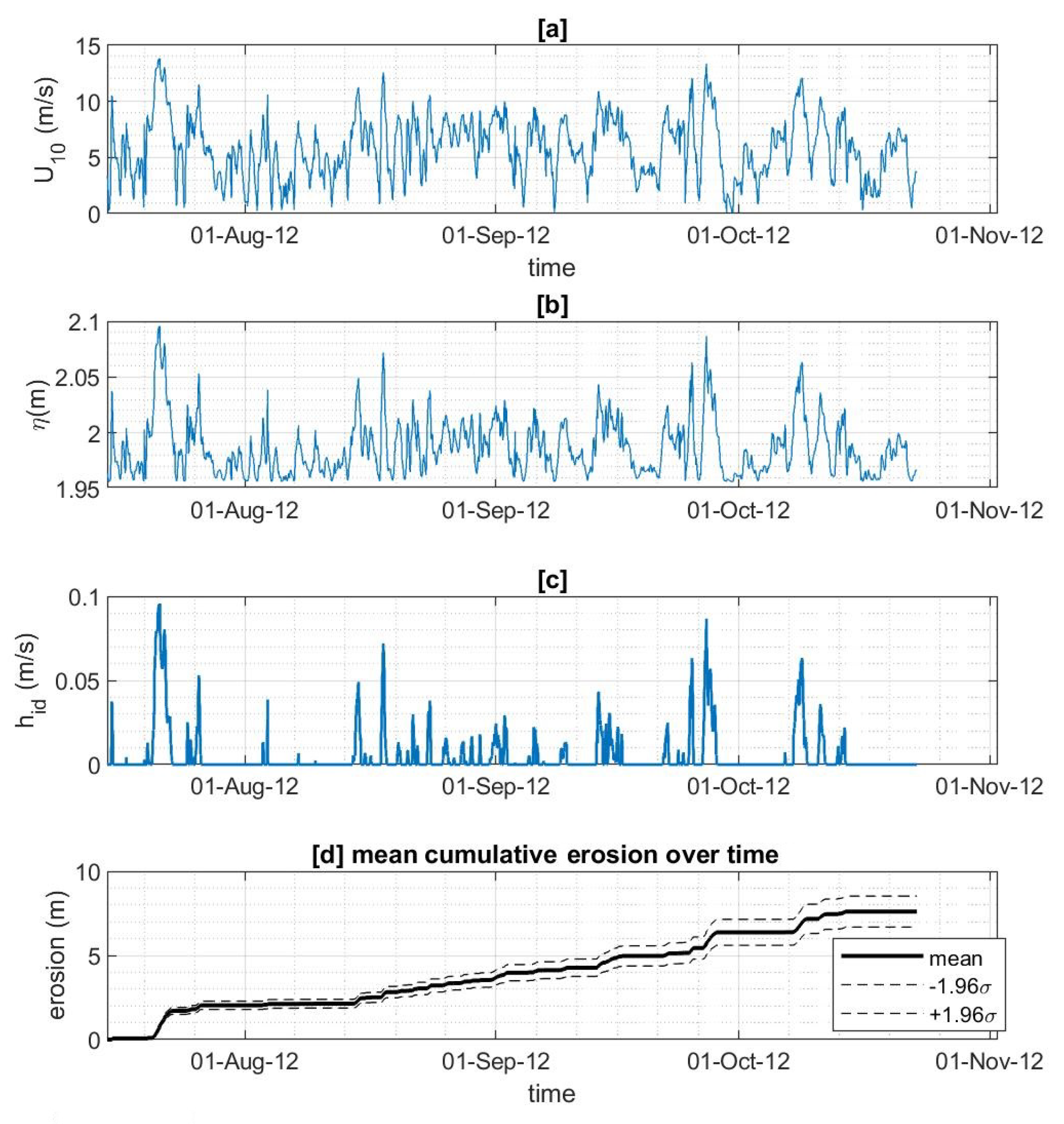
4. Results and Discussion
- horizontal crest retreat (),
- average slope of bluff face (s) and
- height of the bluff ()
- the average slope of the bluff face (s) after the retreat,
- the average slope of the bluff face (s) before the retreat,
- the bluff heights () are defined as, and
- the horizontal crest retreat () is defined as,
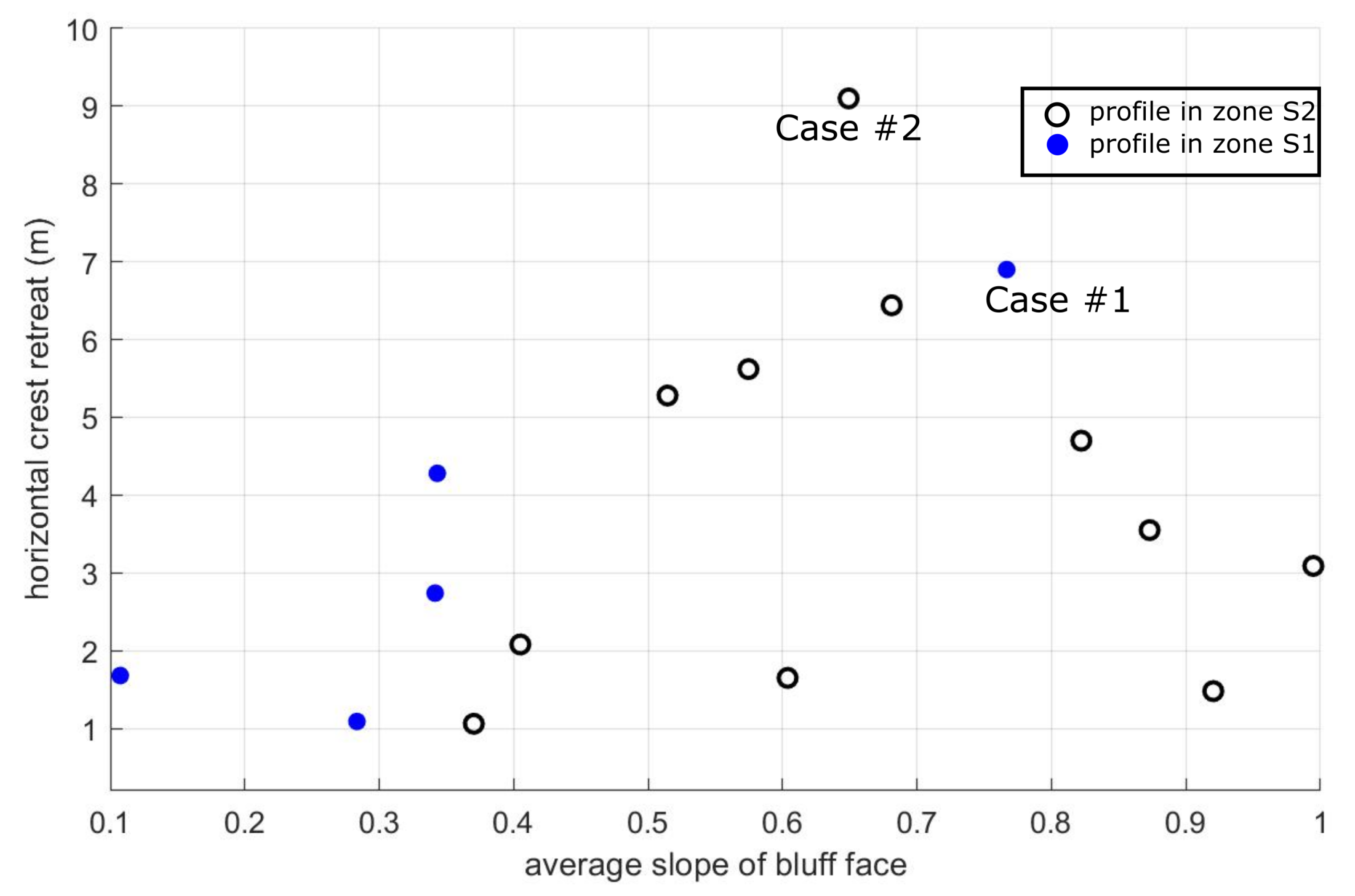
4.1. Determination of Crest Retreat in the Two Cases
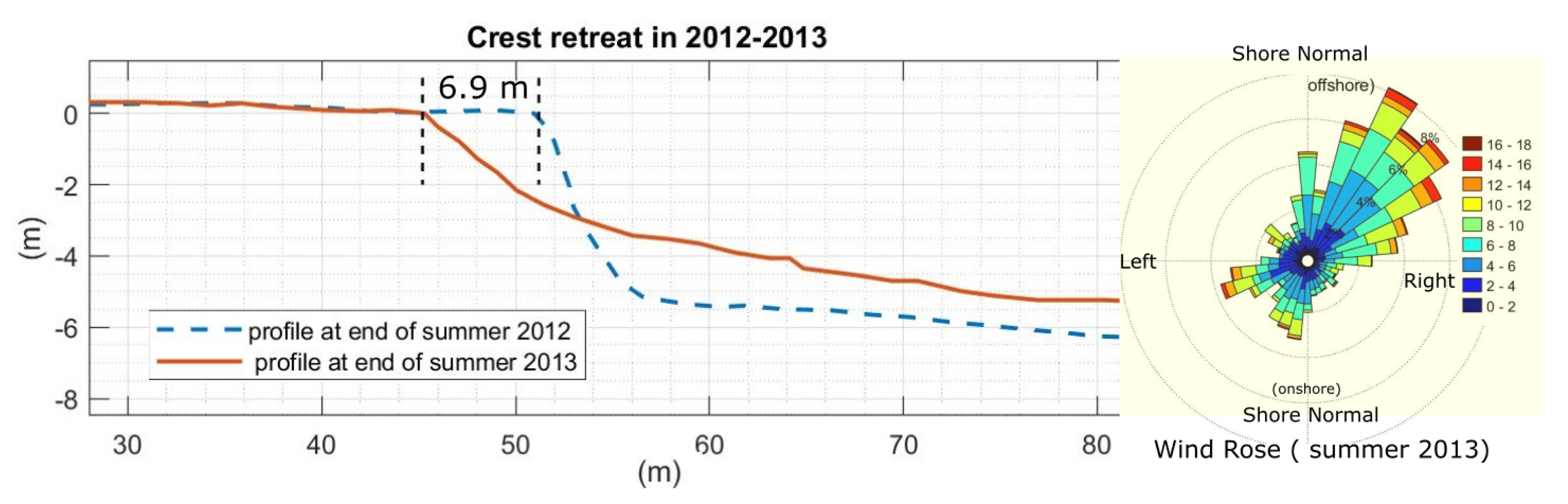
Case #1: Crest Retreat during Summer of 2013
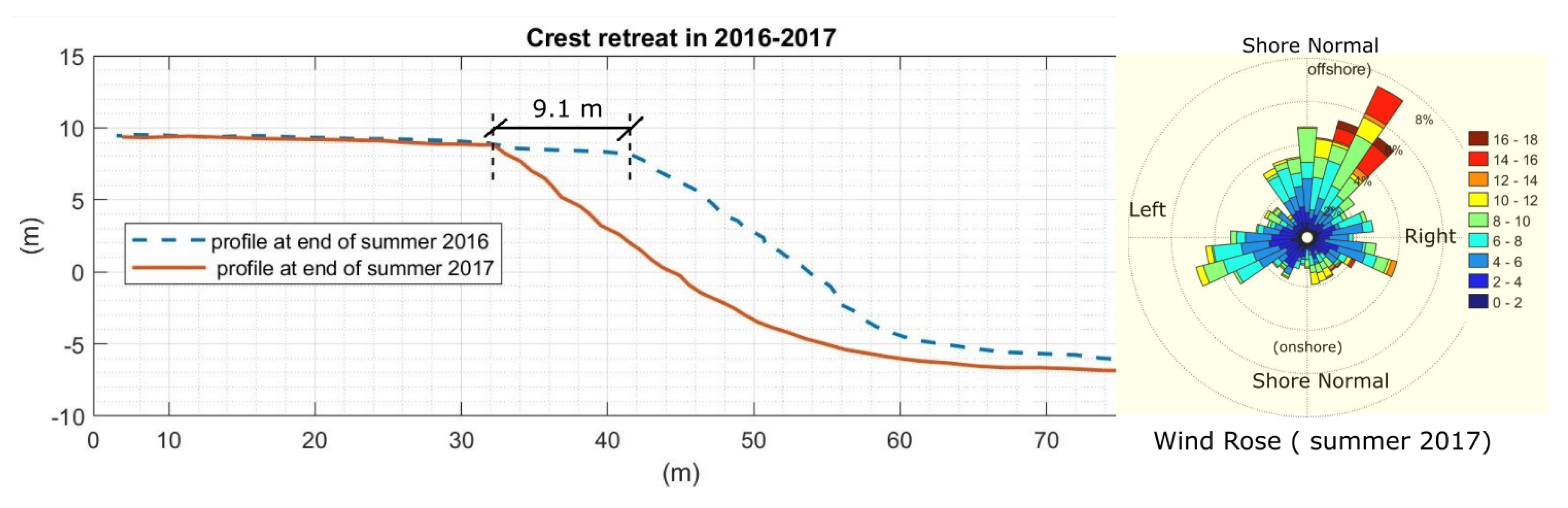
Case #2: Crest Retreat during the Summer of 2017
4.2. Sensitivity Analysis
5. Conclusions
- Thermoabrasion is episodic and discontinuous, not continuous like other Arctic erosion processes.
- There is a small time-lag between the inundation depth and niche growth rate. This time lag can be attributed to the initial resistance of the bluff face to the growth of a niche.
- Coastal erosion is dependent on the intensity of extreme events. Even though Case #1 faced more storms during 2013, the erosion in Case #2 during 2017 is higher than that in Case #1 in 2013 as the intensity and duration of extreme events were significantly higher in 2017.
- The growth of the niche mainly depends on the inundation depth at the base of the bluff, the temperature of incoming waves and the wave height (which is depth-limited).
- The thermoabrasion process is highly sensitive to changes in sea level; therefore, the coasts where thermoabrasion is the dominant erosion process are at higher risk under sea-level rise.
- The sediment concentration and salinity of seawater have very little effect on thermoabrasion when compared to the other input parameters.
- The sensitivity analysis also reveals that the height of the bluff is a secondary factor for thermoabrasion. Field observations also validated this.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, T.; Barry, R.G.; Knowles, K.; Heginbottom, J.; Brown, J. Statistics and characteristics of permafrost and ground-ice distribution in the northern hemisphere. Polar Geogr. 1999, 23, 132–154. [Google Scholar] [CrossRef]
- Anisimov, O.; Reneva, S. Permafrost and changing climate: The Russian perspective. Ambio 2006, 35, 169–175. [Google Scholar] [CrossRef]
- Frederick, J.M.; Thomas, M.A.; Bull, D.L.; Jones, C.A.; Roberts, J.D. The Arctic Coastal Erosion Problem; Technical Report SAND2016-9762; Sandia National Laboratories: Albuquerque, NM, USA, 2016.
- Barnhart, K.R.; Anderson, R.S.; Overeem, I.; Wobus, C.; Clow, G.D.; Urban, F.E. Modeling erosion of ice-rich permafrost bluffs along the Alaskan Beaufort Sea coast. J. Geophys. Res. Earth Surf. 2014, 119, 1155–1179. [Google Scholar] [CrossRef]
- Reimnitz, E.; Graves, S.M.; Barnes, P.W. Beaufort Sea Coastal Erosion, Sediment Flux, Shoreline Evolution, and the Erosional Shelf Profile; U.S. Geological Survey: Reston, VA, USA, 1988.
- Jones, B.M.; Arp, C.D.; Jorgenson, M.T.; Hinkel, K.M.; Schmutz, J.A.; Flint, P.L. Increase in the rate and uniformity of coastline erosion in Arctic Alaska. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Slater, A.G.; Tomas, R.A.; Holland, M.M.; Deser, C. Accelerated Arctic land warming and permafrost degradation during rapid sea ice loss. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Ravens, T.; Peterson, S.; Panchang, V.; Kaihatu, J. Arctic coastal erosion modeling. In Advances in Coastal Hydraulics; World Scientific: Singapore, 2018; p. 47. [Google Scholar]
- Prowse, T.D.; Furgal, C.; Chouinard, R.; Melling, H.; Milburn, D.; Smith, S.L. Implications of climate change for economic development in northern Canada: Energy, resource, and transportation sectors. Ambio 2009, 38, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Soluri, E.; Woodson, V. World vector shoreline. Int. Hydrogr. Rev. 1990, 67, 27–35. [Google Scholar]
- Lantuit, H.; Overduin, P.P.; Couture, N.; Wetterich, S.; Aré, F.; Atkinson, D.; Brown, J.; Cherkashov, G.; Drozdov, D.; Forbes, D.L.; et al. The Arctic coastal dynamics database: A new classification scheme and statistics on Arctic permafrost coastlines. Estuar. Coasts 2012, 35, 383–400. [Google Scholar] [CrossRef] [Green Version]
- Isaev, V.; Koshurnikov, A.; Pogorelov, A.; Amangurov, R.; Podchasov, O.; Sergeev, D.; Buldovich, S.; Aleksyutina, D.; Grishakina, E.; Kioka, A. Cliff retreat of permafrost coast in south-west Baydaratskaya Bay, Kara Sea, during 2005–2016. Permafr. Periglac. Proc. 2019, 30, 35–47. [Google Scholar] [CrossRef]
- Baranskaya, A.; Belova, N.; Kokin, O.; Shabanova, N.; Aleksyutina, D.; Ogorodov, S. Coastal dynamics of the Barents and Kara Seas in changing environment. In Proceedings of the 13th International MEDCOAST Congress on Coastal and Marine Sciences, Engineering, Management & Conservation, Mellieha, Malta, 31 October–4 November 2017; Volume 1, pp. 281–292. [Google Scholar]
- Afzal, M.S.; Lubbad, R. Development of predictive tool for coastal erosion in Arctic—A review. In Proceedings of the Fourth International Conference in Ocean Engineering (ICOE2018); Murali, K., Sriram, V., Samad, A., Saha, N., Eds.; Springer: Singapore, 2019; pp. 59–69. [Google Scholar]
- Guégan, E. Erosion of Permafrost Affected Coasts: Rates, Mechanisms and Modelling; NTNU: Trondheim, Norway, 2015. [Google Scholar]
- Pearson, S.; Lubbad, R.; Le, T.; Nairn, R. Thermomechanical erosion modelling of Baydaratskaya Bay, Russia with COSMOS. In Scour and Erosion, Proceedings of the 8th International Conference on Scour and Erosion (Oxford, UK, 12–15 September 2016); CRC Press: Boca Raton, FL, USA, 2016; p. 281. [Google Scholar]
- Vasiliev, A.; Kanevskiy, M.; Cherkashov, G.; Vanshtein, B. Coastal dynamics at the Barents and Kara Sea key sites. Geo Mar. Lett. 2005, 25, 110–120. [Google Scholar] [CrossRef] [Green Version]
- Hoque, M.A.; Pollard, W.H. Stability of permafrost dominated coastal cliffs in the Arctic. Polar Sci. 2016, 10, 79–88. [Google Scholar] [CrossRef]
- Harper, J.R. The Physical Processes Affecting the Stability of Tundra Cliff Coasts. 1978. Available online: digitalcommons.lsu.edu (accessed on 30 January 2020).
- Hoque, M.A.; Pollard, W.H. Arctic coastal retreat through block failure. Can. Geotech. J. 2009, 46, 1103–1115. [Google Scholar] [CrossRef]
- Kobayashi, N. Formation of thermoerosional niches into frozen bluffs due to storm surges on the Beaufort Sea coast. J. Geophys. Res. Oceans 1985, 90, 11983–11988. [Google Scholar] [CrossRef]
- Kobayashi, N.; Vidrine, J.C. Combined Thermal-Mechanical Erosion Processes Model; Center for Applied Coastal Research, University of Delaware: Newark, DE, USA, 1995. [Google Scholar]
- Nairn, R.; Solomon, S.; Kobayashi, N.; Virdrine, J. Development and testing of a thermal-mechanical numerical model for predicting Arctic shore erosion processes. In Permafrost, Proceedings of the Seventh International Conference, Yellowknife, NWT, Canada, 23–27 June 1998; Centre d’études nordiques, Université Laval: Laval, QC, Canada, 1998; pp. 789–795. [Google Scholar]
- Ravens, T.M.; Jones, B.M.; Zhang, J.; Arp, C.D.; Schmutz, J.A. Process-based coastal erosion modeling for drew point, North Slope, Alaska. J. Waterw. Port Coast. Ocean Eng. 2011, 138, 122–130. [Google Scholar] [CrossRef] [Green Version]
- Isaev, V.; Kokin, O.; Pogorelov, A.; Gorshkov, E.; Komarov, O.; Amangurov, R.; Simonsen, V. Field Investigation and Laboratory Analyses Baydaratskaya Bay 2018; Norwegian University of Science and Technology: Trondheim, Norway, 2019. [Google Scholar] [CrossRef]
- Harms, I.; Karcher, M. Modeling the seasonal variability of hydrography and circulation in the Kara Sea. J. Geophys. Res. Oceans 1999, 104, 13431–13448. [Google Scholar] [CrossRef]
- Stein, R.; Fahl, K.; Fiitterer, D.; Galimov, E.; Stepanets, O. River run-off influence on the water mass formation in the Kara Sea. In Siberian Rer Run-Off in the Kara Sea: Characterisation, Quantification, Variability and Environmental Significance; Elsevier: Amsterdam, The Netherlands, 2003; Volume 6, p. 9. [Google Scholar]
- Odisharia, G.; Tsvetsinsky, A.; Mikhailov, N.; Dubikov, G. Specialized information system on environment of Yamal Peninsula and Baydaratskaya Bay. In Proceedings of the 7th International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 1997. [Google Scholar]
- Leont’yev, I. Coastal profile modeling along the Russian Arctic coast. Coast. Eng. 2004, 51, 779–794. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Coastal Processes with Engineering Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Longuet-Higgins, M.S. Longshore currents generated by obliquely incident sea waves: 1. J. Geophys. Res. 1970, 75, 6778–6789. [Google Scholar] [CrossRef]






| Parameter | Symbol | Estimated Value | Remarks |
|---|---|---|---|
| Physical properties | |||
| Inundation depth | - | to be calculated | |
| Salinity of the seawater inside the niche | S | 0.03 ppt | no salt in the ice inside the bluff |
| Salinity of the ice inside the bluff | 0 | assumption | |
| Suspended sediment (initial) | C | 0 | assumption |
| Porosity of the frozen sediments | n | 0.4 | assumption |
| Density of ice | 916 kg/m | ||
| Density of sediments | 2650 kg/m | measurement | |
| Density of water | 1010 kg/m | ||
| Specific heat of suspended sediment | 0.8374 kJ/kg-K | [4] | |
| Specific heat of seawater | 4.187 kJ/kg-K | ||
| Specific heat of ice | 2.108 kJ/kg-K | ||
| Latent heat of ice | 334 kJ/kg | ||
| Initial conditions | |||
| Sediment concentration | 0 kg/m | [21] | |
| Salinity concentration | 30 ppt | measurements | |
| Temperature | 3 C | measurements (averaged) | |
| Empirical constant of Josberger | m | 0.06 C per ppt | [21] |
| Salinity of the melting point | - | to be calculated | |
| Momentum diffusivity at the melting point | - | to be calculated | |
| Opening of niche (empirical) | 2 | [21] | |
| Empirical parameter of the diffusivity index | A | 0.4 | [31] |
| Module | Input | Output | Remarks |
|---|---|---|---|
| Storm surge module | Bathymetry, wind speed and sea-water density | For every time step | 1D line model, quasi-static equation |
| Niche growth module | Storm surge level (), inundation depth () as defined in Figure 5, temperature of seawater, and diffusivity index Equation (2) | For every time step | 1D, not an empirical formula, based on conservation of mass, energy and salinity |
| Bluff collapse module | Tensile strength of bluff and ice, bluff height and ice content in bluff | Stability | 2D model, highly dependent on the geometry of frozen bluffs |
| Parameter | Symbol | Distribution |
|---|---|---|
| Bluff height | N[5.2,0.52] for case #1 N[14,1.4] for case #2 | |
| Inundation depth | deterministic [calculated] | |
| Ice-wedge size | N[14,1.4] | |
| Salinity of seawater | N[30,3] | |
| Porosity of frozen sediments | n | D[0.4] |
| Density of ice | 916 kg/m | |
| Density of sediments | D[2650 kg/m] | |
| Seawater temperature | N[monthly mean, 10% cov] | |
| Friction factor | D[1 × ] | |
| Longshore current | v | N[1,0.1] |
| Beta (Kobayashi formula) | N[2,0.2] | |
| Tensile strength (ice) | Log N[1 × Pa, V = 100] | |
| Tensile strength (bluff) | Log N[2 × Pa, V = 200] |
| Profile Number | Parameter | 2017 | 2016 | 2015 | 2014 | 2013 | 2012 |
|---|---|---|---|---|---|---|---|
| 1 | s | 0.38 | 0.34 | 0.28 | n.a | n.a | 0.77 |
| cr | n.a | 4.28 | 1.09 | 2.05 | 1.01 | 6.90 | |
| bh | 5.63 | 6.21 | 6.78 | −0.12 | −0.12 | 5.47 | |
| 2 | s | 0.41 | 0.25 | n.a | 0.04 | 0.03 | −0.02 |
| cr | n.a | −5.49 | n.a | n.a | 8.39 | 5.89 | |
| bh | 4.04 | 4.97 | n.a | −1.28 | −1.12 | 1.09 | |
| 3 | s | 0.23 | 0.34 | 0.26 | 0.11 | 0.09 | n.a |
| cr | n.a | 2.74 | −2.06 | 1.68 | −0.16 | n.a | |
| bh | 4.37 | 3.74 | 3.86 | 3.35 | −1.41 | 0.10 | |
| 4 | s | 0.19 | n.a | 0.72 | 0.12 | 0.12 | −0.09 |
| cr | n.a | n.a | n.a | −1.53 | −5.82 | 7.74 | |
| bh | 3.11 | n.a | 3.43 | −2.37 | −1.67 | 1.82 | |
| 5 | s | 0.84 | 0.92 | 1.13 | n.a | n.a | n.a |
| cr | n.a | −0.69 | n.a | 0.23 | n.a | n.a | |
| bh | 13.73 | 13.94 | 12.89 | 15.25 | n.a | n.a | |
| 6 | s | 0.56 | 0.65 | 0.60 | n.a | n.a | n.a |
| cr | n.a | 9.10 | 1.65 | 2.02 | −0.54 | n.a | |
| bh | 14.84 | 13.77 | 13.92 | 8.82 | 9.32 | n.a | |
| 7 | s | 0.31 | 0.57 | 0.99 | n.a | n.a | n.a |
| cr | n.a | 5.62 | 3.09 | −0.33 | 0.98 | n.a | |
| bh | 13.47 | 12.92 | 11.27 | 5.61 | 5.76 | n.a | |
| 8 | s | 0.89 | 0.96 | 0.92 | n.a | n.a | n.a |
| cr | n.a | −0.54 | 1.48 | −1.75 | 0.27 | n.a | |
| bh | 9.86 | 9.61 | 9.43 | 4.81 | 4.90 | n.a | |
| 9 | s | 0.88 | 0.87 | 0.02 | n.a | n.a | n.a |
| cr | n.a | 3.55 | 1.21 | −1.88 | n.a | n.a | |
| bh | 10.77 | 10.91 | 0.19 | 6.04 | n.a | n.a | |
| 10 | s | 0.36 | 0.31 | 0.37 | n.a | 0.51 | n.a |
| cr | n.a | −0.36 | 1.06 | 0.17 | 5.28 | n.a | |
| bh | 13.68 | 13.49 | 12.52 | 6.76 | 12.37 | n.a | |
| 11 | s | 0.48 | n.a | 0.68 | 0.82 | 0.40 | n.a |
| cr | n.a | 2.35 | 6.44 | 4.70 | 2.08 | n.a | |
| bh | 14.80 | 7.96 | 14.25 | 12.47 | 12.88 | n.a |
| Case | Measured Results | Field Measurements | Deviation (%) | |
|---|---|---|---|---|
| Mean | Standard Dev. | |||
| Case #1 | 6.6694 m | 0.3903 | 6.9 m | 3.4% |
| Case #2 | 8.3050 m | 0.4868 | 9.1 m | 8.8% |
| Change in Parameter | Erosion Rate (m/year) | Change Compared to Measured Values (%) |
|---|---|---|
| Reduction of 5 m in the critical niche depth | 14.24 | 113.5 % |
| Decrease of 0.1 m in sea level | 0.647 | −90.3 % |
| Increase of 0.1 m in sea level | 49.11 | 636 % |
| Increase of 10% in wind speed | 20.42 | 0.206 % |
| Increase of 10% in seawater temperature | 7.09 | 6.3 % |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.A.; Lubbad, R.; Afzal, M.S. A Probabilistic Model of Coastal Bluff-Top Erosion in High Latitudes Due to Thermoabrasion: A Case Study from Baydaratskaya Bay in the Kara Sea. J. Mar. Sci. Eng. 2020, 8, 169. https://doi.org/10.3390/jmse8030169
Islam MA, Lubbad R, Afzal MS. A Probabilistic Model of Coastal Bluff-Top Erosion in High Latitudes Due to Thermoabrasion: A Case Study from Baydaratskaya Bay in the Kara Sea. Journal of Marine Science and Engineering. 2020; 8(3):169. https://doi.org/10.3390/jmse8030169
Chicago/Turabian StyleIslam, Mohammad Akhsanul, Raed Lubbad, and Mohammad Saud Afzal. 2020. "A Probabilistic Model of Coastal Bluff-Top Erosion in High Latitudes Due to Thermoabrasion: A Case Study from Baydaratskaya Bay in the Kara Sea" Journal of Marine Science and Engineering 8, no. 3: 169. https://doi.org/10.3390/jmse8030169
APA StyleIslam, M. A., Lubbad, R., & Afzal, M. S. (2020). A Probabilistic Model of Coastal Bluff-Top Erosion in High Latitudes Due to Thermoabrasion: A Case Study from Baydaratskaya Bay in the Kara Sea. Journal of Marine Science and Engineering, 8(3), 169. https://doi.org/10.3390/jmse8030169






