A Numerical Study on Hydrodynamic Performance of an Inclined OWC Wave Energy Converter with Nonlinear Turbine–Chamber Interaction based on 3D Potential Flow

Abstract

In this study, a time-domain numerical method based on three-dimensional potential flow was developed to analyze the hydrodynamic characteristics of an inclined oscillating-water-column (OWC) wave energy converter (WEC). A finite element method was applied to solve the potential flow around and inside the OWC chamber. A turbine–chamber interaction was considered to take into account the pressure drop inside the OWC chamber, which is a nonlinear function of airflow speed via turbine operation. The instantaneous pressure drop was updated on the free-surface boundary condition inside the chamber in the time-domain to account for the coupling effect between the turbine and the chamber. The present numerical method was verified by comparing it with the model test results. The hydrodynamic characteristics of an inclined OWC chamber in terms of potential flow, such as the water column motion and the three-dimensional flow distribution around the chamber, were investigated. In terms of hydrodynamic performance, the energy conversion efficiency of the chamber showed a nonlinear response characteristic dependent on the incident wave height. In addition, numerical calculations were carried out to clarify the relationship between the main geometric parameters and the hydrodynamic response of the inclined OWC chamber.

1. Introduction

In order to utilize ocean wave energy, various technologies for the wave energy converters (WECs) have been developed according to the mode of operation, such as the oscillating water column (OWC); oscillating-wave-surge converter; overtopping device; submerged pressure differential; and point-absorber and attenuator [1]. OWC devices, which is one of the most popular WECs, utilize the pneumatic energy converted from the wave-column motion inside a chamber excited by waves. The air turbine, the power take-off (PTO) system of the OWC wave energy converter, is rotated by reciprocating airflow. The moving part of this PTO system is simple and reliable from a mechanical viewpoint and can be protected from corrosion and mechanical loads because it is located above the seawater [2].

There are several OWC wave energy converters that have been pilot tested, most of which are fixed type. The representative OWC plants are the Pico Plant in Portugal [3], LIMPET OWC Plant in Scotland [4], and Yongsu OWC Plant in Korea. The critical issue for the bottom-fixed structure is how to reduce energy production costs. Generally, it is known that construction of the massive substructure is quite expensive. For this reason, integrating the structure of the OWC device into the breakwater has been proposed to improve accessibility as well as construction, operation, and maintenance costs. [2]. So far, OWC plants combined with breakwaters have been constructed at the harbor of Sakata, Japan [5]; the port of Muturiku, Spain [6]; and the harbor of Civitavecchia, Italy [7].

On the other hand, islands far from the land are not easy to connect to the grid, and where power demand is low, they rely on diesel generators to supply electric power. As part of renewable energy supply to the remote islands, there is an effort to integrate the OWC wave energy converter with the conventional rubble mound breakwater of small fishery harbors [8,9]. An inclined OWC chamber has been proposed, which can improve the economic feasibility of the OWC wave energy converter by improving the applicability to the sloped breakwater section and reducing the construction cost of the chamber structure shown in Figure 1. Model tests and numerical analyses for an inclined OWC wave energy converter were performed to estimate the hydrodynamic performance of the inclined OWC chamber [10,11,12].

In order to investigate the hydrodynamic performance of the OWC wave energy converters, numerical analyses based on the conventional linear potential wave theory have been performed in many previous studies [13,14]. For more reliable performance estimation of the OWC device, efforts have been made to incorporate further complex physical effects such as wave nonlinearity and PTO damping into the numerical analysis. For example, the nonlinear wave model, which includes quadratic terms of the free-surface condition, has been utilized to investigate the hydrodynamics of the OWC chamber [15,16,17]. When the nonlinearity and viscosity are considered in the numerical model, it has been shown that the efficiency of the OWC device is affected by the magnitude of the wave amplitude, and it tends to decrease as the wave height increases [18]. In addition, the pneumatic pressure generated by the operation of the air turbine acts as a damping force on the free surface inside the chamber. Previous studies modeled that the PTO damping is proportional to the airflow speed with the artificial damping coefficient [10,11,19,20,21,22,23]. The time-domain simulations were performed using a two-dimensional, fully nonlinear numerical wave tank technique with the artificial PTO damping proportional to the square of the airflow speed [17,24]. Furthermore, the effect of air compressibility on the estimation accuracy of the OWC’s energy conversion has been studied. The change in an air density due to the air compression and decompression is affected by the pressure, temperature and humidity inside the chamber [25,26,27,28], which leads to a reduction in pneumatic power and a phase difference of the power in the chamber and turbine [25,26,27,29]. Moreover, considering the air compressibility, the OWC’s energy conversion performance may vary depending on the scale effect of the model [29,30].

The main objective of this study is to analyze the hydrodynamic characteristics of an inclined OWC wave energy converter (Figure 1) based on time-domain numerical analysis by using the three-dimensional numerical wave tank (NWT). A turbine–chamber interaction was considered to account for the pressure drop inside the OWC chamber, which is a nonlinear function of airflow speed via turbine operation. This nonlinear function was derived based on the empirical relation between the pressure drop and the airflow speed from the 1/4 scale model test. The instantaneous pressure drop was updated on the dynamic free-surface boundary condition inside the chamber in the time-domain to account for the coupling effect between the turbine and the chamber. Air compressibility is an important characteristic of OWC’s energy conversion but is assumed to be an incompressible gas to simplify the problem in this study.

2. Materials and Methods

2.1. Numerical Method

2.1.1. Boundary Value Problem

In this study, a numerical method based on potential flow theory was developed to evaluate the hydrodynamic performance of an inclined OWC wave energy converter. Figure 2 shows a schematic diagram for the present problem with boundary definitions. It is assumed that an OWC chamber is installed onto the inclined breakwater and that an air-duct for the turbine is connected to the top of the OWC chamber. A skirt with certain depth confines oscillating water inside the OWC chamber. Incident waves directly interact with the OWC chamber, and induced oscillating water interacts with the turbine via air flows. The boundary value problem for the flow around the OWC chamber is as follows;

$${\nabla }^2\varphi =0,\mathrm{in}\Omega$$

(1)

$$\frac{\partial \zeta }{\partial t}=\frac{\partial \varphi }{\partial z}-\beta \zeta ,\mathrm{on}{S}_{F1}\mathrm{and}{S}_{F2}$$

(2)

$$\frac{\partial \varphi }{\partial t}=-g\zeta +\frac{p}{{\rho }_a}-\beta \varphi ,\mathrm{on}{S}_{F1}\mathrm{and}{S}_{F2}$$

(3)

$$\frac{\partial \varphi }{\partial n}=0,\mathrm{on}{S}_B\mathrm{and}{S}_W$$

(4)

The Laplace equation in Equation (1) is the governing equation for the potential flow, where velocity potential $\varphi$ is introduced in the entire fluid domain $\Omega$. The linearized kinematic and dynamic free-surface boundary conditions shown in Equations (2) and (3) are adopted. To satisfy the radiation condition, an artificial damping term is added to free-surface boundary conditions on the numerical damping zone. $\zeta$, $g$, $\beta$, $p$, and ${\rho }_a$ are the wave elevation, gravitational acceleration, damping coefficient, pressure acting on the free-surface, and air density constant, respectively. Here, air is assumed to be an incompressible gas. Equation (4) is the nonpenetration boundary condition for the chamber structure and wall boundary condition on the sea bottom.

Normally, $p$ of the dynamic free-surface boundary condition is set to zero under an atmospheric condition. However, inside the OWC chamber, because the pressure can change due to the turbine, those pressure variations should be considered in Equation (3). It is known that the pressure change due to the turbine–chamber interaction causes the suppression of the free-surface motion inside the OWC chamber.

In this study, a turbine is modeled as an orifice with an empirical nonlinear pneumatic relation between pressure drop ($\Delta p$) and airflow speed ($U_o$), as shown in Equation (5), which takes into account the turbine–chamber interaction in the numerical model. Here, the OWC chamber is sealed and air can flow only through the orifice.

$$\Delta p=p_c-p_{atm.}=\gamma U_o\left|U_o\right|,$$

(5)

where $\gamma$ is the nonlinear pressure drop coefficient. $p_c$ is the pressure inside the chamber. $p_{atm.}$ is the atmospheric pressure.

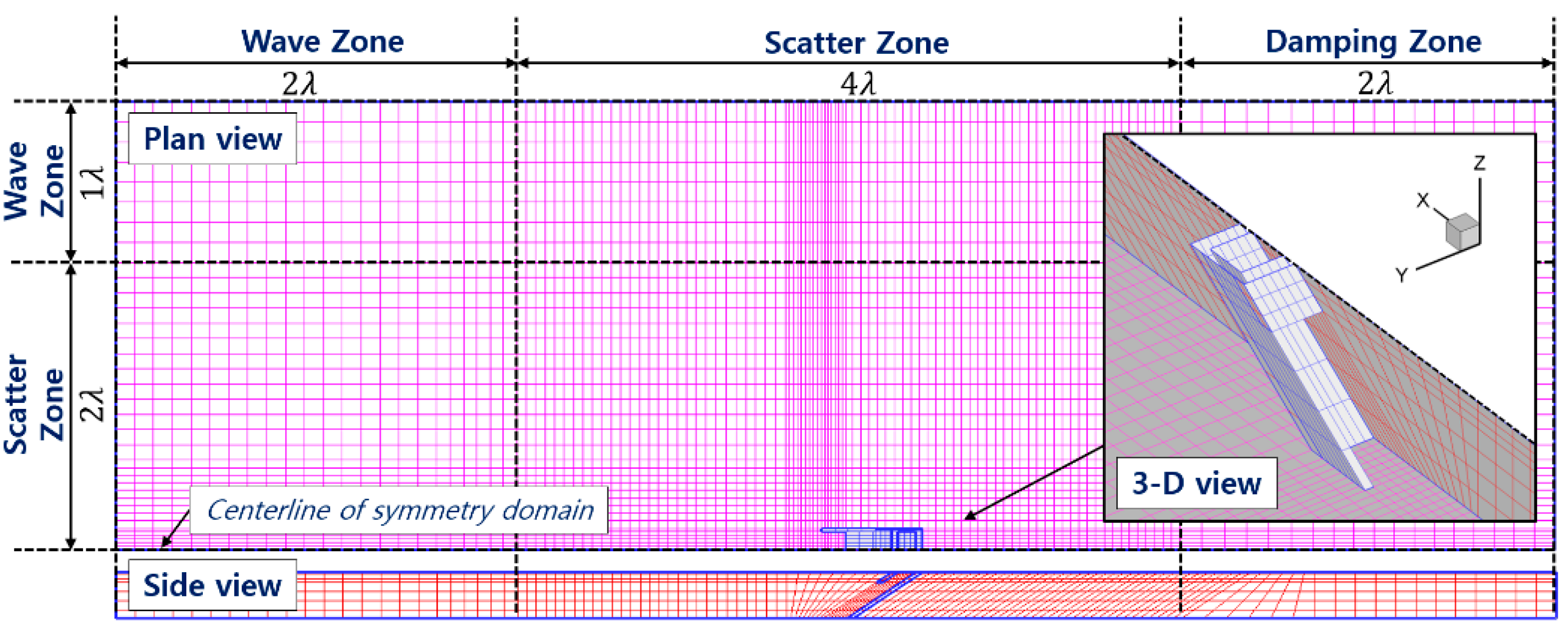
2.1.2. Finite Element Method

In this study, the finite element method is applied to solve the given boundary value problem in Equations (1)–(5). First, the weak formulation of the governing equation could be obtained by applying integration by parts with test functions $\psi$ like Equation (6).

$${\displaystyle {\int }_{\partial \Omega }\nabla \varphi \cdot \nabla \psi dV}-{\displaystyle {\int }_{\partial \Omega }\frac{\partial \varphi }{\partial n}\psi dS}=0,$$

(6)

After the fluid domain is discretized using a finite number of elements, the velocity potential function and wave elevation can be approximated as a linear summation of the continuous and differentiable test functions as shown in Equations (7) and (8).

$$\varphi (x,y,z,t)={\displaystyle \sum _i{\varphi }_i(t)N_i(x,y,z)},$$

(7)

$$\zeta (x,y,z,t)={\displaystyle \sum _k{\zeta }_k(t)M_k(x,y)},$$

(8)

where $N_i$ is a three-dimensional basis function defined in the entire fluid domain, and $M_k$ is a two-dimensional basis function on the free surface. Eight-node hexahedral elements and four-node quadrilateral elements are used in this study. By applying the Galerkin method, the boundary value problem is finally obtained as the following linear algebraic equations:

$$K_{ij}{\varphi }_j=F_i,$$

(9)

$$T_{ik}{\dot{\zeta }}_k=P_{ik}{\varphi }_{n,k},$$

(10)

$$T_{ik}{\dot{\varphi }}_k=-g{P}_{ik}{\zeta }_k$$

(11)

where

$$K_{ij}={\displaystyle {\iiint }_{\Omega }\nabla N_i\cdot \nabla N_{j}dV},$$

(12)

$$F_i={\displaystyle {\iiint }_{S_B}{N}_i\frac{\partial \varphi }{\partial n}dS},$$

(13)

$$T_{ik}=P_{ik}={\displaystyle {\iiint }_{S_F}{M}_i{M}_{k}dS},$$

(14)

The solution of the Laplace equation is obtained from Equation (9). The free-surface velocity potential and elevation are integrated in time by using Equations (10) and (11). In this study, the fourth-order Adams-Bashforth-Moulton method is applied for the time integration of the free-surface boundary condition. The conjugate gradient method is employed for solving Equations (12)–(14). An artificial wave damping zone is introduced to satisfy the radiation condition numerically.

The computational mesh of the three-dimensional numerical wave tank including an inclined OWC chamber is shown in Figure 3. The depth of the entire fluid domain is assumed as constant, and each numerical region length is set to be proportional to the wavelength ($\lambda$). For computational efficiency, the symmetric flow domain was considered at the centerline of the OWC chamber.

2.2. Numerical Validation

2.2.1. Empirical Model for the Duct Orifice

In order to validate the developed numerical method, the present calculation results were directly compared with the model test data of [31], where a series of experiments about an inclined OWC chamber were performed under various wave conditions. The 1/4 scale model of the inclined OWC chamber and its specifications in the test are shown in Figure 4 and

Table 1. Principal dimension of the experimental model (full-scale device).

Item	Symbol	Dimension
Chamber length	$l_c$	5 m
Chamber breadth	$b_c$	10 m
Chamber inclination	$\alpha$	$1\text{:}1.5(\theta =33.69°)$
Skirt draft	$d_s$	2 m
Water depth	$h$	12.8 m
Dia. of air-duct	$d_d$	0.8 m
Dia. of orifice	$d_o$	0.32 m

. In the test, an orifice was installed in place of the turbine at the top of the air chamber to simulate the pressure change due to the turbine–chamber coupling effect. The ratio of the orifice diameter to the air duct ($d_o/d_d$) was set to 0.4 considering the turbine performance under normal operation conditions. The air chamber of this model was tightly sealed so that air could only pass through an air duct with the orifice.

The differential pressure and airflow speed measured at the orifice of the experimental model are shown in Figure 5. The pressure drop inside the chamber has a nonlinear relation with the airflow speed. A previous study [2] also noted that the pressure versus airflow rate is roughly quadratic in most self-rectifying turbines, including impulse types. The quadratic regression function (red line in Figure 5) was derived to define the nonlinear empirical relation by using a least-square method for both experimental pneumatic responses, where the nonlinear pressure drop coefficient ($\gamma /{\rho }_a$) is 1.576. In order to account for the turbine–chamber interaction in the present numerical model, the pneumatic characteristic of the turbine was numerically modeled to an orifice with the nonlinear empirical relation of pneumatic responses as a quadratic function.

2.2.2. Comparison of Airflow Speed and Pneumatic Pressure

Inside the OWC chamber, the total volume of air and water is kept constant under the incompressible flow condition. Thus, the wave-induced oscillatory motion of the water column transforms into the change of the air volume inside the chamber, which in turn causes the airflow through the turbine at the top of the chamber. Therefore, over time, the airflow via the turbine becomes out of phase with the displacement of the free surface inside the chamber because the airflow is in phase with the oscillation speed of the free-surface inside the chamber. The typical time-series of the free-surface elevation ($\zeta$), differential pressure ($\Delta p$), and the airflow rate ($Q$) inside the chamber are shown in Figure 6a. It can be observed that the differential pressure and airflow rate have the same phase while the surface elevation inside the chamber and the pneumatic response show a phase difference of $\pi /2$. These phase relations also demonstrated by Computational Fluid Dynamics (CFD) analysis in a previous study [31].

Figure 6b,c show the wave fields around the OWC chamber at time $t_a$ and $t_b$, respectively. When the pneumatic response is peaked ($t=t_a$), a crest of a standing wave is formed in front of the chamber, shown in Figure 6b. However, when the surface elevation inside the chamber is a peak ($t=t_b$), the wave elevation (z) in front of the chamber decreases, as shown in Figure 6c. It can be said that the pneumatic response was in phase with the surface elevation in front of the chamber.

The validity of the present numerical model was examined by comparing it with the results of the model test, shown in Figure 7. Here, the airflow speed and the pressure difference (drop) are directly compared between the present calculations and the experimental data. The numerical results are suggested with three different mesh resolutions to show their convergence. It can be observed that overall trends of the present calculations are quite similar to those of the experiments. However, some discrepancies are seen, especially in the short-wavelength range (large kh value), where the numerical results slightly underestimate both airflow speed and pressure difference, unlike the experimental data. This is because, under short-wavelength conditions, the free-surface inside the chamber shows nonlinear behavior with a complex sloshing motion which cannot be considered in present potential calculations. In addition, it is understood that the turbulent flow around the skirt structure causes additional dissipation regarding the dynamics of the oscillating water column.

3. Results and Discussions

3.1. Hydrodynamic Characteristics of the Inclined OWC chamber

First, the hydrodynamic response of the OWC chamber was investigated in terms of the wave-chamber as well as chamber-turbine interactions. Naturally, the surface profile inside the OWC chamber is strongly influenced by the incident wave conditions. In particular, it is well-known that under specific wavelength conditions, a resonant response may occur inside the chamber, such as piston-type or sloshing-type resonances. Reflected waves are also developed outside the OWC chamber due to the wave–structure interactions, and those wave fields contribute to increasing the hydrodynamic performance when these standing waves are concentrated in the OWC chamber [32].

Figure 8 shows the free-surface profiles of the water column with various wavelength conditions. The dashed lines indicate the surface profiles corresponding to the crest, while the solid lines indicate the trough of the water column at the time ($t=t_b$) in Figure 6a. The solid black line corresponds to the mean sea level. If the incident wavelength is long enough compared to the chamber length ($l_c/\lambda =0.01$), the free-surface profiles become almost flat, which means a piston-type water column motion is dominant in the OWC chamber. The sloshing-mode motion occurs under the condition of $l_c/\lambda \cong 0.25$, where the surface motion becomes symmetric with respect to the wave direction. The response characteristic of the OWC seems to be affected by the length of the standing wave (${\lambda }^{’}$), which is half of the incident wavelength (${\lambda }^{’}=\lambda /2$). The surface of the water column becomes a more complex shape (i.e., higher-order mode shape). It also categorized the surface motion of the water column inside the chamber into two types: piston-type and sloshing motion [33].

The piston-type motion of the water column can be idealized to a single-degree-of-freedom (SDOF) system, as shown in Figure 9. The natural frequency of the SDOF motion can be calculated, taking into account the mass and restoring force of the system. The effective water mass for the OWC’s piston motion can be defined as $M_e=M_{wc}+M_a$, where $M_{wc}$ is the mass of the water column inside the chamber. $M_a$ is the added mass that behaves together around the chamber when the water column oscillates, which affects the hydrodynamic characteristics of the water column. The natural frequency of the OWC’s piston motion (${\omega }_n$) can be calculated based on the effective fluid mass of the water column ($M_e$) and the restoring force ($K$) due to gravity in Equation (15). The added mass acting on the water column depends on the shape of the chamber with incident wavelength. The inclination of the chamber ($\theta$) is related to the oscillatory direction of the piston motion, which affects the direction of the restoring force acting on the water column. Moreover, the pressure drop inside the chamber acts as a damping force on the oscillating water column.

$${\omega }_n=\sqrt{\frac{K\sin \theta }{M_e}},$$

(15)

where, the mass of the water column inside the chamber ($M_{wc}$) corresponds to $\rho V_{wc}(=\rho l_c{b}_c{d}_s)$, and the gravitational restoring force ($K$) acting on the water column is $\rho g{A}_{wc}(=\rho g{l}_c{b}_c)$.

The pressure change due to the turbine–chamber interaction brings about the suppression of the free-surface motion inside the OWC chamber. To investigate the effect of the turbine modeling on the OWC performance, Figure 10 compares the numerical results of the OWC’s pneumatic responses using a nonlinear empirical pneumatic relation (Figure 5) and with an equivalent linear pneumatic relation under various wave height conditions. Here, the airflow speed and pressure drop are normalized by the wave amplitude.

When the turbine is modeled in a linear pneumatic relation, the numerical results naturally show a linear response to the amplitude of the incident wave. However, when applying the nonlinear empirical pneumatic relation, it can be observed that the pneumatic responses of the OWC chamber changed as a nonlinear function with respect to the wave amplitude. As the wave height increases, the normalized airflow speed dramatically decreases, and at the same time, the differential pressure abruptly increases. It means that the performance of the OWC chamber is not linearly proportional to the wave height owing to the nonlinear turbine–chamber interaction.

The pneumatic power ($P$) converted via the OWC chamber can be expressed as the product of the differential pressure ($\Delta p$) and the airflow rate ($Q$) through the orifice in Equation (16). As shown in Figure 11, it is noteworthy that the differential pressure and airflow rate have signs, but the pneumatic power is a scalar quantity. The pneumatic power of the OWC chamber can be evaluated as a time-averaged value like Equation (17).

$$P=\Delta p\cdot Q,$$

(16)

$$\overline{P}=\frac{1}{t_2-t_1}{\displaystyle {\int }_{t_1}^{t_2}\Delta p\cdot Qdt},$$

(17)

The conversion efficiency ($\eta$) between the pneumatic power ($\overline{P}$) and wave energy flux per unit of wave-crest length ($P_w$) can be defined as follows;

$$\eta =\frac{\overline{P}}{P_w{B}^{*}},$$

(18)

$$P_w=E{c}_g=\frac{1}{8}\rho g{H}^2\left\{\frac{1}{2}\frac{\omega }{k}\left(1+\frac{2kh}{\sinh 2kh}\right)\right\},$$

(19)

where $B^{*}$ is the characteristic length of the breadth, $E$ is the wave energy per unit area, $c_g$ is the group velocity, $H$ is the wave height, $\omega$ is the wave angular frequency, $k$ is the wave number, $\rho$ is the seawater density, and $g$ is the gravitational acceleration constant.

The numerical calculations were performed to investigate the wave height dependency on the hydrodynamic performance of the OWC chamber model (Table 1 and Figure 4) under various wave heights and periods. The primary energy conversion efficiency ($\eta$) of the OWC chamber showed two notable peak responses depending on the incident wavelength (peak A: $kh=1.56$, $T=6.00s$; peak B: $kh=6.20$, $T=2.88s$) in Figure 12a. Here, $B^{*}$ is considered $b_c$. The energy conversion efficiency of the peak A was relatively higher than peak B. As the incident wave height increases, the energy conversion efficiency at both peaks decreases nonlinearly and is more sensitive at lower wave heights, as shown in Figure 12b.

The incident wavelengths of the peak A and B correspond to 0.1 and 0.4 relative to the chamber length ($l_c/\lambda$), respectively. Regarding the free-surface profiles according to the incident wavelength in Figure 8, the peak A and B can be implied as to the resonance responses of the piston-type and sloshing motion, respectively.

3.2. Three-dimensional Hydrodynamic Effect

In real sea operation, OWC structures can be installed in the open sea or sheltered areas. Thus, the hydrodynamic performance of the OWC chamber is affected not only by the two-dimensional shape but also the three-dimensional effect, such as the structure breadth and sidewall. To investigate the three-dimensional effects on the hydrodynamic performance of the OWC chamber, additional numerical simulations were carried out for two- and three-dimensional chamber structure models. Figure 13 shows the comparison of the numerical results for both 2D and 3D models. In this case, the incident wave height was fixed as $H/d_s=0.25$. As shown in the figure, while the second peak B is almost the same, the wavelength and efficiency at the first peak A change significantly due to the three-dimensional effect. For longer incident waves rather than the breadth of the chamber structure ($\lambda >1.5b_c$), the distribution of the three-dimensional wave fields around the chamber structure influences the hydrodynamic performance of the OWC chamber.

Under the condition of peak A, the strong standing waves develop in front of the OWC chamber structure shown in Figure 14a. The standing wave amplifies the oscillating motion of the water column inside the chamber, which improves the hydrodynamic performance of the OWC chamber. The wave frequencies corresponding to peak A of the 2D and 3D models were different in the numerical results (Figure 13). In the 3D simulations, waves are diffracted around the chamber, so the added mass ($M_a$) acting on the water column is relatively smaller than in the 2D model. The difference of the fluid mass affects the hydrodynamic resonance frequency for piston motion, according to Equation (15). This causes the wave frequency of peak A in the 3D simulation to occur under a shorter wavelength than in the 2D simulation.

However, under the condition of peak B, the energy conversion efficiencies of the 2D and 3D simulation results were the same (Figure 13), even though the standing wave in the 3D simulation showed a spatial distribution with a lateral mode in the front of the chamber, as seen in Figure 14b. This corresponds to the geometrical resonance response due to the interaction between the incident wavelength and the cross-sectional shape of the chamber, which is interpreted as peak B irrespective of the 3D flow distribution around the chamber.

The other two conditions of C and D, which show a significant decrease in the hydrodynamic performance of the OWC chamber, showed different characteristics in terms of flow distribution due to wave–structure interaction (Figure 13). The trough C is related to the length of the OWC chamber in the direction of wave propagation and corresponds to a condition where the sum of the skirt and chamber lengths and the wavelength ratio is $\left(l_s+l_c\right)/\lambda =0.25$. A cancelation effect is found under the condition of trough D owing to the crest and trough of the standing wave along the lateral direction of the OWC chamber in Figure 14d.

Figure 15 shows the comparison of the numerical results for the 3D model of the OWC chamber with various sidewall thicknesses ($t_{sw}=0.1,0.5,1.0b_c$). The performance under the condition of peak B is almost the same because there is no three-dimensional effect due to the sidewall thickness. On the other hand, the incident wavelength corresponding to peak A was changed according to the sidewall thickness. The performance of peak A occurred when the standing wave developed to the maximum in front of the structure (Figure 16). As the sidewall gets thicker, the wavelength of peak A becomes longer and the energy conversion efficiency increases. This is because the sidewall thickness corresponds to the capturing width of the wave energy, which contributes to increasing the wave energy concentrated in the chamber.

3.3. Effect of Shape Parameters

In previous numerical results, the energy conversion performance of the OWC chamber was dependent on hydrodynamic characteristics of the OWC’s motion and wave field around the chamber. The effects of the chamber’s shape parameters on the hydrodynamic performance are numerically investigated to clarify the hydrodynamic characteristics of the OWC chamber. The numerical results were analyzed in terms of the change of the wave frequency under both hydrodynamic (peak A) and geometrical (peak B) resonant performance, according to major chamber shape parameters. The four major shape parameters considered in the numerical investigation are chamber length, breadth, inclination, and skirt draft.

3.3.1. Chamber Length

The chamber length ($l_c$), one of the cross-sectional shape parameters, affects the mass ($M_{wc}$) and restoring force ($K$) of the water column inside the chamber. However, changes in mass and restoring force due to chamber length do not affect the natural frequency of the OWC’s piston motion, since the two physical quantities cancel each other out according to Equation (15). The added mass ($M_a$) acting on the oscillating water column, which can be estimated by a numerical analysis, depends on the chamber shape. In Figure 17a, the wave frequency corresponding to peak A is independent of the change in the chamber length, indicating that its effect on the added mass is negligible ($M_a/M_{wc}\simeq 1.48$).

On the other hand, peak B, the peak performance of the sloshing motion, was dependent on the change in the chamber length. The incident wavelength corresponding to peak B (${\lambda }_B$) has a linear relation with the chamber length, $l_c/{\lambda }_B=0.40$, as shown in Figure 17b.

3.3.2. Skirt Draft

The submerged draft of the skirt ($d_s$) is also one of the cross-sectional shape parameters that affect the mass of the water column ($M_{wc}$). According to Equation (15), the change in the water column mass affects the natural frequency (${\omega }_n$). Figure 18a shows that two notable changes with variation of the submerged draft of the skirt are as follows. As the skirt draft increases, the resonance frequency of the piston motion corresponding to the peak A tends to shift to the low frequency due to the increase of the water column mass, as shown in Figure 18b. Another feature is that the energy conversion efficiency on a frequency side higher than peak B is reduced due to the blocking effect of the wave energy entering the chamber by the submerged skirt.

3.3.3. Chamber Inclination

The inclination of the chamber structure ($\alpha$) affects the direction of the OWC’s motion and restoration. According to Equation (15), as the inclination becomes mild (= decrease in $\alpha$), the natural frequency of the water column shifts to a low-frequency side due to the decrease of the restoring force acting on the direction of the OWC’s motion. Both wave frequencies of peaks A and B showed a tendency to shift with the change of the chamber inclination, as shown in Figure 19a,b. Peak B of the sloshing motion’s wave frequency is also more sensitive to the inclination change than peak A, corresponding to the OWC’s piston motion in Figure 19b.

Figure 20 shows the free-surface profiles under the condition of peak B for three inclinations of the chamber structure ($\alpha$ = 1/1.0, 1/1.5, and 1/2.0). Although the inclination of each chamber structure was different, the profiles of the free surface corresponding to peak B were similar to each other as transient sloshing motion, where the nodal point of each profile was equal to $x/l_c=0.6$.

3.3.4. Chamber breadth

The chamber breadth is not included explicitly in the natural frequency of the OWC’s piston motion in Equation (15), because of the SDOF system was idealized in two dimensions. However, the planar geometry of the chamber structure certainly affects the added mass acting on the water column (see Figure 21). The wave frequency of peak A tends to shift toward the lower frequency as the chamber breadth ($b_c$) increases, as shown in Figure 21a.

Assuming the wave frequency of peak A (${\omega }_A$) is the natural frequency of the OWC’s piston motion (${\omega }_n$), which is derived from the numerical results, the added mass ($M_a$) can be estimated based on Equation (15) with the relation of $M_e=M_{wc}+M_a$. Figure 21b shows the change of peak A in wave frequency and ratio of the added mass to the water column mass (${M_a/M}_{wc}$) with respect to various chamber breadths. As the breadth of the chamber increases, the added mass increases. Under infinitely wide chamber breadth, the fluid mass ratio is expected to converge to ${M_a/M}_{wc}=5.68$ derived from the 2D numerical results. As a result, the wave frequency of the hydrodynamic peak performance shifts toward the lower-frequency size as the chamber breadth increases. The change in the three-dimensional flow due to the planar shape of the chamber has a direct effect on the hydrodynamic characteristics of the OWC chamber.

4. Conclusions

In this study, a numerical method based on a potential theory with a finite element method has been developed to simulate the hydrodynamic response of an inclined OWC wave energy converter. The coupling effect between the OWC chamber and air turbine was considered in the numerical model as an orifice with an empirical nonlinear pneumatic relation in the time domain, and the numerical model was verified by comparing it with the model test results. The hydrodynamic performance of the OWC chamber, which means the conversion from incident wave energy to pneumatic energy, was analyzed using the numerical model developed in this study.

The numerical results for the linear and nonlinear pneumatic relation between the pressure drop and the airflow speed were compared to investigate the wave height dependence for the hydrodynamic response of the OWC chamber. The airflow and pressure drop of the OWC chamber tend to decrease or increase nonlinearly with respect to the incident wave height. Since the turbine model with linear pneumatic relation cannot take into account the nonlinear coupling effect, both numerical results showed different pneumatic responses. Therefore, in order to estimate the hydrodynamic performance of the OWC chamber, the turbine–chamber interaction needs to be modeled considering the nonlinear characteristics.

The energy conversion efficiency of the OWC chamber showed a significant peak value at two different wave frequencies depending on the OWC’s motion. The motion type of the water column was dependent on the relation of incident wavelength and chamber length ($l_c/\lambda$). The sloshing motion occurred under the relatively short wave condition ($l_c/\lambda$ < 0.25) compared to the piston motion. The changes in the OWC chamber geometry affect the resonant frequencies of hydrodynamic performance for both sloshing and piston motion. However, according to the dimension of the numerical modeling domain, the resonant frequency and performance for the piston motion of the water column were different. The numerical calculation of a two-dimensional domain cannot take into account the wave diffraction around the chamber structure, making it impossible to properly estimate the added mass that acted on the water column. Therefore, in order to improve the accuracy of the hydrodynamic performance estimation of the finite breadth OWC chamber, it seems that a three-dimensional numerical simulation is required to consider the diffraction of the wave.

In order to clarify the hydrodynamic characteristics of the OWC chamber, the correlation between the wave frequency of the peak performance and the chamber shape parameters was analyzed by numerical calculations. The peak performance due to the OWC’s sloshing motion occurred when the free surface inside the chamber had a profile with the nodal point $x/l_c$ = 0.6. In addition, the resonant frequency of the sloshing motion was dependent on the planar geometry and restoration stiffness of the water column, and the relevant shape parameters are chamber length and inclination, respectively. The piston motion of the water column was analyzed in terms of the natural frequency of the idealized hydrodynamic SDOF system. Each shape parameter of the chamber structure had the dominant influence on the hydrodynamic aspects of the piston motion as follows: the skirt draft (the mass of the water column); the chamber inclination (restoration stiffness); and the sidewall thickness and the chamber breadth (added mass).

It is expected that the numerical technique for estimating hydrodynamic performance can be advanced by considering the nonlinearity and three-dimensional effects, which are essential hydrodynamic characteristics of the OWC chamber investigated in this study. Future research needs to consider air compressibility to improve the accuracy of OWC’s hydrodynamic performance analysis.