Experimental Investigation of the Mooring System of a Wave Energy Converter in Operating and Extreme Wave Conditions
Abstract
:1. Introduction
2. Mooring Solutions for Floating WECs
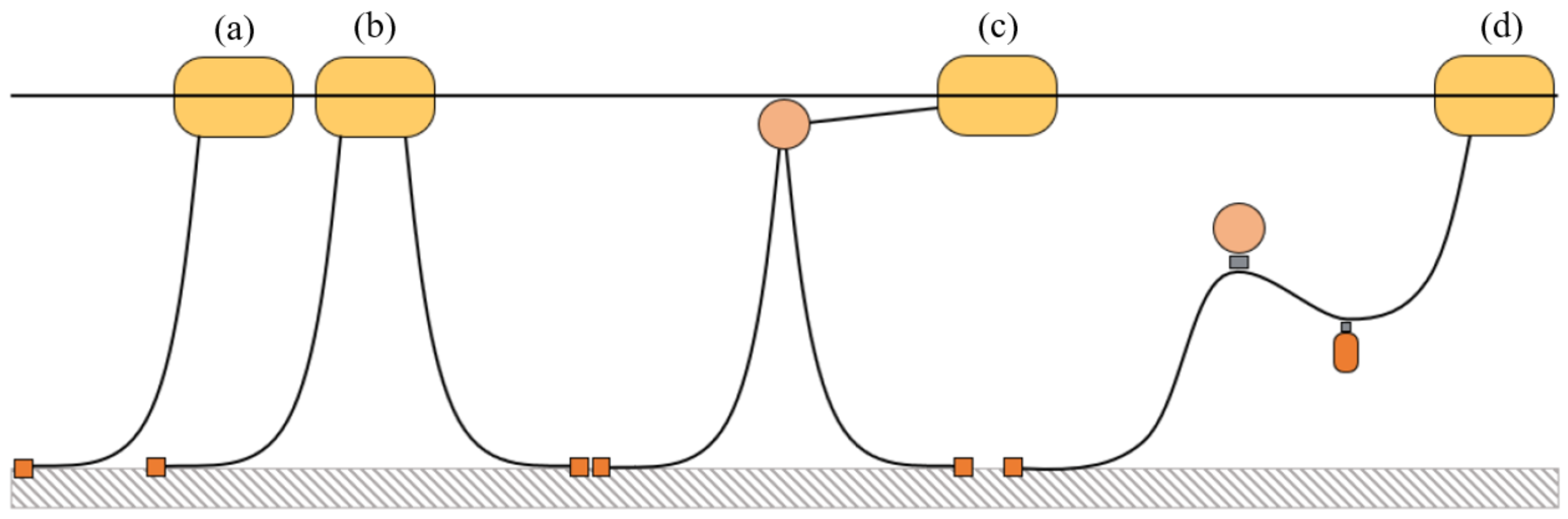
- Single Catenary (a): It is the simplest and least expensive configuration. It belongs to the single point mooring systems and its geometry provides a high compliance, resulting in possible large motions of the device and weather-vaning. The horizontal restoring force is provided only by the weight of the chain. The high footprint and compliance are not suitable for arrays of WECs because collisions may occur. Moreover, no redundancy is present in the case of failure.
- Multi-catenary: this configuration allows the sharing of loads among different lines. Redundancy is provided and allowed motions are reduced by the geometry of the system. However, more components are present, resulting in increased costs.
- CALM: In the Catenary Anchor Leg Mooring, a buoy is introduced close to the surface, minimizing the influence on the vertical motions of the WEC. The upward force exerted by the buoyancy increases the restoring capabilities of the system. This system guarantees larger motions with respect to the multi-catenary, reducing the impedance and the damping related to the mooring. The device can weathervane around the buoy, but, on the other hand, being at the water surface, the buoy is subjected to current and wind loading. Likewise, in the multi-catenary system, more components are present, resulting in higher costs.
- Lazy-wave: In this case, the buoy is submerged, and a clump-weight is introduced. This solution provides lower horizontal loads with respect to the CALM system because no taut lines are present. The geometric compliance of the system is thus increased.
3. ISWEC Device
3.1. ISWEC Device
3.2. ISWEC Mooring System
- Station keeping: the device must be maintained within the specified devoted area.
- Electrical cable safeguard: the motion of the device must avoid tension loads in the electrical transmission cable.
- Compliance: to sustain the environmental loads on the device, the mooring lines and the anchors must comply with the classification and regulations imposed by ruling authorities.
- Passive behavior: the mooring system must minimize the disturbance on the device motion appointed to the power conversion chain (i.e., pitch motion). On the contrary, the horizontal motions need to be constrained, limiting the device drift to ensure station keeping.
- Weathervaning: the ISWEC device should always orientate towards the incident wave, to exploit its pitch motion.: the area dedicated to a single device should be minimized, easing a future installation in an array configuration.
- Reduced maintenance: when possible, the use of high durability component is preferred, to minimize maintenance operations over the service life.
- Redundancy: a degree of redundancy is desirable, according to an appropriate cost analysis.
4. ISWEC Moored Device Experimental Campaign
4.1. Experimental Setup
The 1:20 ISWEC Physical Model
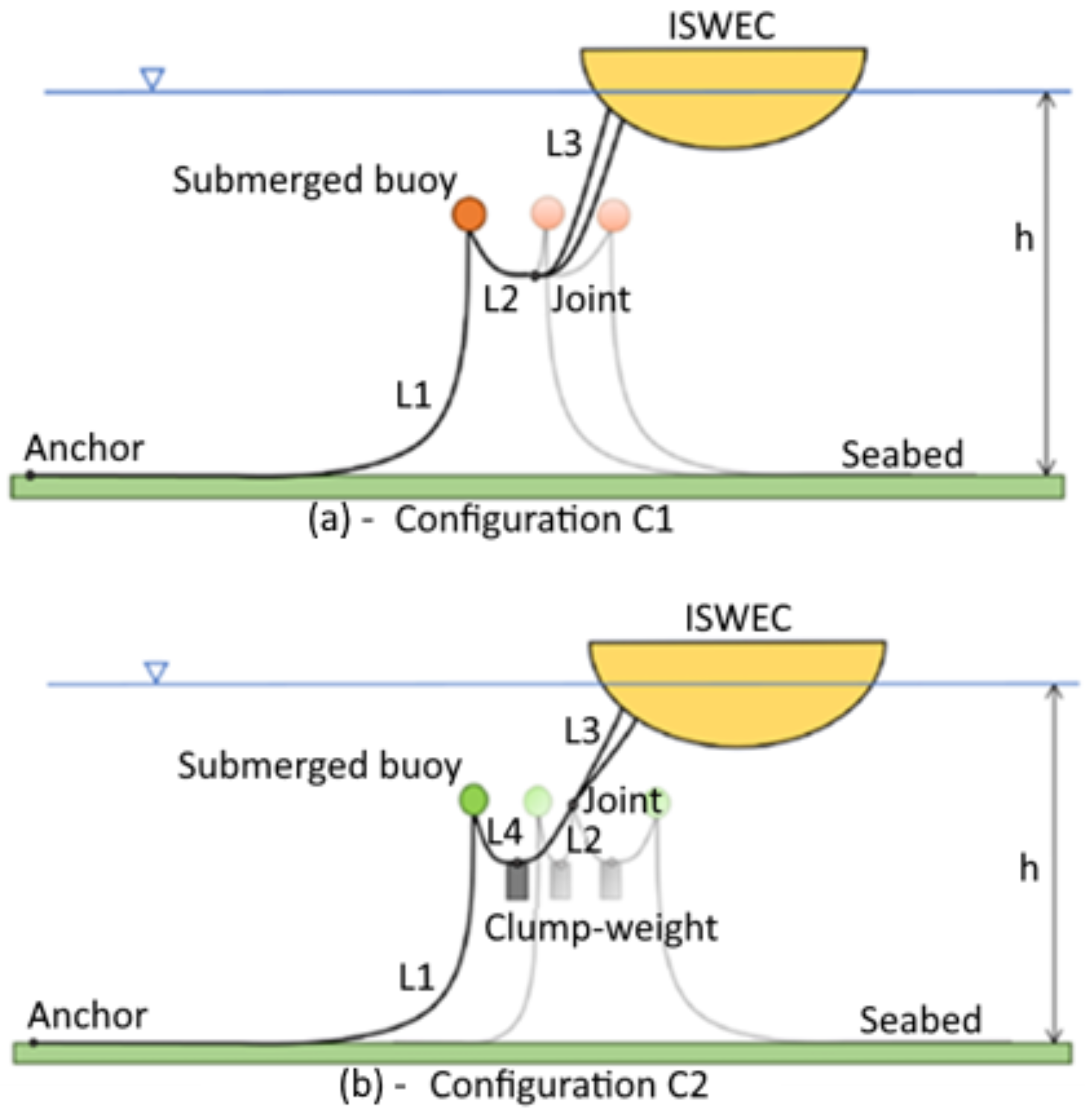
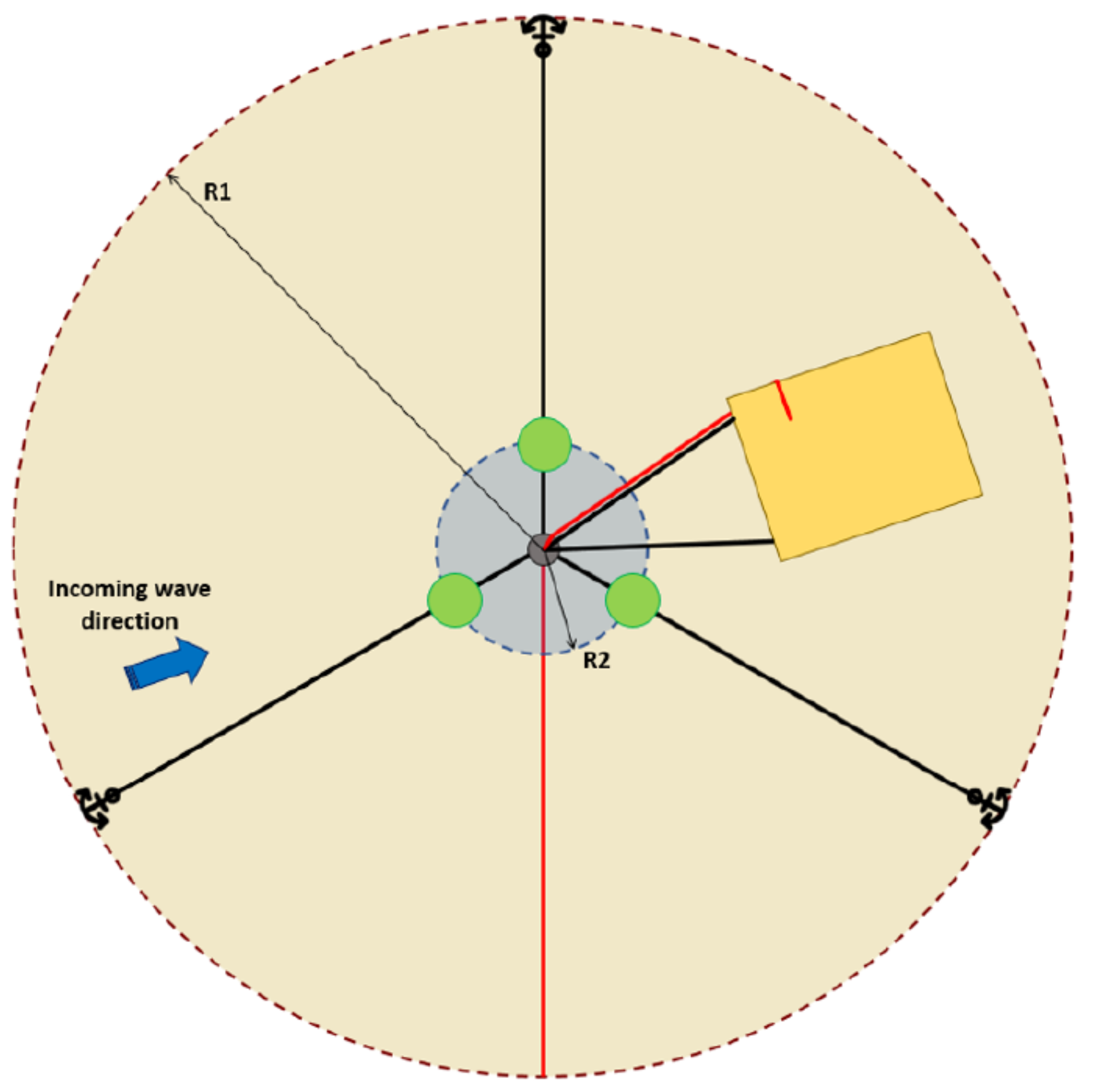
4.2. Mooring System
Acquisition Systems and Data Management
4.3. Meteocean Data
4.4. Experimental Tests
4.4.1. Pull-Out Tests
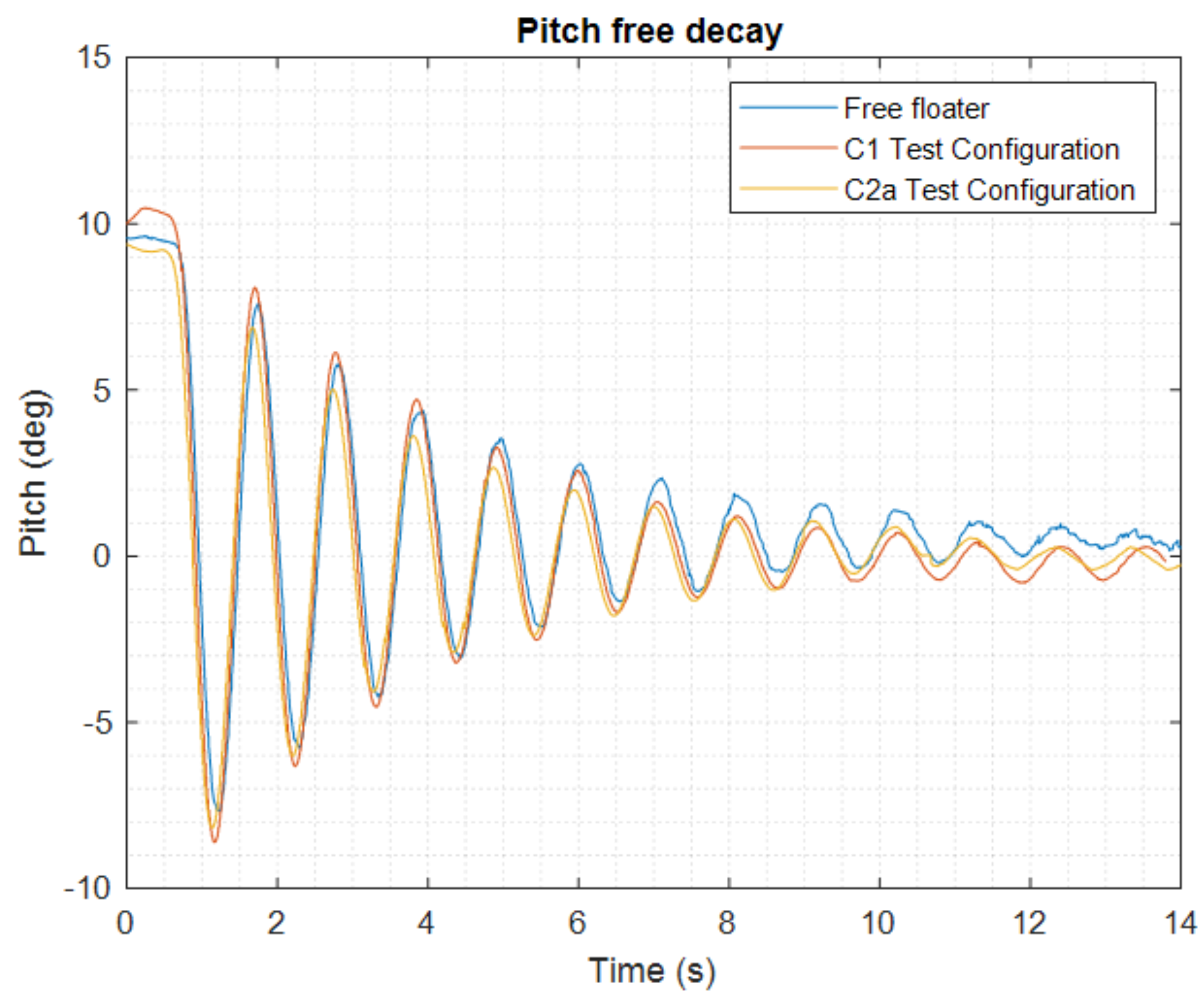
4.4.2. Effect of Mooring on Pitch Natural Period and Damping
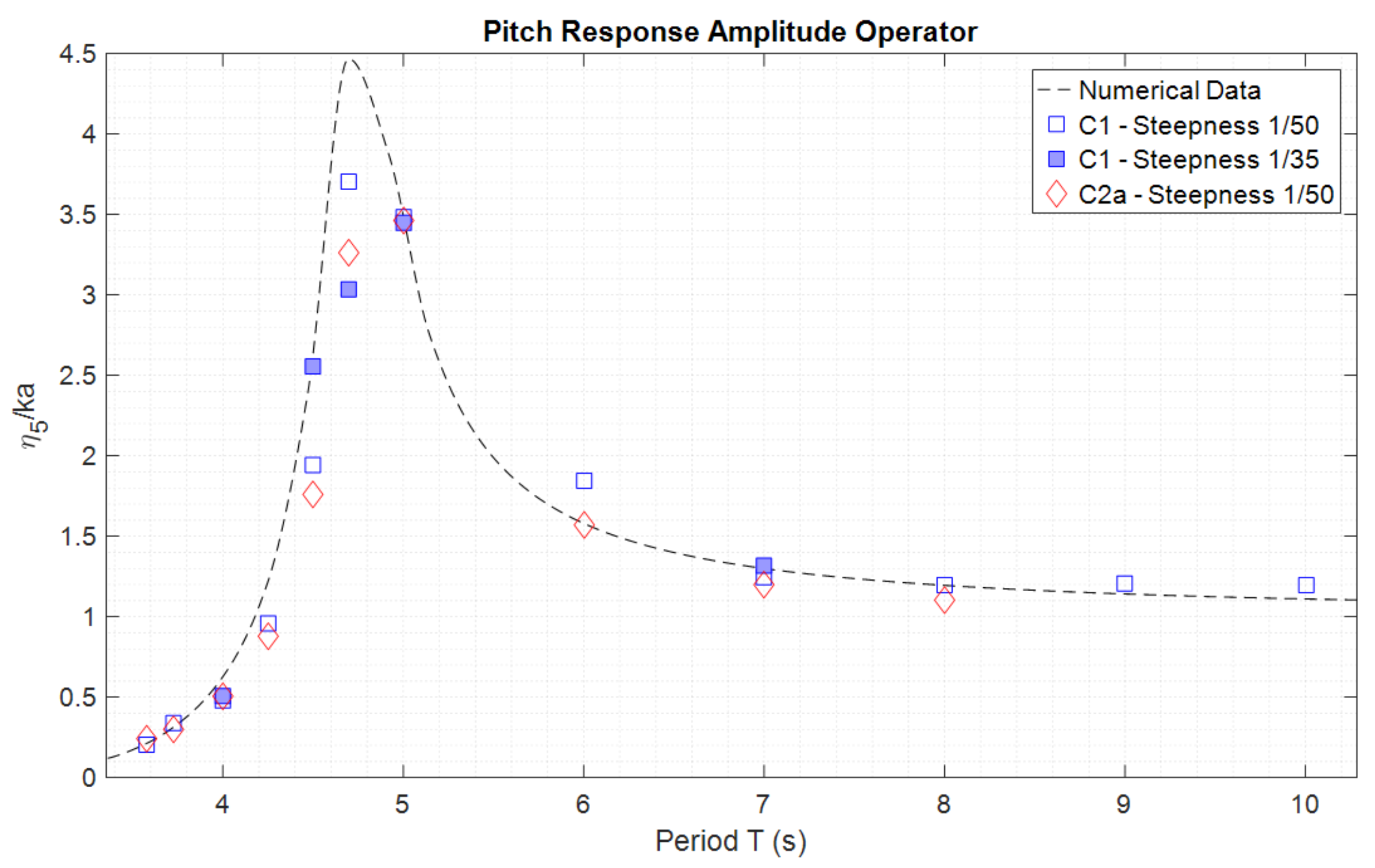
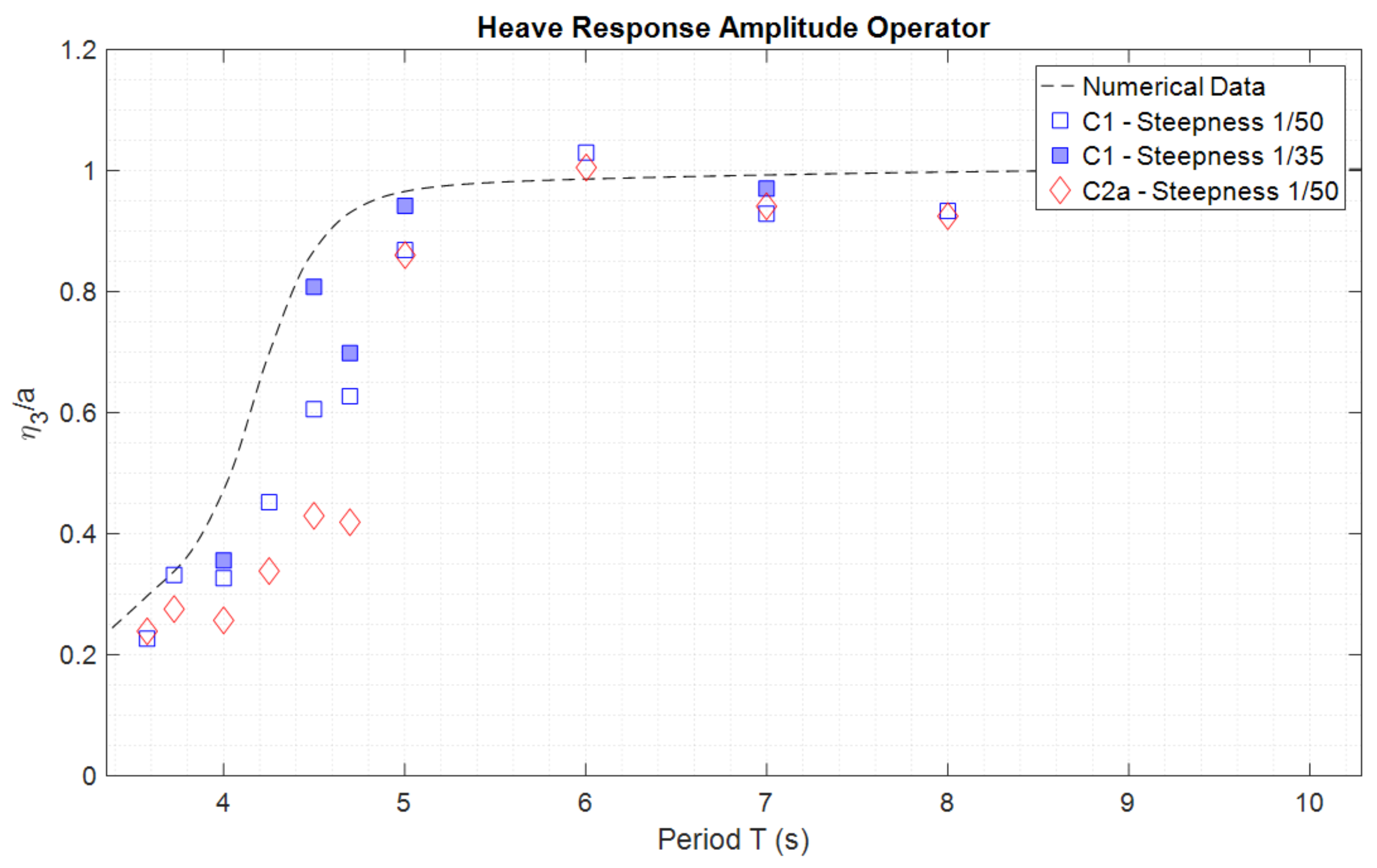
4.4.3. Regular Wave Tests
4.4.4. Irregular Wave Tests
4.4.5. Extreme Wave Tests
4.5. Uncertainty Analysis
5. Experimental Campaign Results
5.1. Regular Wave Results
5.2. Irregular Wave Results
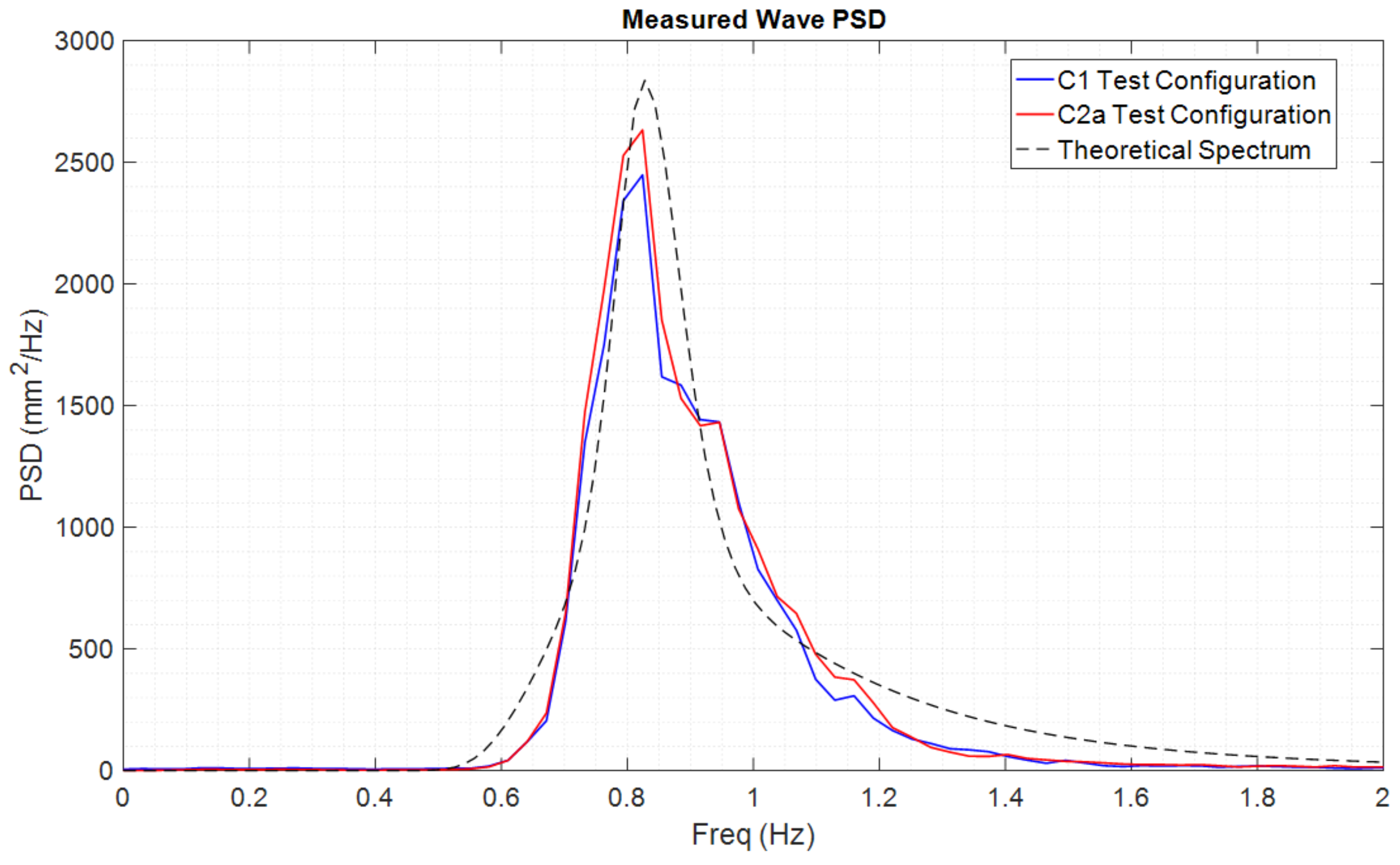
5.2.1. Irregular Wave Spectral Analysis
5.2.2. Device Motion and Mooring Loads Analysis in Operational Wave Conditions
5.3. Extreme Waves Analysis
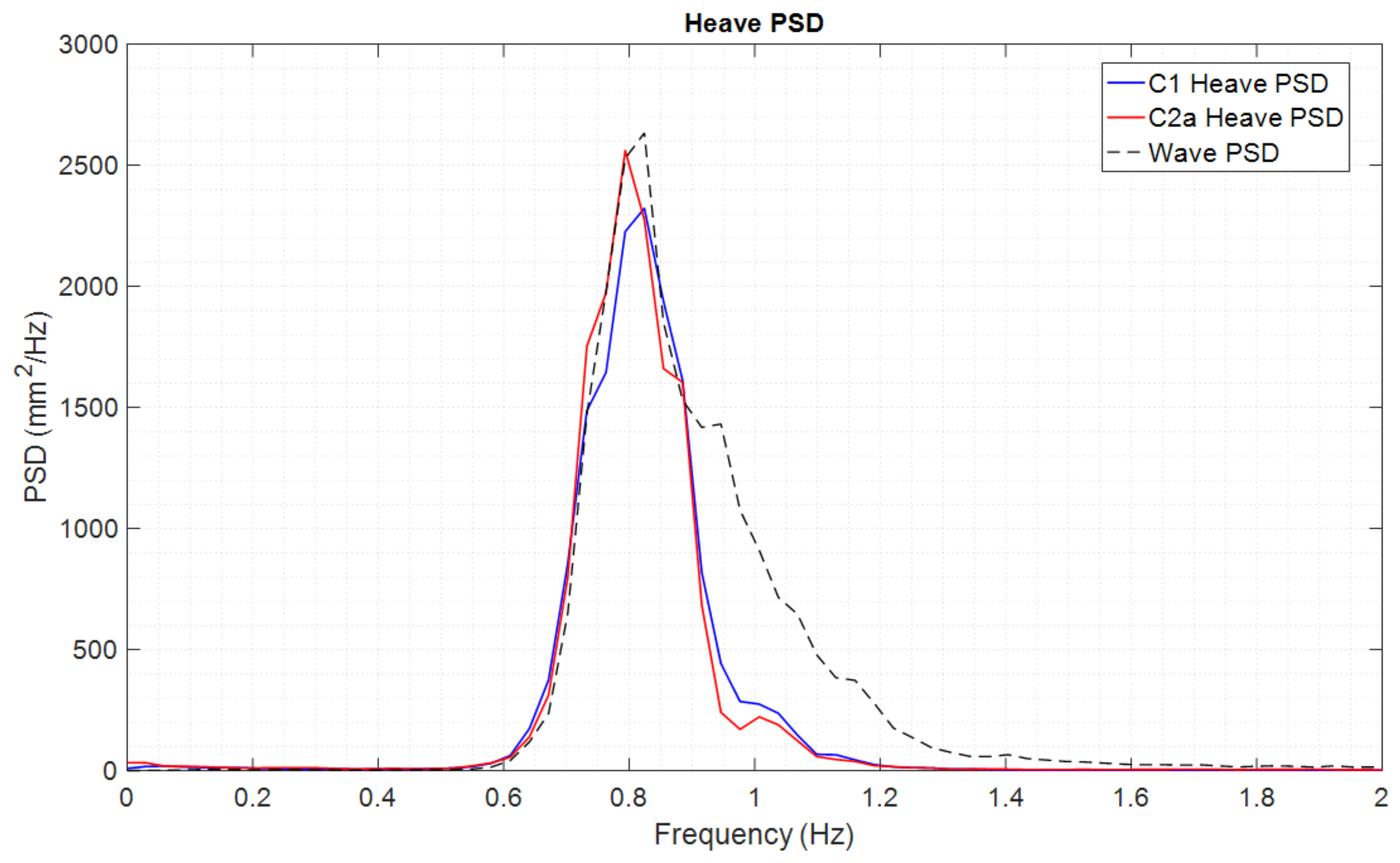
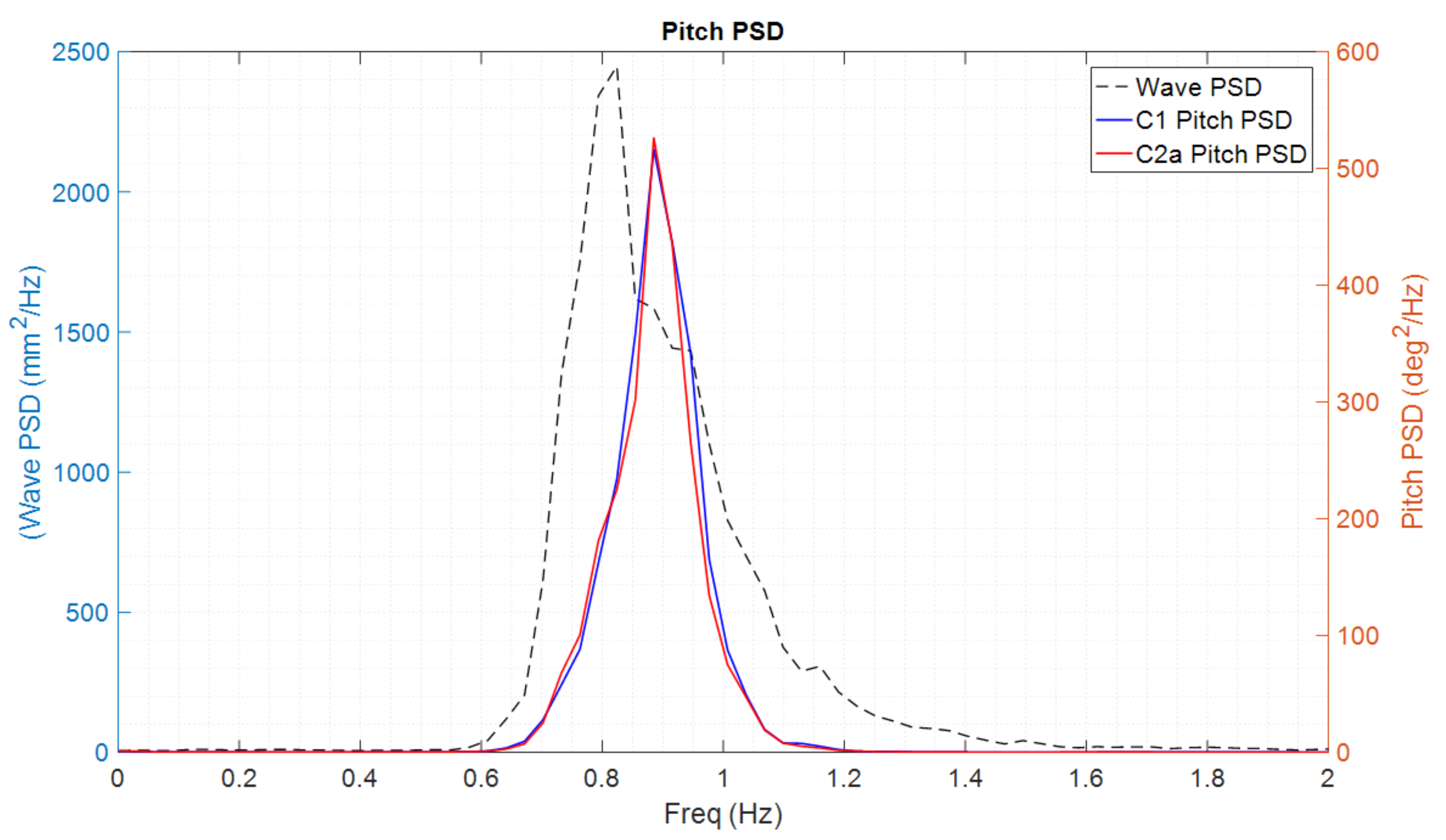
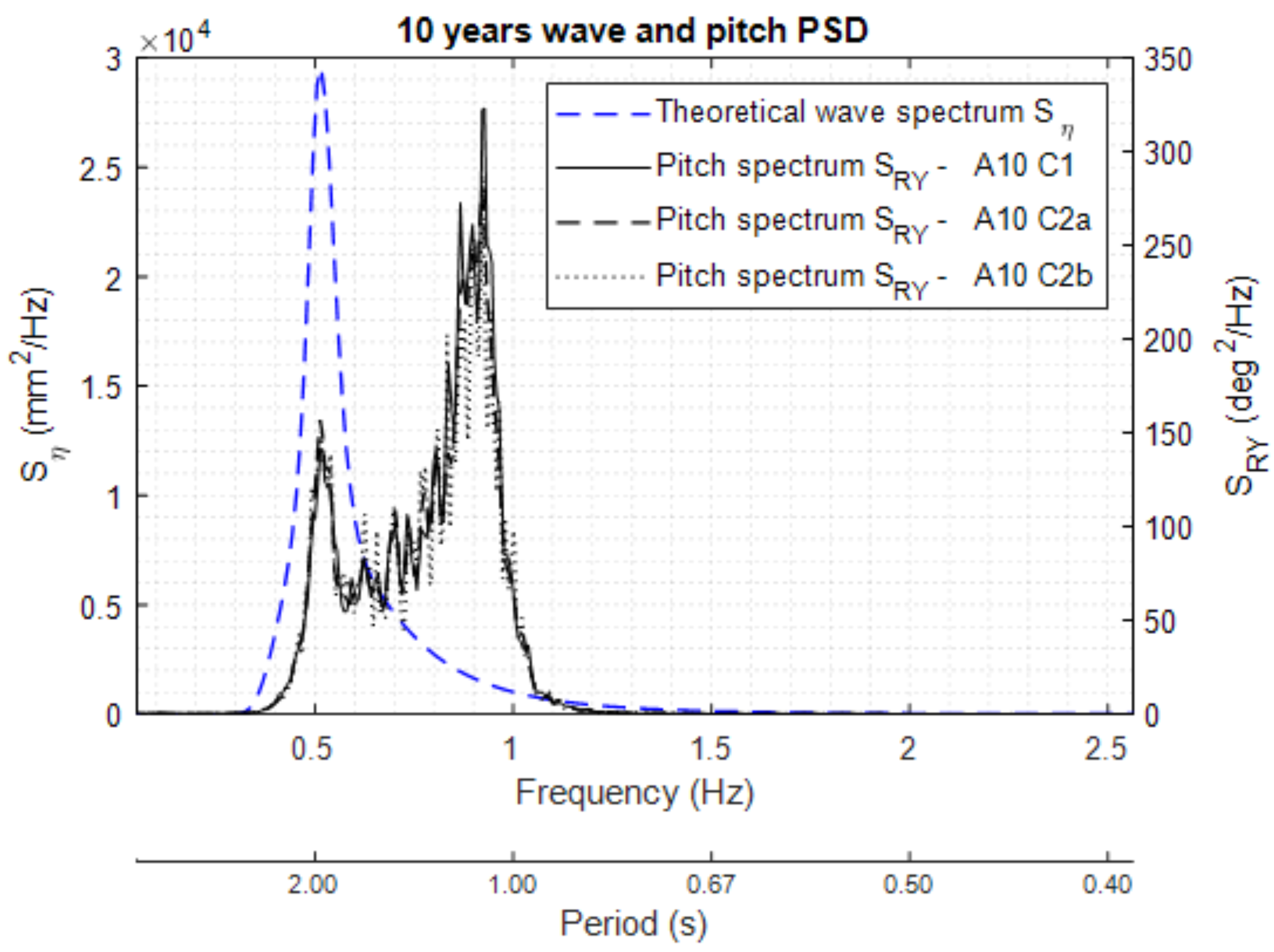
5.3.1. Extreme Waves Spectral Analysis
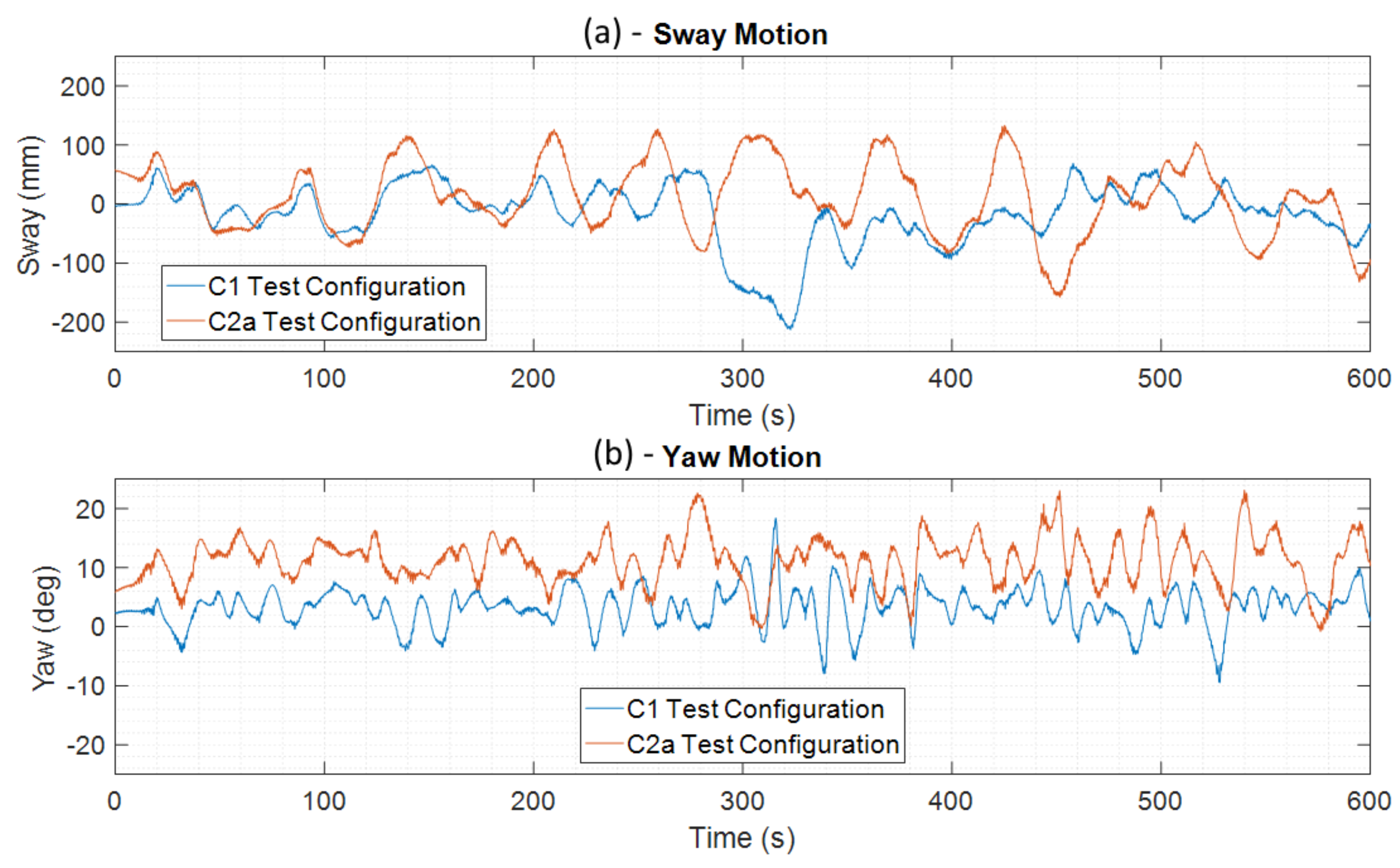
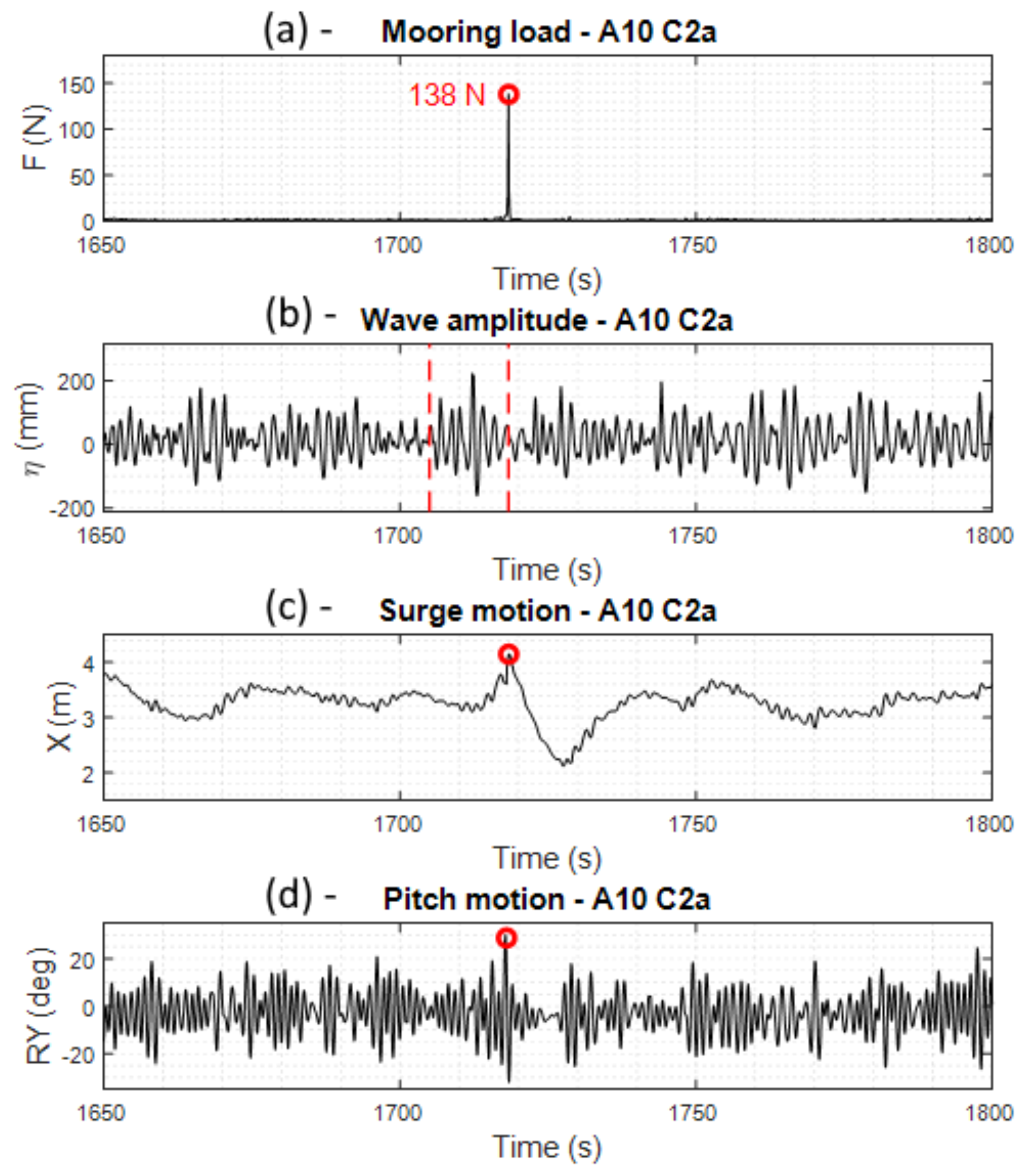
5.3.2. Device Motion Analysis in Extreme Wave Conditions
5.3.3. Mooring Loads Analysis in Extreme Wave Conditions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barltrop, N. Floating Structures: A Guide for Design and Analysis; Oilfield Pubns Inc.: Houston, TX, USA, 1998. [Google Scholar]
- Paredes, G.M.; Bergdahl, L.; Palm, J.; Eskilsson, C.; Pinto, F.T. Station keeping design for floating wave energy devices compared to floating offshore oil and gas platforms. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Articulating parametric resonance for an OWC spar buoy in regular and irregular waves. J. Ocean Eng. Mar. Energy 2018, 4, 311–322. [Google Scholar] [CrossRef]
- Gao, Z.; Bingham, H.B.; Ingram, D.; Kolios, A.; Karmakar, D.; Utsunomiya, T.; Catipovic, I.; Colicchio, G.; Miguel Rodrigues, J.; Adam, F.; et al. Committee V.4 Report: Offshore Renewable Energy, Vol. II; Kamisnski, M.L., Rigo, P., Eds.; International Ship Offshore Structures Congress Press: Amsterdam, The Netherlands, 2018; pp. 193–277. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J.V. Analytical Formulation of Nonlinear Froude-Krylov Forces for Surging-Heaving-Pitching Point Absorbers. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Goggins, J.; Finnegan, W. Shape optimisation of floating wave energy converters for a specified wave energy spectrum. Renew. Energy 2014, 71, 208–220. [Google Scholar] [CrossRef]
- Thomsen, J.B.; Ferri, F.; Kofoed, J.P. Assessment of Current State of Mooring Design in the Danish Wave Energy Sector. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. number 2015 in European Wave and Tidal Energy Conference Series. [Google Scholar]
- Giorgi, G.; Gomes, R.P.F.; Bracco, G.; Mattiazzo, G. The Effect of Mooring Line Parameters in Inducing Parametric Resonance on the Spar-Buoy Oscillating Water Column Wave Energy Converter. J. Mar. Sci. Eng. 2020, 8, 29. [Google Scholar] [CrossRef] [Green Version]
- Sheng, W.; Lewis, T.; Alcorn, R.; Johaning, L.; Kirrane, P. Experimental Investigation of Hydrodynamic Characteristics of a Moored Floating WEC. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010; pp. 1–9. [Google Scholar]
- Hann, M.; Greaves, D.; Raby, A. Snatch loading of a single taut moored floating wave energy converter due to focussed wave groups. Ocean Eng. 2015, 96, 258–271. [Google Scholar] [CrossRef] [Green Version]
- Paredes, G.M.; Palm, J.; Eskilsson, C.; Bergdahl, L.; Taveira-Pinto, F. Experimental investigation of mooring configurations for wave energy converters. Int. J. Mar. Energy 2016, 15, 56–67. [Google Scholar] [CrossRef]
- Wu, M.; Stratigaki, V.; Verbrugghe, T.; Troch, P.; Altomare, C.; Crespo, A.; Kisacik, D.; Cappietti, L.; Dominguez, J.; Hall, M.; et al. Experimental study of motion and mooring behavior of a floating oscillating water column wave energy converter. In Proceedings of the 7th International Conference on Physical Modelling in Coastal Science and Engineering (Coastlab’18), Santander, Spain, 22–26 May 2018; pp. 1–8. [Google Scholar]
- Sirigu, S.A.; Bracco, G.; Bonfanti, M.; Dafnakis, P.; Mattiazzo, G. On-board sea state estimation method validation based on measured floater motion. IFAC-PapersOnLine 2018, 51, 68–73. [Google Scholar] [CrossRef]
- Tarrant, K.R.; Meskell, C. Investigation on parametrically excited motions of point absorbers in regular waves. Ocean Eng. 2016, 111, 67–81. [Google Scholar] [CrossRef]
- Clément, A.H.; Babarit, A.; Gilloteaux, J.C.; Josset, C.; Duclos, G. The SEAREV wave energy converter. In Proceedings of the 6th Wave and Tidal Energy Conference, Glasgow, UK, 29 August–2 September 2005. [Google Scholar]
- Wello, O. Website 2020. Available online: www.wello.eu (accessed on 1 January 2020).
- Falcão, A.F. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean Wave energy converters: Status and challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef] [Green Version]
- Sheng, W. Wave energy conversion and hydrodynamics modeling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Karimirad, M.; Koushan, K.; Weller, S.; Hardwick, J.; Johanning, L. Applicability of offshore mooring and foundation technologies for marine renewable energy (MRE) device arrays. In Renewable Energies Offshore; Guedes Soares, C., Ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 905–912. [Google Scholar]
- Ricci, P.; Rico, A.; Boscolo, F.; Villate, J.L. Design, Modelling and Analysis of an Integrated Mooring System for Wave Energy Arrays. In Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012; pp. 1–6. [Google Scholar]
- Bracco, G.; Cagninei, A.; Casassa, M.; Giorcelli, E.; Giorgi, G.; Mattiazzo, G.; Passione, B.; Poggi, D.; Raffero, M.; Vissio, G. Modeling and optimization of a Wave Energy Converter using ANSYS AQWA. In Innovabook 2015. Paper Anthology. Fluidodinamica, Meccanica, Elettromagnetismo; ANSYS User Group Meeting 2014; Cobalto Casa Editrice: Bergamo, Italy, 2015; pp. 79–86. [Google Scholar]
- Davidson, J.; Ringwood, J.V. Mathematical modeling of mooring systems for wave energy converters—A review. Energies 2017, 10, 666. [Google Scholar] [CrossRef] [Green Version]
- Harris, R.E.; Johanning, L.; Wolfram, J.; Frsa, M. Mooring systems for wave energy converters: A review of design issues and choices. In Proceedings of the 3rd International Conference on Marine Renewable Energy, Blyth, UK, 7–9 July 2004; pp. 159–168. [Google Scholar]
- Martinelli, L.; Ruol, P.; Cortellazzo, G. On mooring design of wave energy converters: The seabreath application. In Proceedings of the Coastal Engineering Conference, Santander, Spain, 1–6 July 2012; pp. 1–12. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Martinelli, L.; Castagnetti, M. Screening of Suitable Mooring Systems; Technical Report; Aalborg University: Aalborg, Denmark, 2011. [Google Scholar] [CrossRef]
- Cagninei, A.; Raffero, M.; Bracco, G.; Giorcelli, E.; Mattiazzo, G.; Poggi, D. Productivity analysis of the full scale inertial sea wave energy converter prototype: A test case in Pantelleria Island. J. Renew. Sustain. Energy 2015, 7, 061703. [Google Scholar] [CrossRef]
- Bracco, G.; Casassa, M.; Giorcelli, E.; Giorgi, G.; Martini, M.; Mattiazzo, G.; Passione, B.; Raffero, M.; Vissio, G. Application of sub-optimal control techniques to a gyroscopic Wave Energy Converter. Renew. Energ. Offshore 2014, 1, 265–269. [Google Scholar]
- Bracco, G.; Giorcelli, E.; Mattiazzo, G.; Orlando, V.; Raffero, M. Hardware-In-the-Loop test rig for the ISWEC wave energy system. Mechatronics 2015, 25, 11–17. [Google Scholar] [CrossRef]
- Bracco, G.; Giorcelli, E.; Giorgi, G.; Mattiazzo, G.; Passione, B.; Raffero, M.; Vissio, G. Performance assessment of the full scale ISWEC system. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 2499–2505. [Google Scholar] [CrossRef]
- Sirigu, S.A.; Bonfanti, M.; Passione, B.; Begovic, E.; Bertorello, C.; Dafnakis, P.; Bracco, G.; Giorcelli, E.; Mattiazzo, G. Experimental investigation of the hydrodynamic performance of the ISWEC 1:20 scaled device. In Proceedings of the NAV International Conference on Ship and Shipping Research, Trieste, Italy, 20–22 June 2018; Number 221499. pp. 551–560. [Google Scholar] [CrossRef]
- Bonfanti, M.; Bracco, G.; Dafnakis, P.; Giorcelli, E.; Passione, B.; Pozzi, N.; Sirigu, S.; Mattiazzo, G. Application of a passive control technique to the ISWEC: Experimental tests on a 1:8 test rig. In Proceedings of the NAV International Conference on Ship and Shipping Research, Trieste, Italy, 20–22 June 2018; Number 221499. pp. 60–70. [Google Scholar] [CrossRef]
- Pozzi, N.; Bonfanti, M.; Mattiazzo, G. Mathematical Modeling and Scaling of the Friction Losses of a Mechanical Gyroscope. Int. J. Appl. Mech. 2018, 10, 1850024. [Google Scholar] [CrossRef]
- Sirigu, A.S.; Gallizio, F.; Giorgi, G.; Bonfanti, M.; Bracco, G.; Mattiazzo, G. Numerical and Experimental Identification of the Aerodynamic Power Losses of the ISWEC. J. Mar. Sci. Eng. 2020, 8, 49. [Google Scholar] [CrossRef] [Green Version]
- Novo, R.; Bracco, G.; Sirigu, S.; Mattiazzo, G.; Merigaud, A.; Ringwood, J. Nonlinear simulation of a wave energy converter with multiple degrees of freedom using a harmonic balance method. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Madrid, Spain, 17–22 June 2018; Volumn 10. [Google Scholar] [CrossRef]
- Genuardi, L.; Bracco, G.; Sirigu, S.A.; Bonfanti, M.; Paduano, B.; Dafnakis, P.; Mattiazzo, G. An application of model predictive control logic to inertial sea wave energy converter. In Mechanisms and Machine Science; Springer: Berlin/Heidelberg, Germany, 2019; Volumn 73, pp. 3561–3571. [Google Scholar] [CrossRef]
- Vissio, G.; Valério, D.; Bracco, G.; Beirão, P.; Pozzi, N.; Mattiazzo, G. ISWEC linear quadratic regulator oscillating control. Renew. Energy 2017, 103, 372–382. [Google Scholar] [CrossRef]
- DNV GL. OFFSHORE STANDARD DNV GL AS Position Mooring; Technical Report. 2015. Available online: https://rules.dnvgl.com/docs/pdf/dnvgl/os/2015-07/DNVGL-OS-E301.pdf (accessed on 1 January 2020).
- Pozzi, N.; Bracco, G.; Passione, B.; Sirigu Sergej, A.; Vissio, G.; Mattiazzo, G.; Sannino, G. Wave Tank Testing of a Pendulum Wave Energy Converter 1:12 Scale Model. Int. J. Appl. Mech. 2017, 9, 1750024. [Google Scholar] [CrossRef] [Green Version]
- Begovic, E.; Bertorello, C.; Prpic Orsic, J. Roll Damping Coefficients Assessment and Comparison for Round Bilge and Hard Chine Hullforms. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
- Begovic, E.; Day, A.; Incecik, A. An experimental study of hull girder loads on an intact and damaged naval ship. Ocean Eng. 2017, 133, 47–65. [Google Scholar] [CrossRef] [Green Version]
- Bencivenga, M.; Nardone, G.; Ruggiero, F.; Calore, D. The Italian data buoy network (RON). WIT Trans. Eng. Sci. 2012, 74, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, V.; Davey, T.; Smith, H.; Smith, G.; Holmes, B.; Barrett, S.; Prevosto, M.; Maisondieu, C.; Cavalieri, L.; Bertotti, L.; et al. EquiMar Project: Wave and Tidal Resource Characterisation; Technical Report. 2011. Available online: https://archimer.ifremer.fr/doc/00250/36152/34706.pdf (accessed on 1 January 2020).
- ITTC. Recommended Procedures and Guidelines 7.5-02-07-03.2: Analysis Procedure for Regular Wave Tests; Technical Report. 2002. Available online: https://ittc.info/media/1323/75-02-07-032.pdf (accessed on 1 January 2020).
- ITTC. Recommended Procedures and Guidelines 7.5-02-07-03.14: Analysis Procedure od Model Tests in Irregular Waves; Technical Report. 2017. Available online: https://www.ittc.info/media/8139/75-02-07-0314.pdf (accessed on 1 January 2020).
- ITTC. Recommended Procedures and Guidelines 7.5-02-01-01: Guide to the Expression of Uncertainty in Experimental Hydrodynamics; Technical Report. 2014. Available online: https://ittc.info/media/1217/75-02-02-01.pdf (accessed on 1 January 2020).
- Begovic, E.; Bertorello, C.; Pennino, S. Experimental seakeeping assessment of a warped planing hull model series. Ocean Eng. 2014, 83, 1–15. [Google Scholar] [CrossRef]
- Pozzi, N.; Bracco, G.; Passione, B.; Sirigu, S.A.; Mattiazzo, G. PeWEC: Experimental validation of wave to PTO numerical model. Ocean Eng. 2018, 167, 114–129. [Google Scholar] [CrossRef]







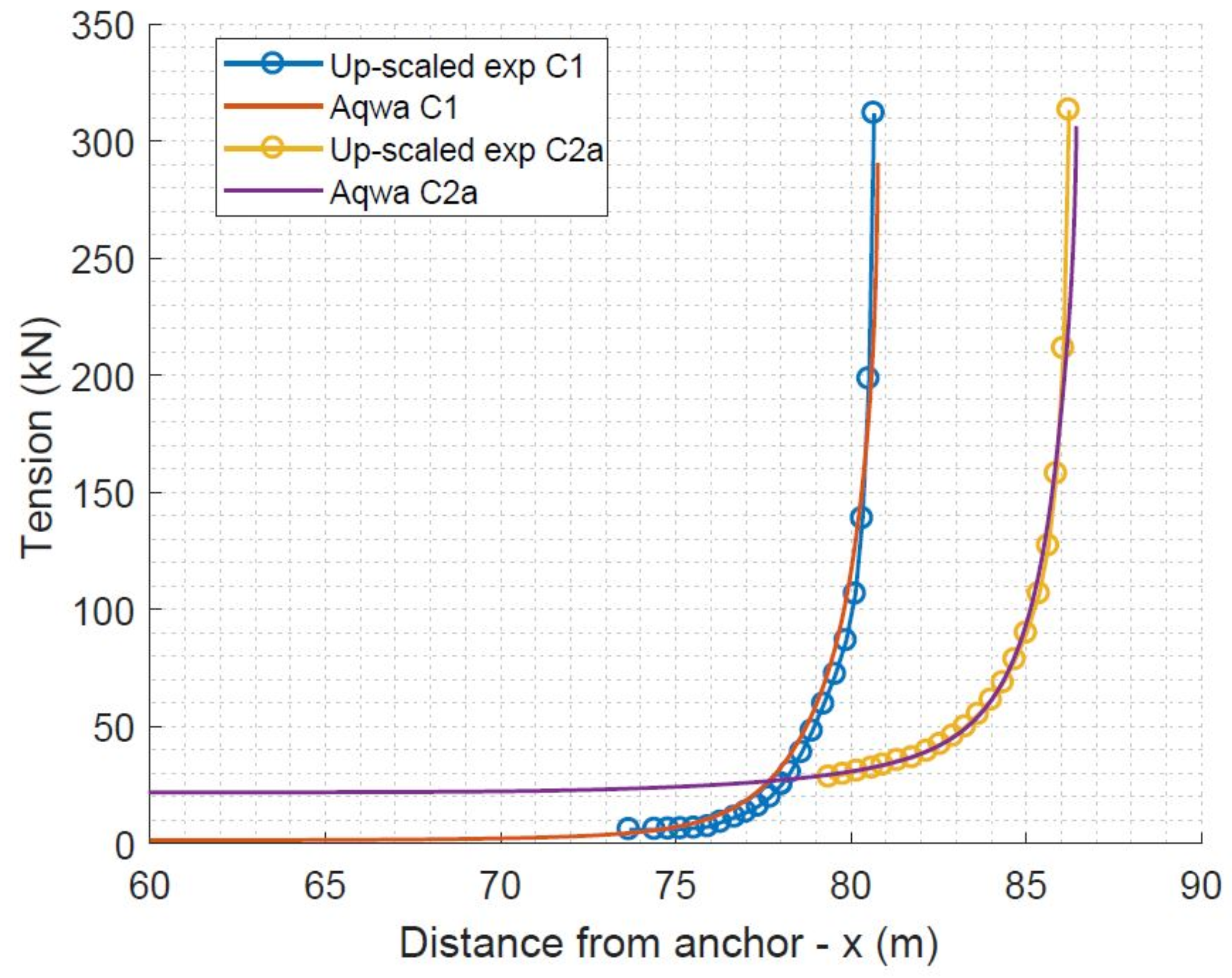
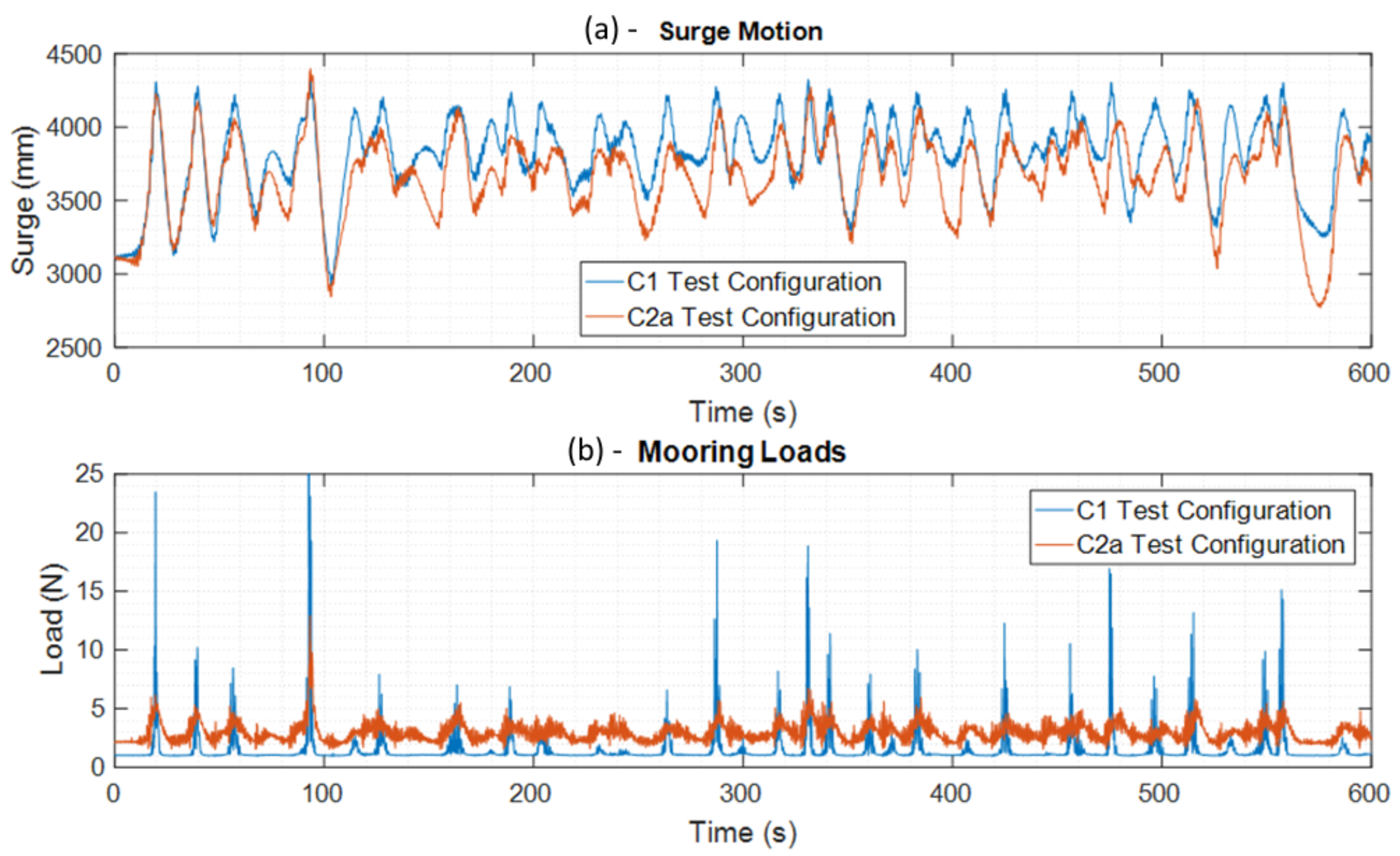

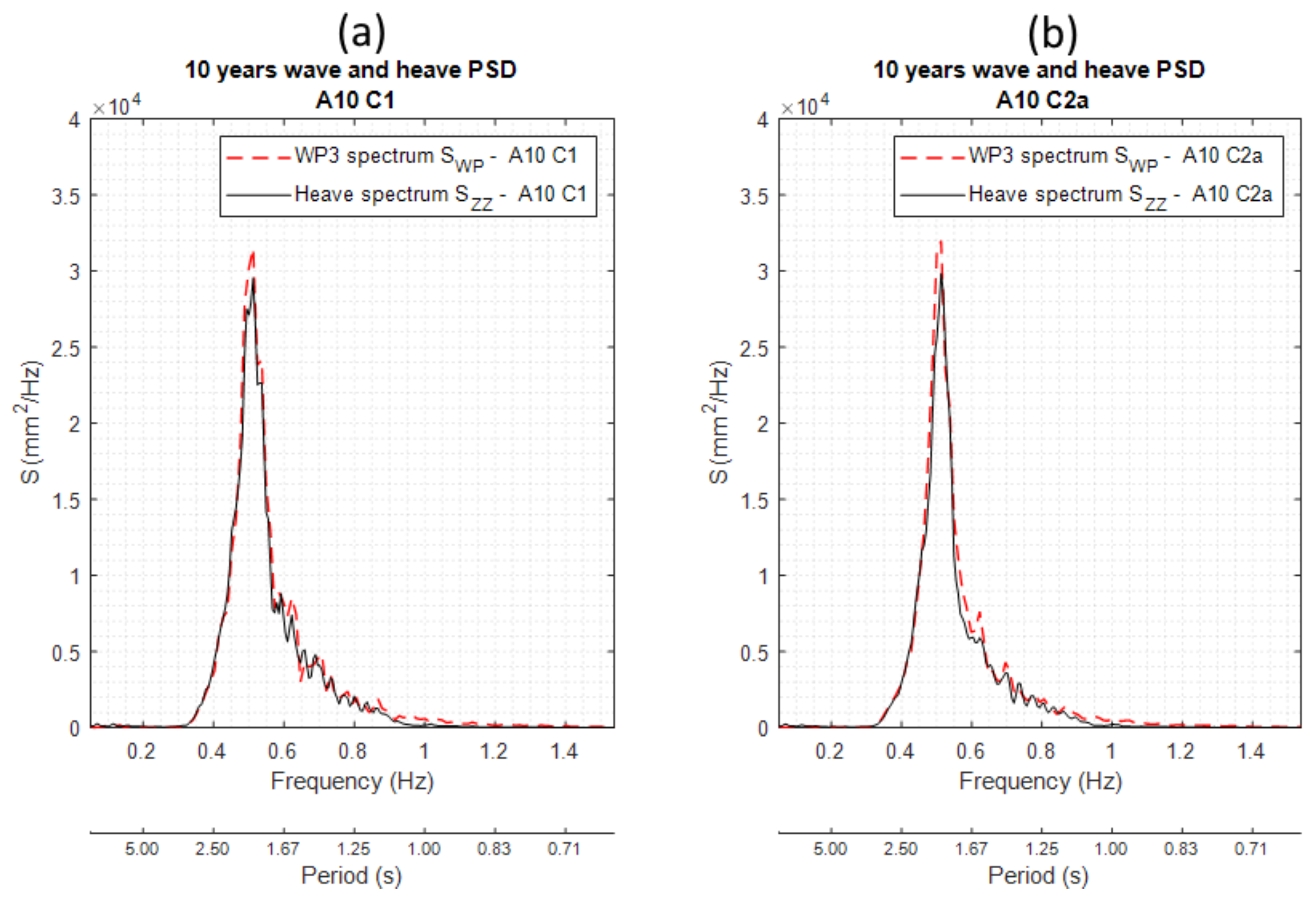

 ) and C2a (in red:
) and C2a (in red:  ) configurations.
) configurations.
 ) and C2a (in red:
) and C2a (in red:  ) configurations.
) configurations.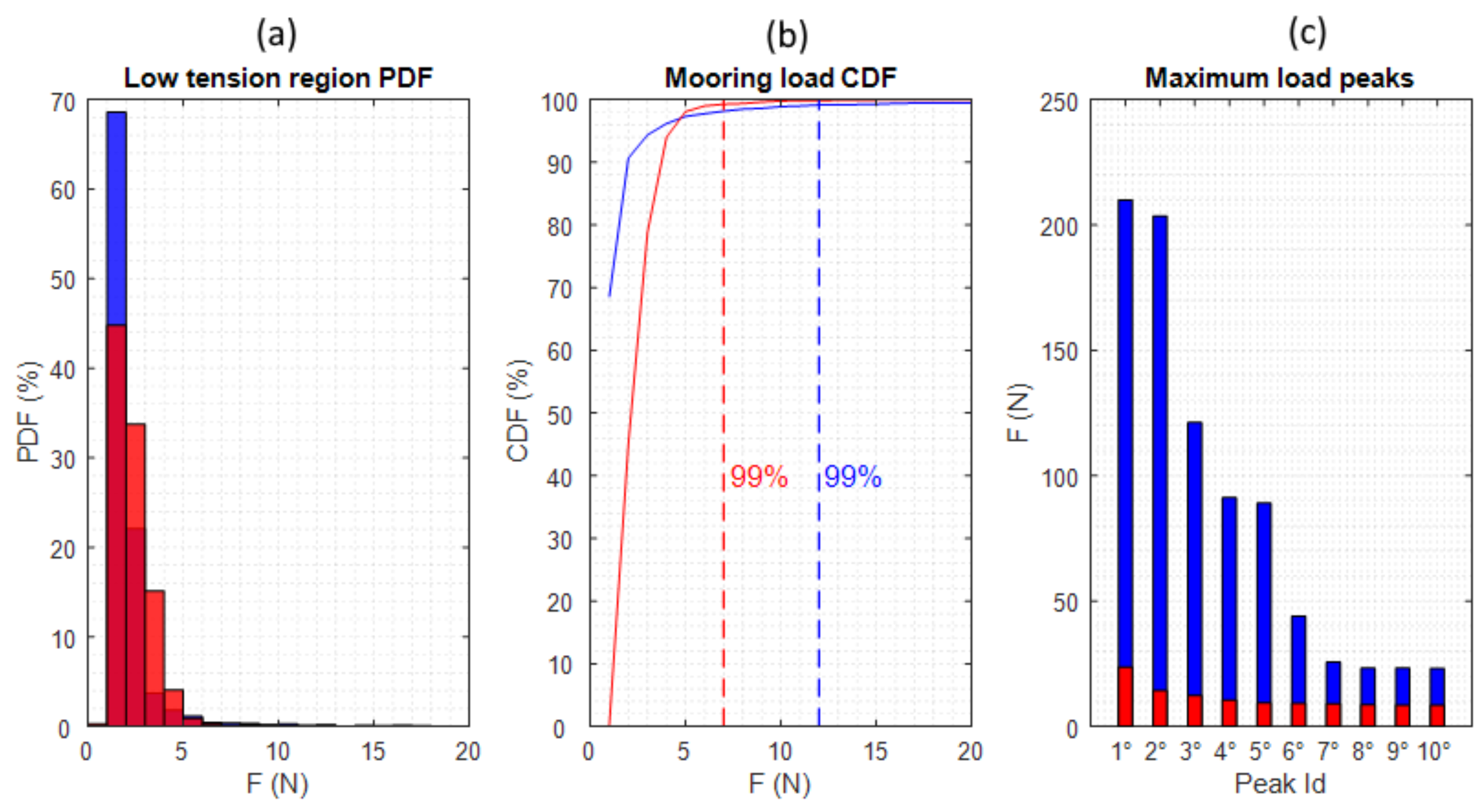

| Parameter | Symbol | Full Scale Model | Scaled Model-TARGET | Experimental Model |
|---|---|---|---|---|
| Length (m) | L | 15.3 | 0.767 | 0.767 |
| Beam (m) | B | 8 | 0.400 | 0.400 |
| Draft (m) | T | 3 | 0.150 | 0.150 |
| Height (m) | D | 4.5 | 0.225 | 0.225 |
| Mass (kg) | M | 288,090 | 35.13 | 35.16 |
| Vertical position of CoG from the bottom (m) | VCG | 2.43 | 0.122 | 0.120 |
| Roll moment of inertia (kgm) | Ixx | 1,923,000 | 0.586 | 0.775 |
| Pitch moment of inertia (kgm) | Iyy | 8,486,000 | 2.587 | 2.513 |
| Roll radi of inertia (m) | 2.584 | 0.129 | 0.149 | |
| Pitch moment of inertia (kgm) | 5.427 | 0.271 | 0.267 |
| Variable | Symbol | Unit | Model | Full-Scale |
|---|---|---|---|---|
| Damped natural period | s | 1.070 | 4.785 | |
| Angular coefficient of the regression curve | a | 1/s | 0.366 | - |
| y-axis intercept of the regression curve | b | 1/s | 0.242 | - |
| Linear extinction coefficient | 1/s | 0.242 | 0.054 | |
| Quadratic extinction coefficient | 1/rad | 0.147 | 0.147 |
| Configuration C1 | Configuration C2a | Configuration C2b | |||||
|---|---|---|---|---|---|---|---|
| Full-Scale | Model | Full-Scale | Model | Full-Scale | Model | ||
| Property | Units | Geometry | |||||
| Water depth | m | 25 | 1.25 | 25 | 1.25 | 25 | 1.25 |
| Anchors Positioning radius | m | 60 | 3 | 60 | 3 | 60 | 3 |
| L1 | m | 65 | 3.25 | 65 | 3.25 | 65 | 3.25 |
| L2 | m | 10 | 0.5 | 10 | 0.5 | 10 | 0.5 |
| L3 | m | 10 | 0.5 | 10 | 0.5 | 10 | 0.5 |
| L4 | m | - | - | 5 | 0.25 | 5 | 0.25 |
| Property | Units | Chain properties for bottom mooring lines (L1, L2, and L4) | |||||
| Nominal Diameter | mm | 60 | 3 | 60 | 3 | 60 | 3 |
| Mass per unit length | kg/m | 74.4 | 0.186 | 74.4 | 0.186 | 74.4 | 0.186 |
| Mass per unit length in water | kg/m | 68.8 | 0.172 | 68.8 | 0.172 | 68.8 | 0.172 |
| Proof Load | N | 1,940,103 | 243 | 1,940,103 | 243 | 1,940,103 | 243 |
| Breaking Load | N | 2,770,103 | 346 | 2,770,103 | 346 | 2,770,103 | 346 |
| Property | Units | Chain properties for top mooring lines (L3) | |||||
| Nominal Diameter | mm | 44 | 2.2 | 44 | 2.2 | 44 | 2.2 |
| Mass per unit length | kg/m | 36 | 0.09 | 36 | 0.09 | 36 | 0.09 |
| Mass per unit length in water | kg/m | 32 | 0.08 | 32 | 0.08 | 32 | 0.08 |
| Proof Load | N | 1,080,103 | 135 | 1,080,103 | 135 | 1,080,103 | 135 |
| Breaking Load | N | 1,540,103 | 193 | 1,540,103 | 193 | 1,540,103 | 193 |
| Property | Units | Submerged buoy and clump mass properties | |||||
| Net buoyancy | kg | 1512 | 0.189 | 3512 | 0.439 | 7042 | 0.878 |
| Clump mass | kg | - | - | 2000 | 0.25 | 4000 | 0.5 |
| Wave Name | (m) | (s) | |
|---|---|---|---|
| Operational wave | 2.20 | 5.41 | 3.3 |
| 10-year wave | 5.00 | 8.70 | 3.3 |
| 100-year wave | 5.90 | 10.30 | 3.3 |
| Configuration | |||
|---|---|---|---|
| ID | C1 | C2a | C2b |
| Pull-out test | ✓ | ✓ | ✗ |
| Wave ID | s | f (Hz) | A (mm) | C1 | C2a | C2b |
|---|---|---|---|---|---|---|
| 1a | 1/50 | 1.250 | 10.00 | ✓ | ✓ | ✗ |
| 2a | 1/50 | 1.200 | 10.80 | ✓ | ✓ | ✗ |
| 3a | 1/50 | 1.118 | 12.50 | ✓ | ✓ | ✗ |
| 4a | 1/50 | 1.052 | 14.10 | ✓ | ✓ | ✗ |
| 5a | 1/50 | 0.994 | 15.80 | ✓ | ✓ | ✗ |
| 6a | 1/50 | 0.952 | 17.20 | ✓ | ✓ | ✗ |
| 7a | 1/50 | 0.894 | 19.50 | ✓ | ✓ | ✗ |
| 8a | 1/50 | 0.745 | 28.10 | ✓ | ✓ | ✗ |
| 9a | 1/50 | 0.639 | 38.20 | ✓ | ✓ | ✗ |
| 10a | 1/50 | 0.559 | 50.00 | ✓ | ✓ | ✗ |
| 11a | 1/50 | 0.497 | 63.20 | ✓ | ✗ | ✗ |
| 12a | 1/50 | 0.447 | 78.10 | ✓ | ✗ | ✗ |
| 3b | 1/35 | 1.198 | 17.83 | ✓ | ✗ | ✗ |
| 5b | 1/35 | 0.994 | 22.57 | ✓ | ✗ | ✗ |
| 6b | 1/35 | 0.952 | 24.59 | ✓ | ✗ | ✗ |
| 7b | 1/35 | 0.894 | 27.93 | ✓ | ✗ | ✗ |
| 9b | 1/35 | 0.639 | 54.63 | ✓ | ✗ | ✗ |
| Wave ID | (s) | C1 | C2a | C2b | ||
|---|---|---|---|---|---|---|
| Irr1 | 0.11 | 1.21 | 3.3 | ✓ | ✓ | ✗ |
| Wave ID | (s) | Seed | C1 | C2a | C2b | ||
|---|---|---|---|---|---|---|---|
| A10 | 0.250 | 1.950 | 3.3 | 1 | ✓ | ✓ | ✓ |
| A101 | 0.295 | 2.303 | 3.3 | 1 | ✓ | ✓ | ✗ |
| A102 | 0.295 | 2.303 | 3.3 | 2 | ✓ | ✓ | ✗ |
| A103 | 0.295 | 2.303 | 3.3 | 3 | ✓ | ✓ | ✗ |
| Wave ID | Configuration | (m) | (s) |
|---|---|---|---|
| Operational wave | Theoretical data | 0.110 | 1.210 |
| Irr1 | C1 | 0.101 | 1.210 |
| Irr1 | C2a | 0.104 | 1.210 |
| Wave ID | Configuration | (deg) | (m) | (deg) |
|---|---|---|---|---|
| Irr1 | C1 | 8.83 | 0.22 | 1.11 |
| Irr1 | C2a | 8.63 | 0.22 | 1.44 |
| Wave ID | Configuration | (m) | (s) |
|---|---|---|---|
| 10-year wave | Theoretical data | 0.250 | 1.950 |
| A10 | C1 | 0.251 | 1.950 |
| A10 | C2a | 0.253 | 1.950 |
| A10 | C2b | 0.253 | 1.950 |
| 100-year wave | Theoretical data | 0.295 | 2.303 |
| A101 | C1 | 0.276 | 2.308 |
| A102 | C1 | 0.286 | 2.307 |
| A103 | C1 | 0.294 | 2.307 |
| A101 | C2a | 0.295 | 2.308 |
| A102 | C2a | 0.294 | 2.310 |
| A103 | C2a | 0.292 | 2.306 |
| Wave ID | Configuration | (m) | (s) |
|---|---|---|---|
| A10 | C1 | 3.050 | 82 |
| A10 | C2a | 2.570 | 34 |
| A10 | C2b | 2.460 | 32 |
| Wave ID | Configuration | (deg) | (s) |
|---|---|---|---|
| A10 | C1 | 8.30 | 1.078 |
| A10 | C2a | 8.23 | 1.085 |
| A10 | C2b | 8.09 | 1.085 |
| Wave ID | Configuration | (N) | (N) |
|---|---|---|---|
| A10 | C1 | 3.4 | 264 |
| A10 | C2a | 2.0 | 138 |
| A10 | C2b | 1.7 | 107 |
| A101 | C1 | 2.7 | 186 |
| A102 | C1 | 3.1 | 210 |
| A103 | C1 | 3.2 | 405 |
| A101 | C2a | 2.3 | 19 |
| A102 | C2a | 1.7 | 23 |
| A103 | C2a | 2.3 | 61 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirigu, S.A.; Bonfanti, M.; Begovic, E.; Bertorello, C.; Dafnakis, P.; Giorgi, G.; Bracco, G.; Mattiazzo, G. Experimental Investigation of the Mooring System of a Wave Energy Converter in Operating and Extreme Wave Conditions. J. Mar. Sci. Eng. 2020, 8, 180. https://doi.org/10.3390/jmse8030180
Sirigu SA, Bonfanti M, Begovic E, Bertorello C, Dafnakis P, Giorgi G, Bracco G, Mattiazzo G. Experimental Investigation of the Mooring System of a Wave Energy Converter in Operating and Extreme Wave Conditions. Journal of Marine Science and Engineering. 2020; 8(3):180. https://doi.org/10.3390/jmse8030180
Chicago/Turabian StyleSirigu, Sergej Antonello, Mauro Bonfanti, Ermina Begovic, Carlo Bertorello, Panagiotis Dafnakis, Giuseppe Giorgi, Giovanni Bracco, and Giuliana Mattiazzo. 2020. "Experimental Investigation of the Mooring System of a Wave Energy Converter in Operating and Extreme Wave Conditions" Journal of Marine Science and Engineering 8, no. 3: 180. https://doi.org/10.3390/jmse8030180
APA StyleSirigu, S. A., Bonfanti, M., Begovic, E., Bertorello, C., Dafnakis, P., Giorgi, G., Bracco, G., & Mattiazzo, G. (2020). Experimental Investigation of the Mooring System of a Wave Energy Converter in Operating and Extreme Wave Conditions. Journal of Marine Science and Engineering, 8(3), 180. https://doi.org/10.3390/jmse8030180












