Virtual Replica of a Towing Tank Experiment to Determine the Kelvin Half-Angle of a Ship in Restricted Water
Abstract
1. Introduction
- (1)
- Levels of inlet turbulence.
- (2)
- Wave reflections and their damping.
- (3)
- The temporal dependency of free surface flows.
2. Case Studies
3. Methodology
3.1. Numerical Aspects
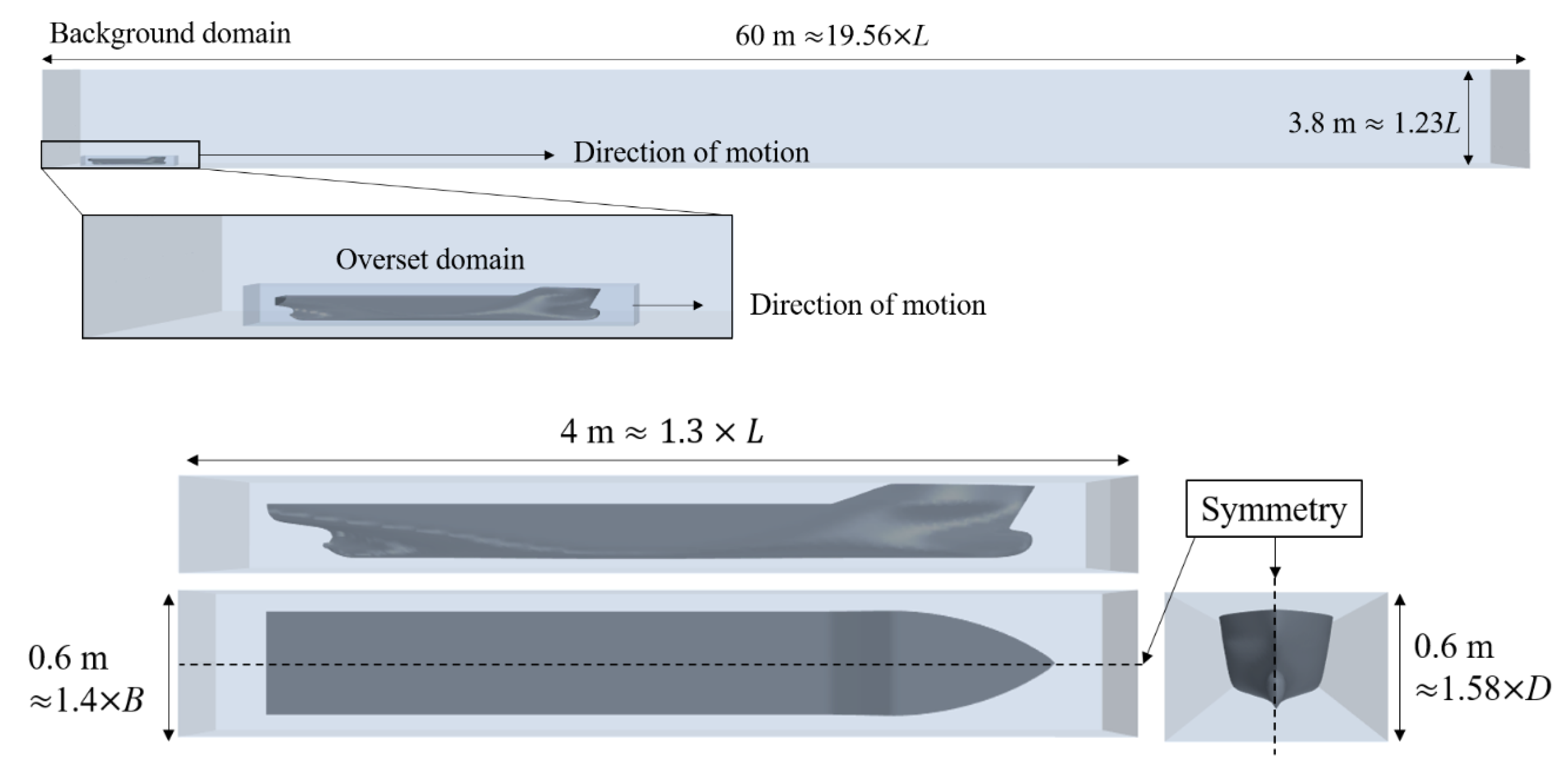
3.1.1. Computational Domain
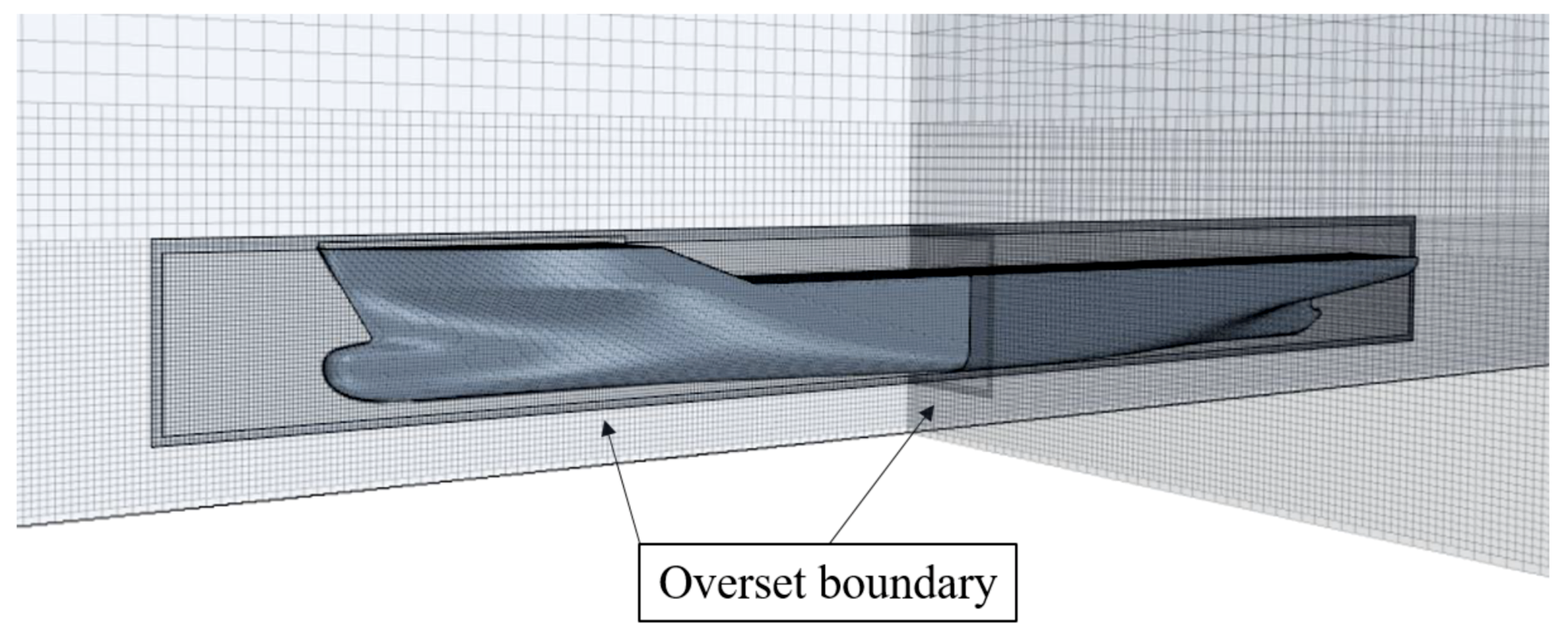
3.1.2. Computational Mesh
3.1.3. Time-Step Selection
3.1.4. Time-History of the Solution
3.1.5. Verification
- Monotonic convergence is observed if 0 < R < 1;
- Oscillatory convergence is observed if R < 0;
- Divergence is observed if R > 1.
3.2. Spectral Representation of the Wave Field
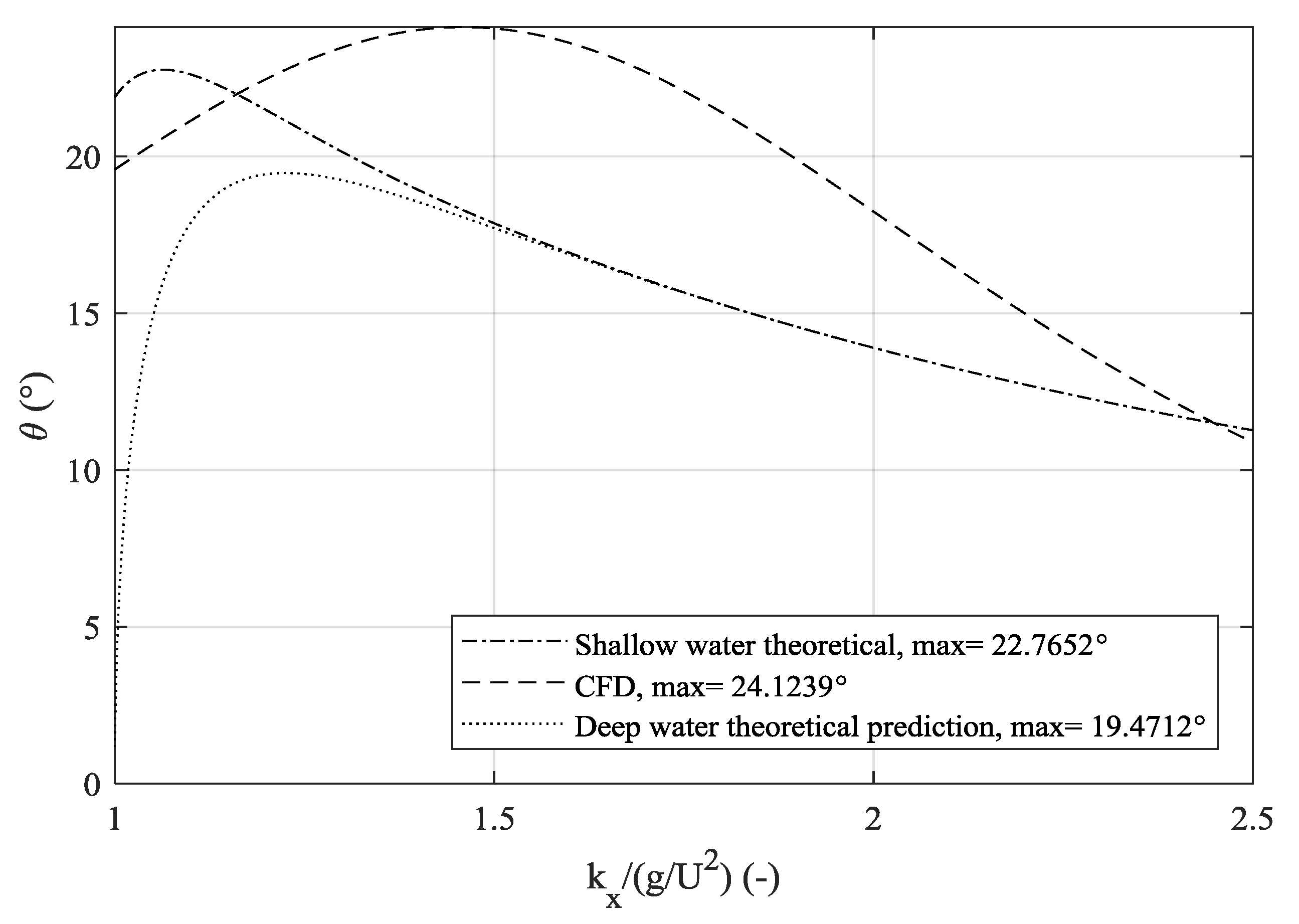
4. Results and Discussion
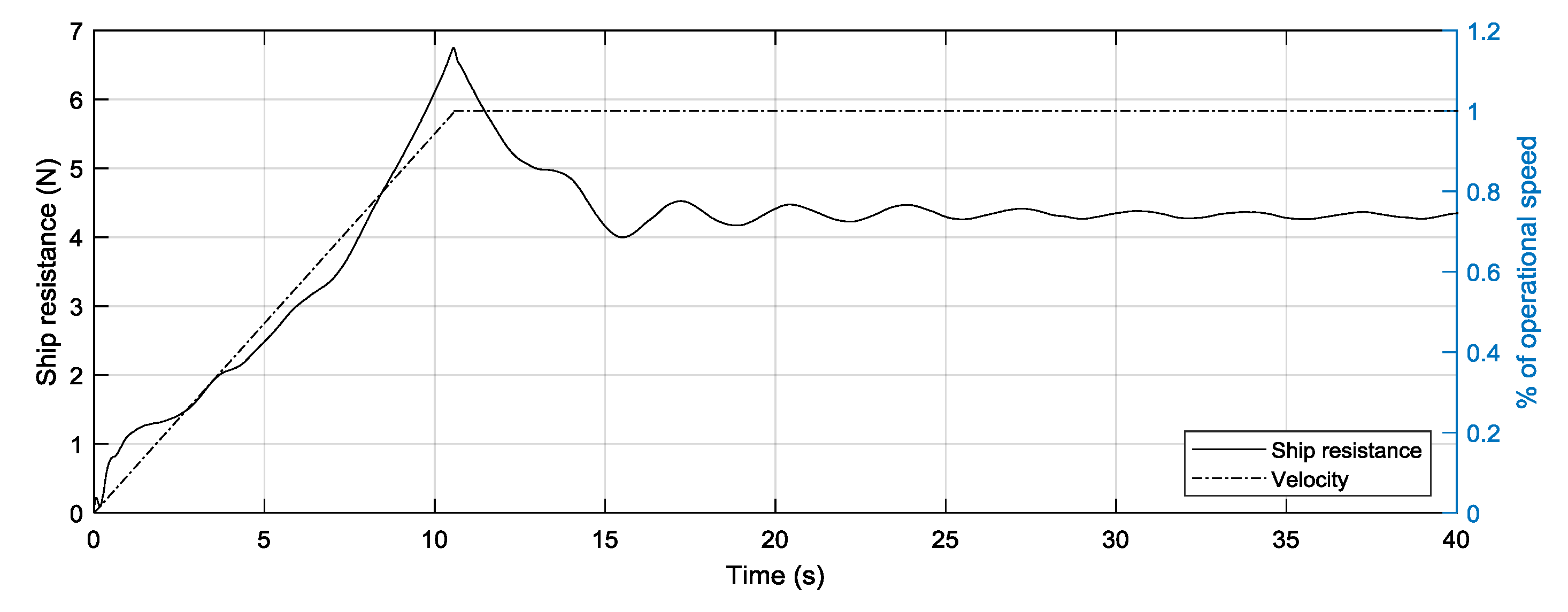
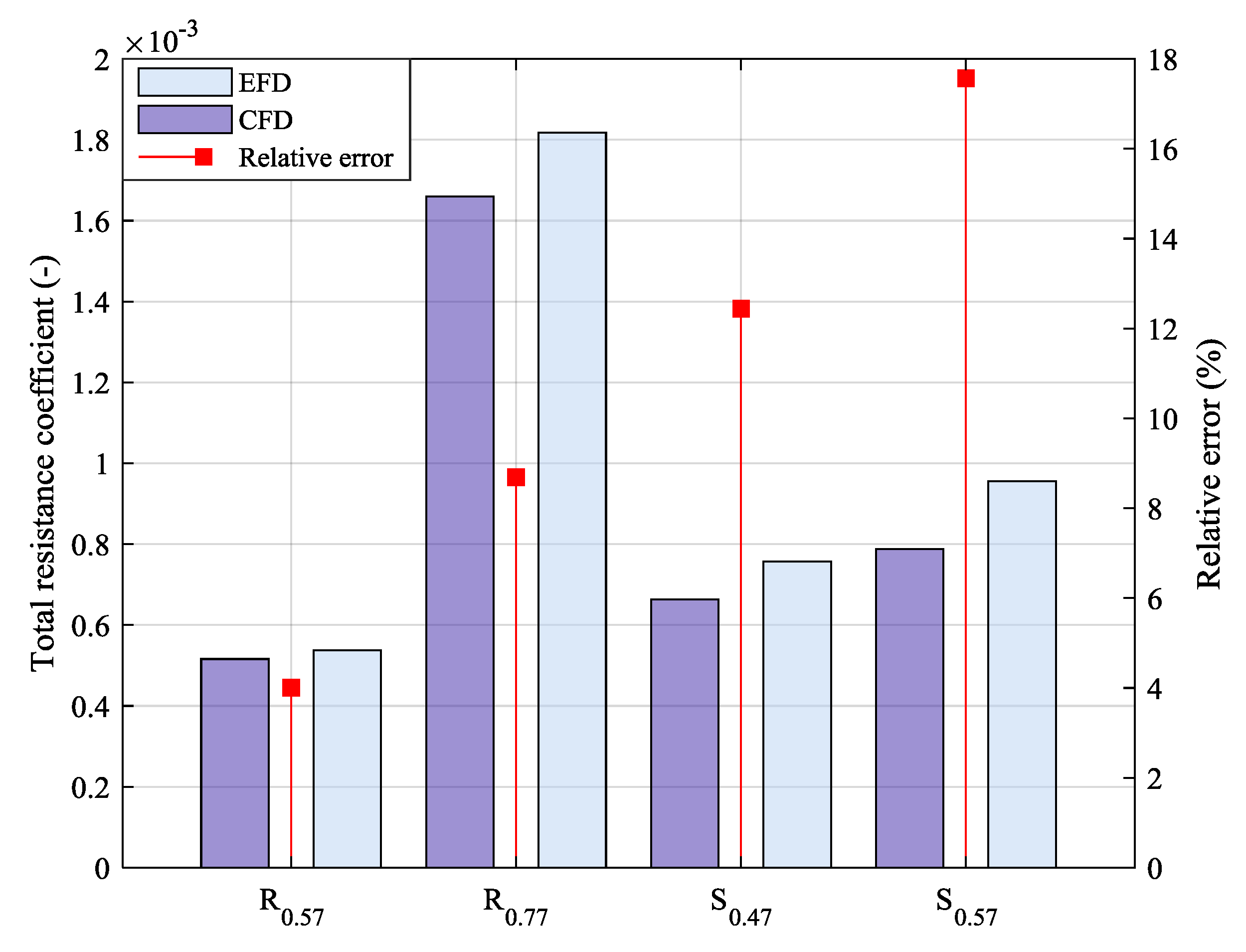
4.1. Ship Resistance
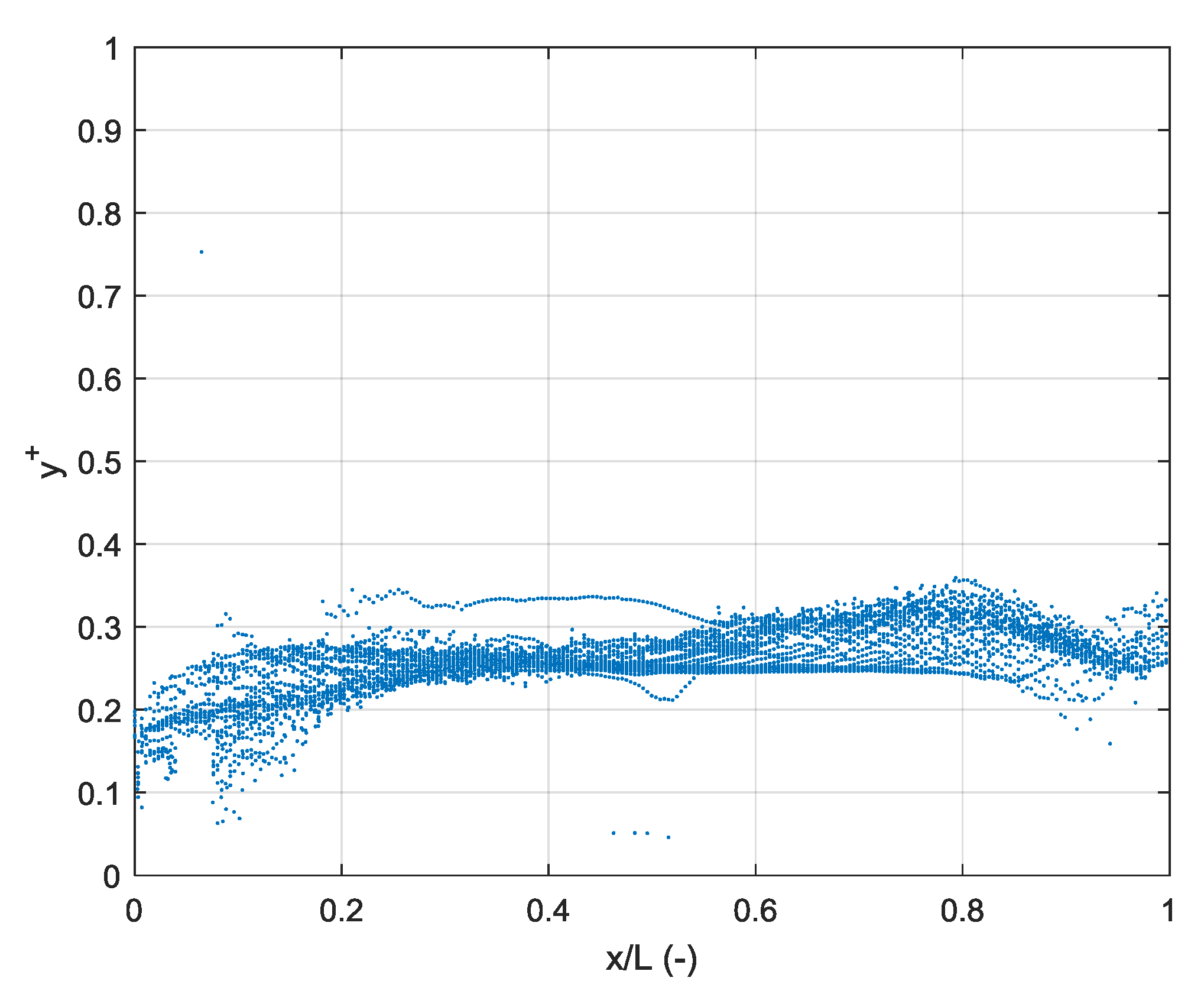
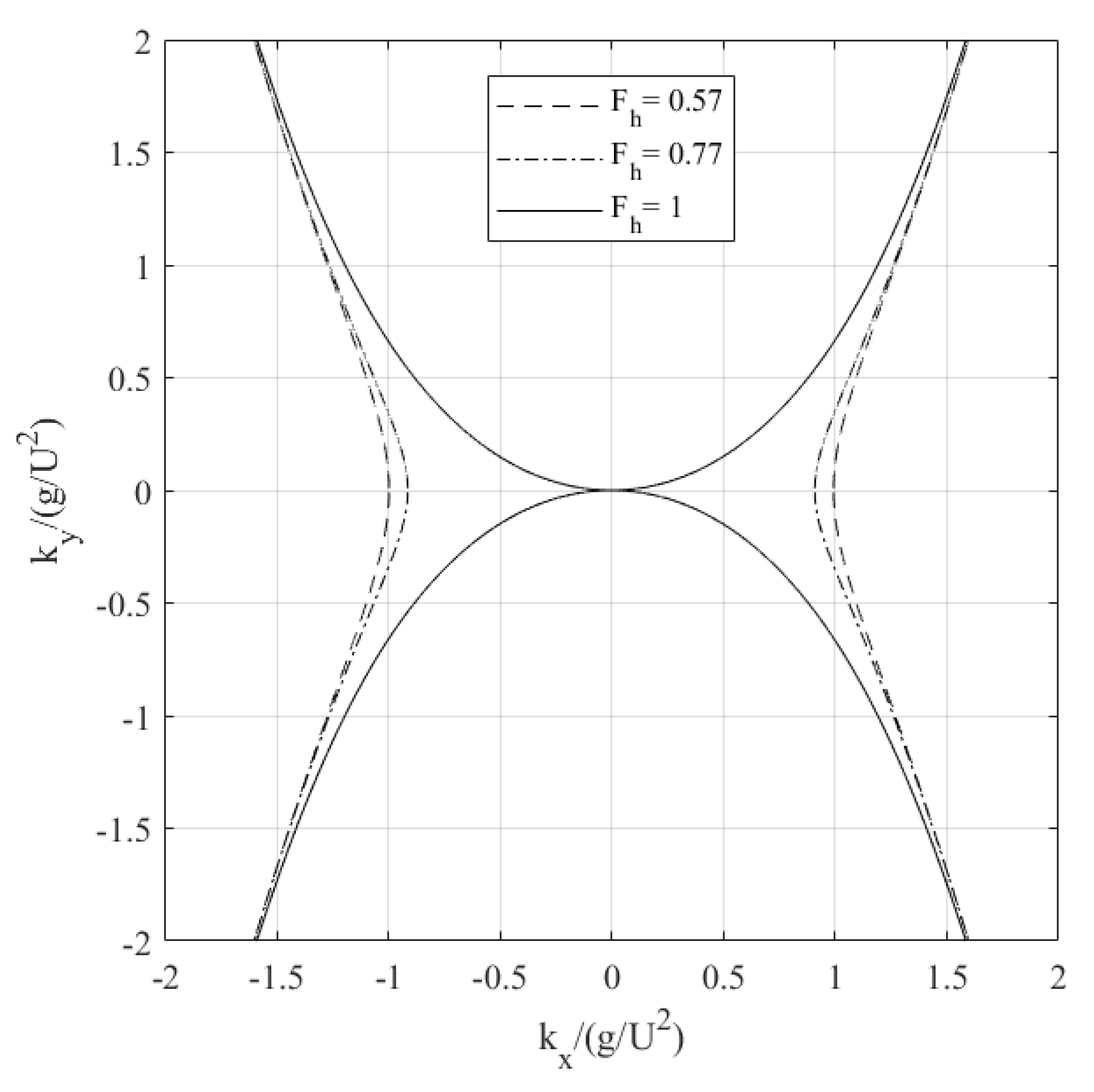
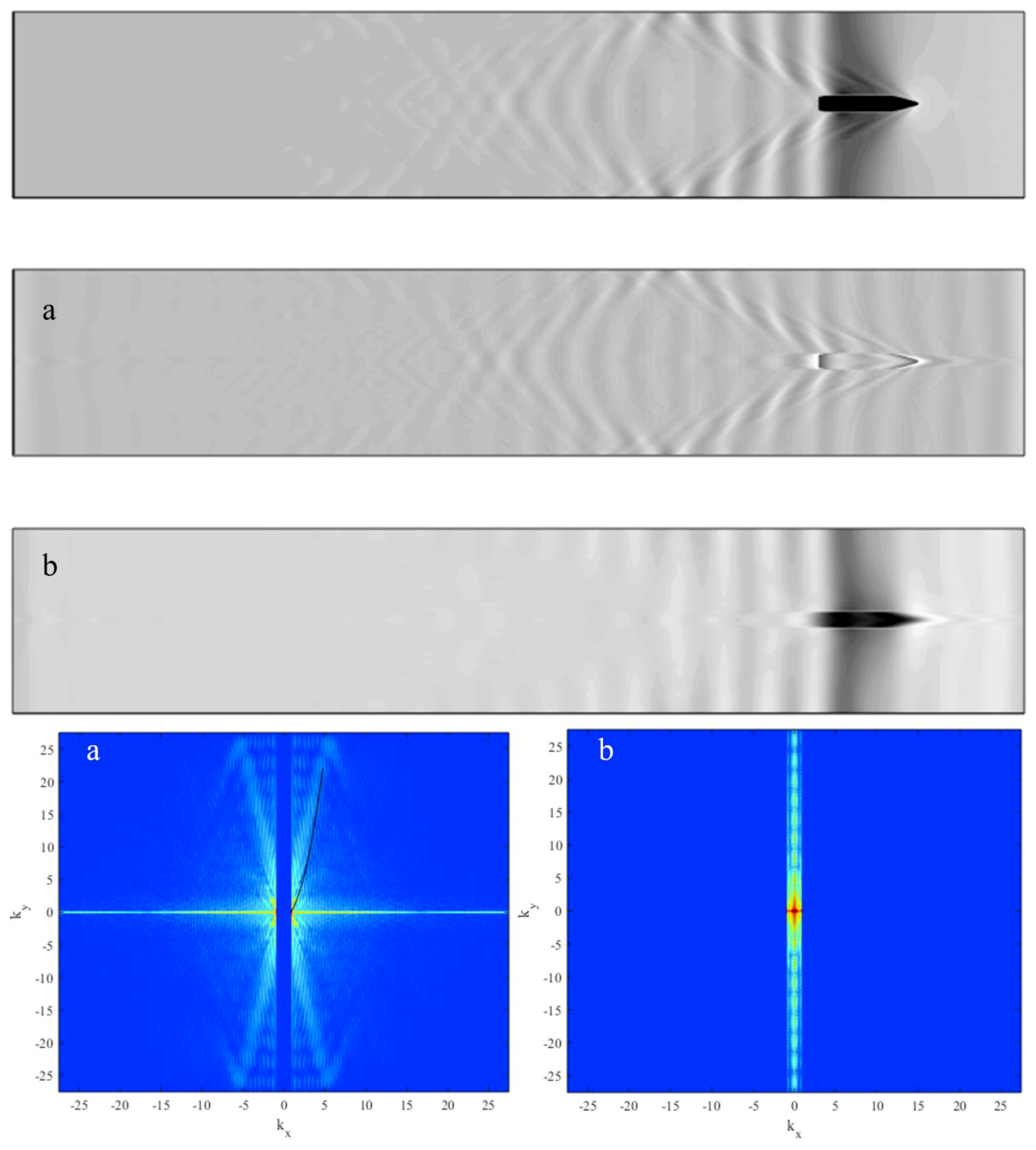
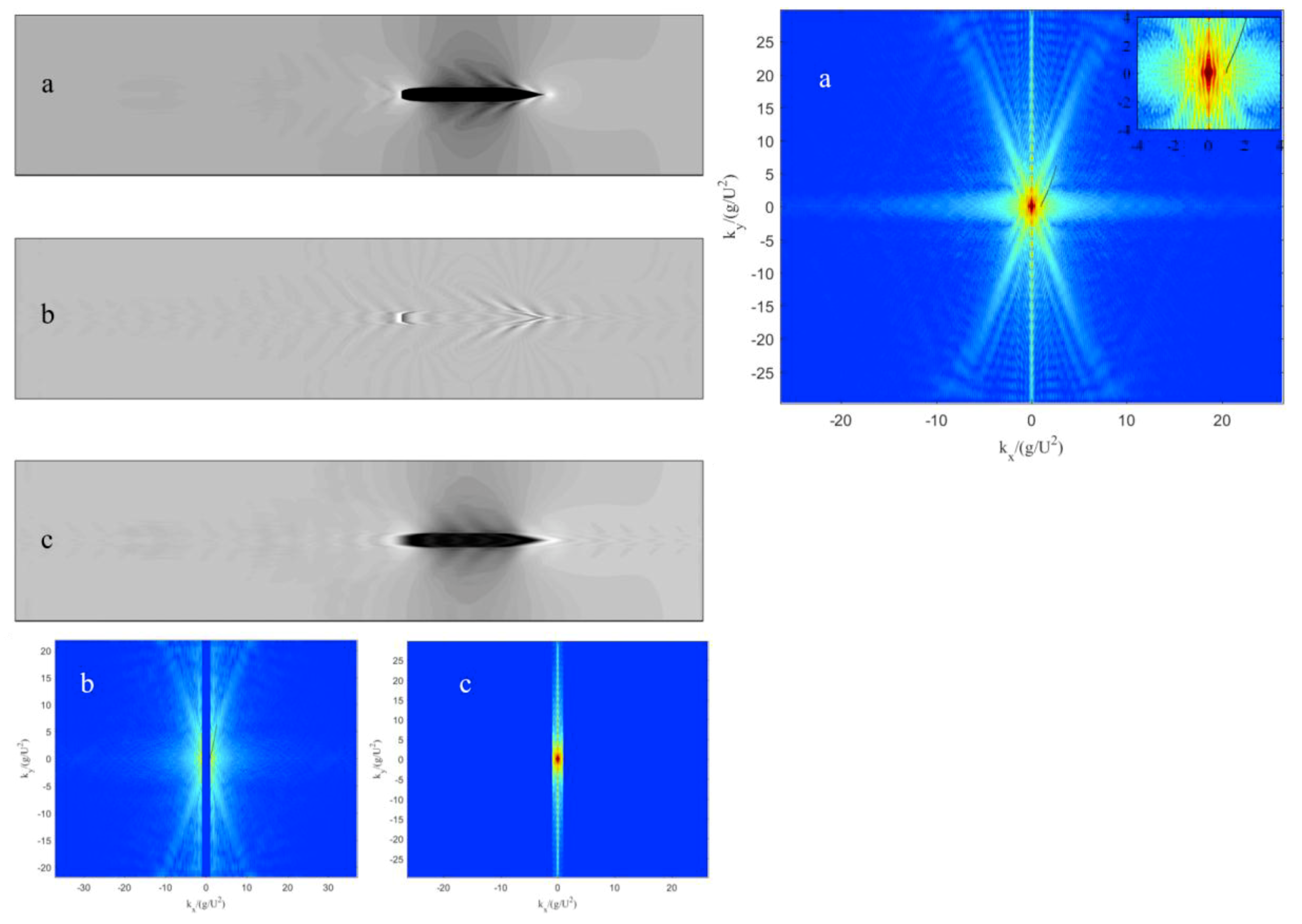
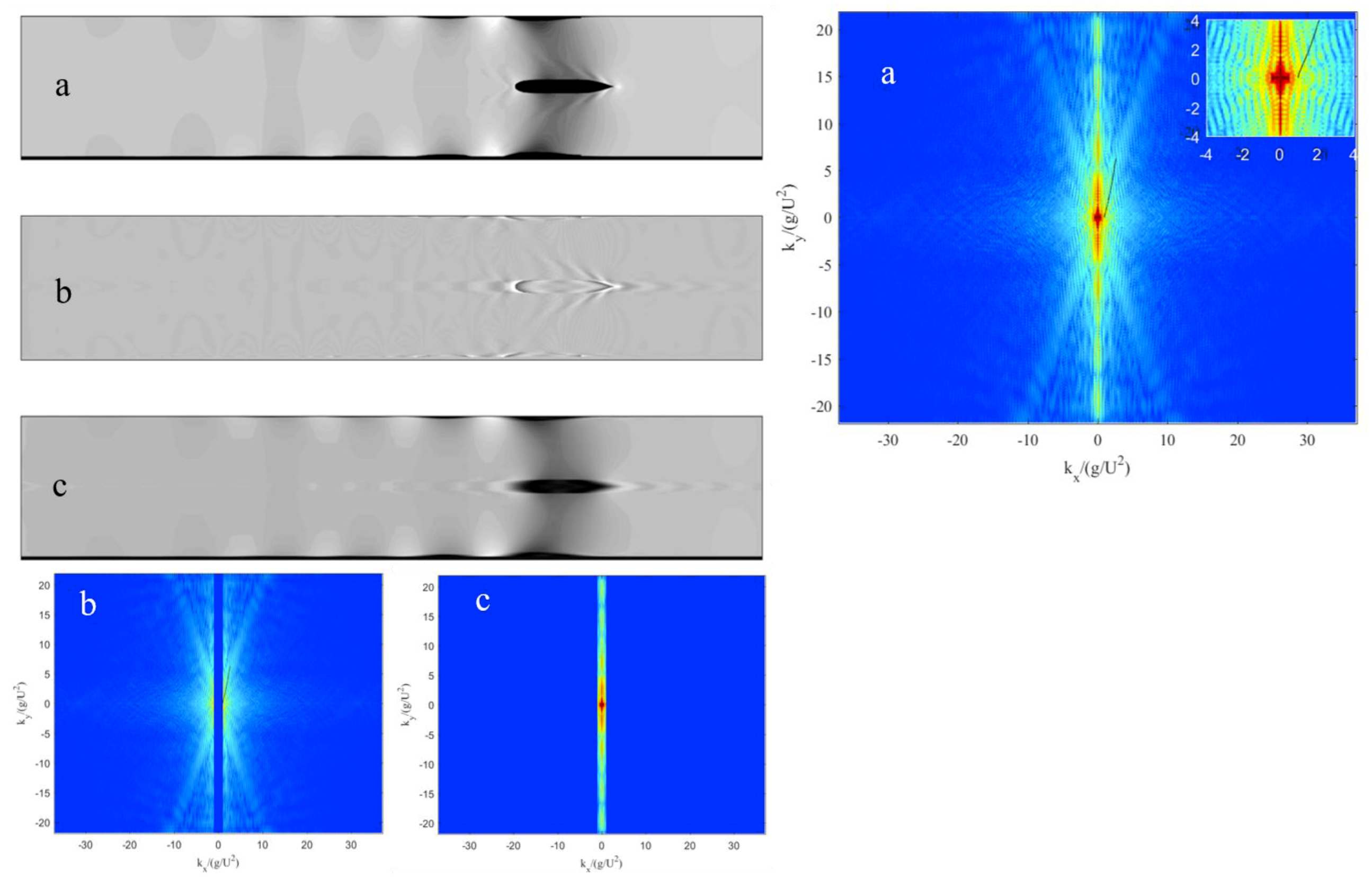
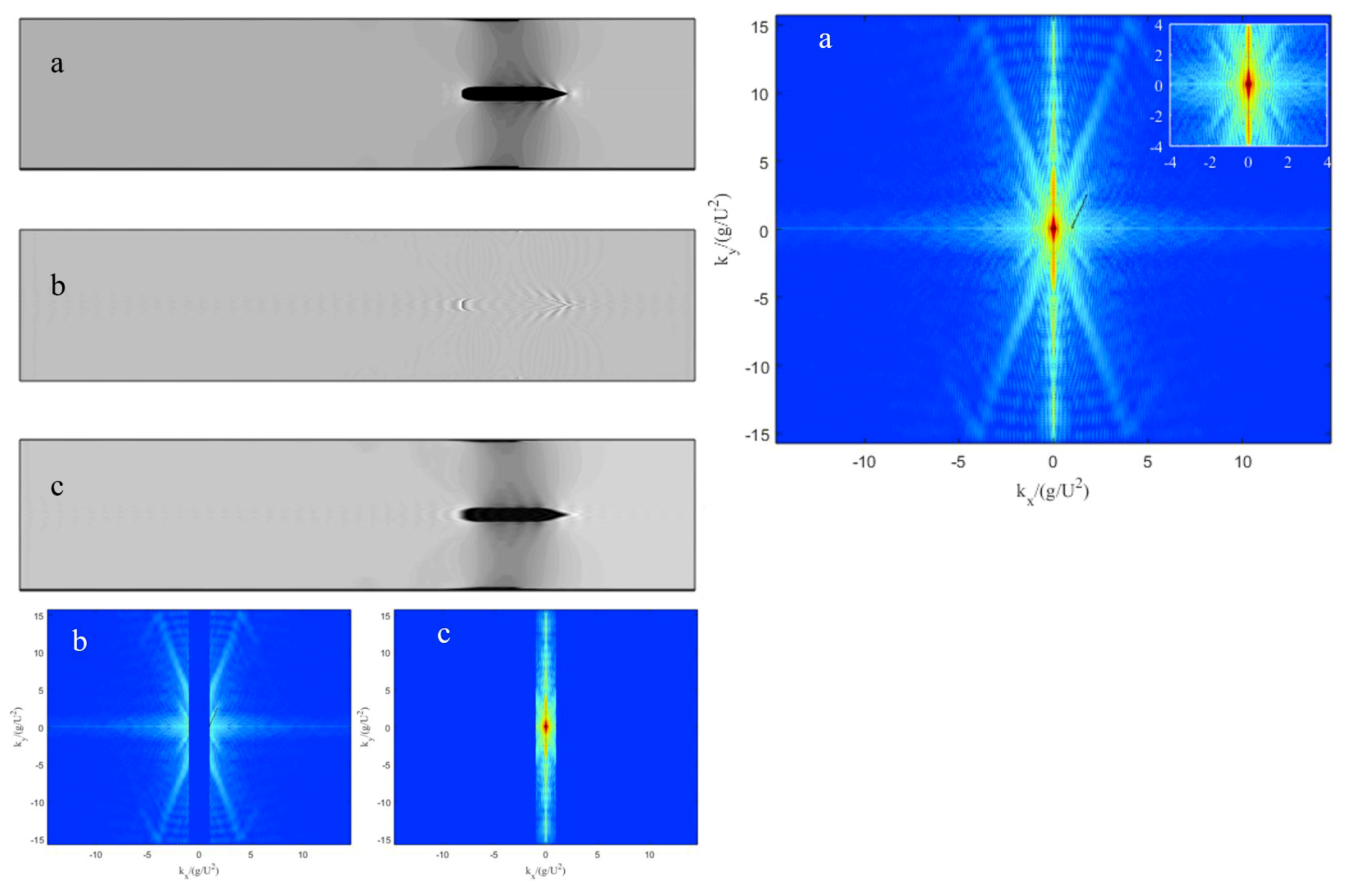
4.2. Spectral Analysis of the Numerical Free Surface
5. Summary and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bašić, J.; Degiuli, N.; Dejhalla, R. Total resistance prediction of an intact and damaged tanker with flooded tanks in calm water. Ocean Eng. 2017, 130, 83–91. [Google Scholar] [CrossRef]
- Bechthold, J.; Kastens, M. Robustness and quality of squat predictions in extreme shallow water conditions based on RANS-calculations. Ocean Eng. 2020, 197, 106780. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. Assessment of hydrodynamic characteristics of a full-scale ship at different draughts. Ocean Eng. 2018, 156, 135–152. [Google Scholar] [CrossRef]
- Larsson, L.; Stern, F.; Visonneau, M. Numerical Ship Hydrodynamics: An Assessment of the Gothenburg 2010 Workshop; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Razgallah, I.; Kaidi, S.; Smaoui, H.; Sergent, P. The impact of free surface modelling on hydrodynamic forces for ship navigating in inland waterways: Water depth, drift angle, and ship speed effect. J. Mar. Sci. Technol. 2018, 1–22. [Google Scholar] [CrossRef]
- Simonsen, C.D.; Otzen, J.F.; Joncquez, S.; Stern, F. EFD and CFD for KCS heaving and pitching in regular head waves. J. Mar. Sci. Technol. 2013, 18, 435–459. [Google Scholar] [CrossRef]
- Toxopeus, S.L. Viscous-flow calculations for KVLCC2 in deep and shallow water. Comput. Methods Appl. Sci. 2013, 29, 151–169. [Google Scholar] [CrossRef]
- Longo, J.; Stern, F. Effects of drift angle on model ship flow. Exp. Fluids 2002, 32, 558–569. [Google Scholar] [CrossRef]
- Tahara, Y.; Longo, J.; Stern, F. Comparison of CFD and EFD for the Series 60 C B = 0.6 in steady drift motion. J. Mar. Sci. Technol. 2002, 7, 17–30. [Google Scholar] [CrossRef]
- Kundu, P.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics; Elsevier: Cambridge, MA, USA, 2012. [Google Scholar]
- Wang, Z.Z.; Xiong, Y.; Shi, L.P.; Liu, Z.H. A numerical flat plate friction line and its application. J. Hydrodyn. 2015, 27, 383–393. [Google Scholar] [CrossRef]
- Lopes, R.; Eca, L.; Vaz, G. On the Numerical Behavior of Rans-based Transition Models. J. Fluids Eng. 2019, 142, 1–14. [Google Scholar] [CrossRef]
- Lopes, R.; Eca, L.; Vaz, G. On the Decay of Free-stream Turbulence Predicted by Two-Equation Eddy-Viscosity Models; NuTTS-2017: Wageningen, The Netherlands, 2017; pp. 1–6. [Google Scholar]
- Wackers, J.; Koren, B.; Raven, H.C.; van der Ploeg, A.; Starke, A.R.; Deng, G.B.; Queutey, P.; Visonneau, M.; Hino, T.; Ohashi, K. Free-Surface Viscous Flow Solution Methods for Ship Hydrodynamics. Arch. Comput. Methods Eng. 2011, 18, 1–41. [Google Scholar] [CrossRef]
- Perić, R.; Abdel-Maksoud, M. Reliable damping of free-surface waves in numerical simulations. Ship Technol. Res. 2016, 63, 1–13. [Google Scholar] [CrossRef]
- Durbin, P.A.; Pettersson Reif, B.A. Statistical Theory and Modelling for Turbulent Flow, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Havelock, T. The Propagation of Groups of Waves in Dispersive Media, with Aplication to Waves on Water produced by a Travelling Disturbance. Proc. R. Soc. London. Ser. A, Math. Phys. Sci. 1933, 140, 359–377. [Google Scholar] [CrossRef]
- Sorensen, R.M. Prediction of Vessel-Generated Waves with Reference to Vessels Common to the Upper Mississippi River System, US Army Corps of Engineers, Waterways Experiment Station, ENV Report 4; 1997. Available online: https://pdfs.semanticscholar.org/6ea7/49e2817a7e9d262e30ba3b5d07a9554a7f1b.pdf (accessed on 3 March 2020).
- Soomere, T. Nonlinear components of ship wake waves. Appl. Mech. Rev. 2007, 60, 120–138. [Google Scholar] [CrossRef]
- Caplier, C.; Rousseaux, G.; Calluaud, D.; David, L. Energy distribution in shallow water ship wakes from a spectral analysis of the wave field. Phys. Fluids 2016, 28, 107104. [Google Scholar] [CrossRef]
- Fourdrinoy, J.; Caplier, C.; Devaux, Y.; Rousseaux, G.; Isae, C.U.D.P.; Jouteur, I.; Poitiers, U.; De France, F.; Martin, P.; Montpellier, U.; et al. The naval battle of actium and the myth of the ship-holder: The effect of bathymetry. arXiv 2019, arXiv:1905.13024. [Google Scholar]
- Gomit, G.; Rousseaux, G.; Chatellier, L.; Calluaud, D.; David, L. Spectral analysis of ship waves in deep water from accurate measurements of the free surface elevation by optical methods. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Elsherbiny, K.; Tezdogan, T.; Kotb, M.; Incecik, A.; Day, S. Experimental analysis of the squat of ships advancing through the New Suez Canal. Ocean Eng. 2019, 178, 331–344. [Google Scholar] [CrossRef]
- Tunaley, J.K.E. Ship Wakes in Shallow Waters; LRDC Report: Pittsburgh, PA, USA, 2014; pp. 6–9. [Google Scholar]
- Yang, R.; Shugan, I.V.; Fang, M. Kelvin ship wake in the wind and waves field and on the finite sea depth. Environment 2011, 27, 71–77. [Google Scholar] [CrossRef]
- Suez Canal Authority. Suez Canal Rules of Navigation. 2019. Available online: https://www.suezcanal.gov.eg/English/Navigation/Pages/RulesOfNavigation.aspx (accessed on 6 January 2020).
- Lee, B.W.; Lee, C. Equation for ship wave crests in the entire range of water depths. Coast. Eng. 2019, 153, 103542. [Google Scholar] [CrossRef]
- Siemens. Star-CCM+ User Guide Version 13.04; Siemens: Munich, Germany, 2018. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Terziev, M.; Tezdogan, T.; Incecik, A. Application of eddy-viscosity turbulence models to problems in ship hydrodynamics. Ships Offshore Struct. 2019. [Google Scholar] [CrossRef]
- Pettersson Reif, B.A.; Mortensen, M.; Langer, C.A. Towards sensitizing the nonlinear v 2-f model to turbulence structures. Flow Turbul. Combust. 2009, 83, 185–203. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Muzaferija, S.; Peric, M. Computation of free-surface ows using interface- tracking and interface-capturing methods. In Chapter 2, Nonlinear Water Wave Interaction, Computational Mechanics Publications; Mahrenholtz, O., Markiewicz, M., Eds.; WIT Press: Southampton, UK, 1999. [Google Scholar]
- Elsherbiny, K.; Terziev, M.; Tezdogan, T.; Incecik, A.; Kotb, M. Numerical and experimental study on hydrodynamic performance of ships advancing through different canals. Ocean Eng. 2019, 106696. [Google Scholar] [CrossRef]
- International Towing Tank Conference. ITTC–Recommended Procedures and Guidelines-Practical guidelines for ship CFD Applications, 7.5-03-02-03 (Revision 01), ITTC–Recomm. Proced. Guidel. 19; ITTC: Zürich, Switzerland, 2014. [Google Scholar]
- Oberkampf, W.L.; Blottner, F.G. Issues in computational fluid dynamics code verification and validation. AIAA J. 1998, 36, 687–695. [Google Scholar] [CrossRef]
- Yuan, Z.M. Ship Hydrodynamics in Confined Waterways. J. Sh. Res. 2019, 63, 1–14. [Google Scholar] [CrossRef]
- Yuan, Z.M.; Zhang, X.; Ji, C.Y.; Jia, L.; Wang, H.; Incecik, A. Side wall effects on ship model testing in a towing tank. Ocean Eng. 2018, 147, 447–457. [Google Scholar] [CrossRef]
- International Towing Tank Conference. ITTC–Recommended Procedures and Guidelines Uncertainty Analysis, Example for Resistance Test; ITTC: Zürich, Switzerland, 2002. [Google Scholar]
- Roy, C.J. Review of code and solution verification procedures for computational simulation. J. Comput. Phys. 1997, 205, 131–156. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.; Shao, J. Quantitative V&V of CFD simulations and certification of CFD codes. Int. J. Numer. Methods Fluids 2006, 50, 1335–1355. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Eca, L.; Hoekstra, M. Evaluation of numerical error estimation based on grid refinement studies with the method of the manufactured solutions. Comput. Fluids 2009, 38, 1580–1591. [Google Scholar] [CrossRef]
- Arnold-Bos, A.; Martin, A.; Khenchaf, A. Obtaining a ship’s speed and direction from its Kelvin wake spectrum using stochastic matched filtering. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 23–27 July 2007; pp. 1106–1109. [Google Scholar]
- Wu, Z. On the Estimation of a Moving Ship’s Velocity and Hull Geometry Information from its Wave Spectra. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1992. [Google Scholar]
- Lighthill, M.J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Carusotto, I.; Rousseaux, G. The Cerenkov Effect Revisited: From Swimming Ducks to Zero Modes in Gravitational Analogues In Analogue Gravity Phenomenology; Springer: Berlin/Heidelberg, Germany, 2013; pp. 109–144. [Google Scholar]
- Crapper, G.D. Surface waves generated by a travelling pressure point. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1964, 282, 547–558. [Google Scholar] [CrossRef]
- Nakos, D.E.; Sclavounos, P.D. On steady and unsteady ship wave patterns. J. Fluid Mech. 1990, 215, 263. [Google Scholar] [CrossRef]
- Tuck, E.O. Sinkage and Trim in Shallow Water of Finite Width. Schiffstechnik 1967, 14, 92–94. [Google Scholar]
- Tuck, E.O. Shallow-Water Flows Past Slender Bodies. J. Fluid Mech. 1966, 26, 81–95. [Google Scholar] [CrossRef]
- Jachowski, J. Assessment of ship squat in shallow water using CFD. Arch. Civ. Mech. Eng. 2008, 8, 27–36. [Google Scholar] [CrossRef]
- Pena, B.; Muk-Pavic, E.; Ponkratov, D. Achieving a high accuracy numerical simulations of the flow around a full scale ship. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE, Scotland, UK, 9–14 June 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley-Interscience: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ma, C.; Zhu, Y.; He, J.; Zhang, C.; Wan, D.; Yang, C.; Noblesse, F. Nonlinear corrections of linear potential-flow theory of ship waves. Eur. J. Mech. B/Fluids 2018, 67, 1–14. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, R.; Ma, C.; Fan, J. Computations of linear and nonlinear ship waves by higher-order boundary element method. Ocean Eng. 2016, 114, 142–153. [Google Scholar] [CrossRef]
- Wu, H.; Wu, J.; He, J.; Zhu, R.; Yang, C.J.; Noblesse, F. Wave profile along a ship hull, short farfield waves, and broad inner Kelvin wake sans divergent waves. Phys. Fluids 2019, 31. [Google Scholar] [CrossRef]
- Noblesse, F.; He, J.; Zhu, Y.; Hong, L.; Zhang, C.; Zhu, R. Why can ship wakes appear narrower than Kelvin’s angle? Eur. J. Mech. -B/Fluids 2014, 46, 164–171. [Google Scholar] [CrossRef]
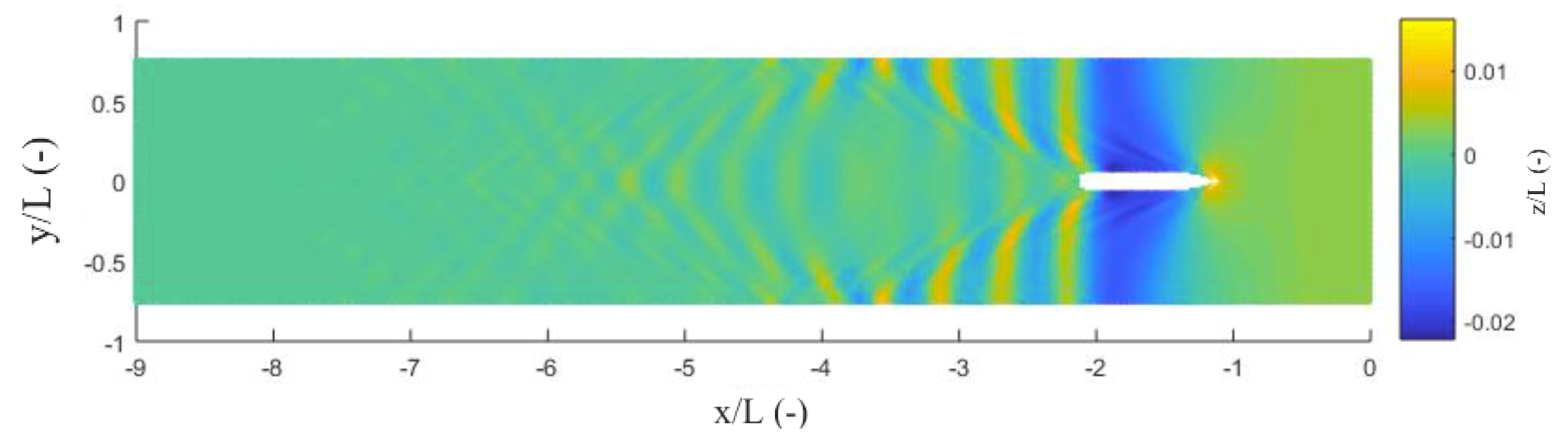
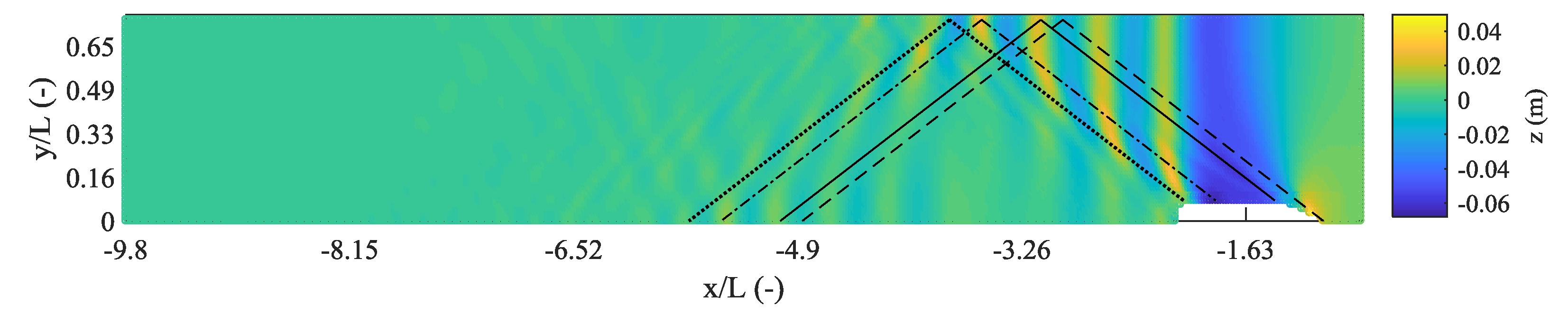
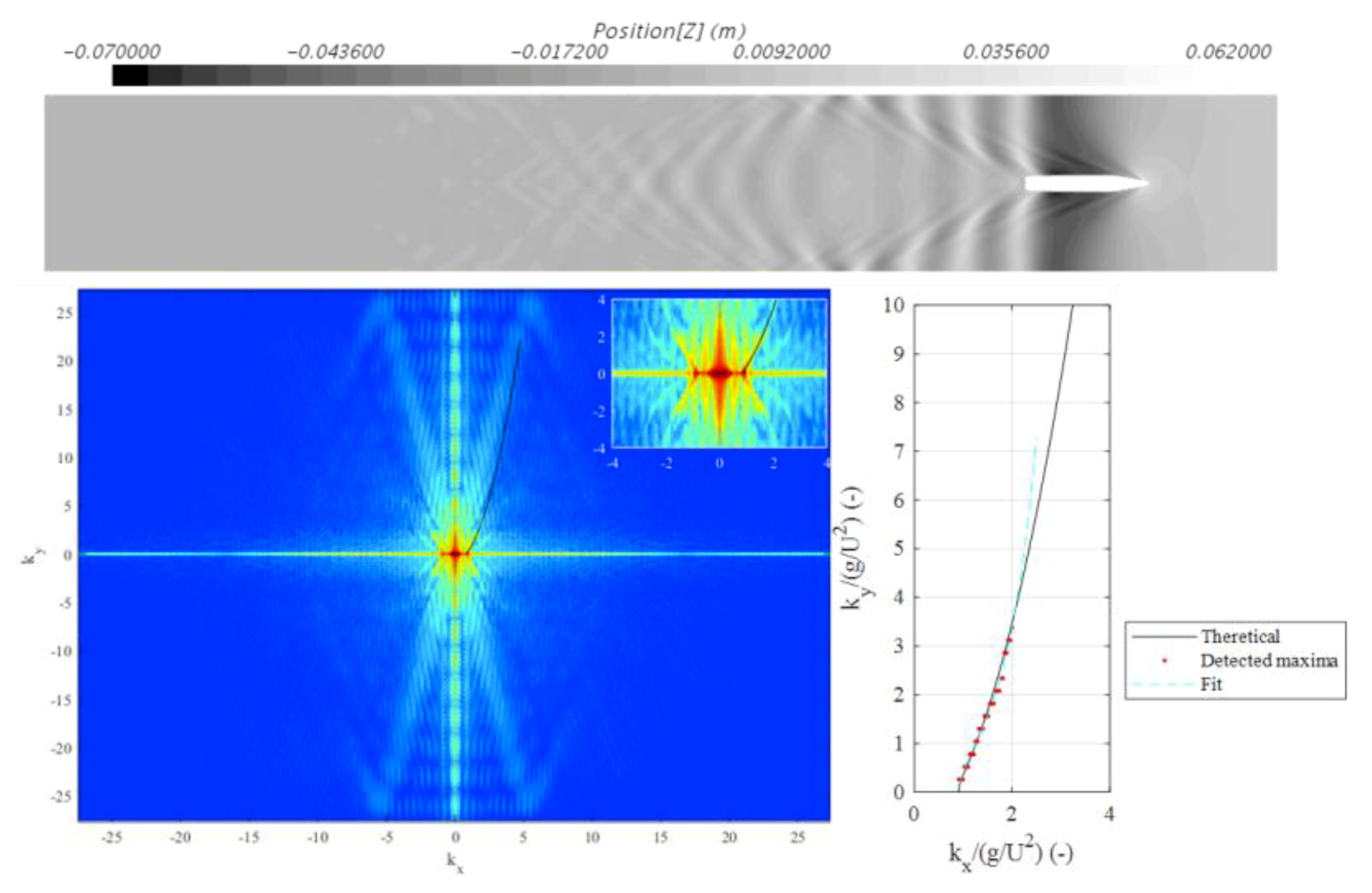
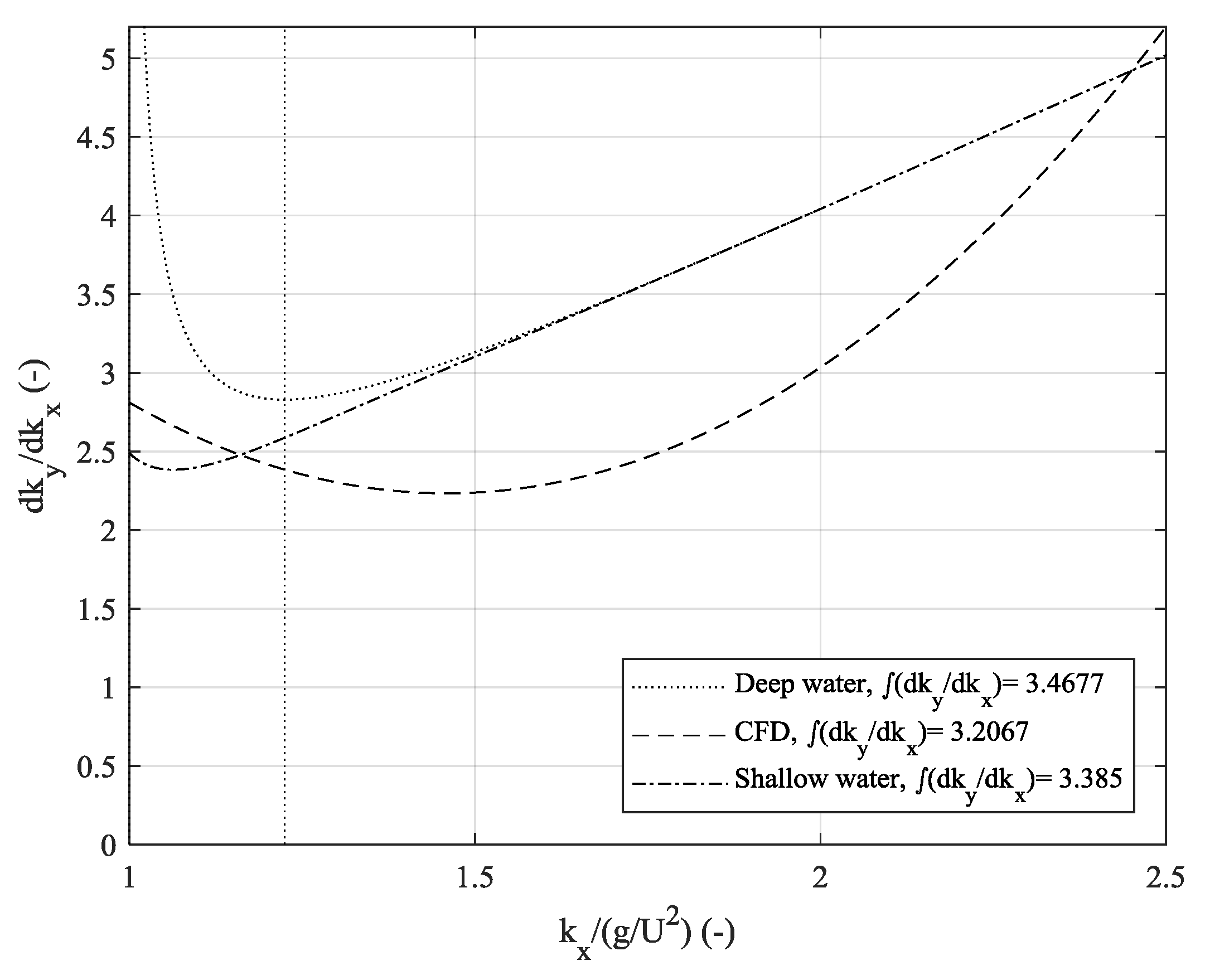
| Quantity | Symbol | Value | Unit |
|---|---|---|---|
| Scale Factor | λ | 75 | - |
| Length | L | 3.067 | m |
| Beam | B | 0.429 | m |
| Draught | T | 0.144 | m |
| Depth | D | 0.253 | m |
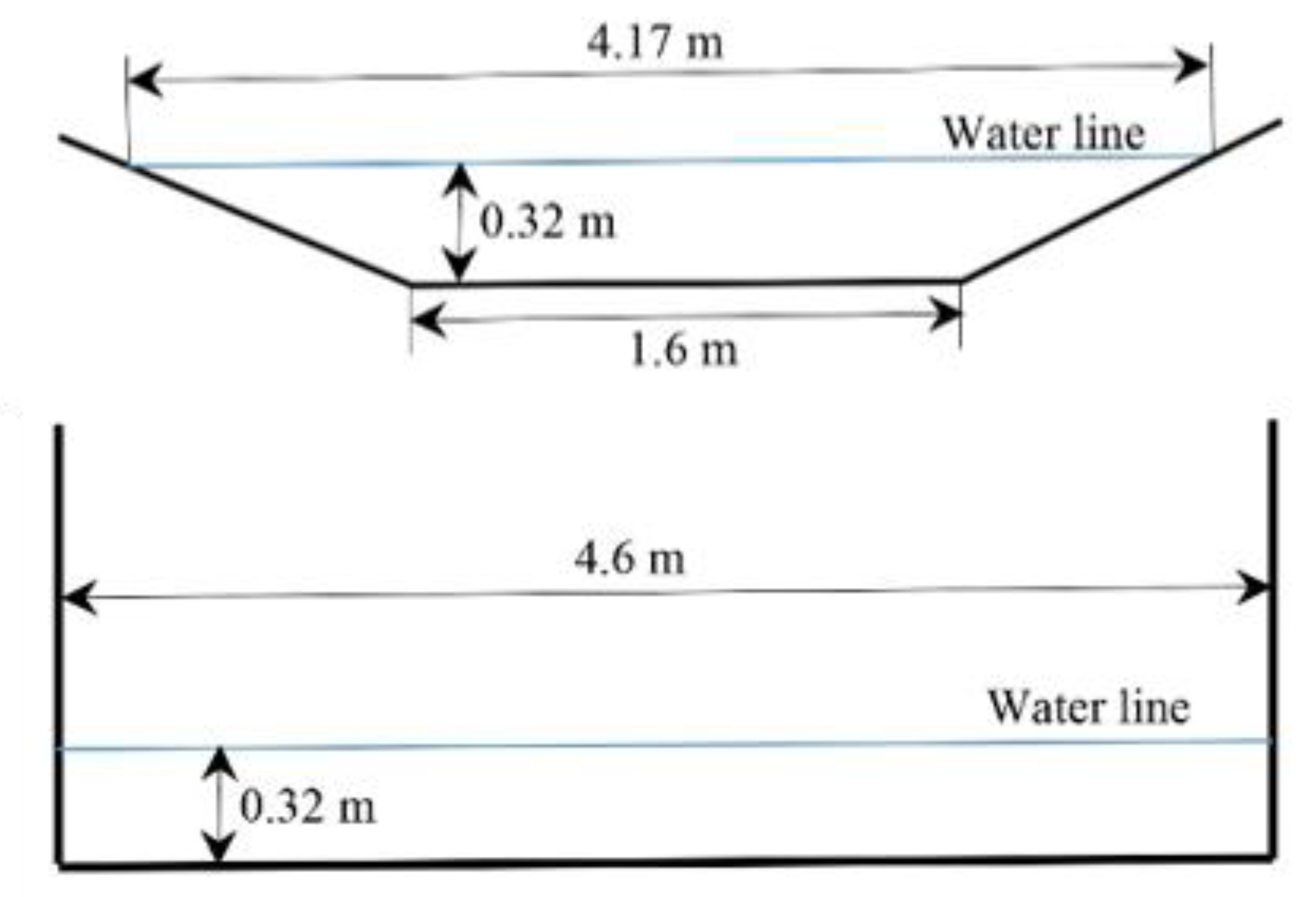
| Water depth | h | 0.32 | m |
| Block coefficient | CB | 0.651 | - |
| Longitudinal Centre of Gravity | LCG | 1.488 | m |
| Wetted area | S | 1.694 | m2 |
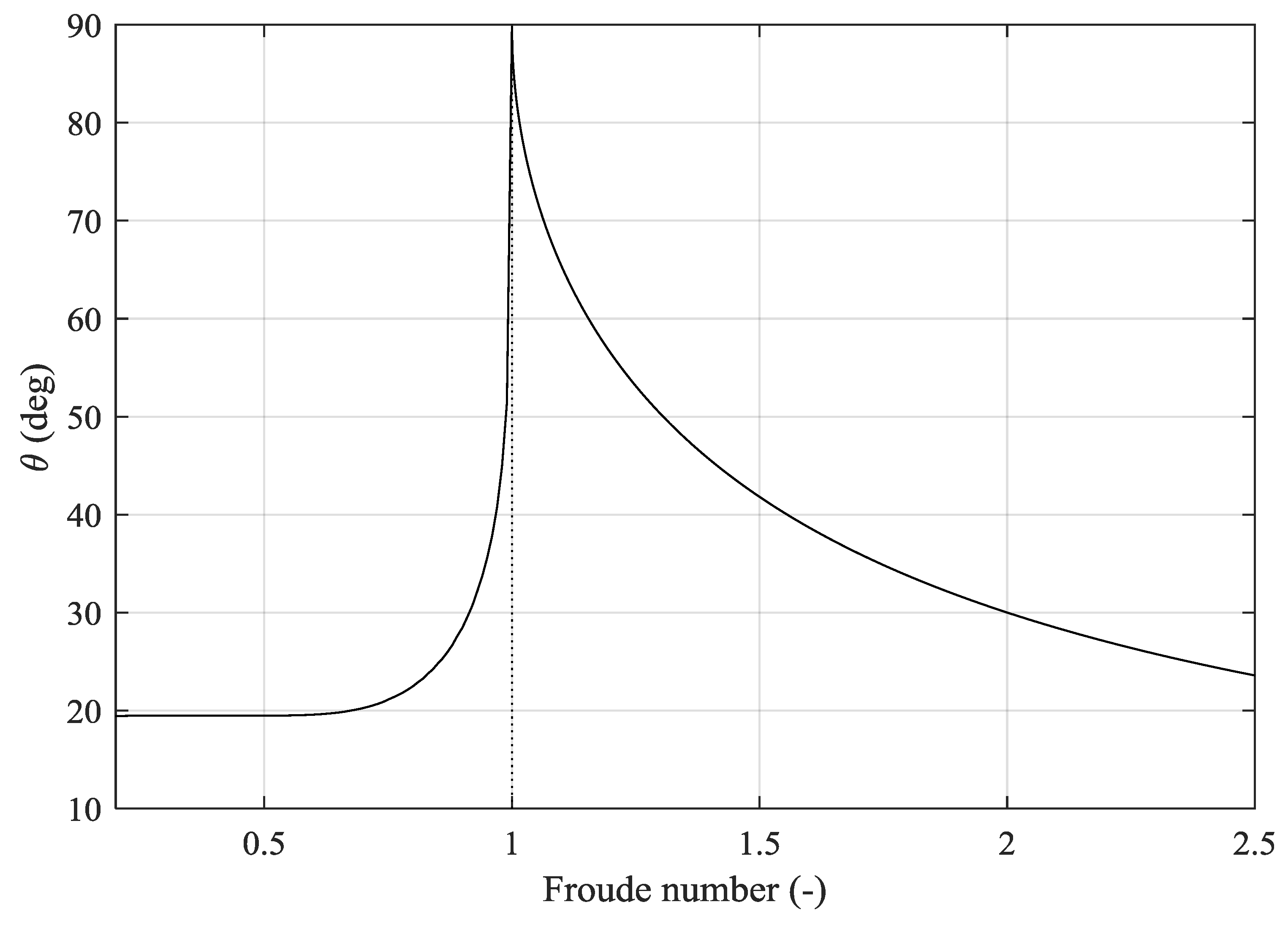
| Canal | Case Number | Depth-to-Draught (h/T) | Depth Froude Number | Ship Speed (m/s) | Kelvin Half-Angle [17] |
|---|---|---|---|---|---|
| Rectangular canal | 1 | 2.2 | 0.57 | 1.01 | 19.52 |
| 2 | 0.77 | 1.364 | 21.58 | ||
| New Suez Canal | 3 | 0.47 | 0.815 | 19.47 | |
| 4 | 0.57 | 1.01 | 19.52 |
| Canal | Background Cells | Overset Cells | Total |
|---|---|---|---|
| Rectangular canal | 29,312,452 | 766,402 | 30,078,854 |
| Suez Canal | 21,496,179 | 766,402 | 22,262,581 |
| Parameter | Mesh | Time-Step | Units |
|---|---|---|---|
| r | - | ||
| f1 | 4.325 (29,312,452 cells) | 4.325 | N |
| f2 | 4.356 (10,955,825 cells) | 4.381 | N |
| f3 | 5.045 (4,155,326 cells) | 4.446 | N |
| R | 0.044 | 0.852 | - |
| p | 9.005 | 0.463 | - |
| GCI (%) | 0.6704 | 19.609 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terziev, M.; Zhao, G.; Tezdogan, T.; Yuan, Z.; Incecik, A. Virtual Replica of a Towing Tank Experiment to Determine the Kelvin Half-Angle of a Ship in Restricted Water. J. Mar. Sci. Eng. 2020, 8, 258. https://doi.org/10.3390/jmse8040258
Terziev M, Zhao G, Tezdogan T, Yuan Z, Incecik A. Virtual Replica of a Towing Tank Experiment to Determine the Kelvin Half-Angle of a Ship in Restricted Water. Journal of Marine Science and Engineering. 2020; 8(4):258. https://doi.org/10.3390/jmse8040258
Chicago/Turabian StyleTerziev, Momchil, Guangwei Zhao, Tahsin Tezdogan, Zhiming Yuan, and Atilla Incecik. 2020. "Virtual Replica of a Towing Tank Experiment to Determine the Kelvin Half-Angle of a Ship in Restricted Water" Journal of Marine Science and Engineering 8, no. 4: 258. https://doi.org/10.3390/jmse8040258
APA StyleTerziev, M., Zhao, G., Tezdogan, T., Yuan, Z., & Incecik, A. (2020). Virtual Replica of a Towing Tank Experiment to Determine the Kelvin Half-Angle of a Ship in Restricted Water. Journal of Marine Science and Engineering, 8(4), 258. https://doi.org/10.3390/jmse8040258






