Numerical Simulation and Validation in Scrubber Wash Water Discharge from Ships
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Chemistry Reaction
2.2. Turbulent Jets
3. Numerical Modeling
3.1. Boundary Conditions
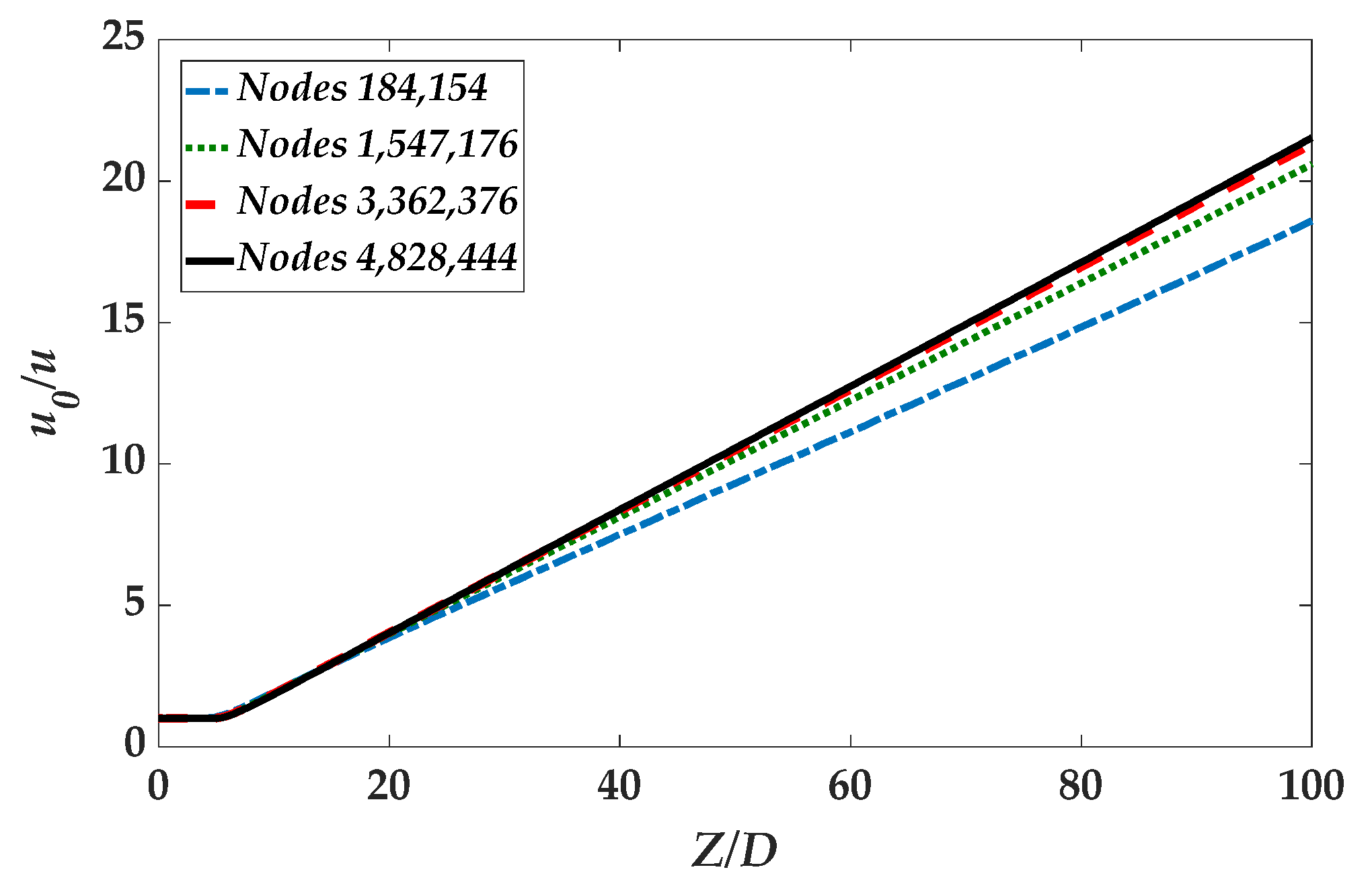
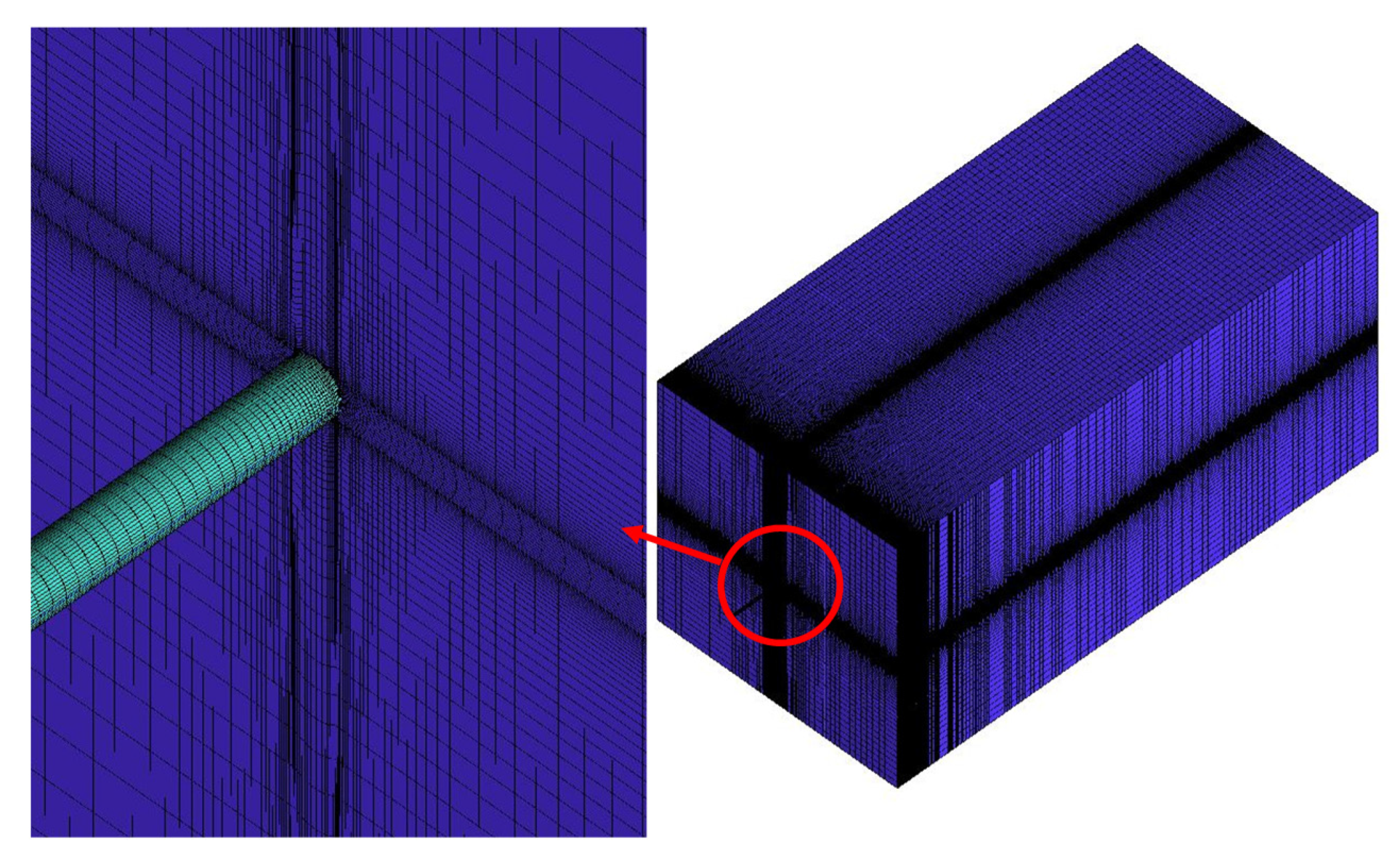
3.2. Mesh
4. Results
4.1. Titration Curves
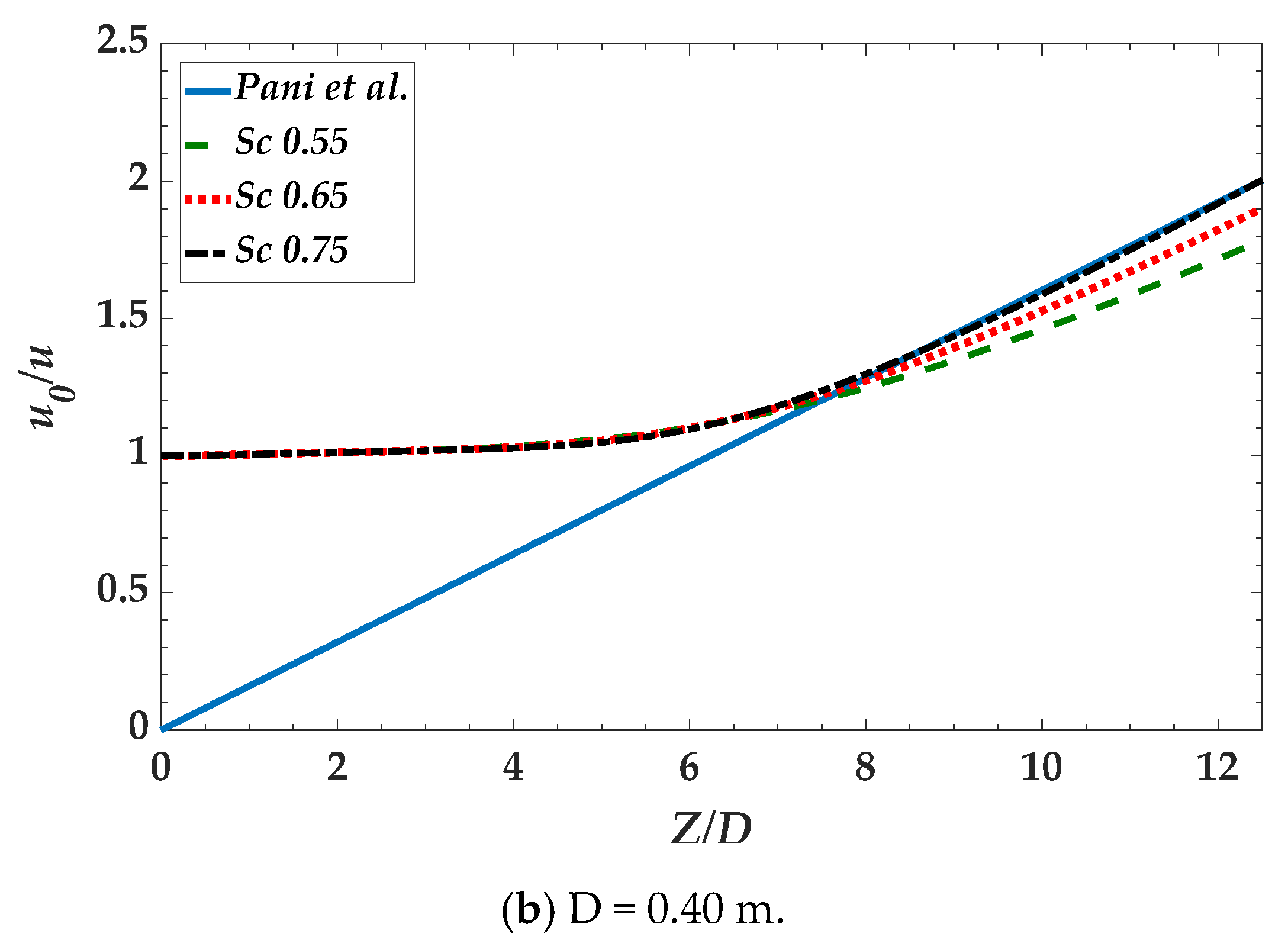
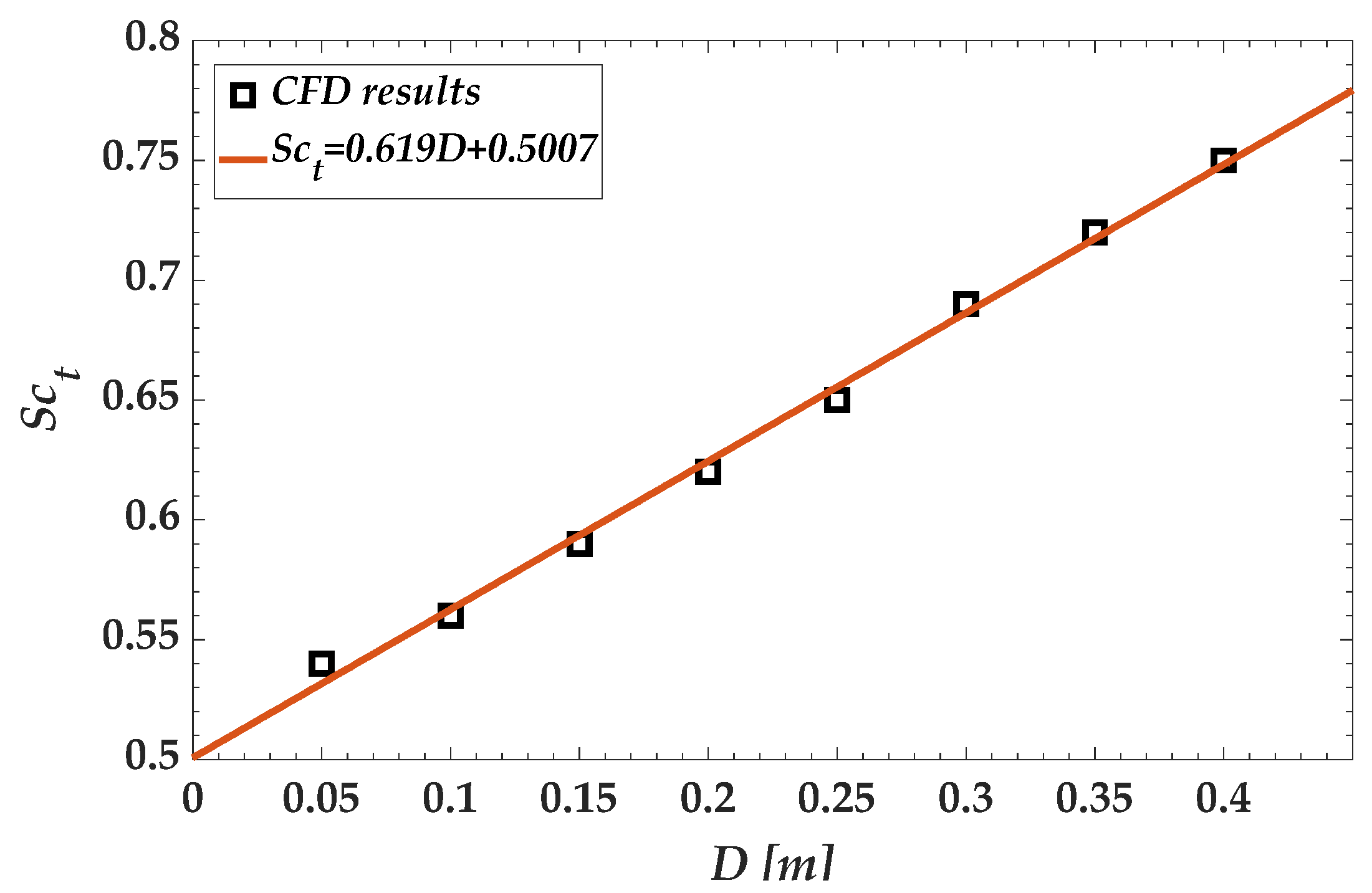
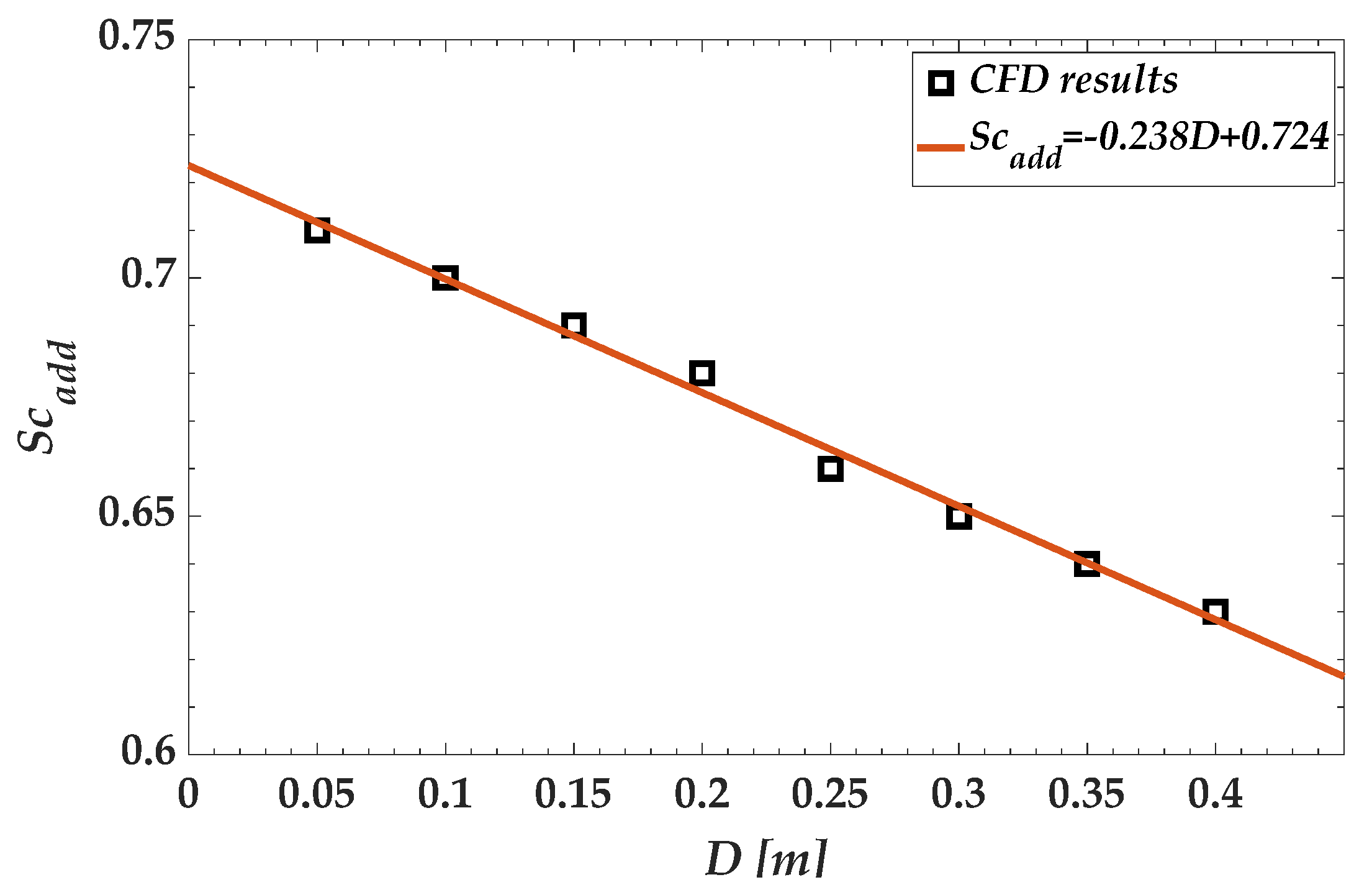
4.2. CFD Validations
4.3. pH Calculations
5. Conclusions
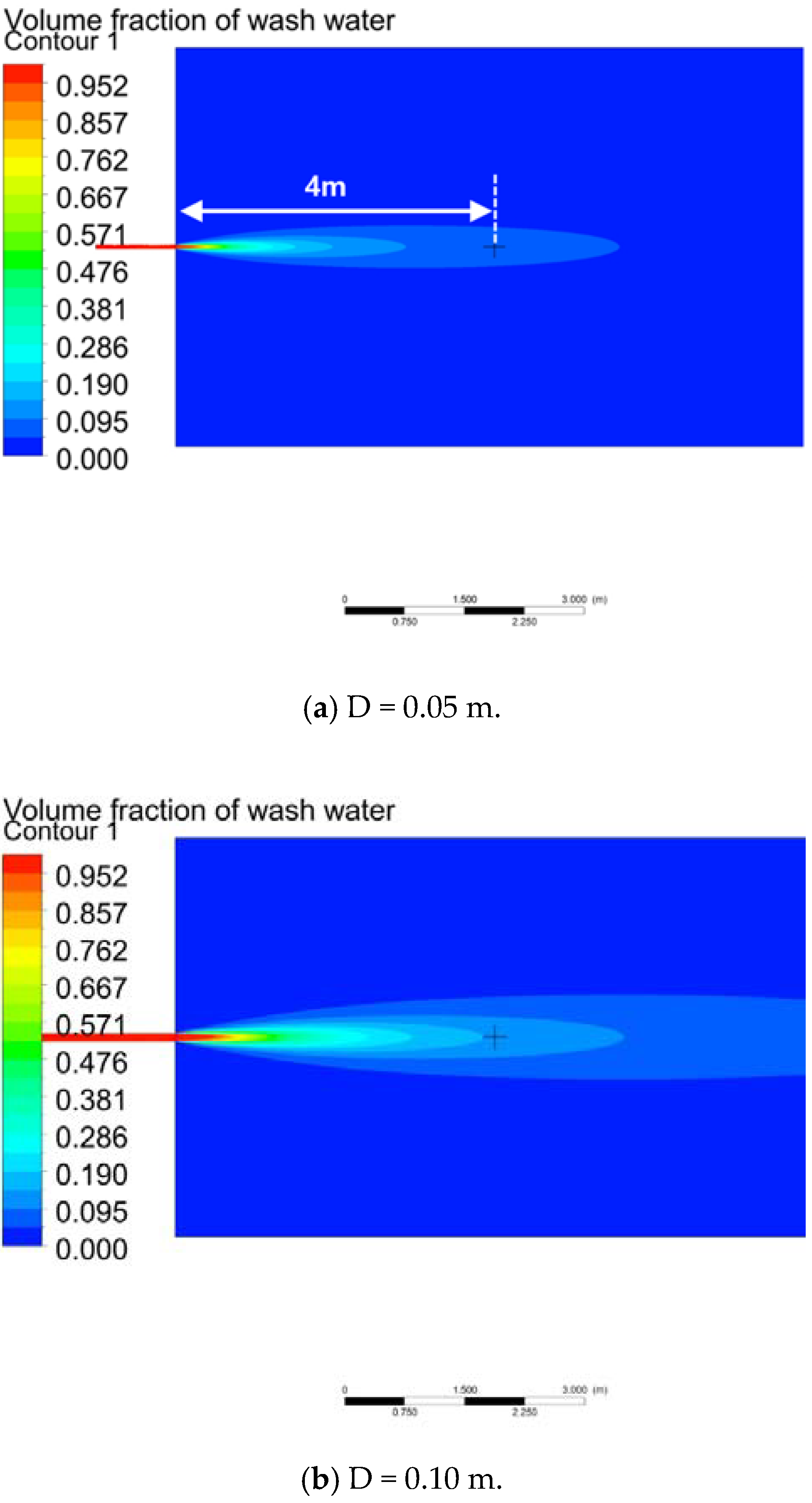
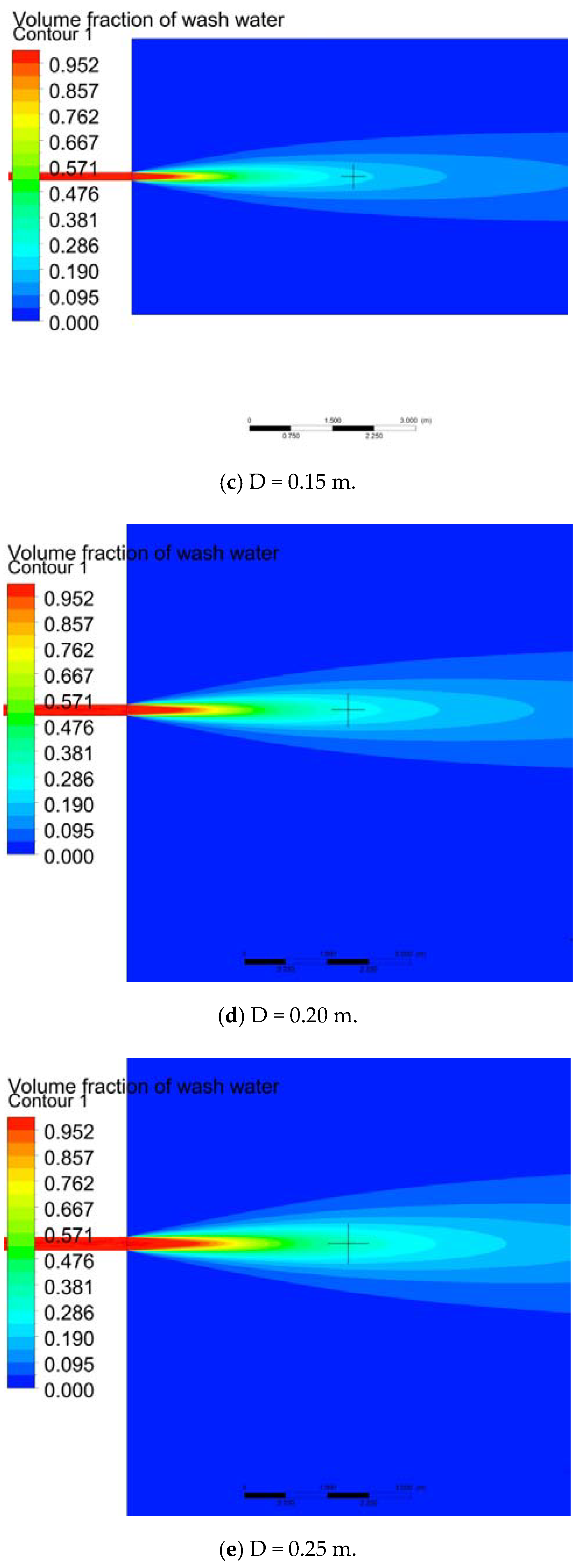
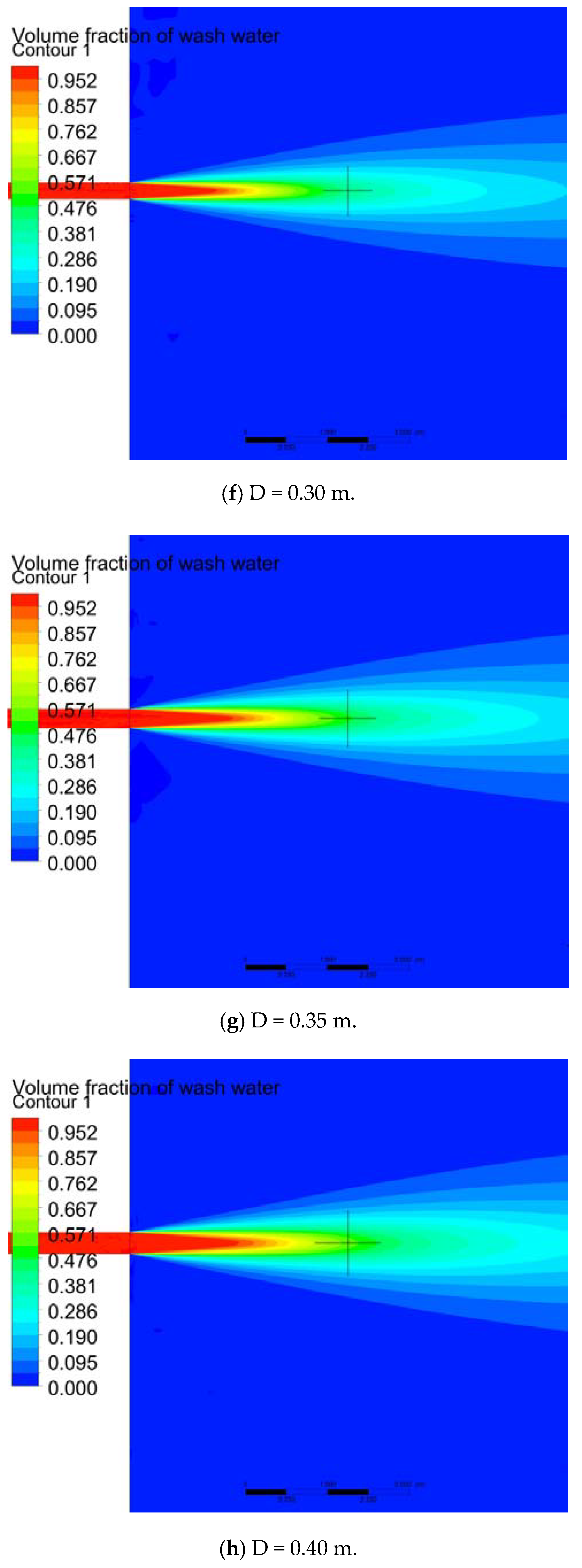
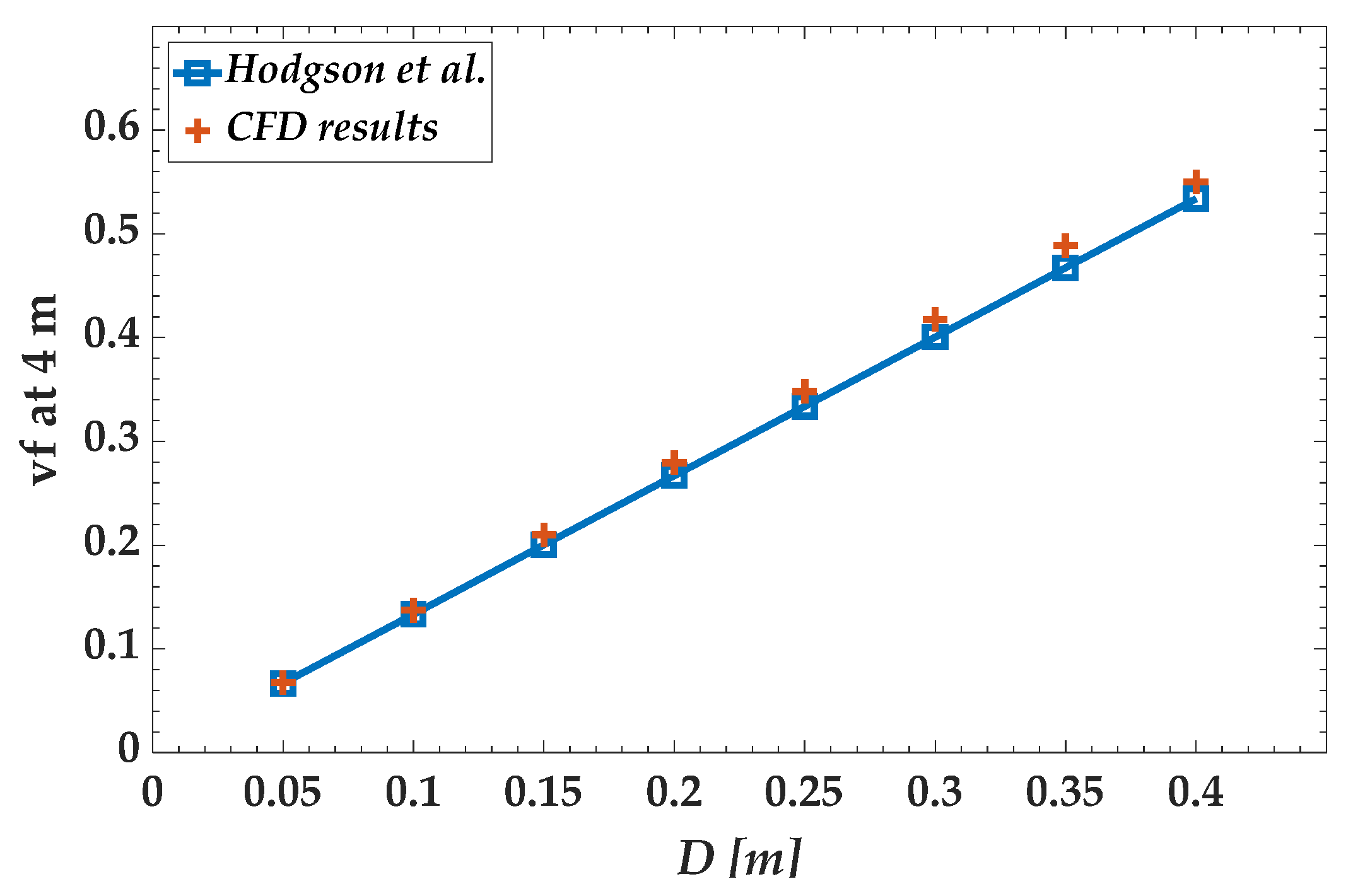
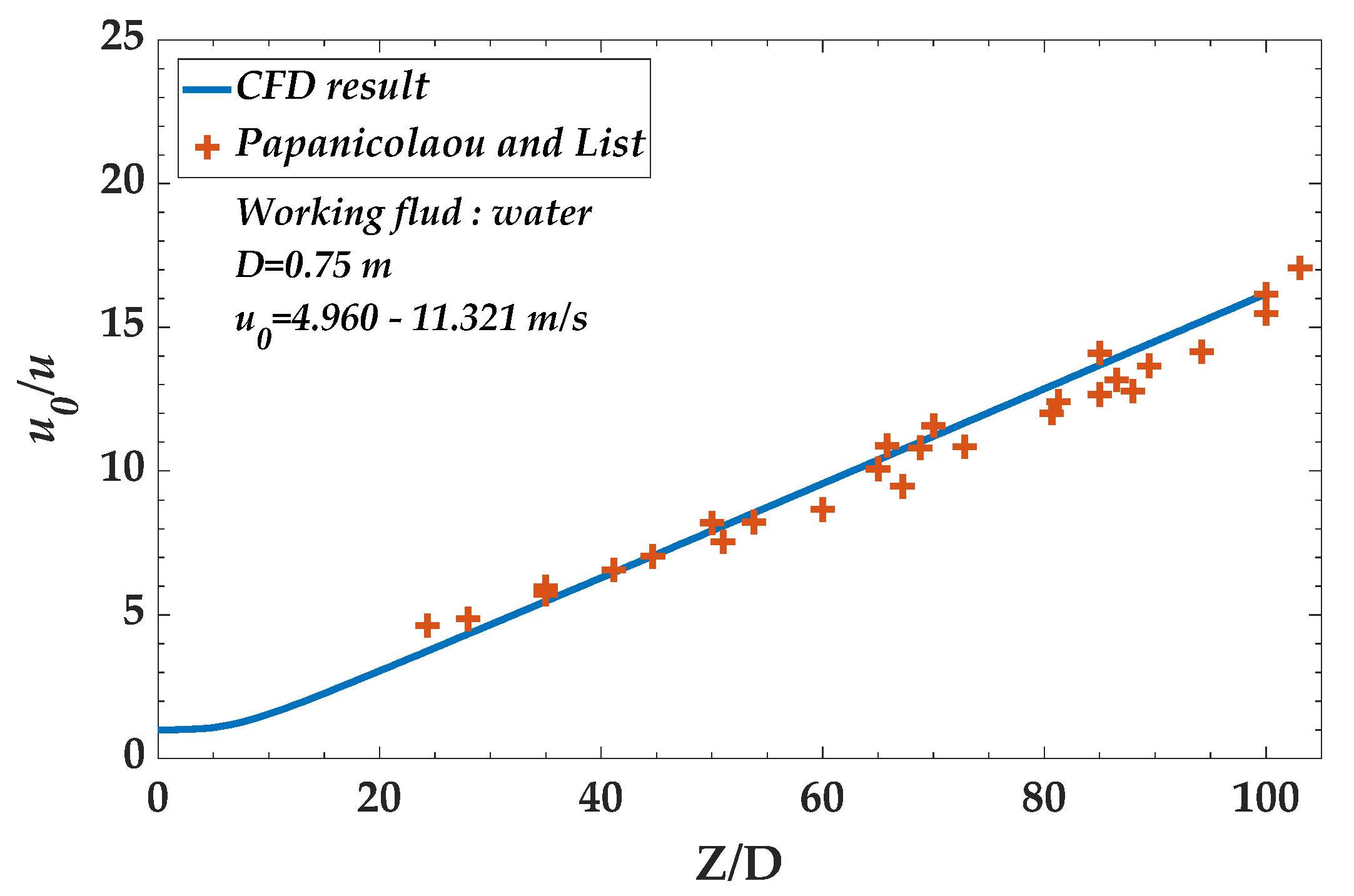
- To simulate the dispersion phenomenon in turbulent jet flow, we solved the transport equation by applying the volume fraction. Simulation was performed for nozzle diameters ranging from 0.05 m to 0.40 m. The turbulent Schmidt number is a critical parameter that exerts a significant effect on dispersion. An appropriate turbulent Schmidt number must be selected according to the nozzle diameter. The appropriate turbulent Schmidt numbers of the transport equations were calculated by comparing them with the existing correlations. The simulation results obtained within 5 m from the discharge point by using the calculated turbulent Schmidt numbers matched well with the results obtained by Pani et al. [14] and Hodgson et al. [20].
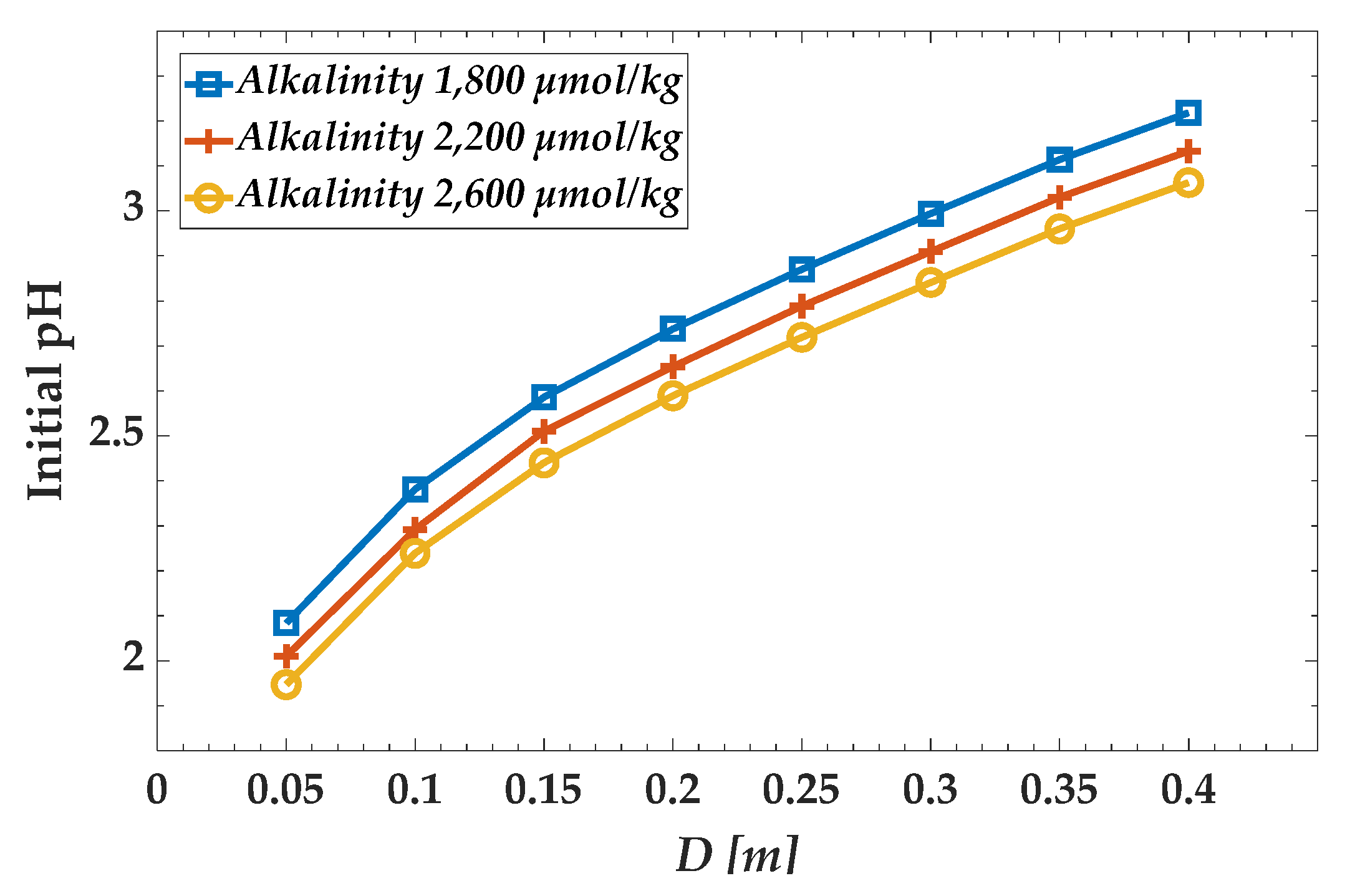
- The volume fraction at 4 m from the discharge point was calculated through simulation, and titration curves were obtained by the theoretical chemical reaction model. The pH value at 4 m can be derived from the initial pH by applying the calculated volume fraction or dilution ratio to the titration curves.
- When the wash water has a low pH, a small diameter nozzle is required to restore the pH to 6.5 at 4 m from the discharge point. When the seawater in the surrounding sea area has a low alkalinity, a large amount of seawater is required. Hence, a small diameter nozzle must be used to promote dispersion. At the initial pH of 3.0 and alkalinity of 2200 μmol/kg, the nozzle diameter should be less than 0.34 m, and at the initial pH of 3.0 and alkalinity of 1800 μmol/kg, it should be less than 0.30 m.
- For future research, we will improve the accuracy of the chemical reaction model through titration experiments by using wash water and seawater obtained from the scrubber of actual ship engines. Moreover, we intend to improve the reliability of the CFD simulation through comparison with correlations derived from more varied turbulent jet flows.
Author Contributions
Funding
Conflicts of Interest
Appendix A. CFD Post Processing Data
References
- IMO MEPC 70/18/Add.1 ANNEX6. Effective Date of Implementation of the Fuel Oil Standard in Regulation 14.1.3 of MARPOL ANNEX VI 2016. Available online: http://www.imo.org (accessed on 9 April 2020).
- Van, T.C.; Ramirez, J.; Rainey, T.; Ristovski, Z.; Brown, R.J. Global impacts of recent IMO regulations on marine fuel oil refining processes and ship emissions. Transp. Res. Part D Transp. Environ. 2019, 70, 123–134. [Google Scholar] [CrossRef]
- Cheenkachorn, K.; Poompipatpong, C.; Gyeung, C. Performance and emissions of a heavy-duty diesel engine fuelled with diesel and LNG (liquid natural gas). Energy 2013, 53, 52–57. [Google Scholar] [CrossRef]
- Armellini, A.; Daniotti, S.; Pinamonti, P.; Reini, M. Evaluation of gas turbines as alternative energy production systems for a large cruise ship to meet new maritime regulations. Appl. Energy 2018, 211, 306–317. [Google Scholar] [CrossRef]
- Tang, X.; Li, T.; Yu, H.; Zhu, Y. Prediction model for desulphurization efficiency of onboard magnesium-base seawater scrubber. Ocean Eng. 2016, 76, 98–104. [Google Scholar] [CrossRef]
- Ammar, N.R.; Seddiek, I.S. Eco-environmental analysis of ship emission control methods: Case study RO-RO cargo vessel. Ocean Eng. 2017, 137, 166–173. [Google Scholar] [CrossRef]
- Koski, M.; Stedmon, C.; Trapp, S. Ecological effects of scrubber water discharge on coastal plankton: Potential synergistic effects of contaminants reduce survival and feeding of the copepod Acartia tonsa. Mar. Environ. Res. 2017, 129, 374–385. [Google Scholar] [CrossRef] [PubMed]
- Ytreberg, E.; Hassellöv, I.M.; Nylund, A.T.; Hedblom, M.; Al-Handal, A.Y.; Wulff, A. Effects of scrubber washwater discharge on microplankton in the Baltic Sea. Mar. Pollut. Bull. 2019, 145, 316–324. [Google Scholar] [CrossRef] [PubMed]
- Ülpre, H.; Eames, I.; Greig, A. Turbulent acidic jets and plumes injected into an alkaline environment. J. Fluid Mech. 2013, 734, 253–274. [Google Scholar] [CrossRef][Green Version]
- Ülpre, H.; Eames, I. Environmental policy constraints for acidic exhaust gas scrubber discharges from ships. Mar. Pollut. Bull. 2014, 88, 292–301. [Google Scholar] [CrossRef]
- Lipari, G.; Stansby, P.K. Review of experimental data on incompressible turbulent round jets. Flow Turbul. Combust. 2011, 87, 79–114. [Google Scholar] [CrossRef]
- Panchapakesan, N.R.; Lumley, J.L. Turbulence Measurements in Axisymmetric Jets of Air and Helium. Part 2. Helium Jet. J. Fluid Mech. 1993, 246, 225–247. [Google Scholar] [CrossRef]
- Boersma, B.J.; Brethouwer, G.; Nieuwstadt, F.T.M. A numerical investigation on the effect of the inflow conditions on the self-similar region of a round jet. Phys. Fluids 1998, 10, 899–909. [Google Scholar] [CrossRef]
- Pani, B.S.; Lai, A.C.H.; Wong, C.K.C. Turbulent Jets: Point-Source and CFD Simulation Results. J. Environ. Res. Dev. 2011, 5, 952–959. [Google Scholar]
- Robinson, D.; Wood, M.; Piggott, M.; Gorman, G. CFD modelling of marine discharge mixing and dispersion. J. Appl. Water Eng. Res. 2016, 4, 152–162. [Google Scholar] [CrossRef]
- Choi, Y.S.; Cha, M.H.; Kim, M.; Lim, T.W. Design of nozzle diameter based on the IMO regulation for discharging scrubber wash-water. J. Korean Soc. Mar. Eng. 2019, 43, 285–291. [Google Scholar] [CrossRef]
- Ülpre, H. Turbulence Acidic Discharges into Seawater. Ph.D. Thesis, University College London, London, UK, 2015. [Google Scholar]
- Frankignoulle, M. A complete set of buffer factors for acid / base CO2 system in seawater. J. Mar. Syst. 1994, 5, 111–118. [Google Scholar] [CrossRef]
- Brown, T.E.; Lemay, H.E.; Bursten, B.E.; Murphy, C.; Woodward, P.; Stoltzfus, M.E. Chemistry: The Central Science, 13th ed.; Pearson: London, UK, 2014. [Google Scholar]
- Hodgson, J.E.; Moawad, A.K.; Rajaratnam, N. Concentration field of multiple circular turbulent jets. J. Hydraul. Res. 1999, 37, 249–256. [Google Scholar] [CrossRef]
- Eigen, M. Methods for investigation of ionic reactions in aqueous solutions with half-times as short as 10–9 sec Application to neutralization and hydrolysis reactions. Discuss. Faraday Soc. 1954, 17, 194–205. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. k-ε Predictions of the initial mixing of desalination discharges. Environ. Fluid Mech. 2008, 8, 617–625. [Google Scholar] [CrossRef]
- Shirzadi, M.; Mirzaei, P.A.; Naghashzadegan, M. Aerodynamics Improvement of k-epsilon turbulence model for CFD simulation of atmospheric boundary layer around a high-rise building using stochastic optimization and Monte Carlo Sampling technique. J. Wind Eng. Ind. Aerodyn. 2017, 171, 366–379. [Google Scholar] [CrossRef]
- ANSYS CFX-Theory Guide; V13.0.; Ansys Inc.: Canonsburg, PA, USA, 2010.
- He, G.; Guo, Y.; Hsu, A.T. The Effect of Schmidt Number on Turbulent Scalar Mixing in a Jet-in-Crossflow. Int. J. Heat Mass Transf. 1999, 42, 3727–3738. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Nguyen, T.C.; Nguyen, J. Numerical Simulation of Turbulent Flow and Pollutant Dispersion in Urban Street Canyons. Atmosphere 2019, 10, 683. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; List, E.J. Investigations of Round Vertical Turbulent Buoyant Jets. J. Flud Mech. 1988, 195, 341–931. [Google Scholar] [CrossRef]



| Initial pH | Alkalinity 1800 μmol/kg | Alkalinity 2200 μmol/kg | Alkalinity 2600 μmol/kg | |||
|---|---|---|---|---|---|---|
| Dilution Ratio | Volume Fraction | Dilution Ratio | Volume Fraction | Dilution Ratio | Volume Fraction | |
| 2.5 | 4.66 | 0.18 | 3.81 | 0.21 | 3.23 | 0.24 |
| 2.6 | 3.63 | 0.22 | 2.97 | 0.25 | 2.51 | 0.28 |
| 2.7 | 2.83 | 0.26 | 2.32 | 0.30 | 1.96 | 0.34 |
| 2.8 | 2.22 | 0.31 | 1.82 | 0.36 | 1.54 | 0.39 |
| 2.9 | 1.74 | 0.36 | 1.43 | 0.41 | 1.21 | 0.45 |
| 3.0 | 1.37 | 0.42 | 1.12 | 0.47 | 0.95 | 0.51 |
| 3.1 | 1.08 | 0.48 | 0.88 | 0.53 | 0.75 | 0.57 |
| 3.2 | 0.85 | 0.54 | 0.70 | 0.59 | 0.59 | 0.63 |
| 3.3 | 0.67 | 0.60 | 0.55 | 0.64 | 0.47 | 0.68 |
| 3.4 | 0.53 | 0.65 | 0.44 | 0.70 | 0.37 | 0.73 |
| 3.5 | 0.42 | 0.70 | 0.35 | 0.74 | 0.29 | 0.77 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.-S.; Lim, T.-W. Numerical Simulation and Validation in Scrubber Wash Water Discharge from Ships. J. Mar. Sci. Eng. 2020, 8, 272. https://doi.org/10.3390/jmse8040272
Choi Y-S, Lim T-W. Numerical Simulation and Validation in Scrubber Wash Water Discharge from Ships. Journal of Marine Science and Engineering. 2020; 8(4):272. https://doi.org/10.3390/jmse8040272
Chicago/Turabian StyleChoi, Yong-Seok, and Tae-Woo Lim. 2020. "Numerical Simulation and Validation in Scrubber Wash Water Discharge from Ships" Journal of Marine Science and Engineering 8, no. 4: 272. https://doi.org/10.3390/jmse8040272
APA StyleChoi, Y.-S., & Lim, T.-W. (2020). Numerical Simulation and Validation in Scrubber Wash Water Discharge from Ships. Journal of Marine Science and Engineering, 8(4), 272. https://doi.org/10.3390/jmse8040272





