Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine
Abstract
1. Introduction
2. Model of DFIG-Based TST
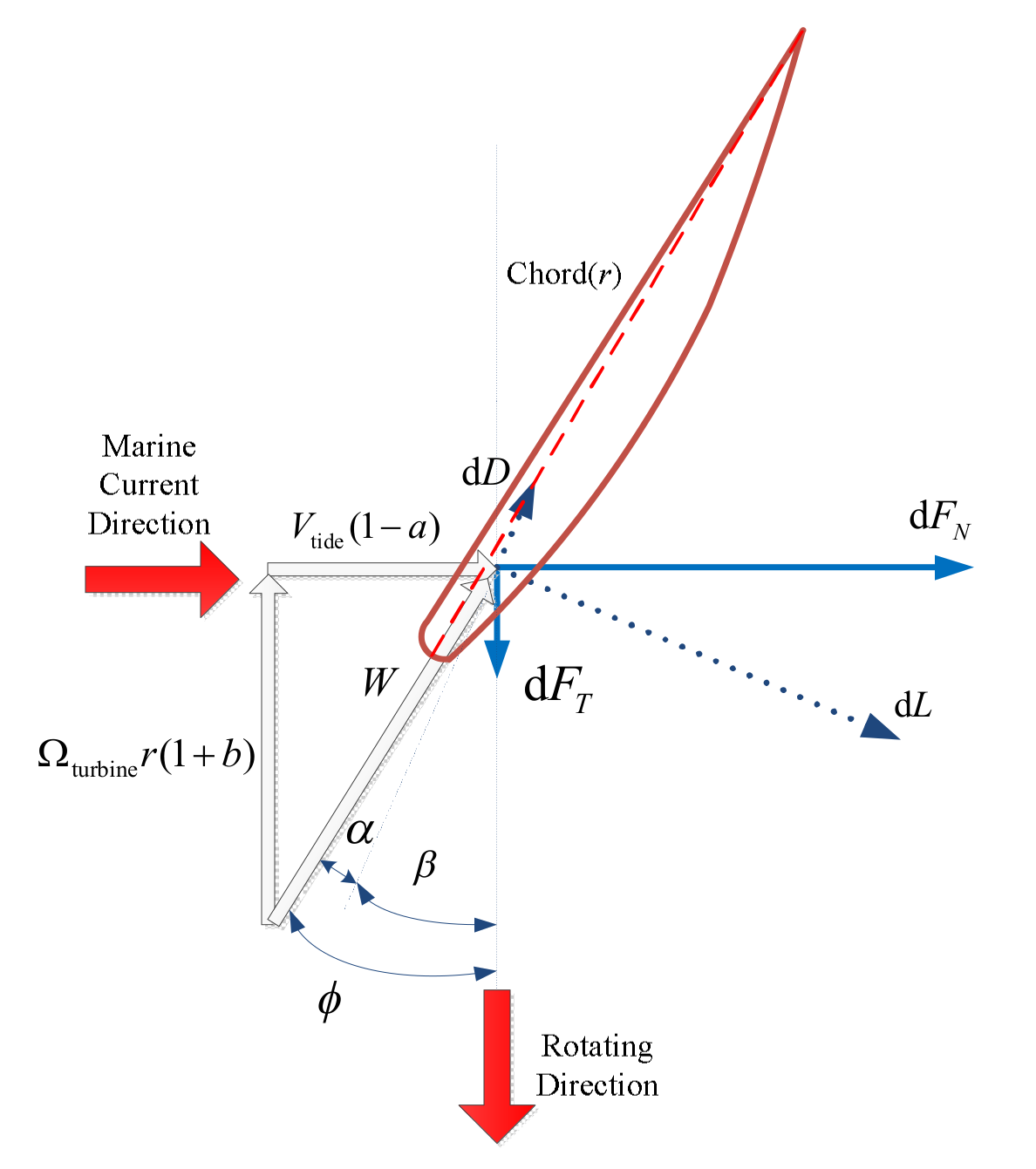
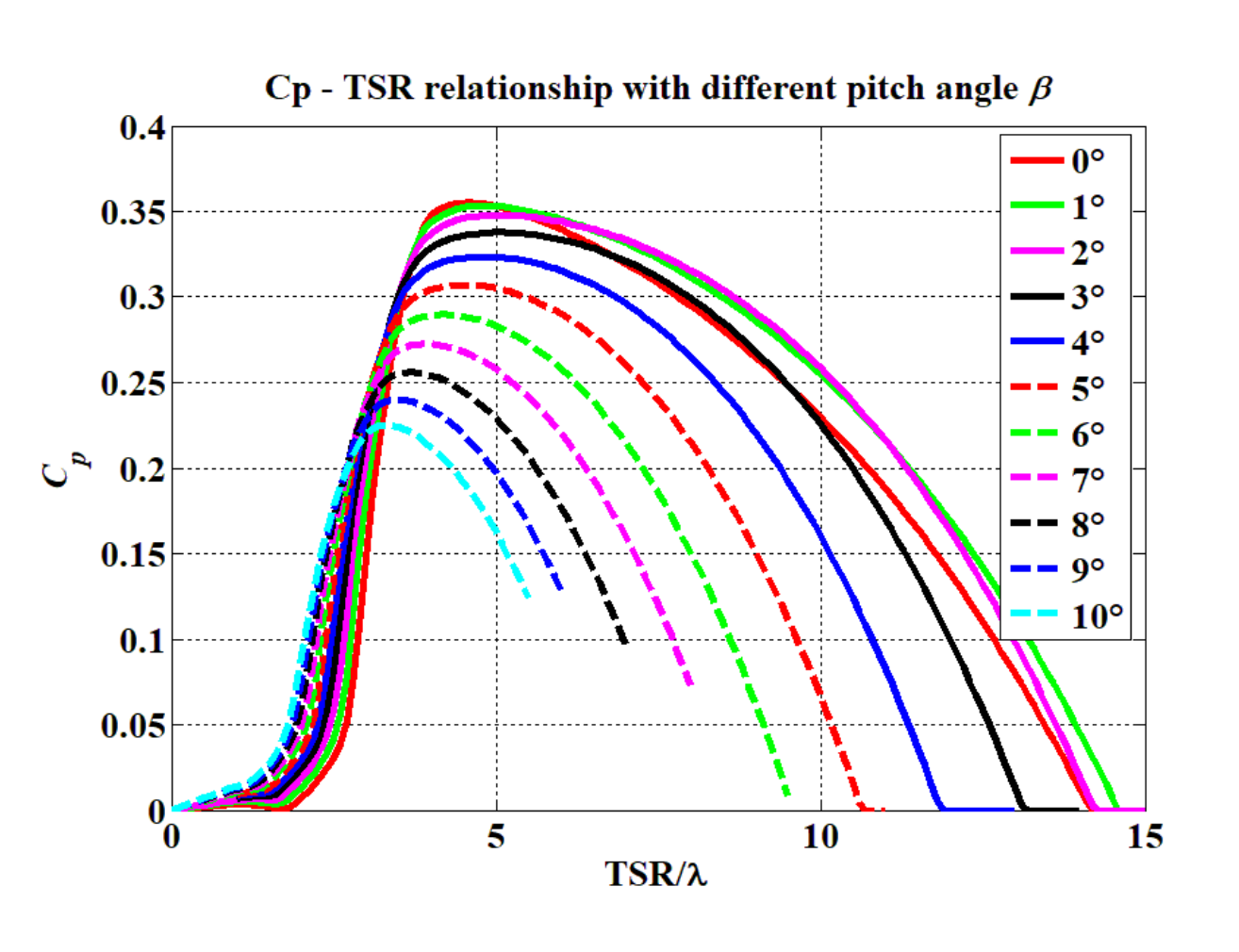
2.1. Tidal Stream Turbine Modeling
2.2. DFIG Modeling
3. Conventional Integer-Order PI Controller
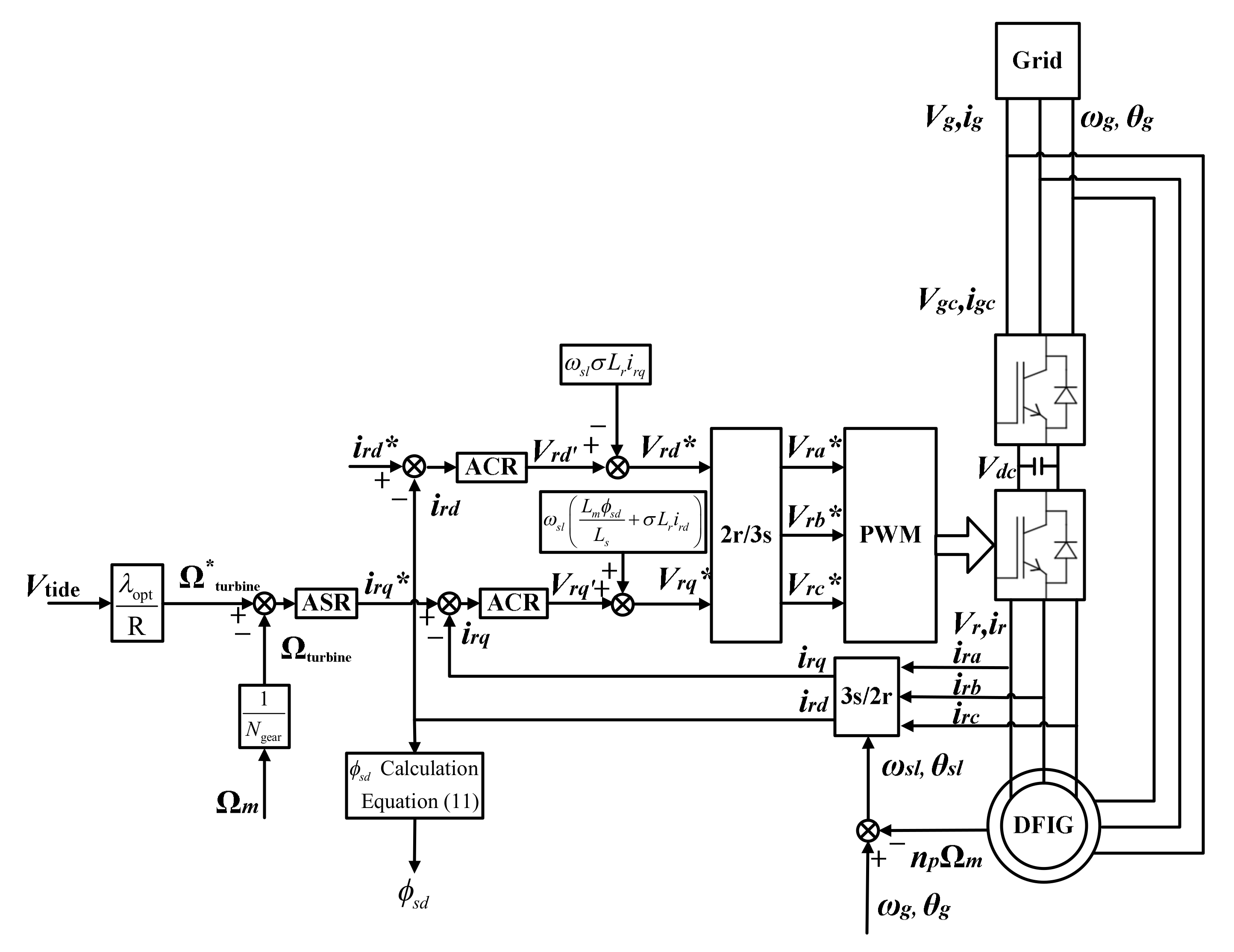
3.1. Control Strategy
3.2. Current Loop
3.3. Speed Loop
4. Fractional-Order PI Controller
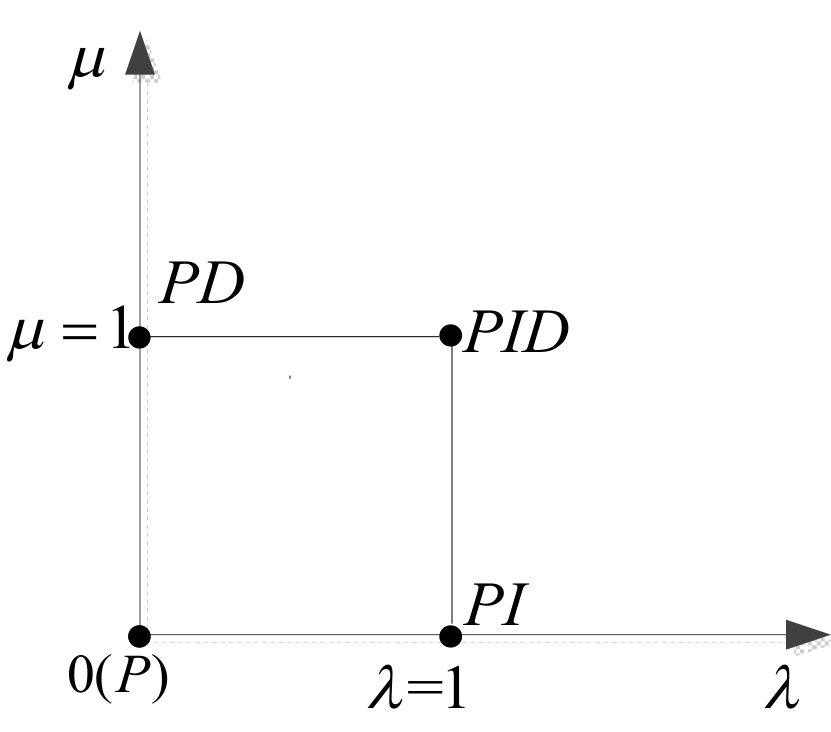
4.1. Basic Introduction of Fractional-Order PID Controller
4.2. Design of FOPI Controller
- (1)
- Determination of the phase-frequency characteristics at ωc:
- (2)
- Determination of the amplitude-frequency characteristics at ωc:
- (3)
- Robustness to the variations of the system gain:
5. Simulation and Comparison
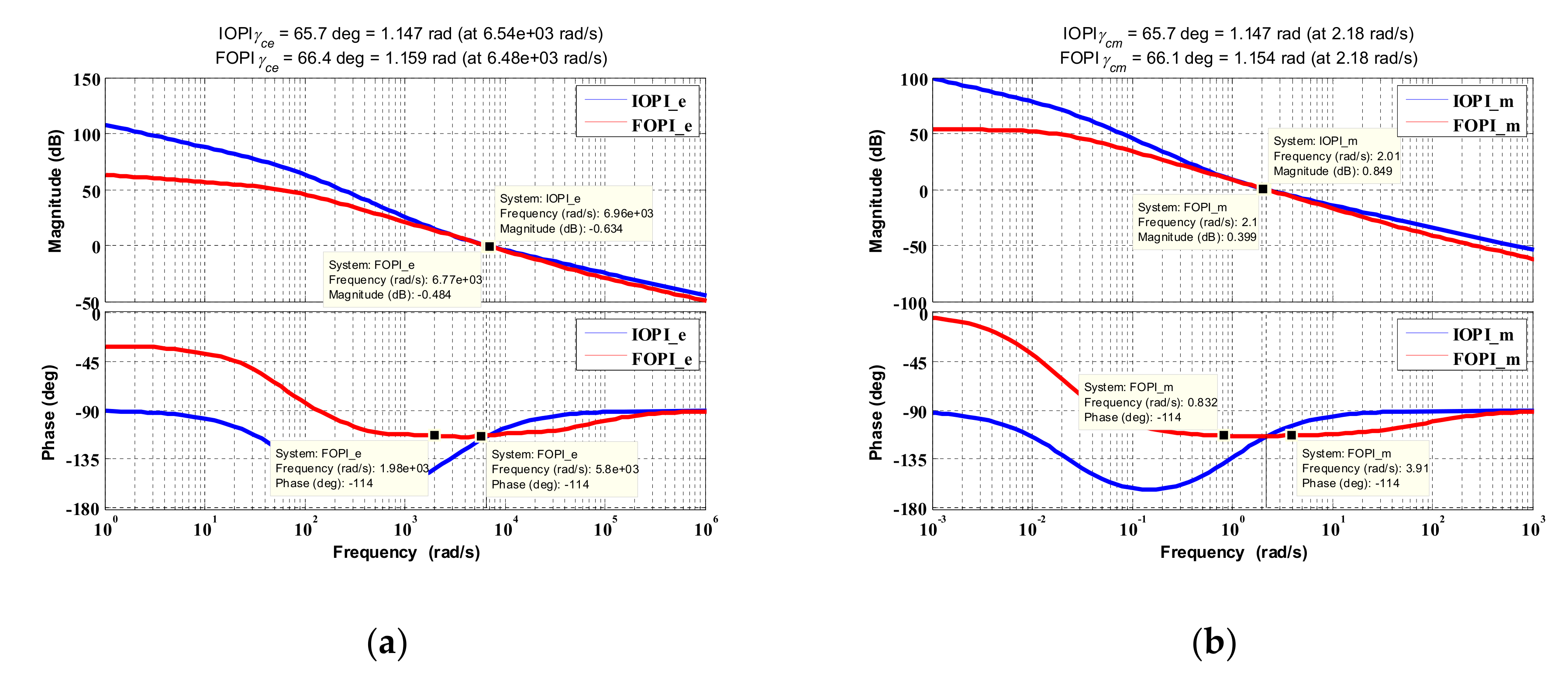
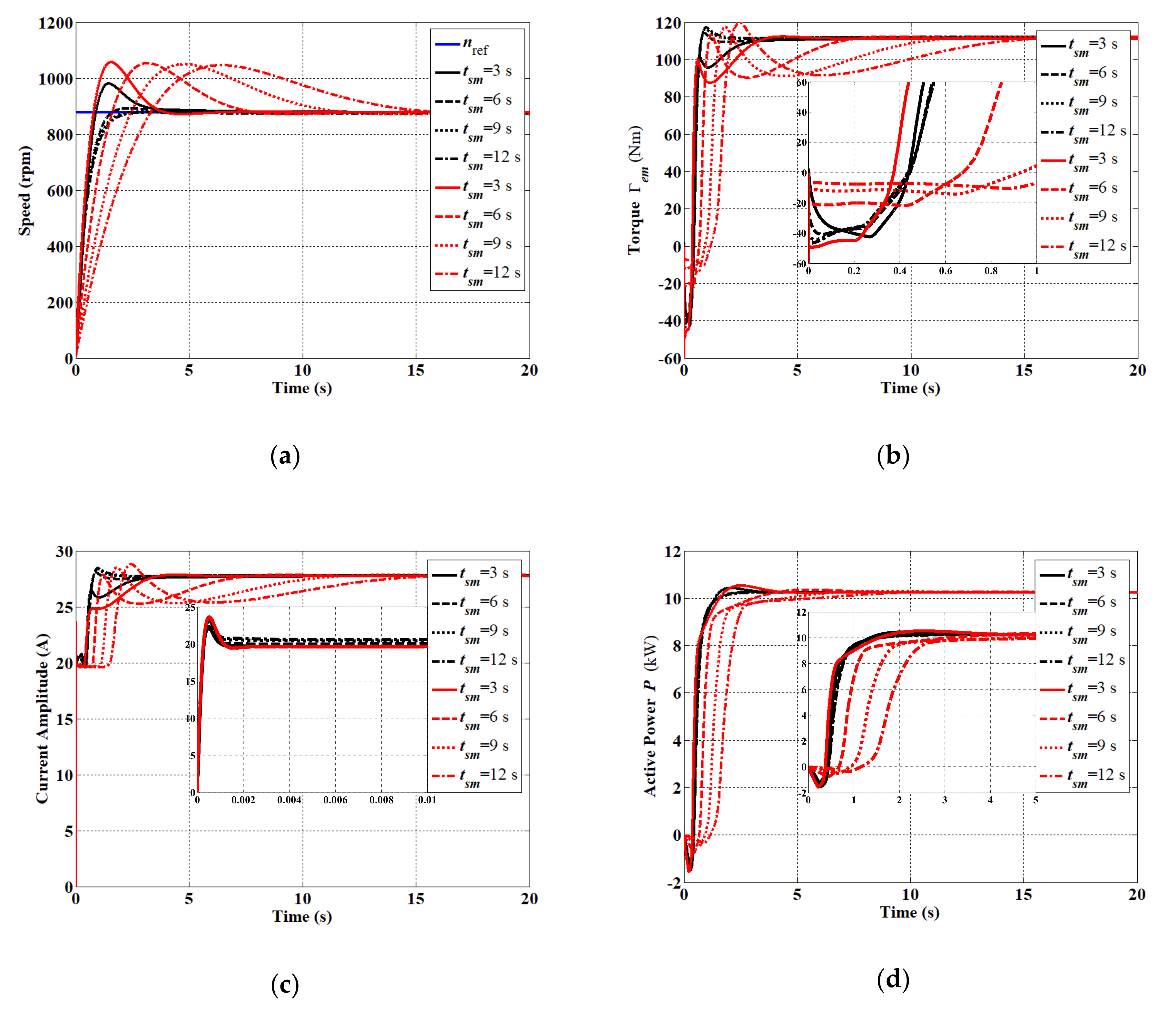
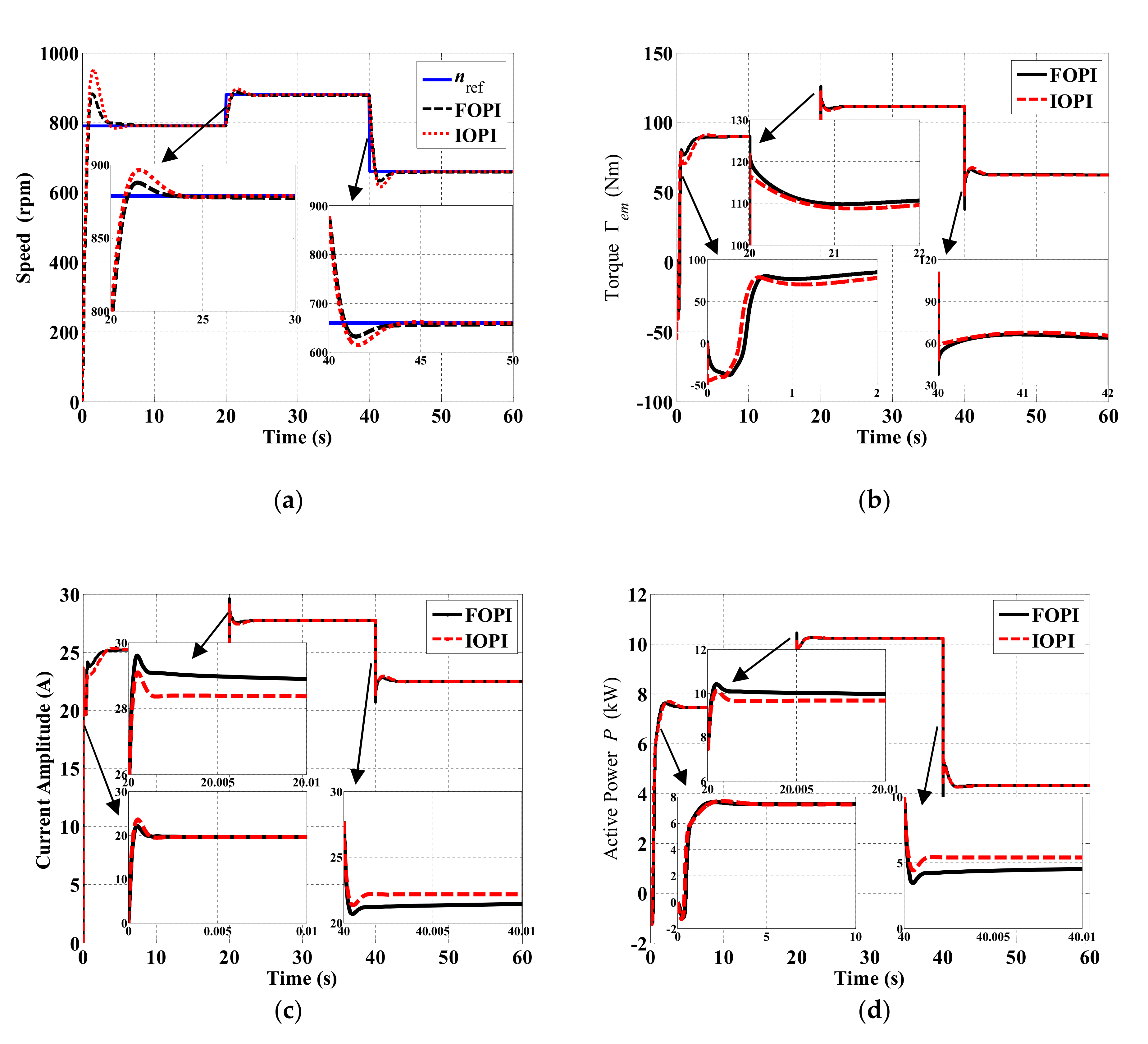
5.1. Comparison of the Two Controllers
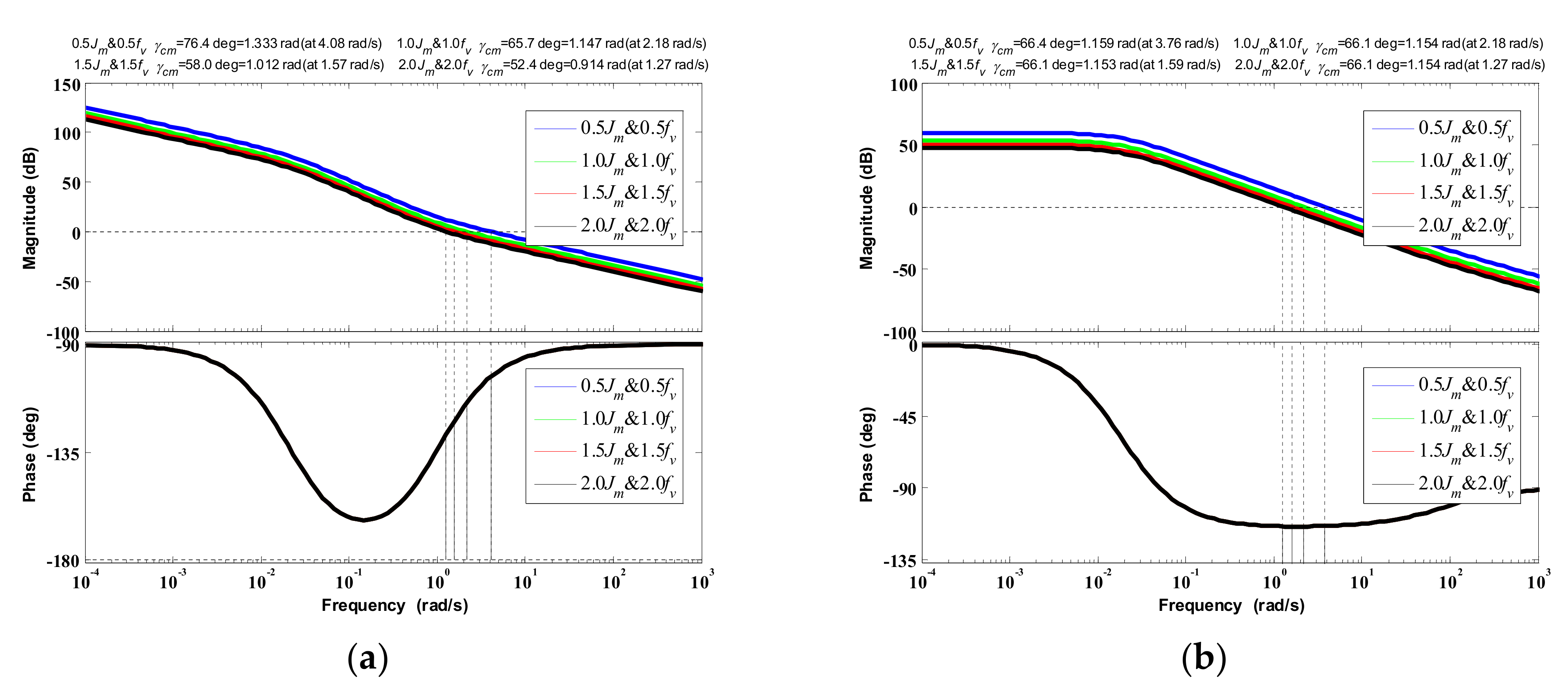
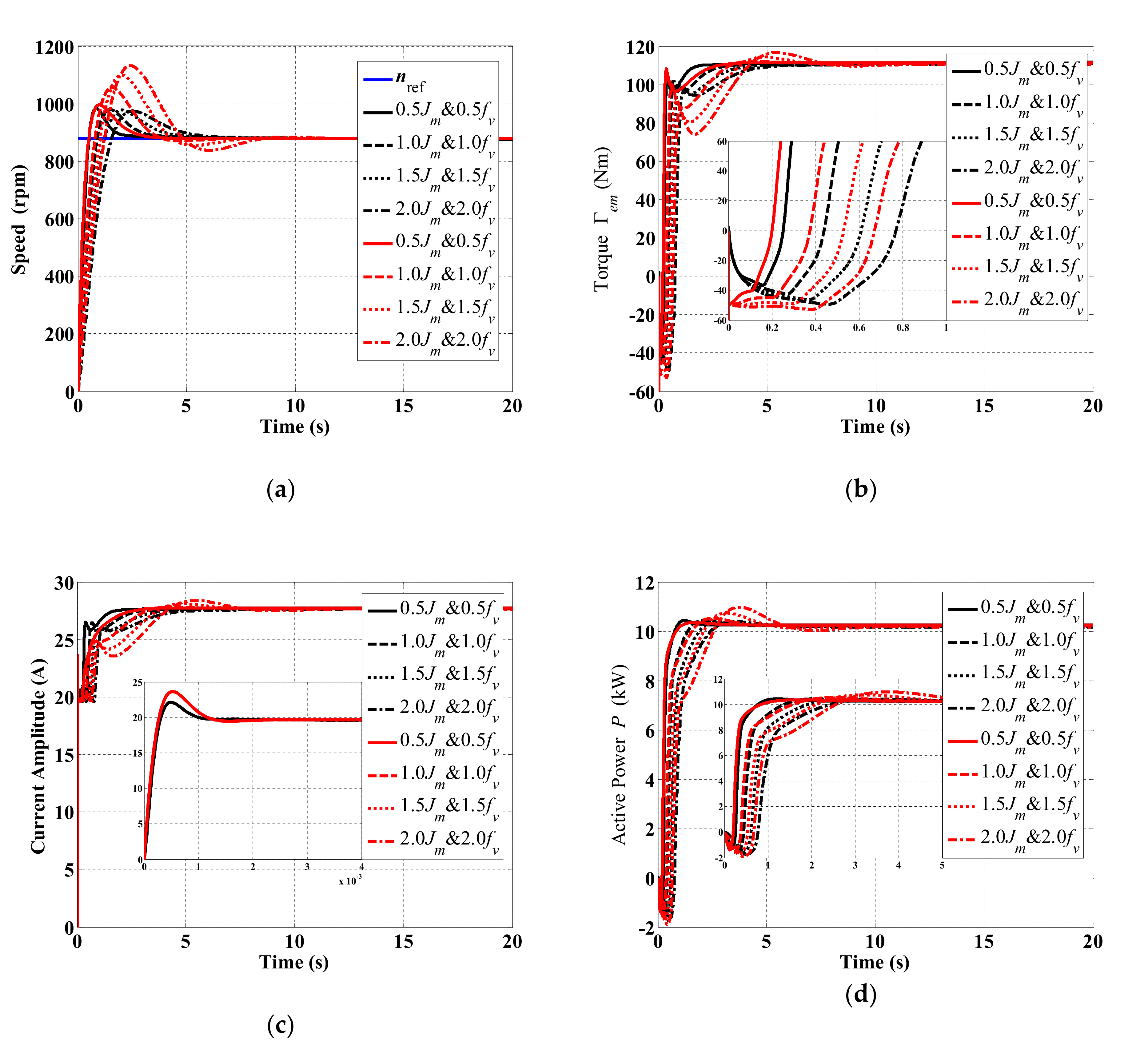
5.2. Robustness Analysis
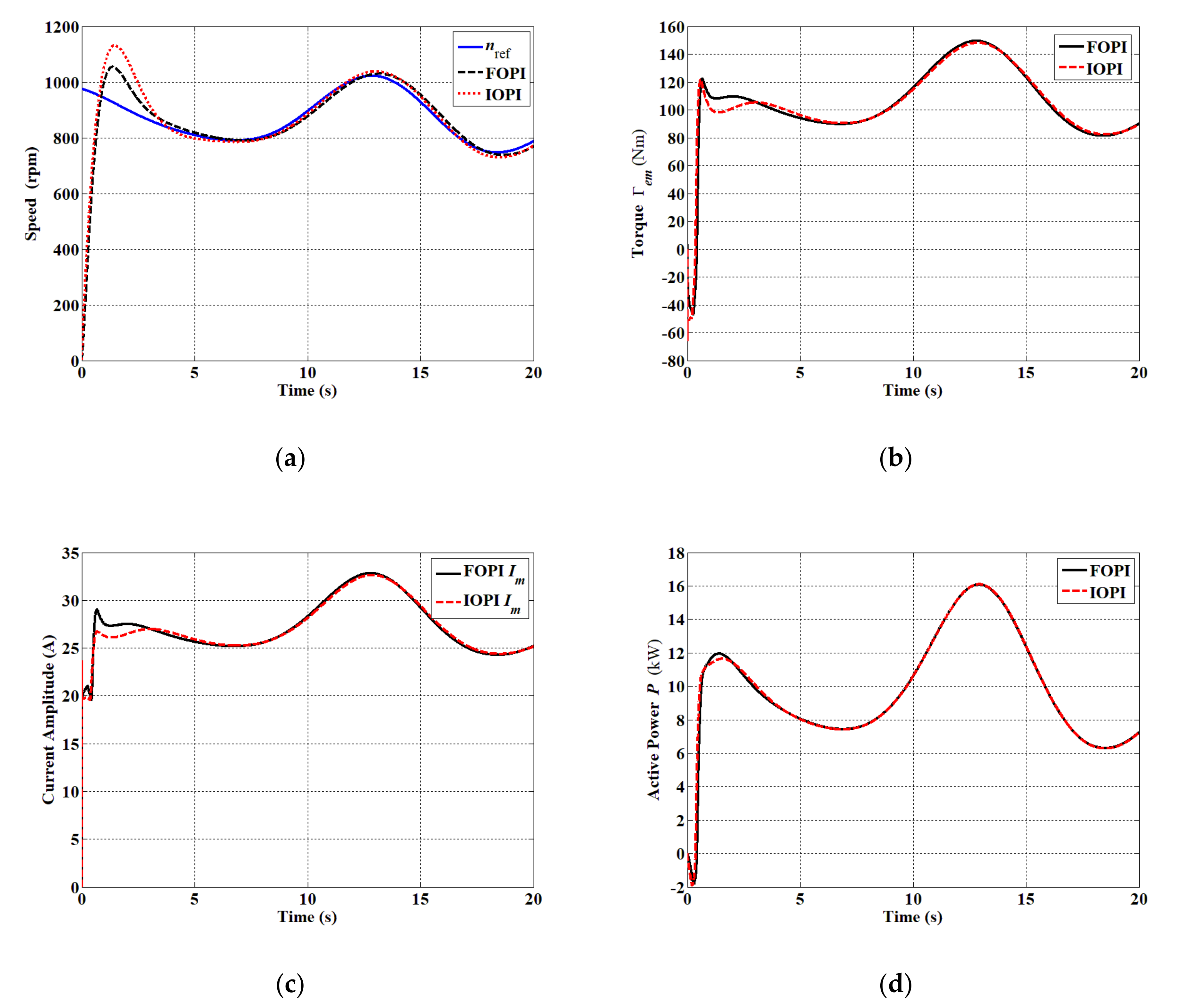
5.3. Performance Analysis with the Tidal Current Variation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| TST | Tidal Stream Turbine |
| WECS | Wind Energy Conversion System |
| IOPI | Integer-Order PI |
| FOPI | Fractional-Order PI |
| TSR | Tip Speed Ratio/λ |
| PMSG | Permanent Magnet Synchronous Generator |
| DFIG | Doubly-Fed Induction Generator |
| DSPM | Doubly Salient Permanent Magnet machine |
| SMC | Sliding Mode Control |
| HOSMC | High-Order Slide Mode Control |
| MPC | Model Predictive Control |
| NPC | Nonlinear Predictive Control |
| ADRC | Active Disturbance Rejection Control |
| ITAE | Integral of Time multiplied by Absolute Error |
| PSO | Particle Swarm Optimization |
| ITSE | Integral of the Time multiplied Square Error |
| BFO | Bacterial Foraging Optimization |
| ASR | Automatic Speed Regulator |
| RSC | Rotor-Side Converter |
| ACR | Automatic Current Regulator |
| CRONE | Commande Robuste d’Ordre Non Entier |
| TID | Tilt-Integral Derivative |
| FOPID | Fractional-Order PID |
| ρ | Seawater density (1024 kg/m3) |
| Cp | Power coefficient, also called Betz’s coefficient |
| λ | Tip Speed Ratio (TSR) |
| Ωturbine, Ωm | Mechanical speed of the turbine/DFIG (rad/s) |
| a, b | Axial and tangential flow induction factors |
| dFN, dFT | Axial and tangential components of the blade element hydrodynamic forces (N) |
| ϕ | Angle of the resultant velocity “W” relative to the rotor plane (rad) |
| R, R | Radius of the turbine (m), the resistance (Ω) |
| Nb | Number of the blades |
| s, r | Stator/rotor index |
| d, q | Synchronous reference frame index |
| V, i, φ, ω | Voltage (V), current (A), flux (Wb) and electrical speed (rad/s) |
| sl | Slip |
| ωsl | Rotor current speed (rad/s) |
| Ls, Lr, Lm | Self inductances of the stator and rotor, and mutual inductances (H, H, H) |
| Γem | Electromagnetic torque (Nm) |
| np | Number of the pole pair |
| Jm | Inertia (kg*m2) |
| fv | Viscosity coefficient |
| Ps, Qs | Stator active and reactive powers (W, VAR) |
| Ngear | Ratio of the gearbox |
| Vs | Voltage amplitude (V) |
| ξ | Damping ratio |
| e, m | electrical/mechanical index |
| ts | Settling time of the closed-loop (s) |
| kp, ki | Proportional and integral coefficients |
| ωc, γc | Gain crossover frequency and the phase margin for the open-loop (rad/s, rad) |
| Kp, Ki, Kd | Proportional, integral and differential constants |
| λ and μ | Integral and differential orders |
| K | Amplification coefficient which can be integrated into the proportional coefficient Kp |
| T | Time constant |
| γ | Peak enhancement factor which indicates the ratio of the maximal spectral energy to the maximum of the corresponding Pierson-Moskowitz spectrum |
| LF | Fetch length (m) |
| Vwind | Wind speed (m/s) |
| g | Acceleration of gravity (m/s2) |
| f, fm | Wave frequency and the frequency at the maximum of the spectrum (Hz, Hz) |
| kJ | Usual Phillips constant |
| Ti | Swell period of each component (s) |
| φi | Initial phase of each term which is given randomly (rad) |
| depth | Sea depth (m) |
| x, z | Horizontal and vertical point for the calculation (m) |
References
- Chen, H.; Tang, T.H.; Aït-Ahmed, N.; Benbouzid, M.; Machmoum, M.; Zaïm, M.E.H. Attraction, challenge and current status of marine current energy. IEEE Access 2018, 6, 12665–12685. [Google Scholar] [CrossRef]
- Zhou, Z.; Benbouzid, M.; Charpentier, J.F.; Scuiller, F.; Tang, T. Developments in large marine current turbine technologies—A review. Renew. Sustain. Energy Rev. 2017, 77, 852–858. [Google Scholar] [CrossRef]
- Touimi, K.; Benbouzid, M.; Tavner, P. Tidal stream turbines: With or without a gearbox? Ocean Eng. 2018, 170, 74–88. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Zhou, Z.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.; Tang, T. Power control of a nonpitchable PMSG-based marine current turbine at overrated current speed with flux-weakening strategy. IEEE J. Ocean. Eng. 2015, 40, 536–545. [Google Scholar] [CrossRef]
- Anwar, M.B.; Moursi, M.S.E.; Xiao, W. Dispatching and frequency control strategies for marine current turbines based on doubly fed induction generator. IEEE Trans. Sustain. Energy 2015, 7, 262–270. [Google Scholar] [CrossRef]
- Zhou, Z.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.; Tang, T. Power Limitation Control for a PMSG-Based Marine Current Turbine at High Tidal Speed and Strong Sea State. In Proceedings of the 2013 International Electric Machines & Drives Conference (IEEE IEMDC′13), Chicago, IL, USA, 12–15 May 2013; pp. 75–80. [Google Scholar]
- Zhou, Z.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.; Tang, T. Grid-Connected Marine Current Generation System Power Smoothing Control Using Supercapacitors. In Proceedings of the IECON 2012, 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4035–4040. [Google Scholar]
- Greco, L.; Testa, C.; Cirrincione, M.; Pucci, M.; Vitale, G. Effectiveness of a GNG-based MPPT and related control system for marine current turbines in unsteady operating conditions. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE2015), Montreal, QC, Canada, 20–24 September 2015; pp. 1027–1034. [Google Scholar]
- Anwar, B.; Moursi, M.S.E.; Xiao, W. A Novel Frequency Control Strategy for Large Scale Marine Current Turbines Based on Doubly Fed Induction Generator. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014; pp. 1–6. [Google Scholar]
- Pucci, M.; Cirrincione, M.; Greco, L.; Testa, C.; Vitale, G. Marine current turbine generator system with induction machine growing neural gas (GNG) MPPT based on sensorless sea speed estimation. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE2015), Montreal, QC, Canada, 20–24 September 2015; pp. 3901–3908. [Google Scholar]
- Ghefiri, K.; Bouallègue, S.; Haggège, J.; Ghefiri, K.; Garrido, I.; Garrido, A.J. Modeling and MPPT control of a Tidal stream generator. In Proceedings of the 2017 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; pp. 1003–1008. [Google Scholar]
- Fall, O.; Charpentier, J.F.; Nguyen, N.K.; Letellier, P. Maximum Torque Per Ampere Control Strategy of a 5-phase PM Generator in healthy and faulty modes for tidal marine turbine application. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition (PEAC), Shanghai, China, 5–8 November 2014; pp. 468–473. [Google Scholar]
- Mademlis, G.; Liu, Y.; Chen, P.; Singhroy, E. Generator Speed Control and Experimental Verification of Tidal Undersea Kite Systems. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1531–1537. [Google Scholar]
- Jahromi, M.J.; Maswood, A.I.; Tseng, K.J. Design and evaluation of a new converter control strategy for near-shore tidal turbines. IEEE Trans. Ind. Electron. 2013, 60, 5648–5659. [Google Scholar] [CrossRef]
- Toumi, S.; Benelghali, S.; Trabelsi, M.; Elbouchikhi, E.; Momouni, M.F. Robustness Analysis and Evaluation of a PMSG-based Marine Current Turbine System under Faulty Conditions. In Proceedings of the 2014 15th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Hammamet, Tunisia, 21–23 December 2014; pp. 631–636. [Google Scholar]
- Barakat, M.R.; Tala-Ighil, B.; Chaoui, H.; Gualous, H.; Slamani, Y.; Hissel, D. Energetic Macroscopic Representation of a Marine Current Turbine System with Loss Minimization Control. IEEE Trans. Sustain. Energy 2018, 9, 106–117. [Google Scholar] [CrossRef]
- BenElghali, S.E.; Benbouzid, M.; Charpentier, J.F. Modeling and control of a marine current turbine driven doubly-fed induction generator. IET Renew. Power Gener. 2010, 4, 1–11. [Google Scholar] [CrossRef]
- Zhou, Z.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.; Tang, T. Power Smoothing Control in a Grid-Connected Marine Current Turbine System for Compensating Swell Effect. IEEE Trans. Sustain. Energy 2013, 4, 816–826. [Google Scholar] [CrossRef]
- BenElghali, S.E.; Benbouzid, M.; Charpentier, J.F.; Ahmed-Ali, T.; Munteanu, I. Experimental Validation of a Marine Current Turbine Simulator: Application to a Permanent Magnet Synchronous Generator-Based System Second-Order Sliding Mode Control. IEEE Trans. Ind. Electron. 2011, 58, 118–126. [Google Scholar] [CrossRef]
- BenElghali, S.E.; Benbouzid, M.; Ahmed-Ali, T.; Charpentier, J.F. High-Order Sliding Mode Control of a Marine Current Turbine Driven Doubly-Fed Induction Generator. IEEE J. Ocean. Eng. 2010, 35, 402–411. [Google Scholar] [CrossRef]
- Mekri, F.; BenElghali, S.E.; Benbouzid, M. Fault-tolerant control performance comparison of three- and five-phase pmsg for marine current turbine applications. IEEE Trans. Sustain. Energy 2013, 4, 425–433. [Google Scholar] [CrossRef]
- BenElghali, S.E.; Mekri, F.; Benbouzid, M.; Charpentier, J.F. Performance Comparison of Three- and Five-Phase Permanent Magnet Generators for Marine Current Turbine Applications Under Open-Circuit Faults. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Chen, H.; Tang, S.F.; Han, J.G.; Aït-Ahmed, N.; Tang, T. Second-Order Sliding Mode Current Control of Doubly Salient Permanent Magnet Generator. In Proceedings of the IECON 2019, 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 7010–7015. [Google Scholar]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust Speed Control of PMSM Using Sliding Mode Control (SMC)—A Review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Gu, Y.J.; Yin, X.X.; Liu, H.W.; Li, W.; Lin, Y.G. Fuzzy terminal sliding mode control for extracting maximum marine current energy. Energy 2015, 90, 258–265. [Google Scholar] [CrossRef]
- Pham, H.T.; Bourgeot, J.M.; Benbouzid, M. Fault-tolerant finite control set-model predictive control for marine current turbine applications. IET Renew. Power Gener. 2018, 12, 415–421. [Google Scholar] [CrossRef]
- Toumi, S.; Amirat, Y.; Trabelsi, M.; Elbouchikhi, E.; Mimouni, M.F.; Benbouzid, M. Backstepping control of a PMSG-based marine current turbine system under faulty conditions. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; pp. 1–6. [Google Scholar]
- Yin, X.; Zhao, X. ADV Preview Based Nonlinear Predictive Control for Maximizing Power Generation of a Tidal Turbine with Hydrostatic Transmission. IEEE Trans. Energy Conv. 2019, 34, 1781–1791. [Google Scholar] [CrossRef]
- Yin, X.X.; Zhang, W.C.; Jiang, Z.S.; Pan, L.; Lei, M.Z. Adaptive backstepping control for maximizing marine current power generation based on uncertainty and disturbance estimation. Int. J. Electr. Power Energy Syst. 2020, 117, 1–11. [Google Scholar] [CrossRef]
- Khan, N.; Rabbi, S.F.; Hinchey, M.J.; Rahman, M.A. An adaptive nonlinear MPPT controller for stand alone marine current energy conversion systems. In Proceedings of the IECON 2013, 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 406–411. [Google Scholar]
- Khan, N.; Rabbi, S.F.; Hinchey, M.J.; Rahman, M.A. Adaptive backstepping based maximum power point tracking control for a variable speed marine current energy conversion system. In Proceedings of the 26th IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Regina, SK, Canada, 5–8 May 2013; pp. 1–5. [Google Scholar]
- Choi, J.S.; Jeong, R.G.; Shin, J.H.; Kim, C.K.; Kim, Y.S. New control method of maximum power point tracking for tidal energy generation system. In Proceedings of the 2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, Korea, 8–11 October 2007; pp. 165–168. [Google Scholar]
- Ghefiri, K.; Garrido, I.; Garrido, A.J.; Bouallègue, S.; Haggège, J. Fuzzy Gain Scheduling of a Rotational Speed Control for a Tidal Stream Generator. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 1271–1277. [Google Scholar]
- Zhou, Z.; BenElghali, S.E.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E.; Feld, G. Control Strategies for Tidal Stream Turbine Systems-A Comparative Study of ADRC, PI, and High-Order Sliding Mode Controls. In Proceedings of the IECON 2019, 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 6981–6986. [Google Scholar]
- Zhou, X.; Wang, T.; Zhang, M.; Xie, T.; Li, Z.; Pandey, S. A Control Strategy for Active Disturbance Rejection Control Based on Marine Current Turbine. In Proceedings of the IECON 2019, 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 6975–6980. [Google Scholar]
- Zhou, Z.; BenElghali, S.E.; Benbouzid, M.; Amirat, Y.; Elbouchikhi, E.; Feld, G. Tidal stream turbine control: An active disturbance rejection control approach. Ocean Eng. 2020, 202, 107190. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 251–256. [Google Scholar]
- Kumar, D.M.; Mudaliar, H.K.; Cirrincione, M.; Mehta, U.; Pucci, M. Design of a Fractional Order PI (FOPI) for the Speed Control of a High-Performance Electrical Drive with an Induction Motor. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 1198–1202. [Google Scholar]
- Tavazoei, M.S. From Traditional to Fractional PI Control: A Key for Generalization. IEEE Ind. Electron. Mag. 2012, 6, 41–51. [Google Scholar] [CrossRef]
- Hammami, R.; Ameur, I.B.; Jelassi, K. Performance evaluation of fractional order controller for induction machine control and comparative study between FOC PI & FOC FOPI. In Proceedings of the 2017 18th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2017; pp. 272–277. [Google Scholar]
- Yu, W.; Chen, Y.Q.; Luo, Y.; Pi, Y.G. Frequency domain modelling and control of fractional-order system for permanent magnet synchronous motor velocity servo system. IET Contr. Theory Appl. 2016, 10, 136–143. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behaviour of real material. J. Appl. Mech. Trans. ASME 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Luo, Y.; Li, H.S.; Chen, Y.Q. Fractional order proportional and derivative controller synthesis for a class of fractional order systems: Tuning rule and hardware-in-the-loop experiment. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 14–18 December 2009; pp. 5406–5465. [Google Scholar]
- Luo, Y.; Chen, Y.Q.; Wang, C.Y.; Pi, Y.G. Tuning fractional order proportional integral controllers for fractional order systems. J. Process Control 2010, 20, 823–831. [Google Scholar] [CrossRef]
- Hammami, R.; Ameur, I.B.; Jelassi, K. Induction machine: Fractional order proportional integral speed control. In Proceedings of the 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2016; pp. 276–288. [Google Scholar]
- Li, C.; Chen, M.; Gao, S. Fractional order PI speed control for permanent magnet synchronous motor drives. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 4681–4685. [Google Scholar]
- Wang, D.; Song, B.; Kang, C.; Xu, J. Design of Fractional Order PI Controller for Permanent Magnet Synchronous Motor. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC 2018), Xi’an, China, 25–27 May 2018; pp. 780–784. [Google Scholar]
- Wang, R.; Pi, Y. Fractional-order PI speed control for permanent magnet synchronous motor. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 2303–2308. [Google Scholar]
- Wang, X.; Jiang, S.; Pan, Z.; Hoang, T.T.G.; Tian, L. Fractional-order Identification and Control of Permanent Magnet AC Servo System. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 3108–3113. [Google Scholar]
- Evangeline, S.J.; Venmathi, K.; Ajayan, S. Speed control of switched reluctance motor using fractional order control. In Proceedings of the 2017 International Conference on Innovations in Electrical, Electronics, Instrumentation and Media Technology (ICEEIMT), Coimbatore, India, 3–4 February 2017; pp. 367–372. [Google Scholar]
- Dieng, A.; Benkhoris, M.F.; Aït-Ahmed, M. Torque control strategy of non-sinusoidal Brushless DC Motor based on fractional regulator. In Proceedings of the 2012 International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM2012), Sorrento, Italy, 20–22 June 2012; pp. 207–212. [Google Scholar]
- Dieng, A.; Benkhoris, M.F.; Aït-Ahmed, M.; Le Claire, J.C. Fault-tolerant control of 5-phase pmsg for marine current turbine applications based on fractional controller. IFAC Proc. Vol. 2014, 47, 11950–11955. [Google Scholar] [CrossRef]
- Dieng, A.; Benkhoris, M.F.; Aït-Ahmed, M. Torque ripples reduction of five-phase PMSM using fractional order regulator. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1114–1120. [Google Scholar]
- Chowdhury, D.R.; Dey, J.; Mondal, R. Optimal parameter selection of fractional order PIλ controller for speed control of DC motor. In Proceedings of the 2017 IEEE Calcutta Conference (CALCON 2017), Kolkata, India, 2–3 December 2017; pp. 347–351. [Google Scholar]
- Ghasemi, S.; Tabesh, A.; Askari-Marnani, J. Application of Fractional Calculus Theory to Robust Controller Design for Wind Turbine Generators. IEEE Trans. Energy Conv. 2014, 29, 780–787. [Google Scholar] [CrossRef]
- Zhang, B.T.; Pi, Y. Robust fractional order proportion-plus-differential controller based on fuzzy inference for permanent magnet synchronous motor. IET Contr. Theory Appl. 2012, 6, 829–837. [Google Scholar] [CrossRef]
- Thakar, U.; Joshi, V.; Vyawahare, V. Design of fractional-order PI controllers and comparative analysis of these controllers with linearized, nonlinear integer-order and nonlinear fractional-order representations of PMSM. Int. J. Dyn. Control 2017, 5, 187–197. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, M.; Yuan, X.; Ruan, Y. Direct instantaneous torque control system for switched reluctance motor in electric vehicles. J. Eng. 2019, 2019, 1847–1852. [Google Scholar] [CrossRef]
- Chen, H.; Aït-Ahmed, N.; Machmoum, M.; Zaïm, M.E.H. Modeling and vector control of marine current energy conversion system based on doubly salient permanent magnet generator. IEEE Trans. Sustain. Energy 2016, 7, 409–418. [Google Scholar] [CrossRef]
- BenElghali, S.E.; Benbouzid, M.; Charpentier, J.F. Generator systems for marine current turbine applications: A comparative study. IEEE J. Ocean. Eng. 2012, 37, 554–563. [Google Scholar] [CrossRef]
- Batten, W.M.J.; Bahaj, A.S. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
- Chen, H.; Chen, X.; Xie, W. Fractional-Order PI Controller for DFIG-Based Marine Tidal Current Applications. In Proceedings of the 2018 International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 11th ed.; Pearson Education Press: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Liu, K.; Hou, C.; Hua, W. A Novel Inertia Identification Method and Its Application in PI Controllers of PMSM Drives. IEEE Access 2019, 7, 13445–13454. [Google Scholar] [CrossRef]
- Sakai, K.; Ishida, Y. A design of an improved anti-windup control using a pi controller based on a pole placement method. Int. J. Simulat. Syst. Sci. Technol. 2016, 17, 1. [Google Scholar]
- Oustaloup, A. The CRONE approach: Theoretical developments and major applications. IFAC Proc. Vol. 2006, 39, 324–354. [Google Scholar] [CrossRef]
- Lurie, B.J. Three-parameter tunable tilt-integral derivative (TID) controller. U.S. Patent 5,371,670, 1994. [Google Scholar]
- Yeroglu, C.; Tan, N. Note on fractional-order proportional-integral-differential controller design. IET Control Theory Appl. 2011, 5, 1978–1989. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Jin, Y. Fractional Order PID controller Synthesis, Auto-Tuning and Experiment Studies for Robust Motion Control Systems. Ph.D. Thesis, Hunan University, Hunan, China, 2010. [Google Scholar]
- Podlubny, I.; Petráš, I.; Skovranek, T.; Terpak, J. Toolboxes and programs for fractional-order system identification, modeling, simulation, and control. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), Tatranska Lomnica, Slovakia, 29 May–1 June 2016; pp. 608–612. [Google Scholar]
- Mahvasha, H.; Tahera, S.A.; Rahimia, M.; Shahidehpourb, M. DFIG performance improvement in grid connected mode by using fractional order [PI] controller. Electr. Power Energy Syst. 2018, 96, 398–411. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, C.; Deng, W. Study on A Combined Optimal Rational Approximation Method of Fractional-order Calculus Operator and Its Application. Recent Adv. Electr. Electron. Eng. 2017, 10, 279–290. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Bhaska, R.; Xue, D.Y. Practical tuning rule development for fractional order proportional and integral controllers. J. Comput. Nonlinear Dyn. 2008, 3, 021403. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Han, Y.M.; Cao, P.L.; Jiang, L. Adaptive fractional-order PID control of PMSG-based wind energy conversion system for MPPT using linear observers. Int. Trans. Electr. Energy Syst. 2019, 29, e2697. [Google Scholar] [CrossRef]
- Nangrani, S.P.; Bhat, S.S. Numerical study of optimized fractional-order controller for chaos control of nonlinear dynamical power system. Int. Trans. Electr. Energy Syst. 2017, 27, e2336. [Google Scholar] [CrossRef]
- Ruszewski, A.; Sobolewski, A. Comparative studies of control systems with fractional controllers. Electr. Rev. 2012, R88, 204–208. [Google Scholar]
- Li, H.; Luo, Y.; Chen, Y. A Fractional Order Proportional and Derivative (FOPD) Motion Controller: Tuning Rule and Experiments. IEEE Trans. Control Syst. Technol. 2010, 18, 516–520. [Google Scholar] [CrossRef]
- Titah-Benbouzid, H.; Benbouzid, M. Marine renewable energy converters and biofouling: A review on impacts and prevention. In Proceedings of the 2015 European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015; pp. 1–8. [Google Scholar]
- Song, S.; Shi, W.; Demirel, Y.K.; Atlar, M. The effect of biofouling on the tidal turbine performance. In Proceedings of the 2019 Applied Energy Symposium: MIT A+B (AEAB2019), Boston, MA, USA, 22–24 May 2019. [Google Scholar]
- Wolfram, J.; Theophanatos, A. The Effects of Marine Fouling on the Fluid Loading of Cylinders: Some Experimental Results. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1985; pp. 517–526. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xie, W.; Chen, X.; Han, J.; Aït-Ahmed, N.; Zhou, Z.; Tang, T.; Benbouzid, M. Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine. J. Mar. Sci. Eng. 2020, 8, 309. https://doi.org/10.3390/jmse8050309
Chen H, Xie W, Chen X, Han J, Aït-Ahmed N, Zhou Z, Tang T, Benbouzid M. Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine. Journal of Marine Science and Engineering. 2020; 8(5):309. https://doi.org/10.3390/jmse8050309
Chicago/Turabian StyleChen, Hao, Wei Xie, Xiyang Chen, Jingang Han, Nadia Aït-Ahmed, Zhibin Zhou, Tianhao Tang, and Mohamed Benbouzid. 2020. "Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine" Journal of Marine Science and Engineering 8, no. 5: 309. https://doi.org/10.3390/jmse8050309
APA StyleChen, H., Xie, W., Chen, X., Han, J., Aït-Ahmed, N., Zhou, Z., Tang, T., & Benbouzid, M. (2020). Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine. Journal of Marine Science and Engineering, 8(5), 309. https://doi.org/10.3390/jmse8050309








