1. Introduction
Many types of offshore structures, including floating islands [
1], floating shelters [
2], floating wind turbines [
3], floating wave energy converters [
4] and floating offshore fish farms [
5], are moored in complicated coastal environments. These structures are exposed to ocean waves, with the possibility of wave reflection and wave shoaling from coastal seabeds. Dynamic responses of these floating bodies are the combined effects of ocean environments and mooring systems. Accurate predictions of dynamic responses are of practical importance for the design and manufacture of these offshore structures.
Compared with that of deep water offshore structures, design and construction of floating structures in coastal environments face unique challenges and the dynamics of these structures could be more complicated because of the seabed effects. Previous researches suggest that shallow waters can excite larger responses of offshore structures under hydrodynamic loading because of the flat seabed effects [
6,
7,
8]. As numerical approaches for flat seabeds are not directly applicable to sloping seabed profiles, refs. [
9,
10] developed second-body models to account for the sloping seabed effect within the boundary element model frame and found that a sloping seabed significantly influences the cross coupling hydrodynamic coefficients. Refs. [
11,
12] developed multi-domain approaches that divide the fluid domain into an interior domain of variable water depth and an exterior domain of constant depth. An extra term accounting for the sloping-bottom effects is introduced to correct the incident wave potential so that the sloping seabed condition is satisfied. They found that the sloping seabed significantly affects the body motion response amplitude operator (RAO). Ref. [
13] coupled a Rankine source model to the Boussinesq equation, which supplies all relevant information concerning the fluid domain. They reported that the peak frequency of the exciting forces and motion responses are shifted ahead due to the sloping seabed effects. Refs. [
14,
15] introduced a reflection velocity potential to account for the sloping seabed effect. Numerical results demonstrated that the sloping seabed alters the symmetrical profile of the fluid domain and the coupled effects between different motion modes become important. However, the mooring lines are not considered in these numerical models.
Mooring systems serve as station-keeping devices used to maintain a floating body in acceptable positions. Mooring systems can be categorised based on the restoring mechanisms, weathervaning characteristics and so forth. For a taut-leg mooring, the elastic stiffness due to line stretch is the dominant source of restoring, while for a catenary mooring configuration, the mooring restoring comes primarily from the geometry stiffness of the lines in normal sea states as the floating structure moves within certain offset ranges [
16]. As a result of the relatively cheap anchoring costs and convenient offshore installation, the catenary mooring configuration has been extensively applied in various water depths [
17,
18] and with different component compositions [
19]. For instance, Ref. [
20] found that proper application of clump weights and buoys can increase the mooring restoring force and floating body capacity, but this will add extra difficulty for practical operation.
Numerical modelling of catenary mooring lines has different levels of fidelity. The quasi-static approach based on the catenary equations does not consider mooring dynamics and facilitates frequency-domain analysis for preliminary design purposes [
21]. For deep-water applications, the dynamic mooring line tension becomes more important, and semi-analytical methods accounting for simplified dynamics were also proposed [
22]. Later, finite element models [
23,
24] and lumped-mass models [
25] were proposed for time-domain simulations, and these models provide accurate representation of the mooring line dynamics at increased computational costs.
Concerning the modelling of floating body and mooring lines, both uncoupled and coupled analysis have been applied. An uncoupled model essentially ignores the interactions between the floating body and treats a mooring line as a simple massless spring [
26,
27]. Such an approach benefits from less computational cost but sacrifices result accuracy. In comparison, a coupled model addresses the interaction between the floating body and mooring lines and can be particularly important if accurate mooring responses are needed. For a coupled model, frequency-domain and time-domain panel models have been developed to describe the wave phenomena and wave forces. As shown by [
28], both frequency- and time-domain models can be used to deal with nonlinear waves around the floating body, although the latter is less ambiguous for the scattered waves.
Many offshore renewable energy facilities such as wave energy converters are moored in coastal areas with shallow water. Depending on the site conditions, the mooring lines may lie on a sloping seabed, which will change the fluid dynamics and eventually affect the mooring dynamics and power production performance. To examine the influence of seabed conditions without loss of generality, we only consider a floating body with mooring lines in this work. A simplified catenary model is adopted together with a boundary integral method to develop a time-domain coupled numerical model. The boundary integral model comprises three boundary element equations accounting for wave diffraction, wave radiation and wave reflection, respectively. This coupled model is validated by comparison against published data for the static offset, free decay and regular wave tests. Furthermore, numerical simulations are performed for various seabed profiles and mooring line conditions. The numerical study shows that the sloping seabed significantly changes the fluid domain and mooring line profile and therefore results in noticeable effects on the dynamic responses of the coupled floating body-mooring line system. These effects also vary under different sloping seabed with asymmetrical mooring lines conditions compared with the flat seabed case.
It should be noticed that in real ocean environments, inclined seabeds can lead to formation of vortices of various scales which affect the mooring line mechanism as well as the floating body motion characteristics. The present fluid domain is described by potential flow and flow viscosity is essentially ignored. The investigation of vortices on the mooring line and body motion is out of the scope of the present study.
4. Case Study
For a floating body moored in coastal areas, if the mooring line anchors are located in different water depths, then the mooring line profiles are not symmetrical. The asymmetry of seabed and mooring line profiles significantly affects fluid domain and hence the body response characteristics. By comparing the asymmetrical seabed and moorings with the flat seabed and symmetrical mooring lines, this section investigates the floating body response characteristics in sloping seabed and asymmetrical mooring lines conditions.
A rectangular cylinder with breadth
B = 20 m and draft
d = 10 m is selected as the floating body. Such a body size is typical of floating bodies in ocean and offshore engineering. An average water depth of
H = 200 m is considered for the first numerical case. Two types of seabed and mooring line configurations are used in the numerical simulations. The first type is a flat seabed with two identical mooring lines, and the second one is a sloping seabed with two different mooring line arrangement.
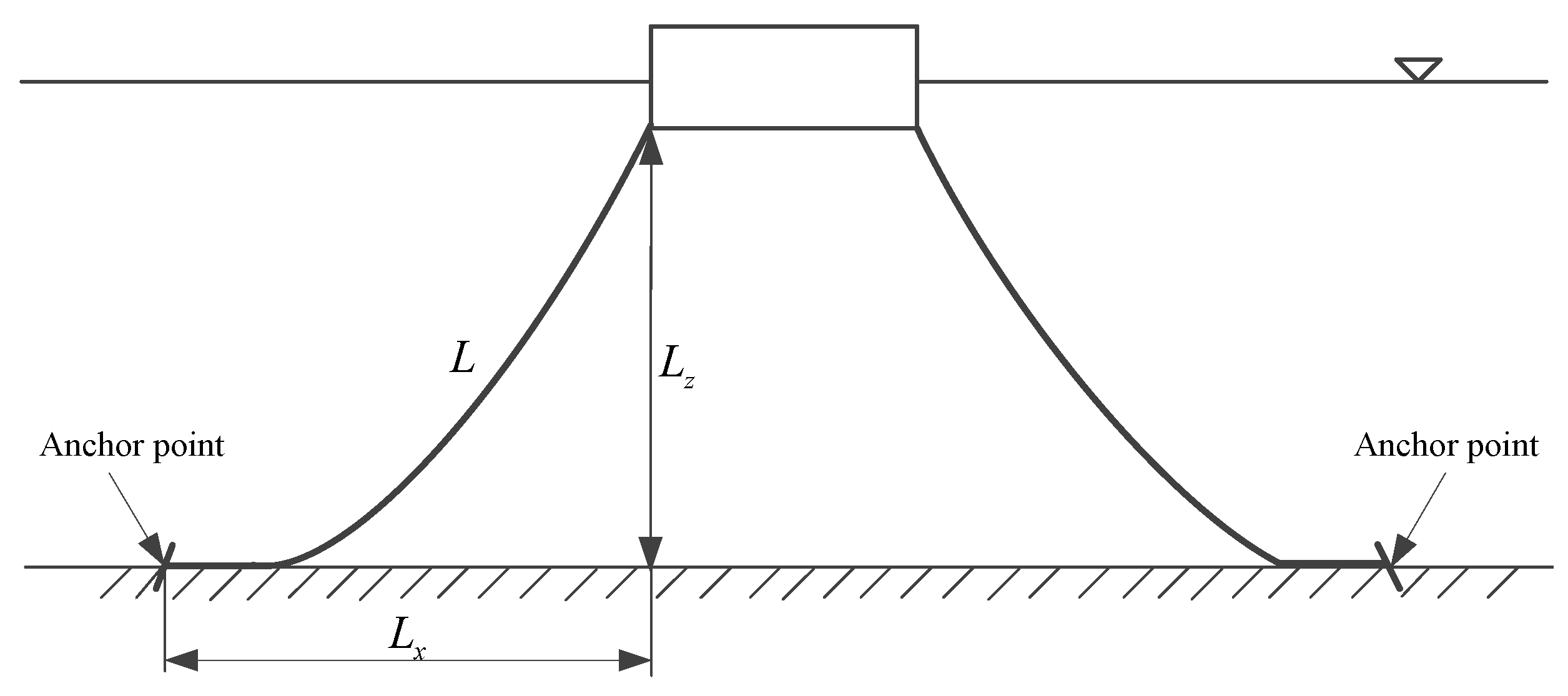
Figure 9 shows the profiles of symmetrical and asymmetrical seabeds with mooring lines. For the flat seabed condition, the left-side mooring line length
and anchor horizontal distance
equal the right-side values
and
. The average water depths
H for the sloping seabeds are same as the flat ones for direct comparisons. Each mooring line has a weight of
W = 5 kN/m in water and two mooring lines are used on each side in the present study unless otherwise stated.
Table 2 shows parameters of the four sets of mooring lines for the symmetrical seabed condition. In the present study,
of the mooring line length are lying on the seabed for all the numerical simulations unless stated otherwise. The incident wave has a wave amplitude
A = 1 m and the mooring line is kept in a catenary profile in all numerical simulations. Free decay test shows the heave nature period for this coupled body and mooring line system are 8.78 s.
Figure 10 shows a comparison of floating body surge motion
between without mooring line condition, mooring line set 1, mooring line set 2, mooring line set 3 and mooring line set 4. It is observed that the mooring line reduces the surge motion
noticeably and the
becomes smaller as the mooring line length increases.
Figure 11 shows a comparison of the heave motion
of the floating body between without mooring line condition, mooring line set 1, mooring line set 2, mooring line set 3 and mooring line set 4. It is noticed that the mooring line reduces the heave motion amplitude significantly. Longer mooring line generates larger restoring force for the floating body and therefore the heave motion amplitude reduces more. The peak value of motion amplitude is shifted towards the high wave frequency as the mooring line length increases. This finding is in line with that of [
36].
In order to investigate the hydrodynamic effects of asymmetrical seabed and mooring line, a symmetrical mooring line set
m is taken as the basis. Two asymmetrical mooring line sets are used in the numerical simulations and the parameters for these two sets of mooring lines are presented in
Table 3. For direct comparison, the total mooring line lengths are same for both symmetrical and asymmetrical mooring line sets. It should be emphasised that the floating body has to be at static equilibrium. This requirement is naturally satisfied for symmetrical mooring line set. For asymmetrical seabed and mooring line set, the left side mooring line is arranged similarly as the symmetrical case, i.e.,
of the mooring line length are laid on the seabed. The right-side mooring line has to be arranged to balance the horizontal mooring line force generated by the left side. An iterative procedure is developed to calculate the anchor horizontal distance
and the anchor vertical distance
is readily available according to the seabed slope once
is obtained. In such arrangement, the difference of vertical mooring line forces generated by the left and right sides is less than
and has marginal effects on the pitch motion of the floating body.
Figure 12 shows a comparison of the surge motion
of the floating body between symmetrical mooring line condition, asymmetrical mooring line set 1 and set 2. It is noticed that the surge motion
reduces appreciably as the asymmetry level increases across the whole wave frequency range. Compared with the symmetrical case, the left-side length of asymmetrical mooring line set 2 increases by
, but it reduces the
by approximately
. If less mooring line length is allowed to lie on the seabed, effects due to the mooring line asymmetry are expected to be more significant. It should be noticed that the difference between the left-and right-side mooring lines is in a reasonable range, otherwise the mooring line set can not keep the floating body at a static equilibrium position. The heave motion
is marginally affected by the asymmetrical mooring line setup and therefore the data are not presented here.
Numerical simulations are further performed for the floating body positioned in a water depth of
m. Both flat seabed with symmetrical mooring lines and sloping seabed with asymmetrical mooring lines are considered. The mooring lines on the sloping seabed have length
but are arranged in asymmetrical position. These mooring lines are lying on flat seabed portion whereas sloping seabed portion is located within two anchor points. Both the symmetrical and asymmetrical mooring line configurations have the same length
m for direct comparison. The
mooring line length is allowed to lie on the seabed for both cases.
Figure 13 shows the profile of an asymmetrical seabed with mooring lines positioned in the water depth
m.
The sloping seabed effect for the incident wave amplitude is first investigated, and no floating body or mooring lines are included in the fluid domain. A linear incident wave with a wave amplitude of
comes from the left-hand side and moves towards the right-hand side as illustrated in
Figure 13.
Figure 14 shows the incident wave amplitude
A on the right- and left-hand sides over a sloping seabed with sloping angle
. The left-hand side has a wave amplitude of
as the incident wave comes from the left. The wave amplitude changes gradually on the sloping part due to the sloping seabed effects. The wave becomes steady when it moves into the flat part on the right-hand side. It is noticed that the incident wave amplitude increases due to the sloping seabed and the sloping seabed has largest effect for the incident wave when the wave frequency is approximately
.
The left-side mooring line weight has a weight of
W = 5 kN/m in water for the sloping seabed case, and the floating body is at a static equilibrium. A preliminary iterative procedure is developed to calculate the right-side mooring line weight per meter to reach static equilibrium.
Figure 15 shows a comparison of the surge motion
of the floating body between a flat seabed and a sloping seabed with
,
and
, respectively. It is noticed that the surge motion
is smaller for the flat seabed than the sloping seabed conditions and
increases as the sloping seabed angle
increases across the frequency range.
Figure 16 shows a comparison of the heave motion
of the floating body between flat seabed, sloping seabed with
,
and
, respectively. It is noticed that the peak responses of the heave motion
are shifted towards lower wave frequency and the peak response values increase along with the sloping seabed angle. The phenomenon presented in
Figure 15 and
Figure 16 implies that the sloping seabed with asymmetrical mooring line arrangement produces less mooring stiffness than does the symmetrical case. In the preliminary study to investigate the right-side mooring weight, numerical simulations show that less weight is required compared with the left side.
Figure 17 shows a comparison of the time record of the floating-body heave motion
for wave frequency
between flat seabed, sloping seabed with
,
and
, respectively. The heave motion
has the largest amplitude for flat seabed condition and the
motion amplitudes decrease as the sloping angles increase. These time-domain results are aligned with those frequency-domain results presented in
Figure 16. In this study, the fluid domain is described by a linear boundary element model. The peak value for heave motion
is around
whereas the trough value is about
. This nonharmonic body motion track demonstrates the nonlinear characteristics of the coupled floating body-mooring line system.
Figure 18 shows a comparison of mooring line force
for wave frequency
between flat seabed, sloping seabed with
,
and
, respectively. The mooring line pretension is excluded in the mooring line force
. The mooring line force
has the largest amplitude for flat seabed condition and
amplitudes decrease as the sloping angles increase. It is also noticed that the force peak values are smaller than the trough values and this phenomenon is due to the fact that the heave motion
peak values are bigger than the trough values.
Figure 19 demonstrates a comparison of time record of floating body surge motion
for wave frequency
between flat seabed, sloping seabed with
,
and
, respectively. The surge motion
peak values are almost same for these different seabed conditions but the
has the least value for flat seabed condition. It is also noticed that the nonlinear characteristics become more obvious as the seabed inclination increases.
Figure 20 shows the wave force
on the moored body excited by an incident wave for the slope seabed angle of
. It is noticeable that the wave force
increases with the wave frequency for
. This wave force
reaches its peak in the period
and decreases gradually with the wave frequency for
. This variation trend is in line with the moored body motion as presented in
Figure 16.
To demonstrate the slope seabed inclination effects for the mooring line force. Numerical simulations are performed for this floating body positioned above a sloping seabed with various inclinations.
Figure 21 shows a comparison of the mooring line force
amplitude for different slope seabed angle
for the floating body experiencing an incident wave with frequency
. It is noticed that the mooring line force
reduces as seabed angle
increases. In the present study, the mooring line and floating body are coupled into an integrated model. The mooring line force is excited mainly due to the floating body motion which is caused by the incident wave. The mooring line force amplitude conforms with the floating body motion amplitude.
It should be noticed that the coupled floating body and mooring line system natural frequency is within the wave frequency range and only the wave-frequency responses are investigated in this paper. The low-frequency responses are very important for large floating bodies.
5. Conclusions
A two-dimensional coupled floating body-mooring line model is developed to study the freely floating body motion responses in both flat and sloping seabed conditions. A continuous Rankine source based boundary element model is established to describe the fluid domain. This model comprises three time-domain boundary integral equations accounting for diffraction problem, radiation problem and reflection problem, respectively. The mooring line is formulated by a catenary mooring line model and coupled with the boundary element model at each time step.
Numerical validations were carried out for the static offset test, free decay test without mooring line, free decay test with mooring line and regular wave simulation. Reasonable agreement with published data demonstrates the accuracy of proposed model.
Two numerical cases are investigated with an emphasis on the hydrodynamic effects of sloping seabed and asymmetrical mooring line. In the first numerical study, both the surge motion and the heave motion decrease as the mooring line length increases for flat seabed condition. For the sloping seabed case, the left and right sides of mooring line have different lengths and are laid on sloping seabed portion. The right-side mooring line is positioned to keep the floating body at static equilibrium. Numerical results show that the surge motion decreases as the asymmetrical level increases across the whole frequency range but the heave motion keeps constant regardless of the asymmetry level. These numerical findings indicate that in such sloping seabed conditions, the mooring line system shows better station-keeping capability than it does in flat seabed conditions.
For the second numerical case, both the left and right sides of mooring lines are laid on flat seabed portion with sloping portion between two anchor points. The left and right mooring line has same length but different weight to keep the floating body in static equilibrium position. Numerical study shows that both the surge motion and heave motion increase as the sloping seabed angle becomes larger. The coupled floating body-mooring line system demonstrates nonlinear characteristics for the body motion and mooring line force responses in the time domain. The surge motion has clearer nonlinear performance than the heave motion. An asymmetrical mooring line configuration demonstrates less station-keeping capability than an symmetrical configuration, but it also requires less mooring line weight and steel consumption. From an economical viewpoint, such a mooring line configuration could be beneficial. In actual industrial projects, the design of asymmetrical mooring line is a trade-off between station-keeping capability and economical benefit.
This paper deals with two-dimensional cases and therefore has academic values, while practical engineering problems are three-dimensional. The study of three-dimensional coupled floating body-mooring line problem and an extention to wave energy converters will be part of our future work.