Suction Bucket Pile–Soil–Structure Interactions of Offshore Wind Turbine Jacket Foundations Using Coupled Dynamic Analysis
Abstract
1. Introduction
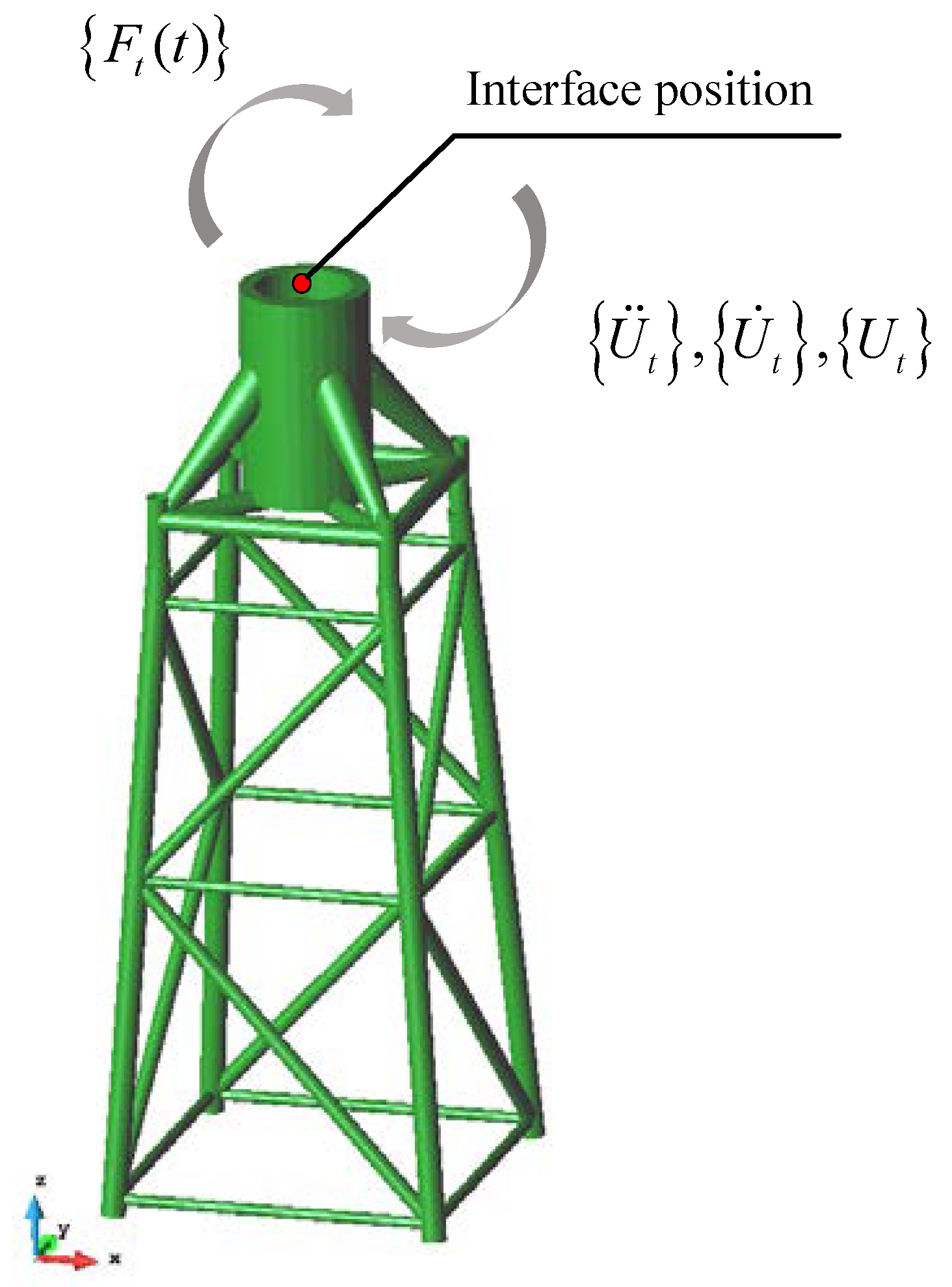
2. Coupled Analysis of Turbine and Support Structure
3. Nonlinear Soil Springs
3.1. Pile Lateral Loads
3.2. Pile Axial Loads and Tip Loads
3.3. Spring Stiffness
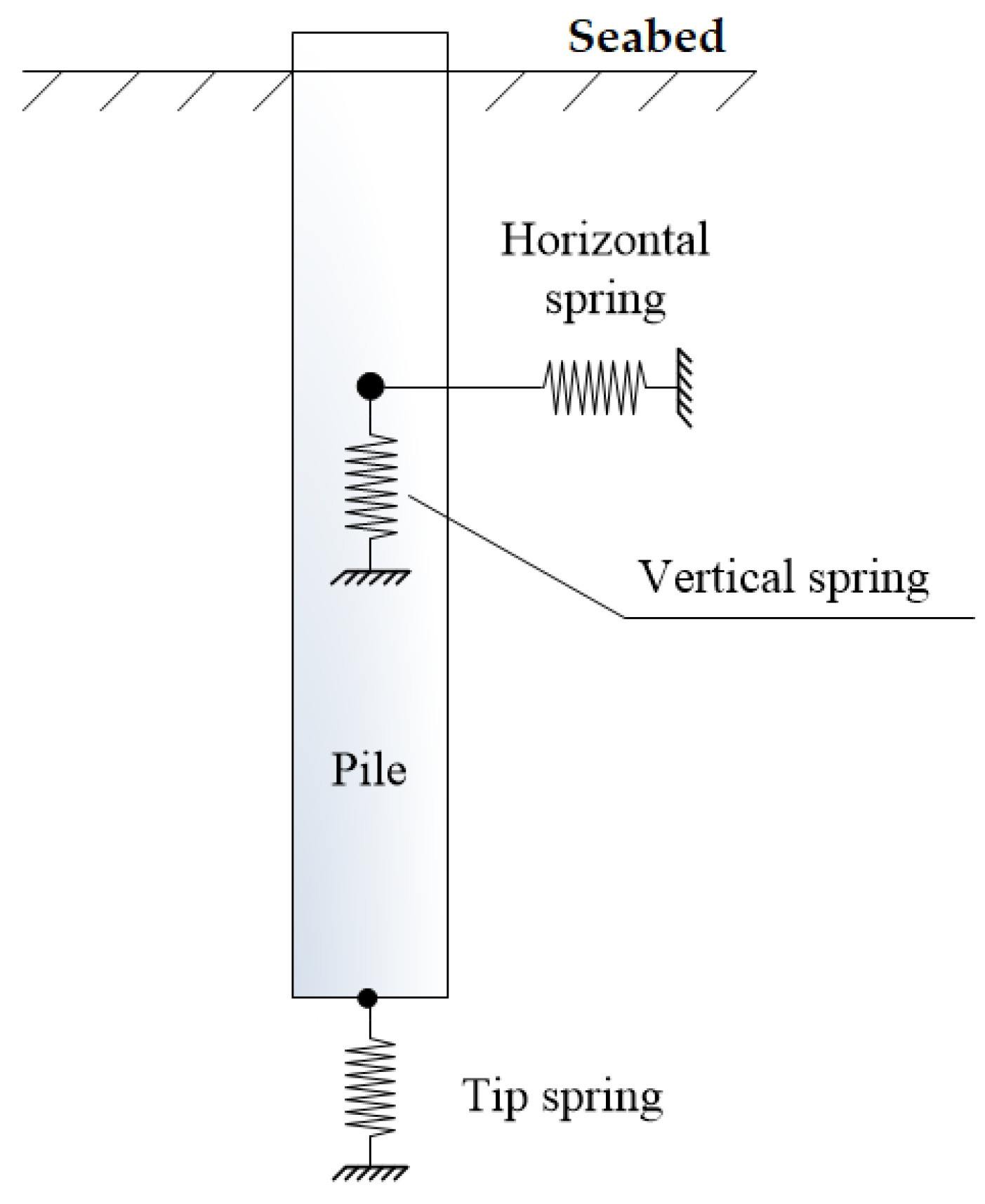
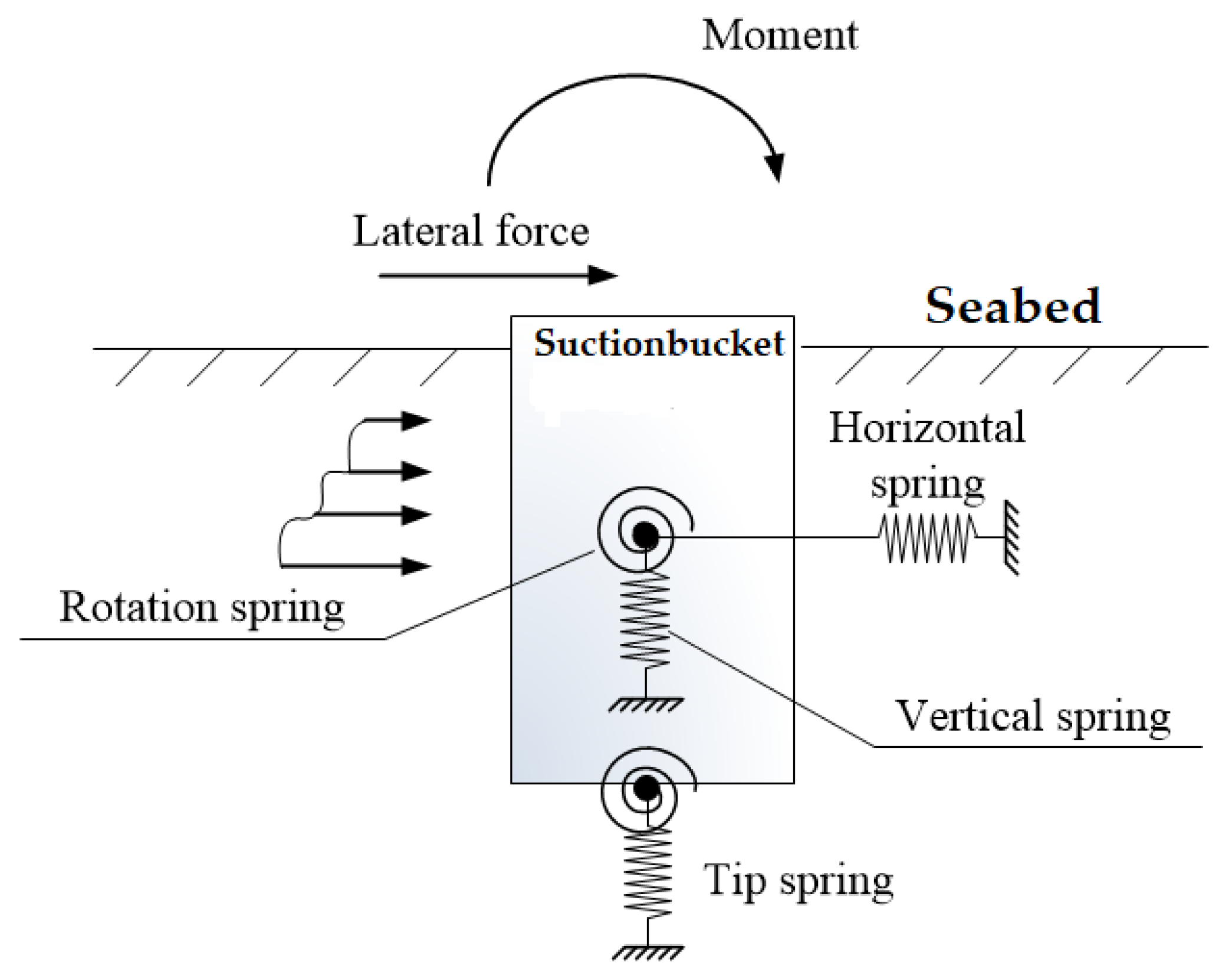
4. Pile–Soil Structure Interaction
5. Wave Excitations and Hydrodynamics
5.1. Hydrodynamic Forces, Added Mass and Damping
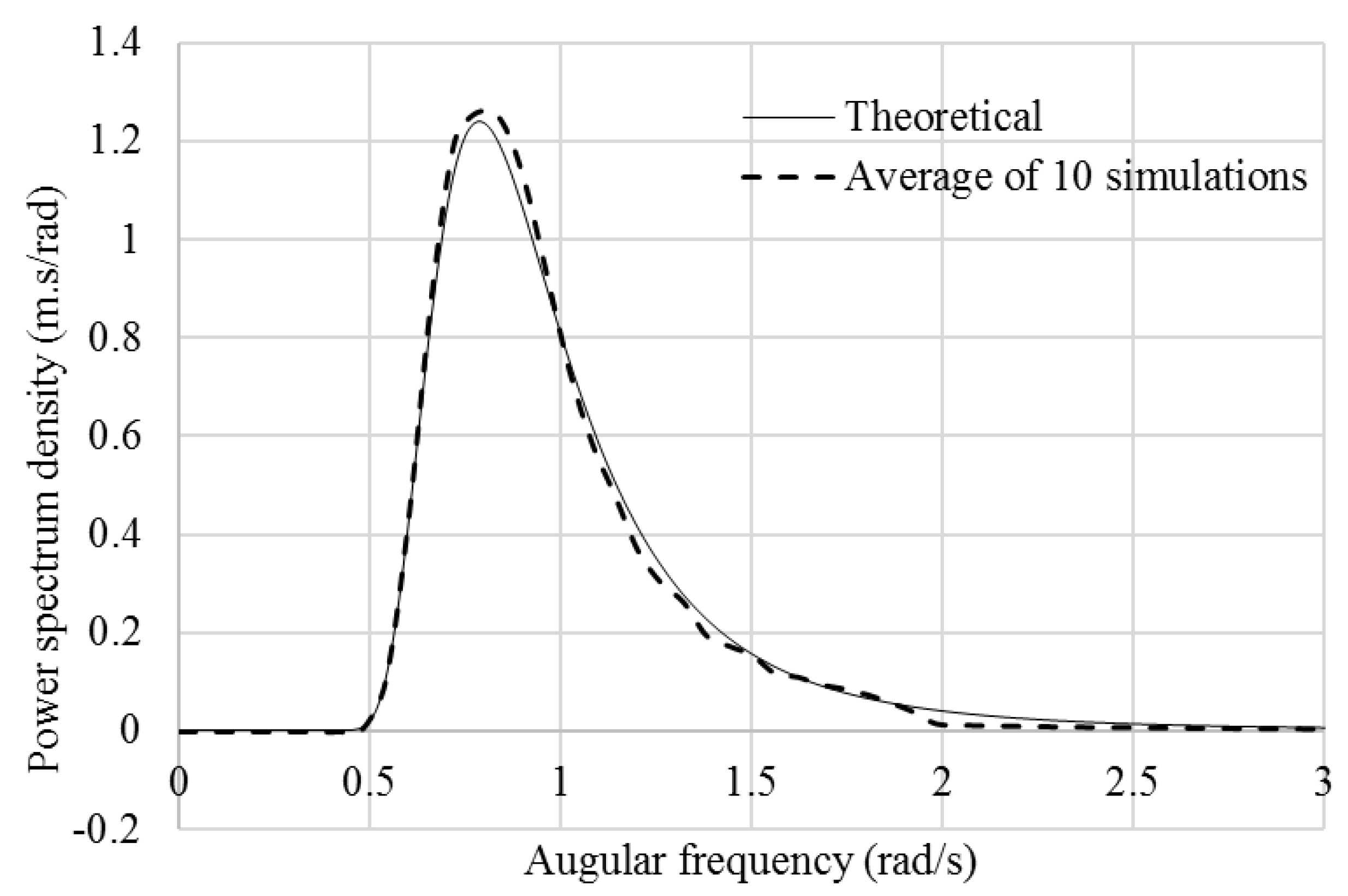
5.2. Random Waves
6. Numerical Study
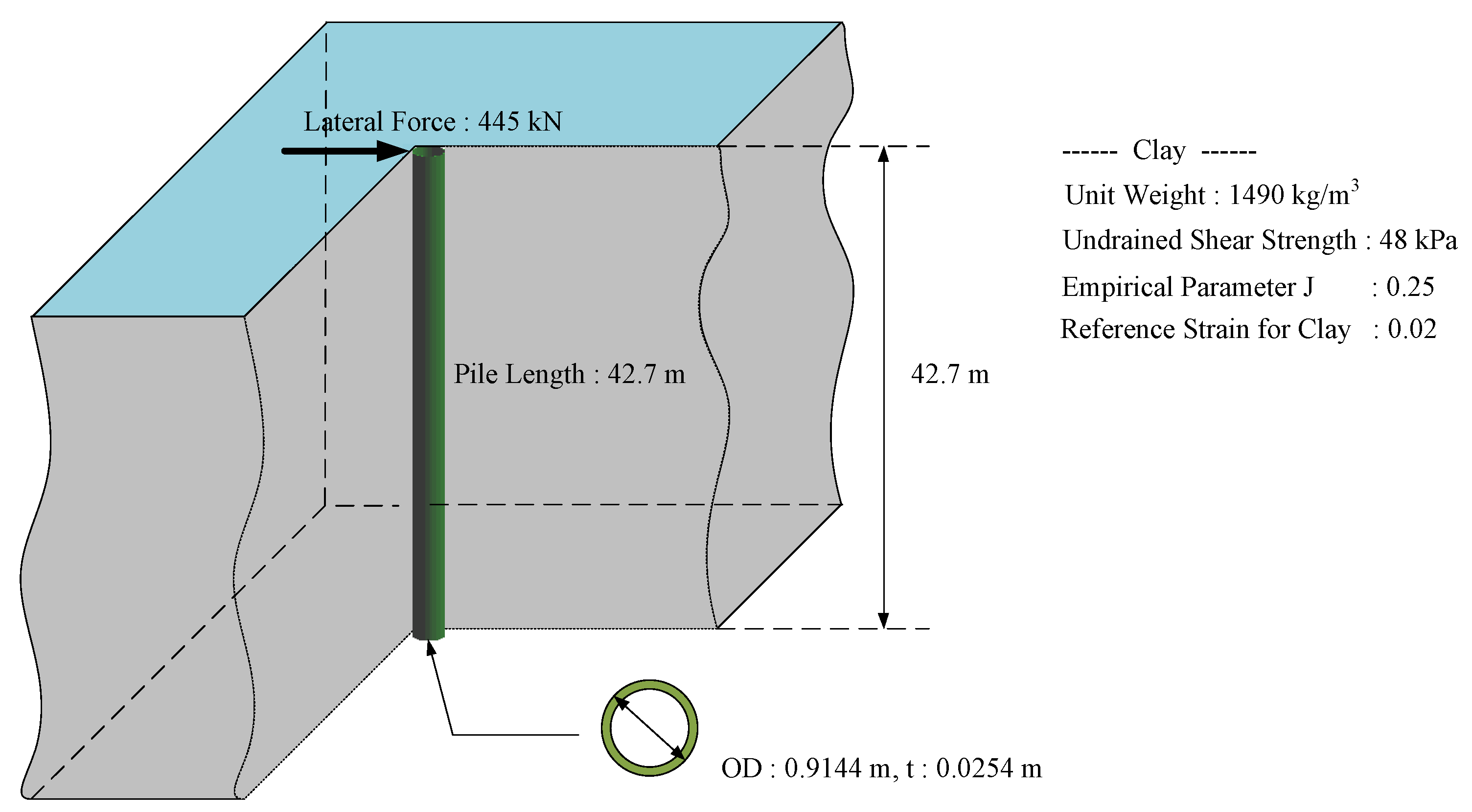
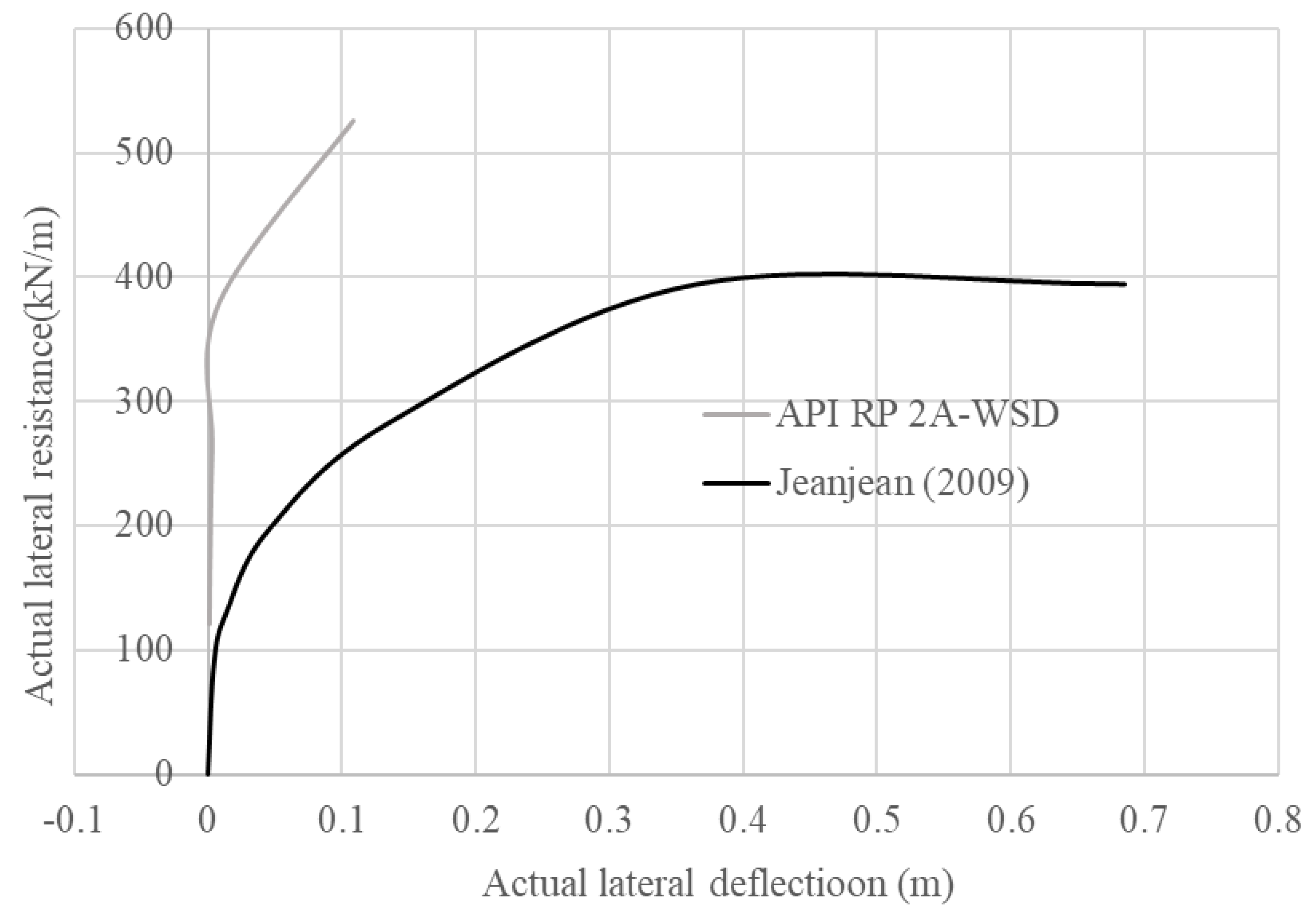
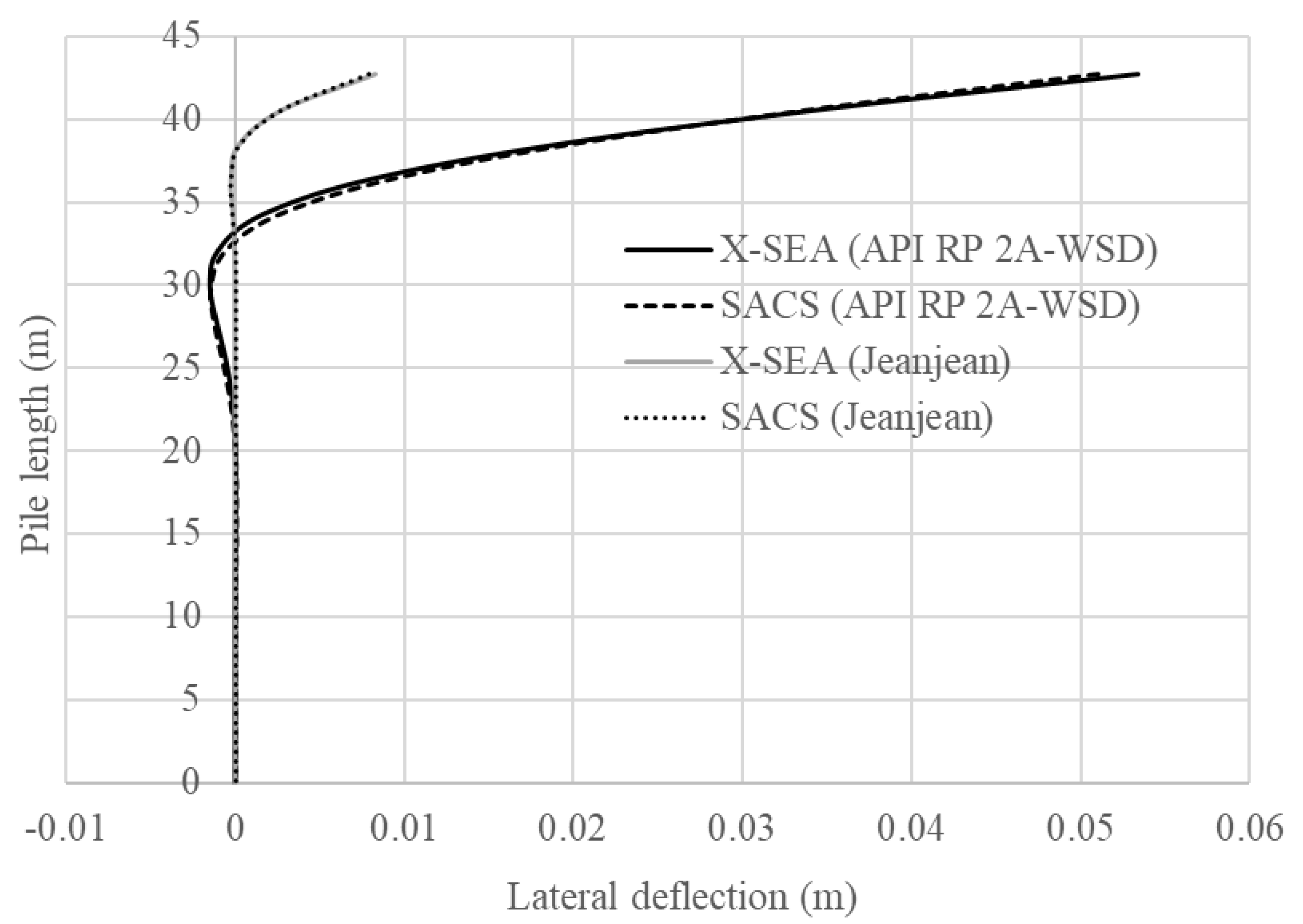
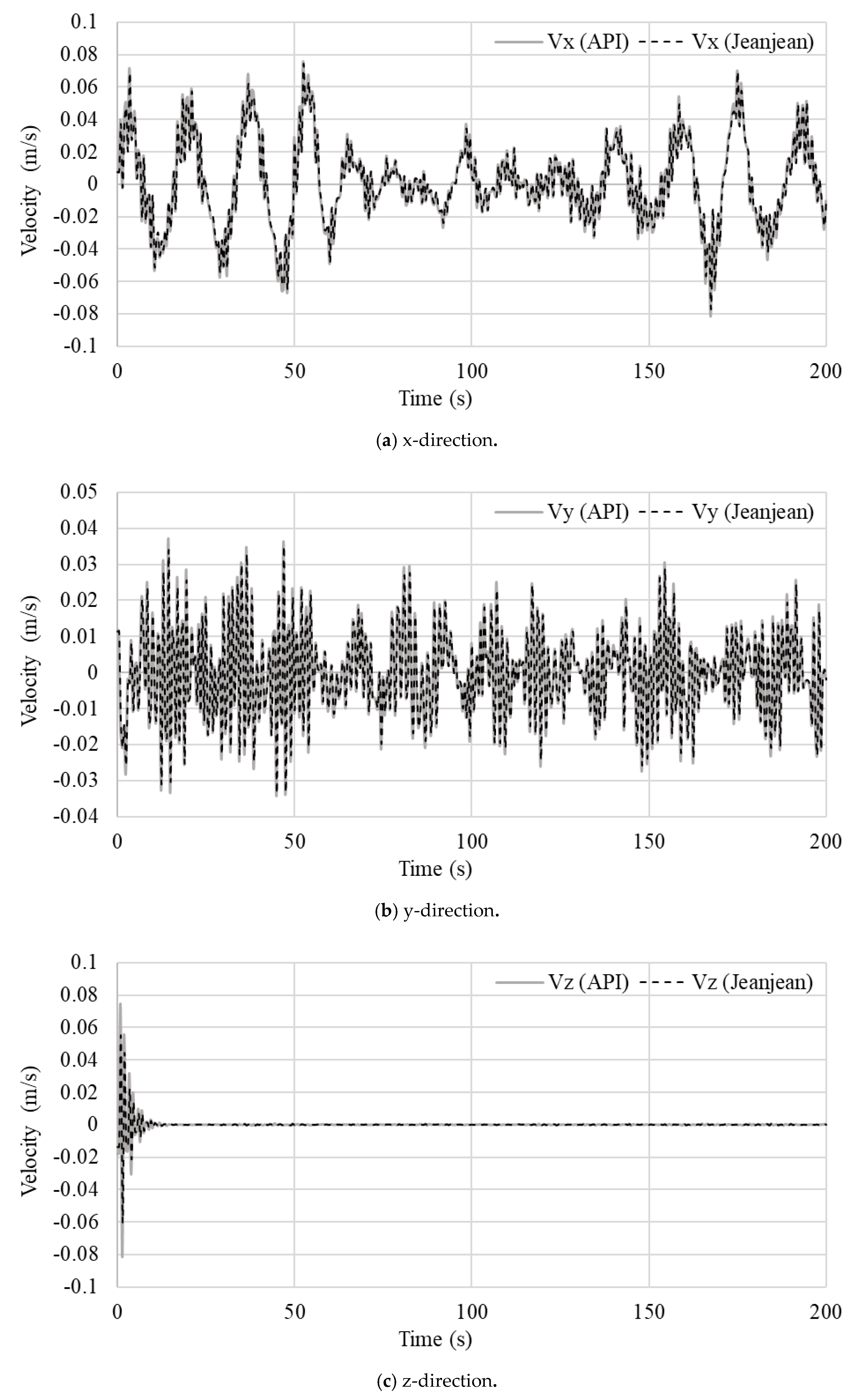
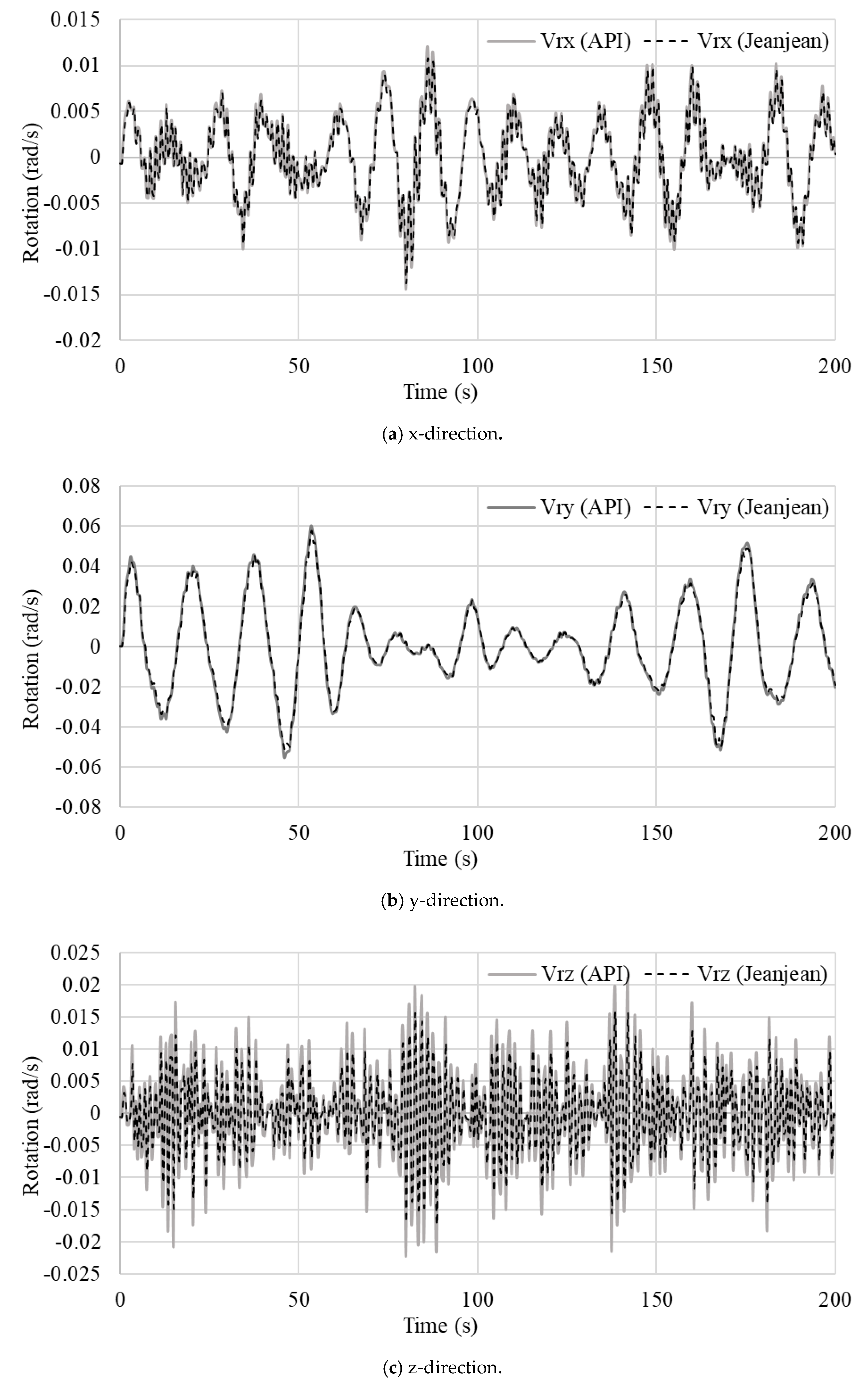
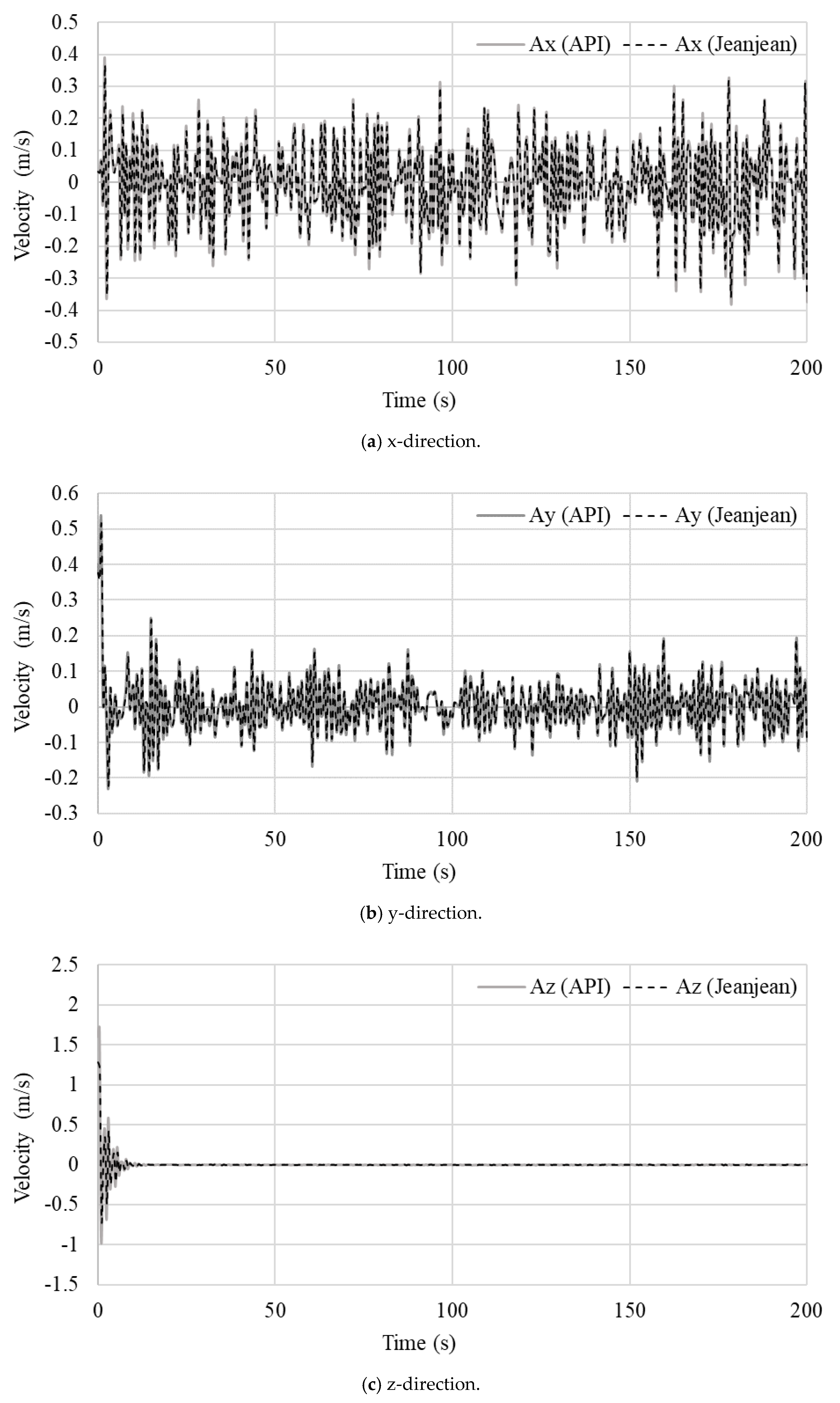
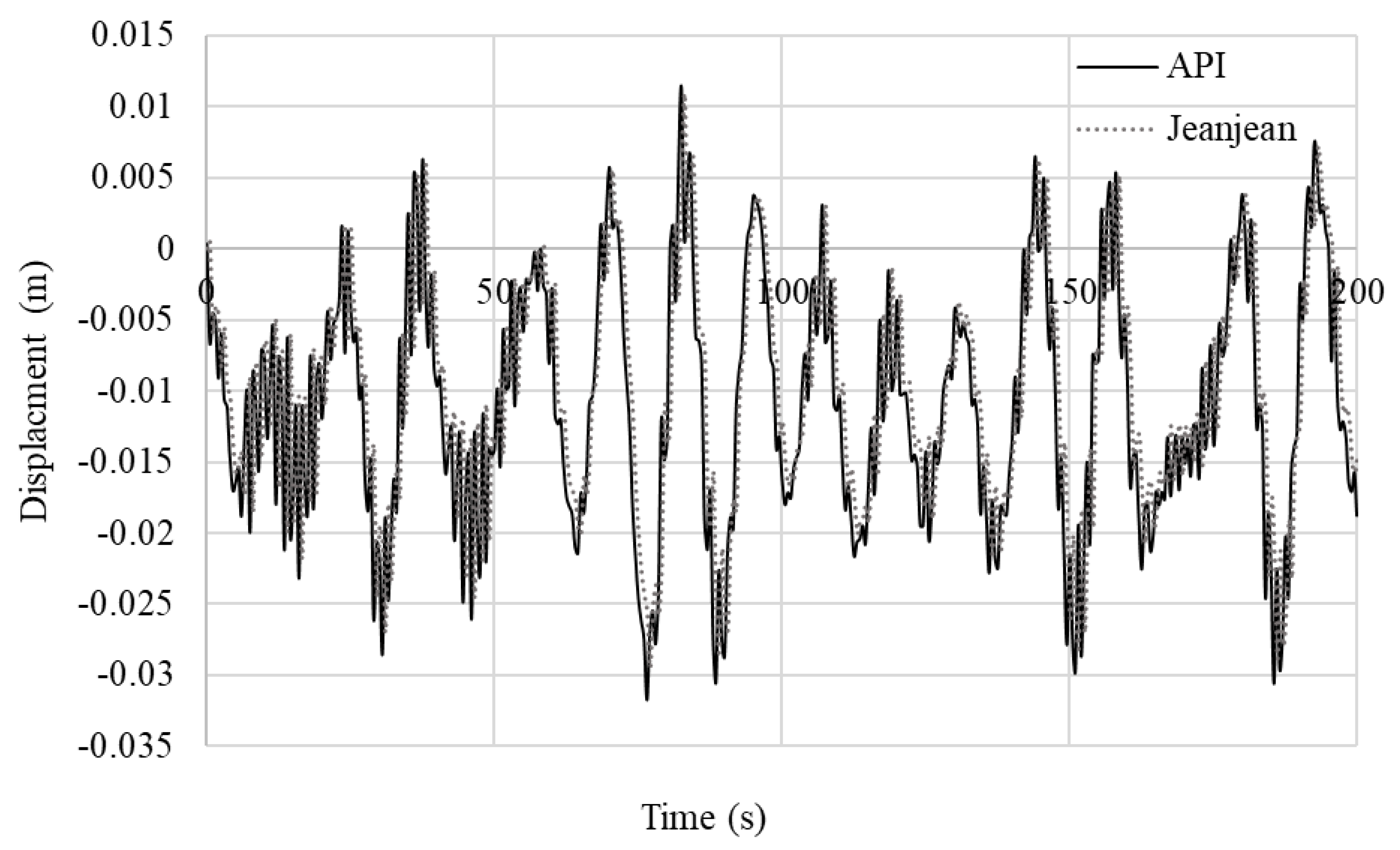
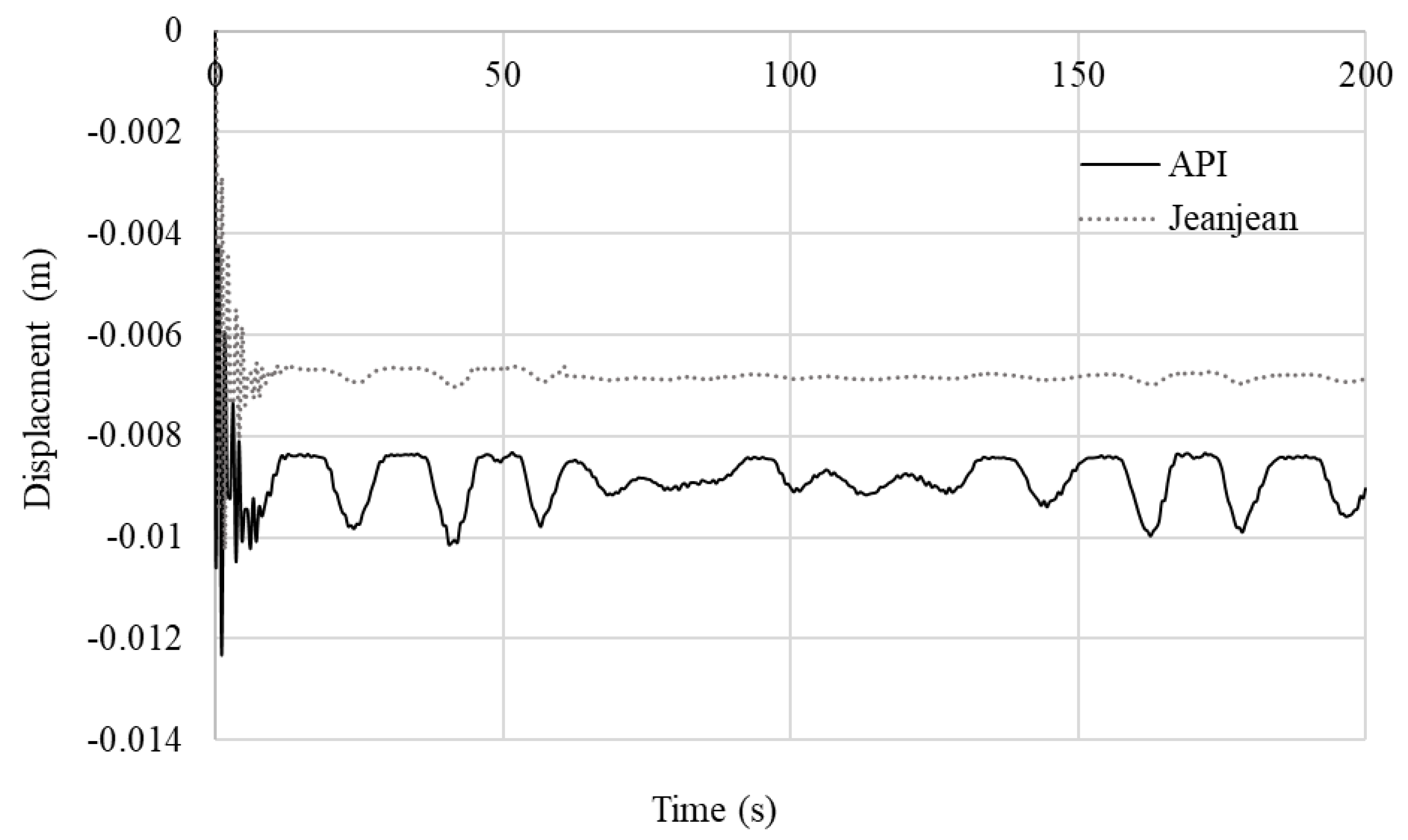
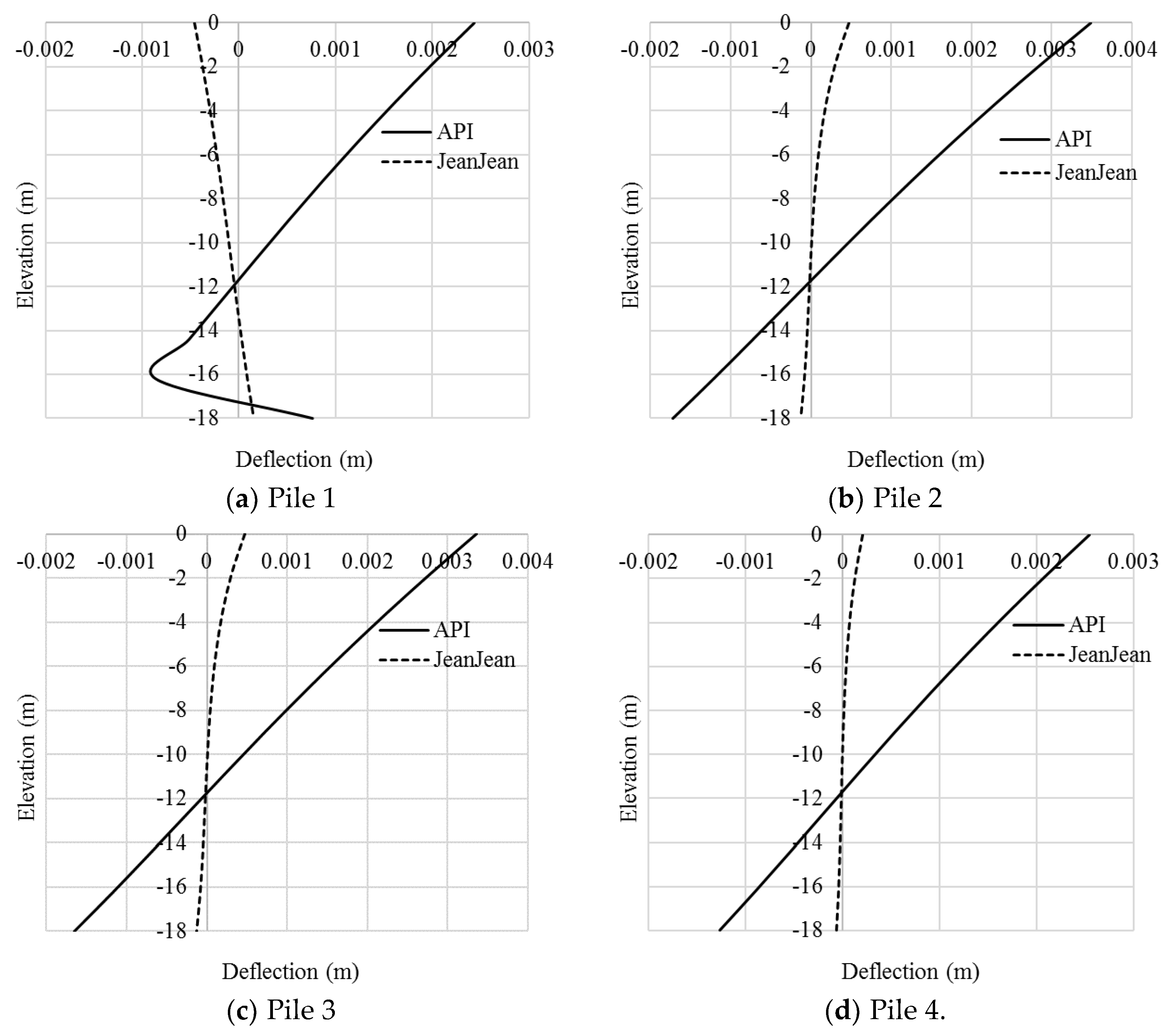
6.1. Verification of Soil–Pile Interactions
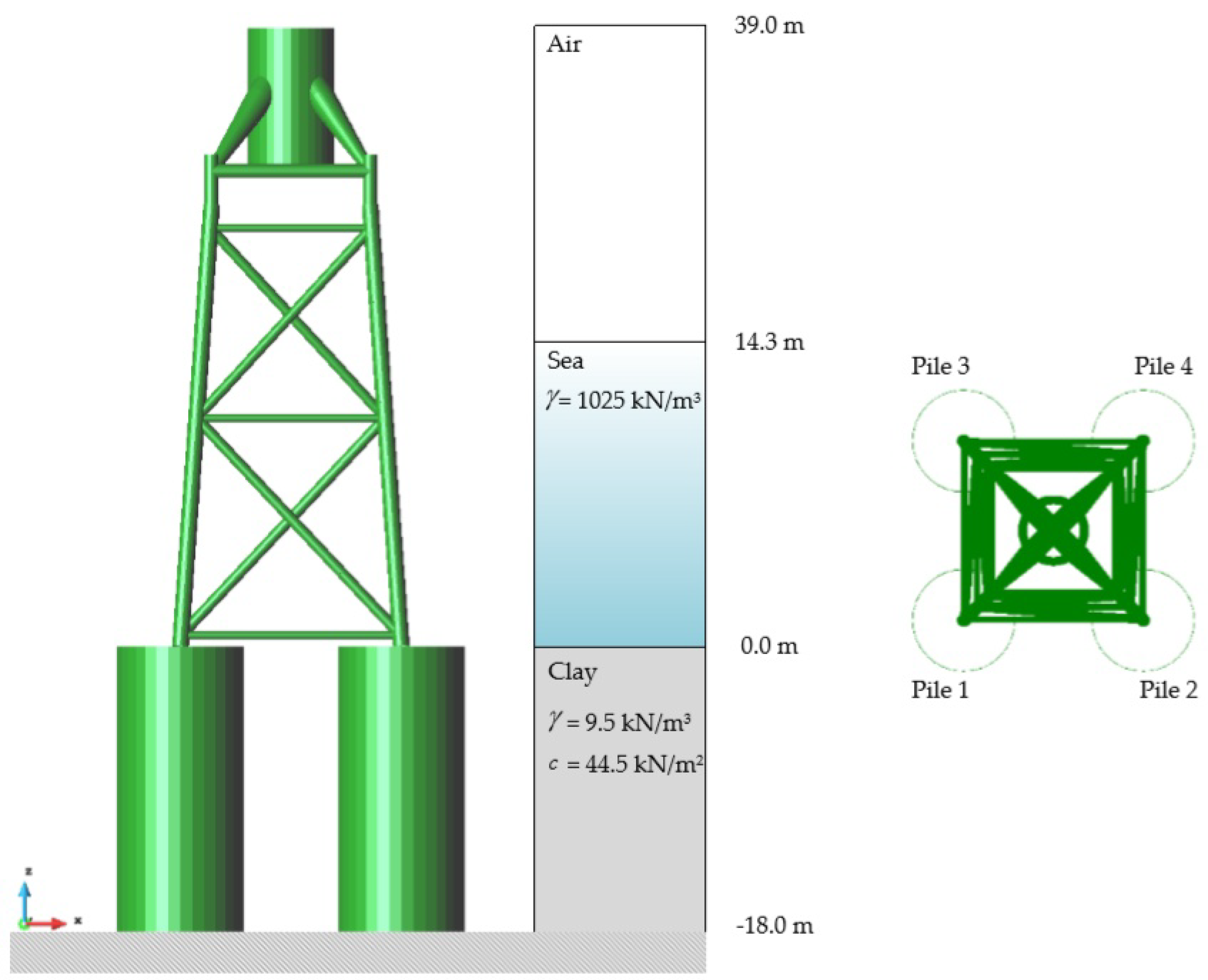
6.2. Coupled Dynamic Analysis of Turbine and Support Structure with Pile–Soil–Structure Interaction (PSSI)
7. Conclusions
- 1)
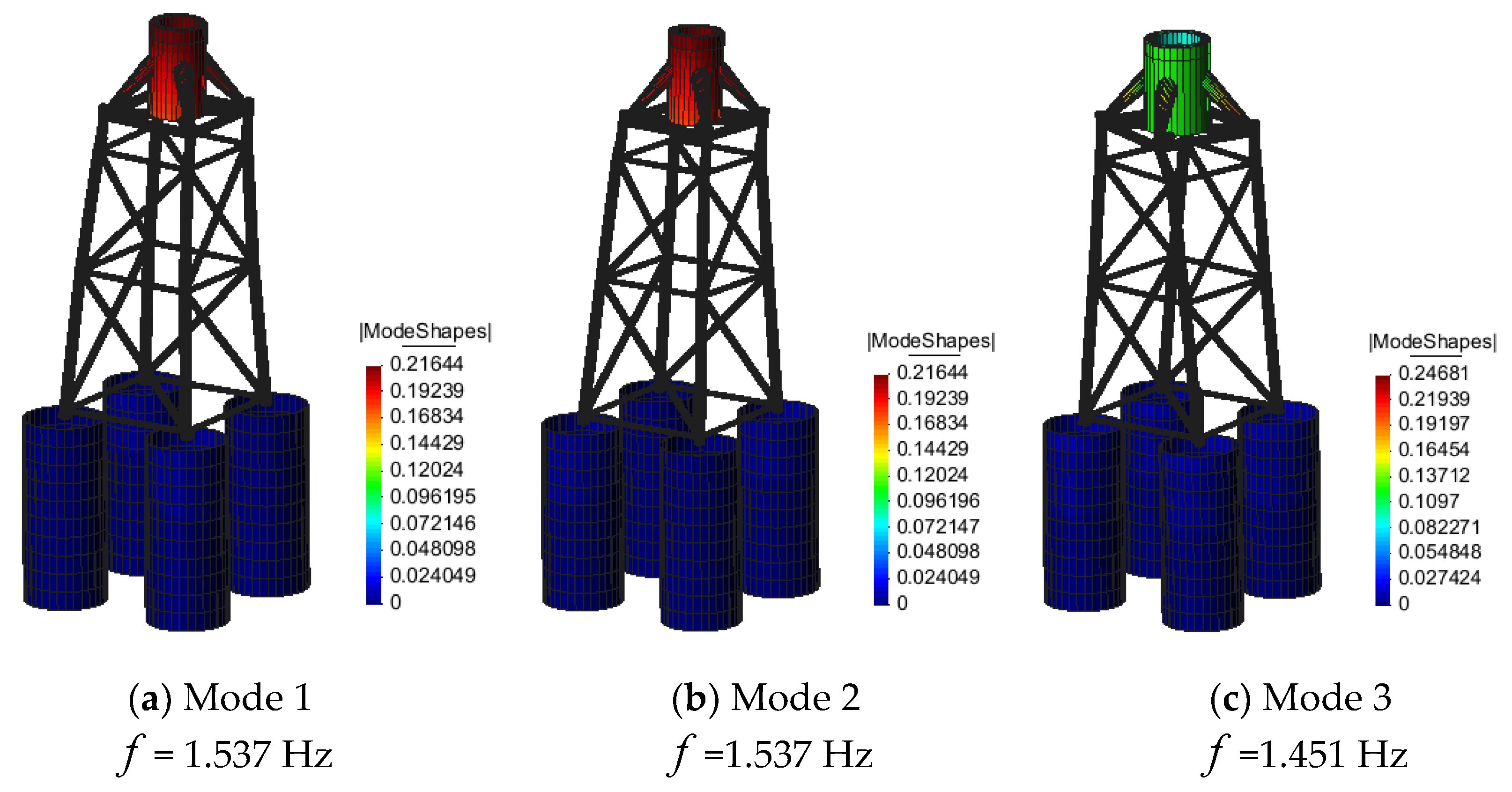
- In the free vibration analysis with fixed boundary conditions (rigid soil), the first and second modes were globally bending and of the same natural frequencies, where the piles oscillated in two horizontal axes. The third mode was torsional about the vertical axis.
- 2)
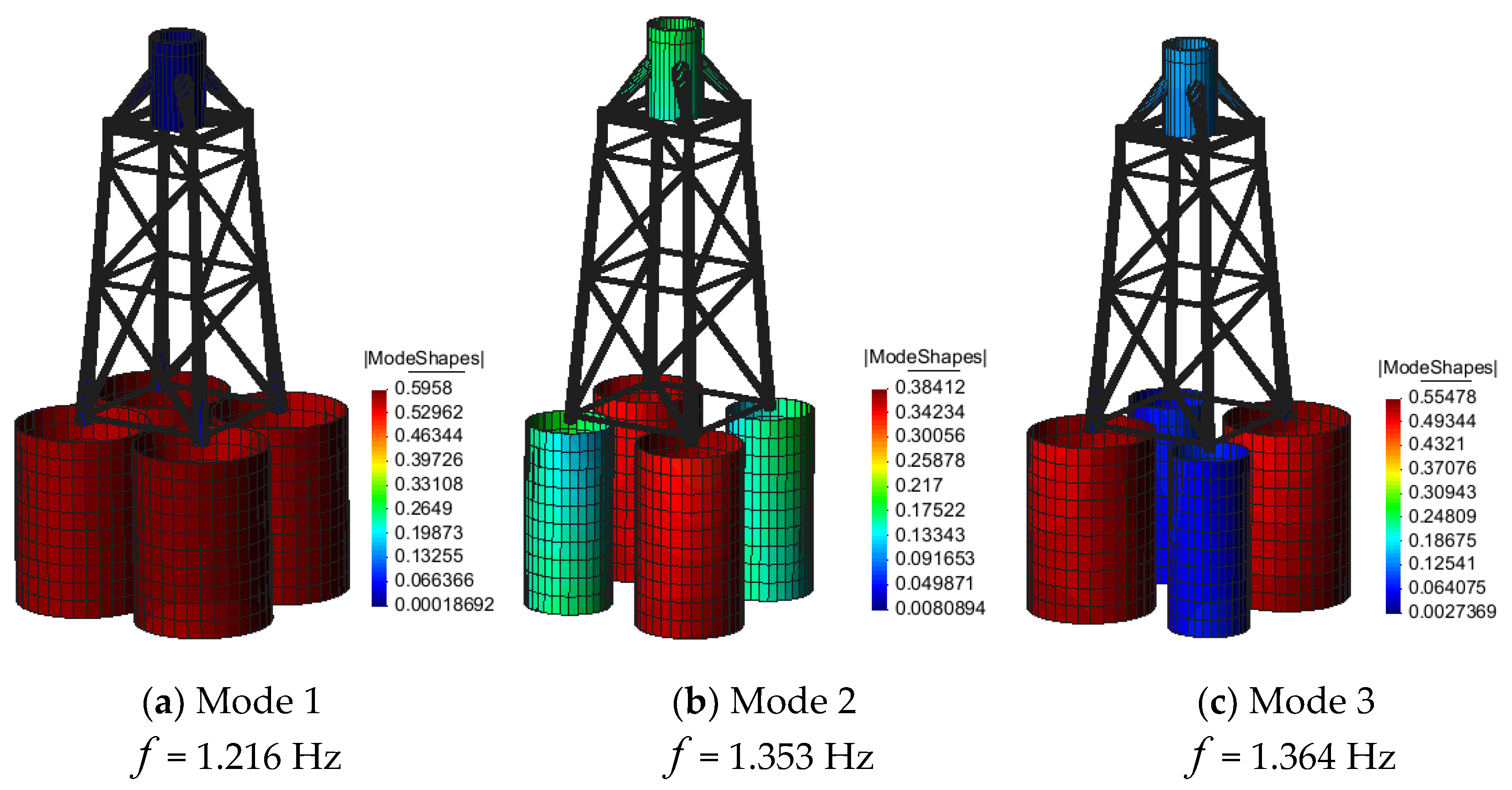
- In the free vibration analysis with the soil spring stiffness determined from P–Y, T–Z, and Q–Z curves using the API method, the suction piles were of lateral movement in the first mode with a distinctly lower natural frequency, and they were twisting in their second and third modes, whereas the first to the third modes of the suction piles using Jeanjean’s method were all twisting. The natural frequencies of the first to the third modes resulting from Jeanjean’s method were higher than those from the API method.
- 3)
- In the forced vibration analysis, the API method made the foundation model more flexible than that of Jeanjean’s method, particularly the pile head. The jacket foundation responses were seen to be significantly influenced by the environmental loads, turbine responses, structural stiffness, and the type of nonlinear soil spring stiffness. The coupled analysis with PSSIs was quite computationally expensive.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Sun, K.; Wang, Z.; Zhang, L. Static and Dynamic Analysis of Monopile Foundation for Offshore Wind Farm. In Proceedings of the International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010. [Google Scholar]
- Scharff, R.; Siems, M. Monopile foundations for offshore wind turbines—Solutions for greater water depths. Steel Constr. 2013, 6, 47–53. [Google Scholar] [CrossRef]
- De, C.; Kai, H.; Lijun, H. Comparison of Structural Properties between Monopile and Tripod Offshore Wind-Turbine Support Structure. Adv. Mech. Eng. 2013, 2013, 1756849. [Google Scholar]
- Georgia, M.; Anastasios, P.; Dimosthenis, B.; Charis, J.G.; Christos, P.G. Design of Monopile and Tripod Foundation of Fixed Offshore Wind Turbine via Advanced Numerical Analysis. In Proceedings of the 8th GRACM International Congress on Computation Mechanics, Volos, Greek, 12–15 July 2015. [Google Scholar]
- Schaumann, P.; Böker, C. Can jackets and tripods compete with monopiles? In Proceedings of the Copenhagen Offshore Wind, Copenhagen, Denmark, 26–28 October 2005.
- Plodpradit, P.; Dinh, V.N.; Kim, K.-D. Coupled Analysis of Offshore Wind Turbine Jacket Structures with Pile-Soil-Structure Interaction Using FAST v8 and X-SEA. Appl. Sci. 2019, 9, 1633. [Google Scholar] [CrossRef]
- Wei, S.; Chinwha, C. Comparison of Dynamic Response of Monopile, Tripod and Jacket Foundation System for a 5-MW Wind Turbine. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Wei, S.; Park, H.C.; Han, J.H.; Na, S.K.; Kim, C.W. A Study on the Effect of Different Modeling Parameters on the Dynamic Response of a Jacket-Type Offshore Wind Turbine in the Korean Southwest Sea. Renew. Energy 2013, 58, 50–59. [Google Scholar]
- Ingrif, B.L.; Amir, M.K. Effect of Foundation Type and Modelling on Dynamic Response and Fatigue of offshore wind turbine. Wind Energy 2012, 22, 12. [Google Scholar]
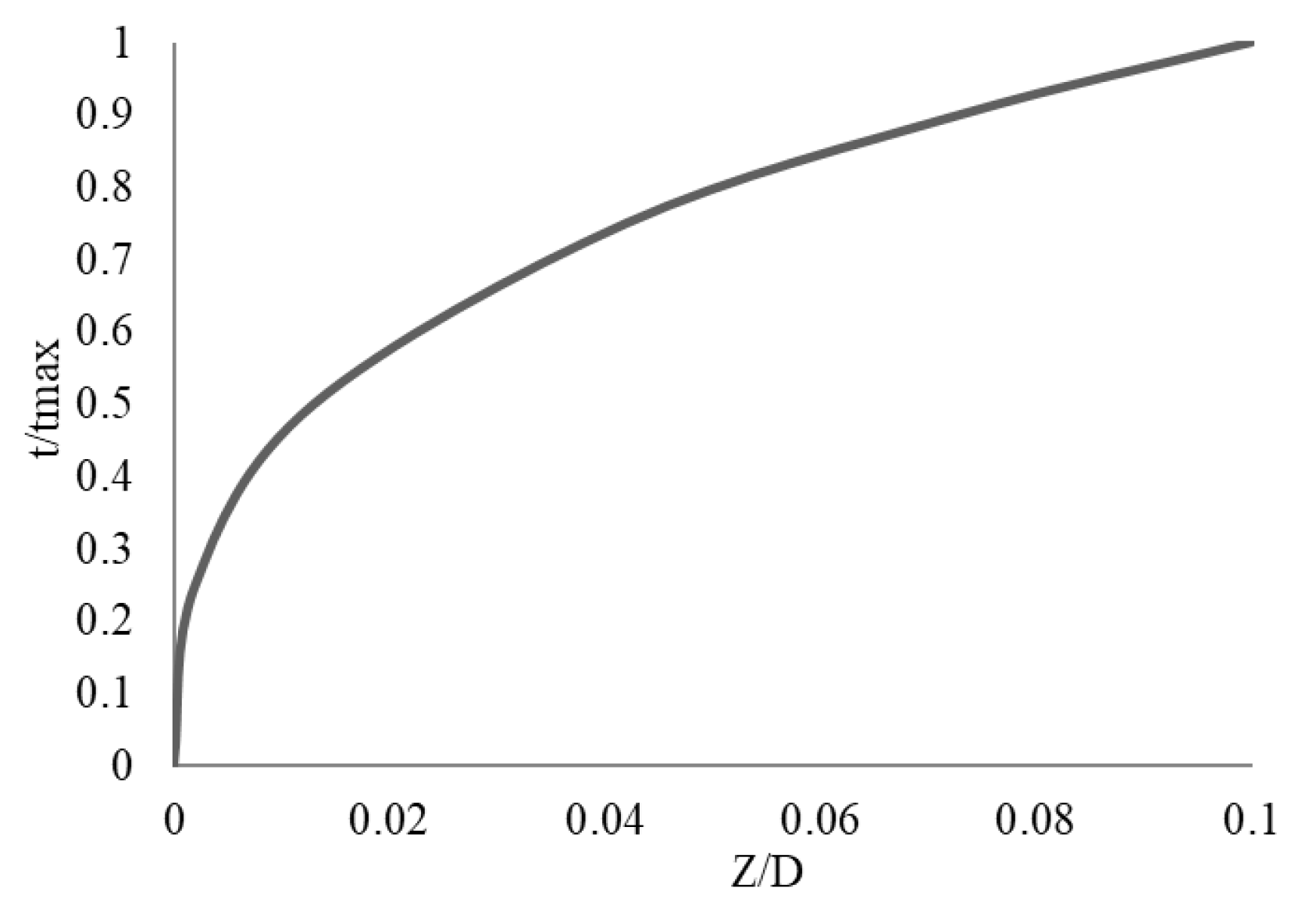
- Wu, Y.; Li, D.; Zhang, Y.; Chen, F. Determination of Maximum Penetration Depth of Suction Caissons in Sand. KSCE J. Civ. Eng. 2017, 22, 2776–2783. [Google Scholar] [CrossRef]
- Wang, X.; Yang, X.; Zeng, X. Lateral response of improved suction bucket foundation for offshore wind turbine in centrifuge modelling. Ocean Eng. 2017, 141, 295–307. [Google Scholar] [CrossRef]
- Tasan, H.E.; Yilmaz, S.A. Effects of installation on the cyclic axial behaviour of suction buckets in sandy soils. Appl. Ocean Res. 2019, 91, 101905. [Google Scholar] [CrossRef]
- Latini, C.; Zania, V. Dynamic lateral response of suction caissons. Soil Dyn. Earthq. Eng. 2017, 100, 59–71. [Google Scholar] [CrossRef]
- Mohammadm, A.; Saif, H. Optimized frequency-based foundation design for wind turbine towers utilizing soil-structure interaction. J. Frankl. Inst. 2010, 348, 1470–1487. [Google Scholar]
- Jonkman, J. FAST v8. National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2018. Available online: https://nwtc.nrel.gov/FAST8 (accessed on 19 September 2017).
- Chen Ong, M.; Bachynski, E.E.; David Økland, O. Dynamic Responses of Jacket-Type Offshore Wind Turbines Using Decoupled and Coupled Models. ASME J. Offshore Mech. Arct. Eng. 2017, 139, 041901. [Google Scholar] [CrossRef]
- Bin, Z.; De-qiong, K.; Ren-peng, C.; Ling-gang, K.; Yun-min, C. Installation and lateral loading tests of suction caissons in silt. Can. Geotech. J. 2011, 48, 1070–1084. [Google Scholar]
- Wang, P.; Zhao, M.; Du, X.; Liu, J.; Xu, C. Wind, wave and earthquake responses of offshore wind turbine on monopile foundation in clay. Soil Dyn. Earthq. Eng. 2018, 113, 47–57. [Google Scholar] [CrossRef]
- Shi, W.; Park, H.; Chung, C.; Baek, J.; Kim, Y.; Kim, C.-W. Load analysis and comparison of different jacket foundations. Renew. Energy 2013, 54, 201–210. [Google Scholar] [CrossRef]
- Matlock, H. Correlations for Design of Laterally Loaded Piles in Soft Clay. In Proceedings of the 2nd Offshore Technology Conference, Houston, TX, USA, 22–24 April 1970; pp. 577–594. [Google Scholar]
- American Petroleum Institute. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms-Load-Working Stress Design API Recommended Practice 2A-WSD; American Petroleum Institute: Washington, DC, USA, 2007. [Google Scholar]
- Asitha, I.M.J.S. Design of Large Diameter Monopiles for Offshore Wind Turbine in Clay. Ph.D. Thesis, University of Texas at Austin, August, TX, USA, 2016. [Google Scholar]
- Ortolani, C. Laterally Loaded Monopiles for Offshore Wind Turbines: Analysis and Improvement of the P-Y Curve; University de Liege: Milano, Italy, 2015. [Google Scholar]
- Kim, K.D.; Vachirapanyaku, S.; Plodpradit, P.; Dinh, V.N.; Park, J.-H. Development of offshore structural analysis software X-SEA and FAST. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore & Arctic Engineering, Glasgow, UK, 9–14 June 2019; p. OMAE 2019-96778. [Google Scholar] [CrossRef]
- Plodpradit, P.; Dinh, V.N.; Kim, K.-D. Tripod-Supported Offshore Wind Turbines: Modal and Coupled Analysis and a Parametric Study Using X-SEA and FAST. J. Mar. Sci. Eng. 2019, 7, 181. [Google Scholar] [CrossRef]
- Jeanjean, P. Re-Assessment of p-y Curve for Soft Clays form Centrifuge Testing and Finite Element Modeling. In Offshore Technology Conference; OTC: Houston, TX, USA, 2015. [Google Scholar]
- Lymon, C.R.; Michael, W.O. Criteria for the Design of Axially Drilled Shafts; The Texas Hight Department; The University of Texas at Austim: Austin, TX, USA, 1971. [Google Scholar]
- Reese, L.C.; O’Neill, M.W. An Evaluation of p-y Relationships in Sands; A report to the American Petroleum Institute; University of Houston: Houston, TX, USA, 1983. [Google Scholar]
- Lam, I.; Martin, G.R. Seismic Design of Highway Bridge Foundations. In Lifeline Earthquake Engineering: Performance, Design and Construction; ASCE: Reston, VA, USA, 1986. [Google Scholar]
- Damiani, R.; Wendt, F. Development and Verification of Soil-Pile Interaction Extension for SubDyn. In Proceedings of the AWEA Offshore WINDPOWER 2017, New York, NY, USA, 24–25 October 2017. [Google Scholar]
- Kim, B.J.; Plodpradit, P.; Kim, K.D.; Kim, H.G. Three-dimensional analysis of prestressed concrete offshore wind turbine structure under environmental and 5-MW turbine loads. J. Mar. Sci. Appl. 2018, 17, 625–637. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas. J. Geophys. Res. 1964, 69, 5181–5203. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. IEC 61400–3 Wind Turbines–Part 3: Design Requirements for Offshore Wind Turbines, 1st ed.; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2009. [Google Scholar]
- Dinh, V.N.; Basu, B. Passive Control of Floating Offshore Wind Turbine Nacelle and Spar Vibrations by Multiple Tuned Mass Dampers. Struct. Control Health Monit. 2015, 22, 152–176. [Google Scholar] [CrossRef]
- Thomas, H.D. Offshore Structure Engineering; Prentice-Hall. Inc.: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- SACS. PSI/Pile User’s Manual; Engineering Dynamic, Inc.: Englewood, CO, USA, 2005. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report, NREL/TP-5000-38060; National Renewable Energy Lab.: Golden, CO, USA, 2009.
- Park, G.S. 5.5 MW Offshore Jacket Modeling of Korean Western Sea; Research Report; Seil Engineering: Seoul, Korea, 2018. [Google Scholar]
- Jonkman, B.J. TurbSim User’s Guide Version 1.50; National Renewable Energy Laboratory Technical report, NREL/TP-500-46198; National Renewable Energy Lab.: Golden, CO, USA, 2009.
- Kim, K.D. X-SEA Validation; Konkuk University: Seoul, Korea, 2018. [Google Scholar]
- Basu, B.; Staino, A.; Dinh, V.N. Vibration of wind turbines under seismic excitations. In Proceedings of the Fifth Asian-Pacific Symposium on Structural Reliability and its Applications, Singapore, 23–25 May 2012. [Google Scholar] [CrossRef]
- MATLAB. Fourier Analysis and Filtering; The MathWorks, Inc.: Natick, MA, USA, 2020; Release. [Google Scholar]








| Geometric Properties | ||
| Parameter | Value | Unit |
| Jacket leg diameter | 1.053 | m |
| Jacket leg thickness | 0.019 | m |
| Diagonal member diameter | 0.508 | m |
| Diagonal member thickness | 0.013 | m |
| Transition piece diameter | 5.500 | m |
| Transition piece thickness | 0.700 | m |
| Material Properties | ||
| Parameter | Value | Unit |
| Steel weight density | 7850 | kg/m3 |
| Elastic of modulus | 2.1 × 1011 | N/m2 |
| Shear modulus | 8.08 × 1010 | N/m2 |
| Motion Components | Factors | ||
|---|---|---|---|
| x-Direction | y-Direction | z-Direction | |
| Rotational displacement | 1.067 | 1.061 | 1.343 |
| Velocity | 1.062 | 1.064 | 1.339 |
| Rotational velocity | 1.073 | 1.067 | 1.336 |
| Acceleration | 1.069 | 1.072 | 1.327 |
| Rotational acceleration | 1.065 | 1.069 | 1.333 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plodpradit, P.; Kwon, O.; Dinh, V.N.; Murphy, J.; Kim, K.-D. Suction Bucket Pile–Soil–Structure Interactions of Offshore Wind Turbine Jacket Foundations Using Coupled Dynamic Analysis. J. Mar. Sci. Eng. 2020, 8, 416. https://doi.org/10.3390/jmse8060416
Plodpradit P, Kwon O, Dinh VN, Murphy J, Kim K-D. Suction Bucket Pile–Soil–Structure Interactions of Offshore Wind Turbine Jacket Foundations Using Coupled Dynamic Analysis. Journal of Marine Science and Engineering. 2020; 8(6):416. https://doi.org/10.3390/jmse8060416
Chicago/Turabian StylePlodpradit, Pasin, Osoon Kwon, Van Nguyen Dinh, Jimmy Murphy, and Ki-Du Kim. 2020. "Suction Bucket Pile–Soil–Structure Interactions of Offshore Wind Turbine Jacket Foundations Using Coupled Dynamic Analysis" Journal of Marine Science and Engineering 8, no. 6: 416. https://doi.org/10.3390/jmse8060416
APA StylePlodpradit, P., Kwon, O., Dinh, V. N., Murphy, J., & Kim, K.-D. (2020). Suction Bucket Pile–Soil–Structure Interactions of Offshore Wind Turbine Jacket Foundations Using Coupled Dynamic Analysis. Journal of Marine Science and Engineering, 8(6), 416. https://doi.org/10.3390/jmse8060416







