Techno-Economic Optimisation for a Wave Energy Converter via Genetic Algorithm

Abstract

Although sea and ocean waves have been widely acknowledged to have the potential of providing sustainable and renewable energy, the emergence of a self-sufficient and mature industry is still lacking. An essential condition for reaching economic viability is to minimise the cost of electricity, as opposed to simply maximising the converted energy at the early design stages. One of the tools empowering developers to follow such a virtuous design pathway is the techno-economic optimisation. The purpose of this paper is to perform a holistic optimisation of the PeWEC (pendulum wave energy converter), which is a pitching platform converting energy from the oscillation of a pendulum contained in a sealed hull. Optimised parameters comprise shape; dimensions; mass properties and ballast; power take-off control torque and constraints; number and characteristics of the pendulum; and other subcomponents. Cost functions are included and the objective function is the ratio between the delivered power and the capital expenditure. Due to its ability to effectively deal with a large multi-dimensional design space, a genetic algorithm is implemented, with a specific modification to handle unfeasible design candidate and improve convergence. Results show that the device minimising the cost of energy and the one maximising the capture width ratio are substantially different, so the economically-oriented metric should be preferred.

1. Introduction

Based on the gradual depletion of conventional fossil fuels, and most importantly, the established awareness of their destructive impact on the environment, recent years have witnessed a compelling momentum towards the energy transition and decarbonisation, shared by industry, governmental bodies and policy-makers. A condition for effective and reliable energy procurement is diversification, especially concerning renewable sources, which are usually more variable and volatile. Ocean energy, wave energy in particular, can play a major role in the overall energy mix, thanks to its high power density and availability [1]. Despite its potential, wave energy still remains substantially untapped since several challenges, hindering commercialisation at industrial scale, remain to be overcome. Wave energy conversion is yet to reach economic viability and is not competitive with other renewable energy technologies, due to an excessive LCOE (levelised cost Of energy) at the current stage of development.

From a high-level perspective, one of the main reasons for the unsuccessful development of effective technologies is that typical development pathways prefer to rapidly increase readiness levels before an acceptable performance is achieved [2]. Considering a matrix composed of technology readiness level (TRL) and the technology performance level (TPL), deficient development pathways tend to increase TRL first, at low TPL; conversely, optimal trajectories should increase TPL first, at low TRL, and then increase TRL towards commercialisation [3]. Although is it challenging to perform an accurate estimation of some performance aspects at low TRL, due to inherent limitations of small-scale devices and subsystems, techno-economic aspects should be taken into account. Changing such a development paradigm involves adopting better design practices, since common approaches are inherently suboptimal. In particular, often, design is performed in sequential fashion, considering different parts of the power conversion chain independently. A representative example is the optimisation of the hydrodynamics and power absorption of an uncontrolled device, followed by a design of an optimal controller, followed by the inclusion of technical constraints and efficiency, finally reaching the stage of cost evaluation and reduction. Although such an incremental approach is justified by the complexity of the system, neglecting mutual interaction typically leads to a suboptimal solution.

An effective design requires one to follow a holistic approach, based on representative wave-to-wire mathematical models [4], including some energy-maximising control strategy [5,6] considering technological constraints [7,8] and costs [9], since all of such aspects are tightly interrelated. Representative hydrodynamic models are advisable, since a controlled device may be affected by strong nonlinearities with major negative effects on power production [10]. Furthermore, unconstrained linear or partially-linear models may predict unrealistic behaviour under the action of an optimal controller [11], which is also sensitive to modelling errors [12,13]. Note that it is essential to include an energy-maximising control strategy, since it has the ability to significantly increase power-production performance over the operational sea states. Moreover, the control strategy has a great influence on the dynamic characteristic of the response of the device [14], making the power-wise optimal solutions for uncontrolled and controlled conditions significantly different [15]. However, the ability of the controller to optimise power absorption is highly dependent on physical constraints, mainly on displacement, speed and force/torque [16]. Such constraints depend on the electrical and mechanical subcomponents characteristics, and ultimately, cost. On the other hand, the hydrodynamic behaviour of the device mainly depends on its shape and dimensions, which entail volume and mass, which are main drivers of capital cost.

A practical implementation of an all-encompassing design optimisation is challenging, mainly due to the vast multi-dimensional search space which cannot be tackled with conventional global optimisation approaches due to computational limitations. Moreover, often there is no analytical representation of the relationship between input and output variables, due to hydrodynamic curves defined by points through panel-based simulations (BEM) and implicit nonlinearities requiring simulation via time-advancing schemes [17], or in some conditions, harmonic balance [18]. Therefore, both cost function and constraints usually behave as grey or black boxes. For such problems, genetic algorithms are among the most common choice, since they can handle design spaces of high dimensionality and complex cost functions and constraints, without relying on the knowledge of their mathematical structure [19]. Genetic algorithms are metaheuristic optimisation codes based on the evolutionary theory, relying on the survival-of-the-fittest principle. Thanks to their stochastic approach, they favour the identification of the global optimum, reducing the risk of convergence to a local minimum. Furthermore, they impose no specific requirement on the system to be optimised, since it is treated as a black box. Genetic algorithms are used in this paper based on previous experience of the authors, although other metaheuristic approaches exist, able to handle a large parameter space, such as covariance matrix adaptation, differential evolution and particle swarm algorithms [20].

Following their use in the general marine engineering field [21], genetic algorithms recently gained popularity in the wave energy field, but are mainly used for the optimisation of the array layout of several wave energy converters (WECs) [22,23]. Although scarce, some single WEC design optimisations via genetic algorithm are found in the literature. Reference [24] optimised the radius and draft of an archetypal cylinder, maximising the absorbed power and bandwidth. The design space is bi-dimensional; the geometry is idealised; and the power take-off (PTO) is a simple linear damper with a frequency-independent damping coefficient. Since power is not an effective single-objective function for practical design, Ref. [25] introduces proxies for costs, structural loads and PTO rating loads into the objective function. Costs are assumed to be proportional to the submerged surface and the maximum reaction force. While [25] considered fixed-axis devices of conventional shape, Ref. [26] attempted to generalise the geometry as much as possible, using B-splines to describe wetted surfaces of arbitrary shapes. Moreover, frequency-dependent energy-maximising control is introduced, also including constraints to limit unrealistically large amplitudes of motion that follow. As a proxy for costs, length and displaced volumes are considered in the cost functions. Finally, Ref. [27] proposes a thorough optimisation of the SEAREV device, attempting to maximise the produced power while minimising the device mass (as a crude proxy for costs), including various constraints and latching-declutching control.

This paper proposes a comprehensive techno-economic optimisation of the PeWEC (pendulum wave energy converter), which is a self-reacting WEC extracting energy from the oscillation of a pendulum sealed in a floating hull [28]. Several novelties, with respect to other design optimisation of WECs, are included. First and foremost, similar only to [27], a high level of detail of a realistic device is considered, as opposed to archetypal or generic geometries. However, a wide design space with high dimensionality is investigated, counting up to 13 design variables, comprising shape and dimensions of the floater; ballast and inertial properties; pendulum properties and numerosity; PTO rated torque; velocity and power; and gearbox speed conversion ratio. Moreover, realistic geometrical, technical and structural constraints are implemented, based on subcomponents characteristics. No idealised proxy is used for estimating costs, which are directly computed based on the cost of different material used for construction and different PTOs from a catalogue. Finally, a simple but realistic energy-maximising control strategy is implemented, including explicit constraint handling, in order to perform a control-informed optimisation. Due to the high-dimensionality and mutual dependence of design variables, a stochastic optimisation approach, treating different variables as independent and random, encounters a high level of unfeasible combinations, which may potentially hinder the success of the optimisation. In order to deal with unfeasible solutions, a tournament-based genetic algorithm is implemented, reducing the impact of mortality rate on the convergence rate. The objective function, which the genetic algorithm tries to minimise, is the ratio between capital cost and annual energy production (AEP). However, in order to highlight the impact of the performance index and to generate a Pareto front, the capture width ratio is also considered as an additional objective. It is shown that hydrodynamic efficiency and cost of energy are contrasting objectives; therefore, this paper provides evidence that challenges the common practice of optimising the hydrodynamic performance during early-stage development, suggesting companies should pursue economic performance instead.

The remainder of the paper is organised as follows: Section 2 describes the technology while Section 3 presents its parametrisation for the optimisation algorithm, also focusing on constraints, cost functions and different objective functions. Finally, Section 4 provides main significant results with a critical discussion. Some final remarks are given in Section 5. Appendix A provides full general details about the genetic algorithm that effectively deals with discrete multi-variate problems with high mortality rate.

2. Technology

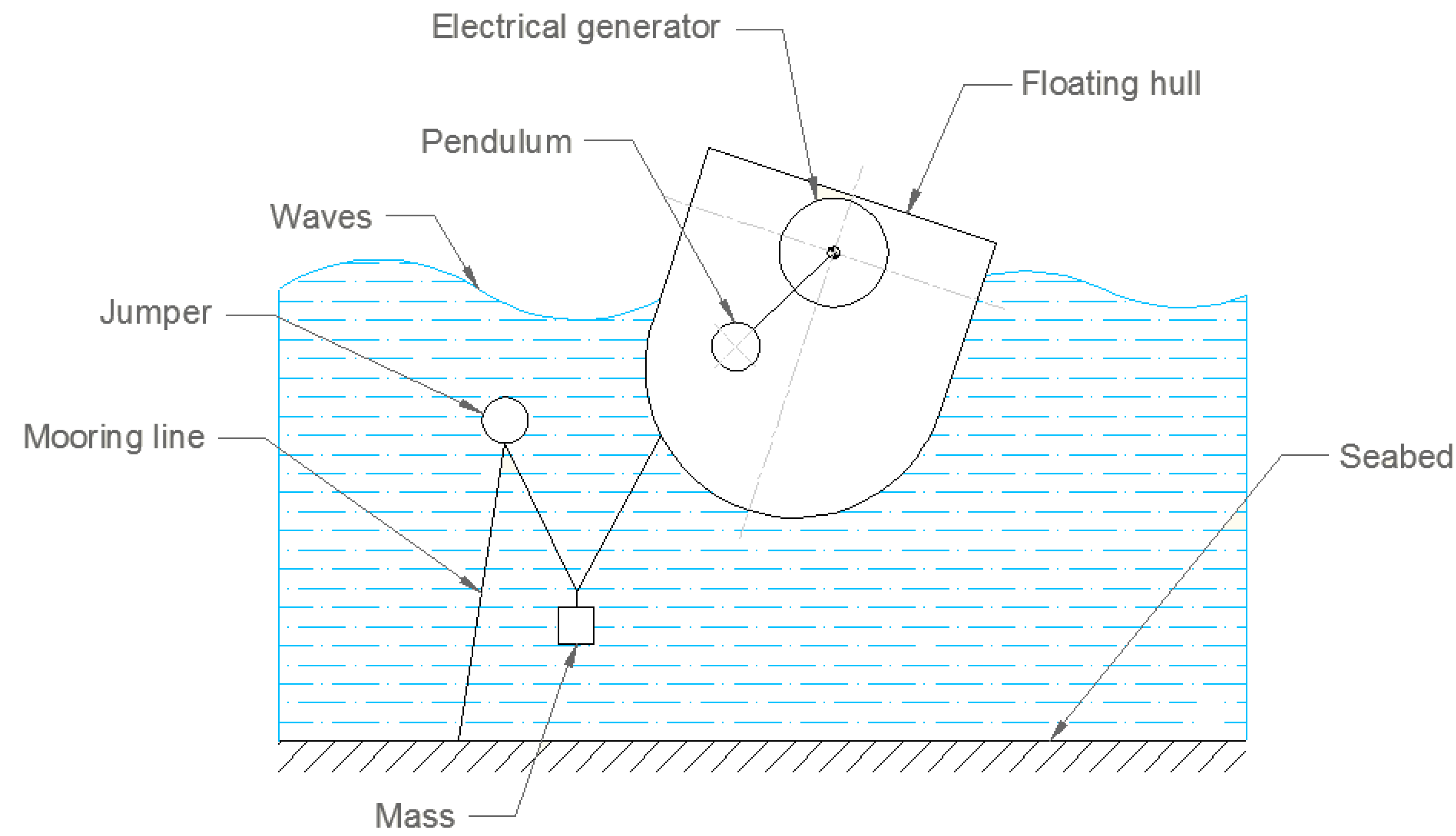
The system under consideration in this optimisation study is the PeWEC, an acronym of pendulum wave energy converter. PeWEC is a self-referenced inertial-based floating WEC, composed of a sealed hull enclosing a pendulum and the power take-off (PTO). There are notional similarities between PeWEC and the SEAREV device [29], both based on an inertial-activated body contained in a floating hull; however, while SEAREV is designed for ocean applications, PeWEC is initially aiming at lower energetic closed seas with lower-period waves (e.g., the Mediterranean Sea). The device is anchored to the seabed by means of a 3-line-3-segment mooring system, with each line composed of a jumper (riser) and a clump-weight [30]. When the device is moved by the waves, a relative motion between the hull and the internal pendulum is obtained, mostly due to the pitching motion. The kinetic energy related to this movement is converted into electrical energy by the PTO connected to the pendulum’s hinge. A control law is implemented in the PTO driver to adjust the pendulum dynamics to the instantaneous sea conditions, with the purpose of maximising the output energy. A schematic of the PeWEC system is shown in Figure 1.

The hull is a sealed steel structure composed of a curved keel, two side walls and a flat topping; three internal sand ballasts (on the keel, stern and bow) ensure the mass distribution necessary to guarantee the required inertial properties, while a trellis structure is used to support the pendulum and the electronic equipment. The pendulum is composed of a cylindrical steel oscillating mass and a shaft, which is connected to the PTO system through a gearbox that ensures an appropriate coupling between the pendulum oscillation velocity and the PTO nominal speed. In order to extract energy from the pendulum movement, the PTO generates a reaction torque, which is adjusted by the driver’s control system. Such constructive and technical features, based on early-development of the device, are here optimised via genetic algorithm. The technology has already been proven to be effective and promising, mainly thanks to wave tank tests at 1:45 and 1:12 scales [31]. Figure 2 shows a 3D digital model of the 1:45 prototype while Figure 3 shows a photo of the 1:12 prototype in the testing wave tank.

The concept of PeWEC germinated from the ISWEC (inertial sea wave energy converter), which generates the inertial coupling between PTO and the hull by means of the gyroscopic effect of a spinning flywheel [32]. While ISWEC requires power to keep the flywheel in rotation and create the self-reaction force [33], PeWEC is entirely passive, hence reducing explicit power loss sources. Further technological improvements are being explored for both the PeWEC and the ISWEC in order to increase the overall power conversion efficiency, such as resonant U-tanks [34], advanced control techniques [35], estimation and forecasting [36]. Moreover, the mooring system is under development, since it can affect the device performance [37]. However, this paper deals with a more fundamental early holistic optimisation of the PeWEC device shape, geometry and subcomponents, as further discussed in Section 3. The mathematical model, used to predict motion and loads of a given device, is presented in Section 2.1. The strategy to parametrically define multiple devices that the genetic algorithm can automatically optimise is presented in Section 3.

2.1. Mathematical Model

The optimisation software relies on a mathematical model to evaluate the objective function which, in this paper, depends on the response of the device to incoming waves. An essential requirement for such a mathematical model is low computational speed, since a high number of individuals (order of tens of thousands) have to be assessed in a reasonable time. Therefore, a fully-linear model based on linear potential flow is implemented in frequency domain, thanks to its computational convenience. However, in order to avoid unrealistic motion that a linear model would predict under controlled conditions, various constraints are included, as further discussed in Section 3.2. Potential-flow-based models are conceptually divided into two phases: Firstly, the linear hydrodynamic curves, namely, excitation coefficients (${\mathbf{F}}_w$), added mass ($\mathbf{A}$) and radiation damping ($\mathbf{B}$), are evaluated at a representative set of frequencies by means of a boundary element method (BEM) software, such as NEMOH [38] (this must be automatised in the genetic algorithm). Secondly, the dynamic response of the device is evaluated for a comprehensive set of sea states, characteristic of the designed installation site, taking care of determining appropriate energy-maximising control parameters. Although the run time of BEM codes depends on the number of simulated frequencies and on the discretised geometry, it is of the order of magnitude of ${10}^2$ s, on average. Since shape and dimensions of the hull are among the optimisation parameters, a detailed description is provided in Section 3.1. On the other hand, the structure of the dynamic response simulator is invariant:

$$\left[\mathbf{M}+\mathbf{A}\left(\omega \right)\right]\ddot{\mathbf{X}}+\mathbf{B}\left(\omega \right)\dot{\mathbf{X}}+({\mathbf{K}}_h+{\mathbf{K}}_p)\mathbf{X}=A_w\left(\omega \right){\mathbf{F}}_w\left(\omega \right)+{\mathbf{T}}_{PTO}$$

(1)

where $\mathbf{M}$ is the mass matrix, ${\mathbf{K}}_h$ is the hydrostatic stiffness, ${\mathbf{K}}_p$ the restoring force of the pendulum, $A_w$ is the wave amplitude, ${\mathbf{T}}_{PTO}$ is the PTO action and $\mathbf{X}$ is the state vector. Under the assumption of mono-directional waves aligned with the longitudinal axis of the hull, a planar motion of the hull can be assumed, namely, in surge (x), heave (z) and pitch ($\delta$). Including the pendulum oscillation ($\epsilon$), the state vector has four dimensions:

$$\mathbf{X}=\left[\begin{array}{c}x\\ z\\ \delta \\ \epsilon \end{array}\right]$$

(2)

The PTO acts on the rotational degree of freedom of the pendulum, applying active and reactive power, proportional to displacement and velocity with constant coefficients, $k_{PTO}$ and $c_{PTO}$, respectively:

$${\mathbf{T}}_{PTO}=\left[\begin{array}{c}0\\ 0\\ 0\\ -k_{PTO}\epsilon -c_{PTO}\dot{\epsilon }\end{array}\right]$$

(3)

Coupling between the pendulum and the hull is provided by the restoring force of the pendulum and inertial reaction forces, which are expressed in ${\mathbf{K}}_p$ and $\mathbf{M}$, respectively. After linearisation [39]:

$${\mathbf{K}}_p=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& -g{m}_p(d-l)& g{m}_{p}l\\ 0& 0& g{m}_{p}l& g{m}_{p}l\end{array}\right]$$

(4)

$$\mathbf{M}=\left[\begin{array}{cccc}(M+m_p+m_b)& 0& m_p(d-l)& -m_{p}l\\ 0& (M+m_p+m_b)& 0& 0\\ m_p(d-l)& 0& I_y+I_p+I_b+m_p{(d-l)}^2& I_p+m_p{l}^2-m_{p}dl\\ -m_{p}l& 0& I_p+m_p{l}^2-m_{p}dl& I_p+m_p{l}^2\end{array}\right]$$

(5)

where M is the mass of the hull; $I_y$ is the hull moment of inertia; g is the acceleration of gravity; d is the distance between the device centre of gravity (CoG) and the pendulum fulcrum; l is the pendulum length; $m_p$ and $m_b$ are the masses of the pendulum and the bar holding the pendulum, respectively, and $I_p$ and $I_b$ are their moments of inertia, respectively.

In order to maintain the model linear, mooring effects are neglected, as are mean drift forces and second order effects. Moreover, viscous effects are neglected, since they would require specific tuning for each device [40]. However, the linearised model has been validated through an experimental campaign [39], ensuring appropriate accuracy and representativeness for global design optimisation problems [41]. Nevertheless, it is worth noticing that these assumptions (planar waves and motion, and absence of a mooring system) are simplifications, since real waves may be short-crested, inducing complex motion in 6 degrees of freedom, which is also possible due to parametric instabilities and nonlinear coupling [42], and the mooring system may significantly affect the dynamics of the system [37].

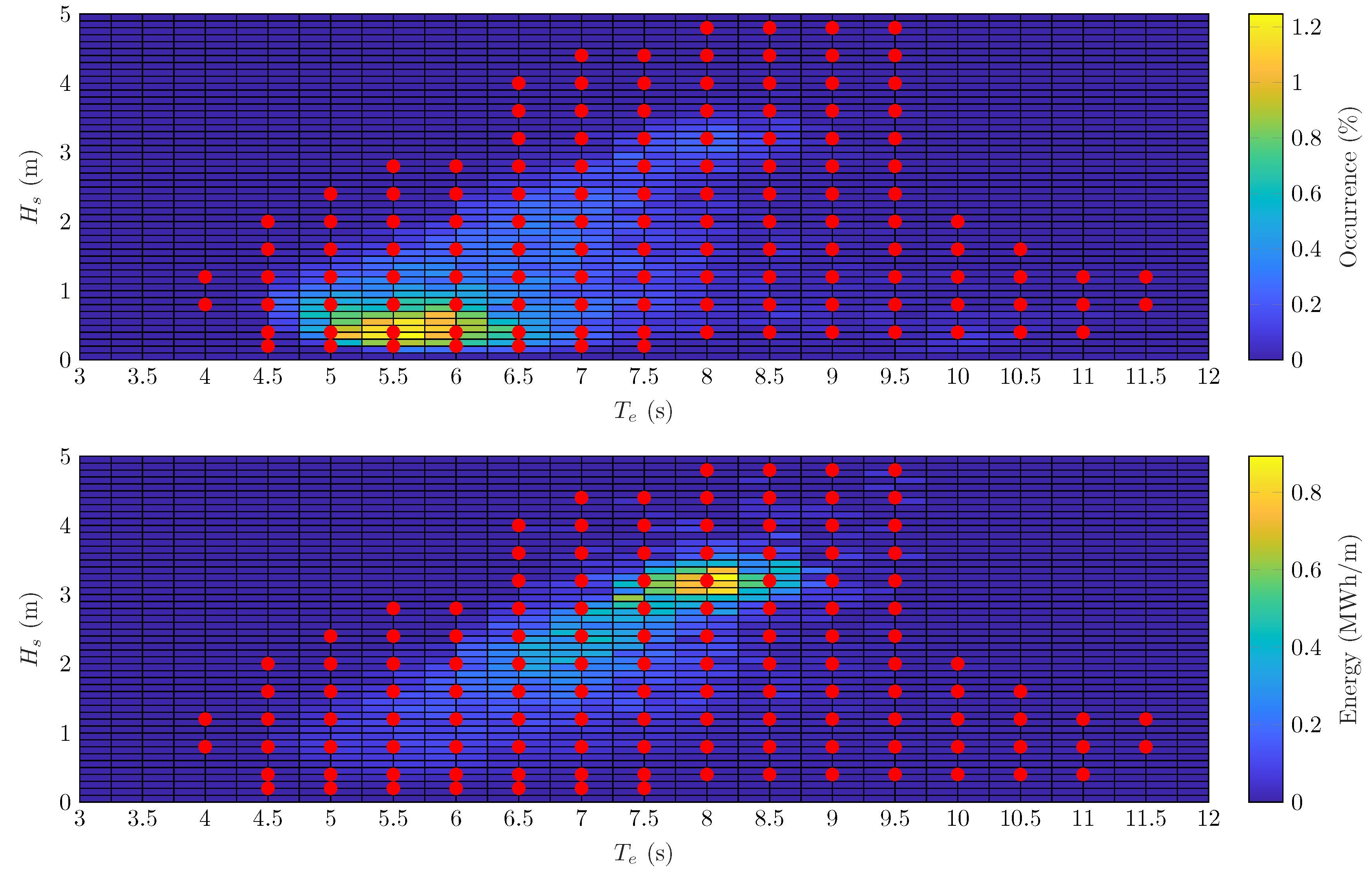
The fully-linear model can be efficiently solved in the frequency domain with a very low computational time. For each wave, the optimal $k_{PTO}$ and $c_{PTO}$ are sought by means of a multi-variate simplex algorithm [43], respecting global constraints on loads and displacements, as discussed in Section 3.2. It is worth remarking that the optimal control (performed by the simplex algorithm for each device) is completely independent of the design optimisation (performed by the genetic algorithm modifying geometrical and technical characteristics of the device). For each individual, the response to each irregular wave (modelled according to a Jonswap spectrum), comprising the simplex optimisation, requires about one second of computation. The productivity is computed over a scatter diagram densely described by 128 waves, accounting for about 100–150 seconds of computation. The targeted installation site is near Pantelleria island, in the Mediterranean Sea. The set of representative waves is chosen in order to adequately cover areas of the scatter diagram with non-negligible occurrence, as shown in Figure 4.

3. Optimisation Software

The implementation of the optimisation software, as presented in Figure A1 and discussed in Appendix A, requires the definition of the design variables, the objective function and the tuning parameters of the genetic algorithm. The system, presented in Section 2, has virtually an infinite number of design variables that define its hydrodynamic behaviour, inertial properties and power absorption/conversion characteristics. Therefore, making some assumptions on the geometry and subcomponents is mandatory. Moreover, a parametric definition is required, allowing the software to fully define the system without direct human intervention. Section 3.1 details such a parametric representation, univocally identifying a device by its shape, dimensions, mass, inertia, ballast’s distribution, pendulum and PTO characteristics. Starting from the shape of the hull, a BEM code automatically computes hydrodynamic curves, used to predict the device response to waves. However, techno-economic considerations should be included in the optimisation process, as extensively discussed in Section 1. Section 3.2 provides all functions that are used to estimate the cost of material and components. Moreover, constraints are imposed on displacements, velocities and loads, in accordance to the characteristics (and costs) of subcomponents. Finally, Section 3.3 presents tuning parameters of the genetic algorithm and the definitions of different performance indexes that the software aims at optimising.

3.1. Parametric Definition

In this work, 13 parameters are chosen to describe the device, summarised in

Table 1. Thirteen design parameters used by the genetic algorithm to univocally define an individual, as discussed in Section 3.1. Discrete values with constant spacing are used, with lower and upper bounds.

Design Parameter	Symbol	Units	Lower Bound	Upper Bound	# Discretisation
Hull length	L	(m)	8	30	23
Hull width	W	(m)	5	30	26
Bow/stern circumference ratio	h	(-)	0.5	1	6
Height ratio	k	(-)	0.5	1	6
Draft ratio	j	(-)	0.65	0.8	4
Ballast filling ratio	BFR	(-)	0.5	1	6
Number of pendulum/PTO	$N_p$	(-)	1	15	15
Unit mass ratio	${\beta }_U$	(-)	0.05	0.95	18
Pendulum shape factor	${\sigma }_p$	(-)	0.05	0.95	10
Pendulum arm factor	${\gamma }_p$	(-)	0.1	1	10
Pendulum fulcrum factor	${\lambda }_p$	(-)	0.1	1	10
Gearbox ratio	$r_g$	(-)	10	30	3
PTO ID	${\mathrm{ID}}_{\mathrm{PTO}}$	(-)	1	11	11

and hereafter discussed in detail: six for the hull, five for the pendulum and two for the PTO.

The shape of the hull is based on previous experience matured during the development of the PeWEC devices. For both manufacturability and hydrodynamic performance, the hull profile is assumed to be composed of a bottom circumference, tangential to two circumferences in the bow/stern sections, as shown in Figure 5, while the transversal section is assumed to be constant. The floater is symmetric with respect to the y-z and x-z planes and it results from the extrusion of the floater profile shape along the y-axis. The x-axis coincides with the floater deck and the z-axis goes from the deck of the floater upwards. The smooth surface with large radius of curvature is easier and cheaper to manufacture [44]. Moreover, the absence of sharp edges in the hull profile guarantee a low impact of vortex shedding and viscous drag losses [41]. Finally, the absence of re-entrant angles significantly reduces the risk of slamming events [27].

The following relevant parameters, with respect to Figure 5, characterise the hull’s profile:

• R: semi-length of the floater;
• H: overall height of the hull—i.e., the distance between the keel and the deck;
• D: draft of the hull;
• $R_1$: radius of circumference $C_1$;
• $(x_A,z_A)$: x- and z-coordinates of the centre of $C_1$, respectively, with $z_A=0$;
• $R_2$: radius of circumference $C_2$;
• $(x_B,z_B)$: x- and z-coordinates of the centre of $C_2$, respectively, with $x_B=0$;
• ${\alpha }_P=\angle \mathrm{PBO}$.

A subset of six independent geometrical and inertial parameters is defined, which are used as design parameters in the genetic algorithm:

• L: length of the floater;
• W: width of the floater;
• $h=x_A/R$: bow/stern circumference ratio;
• $k=H/R$: height ratio;
• $j=D/H$: draft ratio;
• BFR: ballast filling ratio, defined as the ratio of ballast located in aft/fore ballast tanks over the total ballast (BFR = 1: all the ballast is stored in aft/fore ballast tanks; BFR = 0: all the ballast is stored in bottom ballast tank).

Figure 6 shows four examples of the effects of the geometric parameters h and k. Figure 7 shows examples of draft and ballast allocation; namely, j and BFR. Note that the amount of ballast required ($M_{bal}$) is univocally defined by the mass of the displaced volume of water ($M_{tot}$), the mass of the hull structure ($M_h$) and the mass of the pendulum-PTO units. The allocation of $M_{bal}$ between bow/stern and keel compartments determines the total moment of inertia of the system, which is an important parameter to conveniently change the resonant period in pitch. The ballast material is assumed to be sand, with density (${\rho }_{bal}$) of 1400 kg m${}^{-3}$, which is considered to be an appropriate compromise between cost and specific weight. Filling of the ballast compartments is assumed from the extremities inwards, providing higher inertia and being easier from a practical point of view.

The hull is made out of standard naval carpentry steel, with a density (${\rho }_h$) of 7800 kg m${}^{-3}$. Based on previous experience with prototyping of the PeWEC device, $M_h$ is assumed to be 90 times the total volume of the floater. Consequently, assuming the walls of the floater as thin plates, an equivalent thickness is computed from the lateral surface of the floater and $M_h$, making the computation of inertial properties of the hull possible.

On the hull’s centreline, multiple pendulums can be placed, and their number ($N_p$) is one of the design parameters of the genetic algorithm. Each pendulum is composed of an oscillating cylindrical steel-made mass and a steel shaft. A trellis structure envelopes and supports the pendulum, a gearbox and the PTO; the ensemble of these components is referred to as unit, and its mass, inertia and volume are parametrically estimated starting from the pendulum’s properties. The mass and inertia of the entire unit are 20% and 30% higher than the mass and inertia of the pendulum, respectively. The extension of the unit in the y-direction is 2 m longer than the pendulum dimension, in order to account for the required space for machinery and technical operators during assembly and maintenance. The overall mass of the device depends on the submerged volume, defined by j, k and L. Since the mass of the hull is proportional to its total volume, the remaining part has to be composed of the ballast and units. A design parameter (${\beta }_U$) is defined so that the mass of each unit is:

$$M_{unit}=\frac{{\beta }_U\left(M_{tot}-M_h\right)}{N_p}$$

(6)

Consequently, the ballast mass is the complementary fraction of ${\beta }_U$.

Each pendulum is composed of a cylinder with axis parallel to the y-direction, swinging around a fulcrum. The volume of the cylinder is computed from its mass and density (${\rho }_p=$ 7800 kg m${}^{-3}$). Known volume, radius and height are defined by a shape factor (${\sigma }_p$), which is a free design parameter deciding if the pendulum is large and short (${\sigma }_p=0$) or small and long (${\sigma }_p=10$), with respect to the available space. Once the geometry is defined, the length of the swinging arm of the pendulum is defined by a design ratio ${\gamma }_p$, which takes the available space in the hull into account. Finally, the height of the fulcrum is defined by a further design parameter ${\lambda }_p$. Note that the relative geometry of the hull and the pendulum allow for full rotation of the swinging mass around the fulcrum.

Note that not all possible combinations of geometric and pendulum property parameters are feasible due to volume and weight physical restrictions. Consequently, during the optimisation, unfeasible individuals are discarded and the death penalty function is computed, contributing to increase the mortality rate of the genetic algorithm.

Finally, the actual conversion stage is performed by a permanent magnet syncronous motor (PMSM), one for each pendulum, combined with a planetary gearbox that is well suited for high torque and low speed applications. The gearbox ratio $r_g$ is a further design parameter. Finally, different PTO systems are used (${\mathrm{ID}}_{\mathrm{PTO}}$), with different combinations of nominal speed ($n_{PTO}$) and nominal torques ($T_{PTO}$), hence the costs, as shown in Figure 8.

A summarising table of the 13 design parameters is provided in Table 1, including lower and upper bounds, and number of equally spaced steps. Bounds and step sizes are based on the authors’ experience in developing the technology and running the model, ensuring that the minimum allowed variations of the design parameters produce small but relevant variations in the device performance. In this way, the algorithm is forced to consider only substantially different individuals, preventing the risk of simulating almost-equal devices. Although this objective could be achieved with a continuous parameter space by applying appropriate tolerances and checks on parameter variations, the authors believe that a gridded approach is more convenient, since it is easier to inspect and implement.

3.2. Techno-Economic Definitions and Constraints

The definition of the fitness index beholds primary importance in the identification of an optimal device: the genetic algorithm, similarly to other optimisation codes, iteratively tests several devices to find the one that minimises the objective function. In this work, three different fitness functions are used in three independent optimisation cycles, in order to have a deeper understanding of the phenomenon by building the Pareto front. In fact, multi-objective algorithms are usually performed as several single-objective optimisations where the performance index is computed as a weighted average of the multiple objectives [45].

The first objective is to minimise the capital expenditure (CapEx) over productivity (CoP) ratio, computed as the ratio between the overall capital expenditure (CapEx) and the produced energy over the lifetime of the plant ($N_y$, assumed 25 years for PeWEC):

$$\mathrm{CoP}=\frac{\mathrm{CapEx}}{N_y\mathrm{AEP}}$$

(7)

where the annual energy production (AEP) is computed considering net power, affected by efficiencies and baseload: the gearbox is assumed to have a 0.95 mechanical efficiency; the PTO conversion system is considered to have a conversion efficiency of 0.95; the baseload considers all the electrical machinery input energy necessary for their correct operation: 500 W for each pendulum. Power losses from the bearings have been neglected, since the pendulum rotates at low speed [39].

The overall cost considers the device’s capital expenditures to be classified in three main terms: hull’s materials and construction, units’ materials and construction, PTO. The mooring system is not considered, since its layout and cost are device-specific and no clear automatic parametrisation could be tackled in such an early design stage. Similarly, operational and maintenance expenditure (OpEx) is not considered in this work: on the one hand, its assessment requires extensive experience and a mature technology; on the other hand, in sealed WECs such as PeWEC but also ISWEC and SEAREV, OpEx is usually negligible compared to CapEx, since there are no moving parts subject to hostile marine environment (salty water, dust and debris). In fact, for common WECs presenting moving parts in hostile environment, it is estimated that the CapEx accounts for up to 35% only [46]. However, for the SEAREV device (with all moving parts enclosed in a sealed hull, as the PeWEC) it is estimated that OpEx is about 2% of the overall expenses [27]. Moreover, in such conditions, the levelised cost of energy (LCOE) is shown to be mainly sensitive to AEP and CaPex, while Opex, inflation rate, lifetime and expected internal rate of return are less impactful [27].

Several PTO models are considered in this analysis; each of them is characterised by its own maximum and nominal values in torque and speed. PTO costs are assumed to be significantly proportional to the nominal torque, with slope proportional to the nominal velocity, as shown in Figure 8. The PTO costs comprise those of the generator, the gearbox and various power electronic ancillary systems. However, the explicit costs of PTOs have been hidden for confidentiality. Note that a larger PTO provides higher freedom to the controller and is able to convert more energy. However, such a flexibility requires higher investments. The optimisation algorithm attempts to find a suitable compromise, also taking into account technical constraints on speed, torque and power of the PTO.

Material and manufacturing costs of the hull ($C_h$) and the pendulums ($C_p$) are estimated to be proportional to their respective mass, with the specific cost of the pendulums being almost twice the specific cost of the hull. Although simplified, all cost functions (PTO, hull construction and pendulum construction) are notionally based on the experience of the authors in the development and deployment of actual small and full-scale devices.

As discussed in Section 1, it is advisable to optimise the overall CoP, since it takes into account the compromise between techno-economic performance and hydrodynamic performance. However, a popular approach in the literature is to optimise the AEP or the hydrodynamic absorption abilities, regardless of the cost and/or technical characteristics and the limitations of the subcomponents required to achieve such a high conversion efficiency. In order to highlight substantial differences in convergence direction and the obtained optimal device, a second objective is considered: the capture width ratio (CWR), which is a common measure of energy conversion ability, defined as ratio between AEP and annual energy available in the resource ($E_w$):

$$\mathrm{CWR}=\frac{\mathrm{AEP}}{E_w}$$

(8)

Note that the correspondent performance index (to be minimised) is defined as -CWR, since CWR should be maximised. For each sea state, the incoming wave power on the device is defined as:

$$P_w=\frac{\rho g^2}{64\pi }{H}_s^2{T}_{e}W$$

(9)

where $\rho$ is the water density, $H_s$ the significant wave height and $T_e$ the energy period. Equation (9) shows how the incoming available energy is proportional to the width, which is one of the main design parameters in the optimisation. In practice, while maximising AEP will likely maximise (W) in order to have access to larger power, maximising CWR seeks to increase the portion of the converted energy from the wave to the grid, regardless of price of conversion. Finally, maximising CoP focuses on the cost of the conversion, regardless of its efficiency.

Since there are two competing objectives (minimising CoP and maximising CWR), a multi-objective optimisation approach is adopted. By means of a scalarisation technique [47], the two different objectives are aggregated into a unique objective by means of a weighted average, using a pair of weights ($w_1$, $w_2$). Through the choice of different weights, it is possible to build the Pareto-optimal set. Three pairs of weights have been considered, as shown in

Table 2. Multi-objective weights.

Weight Set ID	Explanation	CoP-Weight (${\mathit{w}}_1$)	CWR-Weight (${\mathit{w}}_2$)
(1)	CoP-driven	1	0
(2)	Weight-driven	0.5	0.5
(3)	CWR-driven	0	1

. Effectively, sets (1) and (3) are single-objective optimisations, while set (2) is a proper multi-objective one. However, by aggregating the results of the three optimisations, a Pareto front can be constructed.

Technological constraints are applied to all three optimisations. For each sea state, the optimal control parameters are chosen in order fulfil constraints tabulated in

Table 3. Technological constraints, fulfilled by tuning the control parameters.

Constrained Variable	Units	Constrained Value
$\mathrm{rms}\left(\delta \right)$	(${}^{\circ }$)	15
$\mathrm{rms}\left(\epsilon \right)$	(${}^{\circ }$)	40
$\max \left(\dot{\epsilon }\right)$	(rpm)	$n_{PTO}^{\max }/r_g$
$\max \left(T_{PTO}\right)$	(kNm)	$T_{PTO}^{\max }{r}_g$

. Note that velocity and torque constraints depend on the particular PTO and the gearbox installed, and hence on the design parameters ${\mathrm{ID}}_{\mathrm{PTO}}$ and $r_g$, respectively.

3.3. Genetic Algorithm

In Appendix A, a detailed description of the genetic algorithm is provided. Considering the specific problem, presented in Section 3.1, the tuning factors of the algorithm in

Table 4. Tuning parameters of the genetic algorithm, described in Appendix A.1, Appendix A.2, Appendix A.3, Appendix A.4, Appendix A.5 and Appendix A.6 and shown in red in the flow chart in Figure A1.

Name	Symbol	Value
Population size	N	150
Maximum generation count	M	200
Maximum stall generation	$M_{\Delta }$	50
Convergence threshold	$\Delta$	1.00 × 10${}^{-6}$
Elitism percentage	$ϵ$	5%
Tournament size	k	4

were chosen. The MATLAB built-in implementation of the genetic algorithm has been used, along with its default tuning parameters, which are considered to be suitable. Although beyond of the scope of this paper, a throughout sensitivity analysis can potentially improve the convergence rate of the algorithm.

4. Results

The MI-LXPM genetic algorithm has been chosen since it can effectively handle integer optimisation problems with potentially high number of unfeasible solutions. Figure 9 shows the development of the mortality rate through generations for the example of the CoP-driven optimisation. The first population has a significant number of unfeasible solutions, since it results from a purely stochastic process. However, the mortality rapidly drops to an average value (excluding the first two generations) of 25.5% with a standard deviation of 4.3%. Furthermore, note that there are 118 generations, meaning that the algorithm met convergence criteria before the maximum generation count of 200.

Note that two different seeds for the randomisation of the initial population of each optimisation have been used, reaching consistent results, hereafter discussed. The overall development of the algorithm is shown in Figure 10 for the example of the CoP-driven optimisation. The generic objective function $f^{\ast }$ to be minimised is on the vertical axis. For each generation, individuals are sorted according to $f^{\ast }$, so that the Nth individual has the highest $f^{\ast }$. Unfeasible individuals are missing markers at lowest individual count. The colour code is in accordance with the generation count, showing the evolution of the population. The final population count is 118, as also shown in Figure 9. Therefore, since the maximum stall generation criterion is 50 (see Table 4), improvements of the overall-optimum are found until generation 68. The cloud of points is also projected onto the vertical planes, highlighting relevant trends. The projection on the vertical right plane has the purpose of showing the potentially significant change of theslope as generations advance; i.e., if the ratio of fit individuals over the whole population changes. The fact that such a projection preserves about the same shape shows that the overall distribution of fit individuals remains about constant, apart from early generations. This is also shown in the projection on the vertical left plane: the minimum of $f^{\ast }$ decreases as generations progress, as expected and desired; however, the improvement is abrupt in early generations (until generation 40) and slows down afterwards (until generation 68). Furthermore, the number of devices at a low $f^{\ast }$ is relatively scarce, with a rarefied gap between the fittest individuals and the rest of the population. This suggests that the degradation of performance is quite sensitive to the choice and combination of design parameters. Moreover, the presence of about 20% of unfeasible devices may have an impact on the uniform improvement of the whole population. An alternative, smoother definition of the performance index, a finer parameter grid and different cross-over/mutation strength may smooth the convergence and increase the convergence rate. Moreover, the definition of the design parameters may be appropriately revised in order to structurally reduce the likelihood of unfeasible individuals. However, although such an extensive sensitivity analysis is an interesting topic for future investigation, it is believed that the current setup provides appropriate convergence and satisfactory results to discuss techno-economic aspects of the PeWEC device optimisation.

Three different optimisations have been performed, pursuing different objective functions in order to generate a Pareto front, as discussed in Section 3.2. Figure 11 shows the ensemble of all individuals generated from the three separate optimisations aggregated, plotting on the productivity versus the device cost, with the colour code being proportional to the CoP (left) and CWR (right). Elliptical annotations on the graphs indicated the most convenient region according to the respective metric (low CoP and high CWR, respectively). As expected, the optimal device changes with the optimality metric. In fact the highest AEP, the highest CWR and the lowest CoP are achieved by three significantly different individuals. In particular, it is evident that the increase in AEP is slower than the required increase in cost, so that the lowest CoP is found in the low cost region, in spite of a lower AEP. Moreover, low-CoP devices have also low CWRs, demonstrating the fact that the main driver is the device cost. Conversely, achieving high CWR and/or high AEP typically requires such an increase in device cost that the overall conversion becomes economically unfavourable.

It is interesting to analyse the direction that each optimisation tries to follow in order to improve performance index. Figure 12 shows a map of CWR versus COE, with three shaded areas encompassing individuals generated according to the three optimisation objectives. Individuals are also represented by markers of the same colour of the respective shaded area. As expected, the COE-driven area is attracted towards the bottom CoP-axis and achieves the overall minimum CoP. Similarly the CWR-driven optimisation extends the furthest along the CWR-axis, while obtaining higher CoP. In between, the weighted optimisation reaches good compromises of the two metrics.

Overall, it is important to remark that the CWR-driven optimum has a significantly high CoP, twice the overall minimum CoP. Similarly, also the device with lowest CoP from the CWR-driven optimisation has a high CoP, compared to the entire populations. Conversely, the lowest CoP is obtained by a device with a CWR 6 times smaller than the highest-overall CWR.

From Figure 12 it is possible to extract the Pareto front, shown in Figure 13. Moreover, it is interesting to highlight the evolution of the Pareto front as the algorithm advances through generations. Five different stages of progression are shown, equally spaced from 0% to 100% progression. It is evident that an abrupt improvement is achieved in early stages of the optimisation. Afterwards, although the improvement slows down, the Pareto front is gradually improved, moving downwards and rightwards, namely, to lower CoP and higher CWR.

4.1. CoP and CWR Optima

The characteristics of the optimum devices according to different objective functions are hereafter discussed. Figure 14 and Figure 15 show the cross-section and the top-view, respectively, of the optimal devices according to the three optimisations; namely, the CoP-driven optimum, the weight-driven optimum and the CWR-driven optimum. The same axis scale and dimension are used in order to highlight differences in size. Moreover, position, size and number of pendulums are shown.

Clearly, dimensions in the $x-z$ plane increase from left (CoP-driven) to right (CWR-driven), suggesting that a long and high hull is more hydrodynamically efficient for the considered installation site. However, the CoP-optimum is wider than the CWR-optimum, intercepting more wave-crest, hence the high amount of incoming energy. This suggests that increasing the width requires a lower increment in cost than the consequent increase in AEP, hence lowering the resulting CoP. Moreover, the number of pendulums (and PTOs) increases from left to right, hinting that the cost of the PTO is a limiting constraint in the CoP-driven optimisation. Conversely, higher CWR requires more pendulums with larger cross sectional areas and smaller radius/length ratios.

Figure 16 shows the response amplitude operator (RAO) of the CoP-optimum (left) and CWR-optimum (right), for the pitch ($RA{O}_{55}$, top) and pendulum oscillation ($RA{O}_{77}$, bottom) degrees of freedom. The PTO-free RAO is shown in solid lines and square markers, showing that the natural attitudes of the devices differ according to the pursued objective. In particular, maximising the CWR leads to a higher natural period (about 7 s) than optimising the CoP (about 5.4 s), so that it can be inferred that converting lower energetic waves (lower period) is more economically convenient. Furthermore, Figure 16 also shows RAOs, including optimal control parameters, shown in Figure 17, which significantly modify the dynamics of the system in order to maximise the performance, while remaining compliant with technical constraints. Since the PTO acts directly on the pendulum (under-actuated system), $RA{O}_{77}$ is more affected by the control, with significant increases in amplitude and bandwidth. Conversely, the $RA{O}_{55}$ is damped out, due to the inertial coupling between the hull and the pendulum. Overall, the control increases the energy flux from the hull to the pendulum, and ultimately, the PTO.

Overall, Figure 16 highlights the importance of a controlled-informed optimisation. In fact, the algorithm selects a device that is structurally apt to perform well when controlled, as opposed to select a performing uncontrolled device, and then applies a control.

Figure 17, in accordance with Figure 16, shows that the peak of conversion efficiency, i.e., CWR, is around lower wave periods for the CoP-optimum than the CWR-optimum. The control parameters maps show that $c_{PTO}$ is higher for the CWR-driven optimum, since it has to apply a higher damping torque to convert power in higher-energetic sea states. The reactive term of the PTO control, i.e., $k_{PTO}$, is negative almost across the whole scatter in order to obtain the resonant period of the pendulum $T_{res}$, shown in the last row of Figure 17. The natural period of the pendulum can be affected by the properties of the pendulum (mass, inertia and length) and $k_{pto}$. However, the inertial properties of the pendulum also affect the coupling between hull and pendulum, as shown in the off-diagonal terms of (5) and (4), while $k_{pto}$ only affects the diagonal term of the pendulum. Therefore, it appears that the control-informed optimisation algorithm favours lighter pendulums with negative $k_{PTO}$ rather than heavier pendulums and higher $k_{PTO}$.

4.2. Techno-Economic Trends and Considerations

It is important to remark that Figure 14 and Figure 15, although representative, are just three examples. Moreover, comments so far have no general or absolute validity, since many interrelated parameters comes into play. In order to investigate significant and more informative trends, Figure 18, Figure 19, Figure 20 and Figure 21 show relevant results and design parameters for a selection of 28 devices, chosen in order to be representative of the fittest individuals in the whole population, according to the two evaluation metrics considered (CWR and CoP). In practice, the range of CWR from 0% to 30% is equally divided into 14 bins, and the individual with highest CWR of each bin is selected. Likewise, the range of CoP from 500 EUR/MWh to 1000 EUR/MWh is equally divided into 14 bins, and the individual with lowest CoP of each bin is selected. In order to highlight the most convenient individual, according to each metric, bars colour is proportional to CWR and 1/CoP, for the left and right graphs, respectively, so that best devices are represented by blue bars, while worst devices are in red.

The first row of Figure 18 highlights that high CWRs consistently result in high CoPs and vice versa, remarking that conversion efficiency and economic ability can be contrasting objective. It follows that the best devices in the CWR sense (blue bars in the left column) have high CoP. Conversely, the best devices in the CoP sense (blue bars in the right column) are economically performant in spite of their low CWR. In fact, the second and third rows of Figure 18 show that high AEPs come at high device costs and their ratio is more convenient at low AEP.

Figure 19 explores variations in the hull dimensions, which are the main drivers of hydrodynamic performance, and consequent mass, which is proportional to the hull cost. On the one hand, while CWR consistently increases with the hull length, longer hulls generate high CoP. Conversely, the device width is about constant for all CWR and CoP bins, with strong variations just around the second and third bins of the CWR and CoP scales, respectively. Finally, mainly as a consequence of length and width trends, the hull mass increases for increasing CWR and CoP. In particular, low CoP devices require lighter and cheaper hulls.

Figure 20 shows the total pendulum mass, the geometry ratio and the number of pendulums. The cost of the unit is proportional to the total masses of pendulums and their numbers, since there is one PTO attached to each pendulum. Figure 20 shows that more and overall heavier pendulums increase the CWR but also the CoP, in a similar trend found for the hull dimension and mass, confirming that the incremental investment required to produce more energy is not cost-effective. However, since the pendulums mass and number of pendulums follow the same trend, the single pendulum has about a constant mass in all bins. The geometry ratio ${\sigma }_p$ defines how slender the pendulum is, considering the available space. Overall, although no strong correlation is found, it seems that once the masses and number of pendulums are defined, the algorithm leads to cylinders as long and slim as possible (high ${\sigma }_p$).

Figure 21 shows that CWR and CoP are not particularly sensitive to the single-PTO parameters. In fact, the gearbox ratio is almost always the highest available, while the highest rated torque is often selected, despite the absence of a clear trend, especially in the CWR bins. Similarly, the rated torque is about equally split across both CWR and CoP bins, without any significant pattern. Consequently, the PTOs affect the performance mainly by means of their number, since there is an equal number of PTOs and pendulums: as the optimisation seeks more torque to increase the power conversion, since the largest PTO is already used, the number of pendulum units is increased. Likewise, it seems more cost effective to have fewer pendulums with the largest PTOs than more pendulums with small-medium PTOs.

Finally, Figure 22 shows the total and percentage costs, divided in the hull, pendulum and PTO subcomponents. On the one hand, the absolute cost of each subcomponent tends to increase with both CWR and CoP. On the other hand, the rates of increase seem to be different, since the hull tends to become less relevant in favour of the pendulum/PTO unit. Although the mass (and cost) of the hull increases (from 300 tons to 450 tons), as shown in Figure 19, the number (and cost) of pendulums/PTOs increases at a higher rate (from 1 to 5), as shown in Figure 20. Therefore, Figure 22 shows that the proportional increase of pendulum units has a higher impact than the increase of hull dimension and mass. Alternatively, it can be inferred that the optimisation algorithm reduces the number of pendulum units in order to reduce the CoP. Conversely, in order to increase the CWR, regardless of subcomponents cost, there must be a higher number of conversion units.

The results discussed so far highlight a limitation of the current concept, which is also an opportunity for substantial improvement. In particular, CWR and CoP are partially competing objectives, due to intrinsic limitations and assumptions. In all configurations, while the largest PTO and gearbox ratio possible are selected, the numbers of pendulum/PTO units are mainly selected in order to either maximise CWR or minimise CoP. Therefore, if the total cost of the PTO system could be decreased while maintaining the same conversion ability, both CWR and CoP would benefit. This can be achieved by connecting each PTO to more than one pendulum. However, since this solution implies requiring an even higher PTO torque, electrical generators become ill-suited. Conversely, hydraulic PTOs work better with high loads at low speed, so the gearbox could also be removed. Moreover, virtually, just one hydraulic PTO could be connected to all pendulums by means of an appropriate hydraulic system. Although the hydraulic PTO system introduces more power losses, the overall cost benefits could lead to a significantly lower CoP.

5. Conclusions

The present paper tackles a comprehensive techno-economic optimisation of a floating wave energy converter via genetic algorithm, considering a wide multi-variate design space, including shape and dimensions of the floater, and subcomponent configuration and characteristics. It is crucial to consider both power conversion ability and total cost of the device, taking physical constraints and control into account for a realistic assessment of the overall performance. Results herein presented are preliminary and not meant to have general validity since they are the consequence of specific techno-economic assumptions and hypotheses on the working principle and configuration. However, there is general validity in stating that the optimisation objective has a great influence on the optimised design, so it should be carefully chosen to be as close as possible to the actual intended target. In this paper it is shown that efficient conversion does not necessary imply economical conversion. On the contrary, for the specific case analysed, it resulted that increasing conversion efficiency required an excessive increase in costs, so that the most convenient solution in the economic sense had a relatively low conversion efficiency. Moreover, specific and detailed techno-economic considerations at an early design optimisation stage can lead to substantial conceptual modifications of the system, impossible at a mature development stage, which may be key for the success of such technology.