Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV)
Abstract
1. Introduction
Why Use the Proposed Approach on a UUV?
2. Materials and Methods
2.1. Deterministic Artificial Intelligence Self-Awareness Statement
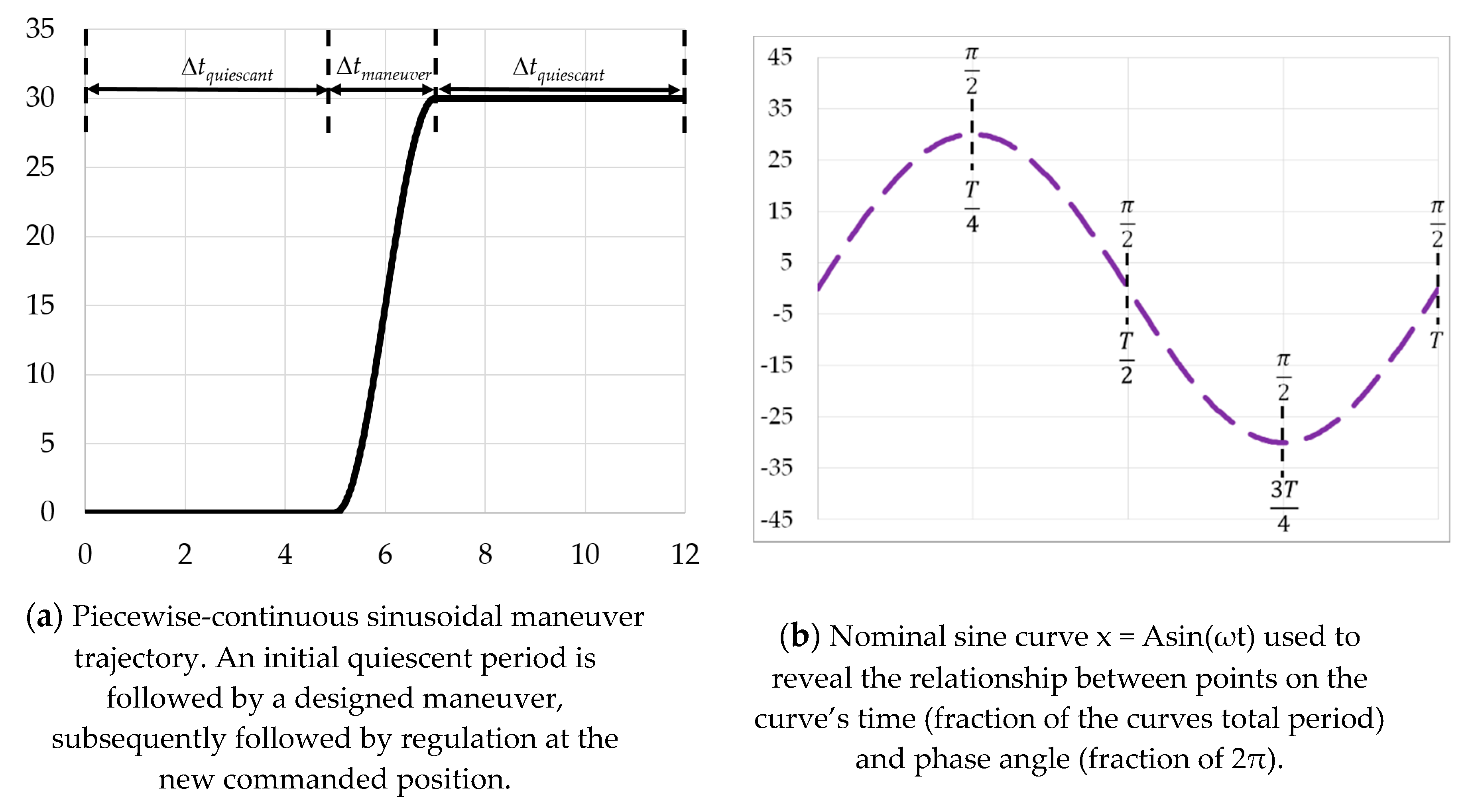
2.2. Autonomous Trajectory Generation
- 1.
- Choose the maneuver time: is used here illustratively. Express the maneuver time as a portion (half) of the total sinusoidal period, , as depicted in Figure 3b.
- -
- The result is Equation (14):
| Important side comment: Δtmaneuver is provided by the user, thus, this time period can be optimized (often represented as t*) to meet any number of cost functions, J and constraint equations. |
- 2.
- Phase shift the curve to place the smooth low-point from to the desired maneuver start time, following the quiescent period at.
- -
- The result is Equation (15) plotted in Figure 4a:
- 3.
- Compress the amplitude for the desired final change in amplitude to equate to the top-to-bottom total of curve.
- -
- The result is Equation (16) plotted in Figure 4b:
- 4.
- Amplitude-shift the curve up for smooth initiation at arbitrary starting position used here by adding.
- -
- The result is Equation (17) plotted in Figure 4c:
- 5.
- Craft a piecewise continuous trajectory such that amplitude is zero until the termination of . Follow the sinusoidal trajectory during the maneuver time indicated by , and then hold the final amplitude afterwards.
- -
- The result is Equation (18) plotted in Figure 4d:
- 6.
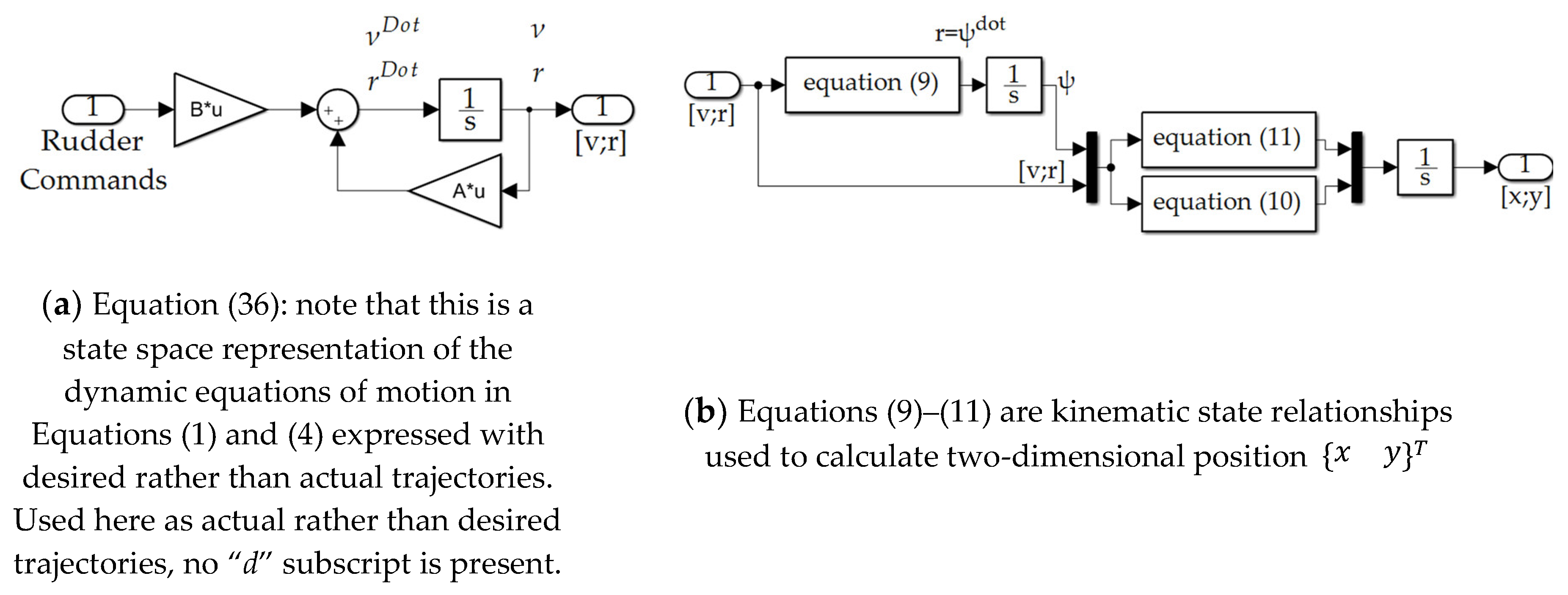
- Differentiating Equation (17), derive the full state trajectory per Equations (19)–(21), establishing the second portion of the piecewise continuous trajectory in Equation (18) and Figure 4d, noting that Equation (19) exactly matches the second portion of Equation (18):
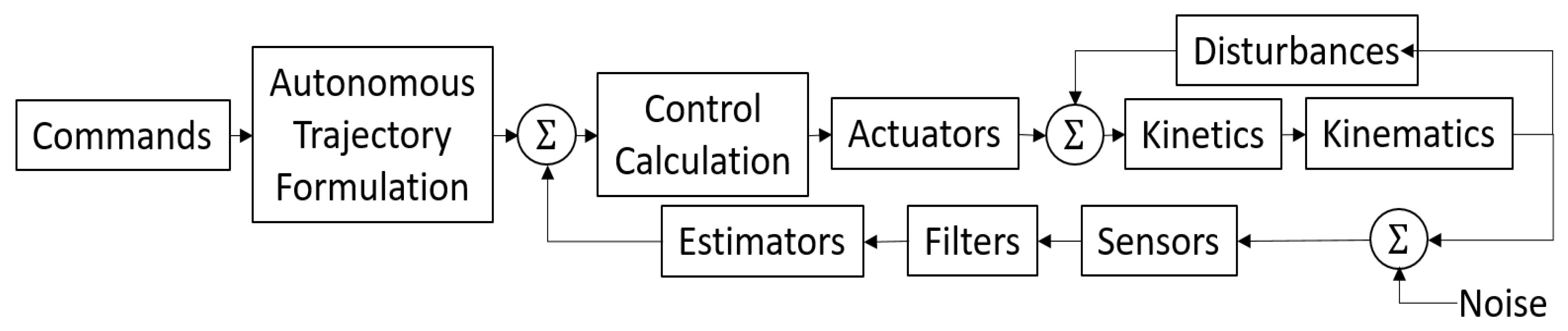
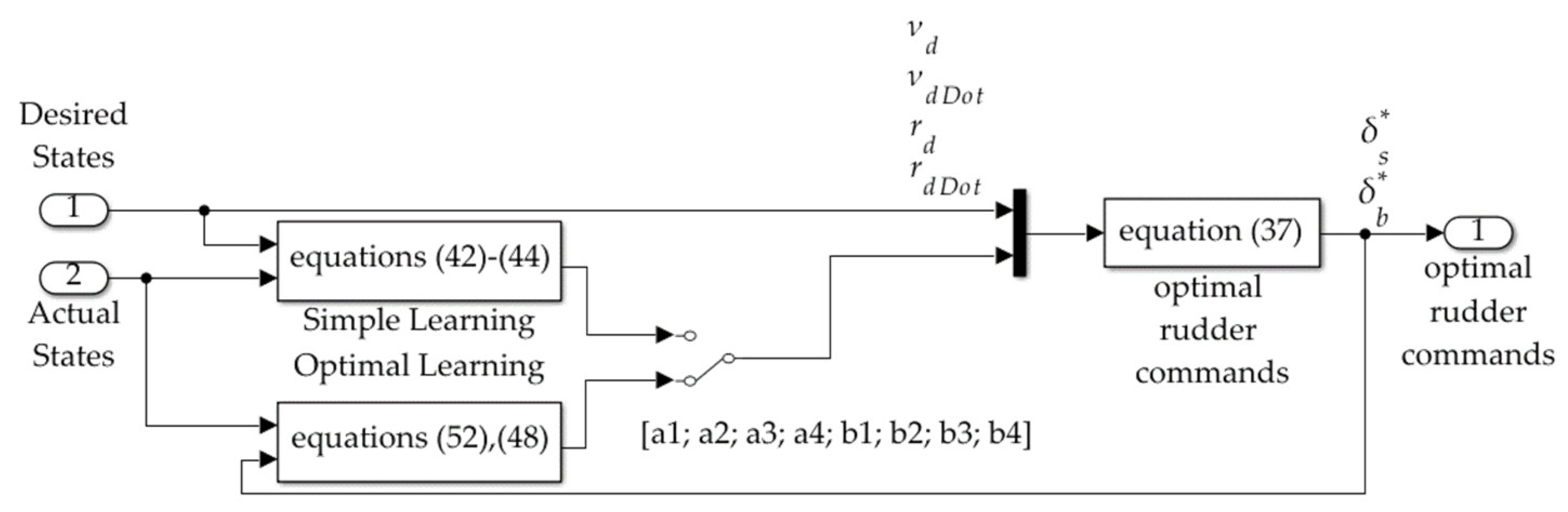
2.3. Topologies and Implementation in SIMULINK
3. Results
3.1. Articulate Optimal Deterministic Self-Awareness Statement
3.2. Formulate Optimal Deterministic Self-Awareness Statement in MIMO State Space Form
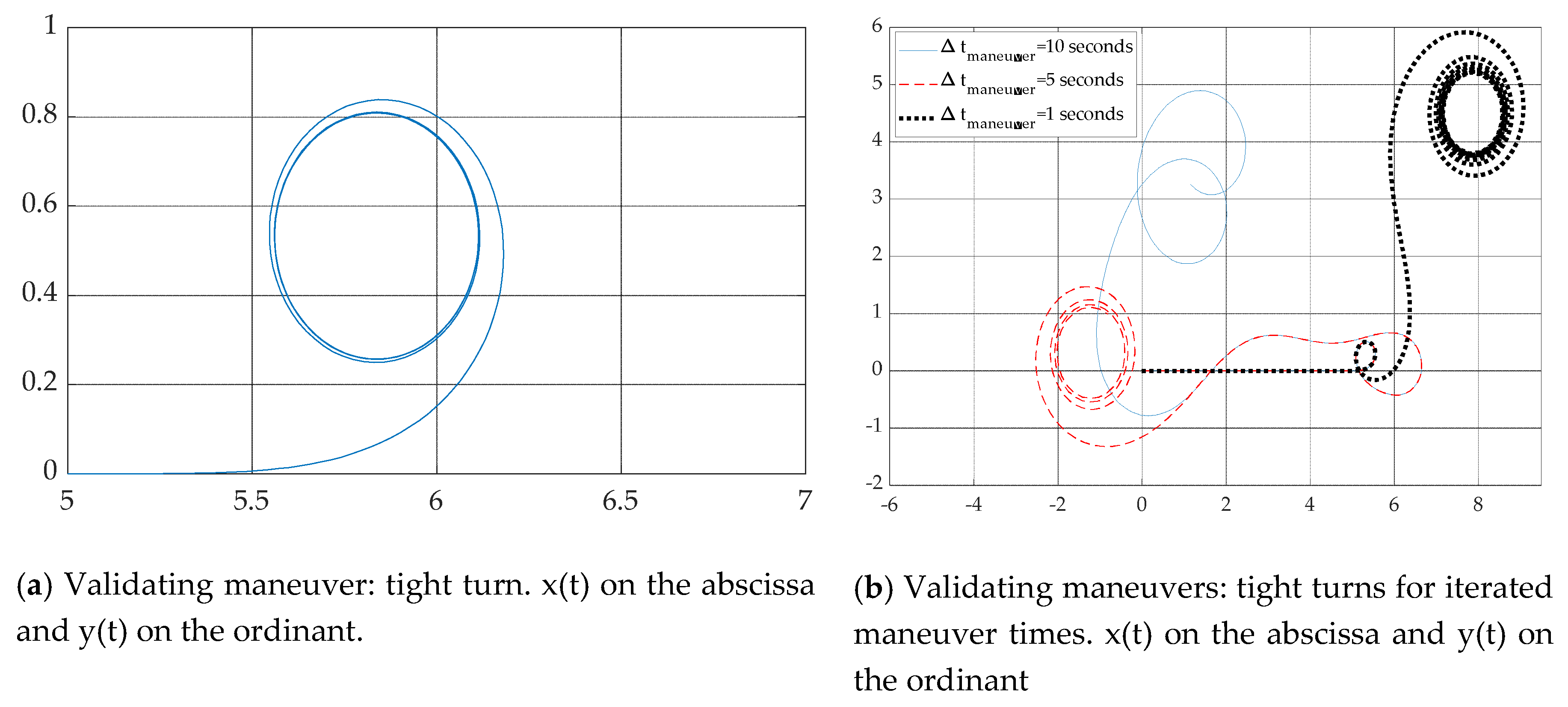
3.3. Validating Simulations
3.4. Deterministic Artificial Intelligence Simple-Learning
3.5. Deterministic Artificial Intelligence Optimal Learning
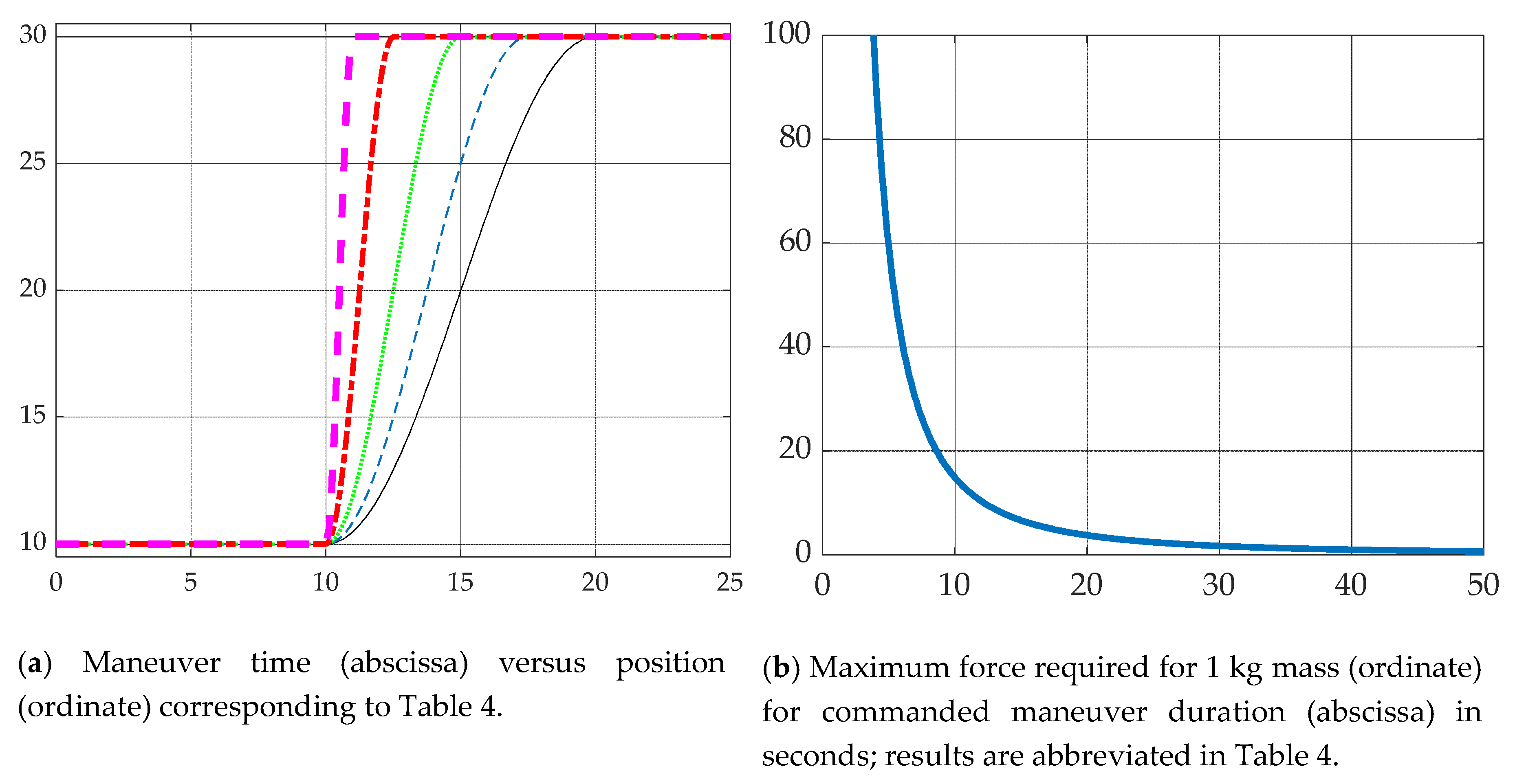
3.6. Optimize maneuver Time for the Allowable Maximum Non-Dimensional Force for a Representative Maneuver
3.7. Procedures to Implement Deterministic Artificial Intelligence as Proposed
|
4. Discussion
4.1. Deterministic Artificial Intelligence Procedure
- 1.
- Use simple learning (Equations (42)–(44)) or optimal learning (Equation (52) with Equation (45)) to update the values of mass and mass moment of inertia, where in the instance of optimal learning the location of the center of gravity is provided by Equation (35). The update begins with substituting the values of the learned parameters into the values of the constants (defined in Equation (2) and Equation (5)), leading to the values of constants (defined in Equation (31) and Equation (34)) used in Equation (37) that command to both rudders.
- a.
- Replace , , and in the deterministic self-awareness statements intermediate constants and in Equations (2) and (5).
- b.
- Use intermediate constants and to find updated intermediate constants and defined in Equations (31) and (34)
- c.
- Use updated intermediate constants and in the optimal rudder commands of Equation (37), which include deterministic artificial intelligence self-awareness statements (thus, we are learning the vehicle’s self).
4.2. Operational Implementation Procedure
- 1.
- Choose for the available control authority (by choice of actuators) from Figure 12b.
- 2.
- Use Equations (19)–(21) to autonomously articulate a trajectory (state, velocity, and acceleration) that starts at the initial point and ends at the commanded point using from step 1.
- 3.
- Use Equation (37) for optimal rudder commands developed using the deterministic self-awareness statement of rigid body motion, where constants are defined in (31) and (34) with constituent constants defined in Equations (2) and (5).
- 4.
- Use Equations (42)–(44) for simple learning or Equation (52) with Equation (45) for optimal learning of time-varying, unknowable parameters .
- 5.
- Use the parameters learned in step 4 to update the constants and constituent constants, repeating step 3 optimal rudder commands
4.3. Follow-On Research
Funding
Conflicts of Interest
Appendix A
| Nondimensional Variable | Definition |
|---|---|
| Mass | |
| Position of center of mass in meters | |
| Mass moment of inertia with respect to a vertical axis that passes through the vehicle’s geometric center (amidships) | |
| , | Lateral (sway) velocity and rate |
| , | Heading angle and rate |
| Cartesian position coordinates | |
| Turning rate (yaw) | |
| , | Deflection of stern rudder and its optimal variant |
| , | Deflection of bow rudder and its optimal variant |
| , | Sway force coefficients: coefficients describing sway forces from resolved lift, drag, and fluid inertia along body lateral axis. These occur in response to individual (or multiple) velocity, acceleration, and plane surface components, as indicated by the corresponding subscripts |
| ,, | Yaw moment coefficients |
| Arbitrarily labeled constants used to simplify expressions | |
| , | Arbitrary motion states (position, velocity, and acceleration) variables used to formulate autonomous trajectories |
| , | Arbitrary motion state displacement amplitude and initial amplitude used to formulate autonomous trajectories |
| Eigenvalue associated with exponential solution to ordinary differential equations | |
| Frequency of sinusoidal functions | |
| Time | |
| Phase angle of sinusoidal functions | |
| Period of sinusoidal functions | |
| User-defined quiescent period used to trouble-shoot and validate computer code (no motion should occur during the quiescent period). | |
| User-defined duration of maneuver (often established by time-optimization problems) | |
| Variables in state-variable formulation (“state space”) of equations of motion associated with motion states | |
| Variables in state-variable formulation (“state space”) of equations of motion associated with controls | |
| Deterministic error-optimal stern rudder displacement commands | |
| Deterministic error-optimal bow rudder displacement commands | |
| Learned vehicle mass | |
| Learned product of vehicle mass and location of center of mass | |
| Learned location of center of mass | |
| Learned mass moment of inertia and initial value | |
| Control gain for mass simple-learning | |
| Control gain for learning product of mass and location of center of mass | |
| , | Control gain for learning mass moment of inertia |
| Variables (combinations of motion states) used to reparametrize problem into optimal learning form |
References
- McCorduck, P.; Cfe, C. Machines Who Think: A Personal Inquiry into the History and Prospects of Artificial Intelligence, 2nd ed.; A.K. Peters, Ltd.: Matick, MA, USA, 2004; ISBN 1-56881-205-1. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003; ISBN 0-13-790395-2. [Google Scholar]
- Berlinski, D. The Advent of the Algorithm. Harcourt Books; Harcourt: San Diego, CA, USA, 2000; ISBN 978-0-15-601391-8. [Google Scholar]
- Turing, A. Machine Intelligence. In The Essential Turing: The Ideas That Gave Birth to the Computer Age; Copeland, B.J., Ed.; Oxford University Press: Oxford, UK, 1948; p. 412. ISBN 978-0-19-825080-7. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2009; ISBN 978-0-13-604259-4. [Google Scholar]
- Dartmouth Summer Research Project on Artificial; Dartmouth College: Hanover, NH, USA, 1956.
- Schaeffer, J. Didn’t Samuel Solve That Game? In One Jump Ahead; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Crevier, D. AI: The Tumultuous Search for Artificial Intelligence; BasicBooks: New York, NY, USA, 1993; ISBN 0-465-02997-3. [Google Scholar]
- Howe, J. Artificial Intelligence at Edinburgh University: A Perspective; Informatics Forum: Edinburgh, UK, 2007. [Google Scholar]
- Simon, H.A. The Shape of Automation for Men and Management; Harper & Row: New York, NY, USA, 1965. [Google Scholar]
- Minsky, M. Computation: Finite and Infinite Machines; Prentice-Hall: Englewood Cliffs, NJ, USA, 1967; ISBN 978-0-13-165449-5. [Google Scholar]
- McCarthy, J. Artificial Intelligence: A paper symposium. In Artificial Intelligence: A General Survey; Lighthill, J., Ed.; Science Research Council: Newcastle, UK, 1973. [Google Scholar]
- ACM Computing Classification System: Artificial Intelligence; ACM: New York, NY, USA, 1998.
- Nilsson, N. Artificial Intelligence: A New Synthesis; Morgan Kaufmann: Burlington, VT, USA, 1998; ISBN 978-1-55860-467-4. [Google Scholar]
- Newquist, H. The Brain Makers: Genius, Ego, and Greed in the Quest for Machines That Think; Macmillan/SAMS: New York, NY, USA, 1994; ISBN 978-0-672-30412-5. [Google Scholar]
- NRC (United States National Research Council). Developments in Artificial Intelligence. In Funding a Revolution: Government Support for Computing Research; National Academy Press: Washington, DC, USA, 1999. [Google Scholar]
- Luger, G.F.; Stubblefield, W. Artificial Intelligence: Structures and Strategies for Complex Problem Solving, 5th ed.; Benjamin/Cummings: San Francisco, CA, USA, 2004; ISBN 978-0-8053-4780-7. [Google Scholar]
- Kurzweil, R. The Singularity Is Near; Penguin Books: London, UK, 2005; ISBN 978-0-670-03384-3. [Google Scholar]
- Markoff, J. Computer Wins on ‘Jeopardy!’: Trivial, It’s Not; The New York Times: New York, NY, USA, 2011. [Google Scholar]
- Ask the AI Experts: What’s Driving Today’s Progress in AI? McKinsey & Company: Brussels, Belgium, 2018.
- Kinect’s AI Breakthrough Explained. Available online: https://www.i-programmer.info/news/105-artificial-intelligence/2176-kinects-ai-breakthrough-explained.html (accessed on 29 July 2020).
- Rowinski, D. Virtual Personal Assistants & The Future Of Your Smartphone [Infographic]. Available online: https://readwrite.com/2013/01/15/virtual-personal-assistants-the-future-of-your-smartphone-infographic/ (accessed on 29 July 2020).
- AlphaGo—Google DeepMind. Available online: https://deepmind.com/research/case-studies/alphago-the-story-so-far (accessed on 29 July 2020).
- Artificial intelligence: Google’s AlphaGo beats Go master Lee Se-dol. BBC News. 12 March 2016. Available online: https://www.bbc.com/news/technology-35785875 (accessed on 10 June 2020).
- Metz, C. After Win in China, AlphaGo’s Designers Explore New AI after Winning Big in China. Available online: https://www.wired.com/2017/05/win-china-alphagos-designers-explore-new-ai/ (accessed on 29 July 2020).
- World’s Go Player Ratings. Available online: https://www.goratings.org/en/ (accessed on 29 July 2020).
- Kē Jié Yíng Celebrates His 19th Birthday, Ranking First in the World for Two Years. 2017. Available online: http://sports.sina.com.cn/go/2016-08-02/doc-ifxunyya3020238.shtml (accessed on 10 June 2020). (In Chinese).
- Clark, J. Why 2015 Was a Breakthrough Year in Artificial Intelligence. Bloomberg News. 8 December 2016. Available online: https://www.bloomberg.com/news/articles/2015-12-08/why-2015-was-a-breakthrough-year-in-artificial-intelligence (accessed on 10 June 2020).
- Reshaping Business with Artificial Intelligence. MIT Sloan Management Review. Available online: https://sloanreview.mit.edu/projects/reshaping-business-with-artificial-intelligence/ (accessed on 10 June 2020).
- Lorica, B. The State of AI Adoption. O’Reilly Media. 18 December 2017. Available online: https://www.oreilly.com/radar/the-state-of-ai-adoption/ (accessed on 10 June 2020).
- Allen, G. Understanding China’s AI Strategy. Center for a New American Security. 6 February 2019. Available online: https://www.cnas.org/publications/reports/understanding-chinas-ai-strategy (accessed on 10 June 2020).
- Review|How Two AI Superpowers—The U.S. and China—Battle for Supremacy in the Field. Washington Post, 2 November 2018.
- Alistair, D. Artificial Intelligence: You Know It Isn’t Real, Yeah? 2019. Available online: https://www.theregister.com/2019/02/22/artificial_intelligence_you_know_it_isnt_real_yeah (accessed on 10 June 2020).
- Stop Calling It Artificial Intelligence. Available online: https://joshworth.com/stop-calling-in-artificial-intelligence/ (accessed on 10 April 2020).
- AI Isn’t Taking over the World—It Doesn’t Exist yet. Available online: https://www.gbgplc.com/inside/ai/ (accessed on 10 April 2020).
- Poole, D.; Mackworth, A.; Goebel, R. Computational Intelligence: A Logical Approach; Oxford Press: New York, NY, USA, 1998. [Google Scholar]
- Legg, S.; Hutter, M. A Collection of Definitions of Intelligence. Front. Artif. Intell. Appl. 2007, 157, 17–24. [Google Scholar]
- Domingos, P. The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World; Basic Books: New York, NY, USA, 2015; ISBN 978-0-465-06192-1. [Google Scholar]
- Lindenbaum, M.; Markovitch, S.; Rusakov, D. Selective sampling for nearest neighbor classifiers. Mach. Learn. 2004, 54, 125–152. [Google Scholar] [CrossRef]
- Brutzman, D. A Virtual World for an Autonomous Underwater Vehicle. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 1994. Available online: https://calhoun.nps.edu/handle/10945/30801 (accessed on 21 April 2020).
- Sands, T.; Bollino, K.; Kaminer, I.; Healey, A. Autonomous Minimum Safe Distance Maintenance from Submersed Obstacles in Ocean Currents. J. Mar. Sci. Eng. 2018, 6, 98. [Google Scholar] [CrossRef]
- Deterministic Artificial Intelligence for Surmounting Battle Damage. FY19 Funded Research Proposal. Available online: https://calhoun.nps.edu/handle/10945/62087 (accessed on 20 April 2020).
- Sands, T.; Kim, J.; Agrawal, B. 2H Singularity-Free Momentum Generation with Non-Redundant Single Gimbaled Control Moment Gyroscopes. In Proceedings of the 45th IEEE Conference on Decision & Control, San Diego, CA, USA, 13–15 December 2006. [Google Scholar]
- Sands, T.; Kim, J.; Agrawal, B. Control Moment Gyroscope Singularity Reduction via Decoupled Control. In Proceedings of the IEEE SEC, Atlanta, GA, USA, 5–8 March 2009. [Google Scholar]
- Sands, T.; Kim, J.; Agrawal, B. Experiments in Control of Rotational Mechanics. Int. J. Autom. Contr. Int. Syst. 2016, 2, 9–22. [Google Scholar]
- Agrawal, B.; Kim, J.; Sands, T. Method and Apparatus for Singularity Avoidance for Control Moment Gyroscope (CMG) Systems without Using Null Motion. U.S. Patent Application No. 9567112 B1, 14 February 2017. [Google Scholar]
- Sands, T.; Lu, D.; Chu, J.; Cheng, B. Developments in Angular Momentum Exchange. Int. J. Aerosp. Sci. 2018, 6, 1–7. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B. Singularity Penetration with Unit Delay (SPUD). Mathematics 2018, 6, 23. [Google Scholar] [CrossRef]
- Lewis, Z.; Ten Eyck, J.; Baker, K.; Culton, E.; Lang, J.; Sands, T. Non-symmetric gyroscope skewed pyramids. Aerospace 2019, 6, 98. [Google Scholar] [CrossRef]
- Baker, K.; Culton, E.; Ten Eyck, J.; Lewis, Z.; Sands, T. Contradictory Postulates of Singularity. Mech. Eng. Res. 2020, 9, 28–35. [Google Scholar] [CrossRef]
- Wikipedia, Deterministic Algorithm. Available online: https://en.wikipedia.org/wiki/Deterministic_algorithm#:~:text=In%20computer%20science%2C%20a%20deterministic,the%20same%20sequence%20of%20states (accessed on 10 June 2020).
- Quora.com. Available online: https://www.quora.com/What-s-the-difference-between-a-deterministic-environment-and-a-stochastic-environment-in-AI (accessed on 10 June 2020).
- Baker, K.; Cooper, M.; Heidlauf, P.; Sands, T. Autonomous trajectory generation for deterministic artificial intelligence. Electr. Electron. Eng. 2019, 8, 59. [Google Scholar]
- Lobo, K.; Lang, J.; Starks, A.; Sands, T. Analysis of deterministic artificial intelligence for inertia modifications and orbital disturbances. Int. J. Control Sci. Eng. 2018, 8, 53–62. [Google Scholar] [CrossRef]
- Sands, T. Physics-based control methods. In Advances in Spacecraft Systems and Orbit Determination; Ghadawala, R., Ed.; InTechOpen: Rijeka, Croatia, 2012; pp. 29–54. [Google Scholar]
- Sands, T.; Lorenz, R. Physics-Based Automated Control of Spacecraft. In Proceedings of the AIAA SPACE, Pasadena, CA, USA, 14–17 September 2009; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Sands, T. Improved magnetic levitation via online disturbance decoupling. Phys. J. 2015, 1, 272. [Google Scholar]
- National Air and Space Administration. Design of Low Complexity Model Reference Adaptive Controllers; Dryden: Fort Worth, TX, USA; California and Ames: Mountain View, CA, USA, 2012; ISBN 978-1793957245.
- Nguyen, N. Model-Reference Adaptive Control: A Primer; Springer: New York, NY, USA, 2019; ISBN 978-3319563923. [Google Scholar]
- National Air and Space Administration. Complexity and Pilot Workload Metrics for the Evaluation of Adaptive Flight Controls on a Full Scale Piloted Aircraft; Dryden: Fort Worth, TX, USA; California and Ames: Mountain View, CA, USA, 2019; ISBN 978-1794408159.
- Sands, T. Space systems identification algorithms. J. Space Exp. 2017, 6, 138–149. [Google Scholar]
- Sands, T.; Kenny, T. Experimental piezoelectric system identification. J. Mech. Eng. Autom. 2017, 7, 179–195. [Google Scholar] [CrossRef]
- Sands, T. Nonlinear-adaptive mathematical system identification. Computation 2017, 5, 47. [Google Scholar] [CrossRef]
- Sands, T.; Armani, C. Analysis, correlation, and estimation for control of material properties. J. Mech. Eng. Autom. 2018, 8, 7–31. [Google Scholar] [CrossRef]
- Sands, T.; Kenny, T. Experimental sensor characterization. J. Space Exp. 2018, 7, 140. [Google Scholar]
- Sands, T. Phase lag elimination at all frequencies for full state estimation of spacecraft attitude. Phys. J. 2017, 3, 1–12. [Google Scholar]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Improved Hamiltonian adaptive control of spacecraft. In Proceedings of the IEEE Aerospace, Big Sky, MT, USA, 7–14 March 2009; IEEE Publishing: Piscataway, NJ, USA, 2009. INSPEC Accession Number: 10625457. pp. 1–10. [Google Scholar]
- Nakatani, S.; Sands, T. Simulation of spacecraft damage tolerance and adaptive controls. In Proceedings of the IEEE Aerospace, Big Sky, MT, USA, 1–8 March 2014; IEEE Publishing: Piscataway, NJ, USA, 2014. INSPEC Accession Number: 14394171. pp. 1–16. [Google Scholar]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Spacecraft Adaptive Control Evaluation. In Proceedings of the Infotech@Aerospace, Garden Grove, CA, USA, 19–21 June 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Sands, T.; Kim, J.J.; Agrawal, B.N. Spacecraft fine tracking pointing using adaptive control. In Proceedings of the 58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007; International Astronautical Federation: Paris, France, 2007. [Google Scholar]
- Nakatani, S.; Sands, T. Autonomous damage recovery in space. Int. J. Autom. Control Intell. Syst. 2016, 2, 23. [Google Scholar]
- Nakatani, S.; Sands, T. Battle-damage tolerant automatic controls. Electr. Electron. Eng. 2018, 8, 23. [Google Scholar]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling chaos—Forced van der pol equation. Mathematics 2017, 5, 70. [Google Scholar] [CrossRef]
- Heshmati-alamdari, S.; Eqtami, A.; Karras, G.C.; Dimarogonas, D.V.; Kyriakopoulos, K.J. A Self-triggered Position Based Visual Servoing Model Predictive Control Scheme for Underwater Robotic Vehicles. Machines 2020, 8, 33. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Nikou, A.; Dimarogonas, D.V. Robust Trajectory Tracking Control for Underactuated Autonomous Underwater Vehicles in Uncertain Environments. IEEE Trans. Autom. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Sands, T. Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms 2019, 12, 232. [Google Scholar] [CrossRef]
- Sands, T. Optimization provenance of whiplash compensation for flexible space robotics. Aerospace 2019, 6, 93. [Google Scholar] [CrossRef]
- Sands, T. Deterministic Artificial Intelligence; IntechOpen: London, UK, 2020; ISBN 978-1-78984-112-1. [Google Scholar]
- Smeresky, B.; Rizzo, A.; Sands, T. Kinematics in the Information Age. Mathematics 2018, 6, 148. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 4th ed.; Prentice Hall: Saddle River, NJ, USA, 2001; ISBN 978-0-13-060907-6. [Google Scholar]
- Ogata, K. System Dynamics; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2004; ISBN 978-0131424623. [Google Scholar]
- Dorf, R.; Bishop, R. Modern Control Systems, 7th ed.; Addison Wesley: Boston, MA, USA, 1998; ISBN 978-02001501742. [Google Scholar]
- Dorf, R.; Bishop, R. Modern Control Systems, 13th ed.; Electronic Industry Press: Beijing, China, 2018; ISBN 978-7121343940. [Google Scholar]
- Franklin, G.; Powell, J.; Emami, A. Feedback Control of Dynamic Systems, 8th ed.; Pearson: London, UK, 2002; ISBN 978-0133496598. [Google Scholar]
- Hamilton, W.R. On a General Method in Dynamics; Royal Society: London, UK, 1834; pp. 247–308. [Google Scholar]
- Merz, J. A History of European Thought in the Nineteenth Century; Blackwood: London, UK, 1903; p. 5. [Google Scholar]
- Whittaker, E. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies; Cambridge University Press: New York, NY, USA, 1904; p. 1937. [Google Scholar]
- Church, I.P. Mechanics of Engineering; Wiley: New York, NY, USA, 1908. [Google Scholar]
- Wright, T. Elements of Mechanics Including Kinematics, Kinetics, and Statics, with Applications; Nostrand: New York, NY, USA, 1909. [Google Scholar]
- Gray, A. A Treatise on Gyrostatics and Rotational Motion; MacMillan: London, UK, 1918; ISBN 978-1-4212-5592-7. [Google Scholar]
- Rose, M. Elementary Theory of Angular Momentum; John Wiley & Sons: New York, NY, USA, 1957; ISBN 978-0-486-68480-2. [Google Scholar]
- Greenwood, D. Principles of Dynamics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1965; ISBN 9780137089741. [Google Scholar]
- Agrawal, B.N. Design of Geosynchronous Spacecraft; Prentice-Hall: Upper Saddle River, NJ, USA, 1986; p. 204. [Google Scholar]
- Wie, B. Space Vehicle Dynamics and Control; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 1998. [Google Scholar]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 1981. [Google Scholar]
- Kane, T. Analytical Elements of Mechanics Volume 1; Academic Press: New York, NY, USA; London, UK, 1959. [Google Scholar]
- Kane, T. Analytical Elements of Mechanics Volume 2 Dynamics; Academic Press: New York, NY, USA; London, UK, 1961. [Google Scholar]
- Kane, T.; Levinson, D. Dynamics: Theory and Application; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Roithmayr, C.; Hodges, D. Dynamics: Theory and Application of Kane’s Method; Cambridge: New York, NY, USA, 2016. [Google Scholar]
- Newton, I. Principia: The Mathematical Principles of Natural Philosophy; Daniel Adee: New York, NY, USA, 1846. [Google Scholar]
- Euler, L. Commentarii Academiae Scientiarum Petropolitanae 13; Academia Scientiarum Imperialis Petropol Publisher: St Petersonsburg, Russia, 1751; pp. 197–219. Available online: https://www.amazon.com/Commentarii-Academiae-Scientiarum-Imperialis-Petropolitanae/dp/1361610832/ref=sr_1_7?dchild=1&keywords=Commentarii+Academiae+Scientiarum+Imperialis+Petropolitanae%2C+Volume+13&qid=1596147535&s=books&sr=1-7 (accessed on 29 July 2020).
- Euler, L. Opera Omnia; Series 2; Birkhäuser: Basel, Switzerland, 1954; Volume 8, pp. 80–99. [Google Scholar]
- Euler, L. Comment. Acad. sc. Petrop, 5th ed.; Nova: Bononiae, Italy, 1744; pp. 133–140. [Google Scholar]
- Euler, L. Memoires de L’academie des Sciences de Berlin 1, 1746, pp. 21–53. Available online: https://books.google.com/books/about/M%C3%A9moires_de_l_Acad%C3%A9mie_des_sciences_de.html?id=OZcDAAAAMAAJ (accessed on 29 July 2020).
- Euler, L. Sur le Choc et la Pression. Hist. de L’acad. d. sc. de Berlin [1], (1745), 1746, pp. 25–28. Available online: https://scholarlycommons.pacific.edu/euler-publications/ (accessed on 29 July 2020).
- Euler, L. Collection Académique (Dijon and Paris) 8, 1770, pp. 29–31 [82a]. Available online: https://www.biodiversitylibrary.org/bibliography/6188#/summary (accessed on 29 July 2020).
- Chasles, M. Note sur les propriétés générales du système de deux corps semblables entr’eux. In Bulletin des Sciences Mathématiques, Astronomiques, Physiques et Chemiques; Ire Section Du Bulletin Universel: Paris, France, 1830; Volume 14, pp. 321–326. (In French) [Google Scholar]






| Nondimensional Variable | Definition |
|---|---|
| Mass | |
| Position of center of mass in meters | |
| Mass moment of inertia with respect to a vertical axis that passes through the vehicle’s geometric center (amidships) | |
| , | Lateral (sway) velocity and rate |
| , | Heading angle and rate |
| Cartesian position coordinates and derivatives | |
| Dummy variables and derivatives for generic motion states | |
| Dummy variables for final and initial amplitude and eigen variable in exponential solution of ordinary differential equations | |
| Sinusoidal frequency and time variables | |
| Dummy variables and derivatives for generic motion states | |
| Turning rate (yaw) | |
| , | Deflection of stern rudder and its optimal variant |
| , | Deflection of bow rudder and its optimal variant |
| , | Sway force coefficients: coefficients describing sway forces from resolved lift, drag, and fluid inertia along body lateral axis. These occur in response to individual (or multiple) velocity, acceleration and plane surface components, as indicated by the corresponding subscripts |
| ,, | Yaw moment coefficients |
| Arbitrarily labeled constants used to simplify expressions | |
| Variable | Definition |
|---|---|
| , | Arbitrary motion states (position, velocity, and acceleration) variables used to formulate autonomous trajectories |
| , | Arbitrary motion state displacement amplitude and initial amplitude used to formulate autonomous trajectories |
| Eigenvalue associated with exponential solution to ordinary differential equations | |
| Frequency of sinusoidal functions | |
| Time | |
| Phase angle of sinusoidal functions | |
| Period of sinusoidal functions | |
| User-defined quiescent period used to trouble-shoot and validate computer code (no motion should occur during the quiescent period). | |
| User-defined duration of maneuver (often established by time-optimization problems) |
| Variable | Definition |
|---|---|
| Variables in state-variable formulation (“state space”) of equations of motion associated with motion states | |
| Variables in state-variable formulation (“state space”) of equations of motion associated with controls | |
| Deterministic error-optimal stern rudder displacement commands | |
| Deterministic error-optimal bow rudder displacement commands | |
| Learned vehicle mass | |
| Learned product of vehicle mass and location of center of mass | |
| Learned location of center of mass | |
| Learned mass moment of inertia and initial value | |
| Control gain for mass simple-learning | |
| Control gain for learning product of mass and location of center of mass | |
| , | Control gain for learning mass moment of inertia |
| Variables (combinations of motion states) used to reparametrize problem into optimal learning form |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sands, T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. https://doi.org/10.3390/jmse8080578
Sands T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). Journal of Marine Science and Engineering. 2020; 8(8):578. https://doi.org/10.3390/jmse8080578
Chicago/Turabian StyleSands, Timothy. 2020. "Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV)" Journal of Marine Science and Engineering 8, no. 8: 578. https://doi.org/10.3390/jmse8080578
APA StyleSands, T. (2020). Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). Journal of Marine Science and Engineering, 8(8), 578. https://doi.org/10.3390/jmse8080578





