Data-Driven, Multi-Model Workflow Suggests Strong Influence from Hurricanes on the Generation of Turbidity Currents in the Gulf of Mexico
Abstract
1. Introduction
2. Materials and Methods
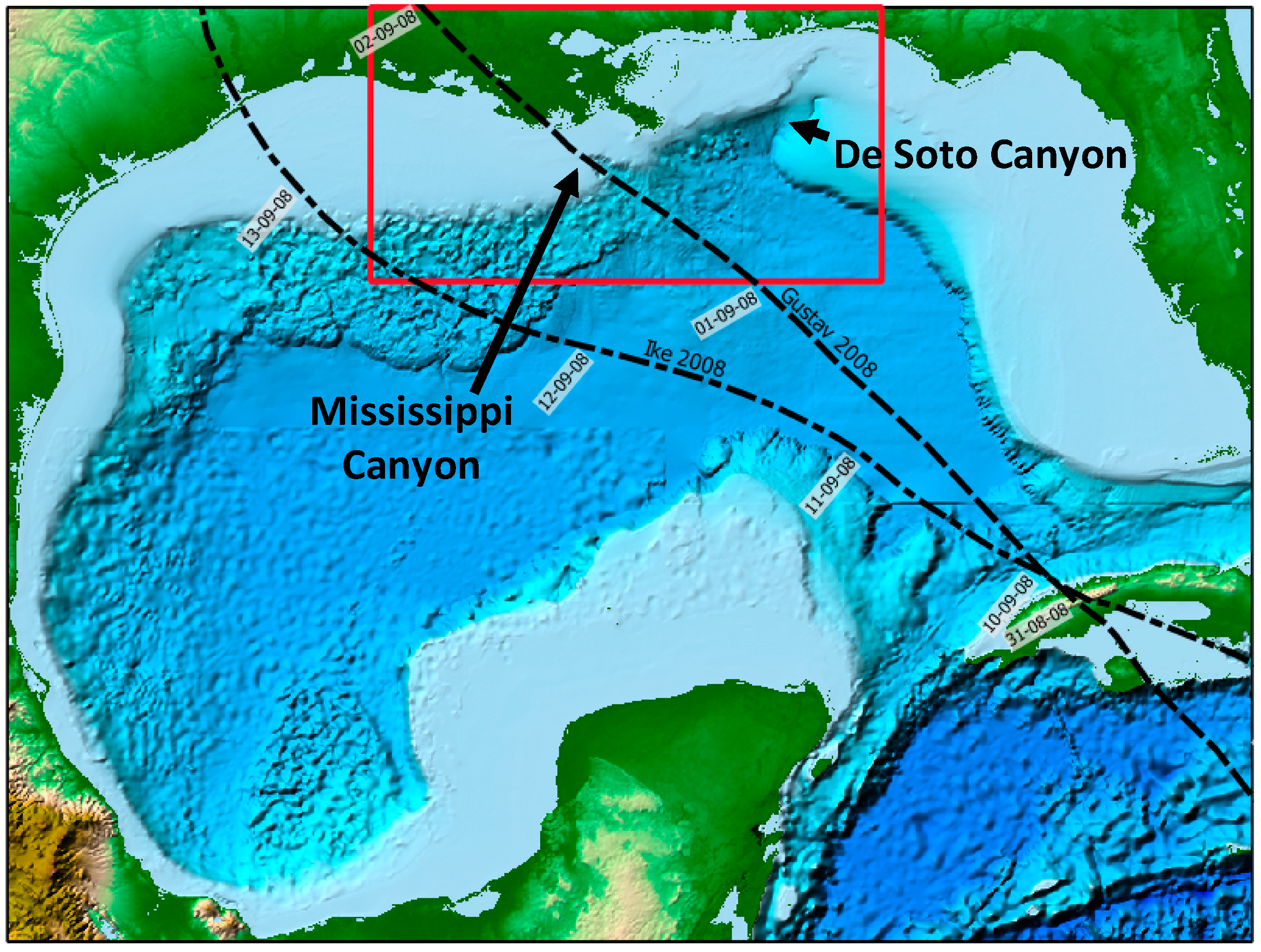
2.1. Environmental Setting
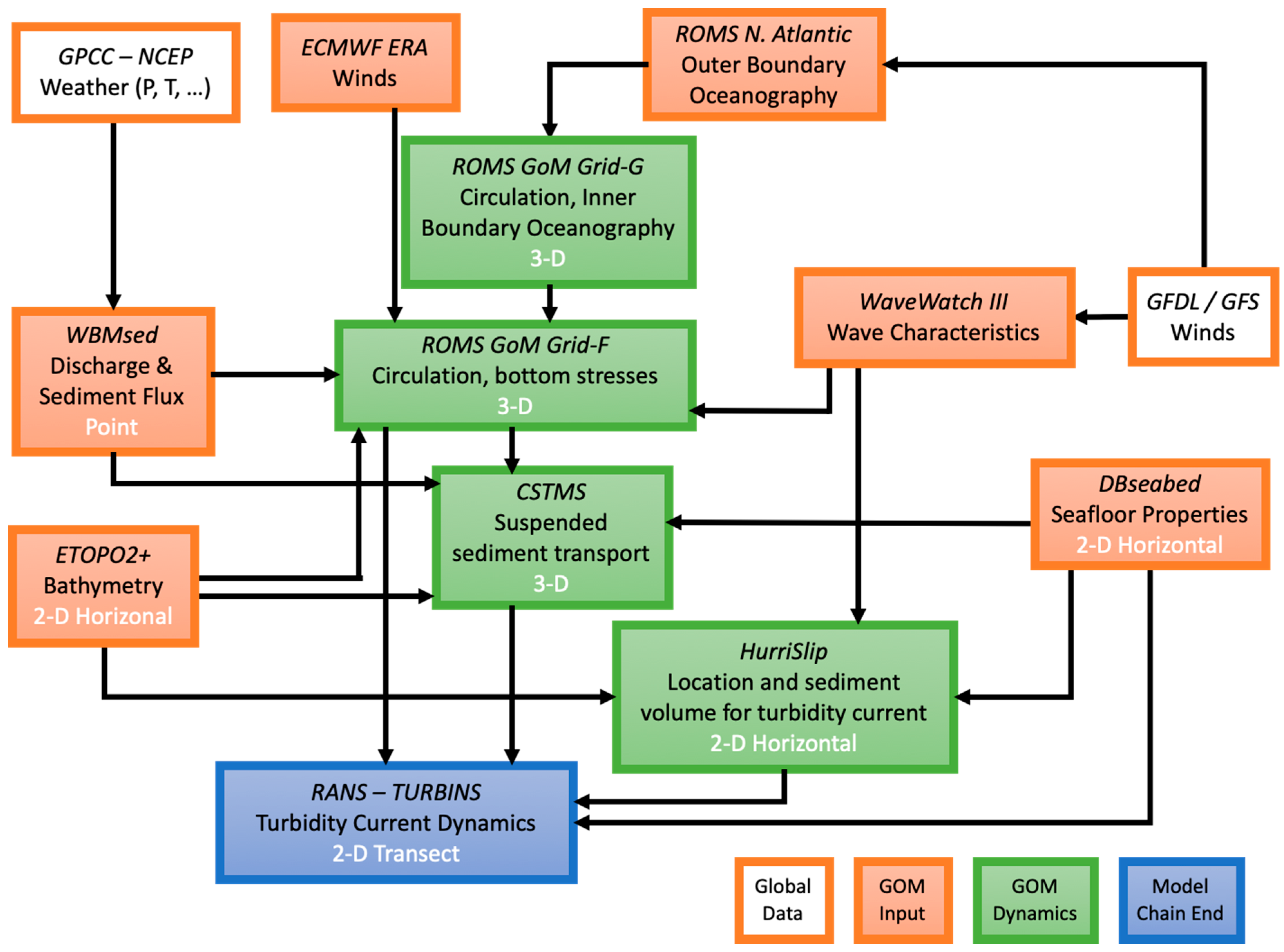
2.2. Workflow Components
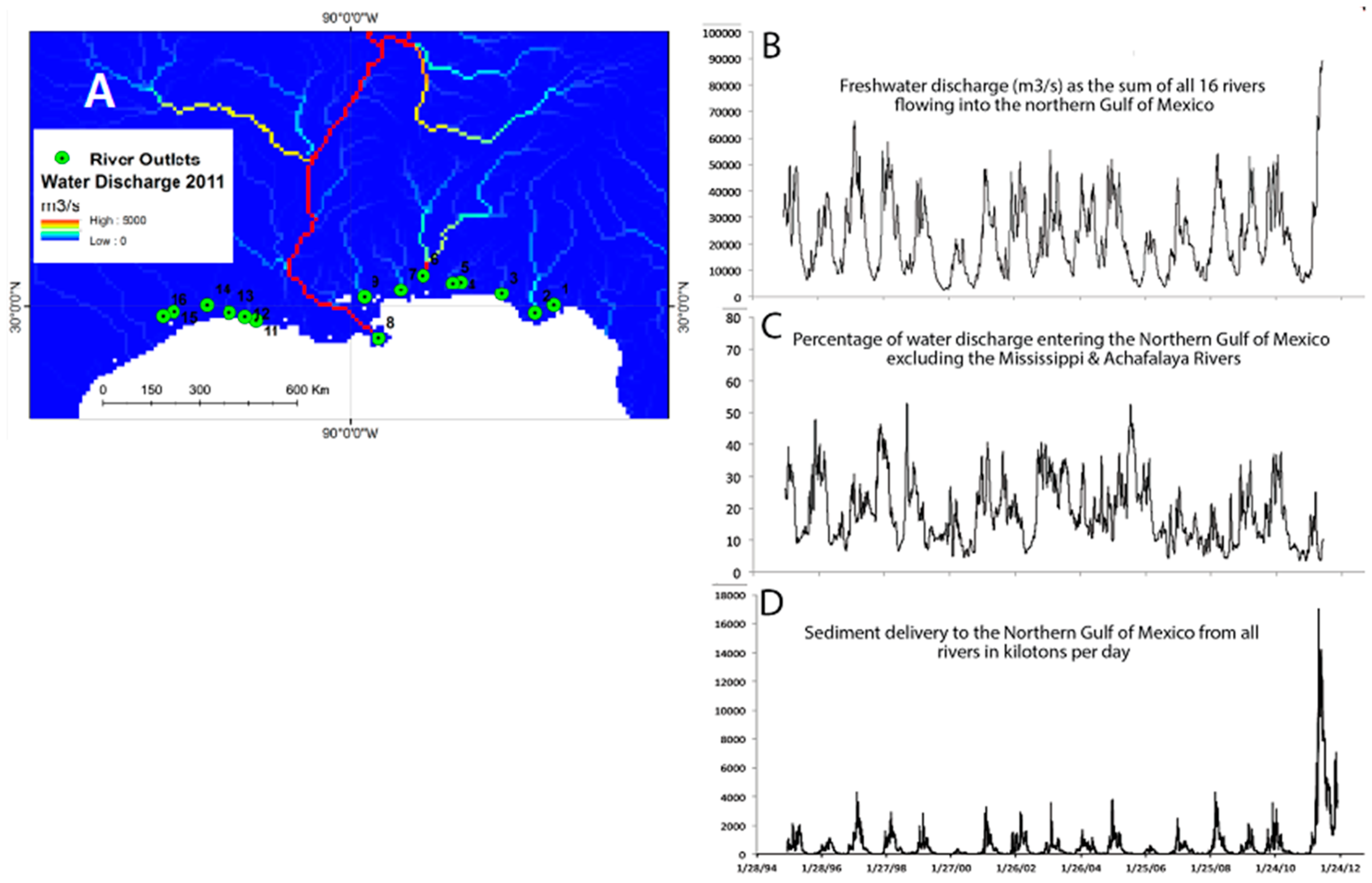
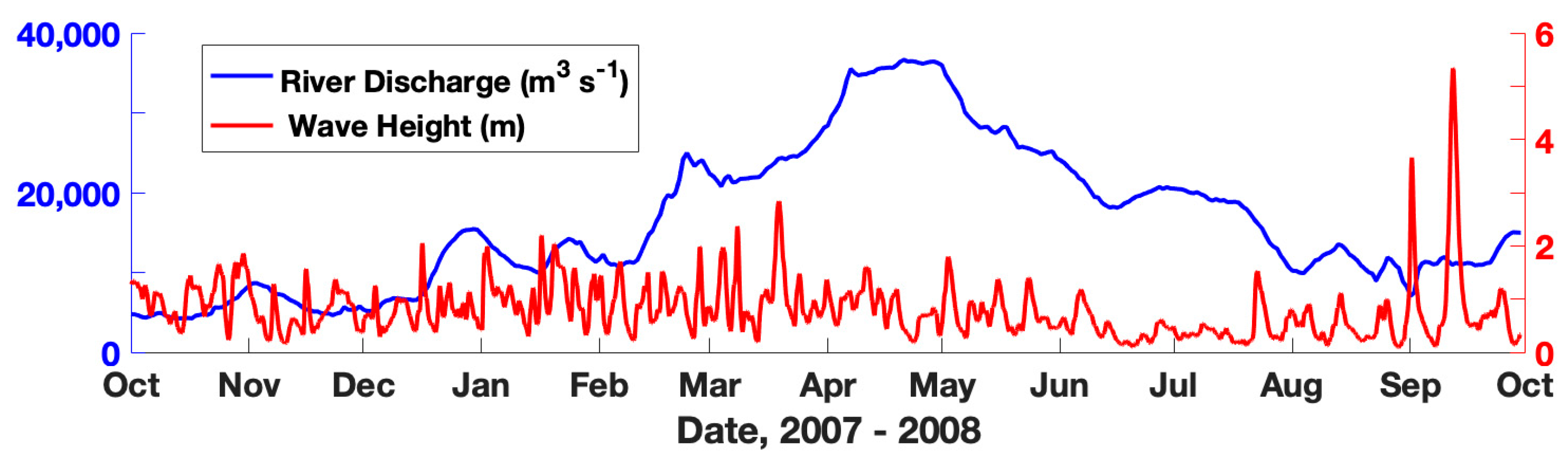
2.2.1. River Discharge Modeling Results and Observations
2.2.2. Ocean Hydrodynamic and Wave Model
2.2.3. Spatial Seabed Datasets
2.2.4. Suspended Sediment Transport Model (CSTMS)
2.2.5. Turbidity Current Ignition Models
2.2.6. RANS/TURBINS: a RANS Sediment Gravity Flow Model
2.3. Modeling Approach
3. Results
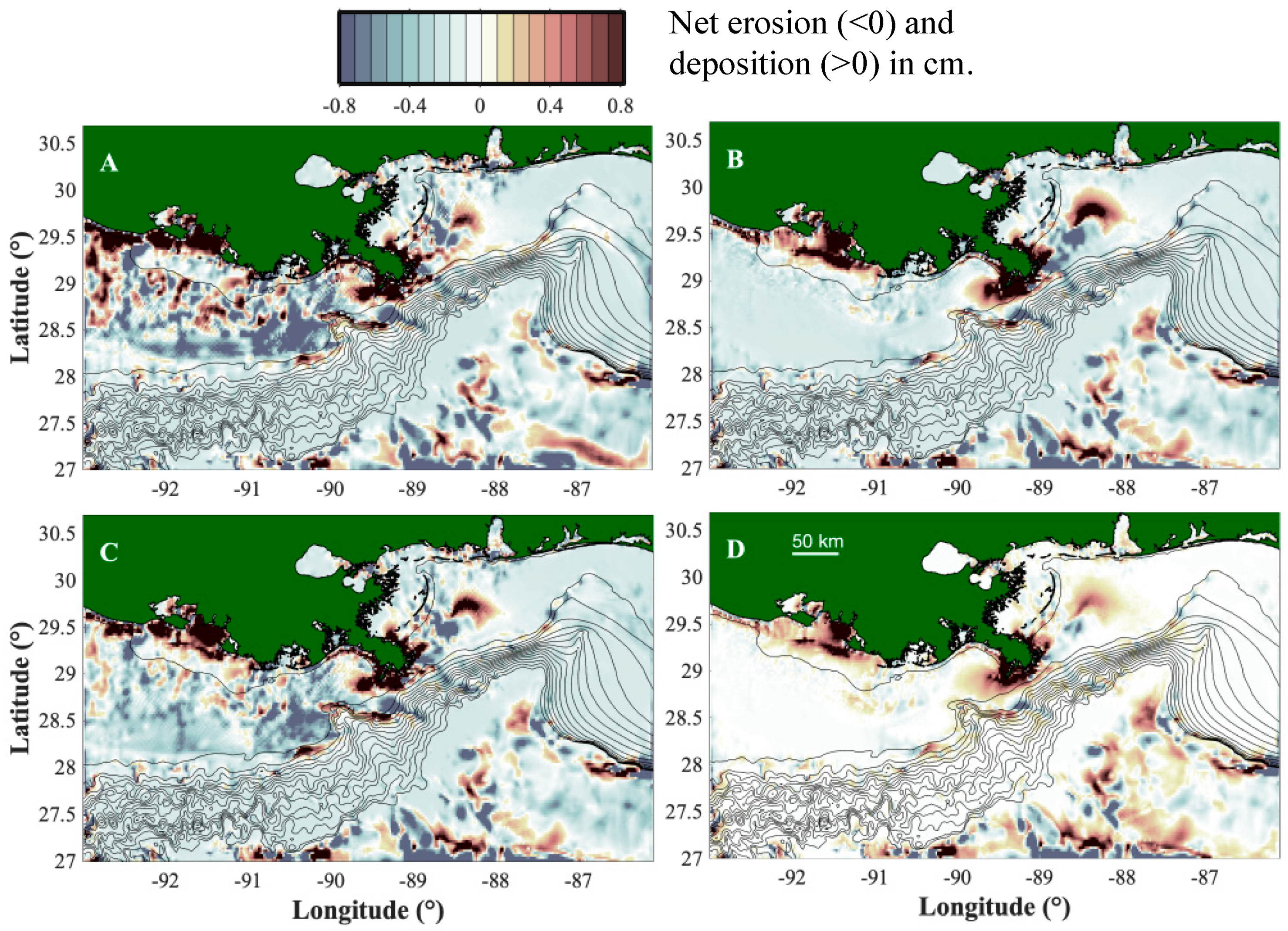
3.1. Suspended Sediment Transport
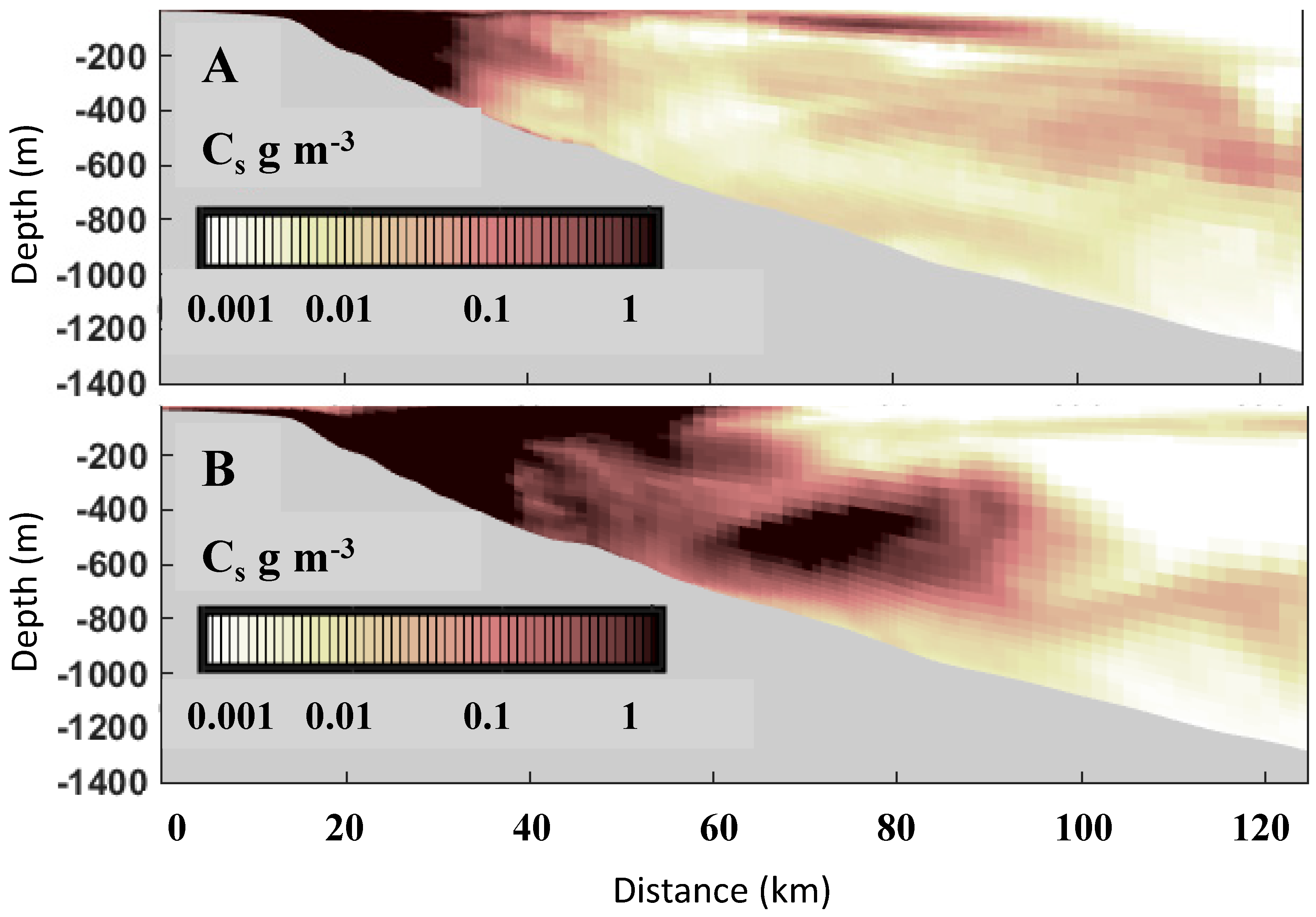
3.2. Density Flow Ignitions
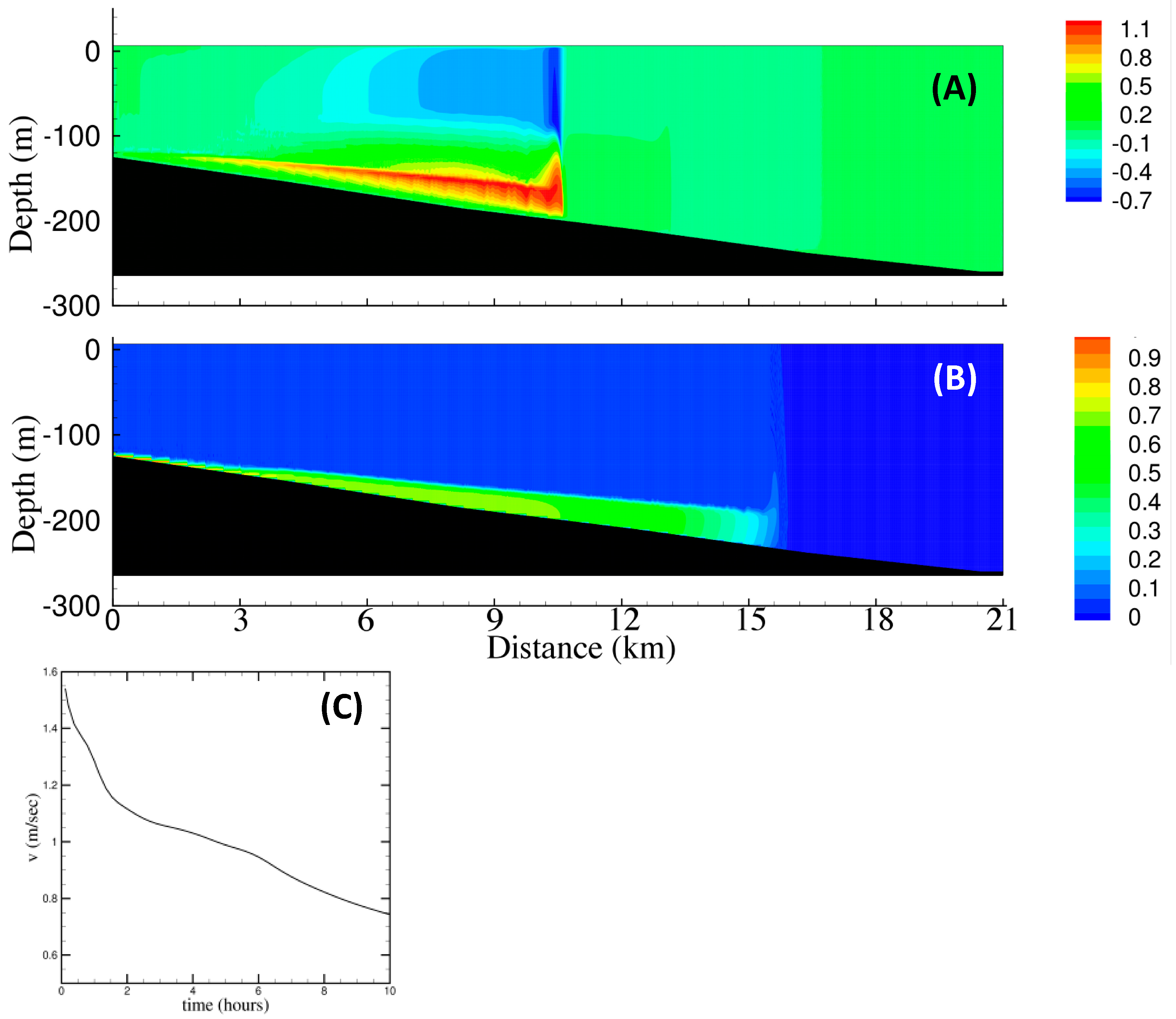
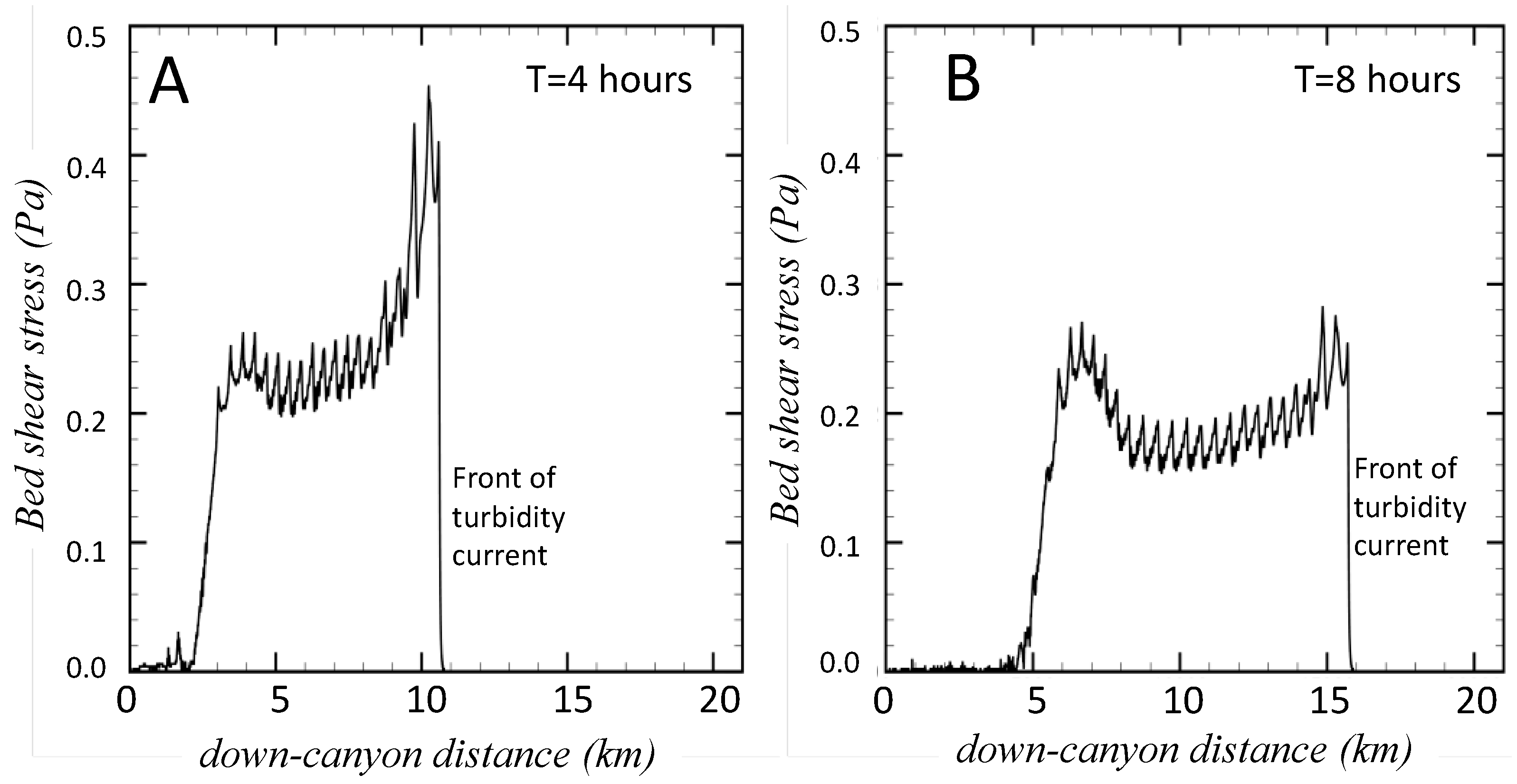
3.3. Turbidity Currents
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bryant, W.L.; Camilli, R.; Fisher, G.B.; Overton, E.B.; Reddy, C.M.; Reible, D.; Swarthout, R.F.; Valentine, D.L. Harnessing a decade of data to inform future decisions: Insights into the ongoing hydrocarbon release at Taylor Energy’s Mississippi Canyon Block 20 (MC20) site. Mar. Pollut. Bull. 2020, 155, 111056. [Google Scholar] [CrossRef] [PubMed]
- Stone, G.W.; McBride, R.A. Louisiana barrier islands and their importance in wetland protection: Forecasting shoreline change and subsequent response of wave climate. J. Coast. Res. 1998, 14, 900–915. [Google Scholar]
- Puig, P.; Palanques, A.; Martin, J. Contemporary sediment-transport processes in submarine canyons. Annu. Rev. Mar. Sci. 2014, 6, 53–77. [Google Scholar] [CrossRef] [PubMed]
- Talling, P.J.; Paull, C.K.; Piper, D.J.W. How are subaqueous sediment density flows triggered, what is their internal structure and how does it evolve? Direct observations from monitoring of active flows. Earth Sci. Rev. 2013, 125, 244–287. [Google Scholar] [CrossRef]
- Cacchione, D.A.; Pratson, L.F.; Ogston, A.S. The shaping of continental slopes by internal tides. Science 2002, 296, 724–727. [Google Scholar] [CrossRef]
- Traykovski, P.; Geyer, W.R.; Irish, J.D.; Lynch, J.F. The role of wave-induced density-driven fluid mud flows for cross-shelf transport on the Eel River continental shelf. Cont. Shelf Res. 2000, 20, 2113–2140. [Google Scholar] [CrossRef]
- Hutton, E.W.H.; Syvitski, J.P.M. Advances in the numerical modeling of sediment failure during the development of a continental margin. Mar. Geol. 2004, 203, 367–380. [Google Scholar] [CrossRef]
- Hutton, E.W.H.; Syvitski, J.P.M. Sedflux 2.0: An advanced process-response model that generates three-dimensional stratigraphy. Comput. Geosci. 2008, 34, 1319–1337. [Google Scholar] [CrossRef]
- Parker, G. Conditions for the ignition of catastrophically erosive turbidity currents. Mar. Geol. 1982, 46, 307–327. [Google Scholar] [CrossRef]
- Blanchette, F.; Strauss, M.; Meiburg, E.; Kneller, B.; Glinsky, M.E. High-resolution numerical simulations of resuspending gravity currents: Conditions for self-sustainment. J. Geophys. Res. Ocean. 2005, 110, 1–15. [Google Scholar] [CrossRef]
- Obelcz, J.; Xu, K.; Georgiou, I.Y.; Maloney, J.; Bentley, S.J.; Miner, M.D. Sub-decadal submarine landslides are important drivers of deltaic sediment flux: Insights from the Mississippi River Delta Front. Geology 2017, 45, 703–706. [Google Scholar] [CrossRef]
- Ross, C.B.; Gardner, W.D.; Richardson, M.J.; Asper, V.L. Currents and sediment transport in the Mississippi Canyon and effects of Hurricane Georges. Cont. Shelf Res. 2009, 29, 1384–1396. [Google Scholar] [CrossRef]
- Dail, M.B.; Corbett, D.R.; Walsh, J.P. Assessing the importance of tropical cyclones on continental margin sedimentation in the Mississippi delta region. Cont. Shelf Res. 2007, 27, 1857–1874. [Google Scholar] [CrossRef]
- Sterling, G.H.; Strohbeck, G.E. The failure of the South Pass 70 Platform B in Hurricane Camille. J. Pet. Technol. 1975, 27, 263–268. [Google Scholar] [CrossRef]
- Wijesekera, H.W.; Wang, D.W.; Teague, W.J.; Jarosz, E. High sea-floor stress induced by extreme hurricane waves. Geophys. Res. Lett. 2010, 37, L11604. [Google Scholar] [CrossRef]
- Teague, W.J.; Jarosz, E.; Keen, T.R.; Wang, D.W.; Hulbert, M.S. Bottom scour observed under Hurricane Ivan. Geophys. Res. Lett. 2006, 33, L07607. [Google Scholar] [CrossRef]
- Shay, L.K.; Elsberry, R.L. Near-inertial ocean current response to Hurricane Frederic. J. Phys. Oceanogr. 1987, 17, 1249–1269. [Google Scholar] [CrossRef]
- Brooks, D.A. The wake of Hurricane Allen in the western Gulf of Mexico. J. Phys. Oceanogr. 1983, 13, 117–129. [Google Scholar] [CrossRef]
- Xu, K.; Harris, C.K.; Hetland, R.D.; Kaihatu, J.M. Dispersal of Mississippi and Atchafalaya sediment on the Texas–Louisiana shelf: Model estimates for the year 1993. Cont. Shelf Res. 2011, 31, 1558–1575. [Google Scholar] [CrossRef]
- Xu, K.; Mickey, R.C.; Chen, Q.J.; Harris, C.K.; Hetland, R.D.; Hu, K.; Wang, J. Shelf sediment transport during hurricanes Katrina and Rita. Comput. Geosci. 2016, 90, 24–39. [Google Scholar] [CrossRef]
- Zang, Z.; Xue, Z.G.; Bao, S.; Chen, Q.; Walker, N.D.; Haag, A.S.; Ge, Q.; Yao, Z. Numerical study of sediment dynamics during hurricane Gustav. Ocean Model. 2018, 126, 29–42. [Google Scholar] [CrossRef]
- Zang, Z.; Xue, Z.G.; Xu, K.; Bentley, S.J.; Chen, Q.J.; D’Sa, E.J.; Ge, Q. A two decadal (1993–2012) numerical assessment of sediment dynamics in the northern Gulf of Mexico. Water 2019, 11, 938. [Google Scholar] [CrossRef]
- Meade, R.H.; Moody, J.A. Causes for the decline of suspended-sediment discharge in the Mississippi River system, 1940–2007. Hydrol. Process. 2010, 24, 35–49. [Google Scholar] [CrossRef]
- Wright, L.D.; Nittrouer, C.A. Dispersal of river sediments in coastal seas: Six contrasting cases. Estuaries 1995, 18, 494–508. [Google Scholar] [CrossRef]
- Neill, C.F.; Allison, M.A. Subaqueous deltaic formation on the Atchafalaya Shelf, Louisiana. Mar. Geol. 2005, 214, 411–430. [Google Scholar] [CrossRef]
- Goñi, M.A.; Alleau, Y.; Corbett, R.; Walsh, J.P.; Mallinson, D.; Allison, M.A.; Gordon, E.; Petsch, S.; DellaPenna, T.M. The effects of Hurricanes Katrina and Rita on the seabed of the Louisiana shelf. Sediment. Rec. 2007, 5, 4–9. [Google Scholar] [CrossRef]
- Kineke, G.C.; Higgins, E.E.; Hart, K.; Velasco, D. Fine-sediment transport associated with cold-front passages on the shallow shelf, Gulf of Mexico. Cont. Shelf Res. 2006, 26, 2073–2091. [Google Scholar] [CrossRef]
- Pepper, D.A.; Stone, G.W. Hydrodynamic and sedimentary responses to two contrasting winter storms on the inner shelf of the northern Gulf of Mexico. Mar. Geol. 2004, 210, 43–62. [Google Scholar] [CrossRef]
- Panchang, V.; Jeong, C.K.; Demirbilek, Z. Analyses of extreme wave heights in the Gulf of Mexico for offshore engineering applications. J. Offshore Mech. Arct. Eng. 2013, 135, 031104. [Google Scholar] [CrossRef]
- Diercks, A.-R.; Dike, C.; Asper, V.L.; DiMarco, S.F.; Chanton, J.P.; Passow, U.; Deming, J.W.; Thomsen, L. Scales of seafloor sediment resuspension in the northern Gulf of Mexico. Elem. Sci. Anthr. 2018, 6, 32. [Google Scholar] [CrossRef]
- Cohen, S.; Kettner, A.J.; Syvitski, J.P.M.; Fekete, B.M. WBMsed, a distributed global-scale riverine sediment flux model: Model description and validation. Comput. Geosci. 2013, 53, 80–93. [Google Scholar] [CrossRef]
- Cohen, S.; Kettner, A.J.; Syvitski, J.P.M. Global suspended sediment and water discharge dynamics between 1960 and 2010: Continental trends and intra-basin sensitivity. Glob. Planet. Chang. 2014, 115, 44–58. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Milliman, J.D. Geology, geography, and humans battle for dominance over the delivery of fluvial sediment to the coastal ocean. J. Geol. 2007, 115, 1–19. [Google Scholar] [CrossRef]
- Morehead, M.D.; Syvitski, J.P.; Hutton, E.W.H.; Peckham, S.D. Modeling the temporal variability in the flux of sediment from ungauged river basins. Glob. Planet. Chang. 2003, 39, 95–110. [Google Scholar] [CrossRef]
- Geological Survey. National Water Information System Data Available on the World Wide Web (USGS Water Data for the Nation); 2016. Available online: http://waterdata.usgs.gov/nwis/ (accessed on 1 February 2020). [CrossRef]
- Brakenridge, G.R.; Cohen, S.; Kettner, A.J.; De Groeve, T.; Nghiem, S.V.; Syvitski, J.P.M.; Fekete, B.M. Calibration of satellite measurements of river discharge using a global hydrology model. J. Hydrol. 2012, 475, 123–136. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.; Budgell, W.P.; Cornuelle, B.D.; Curchitser, E.; Di Lorenzo, E.; Fennel, K.; Geyer, W.R.; Hermann, A.J.; Lanerolle, L.; et al. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2008, 227, 3595–3624. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. J. Geophys. Res. Ocean. 2003, 108, 3090. [Google Scholar] [CrossRef]
- Durski, S.M.; Glenn, S.M.; Haidvogel, D.B. Vertical mixing schemes in the coastal ocean: Comparison of the level 2.5 Mellor-Yamada scheme with an enhanced version of the K profile parameterization. J. Geophys. Res. Ocean. 2004, 109, C01015. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Arango, H.G.; Signell, R.P. Performance of four turbulence closure models implemented using a generic length scale method. Ocean Model. 2005, 8, 81–113. [Google Scholar] [CrossRef]
- Sikirić, M.D.; Janekovic, I.; Kuzmić, M. A new approach to bathymetry smoothing in sigma-coordinate ocean models. Ocean Model. 2009, 29, 128–136. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Tolman, H.L.; Chalikov, D.V. Development of a third-generation ocean wave model at NOAA-NMC. In Physical and Numerical Modelling; Isaacson, M., Quick, M.C., Eds.; The University of British Columbia: Vancouver, BC, Canada, 1994; pp. 724–733. [Google Scholar]
- Wiberg, P.L.; Sherwood, C.R. Calculating wave-generated bottom orbital velocities from surface-wave parameters. Comput. Geosci. 2008, 34, 1243–1262. [Google Scholar] [CrossRef]
- Goff, J.A.; Jenkins, C.J.; Williams, S.J. Seabed mapping and characterization of sediment variability using the usSEABED data base. Cont. Shelf Res. 2008, 28, 614–633. [Google Scholar] [CrossRef]
- Jenkins, C. Dominant bottom types and habitats. In Gulf of Mexico Data Atlas. Stennis Space Center (MS): National Coastal Data Development Center; 2011. Available online: http://gulfatlas.noaa.gov/ (accessed on 27 June 2020).
- Williams, S.J.; Flocks, J.; Jenkins, C.; Khalil, S.; Moya, J. Offshore sediment character and sand resource assessment of the northern Gulf of Mexico, Florida to Texas. J. Coast. Res. 2012, 60, 30–44. [Google Scholar] [CrossRef]
- Brooke, S.; Schroeder, W.W. State of deep coral ecosystems in the Gulf of Mexico region, Texas to the Florida Straits. In The State of Deep Coral Ecosystems of the United States; Lumsde, S.E., Hourigan, T.F., Bruckner, A.W., Dorr, G., Eds.; NOAA Technical Memorandum CRCP-3; U.S. Department of Commerce: Silver Spring, MD, USA, 2007; pp. 271–306. [Google Scholar]
- Gardner, J.V.; Calder, B.R.; Clarke, J.E.H.; Mayer, L.A.; Elston, G.; Rzhanov, Y. Drowned shelf-edge deltas, barrier islands and related features along the outer continental shelf north of the head of De Soto Canyon, NE Gulf of Mexico. Geomorphology 2007, 89, 370–390. [Google Scholar] [CrossRef]
- Cordes, E.E.; Bergquist, D.C.; Fisher, C.R. Macro-ecology of Gulf of Mexico cold seeps. Annu. Rev. Mar. Sci. 2009, 1, 143–168. [Google Scholar] [CrossRef]
- Thompson, D.M.; Wohl, E.E.; Jarrett, R.D. Velocity reversals and sediment sorting in pools and riffles controlled by channel constrictions. Geomorphology 1999, 27, 229–241. [Google Scholar] [CrossRef]
- Ueckermann, M.P.; Chambers, R.D.; Brooks, C.A.; Audette, W.E.; Bieszczad, J. pyDEM: Global digital elevation model analysis. In Proceedings of the 14th Python in Science Conference (SciPy 2015), Austin, TX, USA, 6–12 July 2015; Volume 6, pp. 117–124. [Google Scholar]
- Jenkins, C. Sediment Drainage Streams Important in Benthic Seafloor Classification. In Ocean Solutions, Earth Solutions, 2nd ed.; Wright, D., Ed.; ESRI Press: Redlands, CA, USA, 2016; pp. 431–440. [Google Scholar] [CrossRef]
- Bever, A.J.; Harris, C.K. Storm and fair-weather driven sediment-transport within Poverty Bay, New Zealand, evaluated using coupled numerical models. Cont. Shelf Res. 2014, 86, 34–51. [Google Scholar] [CrossRef]
- Chen, S.-N.; Geyer, W.R.; Hsu, T.-J. A numerical investigation of the dynamics and structure of hyperpycnal river plumes on sloping continental shelves. J. Geophys. Res. Ocean. 2013, 118, 2702–2718. [Google Scholar] [CrossRef]
- Fukushima, Y.; Parker, G.; Pantin, H.M. Prediction of ignitive turbidity currents in Scripps Submarine Canyon. Mar. Geol. 1985, 67, 55–81. [Google Scholar] [CrossRef]
- Piper, D.J.W.; Cochonat, P.; Morrison, M.L. The sequence of events around the epicentre of the 1929 Grand Banks earthquake: Initiation of debris flows and turbidity current inferred from sidescan sonar. Sedimentology 1999, 46, 79–97. [Google Scholar] [CrossRef]
- Parker, G.; Fukushima, Y.; Pantin, H.M. Self-accelerating turbidity currents. J. Fluid Mech. 1986, 171, 145–181. [Google Scholar] [CrossRef]
- Parchure, T.M.; Mehta, A.J. Erosion of soft cohesive sediment deposits. J. Hydraul. Eng. 1985, 111, 1308–1326. [Google Scholar] [CrossRef]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; Advanced Series on Ocean Engineering; World Scientific: Hackensack, NJ, USA, 1992; Volume 4, 340p. [Google Scholar]
- Amos, C.L.; Daborn, G.R.; Christian, H.A.; Atkinson, A.; Robertson, A. In situ erosion measurements on fine-grained sediments from the Bay of Fundy. Mar. Geol. 1992, 108, 175–196. [Google Scholar] [CrossRef]
- Schieber, J.; Southard, J.B.; Schimmelmann, A. Lenticular shale fabricsresulting from intermittent erosion of water-rich muds—Interpreting the rock record in the light of recent flume experiments. J. Sediment. Res. 2010, 80, 119–128. [Google Scholar] [CrossRef]
- Pantin, H.M.; Franklin, M.C. Predicting autosuspension in steady turbidity flow: Ignition points and their relation to Richardson numbers. J. Sediment. Res. 2009, 79, 862–871. [Google Scholar] [CrossRef]
- Mohrig, D.; Marr, J.G. Constraining the efficiency of turbidity current generation from submarine debris flows and slides using laboratory experiments. Mar. Pet. Geol. 2003, 20, 883–899. [Google Scholar] [CrossRef]
- Waltham, D. Flow Transformations in particulate gravity currents. J. Sediment. Res. 2004, 74, 129–134. [Google Scholar] [CrossRef]
- Nodine, M.C.; Cheon, J.Y.; Wright, S.G.; Gilbert, R.B. Mudslides during Hurricane Ivan and an assessment of the potential for future mudslides in the Gulf of Mexico. In C175 Phase I Project Report; Minerals Management Service: College Station, TX, USA, 2006; MMS Project Number 552; 37p. [Google Scholar]
- Nataraja, M.S.; Gill, H.S. Ocean wave-induced liquefaction analysis. J. Geotech. Eng. 1983, 109, 573–590. [Google Scholar] [CrossRef]
- Geremew, A.M. Pore-water pressure development caused by wave-induced cyclic loading in deep porous formation. Int. J. Geomech. 2013, 13, 65–68. [Google Scholar] [CrossRef]
- Jeng, D.-S.; Seymour, B.; Li, J. A new approximation for pore pressure accumulation in marine sediment due to water waves. Int. J. Numer. Anal. Methods Geomech. 2006, 31, 53–69. [Google Scholar] [CrossRef]
- Boudreau, B.P.; Bennett, R.H. New rheological and porosity equations for steady-state compaction. Am. J. Sci. 1999, 299, 517–528. [Google Scholar] [CrossRef]
- Youd, T. Factors Controlling maximum and minimum densities of sands. In Evaluation of Relative Density and Its Role in Geotechnical Projects Involving Cohesionless Soils; Selig, E., Ladd, R., Eds.; ASTM International: West Conshohocken, PA, USA, 2009; pp. 98–112. [Google Scholar] [CrossRef]
- Brooks, G.R.; Kindinger, J.L.; Penland, S.; Williams, S.J.; McBride, R.A. East Louisiana continental shelf sediments: A product of delta reworking. J. Coast. Res. 1995, 11, 1026–1036. [Google Scholar]
- Nasr-Azadani, M.M.; Meiburg, E. TURBINS: An immersed boundary, Navier–Stokes code for the simulation of gravity and turbidity currents interacting with complex topographies. Comput. Fluids 2011, 45, 14–28. [Google Scholar] [CrossRef]
- Nasr-Azadani, M.M.; Meiburg, E. Turbidity currents interacting with three-dimensional seafloor topography. J. Fluid Mech. 2014, 745, 409–443. [Google Scholar] [CrossRef]
- Necker, F.; Härtel, C.; Kleiser, L.; Meiburg, E. High-resolution simulations of particle-driven gravity currents. Int. J. Multiph. Flow 2002, 28, 279–300. [Google Scholar] [CrossRef]
- Necker, F.; Härtel, C.; Kleiser, L.; Meiburg, E. Mixing and dissipation in particle-driven gravity currents. J. Fluid Mech. 2005, 545, 339–372. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Garcia, M.H.; Parker, G. Experiments on the entrainment of sediment into suspension by a dense bottom current. J. Geophys. Res. Ocean. 1993, 98, 4793–4807. [Google Scholar] [CrossRef]
- Gardner, W.D.; Tucholke, B.E.; Richardson, M.J.; Biscaye, P.E. Benthic storms, nepheloid layers, and linkage with upper ocean dynamics in the western North Atlantic. Mar. Geol. 2017, 385, 304–327. [Google Scholar] [CrossRef]
- Prior, D.B.; Coleman, J.B.; Garrison, L.E. Digitally acquired undistorted side scan sonar images of submarine landslides, Mississippi Delta. Geology 1979, 7, 423–425. [Google Scholar] [CrossRef]
- Elverhøi, A.; Breien, H.; De Blasio, F.V.; Harbitz, C.B.; Pagliardi, M. Submarine landslides and the importance of the initial sediment composition for run-out length and final deposit. Ocean Dyn. 2010, 60, 1027–1046. [Google Scholar] [CrossRef]
- Kuehl, S.A.; Alexander, C.R.; Blair, N.E.; Harris, C.K.; Marsaglia, K.M.; Ogston, A.S.; Orpin, A.R.; Roering, J.J.; Bever, A.J.; Bilderback, E.L.; et al. A source-to-sink perspective of the Waipaoa River margin. Earth Sci. Rev. 2016, 153, 301–334. [Google Scholar] [CrossRef]
- Sturges, W.; Leben, R. Frequency of ring separations from the loop current in the Gulf of Mexico: A revised estimate. J. Phys. Oceanogr. 2000, 30, 1814–1819. [Google Scholar] [CrossRef]
- Larson, R.A.; Brooks, G.R.; Schwing, P.T.; Holmes, C.W.; Carter, S.R.; Hollander, D.J. High-resolution investigation of event driven sedimentation: Northeastern Gulf of Mexico. Anthropocene 2018, 24, 40–50. [Google Scholar] [CrossRef]




| Sediment Class | Source | Sediment Type | D (mm) | Tcr (Pa) | ws (mm/s) |
|---|---|---|---|---|---|
| 1 | Seabed | Mud | 0.063 | 0.11 | 1.0 |
| 2 | Sand | 0.125 | 0.13 | 10.0 | |
| 3 | Gravel | 10.0 | 10.0 | 70.0 | |
| 4 | Mississippi River | Small Mud | 0.015 | 0.11 | 0.1 |
| 5 | Larger Mud | 0.063 | 0.11 | 1.0 | |
| 6 | Atchafalaya/Mobile Rivers | Small Mud | 0.015 | 0.03 | 0.1 |
| 7 | Larger Mud | 0.063 | 0.03 | 1.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harris, C.K.; Syvitski, J.; Arango, H.G.; Meiburg, E.H.; Cohen, S.; Jenkins, C.J.; Birchler, J.J.; Hutton, E.W.H.; Kniskern, T.A.; Radhakrishnan, S.; et al. Data-Driven, Multi-Model Workflow Suggests Strong Influence from Hurricanes on the Generation of Turbidity Currents in the Gulf of Mexico. J. Mar. Sci. Eng. 2020, 8, 586. https://doi.org/10.3390/jmse8080586
Harris CK, Syvitski J, Arango HG, Meiburg EH, Cohen S, Jenkins CJ, Birchler JJ, Hutton EWH, Kniskern TA, Radhakrishnan S, et al. Data-Driven, Multi-Model Workflow Suggests Strong Influence from Hurricanes on the Generation of Turbidity Currents in the Gulf of Mexico. Journal of Marine Science and Engineering. 2020; 8(8):586. https://doi.org/10.3390/jmse8080586
Chicago/Turabian StyleHarris, Courtney K., Jaia Syvitski, H.G. Arango, E.H. Meiburg, Sagy Cohen, C.J. Jenkins, Justin J. Birchler, E.W.H. Hutton, T.A. Kniskern, S. Radhakrishnan, and et al. 2020. "Data-Driven, Multi-Model Workflow Suggests Strong Influence from Hurricanes on the Generation of Turbidity Currents in the Gulf of Mexico" Journal of Marine Science and Engineering 8, no. 8: 586. https://doi.org/10.3390/jmse8080586
APA StyleHarris, C. K., Syvitski, J., Arango, H. G., Meiburg, E. H., Cohen, S., Jenkins, C. J., Birchler, J. J., Hutton, E. W. H., Kniskern, T. A., Radhakrishnan, S., & Auad, G. (2020). Data-Driven, Multi-Model Workflow Suggests Strong Influence from Hurricanes on the Generation of Turbidity Currents in the Gulf of Mexico. Journal of Marine Science and Engineering, 8(8), 586. https://doi.org/10.3390/jmse8080586





