Torsional Vibration Stress and Fatigue Strength Analysis of Marine Propulsion Shafting System Based on Engine Operation Patterns

Abstract

Modern merchant ships use marine propulsion systems equipped with an ultra-long-stroke diesel engine that directly drives a large slow-turning propeller. Such systems use fewer cylinders and generate greater power at slower shaft speeds, which affords improved propulsion performance as well as low repair and maintenance costs. However, this also results in higher torsional vibrations, which can lead to the fatigue of the shafting system. Tests performed on various marine propulsion systems with 5- to 7-cylinder engines have shown that engines with fewer cylinders exhibit a correspondingly wider barred speed range (BSR) and higher torsional vibration stresses. Thus, it is necessary to investigate the optimal engine operation patterns required to quickly pass the BSR with smaller torsional vibration. In this study, we carried out a series of BSR passage experiments during actual sea trials to evaluate the intermediate shaft performance under different engine operation patterns. The fractional damage accumulations due to transient torsional vibration stresses were calculated to estimate the fatigue lifetime of the shafting system. Our analysis results show that the torsional fatigue damage during BSR decelerations are small and negligible; however, the fractional damage during accelerations is a matter of concern. Our study determines the optimal main engine operation pattern for quick passage through the BSR with the smallest torsional vibration amplitudes and the least fractional damage accumulation, which can therefore extend the fatigue lifetime of the entire propulsion shafting system. Based on this analysis, we also suggest the optimum engine pattern for safe BSR passage.

1. Introduction

Marine propulsion systems have witnessed rapid improvements owing to the development of ultra-long-stroke diesel engines such as the MAN Energy Solutions (MAN ES) G-type (Green) [1,2] and Winterthur & Gas Diesel (WinGD) X-type models [3,4], which offer lower maximum revolution rates. These engines afford enhanced propulsion efficiencies as well as low repair and maintenance costs, which has contributed to their wide usage. However, such engines afford higher powers at lower speeds, which results in higher torsional vibrations that can adversely affect the fatigue strength of the shafting system. Solutions and techniques to control torsional vibrations include the installation of a torsional damper or turning wheel [5,6,7,8], changing the fillet design of the shaft flange from single-radius to multi-radius [9,10], and the application of the dynamic limiter function [11] proposed by MAN ES or Delta Bypass tuning [12] by WinGD.

Meanwhile, comparisons between the designs of 5- to 7-cylinder engines have indicated that diesel engines with fewer cylinders afford a lower speed and a wider barred speed range (BSR) owing to high torsional vibrations [13]. Increased torsional vibrations during BSR passage can adversely affect the ship’s safety. In particular, the BSR passage time for a “fewer-cylinder engine” is longer than those of engines with more cylinders. Moreover, the torsional vibration during BSR passage depends on the ship maneuvering conditions and engine operation settings. Additionally, the presence of higher torsional vibrations necessitates one or both shafts to be large in size and made of higher-tensile-strength material. Torsional vibration dampers are also increasingly required for vessels equipped with ultra-long-stroke engines.

It is well known that every machine part eventually fails owing to fatigue after a certain number of loading cycles. As per Miner’s rule [14], the fractional fatigue damage is linearly proportional to the torsional vibration stress amplitude (when both are expressed in the log scale). Thus, the fatigue fracture of shafts due to BSR passage is a matter of concern. The torsional fatigue lifetime of the shafting system can be estimated by calculating the accumulated fractional damage during each passage. This can prevent accidents and ensure the safety and reliability of the entire propulsion system.

Against this backdrop, in this study, we carried out a series of BSR passage experiments to evaluate the shaft performance under different engine operation patterns. The fractional damage accumulations due to transient torsional vibration stresses were calculated to estimate the fatigue lifetime of the shafting system. Consequently, we determined the optimal engine operation conditions to ensure optimal BSR passage.

2. Materials and Methods

2.1. Calculation of Accumulated Fractional Fatigue Damage

Miner’s rule is one of the most widely used methods to calculate failures caused by cyclic/time-variant loading [14,15]. The rule is based on a linear damage accumulation model that uses a load time history and the stress-life (S–N) curve as inputs to calculate the damage. The S–N curve refers to the plot of the magnitude of alternating stress as the function of the number of cycles leading to failure for a given structure. Both the stress and number of cycles are plotted on a logarithmic scale. Here, we consider the situation wherein a rotating shaft is subjected to n₁ cycles at torsional vibration stress level ${\tau }_1$, n₂ cycles at torsional vibration stress level ${\tau }_2$, …, and n_N* cycles at torsional vibration stress level ${\tau }_{N\ast }$.

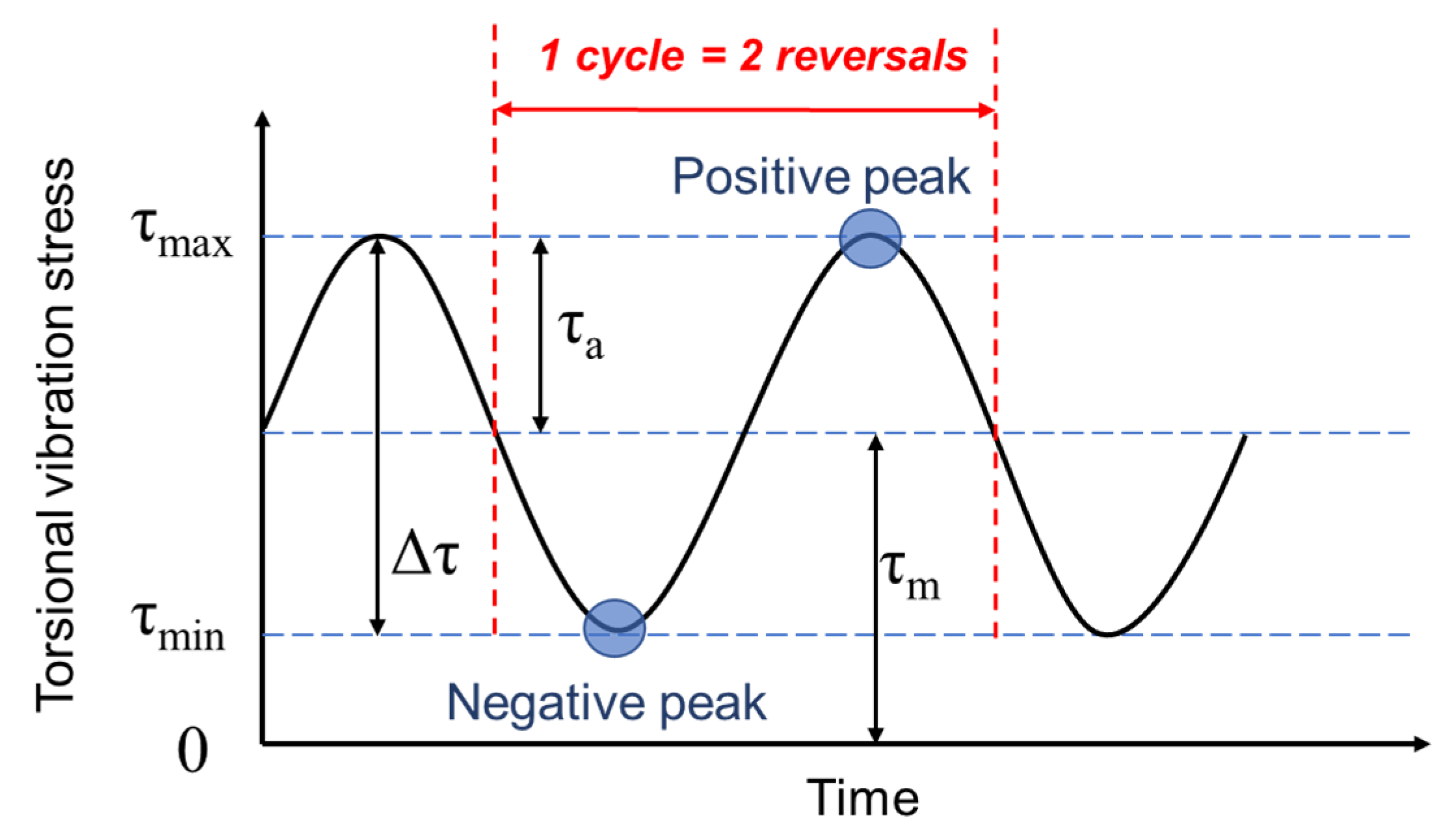
Figure 1 shows the S–N curve in log-log scale for a given shaft, from which the number of torsional vibration cycles leading to failure at each stress level can be determined, i.e., N₁ cycles at stress level ${\tau }_1$, N₂ cycles at stress level ${\tau }_2$, …, N_N* cycles at stress level ${\tau }_{N\ast }$. In S–N testing, the number of cycles to failure is converted to the number of reversals to failure (Figure 2). Here, one cycle includes two stress reversals, and the symbol (2N) is used to indicate this cycle. Miner’s rule states that failure occurs when the accumulated fractional damage reaches the value of 1.

$${\displaystyle \sum _{i=1}^{N\ast }\frac{2n_i}{2N_i}}=1$$

(1)

Here, (2n_i) denotes the number of reversals and (2N_i) the number of reversals leading to failure at stress level ${\tau }_i$. The fractional damage caused by one loading reversal at stress level ${\tau }_i$ is 1/(2N_i).

The most important aspect of the calculation is the estimation of the low-cycle and high-cycle criteria corresponding to each specific torque. For transient torsional vibration during BSR quick passage, Det Norske Veritas (DNV) classification recommends choosing the number of reversals for low-cycle and high-cycle fatigue as 10⁴ and 3 × 10⁶, respectively [16]. Figure 3 shows the relationship between the torsional vibration stress amplitude and fractional damage. From the figure, based on the vibration measurement, we can obtain the fractional damage due to each reversal of torsional stress to calculate the accumulated fatigue damage of the intermediate shaft during BSR passage.

2.2. Low- and High-Cycle Criteria Determination

In this study, we considered a propulsion system of a 160,000-DWT oil tanker fitted with the WinGD W6 × 72 diesel main engine. The specifications of the engine and shafting system are listed in

Table A1. Specifications of engine and propulsion shafting system (courtesy of shipyard).

Main engine	Type	WinGD W6 × 72
	Power	16,300 kW × 73.0 r/min
	No. of cylinders	6
	Bore	700 mm
	Stroke	3086 mm
Torsional vibration damper	Type	Geislinger D290/36/V/M
	Outer inertia	15,400 kg × m2
	Inner inertia	853 kg × m2
	Torsional stiffness	13 MN × m/rad
	Relative damping	230 kN × m × s/rad
	Weight	12,900 kg
Flywheel	Moment of inertia (MOI)	15,300 kg × m2
	Weight	5970 kg
Propulsion shafting system	Intermediate shaft	Φ530 mm × 9241 mm
	Propeller shaft	Φ690 mm × 9456 mm
	IS and PS material	TS ≥ 800/600 N/mm2
Propeller	No. of blades	4
	Diameter	9.0 m
	MOI in water	195,570 kg × m2
	Weight	44,056 kg

, Appendix A. The low- and high-cycle criteria of the torsional fatigue strength were calculated by means of the following procedure and settings:

Engine maximum continuous power rating, P₀ = 16,300 kW

Maximum continuous rate, n₀ = 73.0 r/min

Intermediate shaft diameter, d = 530 mm

Intermediate shaft tensile strength, σ_b = 800 N/mm²

Yield strength, σ_y = 0.7σ_b = 560 N/mm²

Surface roughness at the edge of the slot, R_a = 1.6 µm, R_y ~ 9.6 µm

Torque at maximum continuous power:

$$\begin{array}{ll}{T}_0& =\frac{30P_0}{\pi n_0}=\frac{30\times 16300}{73\pi }\\ & =2132.24 (kN\times m)\end{array}$$

(2)

Shear stress at maximum continuous power:

$${\tau }_0=\frac{16T_0}{\pi d^3}\times {10}^6=\frac{16\times 2132.24}{\pi {(530)}^3}\times {10}^6=72.94 (N/m{m}^2)$$

(3)

2.2.1. Low-Cycle Criteria

The permissible low-cycle torsional vibratory stress can be calculated as [16]

$${\tau }_{vLC}=\frac{{\sigma }_y}{2\cdot S\cdot K_L}-\tau$$

(4)

where, τ = mean torsional stress at variety of shaft speed; S = safety factor = 1.25, as recommended by DNV for low-cycle criteria [9]; K_L = component influence factor for low-cycle fatigue.

We have,

$$\begin{array}{lll}{K}_L=1+& f_{{}_L}\left({\alpha }_t,{\sigma }_y\right)+& f_L\left(R_y,{\sigma }_b\right)\\ & (\mathrm{Term} 1)& (\mathrm{Term} 2)\end{array}$$

(5)

The first component (term 1) refers to the notch influence for low-cycle fatigue including notch sensitivity, where

$$f_{{}_L}\left({\alpha }_t,{\sigma }_y\right)=\left({\alpha }_t-1\right)\frac{{\sigma }_y}{900}$$

(6)

Here, α_t = geometrical stress concentration factor. For multi-radii transition fillet design of the shaft flange, α_t = 1.05.

Substituting this value in Equation (6), we obtain f_L(α_t, σ_y) = 0.04

The second component refers to the surface condition influence term for low-cycle fatigue, where,

$$f_L\left(R_y,{\sigma }_b\right)={10}^{-4}\left({\sigma }_b-200\right)\log R_y$$

(7)

In this equation, surface roughness R_y = 9.6.

Thus, we have

$$\begin{array}{l}{f}_L\left(R_y,{\sigma }_b\right)={10}^{-4}\left(800-200\right)\log 9.6\\ =0.06\end{array}$$

(8)

Upon substitution of the two terms in Equation (5), we have

$$K_L=1+0.031+0.035=1.066\sim 1.1$$

(9)

The mean torsional stress, τ, is defined as the average torsional stress, and it can be estimated from the measured vibration data. Moreover, the engine power and shaft speed exhibit a quadratic relation. In certain cases, the mean torsional stress can be calculated as

$$\tau ={\tau }_0\cdot {\lambda }^2$$

(10)

where, λ = speed ratio = n/n₀ = τ/τ₀.

2.2.2. High-Cycle Criteria

The permissible high-cycle torsional stress can be calculated as [16]

$${\tau }_{vHC}=\frac{0.24{\sigma }_y+42-0.15\tau }{K_{H\tau }}$$

(11)

where, K_Hτ = component influence factor for high-cycle torsional fatigue,

$$\begin{array}{cccc}{K}_{H\tau }=& f_{{}_{H\tau }}\left({\alpha }_t,m_t\right)+& f_{{}_H}\left(r\right)+& f_{{}_{H\tau }}\left(R_y,{\sigma }_B\right)\\ & \left(1^{\mathrm{st}}\right)& \left(2^{\mathrm{nd}}\right)& \left(3^{\mathrm{rd}}\right)\end{array}$$

(12)

The first term denotes the notch influence term for high-cycle torsional fatigue, with

$$f_{{}_{H\tau }}\left({\alpha }_t,m_t\right)=\frac{{\alpha }_t}{m_t},$$

(13)

where, m_t = notch sensitivity coefficient for high-cycle torsional fatigue, calculated as:

$$m_t=1+\left(\frac{60}{{\sigma }_y}-0.05\right)\sqrt{\frac{1}{r}}$$

(14)

In general, r = notch radius = 100 mm. If r > 100, r is set to 100.

Upon substituting Equation (14) in Equation (13), we obtain f_Hτ = 1.044.

The second component refers to the size (statistical) influence term for high-cycle fatigue:

$$f_{{}_H}\left(r\right)=0.01\sqrt{r}=0.1$$

(15)

Finally, the third component refers to the surface condition influence term for high-cycle torsional fatigue, where,

$$\begin{array}{l}{f}_{{}_{H\sigma }}\left(R_y,{\sigma }_b\right)=3\cdot {10}^{-4}\left({\sigma }_b-200\right)\log R_y\\ =3\cdot {10}^{-4}\left(560-200\right)\log 9.6\\ =0.006\end{array}$$

(16)

Upon substituting these values in Equation (12), we have

$$K_{H\tau }=1.044+0.1+0.006=1.15$$

(17)

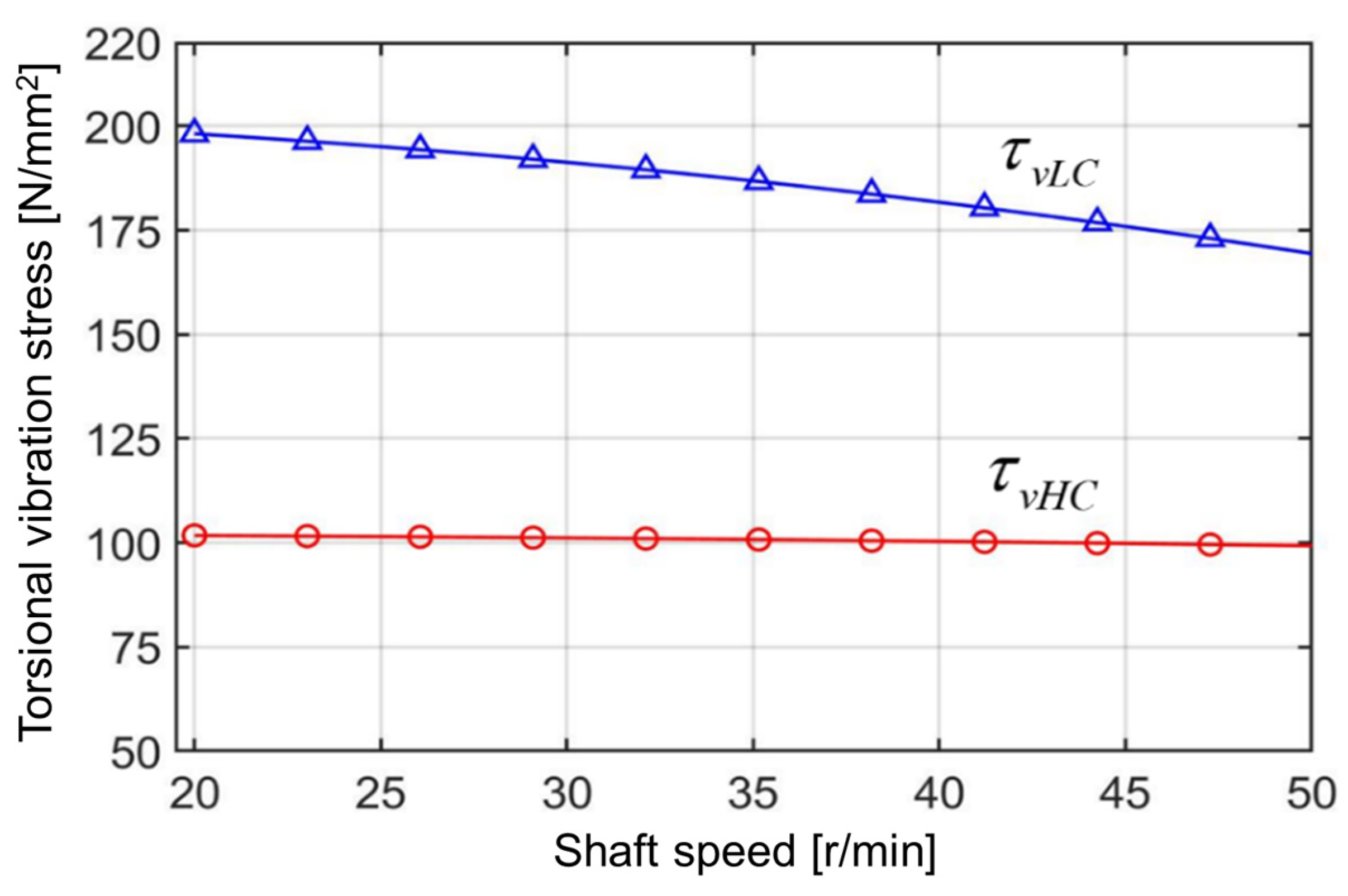
In this calculation, the mean torsional stress is determined based on the corresponding speed as per the relationship with shear stress at maximum continuous power via Equation (10). Finally, the low- and high-cycle criteria over the whole operation speed range are plotted as shown in Figure 4. For each specific value of the mean torsional stress corresponding to a certain speed, the slope of the S–N curve can be obtained as

$$b=\frac{\log \left(2N_{HC}\right)-\log \left(2N_{LC}\right)}{\log {\tau }_{vLC}-\log {\tau }_{vHC}}$$

(18)

As mentioned earlier, Figure 3 shows the linear relationship between the number of reversals and the failure and amplitude of torsional stress vibration; this relationship can be expressed as the following equation:

$$\log \left(2N\right)=\log \left(2N_a\right)-b\cdot \log \left({\tau }_v\right)$$

(19)

or

$$\left(2N\right)=a\times {\tau }_v{}^{\left(-b\right)}$$

(20)

where,

$$\log a=\log \left(2N_a\right)=\log \left(2N_{HC}\right)+b\cdot \log {\tau }_{HC}$$

(21)

3. Results and Discussion

We performed a series of torsional vibration measurement experiments with different engine operation patterns during BSR passage to evaluate the performance of each setting based on the calculated fatigue damage. Figure 5 displays the schematic of the torsional vibration measurement system, and the setup of the computer and device installation for measurements is shown in Figure 6. 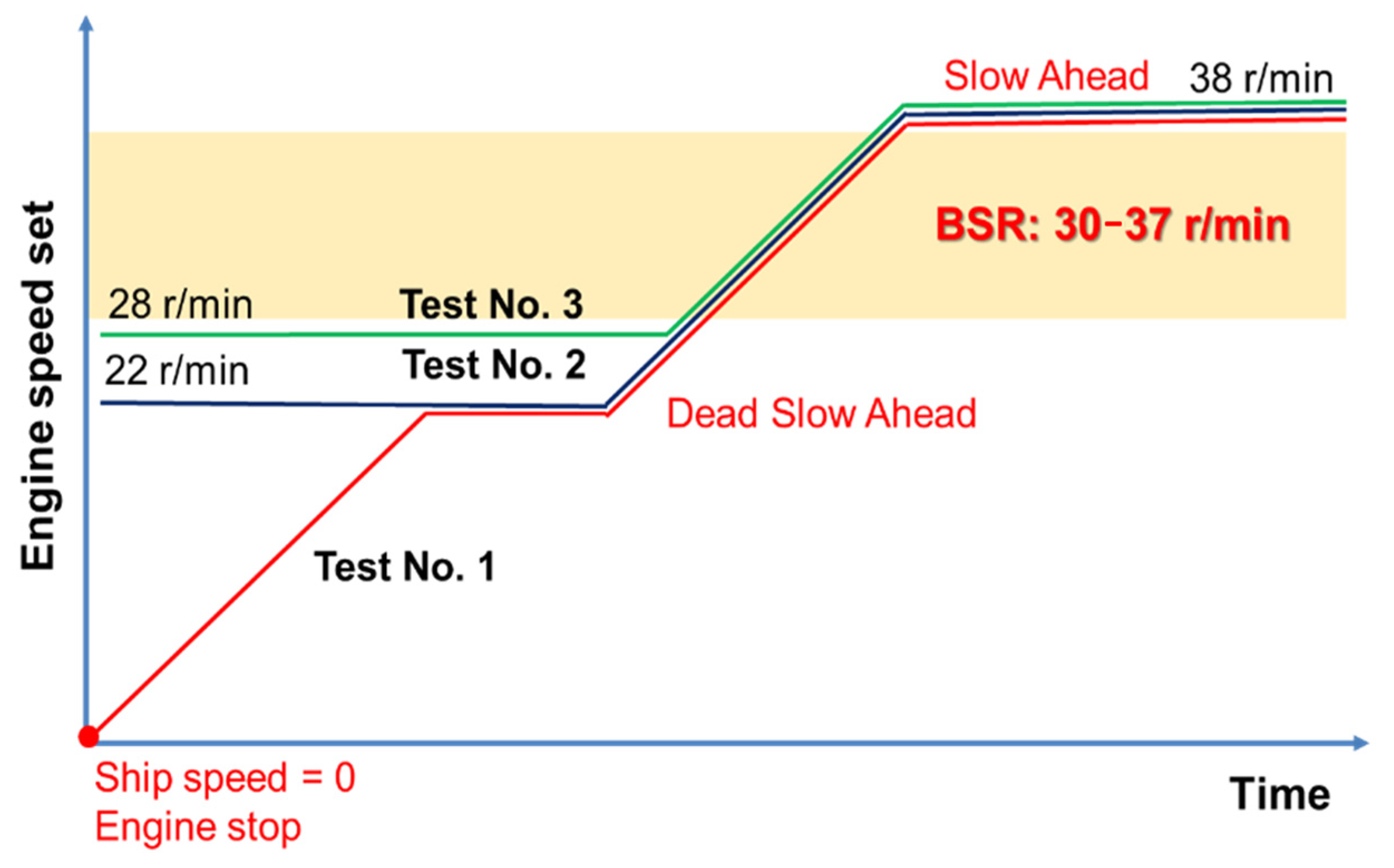All vibration data were measured using the EvamosM software [17,18,19] developed by the Dynamics Lab of the Mokpo National Maritime University. In the experiments, we used three operation modes for BSR quick passage tests. 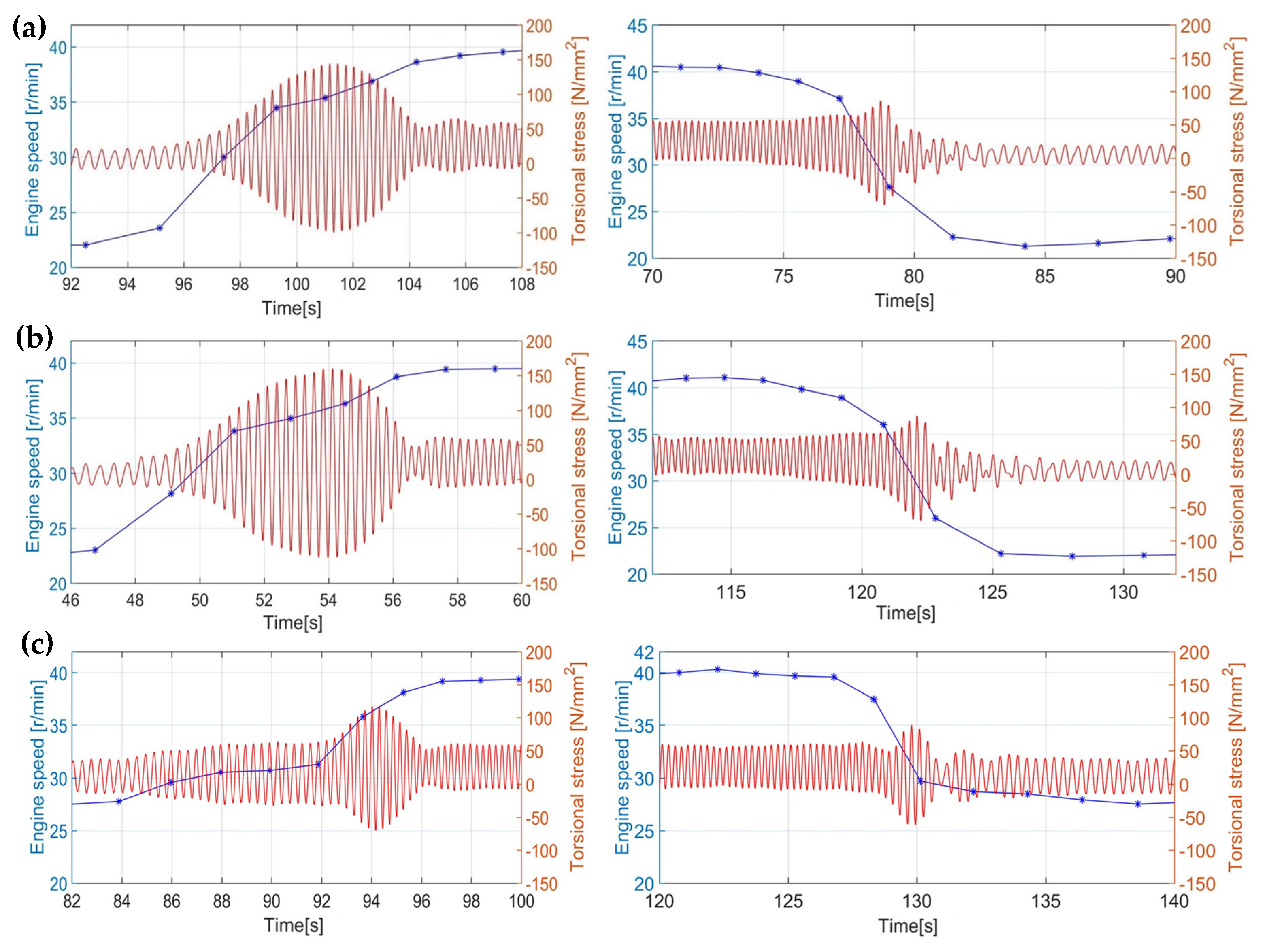The condition and engine control setting of each test is described in Figure 7. The torsional vibration stresses corresponding to the engine speed and time in each test are shown in Figure 8a–c.

From the measurement results, we note that in the BSR deceleration passages, the torsional vibration amplitudes are small and negligible; however, the vibration during BSR accelerations is a matter of concern. Upon comparing the results of the three BSR acceleration tests, we note that the torsional vibration stresses are smallest when the vessel reaches a certain speed and the starting point of the engine rpm is higher.

The calculated fractional fatigue damage during BSR passage for each test is listed in

Table 1. Fractional damage calculation results.

Name of Test	Fractional Damage (×10−5)	Estimated Fatigue Lifetime
BSR quick passage test no. 1	9	33 y (*)
BSR quick passage test no. 2	1.7	175 y (*)
BSR quick passage test no. 3	0.07	4250 y (*)
BSR steady-state (30 s)	26.5	31 h
BSR steady-state—120% (30 s)	325	2.5 h

(*) It is assumed that barred speed range (BSR) passage is performed once a day.

. Here, we note that the intermediate shaft will break when the accumulated fractional damage reaches the value of 1 (Equation (1)). According to the measurement results, for the settings corresponding to test no. 3, the fatigue damage is reduced by nearly 128 times that of test no. 1 and ~24 times that of test no. 2. Obviously, smaller fraction damage indicates that the fatigue life increases. In the case of engine operation in the BSR steady-state normal firing condition (Figure 9), the accumulated fractional damage reaches a value of 26.5 × 10⁻⁵ after 30 s. This result indicates shaft breakage after 31 h under this condition. In general, after many years of ship operation, the operating condition of the whole propulsion system degrades to relative to that of a new vessel. In this case, the damping of the torsional vibration damper may change, and the turbocharging system exhibits a poor performance due to age. In this situation, if we assume that the torsional vibration level increases by 20%, the fatigue lifetime for this shaft is just 2.5 h.

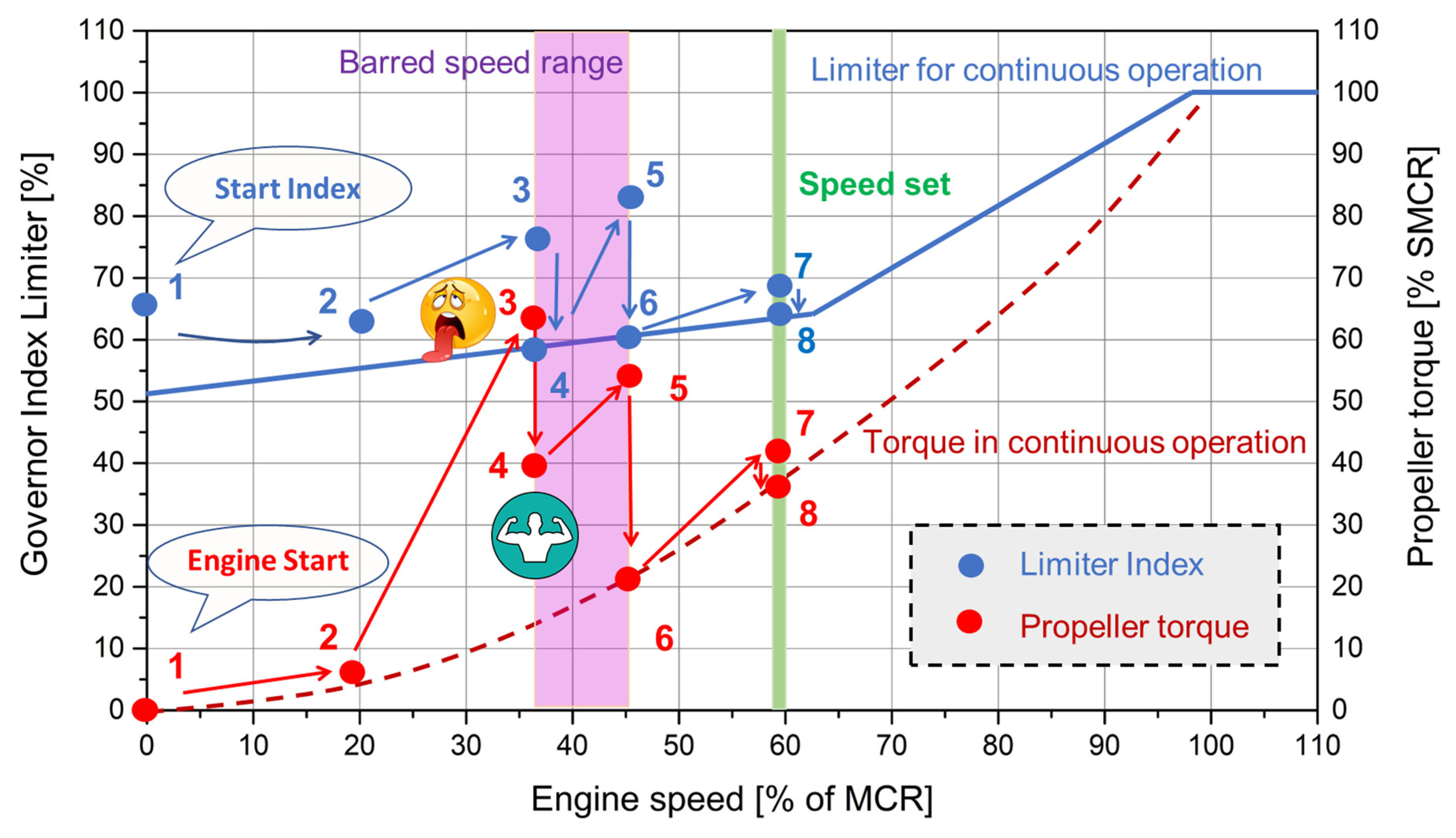
Based on the above-mentioned results, to reduce the torsional vibration stresses amplitude, we recommend the following operating procedure corresponding to test no. 3 for BSR acceleration (Figure 10):

• Step 1: Start main engine (point nos. 1, 2), set engine speed to 28 r/min, immediately below BSR (point no. 3); wait until vessel reaches a certain speed corresponding to the engine speed (point no. 4).
• Step 2: Set engine speed to 38 r/min—right above BSR (point No. 5); wait until engine speed reaches setting speed (point no. 6).
• Step 3: Set desired speed (point nos. 7, 8).

4. Conclusions

The ultra-long-stroke engine affords a higher power at slower shaft speeds; however, the trade-off is the resulting higher torsional vibration, which can affect the fatigue strength of the shafting system. In this study, we investigated the torsional vibration characteristics of the intermediate shaft of a marine propulsion system with the WinGD-W6X72 main engine during BSR passage. To evaluate how different engine operation patterns affect BSR acceleration, we conducted a series of experiments. Our results can be summarized as follows:

(1)

Fatigue failure can occur after a certain number of loading reversals (or number of loading cycles). The fractional fatigue damage varies linearly with the torsional stress amplitude (when both are represented in the log scale). Additionally, it is important to determine the low- and high-cycle criteria to calculate the accumulated fractional damage for each passage. Consequently, the fatigue lifetime of the shafting system can be estimated.

(2)

It is necessary to calculate the accumulated fatigue damage for marine propulsion systems, particularly during BSR passing. Consequently, the fatigue lifetime can be estimated to evaluate the optimal working conditions of the diesel engine and predict and avoid structural failure. In our case, optimization of the operation pattern reduced the fatigue damage by a factor of 128. Furthermore, such optimization ensures that BSR steady-state conditions are avoided. Otherwise, BSR passage can damage the shaft after only 31 h or even 2.5 h of operation in the worst-case scenario (assuming that the torsional vibration level increases by 20%).

(3)

The fatigue lifetime of the shafting system can be extended as follows: the shaft size can be increased, a multi-radii-shaped design can be applied to the fillet, and materials with higher tensile strengths can be used. The dynamic characteristics of the torsional vibration can be improved by installing a torsional damper or tuning wheel. Newer techniques such as the dynamic limiter function (MAN ES) and Delta Bypass (WinGD) are also available. These methods can be combined to improve the engine acceleration torsional vibration behavior at a reasonable cost.

(4)

The torsional vibration during BSR passage depends on the engine operation patterns. To improve the torsion behavior during BSR acceleration and thereby extend the operation lifetime of the shafting system, it is recommended to set the engine speed right below the BSR lower limit and then wait for the ship speed to increase before acceleration to reduce the torsional vibration amplitude during BSR passage.

The ultra-long-stroke engine propulsion system is the future of large vessels, such as “supertankers” including very large and ultra-large crude carriers (VLCCs and ULCCs). All new techniques used to improve the engine acceleration capacity achieved by more power generated should be tested for torsional vibration to evaluate the fractional damage during BSR quick passage. The ultimate purpose is to prevent the risk of fatigue fracture during the entire vessel life expectancy (25–30 years).