Structural Analysis of a Barge Midship Section Considering the Still Water and Wave Load Effects

Abstract

Structural failures in the barge midship sections can cause operational delay, sinking, cargo loss and environmental damage. These failures can be generated by the barge and cargo weights, and wave load effects on the midships sections. These load types must be considered in the design of the barge midship sections. Here, we present the structural analysis of a barge midship section that has decreased up to 36.4% of its deck thickness caused by corrosion. This analysis is developed using finite element method (FEM) models that include the barge and cargo weights, and wave load effects. The FEM models regarded three cargo tanks in the midship section, containing the main longitudinal and transverse structural elements. In addition, the hull girder section modulus and the required deck thickness of the barge were calculated using Lloyd’s Register rules. These rules were applied to estimate the permissible bending stresses at deck and bottom plates under sagging and hogging conditions, which agreed well with those of the FEM models. Based on FEM models, the maximum compressive normal stress and von Mises stress of the hull girder structure were 175.54 MPa and 215.53 MPa, respectively. These stress values do not overcome the yield strength (250 MPa) of the barge material, allowing a safe structural behavior of the barge. The structural modeling of the barge midship section can predict its structural behavior under different sagging and hogging conditions, considering the cargo, weight and wave loads.

1. Introduction

The longitudinal structural strength of the midship section is the most important strength to ensure the safe structural behavior of a ship [1,2]. To calculate this strength must be considered all the different loads types such as ship and cargo weights, and wave load [3,4]. This midship section includes the hull girder, which is a structure formed by shells, deck, interior bottom and longitudinal bulkhead. The design of this structure considers the longitudinal bending moment caused by the combination of lightship weight, load weight, buoyancy forces, and wave effects in different sea routes. The ships’ navigations on sea routes are not always with a calm sea and may have areas with different marine environmental conditions and wave loads. High bending moments in the structure of a ship are generated when the wavelength is equal to the ship length [5]. Generally, the highest bending moments are in the ship’s hull girder, which can cause maximum stresses and deflections in this section of the ship.

Classification societies rules [6,7] can be used to estimate the structural strength of the ship hull. However, these rules only apply to single ship hull and do not take into account the possible stresses in longitudinally connected structural elements with transverse frames. Several researchers [8,9,10,11] have reported works about the design of the midship section using finite element method (FEM) models and regarding different load cases. In the strength assessment of the midship section can be used one of the two approaches described in the classification societies [12,13]. The first approach is based on an FEM model of three cargo tanks in the midship section. For this approach, the strength assessment focuses on the stresses obtained in the central tank. The second approach considers a FEM model of all the cargo and ballast tanks. This second approach is used for the design of ships, in where their structural behavior cannot be determined using beam theory. In particular, this second approach is employed in ships with large deck openings such as bulk carriers and container ships. These types of ships are affected by high torsional deformation and stresses. Rörup et al. [14] used the two approaches for the analysis of the structural behavior of cargo hold model with a full model of a ship with open decks. By using same mesh and load types, they reported identical results for the two approaches. These approaches can be employed to calculate the structural safety of the ship hull under different operation conditions, load cases and corrosion addition. Three types of rules based on corrosion addition models, named previously applied structural rules (pre-CSR), common structural rules (CRS), and harmonized common structural rules (CSR-H) can be considered [15]. First, corrosion addition rules were known as pre-CSR. To achieve safer ships, the International Association of Classification Societies (IACS) adopted CSR for oil tankers and bulk carriers on 1st April 2006. Finally, IACS published CSR-H 2020, in which the corrosion additions were specified for oil tankers and bulk carriers with unrestricted navigation on 1st January 2020 [16].

In shipping, corrosion addition methods were adopted in structural design to prevent structural capacity degradation. Paik et al. [17] investigated the ultimate strength performance of double hull oil tanker structures designed by pre-CSR versus CSR methods in terms of buckling for stiffened plates at deck, bottom part and hull girder. These stiffened plates were determined considering three types of scantlings. They observed that the working stresses of pre-CSR are lesser than CSR designs. Furthermore, Kim et al. [15] presented a study focuses on the historical trend of corrosion addition rules for ship structural design and reported their effects on the ultimate strength performance on hull girder and stiffened panel of double hull oil tankers structures.

Here, we present a structural analysis of a barge midship section that has decreased close 36.4% of its original deck thickness (22 mm) due to corrosion. The original thickness of the deck plates was taken from the midship section drawing of the ship, which is registered and approved by LR class and the maritime authority and was updated the thickness measurement by certified NDE company. The selected barge is a Non-Self-Propelled oceangoing deck barge that transport jackets and heavy cargo up to 14,000 tons on its flat deck, while being towed or pushed. The barge was laid-up in a port in the southeastern part of the state of Tamaulipas, Mexico, for several years. For this, the owner decided to return the barge to service. The structural analysis of the barge midship was done to determine if its mission could be achieved with lowered deck scantling. This analysis considered a FEM model of three cargo tanks, including the barge and cargo weights, and the wave load. This analysis evaluated the structural safety of the barge midship section affected by the corrosion. The value of wave load was obtained through analytical models established by the Lloyd’s Register rules. In addition, these rules were used to verify the parameters of the barge midship section using a reduced deck plate thickness (14 mm) to ensure a safe performance of the barge. The results of the FEM model agreed well with those obtained using the Lloyd’s Register rules. The maximum compressive normal stress and von Mises stress of the midship section of the FEM model were 219.52 and 255.39 MPa, respectively. These stress values do not overcome the yield strength (250 MPa) of the barge material, allowing a safety structural behavior of the barge.

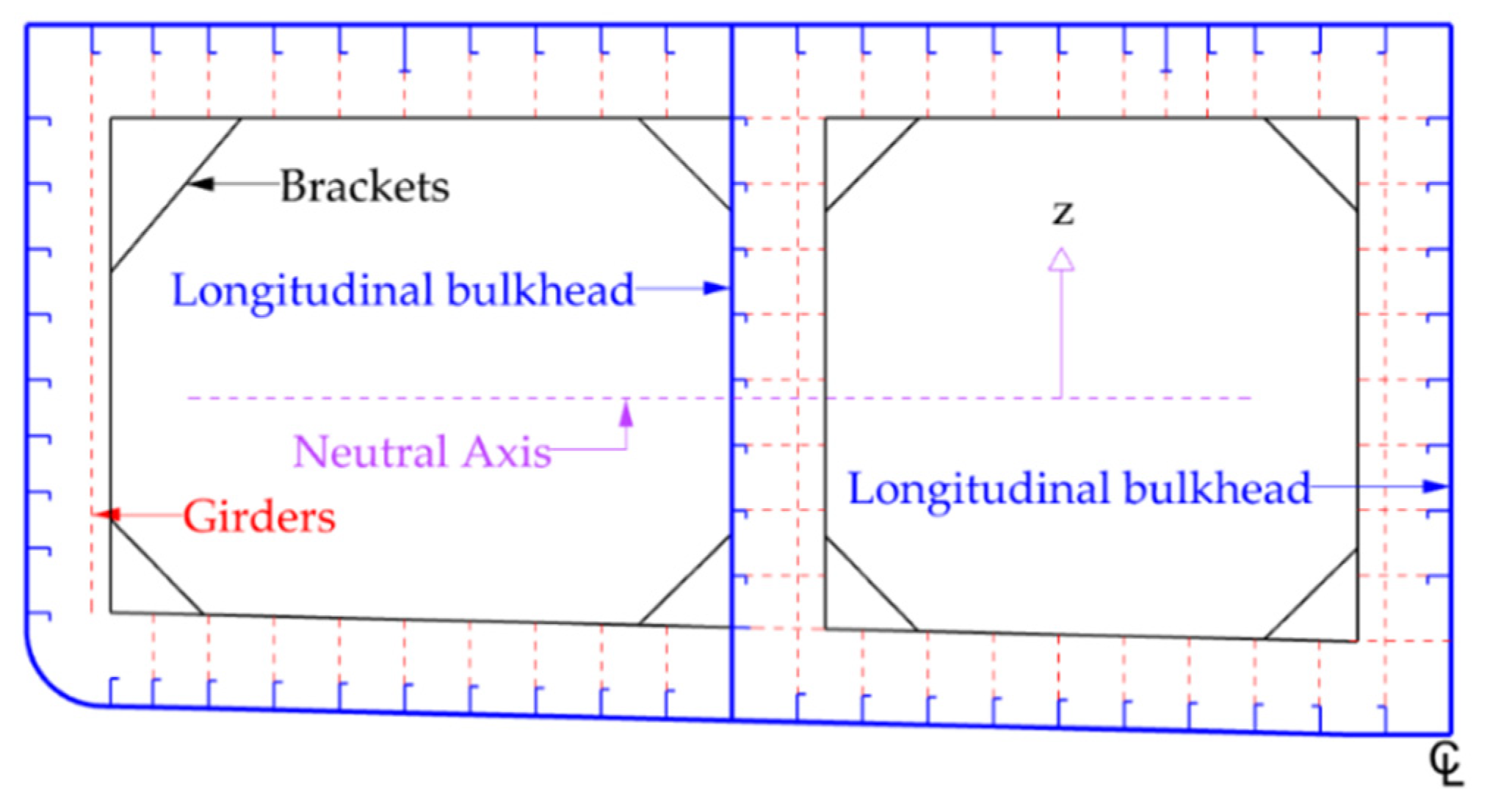
2. Modeling the Barge Midship Section

This section describes the structural components and dimensions of the barge midship section. In addition, it reports the Lloyd’s Register rules to determine the minimum thickness in deck plate, permissible bending stresses of the ship hull, hull section modulus, and still water shear loads and wave bending moments. Furthermore, it includes a FEM model of the barge midship section considering the barge and cargo weights, and wave bending moment.

2.1. Description of the Barge

The barge studied in this work has a midship section affected by corrosion, which has decreased its deck thickness up to 36.4%.

Table 1. Main dimensions of the barge.

Parameters	Value	Unit
Overall length	122.45	m
Loadline length (L)	119.95	m
Breadth (B)	30.5	m
Depth (D)	7.60	m
Loadline draft (T)	6.21	m
Deadweight	15,550	ton

depicts the main dimensions of the barge. Figure 1 depicts a 3D view of the internal and external structural components of the barge midship section. The midship section has a length of 45 m and it contains three cargo tanks. The barge has three longitudinal bulkheads between stations 3 and 44, in where the barge midship section is located between stations 15 and 33. The other two longitudinal bulkheads are placed at the sides of the central bulkhead with a separation of 7.7 m from the centerline. The midship section has a single hull composed by transversal frames with separation of 2.5 m and longitudinal stiffeners with the spacing of 0.7 m, with exception in specific locations close to bilge.

2.2. Lloyd’s Register Rules

In order to determine the overall structural response of the midship section, we applied the Lloyd’s Register rules [6]. The Lloyd’s Register rules establish minimum reference values to reinforce the midship section and classify it as safe structure. For this case, the minimum value of thickness (14 mm) of deck plates was evaluated.

2.2.1. Minimum Thickness of Deck Plates

The maximum bending stresses occur over the midship section on the strength deck and bottom plates [6,7]. The strength deck is the main structural assembly of the ship that maintains its longitudinal strength under the longitudinal bending moment on the hull. The strength deck plate has the 40% of the barge length and has a minimum thickness (t) allowed by the classification societies. The minimum thickness of strength deck plates of the midship section must satisfy the Lloyd’s Register rule appropriate to its structural configuration, which can be longitudinal or transverse type. In particular, the minimum thickness (mm units) of the strength deck plates was calculated for a longitudinal structural configuration using the following Lloyd’s Register rule [6]:

$$t=0.001s_1\left(0.059L_1+7\right)\sqrt{\frac{F_D}{K_L}}$$

(1)

$$F_D=\frac{{\sigma }_D}{\sigma }$$

(2)

where F_D is a local scantling reduction factor for hull members above the neutral axis, σ_D is the bending stress on the strength deck, σ is the allowable tensile stress, s₁ is the spacing of primary members, K_L is a higher tensile steel factor, and L₁ is the length (m units).

2.2.2. Permissible Hull Vertical Bending Stresses

The σ induced by still water plus wave load at the midship section, for the vertical deflection of the hull girder structure, is calculated as:

$$\sigma =\frac{175}{K_L}\mathrm{MPa}$$

(3)

The maximum bending stresses of the hull on the deck (σ_D) and keel (σ_B) are calculated with (4) and (5), respectively. These equations use the appropriate combination of bending moments to determine sagging and hogging stresses:

$${\sigma }_D=\frac{\left|{\overline{M}}_S+M_W\right|}{Z_D}\times {10}^{-3}\mathrm{MPa}$$

(4)

$${\sigma }_B=\frac{\left|{\overline{M}}_S+M_W\right|}{Z_B}\times {10}^{-3}\mathrm{MPa}$$

(5)

where Z_B and Z_D are the hull section modulus (m³ units) at keel and strength deck, $\overline{M}s$ is the maximum permissible still water bending moment calculated with (12) and (13), and M_W is the hull vertical wave bending moment (kNm units) calculated with (15) that can be sagging (negative) and hogging (positive) type.

2.2.3. Hull Section Modulus

Figure 2 depicts the transversal view of the half of midship section, which includes the longitudinal members highlighted in blue color. All the continuous longitudinal structural members of the midship section are considered to determine the moment of inertia and section modulus. The distance z of the midship section is measured from its neutral axis to the top of the keel and the top line of the strength deck. Commonly, the longitudinal members of the hull section modulus are extending through the midship section and towards the ends of ship. The minimum section modulus (Z_min) of the midship section of the hull with respect to transversal neutral axis, on the deck or on the keel (Z_B and Z_D), is obtained by [6]:

$$Z_{\min }=f_1{K}_L{C}_1{L}^{2}B\left(C_b+0.7\right)\times {10}^{-6}{\mathrm{m}}^3$$

(6)

$$C_1=10.75-{\left(\frac{300-L}{100}\right)}^{1.5}$$

(7)

where f₁ is ship service factor, which is equal to 1 for our case of unrestricted sea-going service, C₁ is wave bending moment factor for ships with a length between $90\le L\le 300$, C_b is the block coefficient, and B is breadth (m units).

The moment of inertia (I_min) of the midship section is calculated with (8) the maximum total bending moment in sagging or hogging condition.

$$I_{\min }=\frac{3L\left(|{\overline{M}}_S+M_W|\right)}{K_L\sigma }\times {10}^{-5}{\mathrm{m}}^4$$

(8)

where K_L should be taken equal to 1.0 only for hull moment of inertia

In addition, for vessels with L ≥ 90 m, the minimum moment of inertia of the midship section is determined by Equation (9):

$$I_{\min }=3C_1{L}^{3}B\left(C_b+0.7\right)\times {10}^{-8}{\mathrm{m}}^4$$

(9)

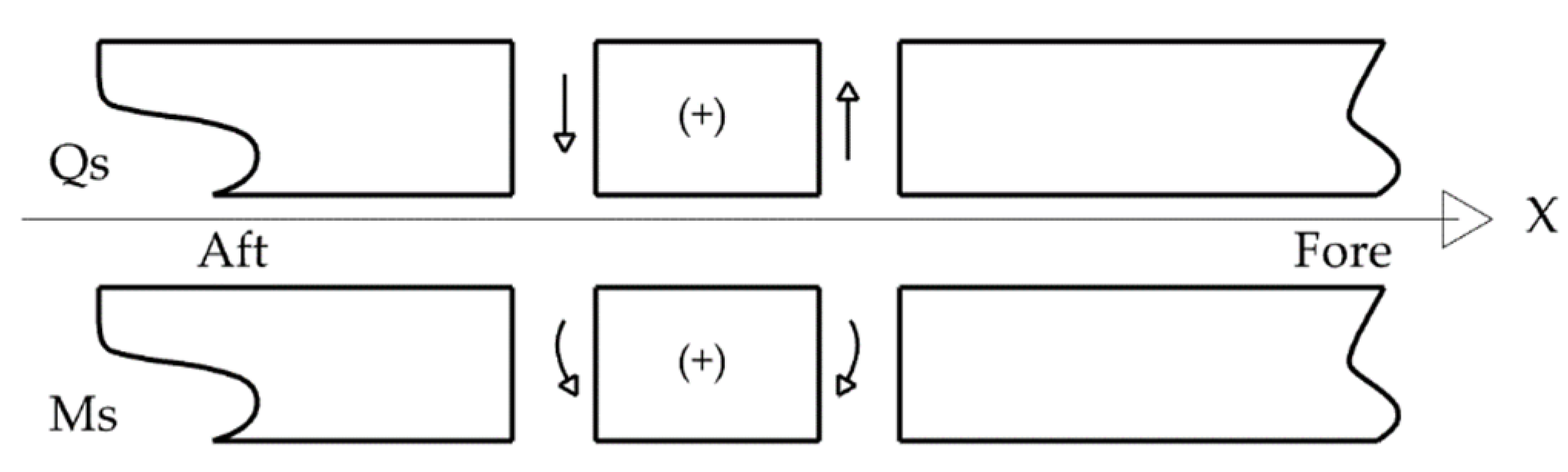
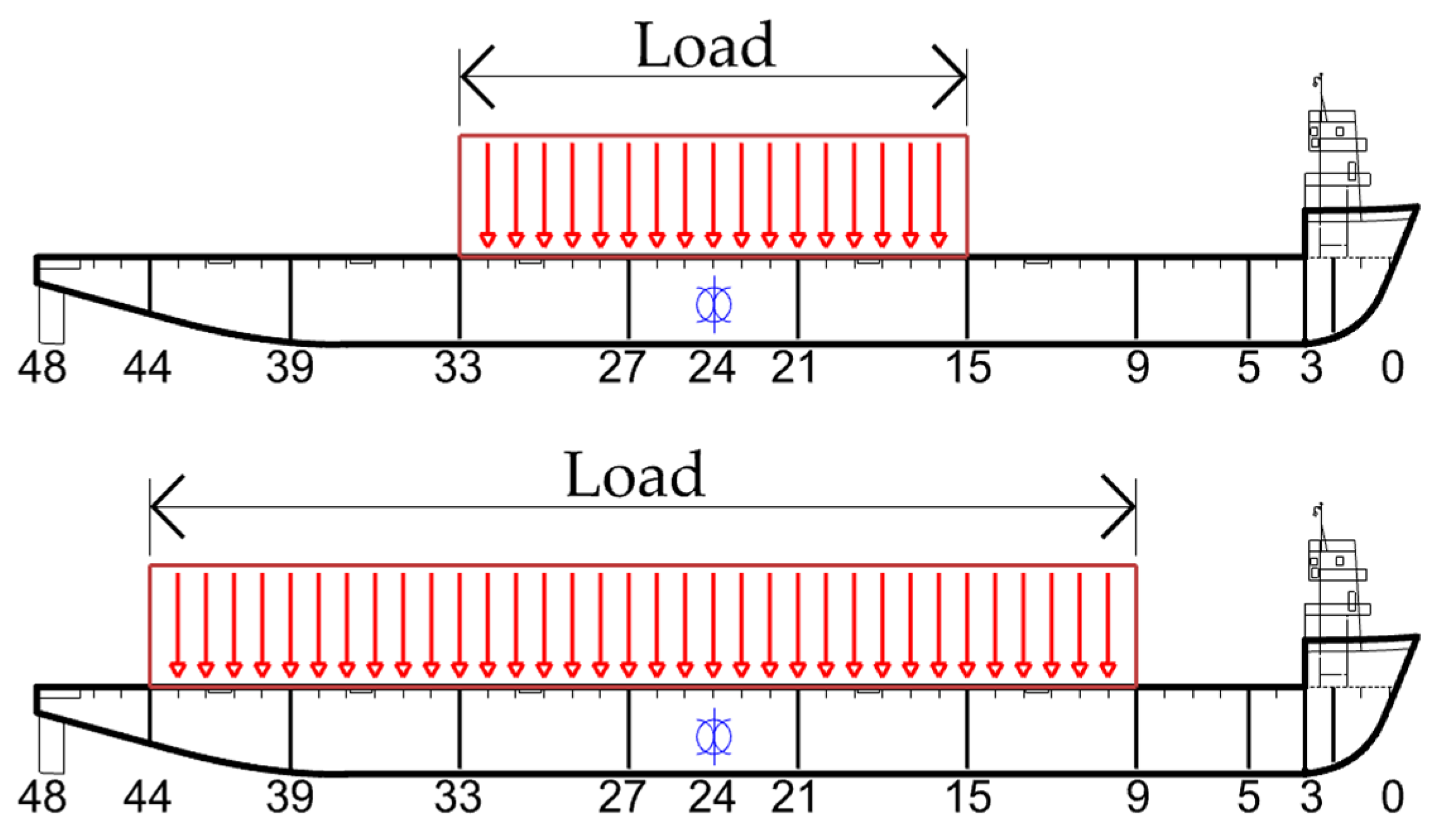
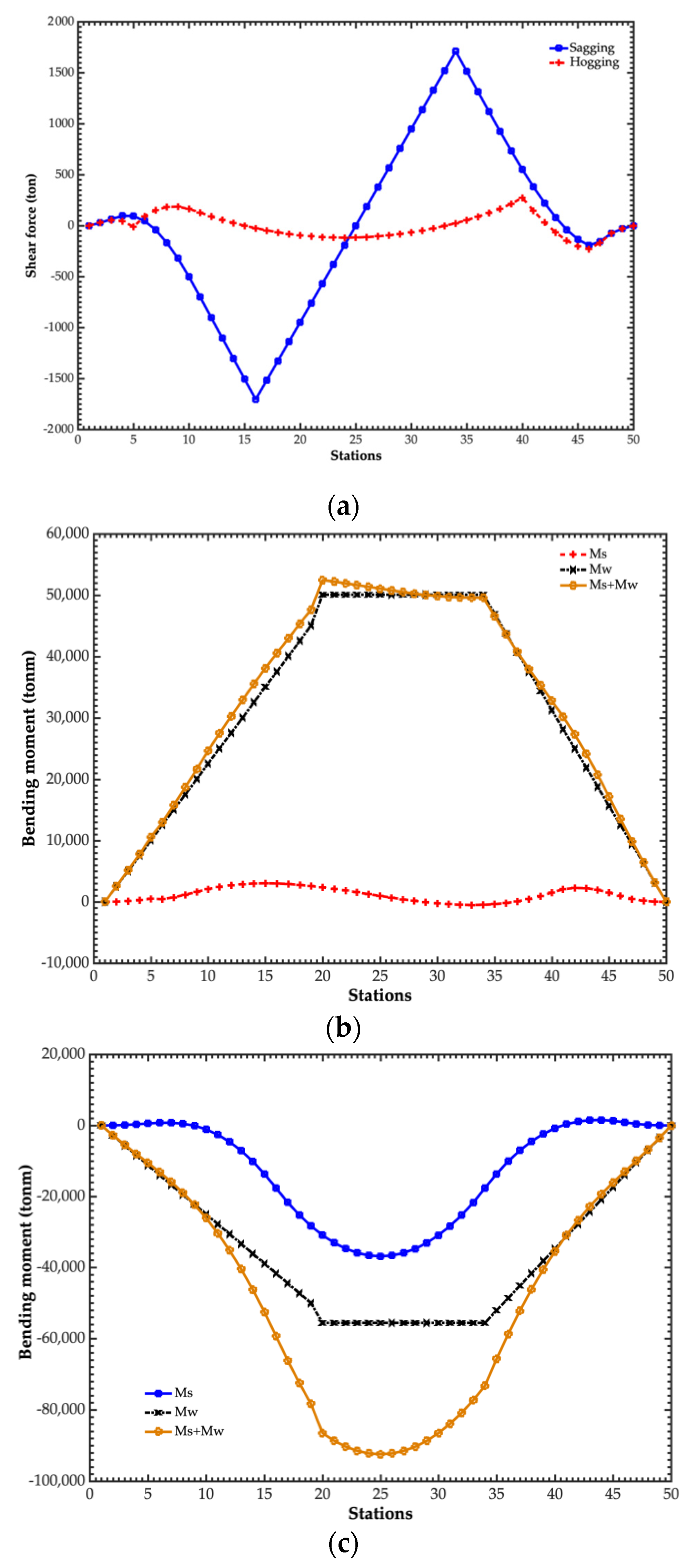
2.2.4. Still Water Shear Forces and Vertical Bending Moments

For vessels with length (L) larger than 65 m, the longitudinal strength must be determined considering the shear forces and bending moments [6]. The shear forces (Q_S(x)) and bending moments (M_S(x)) in still water are estimated using the load stability conditions. These conditions comply the load and ballast conditions for safe operation of ships. Bending moments in still water are calculated by differentiating the non-uniform distribution of the weight (w_(x)) of the ship structure, including its cargo, and buoyancy forces (b_(x)). This w_(x) is integrated using Equations (10) and (11) along x-axis direction. Figure 3 shows the sign convention of Q_S(x) and M_S(x), the positive sign means that the ship is in hogging and negative sign under sagging [18].

$$Q_{S(x)}={\displaystyle {\int }_0^x\left[b_{\left(x\right)}-w_{\left(x\right)}\right]}dx$$

(10)

$$M_{S\left(x\right)}={\displaystyle {\int }_0^x\left[Q_{S\left(x\right)}\right]}dx$$

(11)

Figure 4 shows two load conditions of 7000 tons each one on the barge deck. Based on Lloyd’s Register rules, the minimum bending moments in still water for hogging and sagging should be taken as the lesser value of the that reported by Equations (12) and (13) [6]:

$$\left|{\overline{M}}_S\right|=F_D\sigma Z_D\times {10}^3-\left|M_W\right|\mathrm{kNm}$$

(12)

$$\left|{\overline{M}}_S\right|=F_B\sigma Z_B\times {10}^3-\left|M_W\right|\mathrm{kNm}$$

(13)

The maximum bending moment of a ship obtained using (11) must satisfy the constraint condition of Equation (14) [6]:

$$\left|M_S\right|\le \left|{\overline{M}}_S\right|$$

(14)

where $\left|M_S\right|$ is real bending moment in still water of a midship section considering hogging and sagging conditions.

2.2.5. Vertical Wave Bending Moment

The vertical wave bending moment is calculated with the equations of the classification societies [6,7] using analytical methods based on the main dimensions of the ship. These equations do not include the ship type, load distribution and hull shape. The classification societies use common equations specified by International Association of Classification Societies (IACS) [16] to calculate vertical wave bending moment under sagging and hogging conditions. This moment value is considered equal to the maximum moment that will be obtained during 20 years of ship operation. Generally, this operation time is regarding the ordinary service life of a ship [19,20].

The hydrodynamic analysis using numerical methods can be used to calculate the wave bending moment. Parunov et al. [20] established the steps of a direct hydrodynamic analysis to determine the maximum bending moments of a ship under different types of waves. They reported that wave bending moments of novel ship designs could be higher than those obtained with the IACS equations. However, the direct hydrodynamic analysis requires more detail information about the sea state, which is not always available to estimate the wave bending moment. The vertical wave bending moment (M_w) for sagging or hogging in the midship section is estimated by:

$$M_W=f_1{f}_2{M}_{WO}$$

(15)

$$f_2=\frac{1.9C_b}{C_b+0.7}\mathrm{for}\mathrm{hogging}(\mathrm{positive})$$

(16)

$$M_{WO}=0.1C_1{C}_2{L}^{2}B\left(C_b+0.7\right)\mathrm{kNm}$$

(17)

where C_b is to be taken not less than 0.60, C₂ is the longitudinal distribution factor equal to 1 at midship section, $f_2$ is taken equal to −1 for the sagging moment (negative).

The total vertical bending moment used in FEM models of the ship is composed of the vertical bending moments under still water and wave. This total vertical wave bending moment is given by:

$$M_V=M_S+M_W$$

(18)

3. Buckling and Ultimate Strength of Ship Structure

Buckling and ultimate strength of ship structures are important concepts in the study about local (stiffened panels and plates) and global strengths of the ship (hull girder) [21], as shown Figure 5. The concepts have been widely investigated by employing analytical methods, experimental tests, empirical approaches and non-linear FEM simulations over the years for several researchers.

Comprehensive technical reviews on existing empirical formulations that predict the ultimate limit state (ULS) of a stiffened panel under longitudinal compression were presented by Zhang [21] and Kim et al. [22]. The empirical formulations to predict the buckling and ultimate strength of plates and stiffened panels behavior are strongly related to two parameters shown in (19). In general, relevant parameters representing the geometrical and material properties should be defined in an empirical formulation [22]. These parameters are the plate slenderness ratio (β) and column slenderness ratio (λ) in (20) and (21), respectively.

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=f(\lambda ,\beta )$$

(19)

$$\beta =\frac{b}{t_p}\sqrt{\frac{{\sigma }_{Yp}}{E}}$$

(20)

$$\lambda =\frac{a}{\pi r}\sqrt{\frac{{\sigma }_{Yseq.}}{E}}$$

(21)

where σ_xu is ultimate compressive stress, ${\sigma }_{Yeq}$ is the yield stress equivalent calculated with (22), ${\sigma }_{Yp}$ is the yield strength of plate attached to stiffener, ${\sigma }_{Yeq}$ is the yield strength of the equivalent stiffener, E is the Young’s modulus, and t_p is the plate thickness, r = $\sqrt{I/A}$ is the radius of gyration of the stiffener including associated full width (b) plating, I is the moment of inertia calculated with (23) and A is the cross-section area of the stiffener including associated full width plating, z₀ is the neutral axis of the stiffener with its attached plate. Figure 6 shows the geometrical parameters of the cross-sections of the stiffener types considered in the empirical formulations.

$${\sigma }_{Yseq}=\frac{{\sigma }_{yp}b{t}_p+{\sigma }_{ys}\left(h_w{t}_w+b_f{t}_f\right)}{b{t}_p+h_w{t}_w+b_f{t}_f}$$

(22)

$$\begin{array}{l}I=\frac{b{t}_p^3}{12}+b{t}_p{\left(z_0-\frac{t_p}{2}\right)}^2+\frac{h_w^3{t}_w}{12}+h_w{t}_w{\left(z_0-t_p-\frac{h_w}{2}\right)}^2\\ +\frac{b_f{t}_f^3}{12}+b_f{t}_f{\left(t_p+h_w+\frac{t_f}{2}-z_0\right)}^2\end{array}$$

(23)

$$z_0=\frac{0.5b{t}_p^2+h_w{t}_w\left(t_p+0.5h_w\right)+b_f{t}_f\left(t_p+h_w+0.5t_f\right)}{b{t}_p+h_w{t}_w+b_f{t}_f}$$

(24)

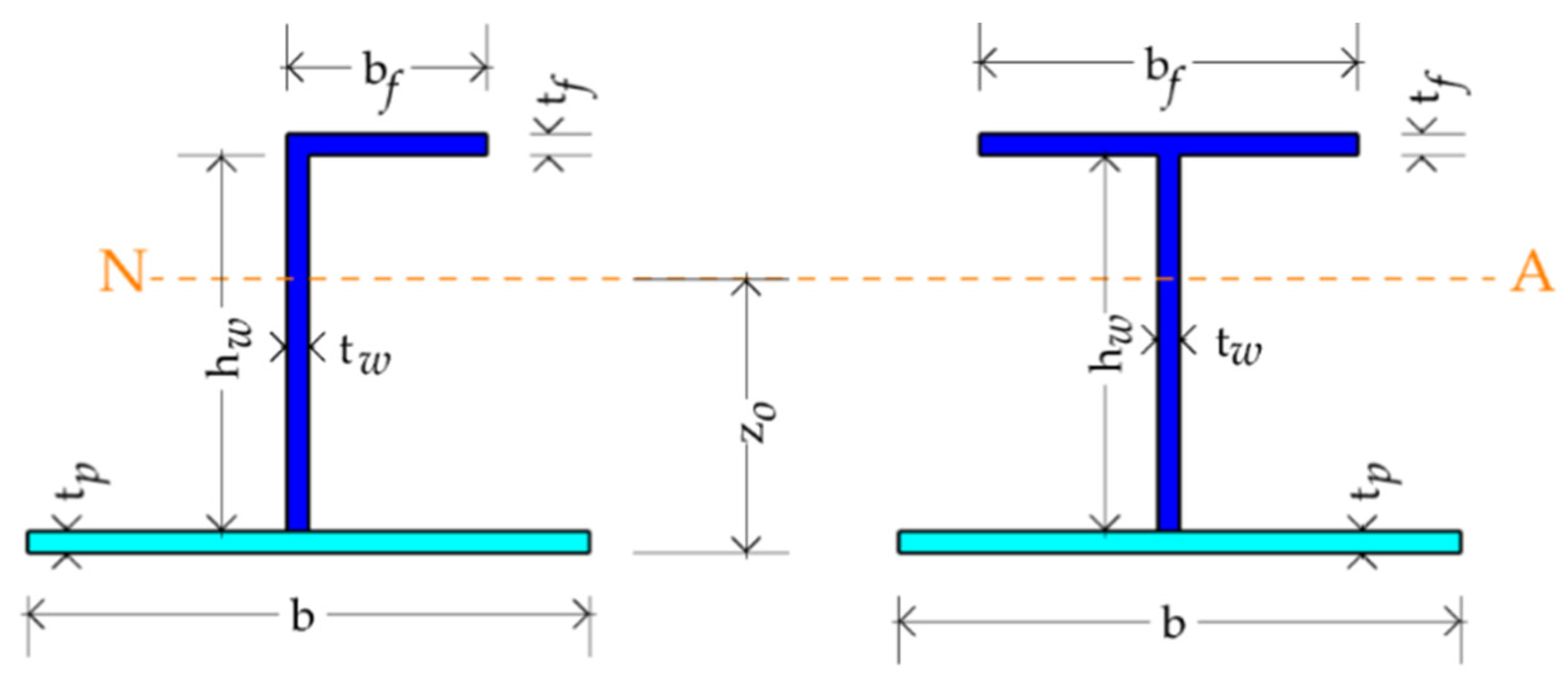
Empirical Formulas for Stiffened Panels and Unstiffened Plates

In order to calculate the ultimate compressive strength of the stiffened panel and unstiffened panel (plate) at the deck, which is under axial compression caused by sagging moment, the empirical equations were applied. These equations consider both the T-bar stiffener and angle-bar stiffener, which are expressed in terms of the plate slenderness ratio (β) and the column (stiffener) slenderness ratio (λ). Recently, more refine equations expressed with four terms (λ, β, h_w/t_w, I_pz/I_sz) were developed by Kim et al. [23] for the T-bar stiffened panel and Kim et al. [24] for the Flat-bar stiffened panel. In addition, Kim et al. [23] obtained a better empirical formulation (28) to predict the ultimate strength of stiffened panel considering fifteen coefficients (i.e., c₀ to c₁₄), which are indicated in

Table 2. Coefficients of empirical formulations proposed by Kim et al. [23,24].

Terms	Coefficients
	T-bar	Flat-bar
C0	−0.1449	−1.5721
C1	2.9787	5.6591
C2	−2.6098	−3.7336
C3	−0.2418	−0.6934
C4	1.2374 × 10−3	−1.8581 × 10−2
C5	1.3470 × 10−3	1.7858 × 10−2
C6	0.8841	1.3546
C7	−0.3361	−0.3482
C8	1.5975 × 10−3	−1.9443 × 10−3
C9	2.7745 × 10−3	0.8850 × 10−3
C10	−7.5919 × 10−3	1.8299 × 10−2
C11	3.2442 × 10−5	−1.2316 × 10−4
C12	4.9670 × 10−5	1.4994 × 10−4
C13	1.3267 × 10−2	−1.8752 × 10−4
C14	−5.4149 × 10−5	−1.6306 × 10−5

. Furthermore, these authors reported a limitation of the range of stiffened panel’s geometry, which was a function of plate slenderness ratio (25) and column slenderness ratio (26).

$$0.7297\le \beta \le 3.4181$$

(25)

$$0.1240\le \lambda \le 0.0462{\beta }^2-0.3104\beta +1.1898$$

(26)

$$\frac{I_{pz}}{I_{sz}}=\frac{t_p{b}^3}{h_w{t}_w^3+t_f{b}_f^3}$$

(27)

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\left[\begin{array}{l}{c}_0+\left(c_1+c_2\sqrt{\lambda }+\frac{c_3}{\beta }+c_4\frac{h_w}{t_w}+c_5\sqrt{\frac{I_{pz}}{I_{sz}}}\right)\sqrt{\lambda }+\left(c_6+\frac{c_7}{\beta }+c_8\frac{h_w}{t_w}+c_9\sqrt{\frac{I_{pz}}{I_{sz}}}\right)\frac{1}{\beta }\\ +\left(c_{10}+c_{11}\frac{h_w}{t_w}+c_{12}\sqrt{\frac{I_{pz}}{I_{sz}}}\right)\frac{h_w}{t_w}+\left(c_{13}+c_{14}\sqrt{\frac{I_{pz}}{I_{sz}}}\right)\sqrt{\frac{I_{pz}}{I_{sz}}}\end{array}\right]\le 1.0$$

(28)

The ultimate compressive strength of the stiffened panels can be approximated by the following empirical formula [25,26,27]:

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{\sqrt{C_1+C_2{\lambda }^2+C_3{\beta }^2+C_4{\lambda }^2{\beta }^2+C_5{\lambda }^4}}$$

(29)

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{\sqrt{0.960+0.765{\lambda }^2+0.176{\beta }^2+0.131{\lambda }^2{\beta }^2+1.046{\lambda }^4}}$$

(30)

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{\sqrt{0.995+0.936{\lambda }^2+0.170{\beta }^2+0.188{\lambda }^2{\beta }^2-0.067{\lambda }^4}}\le \frac{1}{{\lambda }^2}$$

(31)

A semi-analytical formula (32) for ultimate compressive strength assessments of stiffened panels was proposed by Zang and Khan [28] with the restriction as long as β = 1, if β < 1. This formula is for the next parameters β < 5 and λ < $\sqrt{2}$. Zang and Khan’s formula was applied by the classification society Lloyd’s Register to carry out a comprehensive analysis on the ultimate strength of stiffened panels [21]. By regarding non-linear FEM simulations, Zang and Khan [28] modified the parameter values of the plate slenderness and column slenderness ratio expression taking β = 1.25, if β < 1.25. Thus, this formula is now for β < 5 and λ < 1.0.

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{{\beta }^{0.28}\sqrt{1.0+{\lambda }^{3.2}}}for\lambda \le \sqrt{2}rangeonly$$

(32)

Xu et al. [22,29] proposed an empirical formulation (33) with ten coefficients (X₀–X₁₀). The formulation considers the influence of lateral pressure in the ten finalized coefficients (X₀–X₁₀) and its values are given in function of the water head in meters (h) and stiffener type. These coefficients for the angle-bar stiffener are show in (34). We determined the ultimate axial compression strength with the water head of cero meters and considering the final equation for angle-bar stiffened panel as (35) with water head of cero meters (h = 0).

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{\sqrt{\left(X_0+X_1\lambda +X_2\beta +X_3\lambda \beta +X_4{\lambda }^2+X_5{\beta }^2+X_6{\lambda }^2{\beta }^2+X_7{\lambda }^3+X_8{\beta }^3+X_9{\lambda }^3{\beta }^3+X_{10}{\lambda }^4\right)}}\le \frac{1}{{\lambda }^2}$$

(33)

$$coefficients\{\begin{array}{l}{X}_0=-0.006h^2+0.177h+1.192,X_1=-0.020h^2-0.024h-1.583,X_2=0.013h^2-0.256h-0.355,\\ X_3=0.028h^2-0.165h+0.289,X_4=-0.019h^2+0.375h+3.407,X_5=-0.009h^2+0.125h+0.462,\\ X_6=-0.009h^2+0.076h-0.018,X_7=0.026h^2-0.389h-2.260,X_8=0.001h^2-0.017h-0.084,\\ X_9=0.001h^2-0.007h-0.002,X_{10}=-0.007h^2+0.100h+0.456\end{array}$$

(34)

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{\sqrt{\left(\begin{array}{l}1.192-1.583\lambda -0.355\beta +0.289\lambda \beta +3.407{\lambda }^2+0.462{\beta }^2\\ -0.018{\lambda }^2{\beta }^2-2.260{\lambda }^3-0.084{\beta }^3-0.002{\lambda }^3{\beta }^3+0.456{\lambda }^4\end{array}\right)}}\le \frac{1}{{\lambda }^2}$$

(35)

Kim et al. [30] proposed a simple empirical formula (36) as a function of plate slenderness (β) and column slenderness (λ) ratios for the estimation of ultimate strength performance of stiffened panels. In this empirical formula, four plate slenderness ratios (i.e., β = 1.0023, 1.4834, 2.0046, and 2.4723), and 0.0 ≤ λ < 5.0 range of column slenderness ratios were adopted. Furthermore, the effects of residual strength were not considered. The empirical formula (37) shows good agreement with the ANSYS nonlinear finite element analysis results and is recommended to be used in the range of 0.5 ≤ λ < 5.0 and in the case of relatively small values of column slenderness ratio (λ).

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{C_1+e^{{\lambda }^2}}+\frac{1}{C_2+e^{\sqrt{\beta }}}$$

(36)

$$\frac{{\sigma }_{xu}}{{\sigma }_{Yeq}}=\frac{1}{0.8884+e^{{\lambda }^2}}+\frac{1}{0.4121+e^{\sqrt{\beta }}}$$

(37)

Unstiffened plates are the main structural components of ships and the ultimate strength of these elements is key for the design and safety of ships [31]. The ultimate strength model of unstiffened plates can be considered is a simply supported long plate subjected to axial compressive loads. These loads can be applied at short edges of the plate when a ship is under vertical bending moments. Useful formulations have been developed under simple supported plate and the formulation (38) proposed by Faulkner [32] shows good agreement with extensive experimental data and with non-linear FEM simulations [21]. The ultimate strength of unstiffened plates can be influenced by initial imperfections and Faulkner’s formulation is used for the average geometrical initial imperfections [28,32]:

$$\frac{{\sigma }_{xu}}{{\sigma }_Y}=\frac{2}{\beta }-\frac{1}{{\beta }^2}$$

(38)

Initial imperfections such as the effects of welding distortions and residual stresses on the ultimate compressive strength of unstiffened plates were studied by Cui and Mansour [31]. The ultimate strength of the imperfect plate (ϕ_u = σ_xu/σ_Y) is a function of the aspect radio (α = a/b), plate slenderness (β), and normalized residual stress (η = −σ_rc/σ_Y). The effect of welding residual stresses (−σ_rc) on the progressive collapse behavior of a Suezmax class double hull tanker hull proved that the effect of welding residual stresses of plates on an ultimate hull girder strength is small [31]. Based on the results of Cui and Mansour [31], the ultimate strength (${\varphi }_u$) equation of an imperfect plate is given by Equation (39):

$${\varphi }_u={\varphi }_{up}{R}_d{R}_r$$

(39)

$${\varphi }_{up}=\{\begin{array}{ll}1& if\beta \le 1.9\\ 0.08+\frac{1.09}{\beta }+\frac{1.26}{{\beta }^2}& if\beta >1.9\end{array}$$

(40)

$$R_d=1-0.2433f\left(\alpha \right)g\left(\beta \right){\psi }_{0\max }^{0.911}$$

(41)

$$f\left(\alpha \right)=2.05-1.376\alpha +0.366{\alpha }^2-0.0345{\alpha }^3$$

(42)

$$g\left(\beta \right)=\{\begin{array}{ll}2.28-2.568\beta +1.288{\beta }^2& for1.0\le \beta \le 1.9\\ 8.191-4.224\beta +0.522{\beta }^2& for1.9<\beta \le 2.5\\ 4.593-2.162\beta +0.273{\beta }^2& for2.5<\beta \le 4\end{array}$$

(43)

$${\psi }_{0\max }=\{\begin{array}{ll}0.1{\beta }^2& 1\le \beta \le 2.5\\ 0.25\beta & 2.5<\beta \le 4\end{array}$$

(44)

$$Rr=1-0.46{(\beta -1.5)}^{0.275}{\eta }^{0.725}$$

(45)

Kim et al. [33] proposed an advanced empirical formulation (46) to predict the ultimate strength of initially deflected steel plate subjected to longitudinal compression. This formulation was proposed with two parameters for plate element, which is a function of plate slenderness ratio (β) and coefficient of initial deflection index (IDI) (see

Table 3. Sub-coefficients of IDI obtained with slight level until severe level of deflection.

${\mathit{C}}_{\mathit{I}\mathit{D}}$	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
0.025 (slight level)	−10.749	31.246	−37.009	0.480
0.05	−2.948	8.138	−13.839	−0.368
0.10 (average level)	−0.029	0.322	−4.680	−0.745
0.15	0.735	−1.554	−2.172	−0.859
0.20	1.064	−2.321	−1.060	−0.912
0.25	1.241	−2.719	−0.448	−0.943
0.30 (severe level)	1.349	−2.956	−0.068	−0.963

). The IDI consists of four sub-coefficients (c₁, c₂, c₃, and c₄) as shown in Equation (47) and considers different levels of initial deflection in the empirical formulation. The empirical formula of the ultimate strength for steel plate, obtained by Kim et al. [33], is expressed as:

$$\frac{{\sigma }_{xu}}{{\sigma }_Y}=1-{\mathrm{e}}^{IDI}$$

(46)

$$IDI=\frac{c_1}{\beta }+\frac{c_2}{{\beta }^2}+\frac{c_3}{{\beta }^3}+c_4$$

(47)

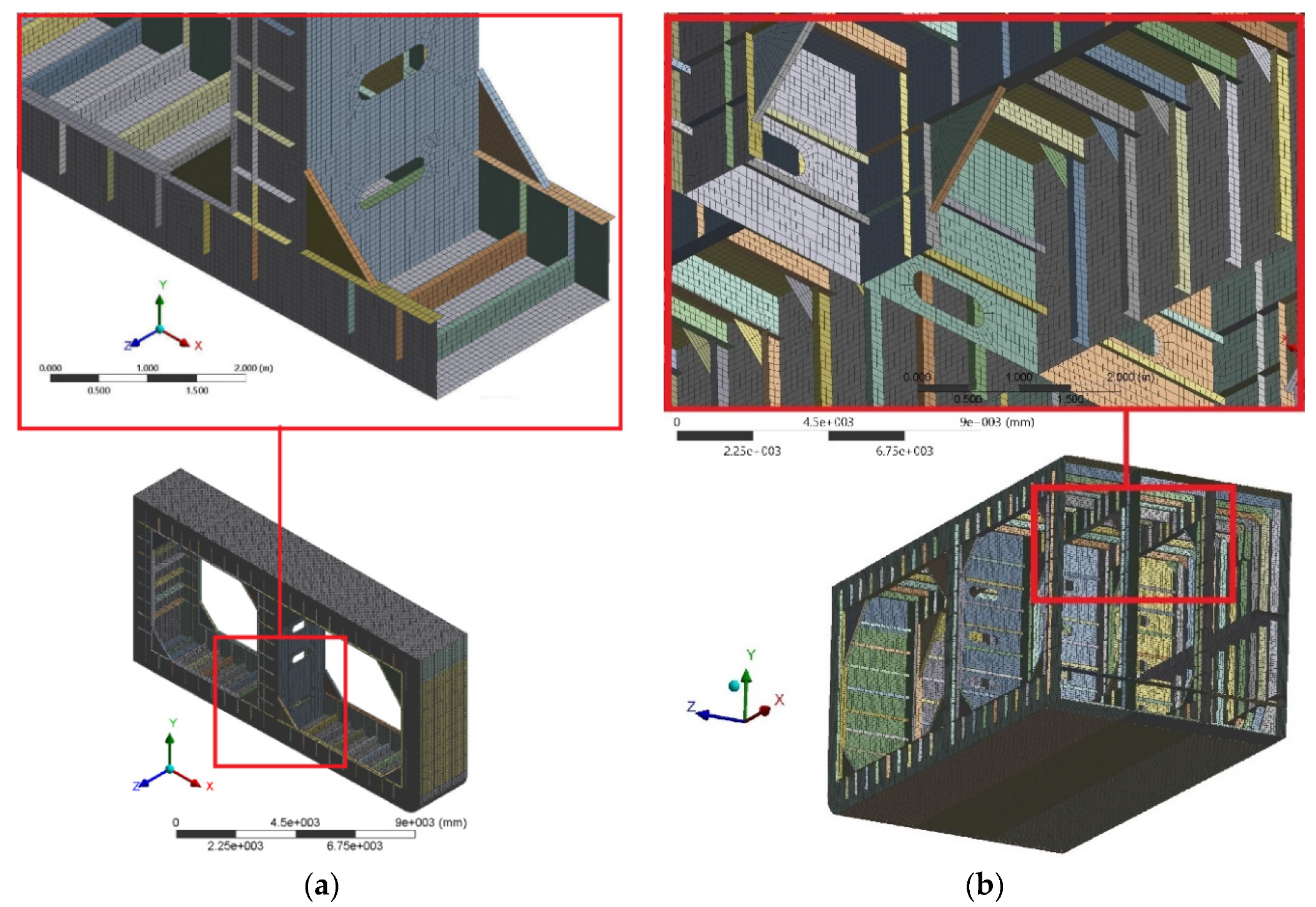
4. FEM Models of Midship Section

Figure 7 depicts a FEM model of the barge midship section used for its structural analysis, which was developed using the ANSYS 2017 Workbench software. This model included the cargo tanks with their longitudinal hull structural elements previously verified with Lloyd’s Register rules. In addition, the FEM model considered the port and starboard sides of the tanks, overall depth and transversal frames at the ends. Furthermore, this model added the internal structure (grade A36, tensile stress 400 MPa) of the midship section formed by the transversal bulkheads, longitudinal bulkheads in the tanks and all main longitudinal and transverse structural elements.

The FEM model used the real geometry of the cargo tanks, applying uniform mesh that included the reinforcement system with plate elements. In general, the mesh of the plate elements must comply the following minimum requirements [34]:

(i)

The length of one mesh element between each longitudinal stiffener must not be greater than two longitudinal spaces.

(ii)

The free edge on large brackets of the primary members must have a fine mesh to avoid unreal high stress due to discontinuities in geometry. In general, a mesh size equal to the spacing of the stiffener is recommended.

Figure 8 depicts the mesh in the common structure between two transverse frames of the cargo tanks and the longitudinal bulkhead. Shell elements were generated to solve the model, with an average size of 70 mm. This modeling resulted in a very fine mesh: the final model includes approximately 1,254,906 nodes and 1,271,880 shell elements. The mesh quality has an element quality with the values between 0.192 and 0.999 and an average of 0.973 of which 92.7% has a value of 0.959. The mesh quality has an aspect ratio with the values between 1 and 2.778 and an average of 1.078 of which 86.6% has a value of 1.09.

4.1. Verification of the FEM Model

The FEM model of the midship section must satisfy the criteria and requirements of the classification societies [6,7]. For this, the ABS and Lloyds’s Register criteria [12,13] were considered to check the FEM model. These criteria include an aspect ratio on the shell elements less than three and the use of triangular elements should be minimum. Furthermore, the aspect ratio of plate elements in high stress regions of the FEM model must be close to one and the use of triangular elements must not be allowed. The verification of the FEM model includes the following basic specifications [13]:

Material definitions: modulus of elasticity, Poisson’s ratio, and material density are defined in a coherent system of units.

(i)

Element thickness: the total thickness of the plate is correctly defined. Duplicate elements can cause incorrect plate thickness and element properties.

(ii)

Element shape: model elements should be examined in unconnected free edges, nodes, and coincident elements.

(iii)

Commonly, the tolerance limits of the model are the follows: aspect ratio should be less than 3, taper should be less than 10, warping should be less than 5 degrees, internal angle should be not less than 30 degrees, no free edge caused by wrong element connectivity, and coincident (duplicated) nodes should be checked and merged.

4.2. Total Vertical Bending Moment

The total vertical bending moments calculated with (18) were applied to the FEM model using multipoint constraints (MPCs) in ANSYS software for sagging and hogging conditions. The MPCs allow the connection of different nodes and degrees of freedom together for the FEM analysis. Figure 9 illustrates these MPCs used in the two ends of the midship section to apply the bending moments. Figure 10 shows the direction of the total vertical bending moment for sagging condition using the IACS convection signs [18]. The value of the total vertical bending moment (906.88 × 10⁶ Nm) was applied in all the longitudinal stiffeners and hull located in the ends of the FEM model.

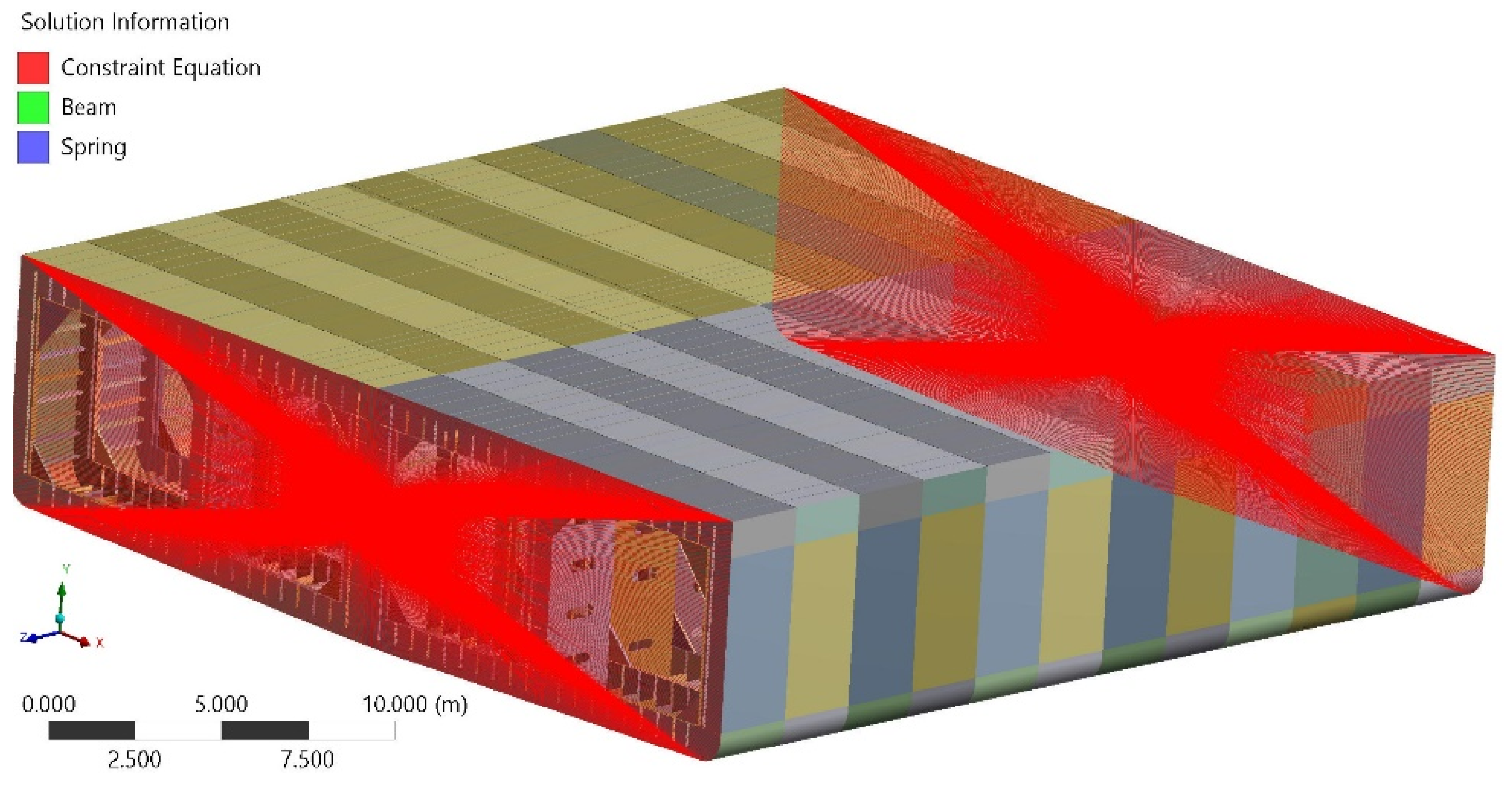
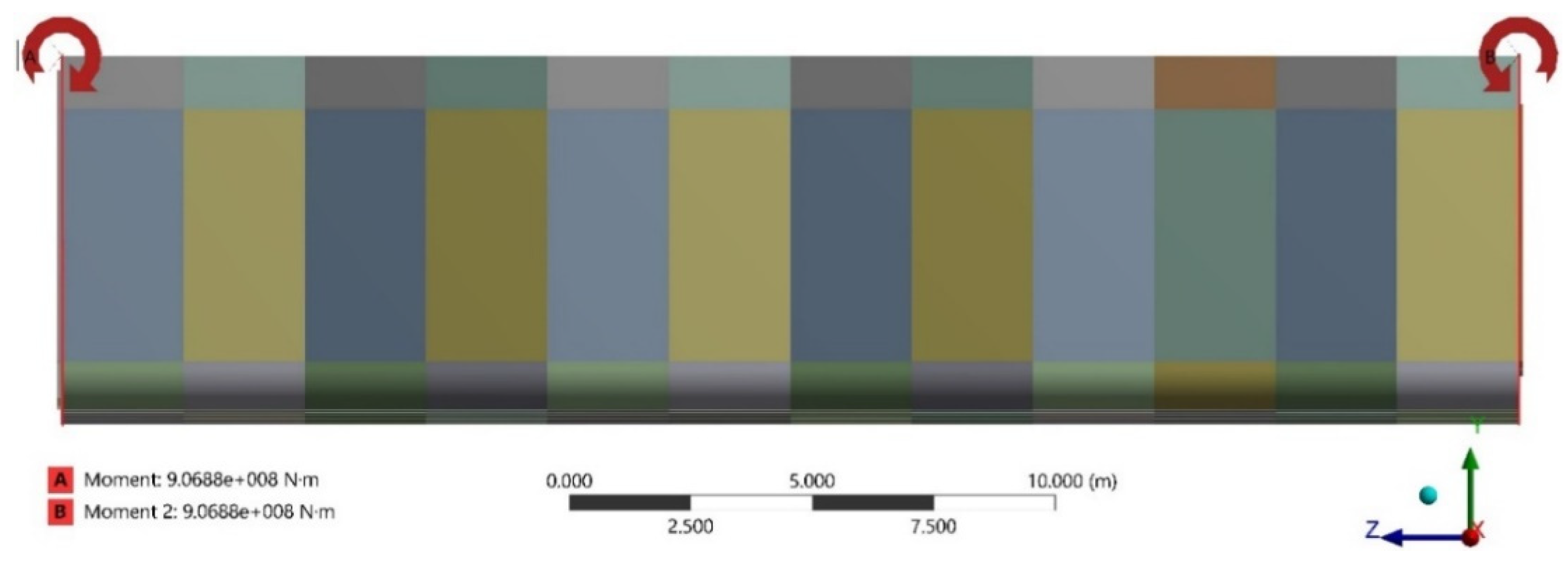
4.3. Boundary Conditions

The boundary conditions of the FEM model allow a bending behavior for different longitudinal resistance loads. In case of longitudinal resistance, no other loads should be applied to the FEM model [35].

The planes at the ends (fore and aft) of the FEM model must remain flat under the action of the bending moment while the cross-section must be able to rotate freely [35]. For this purpose, all nodes related to the continuous longitudinal stiffeners at the ends of the model must be rigidly linked to an independent point. The independent point was located on the center line at a height close to the position of the neutral axis. These independent points are connected to the model by the rigid links and have free rotation only in the x axis, wherein the bending moment is supplied. The required vertical bending moment was applied to the independent point at each end of the model, as shown in Figure 9.

4.4. Utilization Factor

The utilization factor (λ_y) of the midship section is determined using the von Mises stress results of the structural analysis of the FEM model [34]. This factor is obtained as the ratio of von Mises stress (σ_vM) to yield stress (σ_yd) of the midship section material and it must not overcome to 0.9 for a safe operation of the barge. Thus, the stress results of the structural members of the central tank must satisfy this condition for the utilization factor. The yield stress of the structural members material is 250 MPa.

5. Results and Discussion

The structural assessment of the barge midship section was made complying with Lloyd’s Register rules. With this assessment, the maximum bending stress at strength deck plate and bottom plate was determined, which were compared to permissible yield stress. The results of the stress distribution on the midship section allow to know the barge ability to withstand the loads applied on the deck.

The classification societies recommend the beam theory to obtain the stresses in the deck and bottom plates. We compared the results obtained with the beam theory with respect those of the FEM model. This procedure was done considering the central tank region of the FEM model. The theoretical hogging normal stress is 112.24 MPa, which is close to results (85.82 to 114.21 MPa) determined by the FEM model at the deck (see Figure 11b). The maximum hogging normal stress of 142.59 MPa is located at the intersection with the transverse frames. Theoretical sagging (compression) normal stress of 174.23 MPa is close to the results (−131.56 to −175.54 MPa) of the FEM model in the deck (see Figure 11a). The maximum sagging normal stresses of −219.52 MPa is registered at the intersection with the transverse frames. In both cases, the values calculated with (4) and (5) were approximated.

The shear forces and bending moments in still water along barge were calculated with (10) and (11). Figure 12 depicts the distribution of the shear forces and bending moments regarding the sagging and hogging conditions. The most critical condition was sagging due to the location of the load near the midship section. In addition, the wave bending moment was calculated with (15) and it is plotted using black line, and the total bending moment is obtained with (18) and it is illustrated with orange line (see Figure 12b,c). The total calculated sagging and hogging bending moments were 906.88 × 10⁶ Nm and 599.10 × 10⁶ Nm, respectively.

Table 4. Bending moments (tonm units) of the barge calculated considering still water and wave load.

Condition	Wave	Still Water		Total	Status
	MW	MS	$\left|\overline{M_S}\right|$	MV	$\left|M_S\right|\le \left|\overline{M_S}\right|$
Sagging	−55583	−36861	43610	−92444	OK
Hogging	50102	10968	44702	61070	OK

indicates the bending moments of the barge calculated by regarding still water and wave load. The value of the bending moment in still water satisfies the relation established by (14). When this value is unknown, the higher value of Equations (12) and (13) can be used for the structural evaluation of the barge midship section. We observed that the most critical condition for the vessel is sagging with a total vertical moment 33.93% greater than the hogging.

Table 5. Parameters of barge determined using Lloyd’s Register rules.

Section Modulus (m3)			Moment of Inertia (m4) at Midship Section		Deck Plate Thickness (mm)		Status
ZD	ZB	Zmin	INA	Imin	t	tmin
5.338	5.974	4.961	21.426	17.247	14	9.562	OK
Hull Vertical Bending Stresses (MPa)
Results			Permissible
Condition	${\sigma }_D$	${\sigma }_B$	$\sigma$
Sagging	174.23	155.68	182.29				OK
Hogging	112.24	100.28	182.29				OK

shows the calculations made with the Lloyds’s Register rules. These calculations included the required minimum thickness of the deck plates (t_min), the section modulus, the moment of inertia and the normal stresses of the hull at deck and bottom under sagging and hogging conditions.

The displacements and von Mises stresses of the FEM model were estimated under the action of both sagging and hogging bending moments (see Figure 13a,b). Figure 13 depicts the displacements in y-direction of the FEM model. The maximum displacement of the midship section with sagging condition was 10.95 mm at the ends and 9.85 mm at the side shell center, respectively.

The maximum von Mises stresses of the central tank FEM model under sagging and hogging conditions were 215.53 MPa and 138.83 MPa, respectively (see Figure 14). The results satisfy the criterion of yield utilization factor (see

Table 6. Results of the FEM model of the barge midship section.

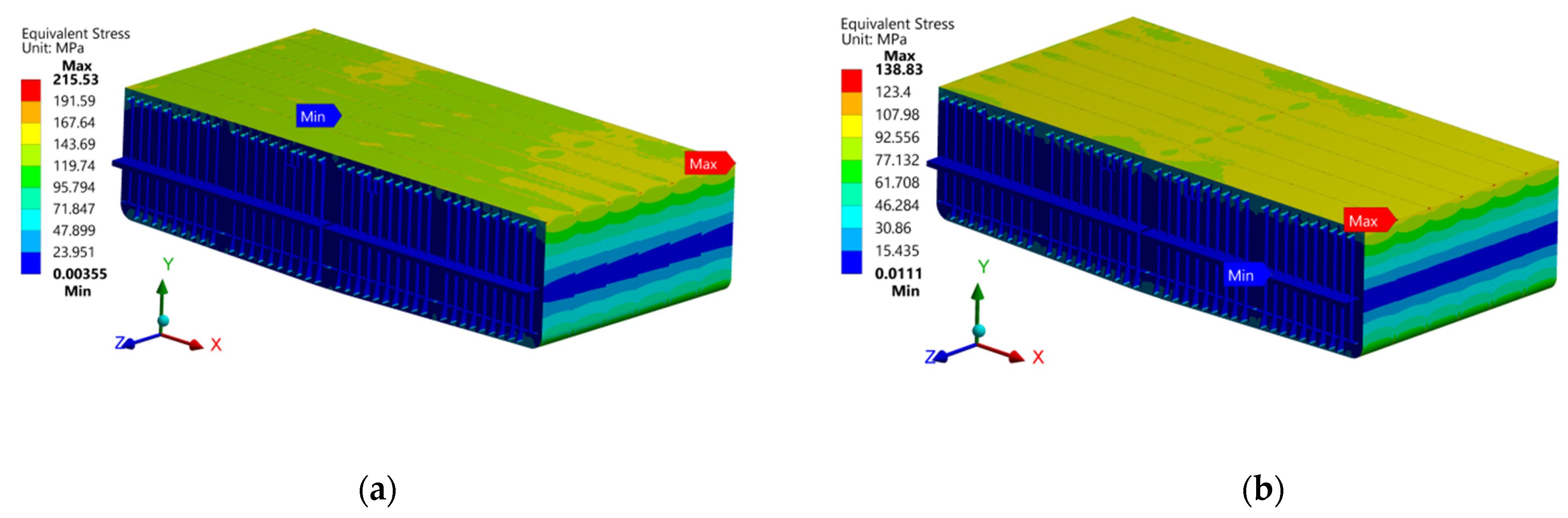
Maximum Stress			Yield Utilization Factor		Status
Condition	Yield stress (MPa) [6,11]	von Mises stress (MPa)	Design	Permissible [34]
Sagging	250	215.53	0.86	0.9	OK
Hogging	250	138.83	0.55	0.9	OK

). The values of the yield utilization factor in sagging and hogging conditions are 0.86 and 0.55, respectively. These values are below the limit value (0.9) of utilization factor. Furthermore, the von Mises stresses did not overcome the yield stress of the barge material (yield strength 250 MPA, Grade A36).

The ultimate compressive stresses in stiffened panels and unstiffened plates were calculated with empirical formulas and with Lloyd’s Register rules. Thus, these compressive stresses were compared with working stresses. The working stresses were determined using FEM for as-built panels.

Table 7. Parameters of stiffened panel with angle-bar stiffener at deck and bottom and related properties of barge.

Parameter	Value		Unit	Details
	Deck	Bottom
$a$	2500	2500	mm	Length of stiffener and plate
$b$	700	700	mm	Breadth of plate
$b_f$	90	90	mm	Breadth of flange
$t_f$	17.4	17.4	mm	Thickness of flange
$h_w$	282.6	282.6	mm	Height of web
$t_w$	17.4	17.4	mm	Thickness of web
$t_p$	14	22	mm	Thickness of plate
$r$	108.733	100.784	mm	Radius of gyration
$\lambda$	0.2588	0.2792	−	Column slenderness ratio
$\beta$	1.7678	1.1249	−	Plate slenderness ratio
${\sigma }_{Yp}$	250	250	MPa	Yield strength of plate
${\sigma }_{Yeq}$	250	250	MPa	Equivalent yield strength
$E$	200	200	GPa	Elastic modulus

indicates the parameters and values of the scantlings of stiffened panels at deck and bottom, plate slenderness, stiffener slenderness, and radius of gyration.

The advanced formulation by Kim et al. [33] was used to calculate the ultimate compressive stresses in plates with slight and severe deflection. The results of compressive stresses with slight and severe deflection were 206.30 MPa and 264.71 MPa, respectively. In addition, the results of the empirical formulas of Falkner [32], Cui and Mansour [31], and Lloyd’s Register rules show intermediate values of Kim’s compressive stresses.

Table 8. Summary of ultimate strength and working stresses of stiffened panels of barge.

Panel	Ultimate Strength Compressive Stresses $\left(\mathbf{MPa}\right)\mathbf{Empirical}\mathbf{Formulation}{\mathit{\sigma }}_{\mathit{x}\mathit{u}}$		Working Stresses (MPa) $\mathbf{FEM}{\mathit{\sigma }}_{\mathit{x}}$	$\frac{{\mathit{\sigma }}_{\mathit{x}\mathit{u}}}{{\mathit{\sigma }}_{\mathit{x}}}$
Deck (sagging)	Lin [25]	198.06	175.54	1.13
	Paik and Thayamballi [26,27]	195.94	175.54	1.12
	Zhang and Khan [28]	211.74	175.54	1.21
	Xu et al. [29]	207.34	175.54	1.18
	Kim et al. [30]	187.35	175.54	1.07
	Kim et al. [23]	208.86	175.54	1.19
	Lloyd’s Register [6]	248.35	175.54	1.41
Bottom (hogging)	Lin [25]	222.58	112.84	1.97
	Paik and Thayamballi [26,27]	219.16	112.84	1.94
	Zhang and Khan [28]	239.88	112.84	2.13
	Xu et al. [29]	235.82	112.84	2.09
	Kim et al. [30]	202.69	112.84	1.80
	Kim et al. [23]	232.71	112.84	2.06
	Lloyd’s Register [6]	248.08	112.84	2.20

indicates the ultimate compressive stresses and working stresses for stiffened panels.

Table 9. Summary of ultimate strength and working stresses of unstiffened plates of barge.

Plate	Ultimate Strength Compressive Stresses (MPa) $\mathbf{Empirical}\mathbf{formulation}{\mathit{\sigma }}_{\mathit{x}\mathit{u}}$		$\mathbf{Working}\mathbf{Stresses}\left(\mathbf{MPa}\right)\mathbf{FEM}{\mathit{\sigma }}_{\mathit{x}}$	$\frac{{\mathit{\sigma }}_{\mathit{x}\mathit{u}}}{{\mathit{\sigma }}_{\mathit{x}}}$
Deck (sagging)	Faulkner [32]	202.84	175.54	1.16
	Cui and Mansour [31]	209.07	175.54	1.19
	Kim et al. (severe level) [33]	171.48	175.54	0.98
	Kim et al. (average level) [33]	199.44	175.54	1.13
	Kim et al. (slight level) [33]	224.96	175.54	1.28
	Lloyd’s Register [6]	195.75	175.54	1.12
Bottom (hogging)	Faulkner [32]	246.92	112.84	2.19
	Cui and Mansour [31]	224.19	112.84	1.99
	Kim et al. (severe level) [33]	220.80	112.84	1.96
	Kim et al. (average level) [33]	245.57	112.84	2.17
	Kim et al. (slight level) [33]	249.99	112.84	2.22
	Lloyd’s Register [6]	228.03	112.84	2.02

depicts the ultimate compressive stresses and working stresses for unstiffened plates.

6. Conclusions

The structural behavior of a barge’s midship section was studied using Lloyd’s Register rules and FEM modeling. The thickness of this midship section has decreased 36.4% from its original deck thickness (22 mm) due to corrosion. This structural performance was determined with different sagging and hogging conditions, considering the barge and cargo weights, and wave loads. The ultimate compressive strengths of the midship decks and bottom plates were calculated with empirical formulas for stiffened panels and unstiffened plates. The maximum compressive working stresses on deck and bottom plates were 175.53 MPa and 112.84 MPa, respectively. These ultimate strength results registered a safe structural performance of both stiffened and unstiffened plates, except for the severe deflection formulas of Kim et al. [33] at unstiffened deck plates. However, ultimate strength results of average deflection formulas of Kim et al. [33] showed good strength at unstiffened deck plates. The ultimate strength performance of the stiffened deck panel was decreased 42.40% and 35.91% due to corrosion, calculated with empirical and Lloyd’s Register rules, respectively. The von Mises stress in sagging and hogging conditions at deck plates were 215.53 MPa and 138.83 MPa, respectively. The results of the structural behavior of the total hull girder, taking into consideration the corrosion decrease along the deck plate, are suitable to ensure a safe performance.

The methodology proposed for the structural analysis of hull girder of a barge midship section allowed to determine its maximum normal stresses and von Mises stress. Future research work will include the simulation of stiffened panel of barge using non-linear FEM methods.