Numerical Investigation of Shallow Liquid Sloshing in a Baffled Tank and the Associated Damping Effect by BM-MPS Method
Abstract
:1. Introduction
2. BM-MPS Method
2.1. Basic Algorithm of MPS Method
2.2. BM-Scheme for the Calculation of Source Term of PPE
2.3. A high-Order Pressure Gradient Model
2.4. Boundary Conditions
3. Results
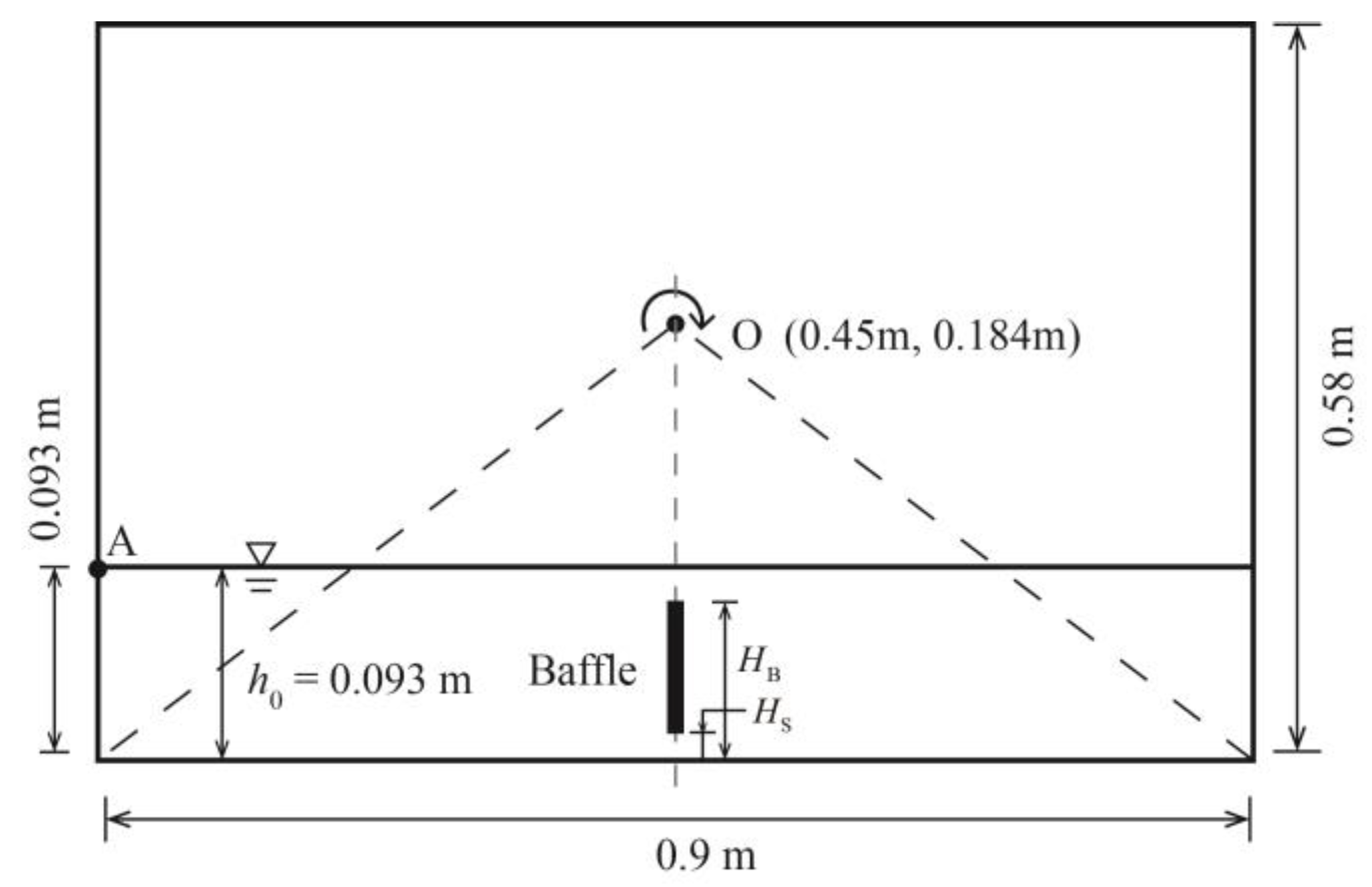
3.1. Calculation Conditions
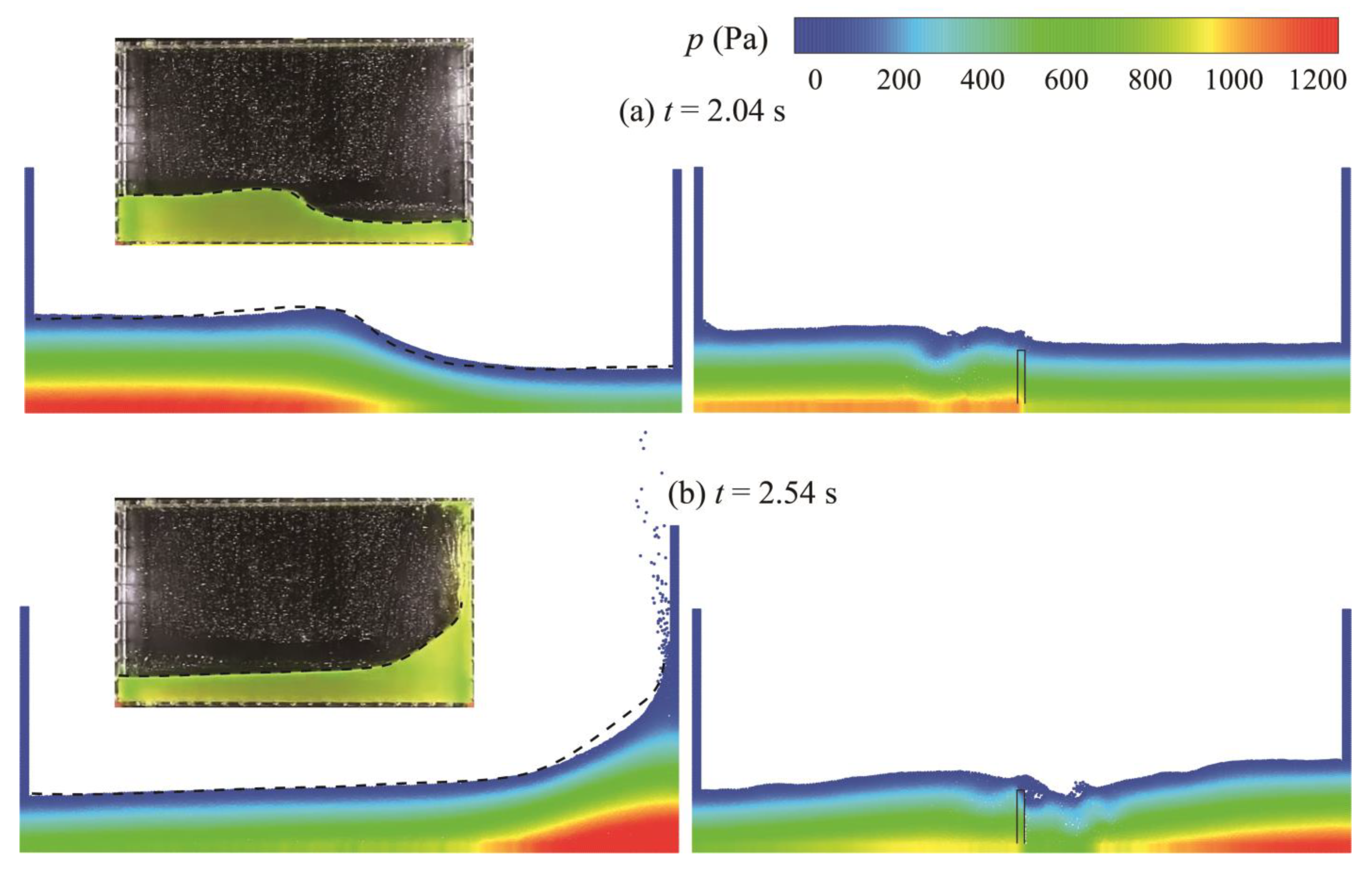
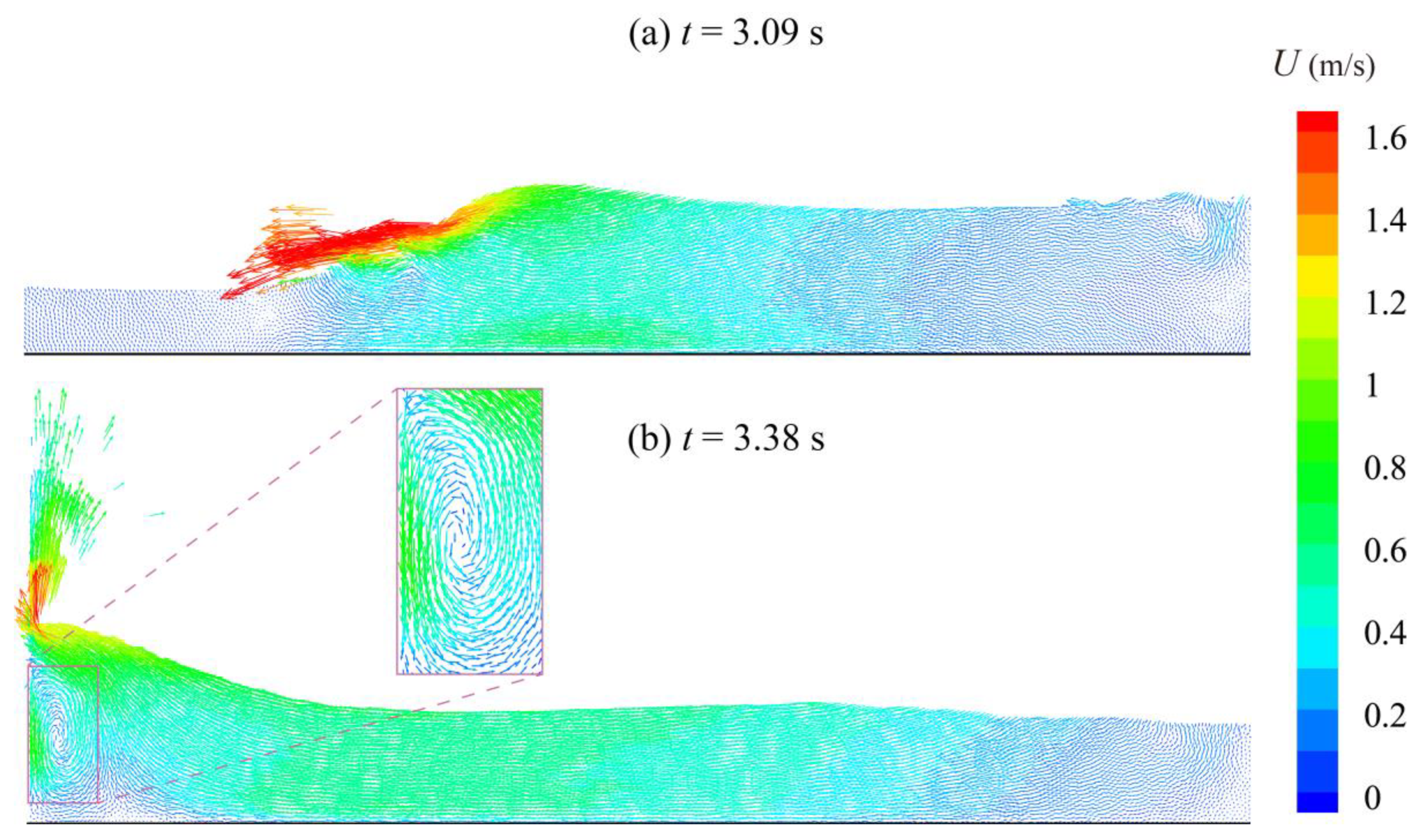
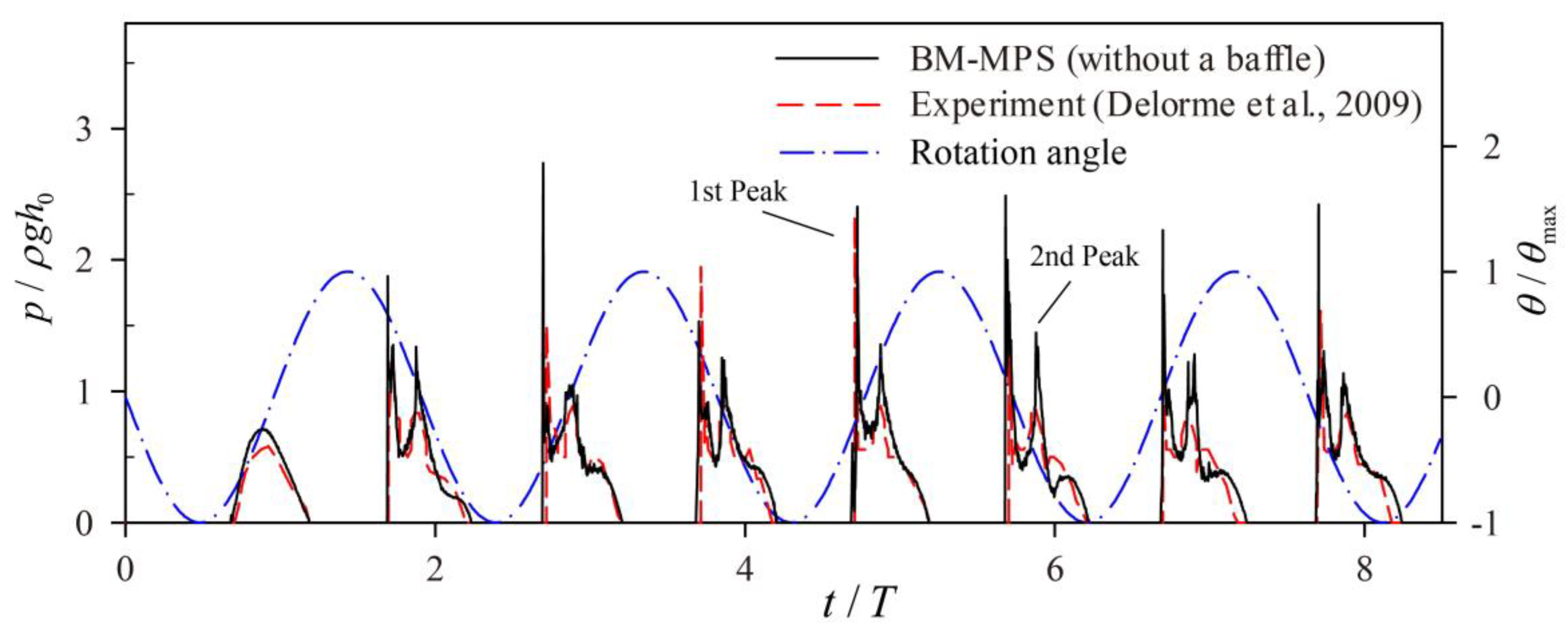
3.2. Sloshing Simulated by BM-MPS
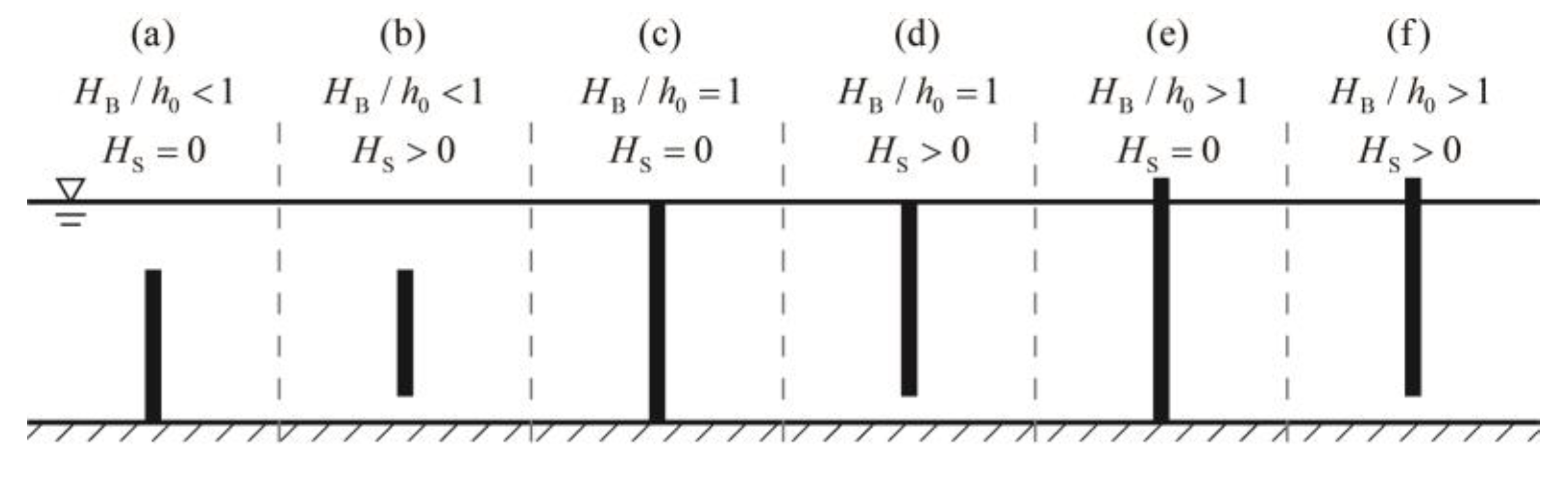
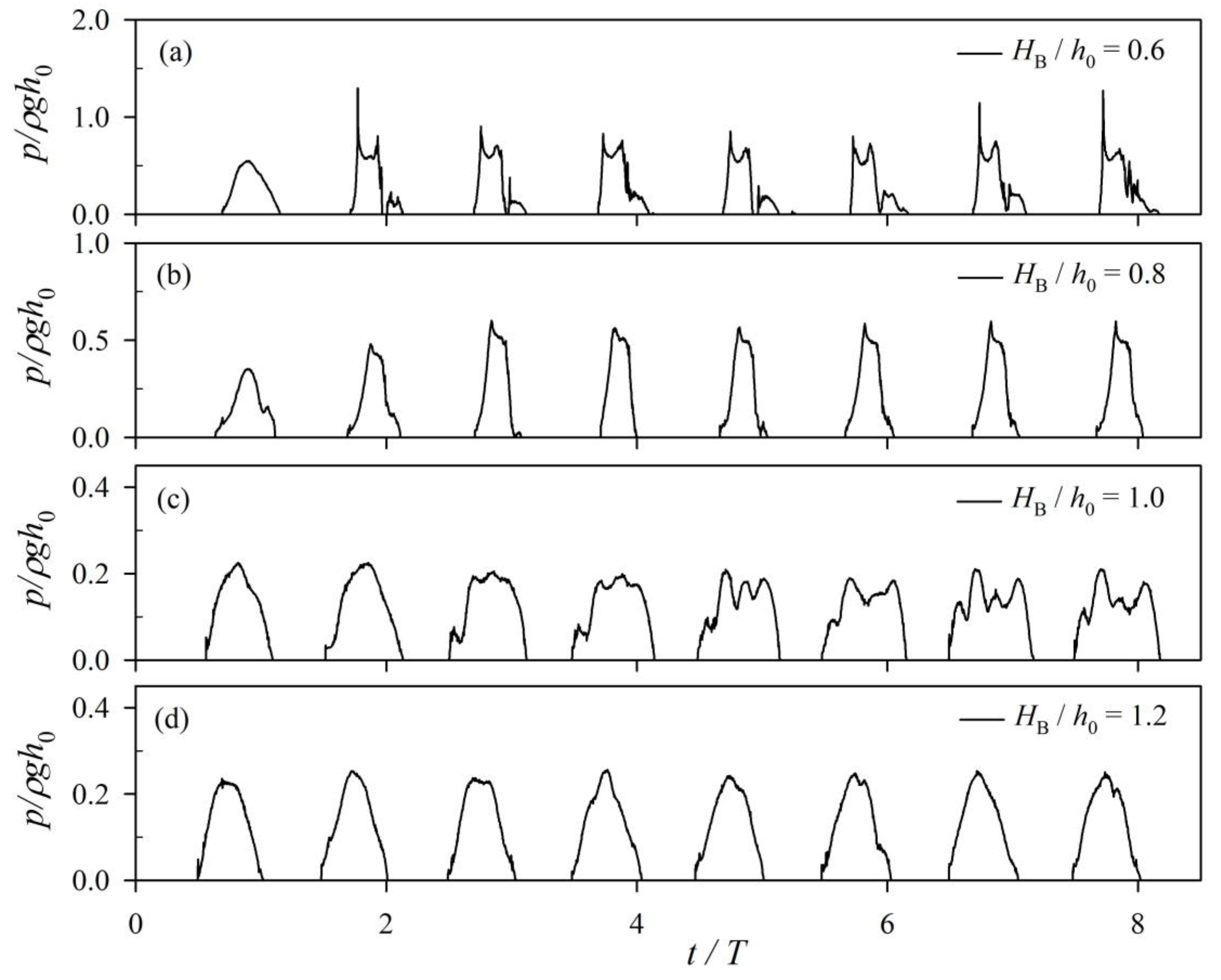
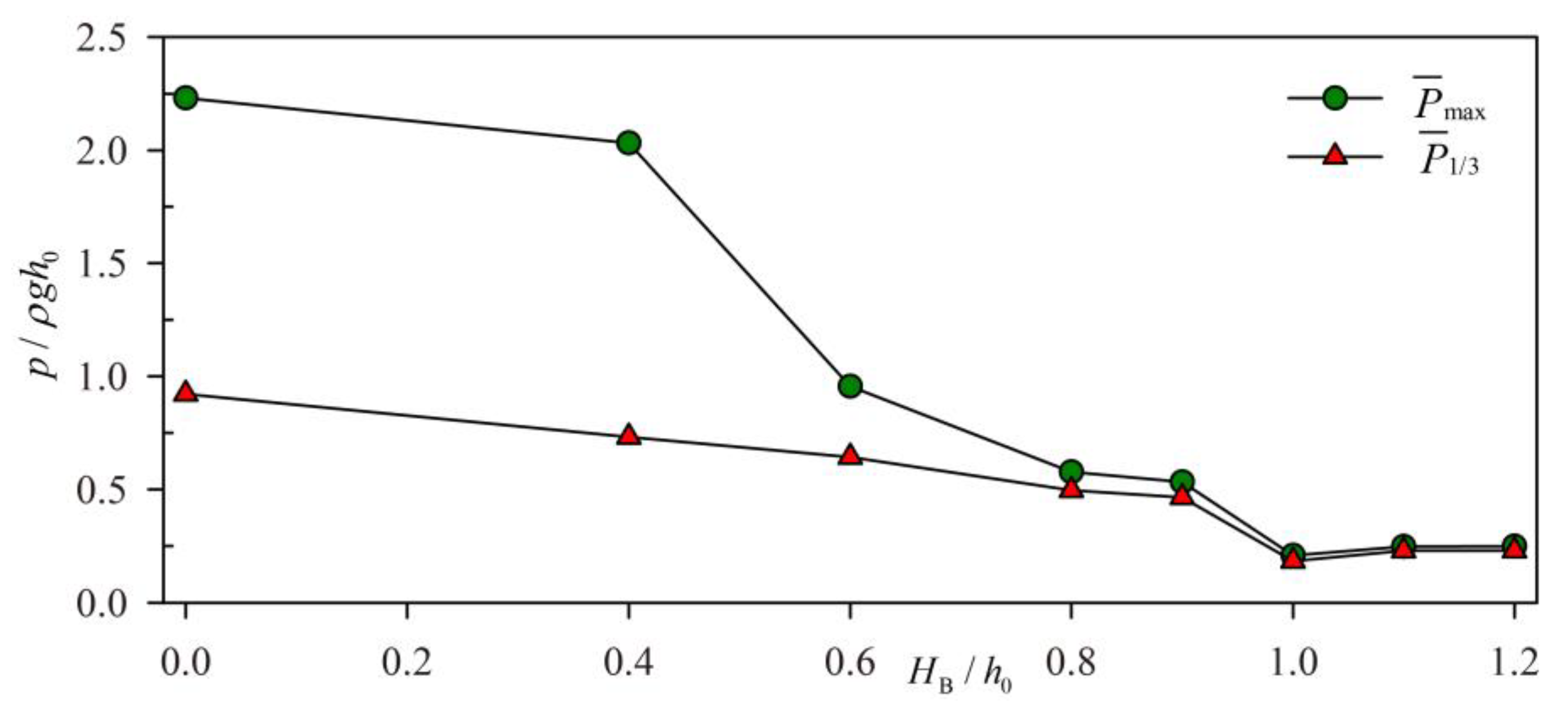
3.3. The Effect of Baffle Height on Restraining Sloshing
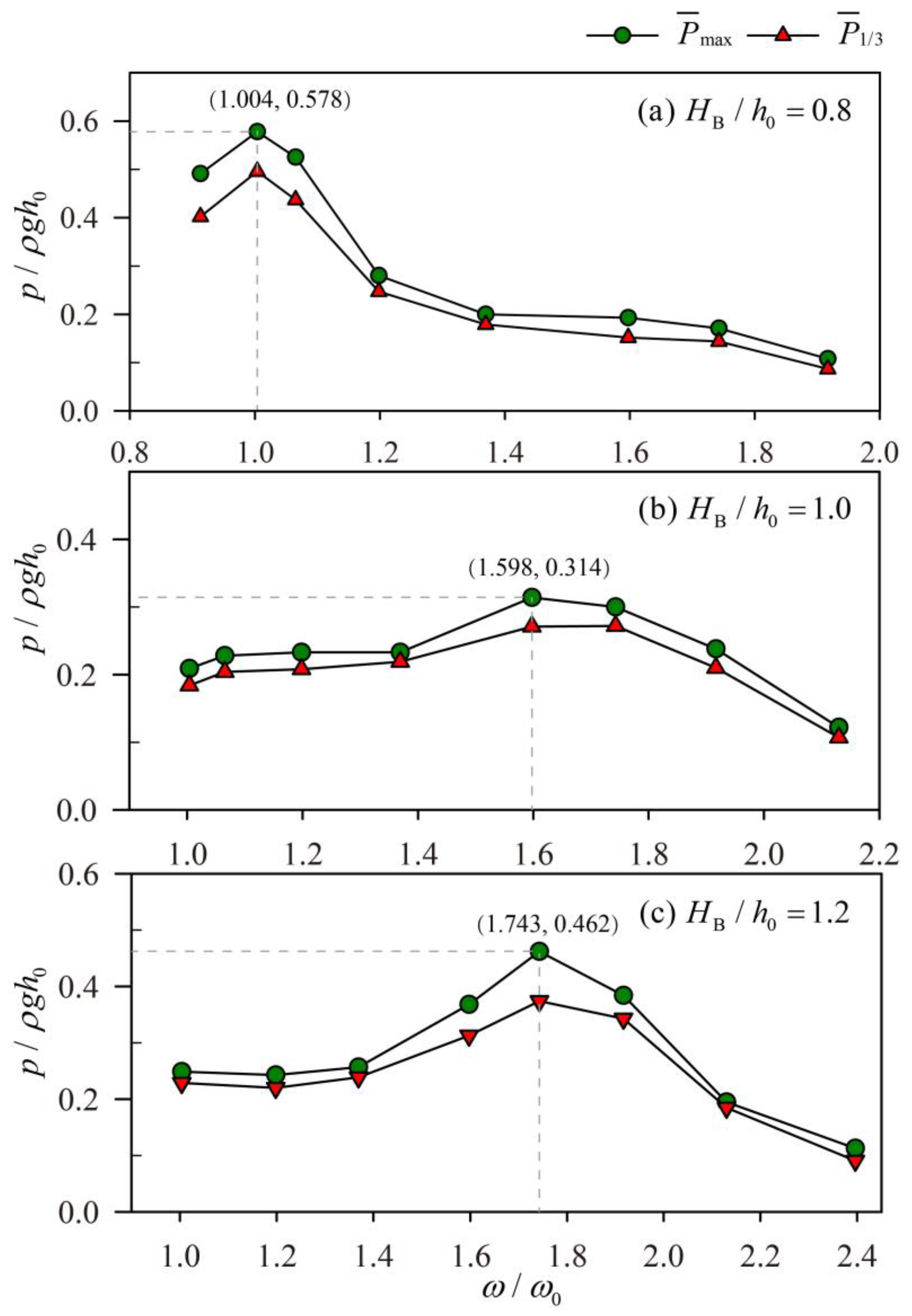
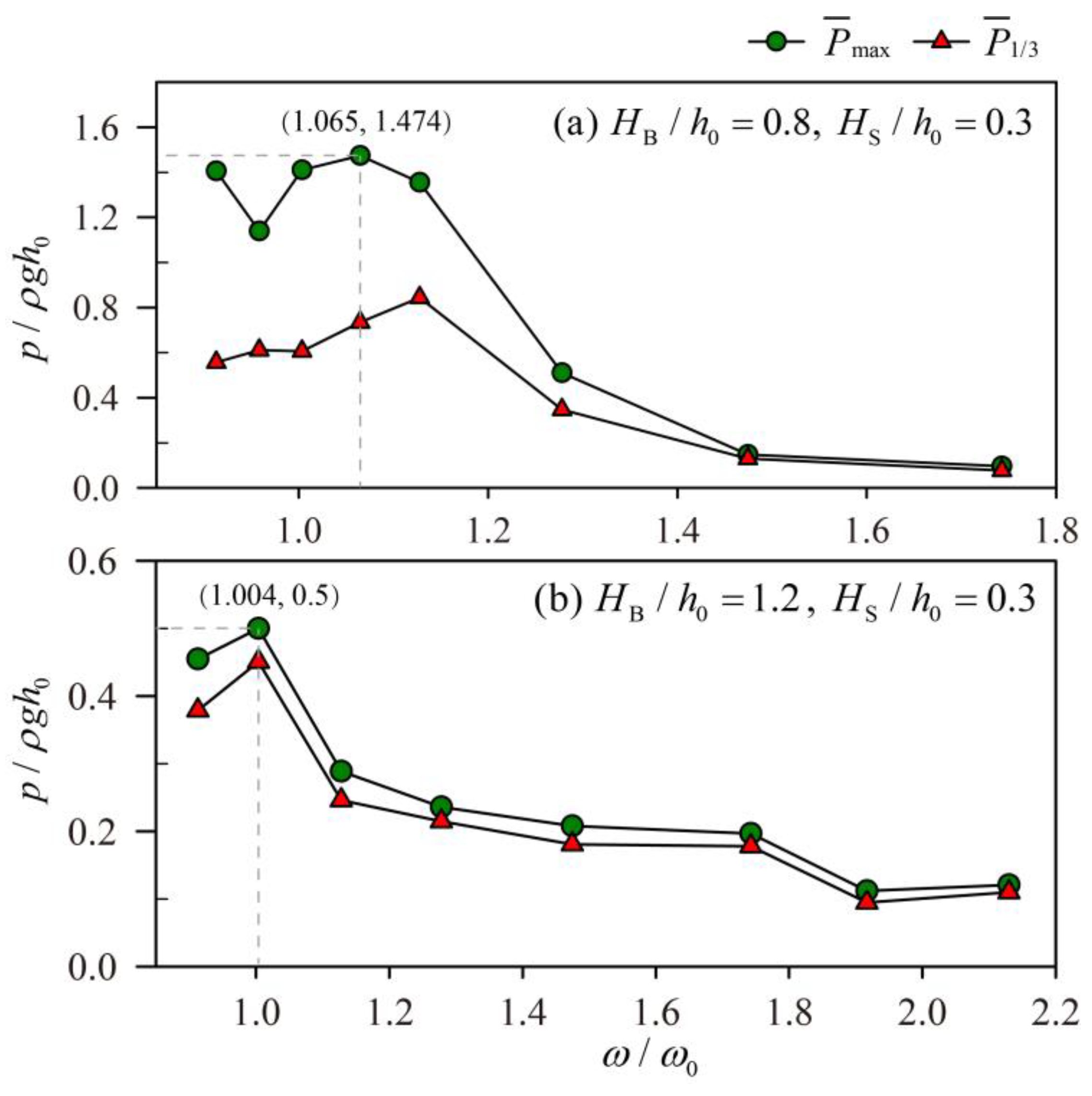
3.4. The Effect of Baffle Height on Resonance
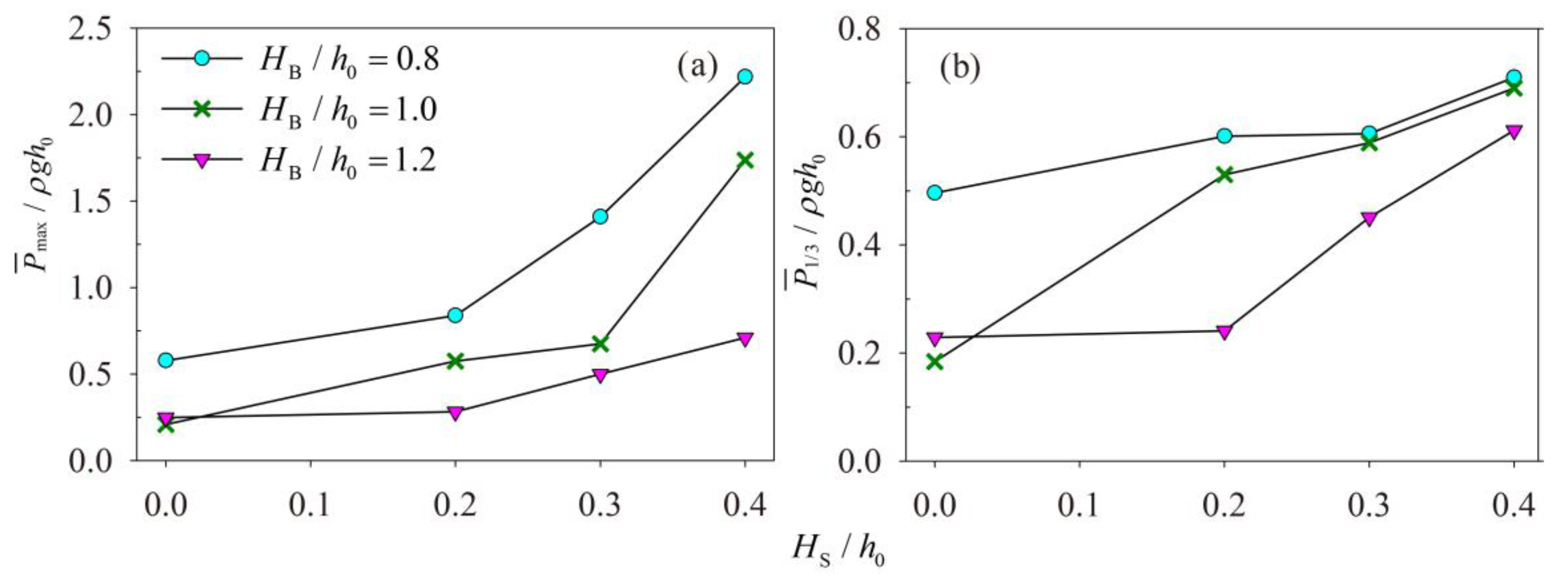
3.5. The Damping Effect of Wall-Mounted Baffles
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| HB/h0 | HS/h0 | T (s) | ω/ω0 | Pmax/ρgh0 | P1/3/ρgh0 | ||
|---|---|---|---|---|---|---|---|
| Maximum | Mean | Maximum | Mean | ||||
| 0 | 0 | 1.91 | 1.004 | 2.736 | 2.231 | 0.981 | 0.921 |
| 0.4 | 0 | 1.91 | 1.004 | 2.467 | 2.032 | 0.779 | 0.732 |
| 0.6 | 0 | 1.91 | 1.004 | 1.298 | 0.955 | 0.668 | 0.643 |
| 0.8 | 0 | 1.91 | 1.004 | 0.602 | 0.578 | 0.532 | 0.496 |
| 0.2 | 1.11 | 0.839 | 0.666 | 0.601 | |||
| 0.3 | 1.594 | 1.41 | 0.667 | 0.606 | |||
| 0.4 | 2.661 | 2.218 | 0.749 | 0.71 | |||
| 0 | 2.1 | 0.913 | 0.567 | 0.491 | 0.497 | 0.402 | |
| 1.8 | 1.065 | 0.561 | 0.525 | 0.467 | 0.437 | ||
| 1.6 | 1.198 | 0.333 | 0.28 | 0.288 | 0.247 | ||
| 1.4 | 1.369 | 0.228 | 0.2 | 0.198 | 0.179 | ||
| 1.2 | 1.598 | 0.213 | 0.193 | 0.167 | 0.152 | ||
| 1.1 | 1.743 | 0.185 | 0.171 | 0.153 | 0.144 | ||
| 1 | 1.917 | 0.128 | 0.108 | 0.099 | 0.087 | ||
| 0.3 | 2.1 | 0.913 | 1.721 | 1.406 | 0.59 | 0.557 | |
| 2 | 0.959 | 1.286 | 1.139 | 0.65 | 0.611 | ||
| 1.8 | 1.065 | 2.528 | 1.474 | 0.771 | 0.735 | ||
| 1.7 | 1.128 | 2.535 | 1.355 | 0.869 | 0.844 | ||
| 1.5 | 1.278 | 0.631 | 0.51 | 0.519 | 0.347 | ||
| 1.3 | 1.475 | 0.212 | 0.148 | 0.157 | 0.13 | ||
| 1.1 | 1.743 | 0.177 | 0.096 | 0.146 | 0.077 | ||
| 0.9 | 0 | 1.91 | 1.004 | 0.576 | 0.533 | 0.506 | 0.465 |
| 1 | 0 | 1.91 | 1.004 | 0.216 | 0.209 | 0.193 | 0.184 |
| 0.2 | 0.617 | 0.575 | 0.552 | 0.53 | |||
| 0.3 | 0.75 | 0.676 | 0.601 | 0.589 | |||
| 0.4 | 2.545 | 1.737 | 0.708 | 0.69 | |||
| 0 | 1.8 | 1.065 | 0.246 | 0.228 | 0.215 | 0.204 | |
| 1.6 | 1.198 | 0.24 | 0.233 | 0.216 | 0.208 | ||
| 1.4 | 1.369 | 0.24 | 0.233 | 0.22 | 0.219 | ||
| 1.2 | 1.598 | 0.342 | 0.314 | 0.285 | 0.271 | ||
| 1.1 | 1.743 | 0.318 | 0.3 | 0.277 | 0.272 | ||
| 1 | 1.917 | 0.263 | 0.238 | 0.225 | 0.21 | ||
| 0.9 | 2.13 | 0.155 | 0.122 | 0.135 | 0.107 | ||
| 1.1 | 0 | 1.91 | 1.004 | 0.26 | 0.248 | 0.238 | 0.229 |
| 1.2 | 0 | 1.91 | 1.004 | 0.257 | 0.249 | 0.236 | 0.229 |
| 0.2 | 0.307 | 0.283 | 0.267 | 0.241 | |||
| 0.3 | 0.514 | 0.5 | 0.462 | 0.451 | |||
| 0.4 | 0.792 | 0.711 | 0.653 | 0.612 | |||
| 0 | 1.6 | 1.198 | 0.27 | 0.243 | 0.244 | 0.22 | |
| 1.4 | 1.369 | 0.278 | 0.257 | 0.245 | 0.239 | ||
| 1.2 | 1.598 | 0.402 | 0.368 | 0.325 | 0.313 | ||
| 1.1 | 1.743 | 0.531 | 0.462 | 0.393 | 0.374 | ||
| 1 | 1.917 | 0.546 | 0.384 | 0.361 | 0.343 | ||
| 0.9 | 2.13 | 0.222 | 0.195 | 0.206 | 0.185 | ||
| 0.8 | 2.396 | 0.165 | 0.113 | 0.142 | 0.091 | ||
| 0.3 | 2.1 | 0.913 | 0.462 | 0.455 | 0.408 | 0.379 | |
| 1.7 | 1.128 | 0.33 | 0.289 | 0.252 | 0.246 | ||
| 1.5 | 1.278 | 0.279 | 0.236 | 0.233 | 0.215 | ||
| 1.3 | 1.475 | 0.284 | 0.208 | 0.249 | 0.181 | ||
| 1.1 | 1.743 | 0.208 | 0.197 | 0.189 | 0.178 | ||
| 1 | 1.917 | 0.122 | 0.112 | 0.098 | 0.095 | ||
| 0.9 | 2.13 | 0.131 | 0.121 | 0.114 | 0.11 | ||
References
- Golla, S.T.; Venkatesham, B. Experimental study on the effect of centrally positioned vertical baffles on sloshing noise in a rectangular tank. Appl. Acoust. 2021, 176, 107890. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.; Zhu, A. Numerical Investigation of Sloshing in Rectangular Tank with Permeable Baffle. J. Mar. Sci. Eng. 2020, 8, 671. [Google Scholar] [CrossRef]
- Xue, M.; Zheng, J.; Lin, P.; Yuan, X. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure. Ocean. Eng. 2017, 136, 178–189. [Google Scholar] [CrossRef]
- Nayak, S.K.; Biswal, K.C. Fluid damping in rectangular tank fitted with various internal objects—An experimental investigation. Ocean. Eng. 2015, 108, 552–562. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P. Three-dimensional liquid sloshing in a tank with baffles. Ocean. Eng. 2009, 36, 202–212. [Google Scholar] [CrossRef]
- Akyildız, H.; Erdem Ünal, N. Sloshing in a three-dimensional rectangular tank: Numerical simulation and experimental validation. Ocean. Eng. 2006, 33, 2135–2149. [Google Scholar] [CrossRef]
- Celebi, M.S.; Akyildiz, H. Nonlinear modeling of liquid sloshing in a moving rectangular tank. Ocean. Eng. 2002, 29, 1527–1553. [Google Scholar] [CrossRef]
- Younes, M.F.; Younes, Y.K.; El-Madah, M.; Ibrahim, I.M.; El-Dannanh, E.H. An experimental investigation of hydrodynamic damping due to vertical baffle arrangements in a rectangular tank. Proc. Inst. Mech. Eng. Part. M J. Eng. Marit. Environ. 2007, 221, 115–123. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Panigrahy, P.K.; Saha, U.K.; Maity, D. Experimental studies on sloshing behavior due to horizontal movement of liquids in baffled tanks. Ocean. Eng. 2009, 36, 213–222. [Google Scholar] [CrossRef]
- Jung, J.H.; Yoon, H.S.; Lee, C.Y.; Shin, S.C. Effect of the vertical baffle height on the liquid sloshing in a three-dimensional rectangular tank. Ocean. Eng. 2012, 44, 79–89. [Google Scholar] [CrossRef]
- Poguluri, S.K.; Cho, I.H. Liquid sloshing in a rectangular tank with vertical slotted porous screen: Based on analytical, numerical, and experimental approach. Ocean. Eng. 2019, 189, 106373. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.; Jiang, Z. Experimental investigation of parametric sloshing in a tank with vertical baffles. Ocean. Eng. 2020, 213, 107783. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Y.; Chen, C.; Chen, Z.; He, Y.; Zheng, M. Numerical study of liquid sloshing in 3D LNG tanks with unequal baffle height allocation schemes. Ocean. Eng. 2021, 234, 109181. [Google Scholar] [CrossRef]
- Kamath, A.; Grotle, E.L.; Bihs, H. Numerical Investigation of Sloshing Under Roll Excitation at Shallow Liquid Depths and the Effect of Baffles. J. Mar. Sci. Appl. 2021, 20, 185–200. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron Astr. 1992, 30, 543–573. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Shimizu, Y.; Gotoh, H.; Khayyer, A. An MPS-based particle method for simulation of multiphase flows characterized by high density ratios by incorporation of space potential particle concept. Comput. Math. Appl. 2018, 76, 1108–1129. [Google Scholar] [CrossRef]
- Hermange, C.; Oger, G.; Le Chenadec, Y.; Le Touze, D. A 3D SPH-FE coupling for FSI problems and its application to tire hydroplaning simulations on rough ground. Comput. Method Appl. M 2019, 355, 558–590. [Google Scholar] [CrossRef]
- Zhang, Y.; Wan, D.; Hino, T. Comparative study of MPS method and level-set method for sloshing flows. J. Hydrodyn. Ser. B 2014, 26, 577–585. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A.; Ikari, H.; Arikawa, T.; Shimosako, K. On enhancement of Incompressible SPH method for simulation of violent sloshing flows. Appl. Ocean. Res. 2014, 46, 104–115. [Google Scholar] [CrossRef]
- Delorme, L.; Colagrossi, A.; Souto-Iglesias, A.; Zamora-Rodríguez, R.; Botía-Vera, E. A set of canonical problems in sloshing, Part I: Pressure field in forced roll—comparison between experimental results and SPH. Ocean. Eng. 2009, 36, 168–178. [Google Scholar] [CrossRef]
- Zheng, X.; You, Y.; Ma, Q.; Khayyer, A.; Shao, S. A Comparative Study on Violent Sloshing with Complex Baffles Using the ISPH Method. Appl. Sci. 2018, 8, 904. [Google Scholar] [CrossRef] [Green Version]
- Khayyer, A.; Tsuruta, N.; Shimizu, Y.; Gotoh, H. Multi-resolution MPS for incompressible fluid-elastic structure interactions in ocean engineering. Appl. Ocean. Res. 2019, 82, 397–414. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, J.; Sun, Z.; Moctar, O.E.; Zong, Z. Numerically simulated flooding of a freely-floating two-dimensional damaged ship section using an improved MPS method. Appl. Ocean. Res. 2020, 101, 102207. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Modified Moving Particle Semi-implicit methods for the prediction of 2D wave impact pressure. Coast. Eng. 2009, 56, 419–440. [Google Scholar] [CrossRef]
- Wang, L.; Khayyer, A.; Gotoh, H.; Jiang, Q.; Zhang, C. Enhancement of pressure calculation in projection-based particle methods by incorporation of background mesh scheme. Appl. Ocean. Res. 2019, 86, 320–339. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, Q.; Zhang, C. Improvement of moving particle semi-implicit method for simulation of progressive water waves. Int. J. Numer. Meth. Fl. 2017, 85, 69–89. [Google Scholar] [CrossRef]
- Koshizuka, S.; Nobe, A.; Oka, Y. Numerical analysis of breaking waves using the moving particle semi-implicit method. Int. J. Numer. Meth. Fl. 1998, 26, 751–769. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, Q.; Zhang, C. Numerical simulation of solitary waves overtopping on a sloping sea dike using a particle method. Wave Motion. 2020, 95, 102535. [Google Scholar] [CrossRef]
- Faltinsen, O.M. A numerical nonlinear method of sloshing in tanks with two-dimensional flow. J. Ship Res. 1978, 22, 193–202. [Google Scholar] [CrossRef]

| BM-MPS | Experiment | |
|---|---|---|
| Maximum peak value | 2.74 | 2.33 |
| Mean value | 2.23 | 1.71 |
| Standard deviation | 0.378 | 0.593 |
| Configurations | Baffle Height | ||
|---|---|---|---|
| HB/h0 = 0.6, HS/h0 = 0.0 | 0.6h0 | 0.955 | 0.643 |
| HB/h0 = 0.8, HS/h0 = 0.2 | 0.839 | 0.601 | |
| HB/h0 = 1.0, HS/h0 = 0.4 | 1.737 | 0.69 | |
| HB/h0 = 0.8, HS/h0 = 0.0 | 0.8h0 | 0.578 | 0.496 |
| HB/h0 = 1.0, HS/h0 = 0.2 | 0.575 | 0.53 | |
| HB/h0 = 1.2, HS/h0 = 0.4 | 0.711 | 0.612 | |
| HB/h0 = 1.0, HS/h0 = 0.0 | 1.0h0 | 0.209 | 0.184 |
| HB/h0 = 1.2, HS/h0 = 0.2 | 0.283 | 0.241 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xu, M.; Zhang, Q. Numerical Investigation of Shallow Liquid Sloshing in a Baffled Tank and the Associated Damping Effect by BM-MPS Method. J. Mar. Sci. Eng. 2021, 9, 1110. https://doi.org/10.3390/jmse9101110
Wang L, Xu M, Zhang Q. Numerical Investigation of Shallow Liquid Sloshing in a Baffled Tank and the Associated Damping Effect by BM-MPS Method. Journal of Marine Science and Engineering. 2021; 9(10):1110. https://doi.org/10.3390/jmse9101110
Chicago/Turabian StyleWang, Lizhu, Min Xu, and Qian Zhang. 2021. "Numerical Investigation of Shallow Liquid Sloshing in a Baffled Tank and the Associated Damping Effect by BM-MPS Method" Journal of Marine Science and Engineering 9, no. 10: 1110. https://doi.org/10.3390/jmse9101110
APA StyleWang, L., Xu, M., & Zhang, Q. (2021). Numerical Investigation of Shallow Liquid Sloshing in a Baffled Tank and the Associated Damping Effect by BM-MPS Method. Journal of Marine Science and Engineering, 9(10), 1110. https://doi.org/10.3390/jmse9101110





