Spatial Rigid-Flexible-Liquid Coupling Dynamics of Towed System Analyzed by a Hamiltonian Finite Element Method

Abstract

An effective Hamiltonian finite element method is presented in this paper to investigate the three-dimensional dynamic responses of a towed cable-payload system with large deformation. The dynamics of a flexible towed system moving in a medium is a classical and complex rigid-flexible-liquid coupling problem. The dynamic governing equation is derived from the Hamiltonian system and built-in canonical form. A Symplectic algorithm is built to analyze the canonical equations numerically. Logarithmic strain is applied to estimate the large deformation effect and the system stiffness matrix will be updated for each calculation time step. A direct integral solution of the medium drag effect is derived in which the traditional coordinate transformation is avoided. A conical pendulum system and a 180° U-turn towed cable system are conducted and the results are compared with those retraced from the existing Hamiltonian method based on small deformation theory and the dynamic software of Livermore software technology corp. (LS-DYNA). Furthermore, a circularly towed system is analyzed and compared with experimental data. The comparisons show that the presented method is more accurate than the existing Hamiltonian method when large deformation occurred in the towed cable due to the application of logarithmic strain. Furthermore, it is more effective than LS-DYNA to treat the rigid-flexible-liquid coupling problems in the costs of CPU time.

1. Introduction

There are many applications in which payloads are towed by three-dimensional airborne platforms: towed remotely operated vehicles (ROVs) [1], flexible aerial refueling hose system [2], aircraft-towed cables [3], and tethered satellite systems [4]. The missions of three-dimensional towed systems have expanded from mapping the benthic and spatial morphology to various objectives, such as mine hunting, collecting biological samples, fuel make-up, and even exploring other celestial bodies [5]. The dynamics of cable-payload systems have been of major interest for several decades due to their nonlinear features caused by the flexible cable and airflow drag, the prediction of the nonlinear dynamic responses of cable-payload systems has become to be an active field of investigations. The towed systems moved in the fluid medium will be subject to fluid resistance such as airflow drag force and water resistance, coupling with the rigid payload and flexible cables, it will become to be classical and complex rigid-flexible-liquid coupling problems. An analytical solution is difficult to be acquired, and commercial software such as LS-DYNA will cost plenty of computation time to tackle the rigid-flexible-liquid coupling problems [6]. Researchers proposed many numerical methods to analyze the towing process dynamics, mainly including lumped mass method, finite difference method, and finite element method.

Asuma and Masayoshi [7] introduced a lumped mass approximation for the towed underwater vehicles, but the environmental water currents are ignored throughout the paper for simplicity. Du et al. [8] discretized the cable into a series of massless springs and lumped-mass points for analyzing the influence of underwater vehicle flow field on the dynamic behavior of the towed sonar cable array, and the drag force on the towed sonar cable array is obtained by calculating the drag force on each lumped-mass point. The lumped mass method is simple and convenient to implement. but it is not effective in handling flexible cables with large deformation and is prone to diverge due to the simplification. Sun et al. [9] applied the finite difference method to study the static and dynamic tug-cable-barge coupling motion problems. Zhao et al. [5] presented a finite difference method taking the axial elasticity, bending stiffness, and torsional stiffness into consideration to study the transient dynamics of straight towing and the U-turn towing process, the numerical simulations are validated by sea trial experimental data. However, the finite difference method cannot be implemented for complex geometries or variable properties of the towed system. Luis et al. [10] proposed a finite element method based on catenary line theory to study the towing dynamics for floating and submerged bodies, and the influence of internal damping was considered. Abhinav et al. [11] modeled the tow cable as a geometrically exact beam and applied a nonlinear finite element method to analyze the three-dimensional transient dynamics of towed underslung systems. Htun et al. [12] proposed a new tether cable element based on the radially multilayered modeling approach and applied the absolute nodal coordinate formulation to study the dynamics of a remotely operated underwater vehicle. Zhu et al. [13,14] proposed a new nodal position finite element to model the towed system dynamics. By assembling elements together, the complex geometries and/or the different properties of cable will be easily modeled, therefore, the finite element method is probably the most appealing technique in existing numerical methods to analyze the dynamic problem of the towed cable-payload system.

However, the moving process of the towed cable-payload system is prone to be a long-term work in practical engineering cases, and the numerical simulation is required to be stable and accurate for long-term calculation. Traditional time integration schemes such as Runge-Kutta, Newmark, and Generalized-α methods are effective, but their accuracies are sensitive to the size of time integration step and are prone to the accumulated error due to the co-existence of rigid-flexible-liquid coupling motion [15]. The conservation of system energy cannot be guaranteed, which may even lead to the divergence of the numerical solution over a long simulation period. To tackle this problem, Ding et al. [16,17] proposed a new nodal position method based on Hamiltonian theory to analyze the nonlinear dynamic responses of spatial flexible tether systems which had low numerical error accumulation. The Hamiltonian formalism solved by the Symplectic algorithm [18,19] could preserve the linear and the quadratic conservative quantities of the differential equations. It has been applied to analyze the vibration problems of beam and plate [20] and the tethered satellite system dynamics [21].

Furthermore, the towing cable is prone to nonlinear large strain due to its high flexibility, therefore, the large deformation influence [22] is a critical point to study the three-dimensional rigid-flexible liquid coupling dynamics of towed cable-payload system. Chucheepsakul et al. [23] developed finite element formulations for large strain analysis of extensible flexible marine pipes which transport fluid. Xu [24] proposed a flexible segment model to evaluate the dynamics of slender underwater cables undergoing high tension and large deformations. However, they are limited to the linear elastic cases and the large deformation is exactly related to the large-scale movement. Actually, the real strain to flexible cable is accumulated since the initial time. Assuming that the cable material is homogeneous and isotropic, the accumulated large strain can be described by the logarithmic strain. Logarithmic strain theory with Kirchhoff stress has been applied to the dynamic analysis of spatial truss systems with large deformation occurred [25].

In addition, the medium resistance is usually analyzed in local coordinate systems firstly and subsequently transformed to be the expression in a global coordinate system [26]. The complex discussions about whether the normal or tangential component of resistance is along with the global coordinate axis are required in the transformation. On the other hand, the medium resistance rigid-flexible liquid coupling problem is time-varying in the movement process [27], it is mainly due to that the medium resistance is related to the cable posture and the relative velocity between the moving structure and the medium. Plenty of medium elements and the enormous cost of computation will be required in existing commercial software. A more effective solution method is required to numerically analyze the rigid-flexible-liquid coupling dynamics of towed cable-payload systems.

This paper aims at the three-dimensional rigid-flexible-liquid coupling dynamic problems of the towed cable-payload systems, a numerical model based on Hamiltonian theory is proposed and solved by finite element method, in which the large strain influence, the damping effect, and the aerodynamic effect are taken into consideration. Following the introduction, the Hamiltonian nodal position finite element formulism is derived, a new solution of aerodynamic resistance is derived and expressed in form of the Morison equation, and the Symplectic solution scheme is formulated in Section 2 and Section 3. Subsequently, the validation of the proposed model using a conical pendulum system, a 180° U-turn towed system, and an experimental work published in the literature is presented in Section 4. Finally, Section 5 discusses and concludes the present study.

2. Dynamic Modeling of Cable Element

Most of the existing finite element methods to analyze the dynamic responses of towed cable-payload systems are derived based on small deformation theory. Besides, the solution of medium drag force is too complex due to the complex discussion about the directions of normal and tangent components. In this section, a discrete formalism is used for dynamic cable modeling. The differential dynamic governing equations are derived based on finite elasticity theory and Hamiltonian theory, in which the logarithmic strain is applied to describe the large strain of the towed cable. The application of logarithmic strain effectively depicts the actual accumulative strain of the flexible cable. Then, the Morison equation is used to represent the influence of aerodynamic, the Rayleigh damping is applied to take the damping influence into consideration. Finally, the Symplectic solution scheme is derived to solve the obtained finite element equations.

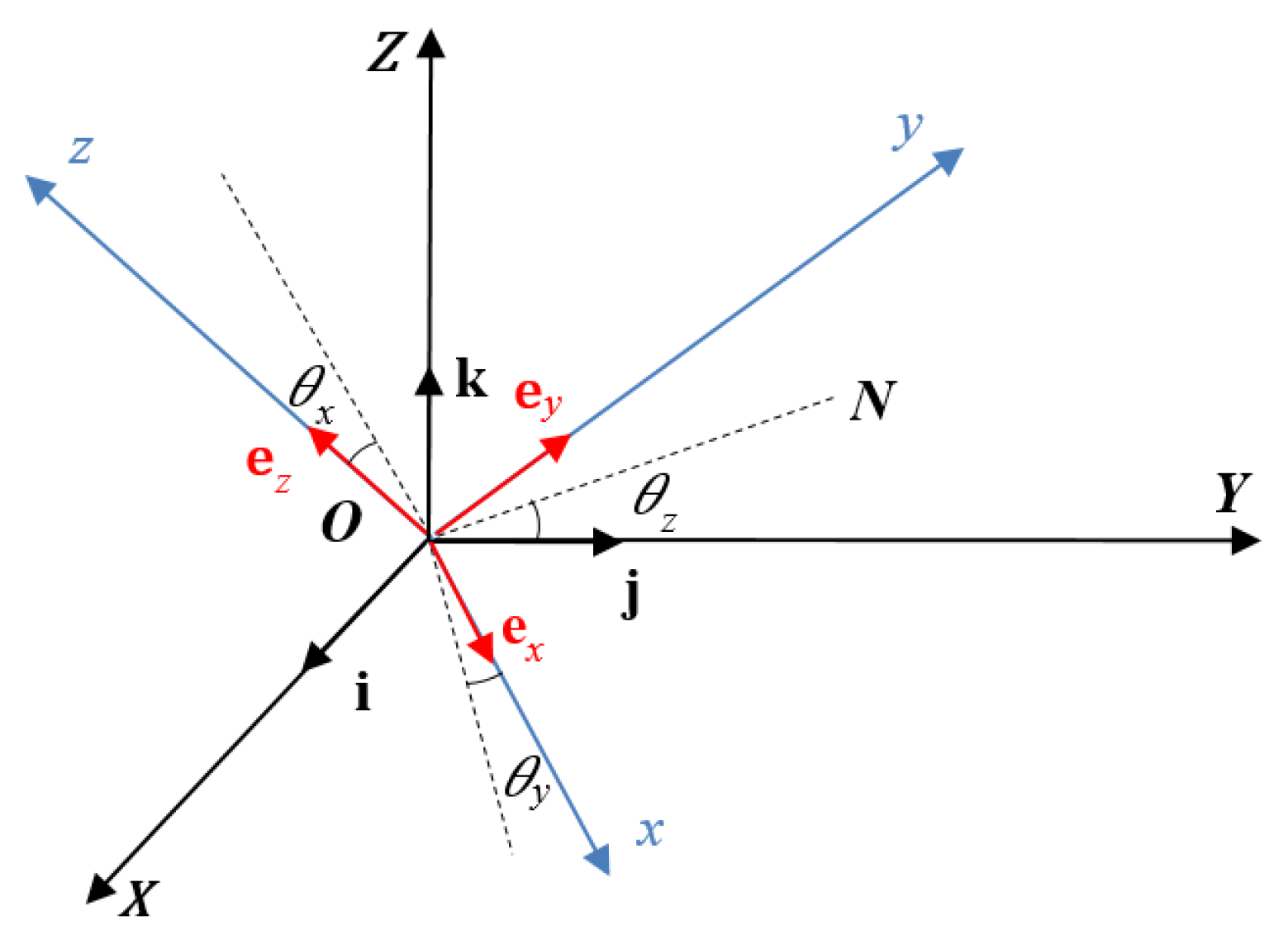
2.1. Three-Dimensional Tait-Bryan Transformation and Shape Function

The flexible cable undergoes large scale motion and large deformation in the motion process of the towed cable-payload system, the flexible cable is in the taut state when large deformation existed due to the flexibility and the bending and torsion effects are not the major dynamic response factors of the flexible cables, furthermore, the bending effects can be also calculated by the selection of much more suitable straight cable elements, therefore, the bending and torsion effects are neglected in the exiting nodal position finite element method. According to the nodal position finite element theory [6], we discretize the towed cable by n segments.

Consider a two-node straight cable element in a three-dimensional space, the elemental position is described by its nodal coordinates (X_i, Y_i, Z_i, X_j, Y_j, Z_j) in a global Cartesian coordinate system O-XYZ with the unit base vectors (i, j, k). A local right-hand coordinate system o-xyz to each cable element is defined with ox-axis along with the cable, oy-axis and oz-axis perpendicular to the ox-axis, respectively, and the unit base vectors of o-xyz are (e_x, e_y, e_z). As shown in Figure 1, ON is set to be the intersection line of surfaces O-XY and o-yz, the Tait–Bryan transformations from the global coordinate system O-XYZ to the local coordinate o-xyz system are θ_z-yaw, θ_y-pitch, and θ_x-roll, respectively.

(1)

Rotating OZ counterclockwise by an angle θ_z (0 ≤ θ_z < π) to overlap OY with ON, the new OY is perpendicular to the new OX, OZ and the local ox.

(2)

Rotating the new OY clockwise by an angle θ_y (0 ≤ θ_y < π) to overlap OX with the local ox.

(3)

Rotating the new OX counterclockwise by an angle θ_x (0 ≤ θ_x < π) to overlap OZ with the local oz and OY with the local oy.

The Tait-Bryan transformation matrix T can be derived from the three sequential coordinate transformations.

$$\begin{array}{c}{\left[\begin{array}{ccc}{\mathbf{e}}_x& {\mathbf{e}}_y& {\mathbf{e}}_z\end{array}\right]}^T=\mathbf{T}{\left[\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\end{array}\right]}^T\\ \mathbf{T}=\left[\begin{array}{ccc}\cos {\theta }_y\cos {\theta }_z& \cos {\theta }_{y}s{\theta }_z& -\sin {\theta }_y\\ -\cos {\theta }_x\sin {\theta }_z+\sin {\theta }_x\sin {\theta }_y\cos {\theta }_z& \cos {\theta }_x\cos {\theta }_z+\sin {\theta }_x\sin {\theta }_y\sin {\theta }_z& \sin {\theta }_x\cos {\theta }_y\\ \sin {\theta }_x\sin {\theta }_z+\cos {\theta }_x\sin {\theta }_y\cos {\theta }_z& -\sin {\theta }_x\cos {\theta }_z+\cos {\theta }_x\sin {\theta }_y\sin {\theta }_z& \cos {\theta }_x\cos {\theta }_y\end{array}\right]\end{array}$$

(1)

The three rotational angles can be calculated at any instant in the simulation process in which the endpoints of the straight cable element are frequently updated. Correspondingly, the nodal position vector r, velocity vector v, and acceleration vector a of an arbitrary point in a local coordinate system can be expressed in a global system, respectively.

$$\begin{array}{l}\mathbf{r}=\left[\begin{array}{ccc}{r}_x & r_y & r_z\end{array}\right]{\left[\begin{array}{ccc}{\mathbf{e}}_x& {\mathbf{e}}_y& {\mathbf{e}}_z\end{array}\right]}^T=\left[\begin{array}{ccc}{r}_x & r_y & r_z\end{array}\right]\mathbf{T}{\left[\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\end{array}\right]}^T\\ \mathbf{v}=\left[\begin{array}{ccc}{v}_x & v_y & v_z\end{array}\right]{\left[\begin{array}{ccc}{\mathbf{e}}_x& {\mathbf{e}}_y& {\mathbf{e}}_z\end{array}\right]}^T=\left[\begin{array}{ccc}{v}_x & v_y & v_z\end{array}\right]\mathbf{T}{\left[\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\end{array}\right]}^T\\ \mathbf{a}=\left[\begin{array}{ccc}{a}_x & a_y & a_z\end{array}\right]{\left[\begin{array}{ccc}{\mathbf{e}}_x& {\mathbf{e}}_y& {\mathbf{e}}_z\end{array}\right]}^T=\left[\begin{array}{ccc}{a}_x & a_y & a_z\end{array}\right]\mathbf{T}{\left[\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\end{array}\right]}^T\end{array}$$

(2)

Assume that the local position vector r(x, t) of an arbitrary point x(x, y, z) along the straight cable element is expressed by the linear shape functions and nodal coordinates x_e (t) = [x_i y_i z_i x_j y_j z_j]^T, such that:

$$\mathbf{r}(\mathbf{x},t)=\left[\mathbf{N}(s)\right]{\mathbf{x}}_e(t)$$

(3)

the linear shape function N(s) is defined as:

$$\mathbf{N}(s)=\left[\begin{array}{cccccc}1-\xi & 0& 0& \xi & 0& 0\\ 0& 1-\xi & 0& 0& \xi & 0\\ 0& 0& 1-\xi & 0& 0& \xi \end{array}\right]$$

(4)

where ξ = s/L_e (0 ≤ ξ ≤ 1) is the length ratio of the deformed cable element, and s = [(x−x_i)² + (y−y_i)² + (z−z_i)²]^1/2 is the length along the deformed cable element measured from node i, L_e is the instantaneous length of the cable element.

According to the interpolation of the position vector, the given linear shape functions would be appropriate to the velocity vector v(x, t) = [v_x v_y v_z]^T and acceleration vector a(x, t) = [a_x a_y a_z]^T.

$$\begin{array}{l}\mathbf{v}(\mathbf{x},t)=\dot{\mathbf{r}}\left(\mathbf{x},t\right)=\mathbf{N}(\mathbf{x}){\mathbf{v}}_e(t)\\ \mathbf{a}(\mathbf{x},t)=\ddot{\mathbf{r}}\left(\mathbf{x},t\right)=\mathbf{N}(\mathbf{x}){\mathbf{a}}_e(t)\end{array}$$

(5)

where v_e (t) = [v_xi v_yi v_zi v_xj v_yj v_zj]^T and a_e (t) = [a_xi a_yi a_zi a_xj a_yj a_zj]^T are the nodal velocity and acceleration components of the deformed cable element in a local coordinate system.

2.2. Elemental Virtual Work and Elemental Matrix

In the movement process of a towed cable-payload system, the cable is in the tensional state with large deformation, especially for the flexible ones. The actual strain of cable element e is accumulated over the movement process, which can be expressed using the logarithmic strain if the cable material is homogeneous and isotropic [28]:

$${}^t\epsilon _L=\ln \frac{L_e}{L_0}$$

(6)

where L₀ and L_e are the initial length and current length at the moment t of the cable element e, respectively. Compared with the engineering strain, the logarithmic strain has a wider range of application which is suitable for both small and large deformation circumstances of flexible structures [28]. The axial Kirchhoff stress will be correspondingly calculated using the linear constitutive relationship, such that:

$${}^t\sigma =E{}^t\epsilon {}_L$$

(7)

and E is the Young’s modulus of the cable material.

Correspondingly, the virtual elastic potential energy δU_e of the cable element e would be obtained by integrating the logarithm strain and the Kirchhoff stress over the element and expressed in a local coordinate system, such as:

$$\delta U_e={\displaystyle {\mathsf{\int }}_{{}^0{V}_e}{}_0{}^t\sigma \delta {}_0{}^t\epsilon {}_{L}d {}^{0}V}={\displaystyle {\mathsf{\int }}_{{}^0{V}_e}E\ln \frac{L_e}{L_0}\delta \ln \frac{L_e}{L_0}d {}^{0}V}={}^t\mathbf{x}{}_e^T{\mathbf{k}}_e\delta {}^t\mathbf{x}{}_e$$

(8)

$${\mathbf{k}}_e=\frac{\partial ({\mathbf{k}}_e{\mathbf{x}}_e)}{\partial {\mathbf{x}}_e^T}=\frac{E{A}_0}{L_e}\ln \frac{L_e}{L_0}\left[\begin{array}{cc}{\mathbf{I}}_{(3\times 3)}& -{\mathbf{I}}_{(3\times 3)}\\ -{\mathbf{I}}_{(3\times 3)}& {\mathbf{I}}_{(3\times 3)}\end{array}\right]$$

(9)

where A₀ is the initial elemental cross-section and ⁰V_e is the initial elemental volume, both A₀ and ⁰V_e keep constant in the analyzing process, ⁰V denotes that the integral is built based on initial volume. Equation (8) is a definite integral to the elemental volume ⁰V_e, the upper left subscripts 0 in Equation (8) denote that the integral is calculated with respect to the initial state of the cable element, and the upper left subscripts t denotes the real-time value at time t. I_{(3 × 3)} denotes the 3 × 3 unit matrix. k_e is the elemental stiffness matrix and analyzed by δU_e. L_e is the function of the nodal position components in a local coordinate system and its value is variable in the movement process, especially for flexible cable elements. Therefore, the value of k_e is a variable and nonlinear matrix, it should be updated with each simulation time step.

Similarly, the elemental virtual kinetic energy δT_e can be obtained and expressed in terms of nodal velocity vectors in a local coordinate system, such as:

$$\delta T_e={\displaystyle {\int }_{{}^0{V}_e}{}^0\rho {}_0{}^t\ddot{u}_k\delta {}_0{}^{t}u_k{}^{0}dV}={\displaystyle {\int }_0^{L_0}{}^0\rho {}^{0}A{}_0{}^t\ddot{u}_k\cdot \delta {}_0{}^{t}u_{k}d {}^{0}s}={}^t\ddot{\mathbf{x}}{}_e^T{\mathbf{m}}_e\delta {}^t\mathbf{x}{}_e$$

(10)

$${\mathbf{m}}_e={\displaystyle {\int }_0^{L_0}\rho A_0{\mathbf{N}}^T{\mathbf{N}}^{T}d {}^{0}s}=\frac{\rho A_0{L}_0}{6}\left[\begin{array}{cc}2{\mathbf{I}}_{(3\times 3)}& {\mathbf{I}}_{(3\times 3)}\\ {\mathbf{I}}_{(3\times 3)}& 2{\mathbf{I}}_{(3\times 3)}\end{array}\right]$$

(11)

where ρ is the density of cable material, m_e is the elemental mass matrix and its value keeps constant in the simulation process, the upper right subscript T denotes the transposed matrix form.

The virtual elastic potential energy and virtual kinetic energy of cable element can also be expressed in a global coordinate system and their values remain unchanged. By the application of the elemental transformation T_e, the elemental stiffness matrix and mass matrix can be expressed in a global coordinate system:

$$\begin{array}{l}{\mathbf{K}}_e={\mathbf{T}}_e^T{\mathbf{k}}_e{\mathbf{T}}_e\\ {\mathbf{M}}_e={\mathbf{T}}_e^T{\mathbf{m}}_e{\mathbf{T}}_e\end{array}$$

(12)

where K_e and M_e are the elemental stiffness and mass matrix in a global system, the elemental transformation matrix from global system to local system T_e depicts the transformation of the elemental position and acceleration components, which can be expressed as:

$${\mathbf{T}}_e=\left[\begin{array}{cc}\mathbf{T}& 0\\ 0& \mathbf{T}\end{array}\right]$$

(13)

The towed cable-payload system is subjected to gravity and medium resistance in the movement process. Due to the gravity vector remains to be constant, the elemental gravity matrix would be analyzed in a global coordinate system directly. A new solution scheme is presented in this paper to analyze the medium resistance, Morison’s equation [29] is applied to modeling the medium resistance and analyzed in a global coordinate system directly. In the solution scheme of medium resistance, the complex transformation process from local coordinate system to global coordinate system is avoided.

The linear interpolation function N_G to global OZ-axial direction would be applied to interpolate the elemental gravity components. The virtual potential energy δU_Ge can be correspondingly expressed as:

$$\delta U_{Ge}={\displaystyle {\int }_{{}^0{V}_e}{}^0\rho {\mathbf{g}}^T\delta {}^t\mathbf{X}{}^{0}dV}={\displaystyle {\int }_{{}^0{V}_e}{}^0\rho {\mathbf{g}}^T{\mathbf{N}}_G{}^{0}dV}\delta {}^t\mathbf{X}{}_e$$

(14)

in which g = [0 0 -g]^T is the gravitational acceleration vector and N_G is assumed to be:

$${\mathbf{N}}_G=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 1-\xi & 0& 0& \xi \end{array}\right]$$

(15)

and the elemental gravity matrix F_Ge would be:

$${\mathbf{F}}_{Ge}={\displaystyle {\int }_{{}^0{V}_e}{}^0\rho {\mathbf{g}}^T{\mathbf{N}}_G{}^{0}dV}=-\frac{\rho A_{0}g{L}_0}{2}{\left[\begin{array}{cccccc}0& 0& 1& 0& 0& 1\end{array}\right]}^T$$

(16)

To tackle the previously mentioned difficulty of complex transformation and enormous computational cost when the medium resistance is analyzed, a direct integral method is proposed in this paper. The medium resistance will be solved by Morison’s equation [30,31] when the diameter size D is much smaller than the cable length,

$${\mathbf{f}}_d=-C_d\frac{{\rho }_{f}D}{2}{\mathbf{V}}_r\left|{\mathbf{V}}_r\right|=\{\begin{array}{l}-C_{dt}(\alpha )\frac{{\rho }_{f}D}{2}\left|{\mathbf{V}}_r\right|{\mathbf{V}}_{rt}={\mathbf{f}}_{d\mathrm{t}}\\ -C_{dn}(\alpha )\frac{{\rho }_{f}D}{2}\left|{\mathbf{V}}_r\right|{\mathbf{V}}_{rn}={\mathbf{f}}_{dn}\end{array}$$

(17)

in which f_d is the medium resistance per unit cable length, f_dt and f_dn are the tangent and normal components, V_r = V-V_f is the relative velocity of cable to fluid, V_f is the fluid velocity, V_rt and V_rn are the tangent and normal components. C_d is the resistance coefficient which is related to the attack angle α, C_dt(α) and C_dn(α) are the tangent and normal components, ρ_f is the fluid density.

Similar to the cable velocity V = NV_e, the fluid velocity of arbitrary location V_f is analyzed by applying the same linear shape function N to elemental fluid velocity vector V_fe, such as V_f = NV_fe. Then, the virtual work conducted by drag force would be obtained without the discussion of tangent and normal components, such as:

$$\delta W_{de}={\displaystyle {\int }_{{}^{0}V}{\mathbf{f}}_d\delta {}^t\mathbf{X}{}^{0}dV}=-C_d\frac{{\rho }_{f}D}{2}{\displaystyle {\int }_{{}^{0}V}{\mathbf{N}}^T\sqrt{{\mathbf{V}}_{re}^T{\mathbf{N}}^T\mathbf{N}{\mathbf{V}}_{re}}\mathbf{N}{\mathbf{V}}_{re}{}^{0}dV}\delta {\mathbf{X}}_e={\mathbf{F}}_{de}\delta {\mathbf{X}}_e$$

(18)

in which F_de is the elemental drag force vector, Fourth-order closed Newton–Cotes formulate [32] is applied to analyze the integrant item

$$\mathbf{f}(s)={\mathbf{N}}^T\sqrt{{\mathbf{V}}_{re}^T{\mathbf{N}}^T\mathbf{N}{\mathbf{V}}_{re}}\mathbf{N}{\mathbf{V}}_{re}$$

(19)

in which V_re is the elemental relative velocity vector, the expansion form of f (s) would be:

$$\mathbf{f}(s)=l\_v(s)\left(\begin{array}{c}s(L_0-s)(L\times V_{rXi}+(V_{rXj}-V_{rXi}))\\ s(L_0-s)(L\times V_{rYi}+(V_{rYj}-V_{rYi}))\\ s(L_0-s)(L\times V_{rZi}+(V_{rZj}-V_{rZi}))\\ s(L_0\times V_{rXi}+s(V_{rXj}-V_{rXi}))\\ s(L_0\times V_{rYi}+s(V_{rYj}-V_{rYi}))\\ s(L_0\times V_{rZi}+s(V_{rZj}-V_{rZi}))\end{array}\right)$$

(20)

$$l\_v(s)=\frac{\sqrt{L_0^2(V_{rXi}^2+V_{rYi}^2+V_{rZi}^2)-2s{L}_0(V_{rXi}^2-V_{rXi}{V}_{rXj}+V_{rYi}^2-V_{rYi}{V}_{rYj}+V_{rZi}^2-V_{rZi}{V}_{rZj})+s^2({(V_{rXj}-V_{rXi})}^2+{(V_{rYj}-V_{rYi})}^2+{(V_{rZj}-V_{rZi})}^2)}}{L_0^3}$$

(21)

where s is the real-time length of cable element. Correspondingly, the elemental drag force vector F_de would be expressed as:

$${\mathbf{F}}_{de}=-C_d{\rho }_{f}DL\left[7\mathbf{f}(0)+32\mathbf{f}(0.25L)+12\mathbf{f}(0.5L)+32\mathbf{f}(0.75L)+7\mathbf{f}(L)\right]/180$$

(22)

in which the elemental drag force vector F_de is related to the real-time length of the cable element, the calculating time step should be small enough to ensure the tiny change of elemental length for each step.

Generally, the structural damping of cable especially for large deformed ones would be considered in the spatial movement process. Rayleigh damping is applied to depict the structural damping effect which provides resistance to the structure with time-varying acceleration, such that:

$$\begin{array}{c}{\mathbf{C}}_e=\alpha {\mathbf{M}}_e+\beta {\mathbf{K}}_e\\ \alpha =\frac{2\left({\xi }_i{\omega }_j-{\xi }_j{\omega }_i\right)}{\left({\omega }_j^2-{\omega }_i^2\right)}{\omega }_i{\omega }_j,\beta =\frac{2\left({\xi }_j{\omega }_j-{\xi }_i{\omega }_i\right)}{\left({\omega }_j^2-{\omega }_i^2\right)}\end{array}$$

(23)

where C_e is the elemental Raleigh damping matrix, α and β are the Rayleigh coefficients, ω_i and ω_j are the cut-off frequencies of lower and upper bounds in the frequency domain, and ξ_i and ξ_j are the corresponding damping ratios, respectively.

2.3. Elemental Dynamic Equation in Canonical Form

Based on Lagrangian theory and the elemental mass matrix, stiffness matrix, Raleigh damping matrix, gravity vector and external force vector, the dynamic equation of cable element in the Lagrangian form will be derived as:

$${ℒ}_e=\frac{1}{2}{\dot{\mathbf{X}}}_e^T{\mathbf{M}}_e{\dot{\mathbf{X}}}_e-\frac{1}{2}{\mathbf{X}}_e^T{\mathbf{K}}_e{\mathbf{X}}_e-{\mathbf{X}}_e^T{\mathbf{C}}_e{\dot{\mathbf{X}}}_e+{\mathbf{X}}_e^T{\mathbf{F}}_{Ge}+{\mathbf{X}}_e^T{\mathbf{F}}_{de}$$

(24)

Equation (24) is widely used in the traditional finite element method to model the cable element dynamics, however, the accuracy of the solution procedure would not be ensured in long-term dynamic simulation cases due to the structural discretization [33]. In this paper, the Hamiltonian equation which conserves the system energy and momentum exactly is used to eliminate the dispersion, Symplectic integration algorithm will be applied to analyze the Hamiltonian equation of the towed system. By the definition of generalized momentum P_e = M_eV_e = [P_Xi P_Yi P_Zi P_Xj P_Yj P_Zj]^T, the elemental Hamiltonian function can be expressed as:

$$H({\mathbf{P}}_e,{\mathbf{X}}_e)={\mathbf{P}}_e^T{\dot{\mathbf{X}}}_e-{ℒ}_e=\frac{1}{2}{\mathbf{P}}_e^T{\mathbf{M}}_e^{-1}{\mathbf{P}}_e+\frac{1}{2}{\mathbf{X}}_e^T{\mathbf{K}}_e{\mathbf{X}}_e+{\mathbf{X}}_e^T{\mathbf{C}}_e{\dot{\mathbf{X}}}_e-{\mathbf{X}}_e^T{\mathbf{F}}_{Ge}-{\mathbf{X}}_e^T{\mathbf{F}}_{de}$$

(25)

in which the upper right subscript -1 denotes the inverse matrix form, P_e and X_e are the canonical variables and solved in canonical form, such as:

$$\begin{array}{l}{\dot{\mathbf{P}}}_e=-\partial H({\mathbf{P}}_e,{\mathbf{X}}_e)/\partial {\mathbf{X}}_e=-{\mathbf{K}}_e{\mathbf{X}}_e-{\mathbf{C}}_e{\dot{\mathbf{X}}}_e+{\mathbf{F}}_{Ge}+{\mathbf{F}}_{de}\\ {\dot{\mathbf{X}}}_e=\partial H({\mathbf{P}}_e,{\mathbf{X}}_e)/\partial {\mathbf{P}}_e={\mathbf{M}}_e^{-1}{\mathbf{P}}_e\end{array}$$

(26)

3. Symplectic Integration Algorithm for Towed Cable-Payload System

Based on the second-order high accuracy method developed by Ding et al. [6], a new Symplectic integration algorithm is derived to solve the Hamiltonian canonical Equation (26), in which both the linear and the quadratic conservative quantities will be preserved. The effect of large deformation, medium resistance, and structural damping is considered in the movement procedure of a towed cable-payload system.

3.1. Assembly of System Dynamic Equations

Based on the continuity theory, the nodal position, velocity, and acceleration of the same node by two adjacent elements always keep consistent, the system dynamic equations will be assembled by all the elemental canonical equations. In this paper, the payload is treated as a lumped mass attached to the tail point of the towed cable, the movement of a towed point is previously identified. Finally, the system dynamic equations will be obtained as:

$$\begin{array}{l}\dot{\mathbf{P}}=-\mathbf{K}\mathbf{X}-\alpha \mathbf{P}-\beta \mathbf{K}{\mathbf{M}}^{-1}\mathbf{P}+{\mathbf{F}}_G+{\mathbf{F}}_d\\ \dot{\mathbf{X}}={\mathbf{M}}^{-1}\mathbf{P}\end{array}$$

(27)

where M is the global mass matrix in which the mass of towed payload is attached to the last elemental node, M⁻¹ is the inverse form of M, F_G is the global gravity vector which takes the gravity of towed payload into consideration, K, P, F_d are the global stiffness matrix, momenta matrix, and medium resistance force vector, respectively, the dot above M and P denotes the derivative with respect to time.

3.2. Symplectic Difference Algorithms

According to the Symplectic algorithm theory, the Hamiltonian canonical variables can be analyzed by a step-by-step iterative approach to preserve the linear and the quadratic conservative quantities. To analyze differential Equation (27) precisely, the second-order Symplectic difference scheme for the k+1 step can be expressed as:

$$\begin{array}{l}{\mathbf{P}}^{k+1}={\mathbf{P}}^k-h{H}_{\mathbf{X}}\left({\mathbf{P}}^{k+1},{\mathbf{X}}^k\right)-\frac{h^2}{2}{\left({\displaystyle \sum _{j=1}^n{H}_{{\mathbf{X}}_j}{H}_{{\mathbf{P}}_j}}\right)}_{\mathbf{X}}\left({\mathbf{P}}^{k+1},{\mathbf{X}}^k\right)\\ {\mathbf{X}}^{k+1}={\mathbf{X}}^k+h{H}_{\mathbf{P}}\left({\mathbf{P}}^{k+1},{\mathbf{X}}^k\right)+\frac{h^2}{2}{\left({\displaystyle \sum _{j=1}^n{H}_{{\mathbf{X}}_j}{H}_{{\mathbf{P}}_j}}\right)}_{\mathbf{P}}\left({\mathbf{P}}^{k+1},{\mathbf{X}}^k\right)\end{array}$$

(28)

where h is the time step, H_X(P^k+1, X^k) and H_P(P^k+1, X^k) are the partial differentiation form with respect to the Hamiltonian canonical variables X and P, the upper right subscript k+1 and k denote the time step which is under calculation. In each time step, repeated iterations will be required in the solution procedure to confirm a converge value of P^k+1.

Based on the second-order Symplectic difference theory (28) and the system Hamiltonian function, the dynamic equations of the towed cable-payload system (27) will be analyzed by each time step, such that:

$$\begin{array}{lll}{\mathbf{P}}^{k+1}& =& {\mathbf{P}}^k-h\left(\mathbf{K}{\mathbf{X}}^k+\alpha {\mathbf{P}}^{k+1}+\beta \mathbf{K}{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}-{\mathbf{F}}_G-{\mathbf{F}}_d\right)\\ & & -\frac{h^2}{2}\frac{\partial {\left({\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}\right)}^T\left(\mathbf{K}{\mathbf{X}}^k+\alpha {\mathbf{P}}^{k+1}+\beta \mathbf{K}{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}-{\mathbf{F}}_G-{\mathbf{F}}_d\right)}{\partial {\mathbf{X}}^k}\\ {\mathbf{X}}^{k+1}& =& {\mathbf{X}}^k+h{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}+\frac{h^2}{2}\frac{\partial {\left(\mathbf{K}{\mathbf{X}}^k+\alpha {\mathbf{P}}^{k+1}+\beta \mathbf{K}{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}-{\mathbf{F}}_G-{\mathbf{F}}_d\right)}^T{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}}{\partial {\mathbf{P}}^{k+1}}\end{array}$$

(29)

Omitting the high-order item in Equation (29), the second-order analytical formulation of towed system for k+1 step would be:

$$\begin{array}{l}{\mathbf{P}}^{k+1}={\mathbf{P}}^k-h\left(\mathbf{K}{\mathbf{X}}^k+\alpha {\mathbf{P}}^{k+1}+\beta \mathbf{K}{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}-{\mathbf{F}}_G-{\mathbf{F}}_d\right)-\frac{h^2}{2}\left(\mathbf{K}+{\mathbf{K}}^{\prime }\right)\left({\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}\right)\\ {\mathbf{X}}^{k+1}={\mathbf{X}}^k+h{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}+\frac{h^2}{2}{\mathbf{M}}^{-1}\left(\mathbf{K}{\mathbf{X}}^k+\alpha {\mathbf{P}}^{k+1}+\beta \mathbf{K}{\mathbf{M}}^{-1}{\mathbf{P}}^{k+1}-{\mathbf{F}}_G-{\mathbf{F}}_d\right)\end{array}$$

(30)

Due to the system stiffness matrix is a time-varying function respects to the nodal position, thus a derivative matrix K’ will be derived as:

$$\mathbf{K}+{\mathbf{K}}^{\prime }=\frac{\partial \left({\mathbf{X}}^T{\mathbf{K}}^T\right)}{\partial \mathbf{X}}$$

(31)

And,

$${\mathbf{K}}^{\prime }=\frac{E{}^{0}A}{L_e^3}\left(1-2\ln \frac{L_e}{L_0}\right)\left[\begin{array}{ccccc}\mathbf{I}& -\mathbf{I}& 0& 0& 0\\ -\mathbf{I}& 2\mathbf{I}& -\mathbf{I}& 0& 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& 0& -\mathbf{I}& 2\mathbf{I}& -\mathbf{I}\\ 0& 0& 0& -\mathbf{I}& \mathbf{I}\end{array}\right]\mathbf{X}{\mathbf{X}}^T{\left[\begin{array}{ccccc}\mathbf{I}& -\mathbf{I}& 0& 0& 0\\ -\mathbf{I}& 2\mathbf{I}& -\mathbf{I}& 0& 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& 0& -\mathbf{I}& 2\mathbf{I}& -\mathbf{I}\\ 0& 0& 0& -\mathbf{I}& \mathbf{I}\end{array}\right]}^T$$

(32)

in which I and 0 are the 3 × 3 unit matrix and null matrix, respectively.

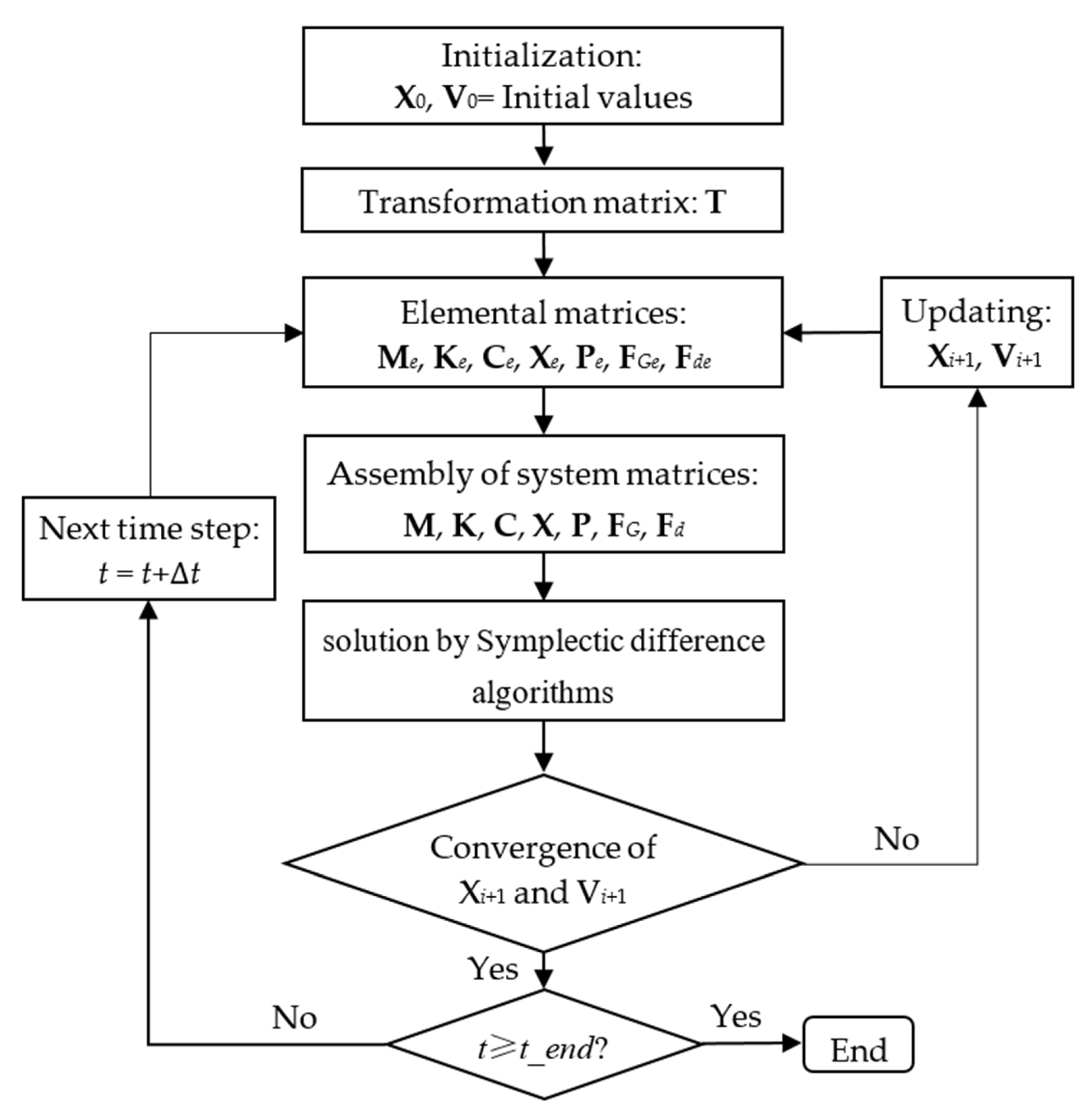
3.3. Initialization and Solution Procedure

As previously mentioned, the system dynamic Equation (27) are the first-order differential equations that have n position variates and n momentum variates. Initialization of 2n variates will be required for the solution of system dynamic equations, and their values would be updated by each time step. In the solution procedure, the momentum matrix is constructed by the constant mass matrix and velocity vector of the towed system. Figure 2 presents a flow chart for the major steps in the proposed numerical solving procedure. The Symplectic solution code of the towed cable-payload system is compiled in VC++ 6.0 environment which is a product of Microsoft corporation.

Where t_end is the pre-set calculating termination time, Δt = h is the time step in the calculation process which is determined according to the calculation rule of finite element method, such that:

$$\begin{array}{l}t\le 0.9\times l/c\\ c=\sqrt{E/\rho }\end{array}$$

(33)

in which l is the characteristic length of cable element, c is the stress wave speed which can be analyzed by the Young’s modulus E and density ρ of cable material.

4. Numerical and Experimental Validations

For nonlinear dynamic systems, many researchers [34,35,36,37] have presented comparative studies between the conventional non-Symplectic algorithms and the Symplectic algorithms. Symplectic algorithms have the conservation characteristic for the conservative Hamiltonian system and have higher calculation accuracy for either conservative or non-conservative Hamiltonian systems. Ding et al. [6,16] have done the detailed validation about the Hamiltonian nodal position finite element method from three aspects: Symplectic conservation features, the higher accuracy, and wider applicability than the conventional numerical methods. In this section, the presented Hamiltonian nodal position finite element method based on logarithmic strain solved by the second-order Symplectic difference algorithm is named HFML.

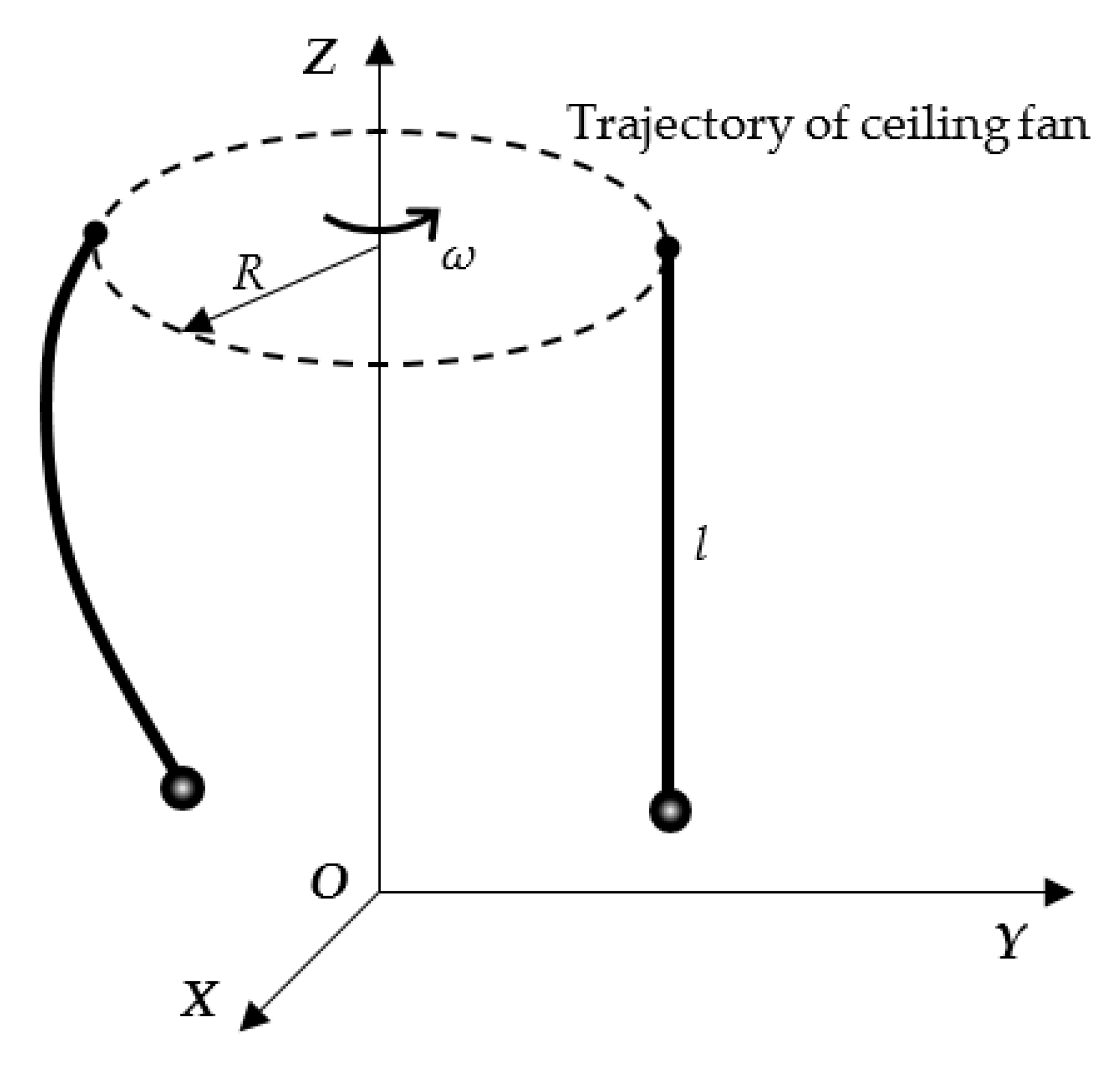
4.1. Flexible Conical Pendulum Modeling

As shown in Figure 3, the dynamic responses of a flexible polyethylene rubber conical pendulum without damping effect are modeled in this section. The pendulum rod rotates about the vertical OZ-axis with the intersection angle θ = π/3 rad, the physical parameters of polyethylene rubber pendulum rod are set as density ρ = 1300 kg/m³, Young’s modulus E = 7.8 MPa, cross-sectional area A = 1 × 10⁻⁵ m², length of pendulum rod L = 2.0 m. The lumped mass m = 1.5789 kg is attached to the tail point of the pendulum rod and the gravity acceleration is g = 9.8 m/s². The conical pendulum system is initially set in O-YZ plan which has the initial velocity V_X0 = −5.422 m/s, V_Y0 = V_Z0 = 0 m/s. The polyethylene rubber conical pendulum is modeled by one isoparametric cable element.

Firstly, a quasi-static tensional process is modeled in which the static tensile strain of the polyethylene rubber pendulum rod will reach 0.2 which is equal to the theoretical value. This attached lumped weight is applied to excite large deformation rotation of the polyethylene rubber conical pendulum. Due to the inertia of the attached lumped weight, the maximum dynamic axial strain will be much larger than the static tensile strain.

Furthermore, the rotation process was modeled by the proposed HFML, the HMSS presented by Ding et al. [6], and the commercial software LS-DYNA SMP R11.0.0 which is a product of ANSYS Inc.. The commercial software LS-DYNA already has the cable element which can take the large deformation into consideration, besides, we have done the comparison about a two-dimensional pendulum system between theoretical solution and LS-DYNA result which demonstrates the solution of LS-DYNA is accurate and credible. In HFML and Ding’s HMSS simulation cases, the calculating time step is Δt = 2 × 10^-4 s and the terminal calculating time is t_end = 6 s. The cable element is modeled by a link 160 element and the lumped mass is treated as an attached particle in LS-DYNA, the time step of LS-DYNA is self-adapting. Figure 4a–c and d–f show the position and velocity responses of the lumped weight simulated by HFML, Ding’s HMSS, and LS-DYNA. The position and velocity responses of HFML match the results of LS-DYNA almost exactly, even for the large dynamic strain much greater than 20% occurred in the swing process. Meanwhile, the non-negligible error exists for Ding’s HMSS which is derived based on small deformation theory. By the comparison of HFML and LS-DYNA, the maximum error of the nodal position in Z-axial is less than 0.1%, and the maximum error of nodal velocity in Z-axial is less than 0.5%. The maximum pendulum length extends to 3.4948m and the dynamic logarithm strain is 55.81%.

The zero potential energy plan is set to Z = −L. As depicted in Figure 5, the system energy-time curve illustrates the proposed HFML will almost exactly keep the energy of the conical pendulum system constant as expected, a slight oscillation occurred due to the value discontinuity. However, the oscillation of system energy exists in Ding’s HMSS for the large deformation calculation, and the oscillation has a tendency to be larger along with the calculation time.

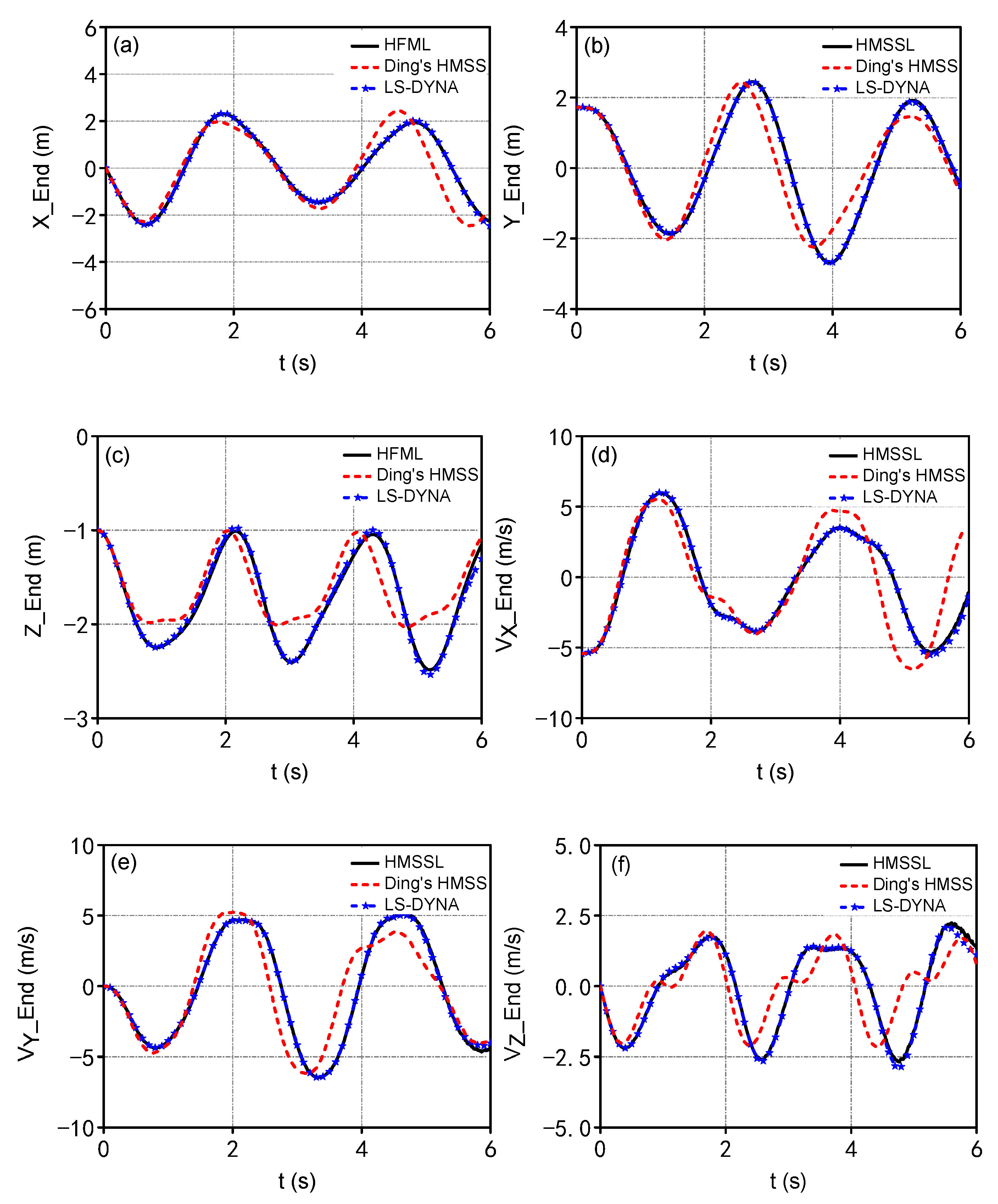
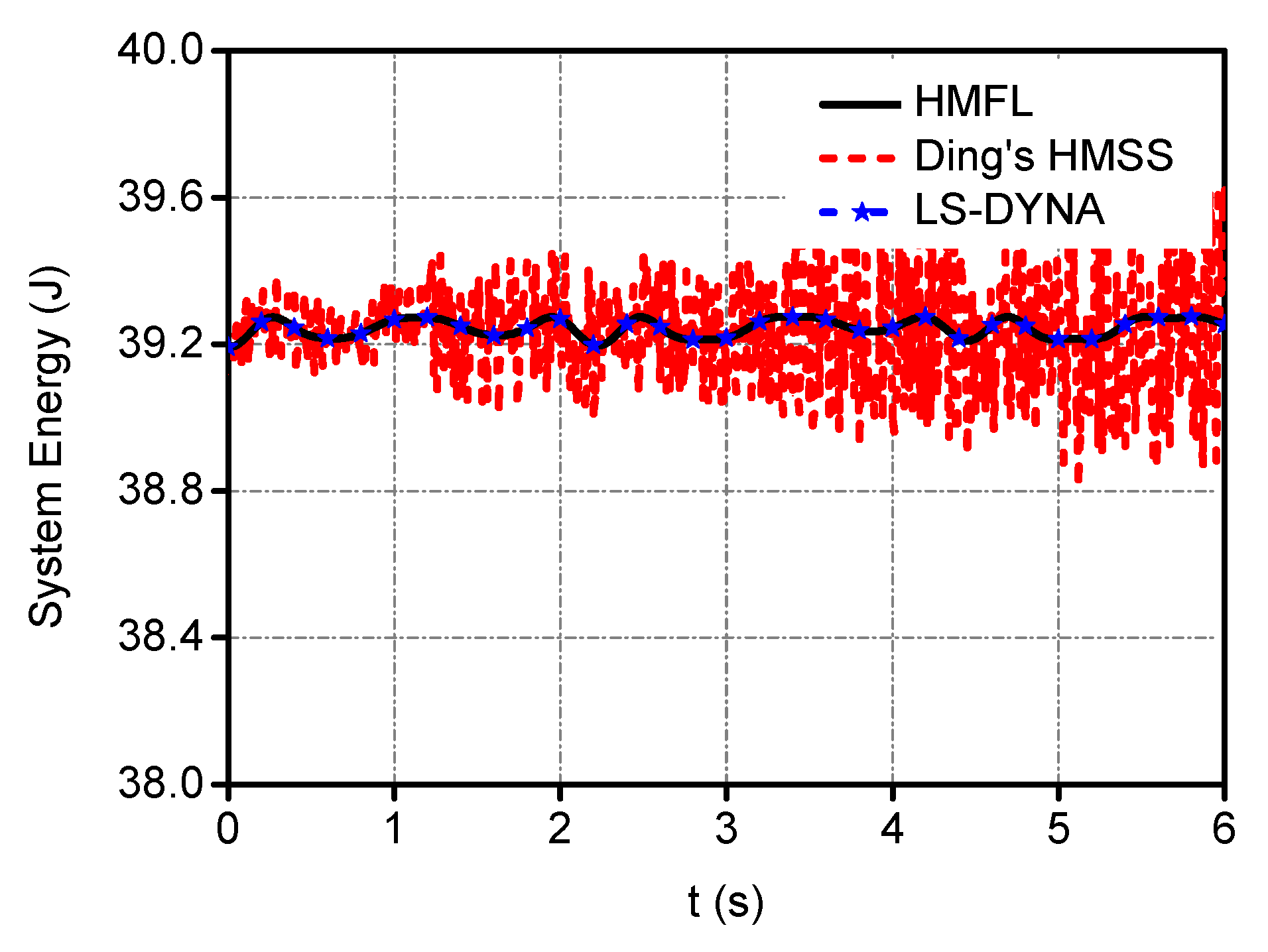
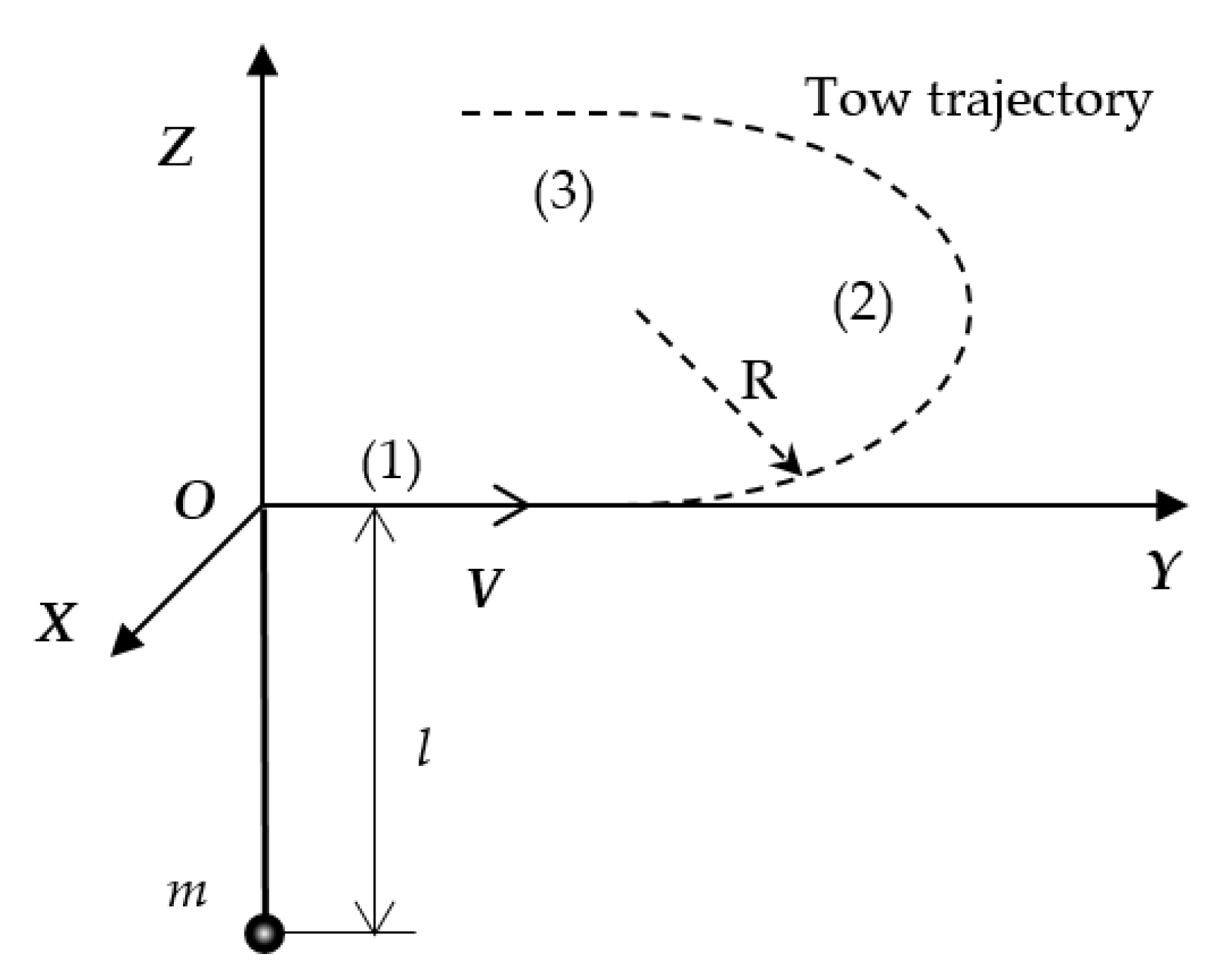
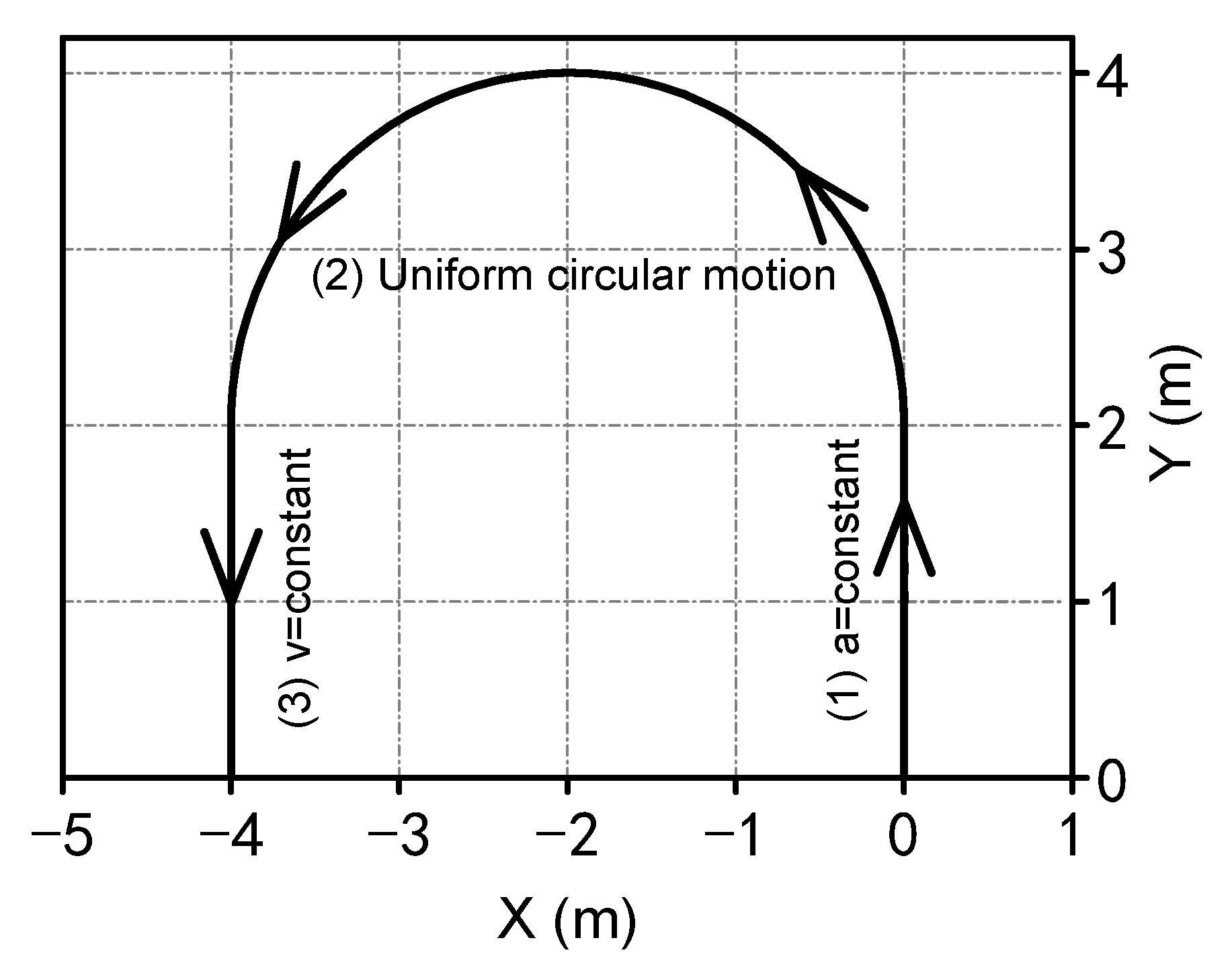
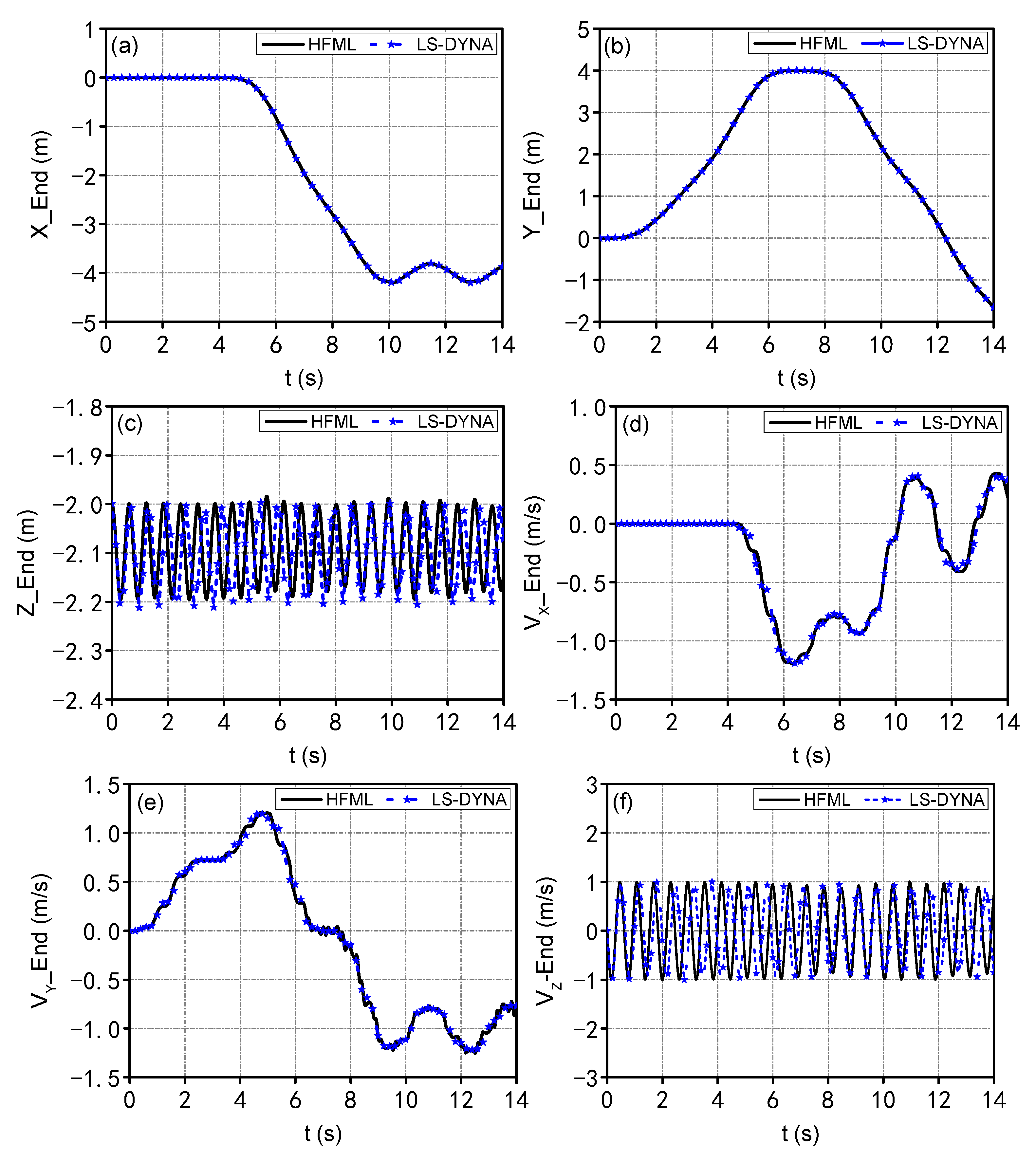
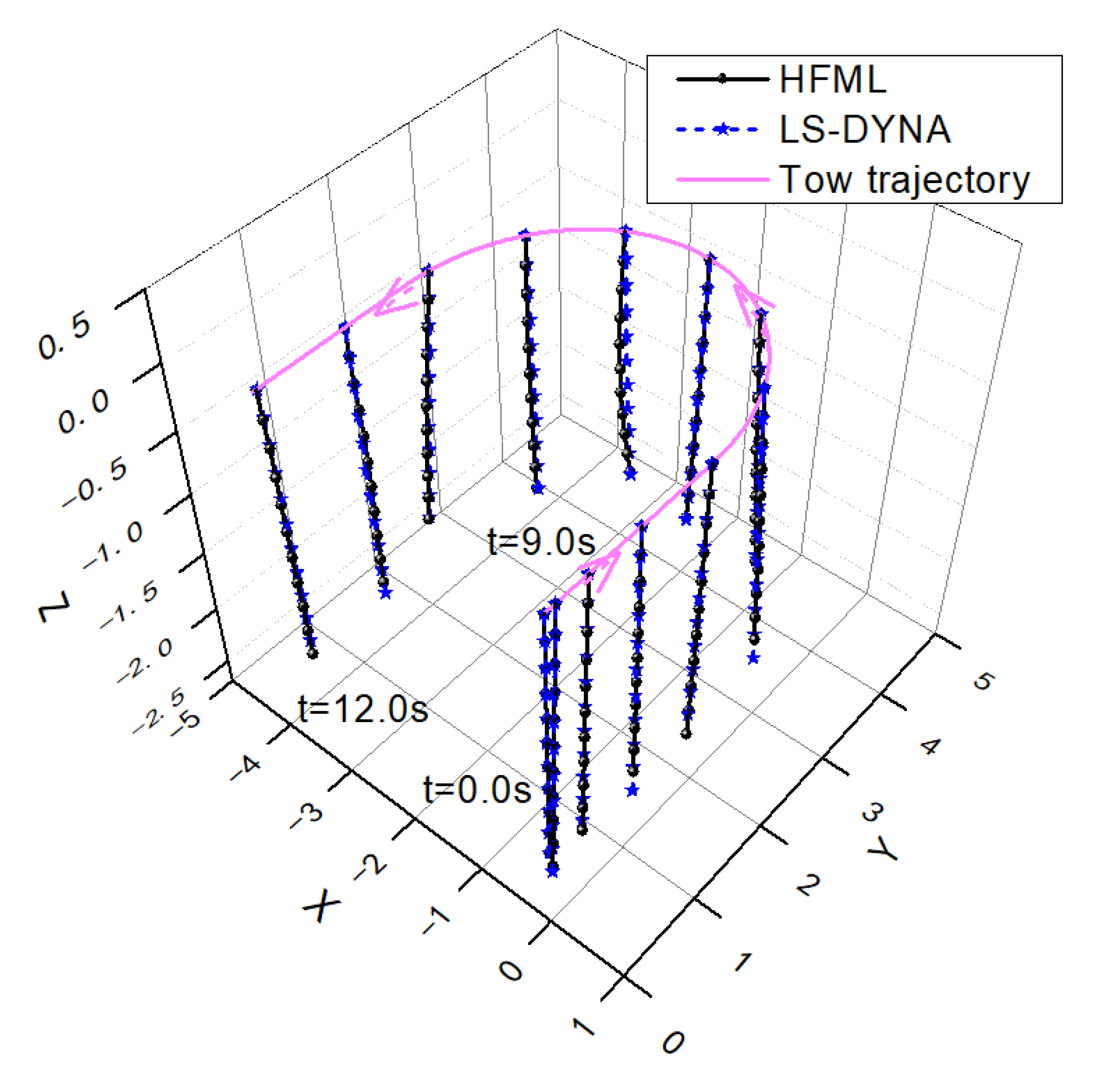
4.2. Towed Cable-Payload System in 180° U-Turn Maneuver

In this section, a towed cable-payload system in the 180° U-turn maneuver (Figure 6) is simulated by HFML and LS-DYNA. The towed system consists of a rubber tow cable and a lumped mass. Yang et al. [38] have investigated the dynamic analysis of cable-towed systems during the ship in a 180° U-turn process, the towed body is treated as a lumped mass. In the simulations, large deformation and displacements might occur if the mass of the towed weight is large enough, and then the logarithm strain will be applied. The material properties and sizes of the rubber cable are the same as those in Section 4.1. The towed lumped mass is m = 0.4 kg and 4% static tensile strain will be generated.

As shown in Figure 6, the 180° U-turn maneuver is set in three phases. The first phase is linear towing. The towing starts from the origin point of the global coordinates, and the linear towing trajectory (dotted portion) lies in the Z = 0 plane and along the positive OY-axis, the phase experiences 4 s and the acceleration is constant (0.25 m/s²). The second phase is circular towing in the Z = 0 plane. The tow node turns left after the first phase and moves constantly along the semicircular towing trajectory with the towing radius R = 2 m. The towing tangential velocity is 1 m/s. The last phase is linear towing again in the Z = 0 plane. The velocity vector is the same as the last one of the second phase. The towing velocity vector is invariable during the third phase. Hence, the three towing phases have the position boundary conditions:

$$\begin{array}{l}\{\begin{array}{l}X=0\\ Y=0.5a{t}^2\end{array} 0\le t<t_0,\{\begin{array}{l}X=-R+R\cos \left[\omega (t-t_0)\right]\\ Y=0.5a{t}_0^2+R\sin \left[\omega (t-t_0)\right]\end{array} t_0\le t<t_1,\{\begin{array}{l}X=-2R\\ Y=0.5a{t}_0^2-a{t}_0(t-t_1)\end{array} t_1\le t\le t_2\\ \hfill Z=0\hfill \end{array}$$

(34)

and the velocity boundary conditions:

$$\begin{array}{l}\{\begin{array}{c}{V}_X=0\\ V_Y=at\end{array}\hspace{1em}0\le t<t_0,\{\begin{array}{l}{V}_X=-Rw\sin \left[\omega (t-t_0)\right]\\ V_Y=Rw\cos \left[\omega (t-t_0)\right]\end{array}\hspace{1em}{t}_0\le t<t_1,\{\begin{array}{l}{V}_X=0\\ V_Y=-a{t}_0\end{array}\hspace{1em}{t}_1\le t\le t_2\\ \hfill V_Z=0\hfill \end{array}$$

(35)

where a = 0.25 m/s², t₀ = 4 s, t₁ = 4 + 2π s, and t₂ = 6 + 2π s. (X, Y, Z) and (V_X, V_Y, V_Z) are the position and velocity components of the tow point, respectively. The angular velocity of the circular towing is ω = 0.5 rad/s, respectively. Figure 7 illustrates the towing trajectory of the tow point in the Z = 0 plane.

Figure 8a–f shows the position and velocity responses of the free end of the rubber cable simulated by HFML and LS-DYNA. In the simulations, 10 logarithm strain elements are used by HFML, and 10 Link 160 elements are used by LS-DYNA. The time step for HFML is Δt = 2 × 10⁻⁴ s and the terminal calculating time is t_end = 6 s. By comparing the simulations by HFML and LS-DYNA, Figure 8a–c illustrates that the position responses in X-axis and Y-axis directions coincide with each other perfectly. A slight error occurs in the position oscillation in the Z-axis direction. The high-frequency oscillation is excited in the Z-axis direction mainly due to the gravity of lumped mass and the high towed speed, the dynamic response error in the Z-axis direction would be decreased by reducing the response frequency, such as reducing the time step, adopting longer cable or lower towed speed. The vibrational periods of the responses by HFML and LS-DYNA are 0.618 s and 0.665 s, respectively. They are slightly different from the theoretical period of the stretching vibration of the cable-towed system, 0.636 s. The two simulation periods have an error of about 7%. Figure 8d–f illustrates that the velocity responses in X-axis and Y-axis directions coincide with each other well. A slight error also occurs in the velocity oscillation in the Z-axis direction.

For the 180° U-turn towing process, Figure 9 illustrates the configurations of the cable calculated by HFML and LS-DYNA. The maximum dynamic strain is 9.75%. The simulating configurations by HFML and LS-DYNA fit perfectly with each other. The comparisons show that HFML using the logarithm strain representation can predict accurately the dynamic large strain configurations of the flexible cable.

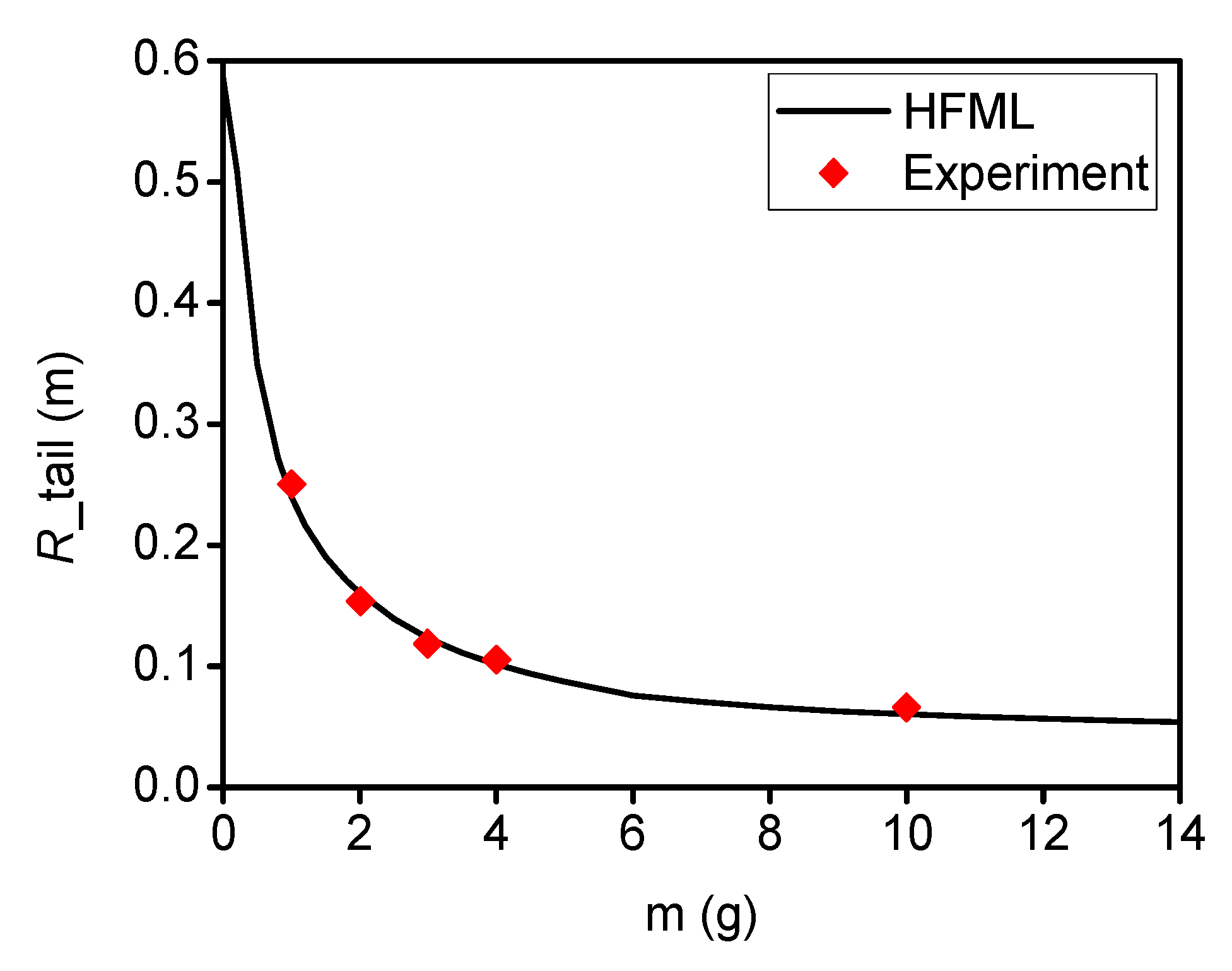
4.3. Experimental Validation of Circularly Towed System in Air

In this section, the proposed HFML will be validated by the towed cable-payload experiments of Williams et al. [39,40]. The aerodynamic resistance effect is taken into consideration due to the relative movement of towed system and air. In the experiments, the nylon cable with an attached mass is towed by a ceiling fan, in which the cable length l = 3.0 m, radius r = 7 × 10⁻⁴ m, density ρ = 1195.3 kg/m³ and Young’s modulus E = 1.0 GPa. The blade length of the ceiling fan is l_b = 0.645 m. The mass of the towed body is gradually increased from m = 0~10 g. The acceleration of gravity is set as g = 9.8 m/s². For different towed bodies, Williams et al. [39,40] measured the orbital radius of the cable tail in a steady state with the towed angular velocity ω = 7.54 rad/s.

The equivalent description is shown in Figure 10, HMFL is applied in this section to model the rotation processes of the towed pay-load systems in which the cable is modeled by 20 uniform elements, the drag coefficient of the cylinder cable is chosen as C_d = 1.2 for towed mass m ≤ 5 g and C_d = 1.72 for m > 5 g according to Sun [26]. The time step for HFML is Δt = 5 × 10⁻⁴ s and the terminal calculating time is dependent on whether the orbital radius of the cable tail can keep constant.

Due to that, Williams et al. [39,40] mentioned that the circularly towed system would achieve a reasonably stable motion state and the data about towing process was not offered, the turning radius of the free ends from the experiments by Williams et al. [39,40] when the towed systems achieve stable motion states would be calculated by the proposed HFML in this section. The time for the towed system achieving a steady towed state would be range from 10 s to 160 s with the mass range from 0 g to 14 g.

Figure 11 shows the variations of the stable R_tail for different towed mass retraced by HFML and experimental data [39,40]. The predicting results of HFML perfectly agree with the experimental data, HFML could effectively model the aerodynamic resistance. However, the calculation time of HFML is just several minutes which is higher efficient than the experimental study of the towed system moved in the medium. Meanwhile, the proposed HMFL is much more suitable for flexible cable analyses since it would keep convergent even for the mass of towed payload reach to 14 g while the lumped mass method presented by Williams et al. [39,40] would be non-convergent when the mass m ≥ 11 g.

The time costs of the presented HFML and the LS-DYNA is compared. In the simulation of LS-DYNA, the cable is modeled by 10 links 160 elements, and a mass element is applied to model the towed mass 14 g, 6 m × 6 m × 3.8 m air domain is modeled and divided into 136800 elements with an element size of 0.1 m; the material parameters are set to be the same with experimental tether. The simulation is carried out on an Intel (R) Core (TM) Quad i5-3470 CPU @ 3.20 GHz and 16 GB RAM. For the simulation up to 10s, it takes about 40 s by the presented HFML compiled in Visual C++ 6.0 environment, while it costs about 2 hours and 25 minutes by LS-DYNA—about 99.55% of computational time is saved by the proposed HFML. The comparison of the calculation efficiency with LS-DYNA shows that HFML is higher efficient and suitable for rigid-flexible-liquid coupling dynamic problems.

5. Conclusions

A robust Hamiltonian finite element method HFML is presented in this paper to analyze the spatial dynamics of the towed cable-payload system which is a rigid-flexible-liquid coupling problem, in which logarithmic strain is applied to model the large deformation cable. A direct integral method is derived to calculate the aerodynamic effect in which the traditional coordinate transformation is avoided, fourth-order closed Newton-Cotes formulate is applied to analyze the integration of Morison’s equation. The proposed HFML can exactly conserve the system energy and accurately predict the dynamic responses of the towed cable-payload system. It is more accurate to analyze the towed dynamic problem with large deformation than existing Ding’s HMSS in which the dynamic equations are derived based on small deformation theory. Furthermore, the efficiency to treat the rigid-flexible-liquid coupling dynamic problem of HMFL is much higher than LS-DYNA since plenty of medium elements are not required in LS-DYNA simulations. The proposed HFML would be further applied to the technical improvement of towed-payload systems in more engineering fields.