Integral Sliding Mode Based Finite-Time Tracking Control for Underactuated Surface Vessels with External Disturbances
Abstract
:1. Introduction
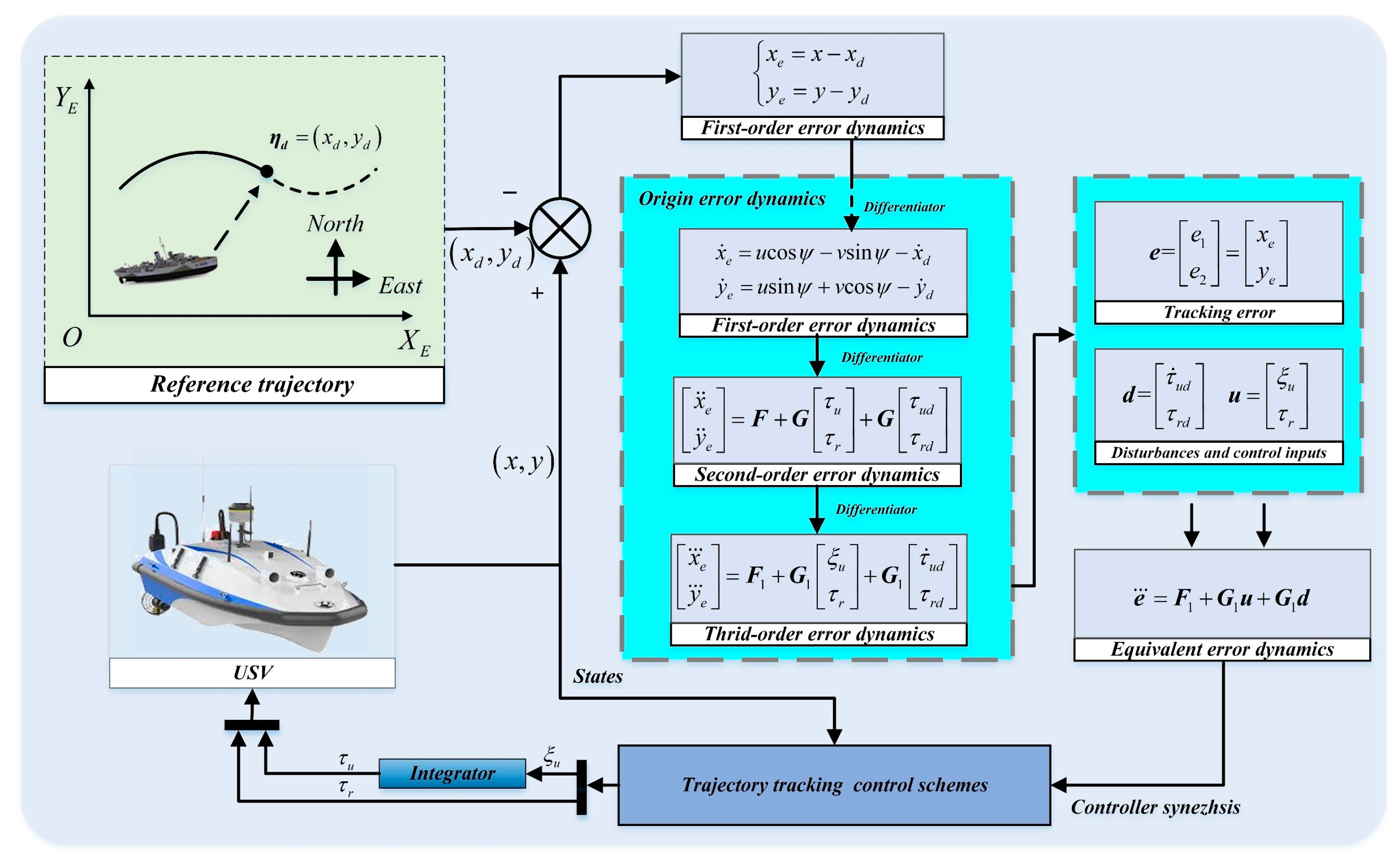
2. System Dynamics and Problem Formulation
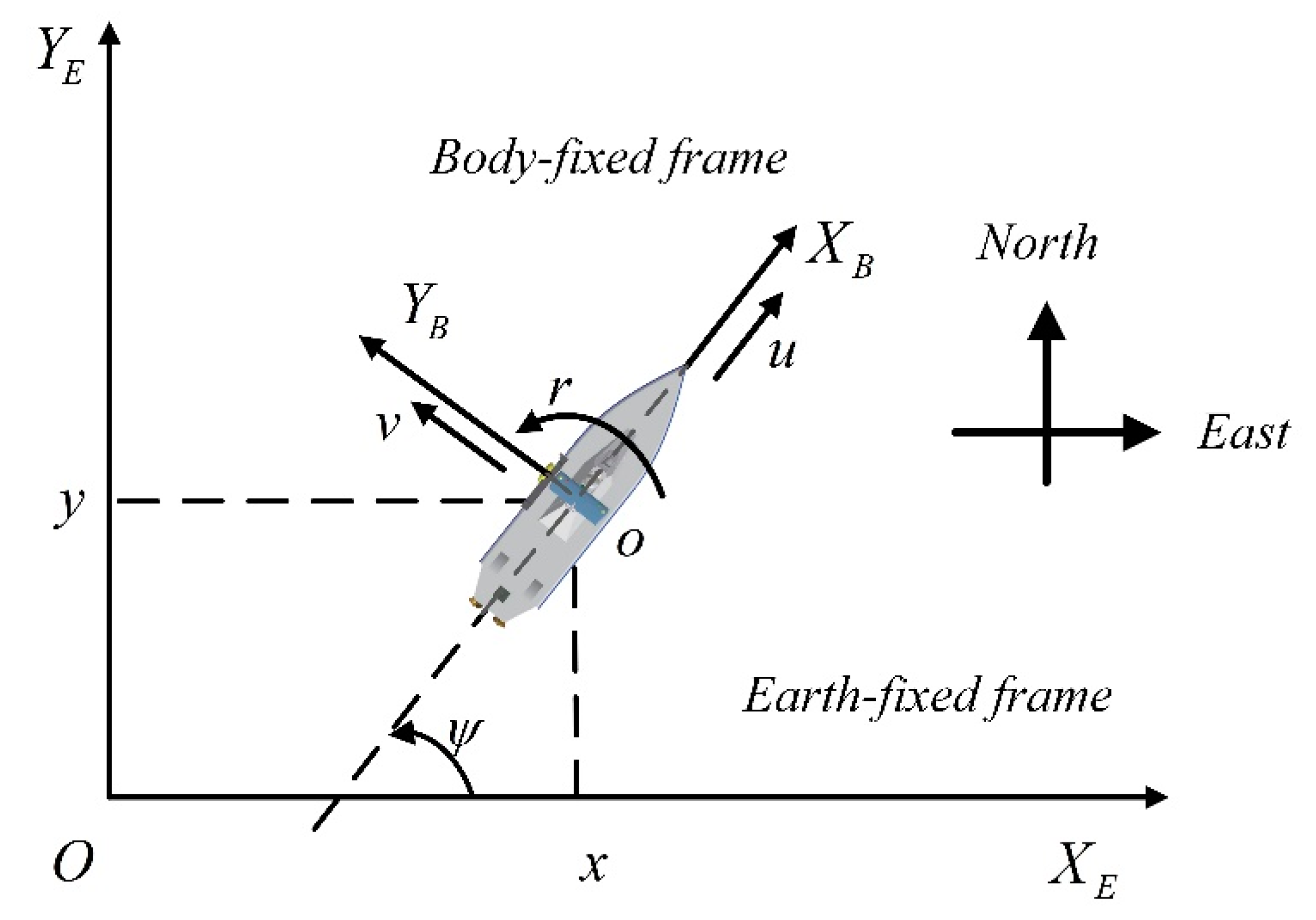
2.1. Modeling of USV
2.2. Notations, Lemmas and Assumptions
3. Controller Design
3.1. Model Transformation
3.2. Adaptive Controller Design with External Disturbances
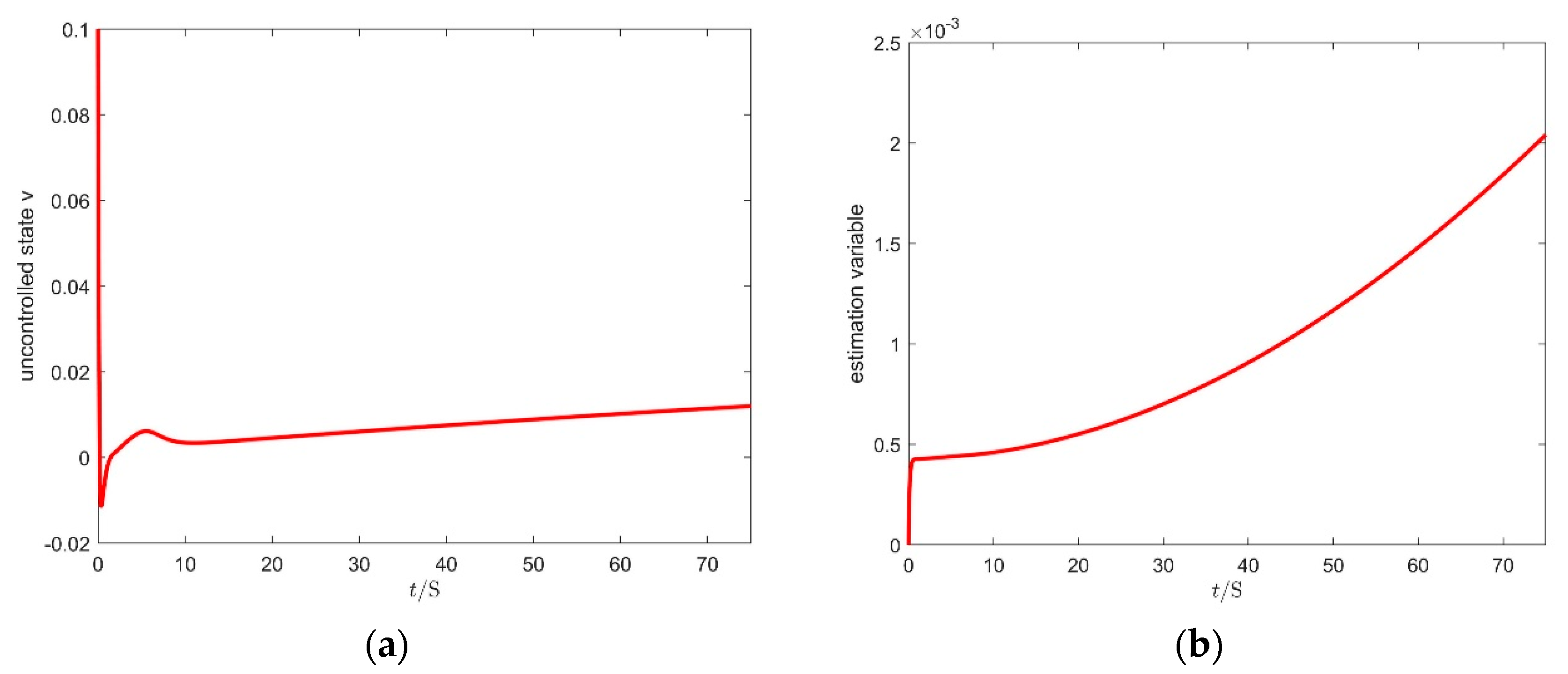
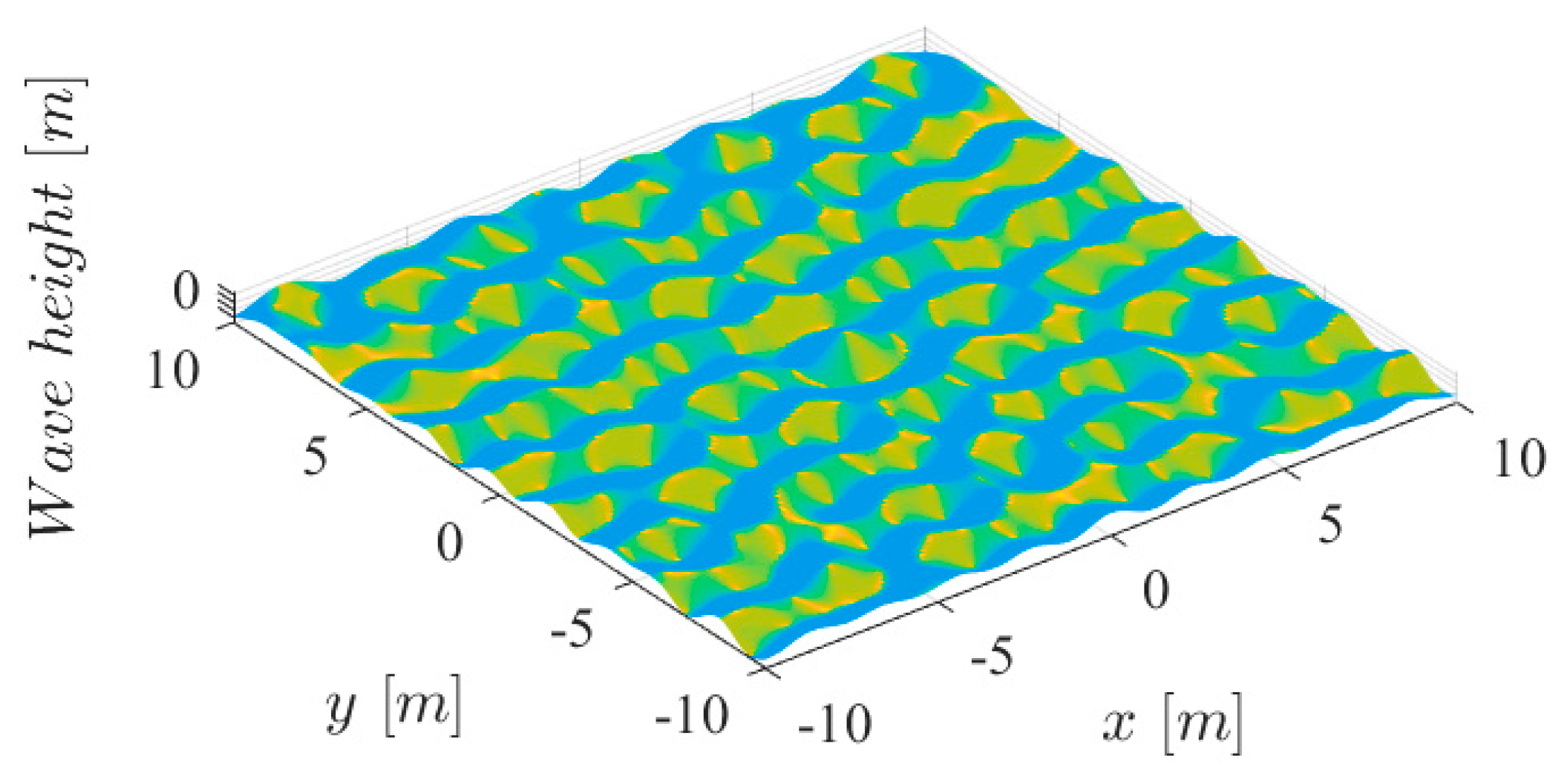
4. Simulation Results
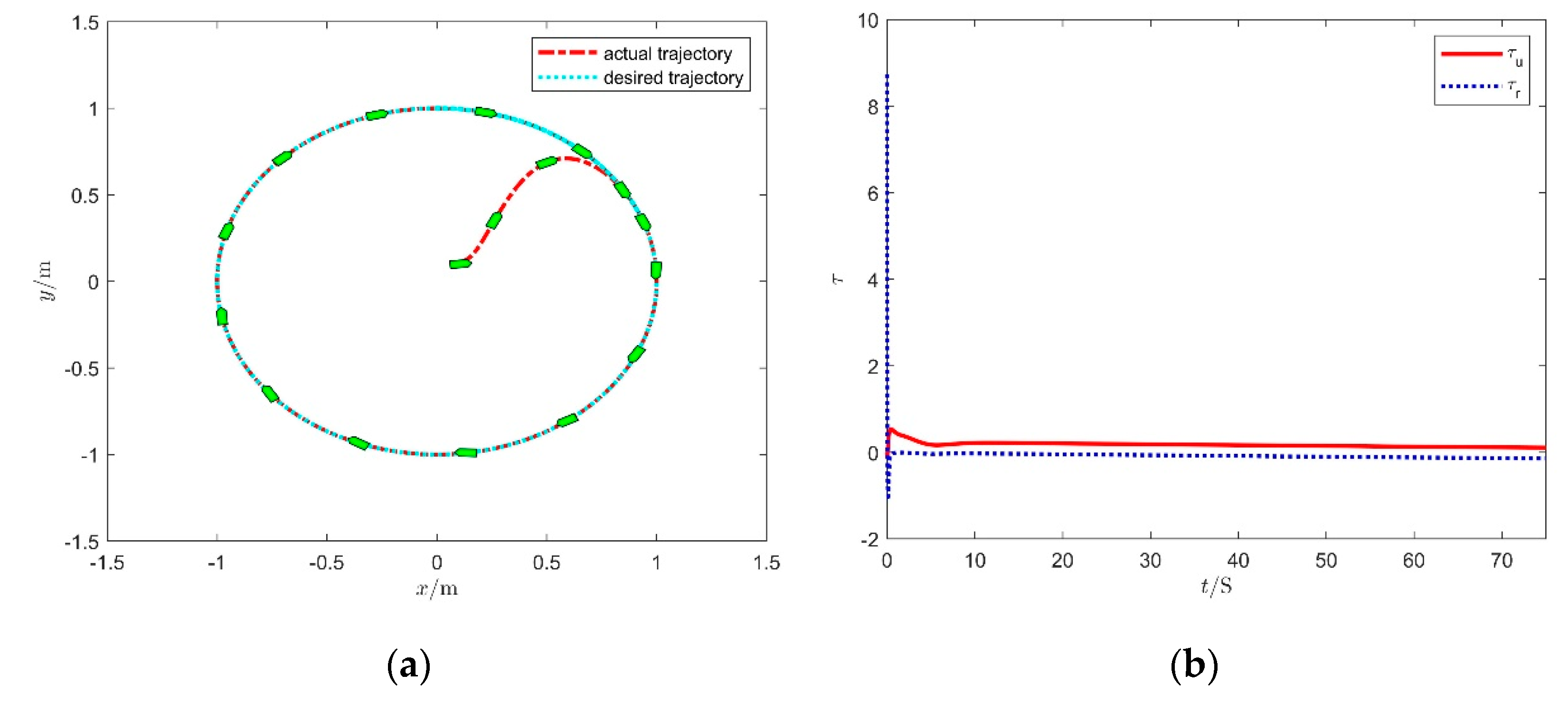
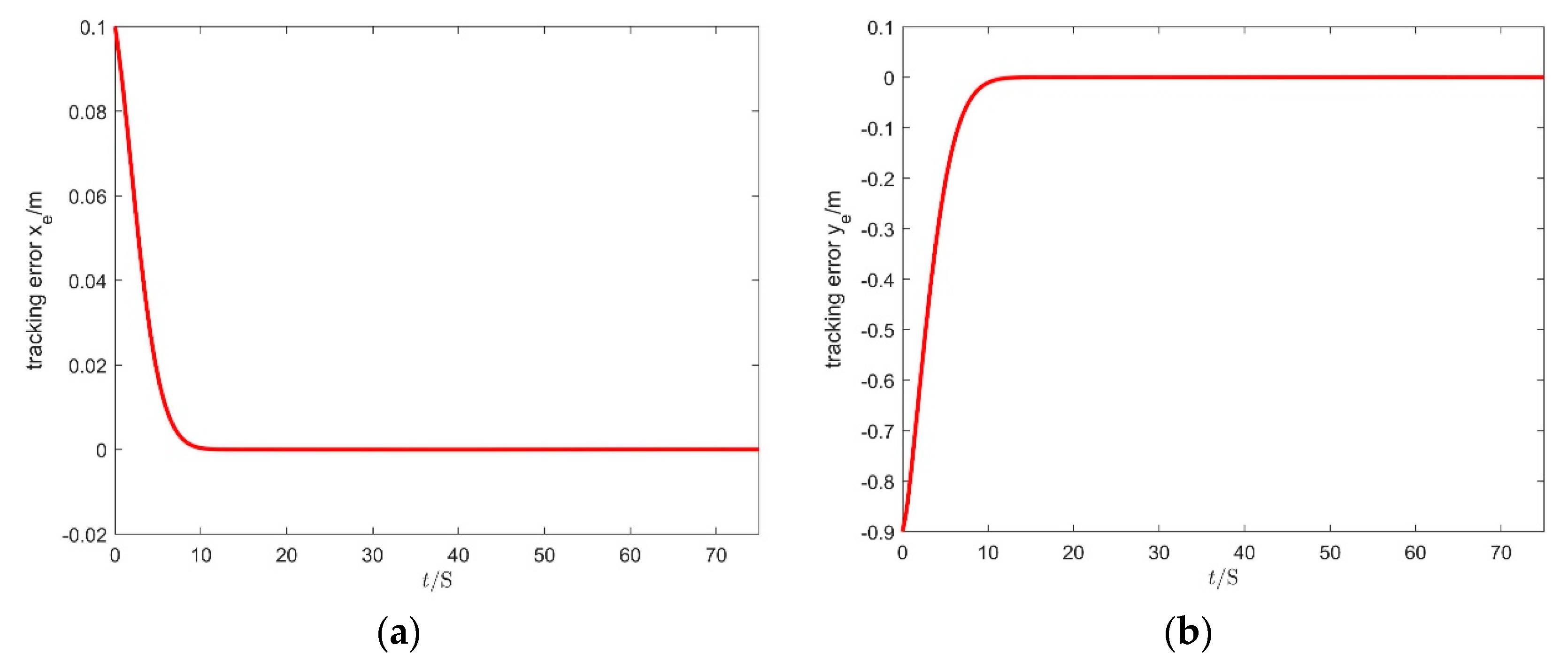
4.1. Simulation of ISMS Controller
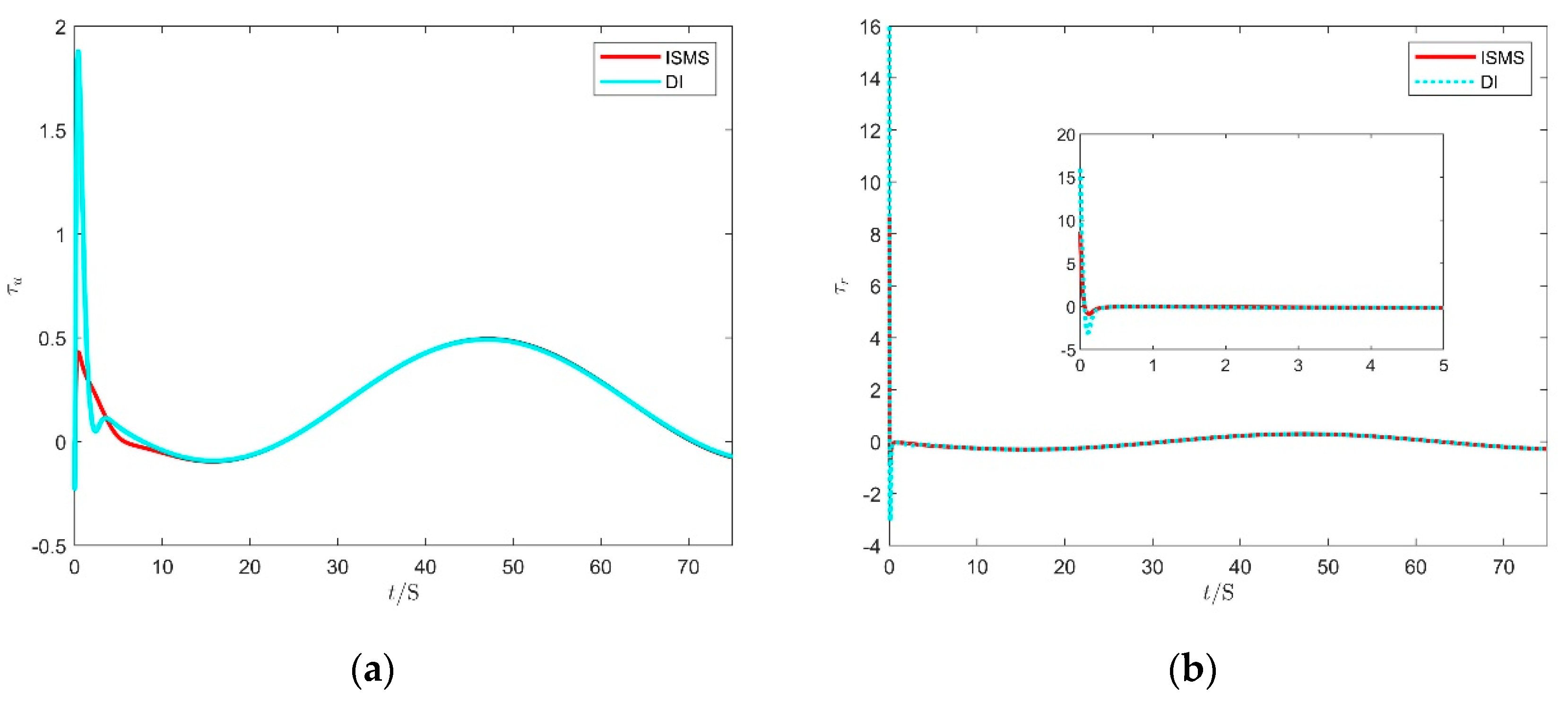
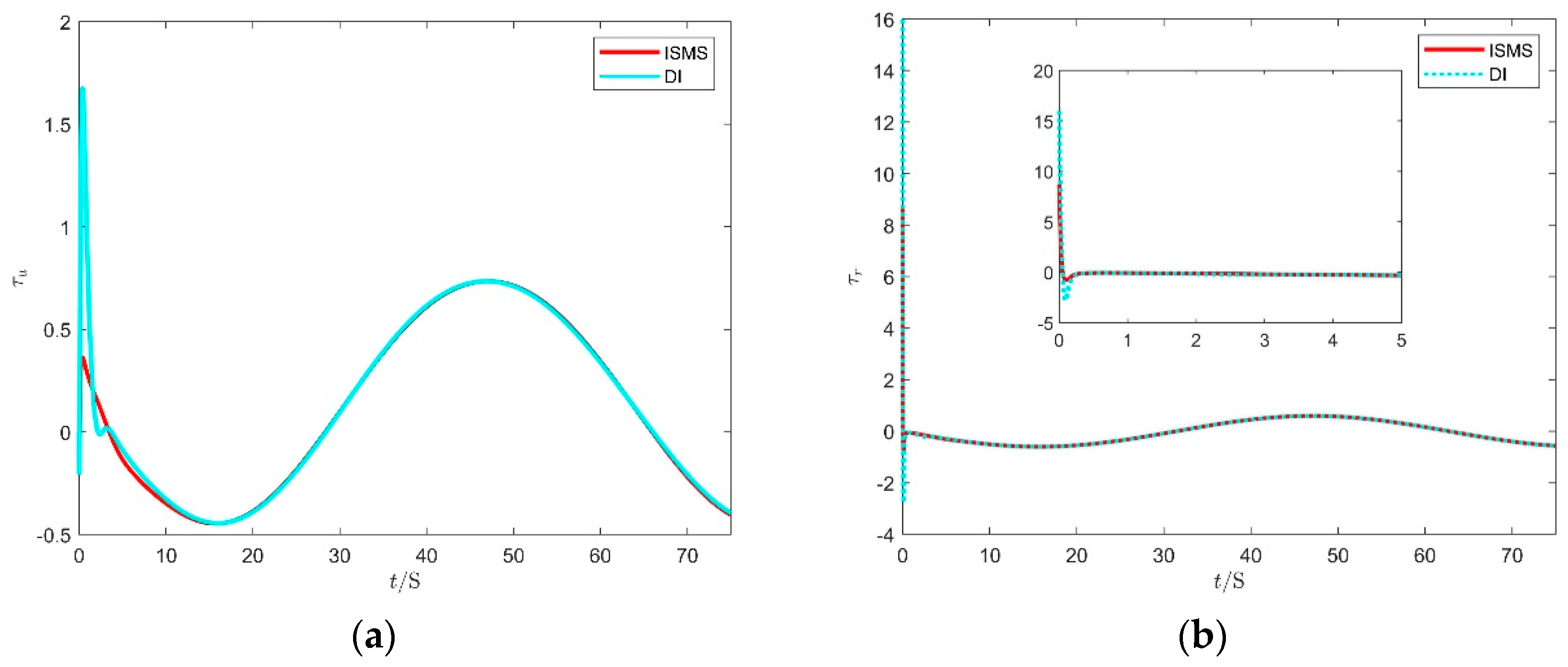
4.2. Comparative Simulation Results on the Different Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
References
- Dai, S.-L.; He, S.; Wang, M.; Yuan, C. Adaptive Neural Control of Underactuated Surface Vessels with Prescribed Performance Guarantees. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3686–3698. [Google Scholar] [CrossRef]
- He, S.; Dai, S.-L.; Luo, F. Asymptotic Trajectory Tracking Control With Guaranteed Transient Behavior for MSV with Uncertain Dynamics and External Disturbances. IEEE Trans. Ind. Electron. 2018, 66, 3712–3720. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, Z.; Zhang, W. Adaptive output-feedback control with prescribed performance for trajectory tracking of underactuated surface vessels. ISA Trans. 2019, 95, 18–26. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Robust adaptive formation control of underactuated autonomous surface vessels based on MLP and DOB. Nonlinear Dyn. 2018, 94, 503–519. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y.; Wang, N. Adaptive trajectory tracking algorithm of unmanned surface vessel based on anti-windup compensator with full-state constraints. Ocean Eng. 2020, 200, 106906. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y.; Li, X.; Du, Y.; Deng, Z. Finite-time trajectory tracking control of unmanned surface vessel with error constraints and input saturations. J. Frankl. Inst. 2019, 357, 11472–11495. [Google Scholar] [CrossRef]
- Zhang, P.; Guo, G. Fixed-time switching control of underactuated surface vessels with dead-zones: Global exponential stabilization. J. Frankl. Inst. 2020, 357, 11217–11241. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time velocity-free sliding mode tracking control for marine surface vessels with uncertainties and unknown actuator faults. Ocean Eng. 2020, 201, 107107. [Google Scholar] [CrossRef]
- Weng, Y.; Wang, N.; Soares, C.G. Data-driven sideslip observer-based adaptive sliding-mode path-following control of underactuated marine vessels. Ocean Eng. 2020, 197, 106910. [Google Scholar] [CrossRef]
- Mina, T.; Singh, Y.; Min, B.-C. Maneuvering Ability-Based Weighted Potential Field Framework for Multi-USV Navigation, Guidance, and Control. Mar. Technol. Soc. J. 2020, 54, 40–588. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive sliding mode trajectory tracking control for unmanned surface vehicle with modeling uncertainties and input saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Sun, X.; Wang, G.; Fan, Y. Adaptive Backstepping Sliding Mode Tracking Control for Underactuated Unmanned Surface Vehicle With Disturbances and Input Saturation. IEEE Access 2020, 9, 1304–1312. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Shuailin, L.; Er, M.J. Integral sliding mode based finite-time trajectory tracking control of unmanned surface vehicles with input saturations. India J. Geo Mar. Sci. 2017, 46, 2493–2501. [Google Scholar]
- Yao, Q. Fixed-time trajectory tracking control for unmanned surface vessels in the presence of model uncertainties and external disturbances. Int. J. Control 2020, 1–11. [Google Scholar] [CrossRef]
- Yao, Q. Adaptive finite-time sliding mode control design for finite-time fault-tolerant trajectory tracking of marine vehicles with input saturation. J. Frankl. Inst. 2020, 357, 13593–13619. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, C.; Yu, H. Finite-Time PLOS-Based Integral Sliding-Mode Adaptive Neural Path Following for Unmanned Surface Vessels With Unknown Dynamics and Disturbances. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1500–1511. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time output feedback trajectory tracking control of marine surface vessels subject to unknown external disturbances and uncertainties. ISA Trans. 2019, 93, 145–155. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, B.; Su, Y.; Zheng, Y.; Zheng, S. Fixed-time neural network trajectory tracking control for underactuated surface vessels. Ocean. Eng. 2021, 236, 109416. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fault-Tolerant Fixed-Time Trajectory Tracking Control of Autonomous Surface Vessels with Specified Accuracy. IEEE Trans. Ind. Electron. 2019, 67, 4889–4899. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, G.; Qiao, L.; Zhang, W. Adaptive output-feedback formation control for underactuated surface vessels. Int. J. Control. 2018, 93, 400–409. [Google Scholar] [CrossRef]
- Dai, S.L.; He, S.; Lin, H. Transverse function control with prescribed performance guarantees for underactuated marine surface vehicles. Int. J. Robust Nonlinear Control 2019, 29, 1577–1596. [Google Scholar] [CrossRef]
- Wang, S.; Tuo, Y. Robust trajectory tracking control of underactuated surface vehicles with prescribed performance. Pol. Marit. Res. 2020. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, B.S. Guaranteed performance design for distributed bounded containment control of networked uncertain underactuated surface vessels. J. Frankl. Inst. 2017, 354, 1584–1602. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. An error transformation approach for connectivity-preserving and collision-avoiding formation tracking of networked uncertain underactuated surface vessels. IEEE Trans. Cybern. 2018, 49, 2955–2966. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Yao, M.; Xu, J.; Zhang, W. Robust neural event-triggered control for dynamic positioning ships with actuator faults. Ocean Eng. 2020, 207, 107292. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, W.; Wang, D.; Peng, Z. Event-triggered extended state observers design for dynamic positioning vessels subject to unknown sea loads. Ocean Eng. 2020, 209, 107242. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Im, N.; Zhang, G.L.; Zhang, Q. Model-based event-triggered tracking control of underactuated surface vessels with minimum learning parameters. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4001–4014. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Nie, Z.; Yu, Y.; Hu, S.; Peng, Z. Event-triggered fuzzy control of networked nonlinear underactuated unmanned surface vehicle. Ocean Eng. 2020, 213, 107540. [Google Scholar] [CrossRef]
- Ye, L.; Zong, Q. Tracking control of an underactuated ship by modified dynamic inversion. ISA Trans. 2018, 83, 100–106. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, S.; Sun, C. Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dyn. 2013, 73, 229–244. [Google Scholar] [CrossRef]




| Model Parameters | Values |
|---|---|
| [m11, m22, m33]T | [1.956, 2.405, 0.043]T (Unit: kg) |
| [d11, d22, d33]T | [2.436, 12.992, 0.0564]T |
| Control Parameters | Values |
|---|---|
| [k1, k2, k3]T | [1, 3, 3]T |
| [η1, η2, η3]T | [5, 5, 0.5]T |
| γ, α | 0.05, 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Feng, Y.; Liu, T.; Yu, X.; Wang, X. Integral Sliding Mode Based Finite-Time Tracking Control for Underactuated Surface Vessels with External Disturbances. J. Mar. Sci. Eng. 2021, 9, 1204. https://doi.org/10.3390/jmse9111204
Xiao Y, Feng Y, Liu T, Yu X, Wang X. Integral Sliding Mode Based Finite-Time Tracking Control for Underactuated Surface Vessels with External Disturbances. Journal of Marine Science and Engineering. 2021; 9(11):1204. https://doi.org/10.3390/jmse9111204
Chicago/Turabian StyleXiao, Yunfei, Yuan Feng, Tao Liu, Xiuping Yu, and Xianfeng Wang. 2021. "Integral Sliding Mode Based Finite-Time Tracking Control for Underactuated Surface Vessels with External Disturbances" Journal of Marine Science and Engineering 9, no. 11: 1204. https://doi.org/10.3390/jmse9111204






