Effects of Clay Mineral Composition on the Dynamic Properties and Fabric of Artificial Marine Clay

Abstract

Marine clays are easily affected by different mineral composition in cyclic load-based geological hazards. Therefore, based on analyzing the mineral composition of natural marine clay, it is the key to predict the dynamic properties of natural materials under cyclic loading by using quantitated artificial marine clay. In this study, the marine clay found in the South China Sea deltas was investigated. Based on the results of geological conditions and mineral composition analyses, raw non-clay minerals (such as quartz, albite) and clay minerals (such as Na-montmorillonite and kaolinite) were used to produce artificial marine clay, the dynamic properties of which were studied from the impact of mineral composition. Dynamic triaxial laboratory testing for artificial marine clay comprising various clay minerals was performed under identical test conditions. The artificial marine clay with high montmorillonite content exhibited slower development of strain, more sluggish growth in pore water pressure, more rounded hysteresis curves, greater stiffness, and more prolonged viscous energy growth than the clay with low montmorillonite content. In addition, the flocculated fabric of the artificial marine clay with high montmorillonite content demonstrated sufficient pore space changes, more uniform pore distribution, and larger specific surface area than the dispersed fabric of the clay with low montmorillonite content. The factors arising from the influence of montmorillonite may lead to microstructural and fabric changes, hinder the development of pore water, and increase intergranular contact stiffness as well as delay the cyclic strain amplitude at the breakpoint of viscous energy dissipation. In general, the results presented in this study confirm that clay minerals, especially montmorillonite, have significant influence on the dynamic properties of large strain.

1. Introduction

The dynamic properties of marine clay under cyclic loading have received extensive attention to date. This is primarily due to marine clay being significantly affected by earthquakes [1,2,3,4,5], traffic loads [6,7,8], and wave loads [9,10,11]. For example, in the Alaska earthquake of 1964 [12] and the Mexican earthquake of 1985 [13], marine clays along the respective coastal and delta areas of these regions were severely affected, leading to the clay-related failure of marine infrastructures and slopes, as well as a large number of casualties and property losses. The studies relating to these disasters so far were aimed at informing on and understanding the cyclic behavior of marine clays [14,15].

Generally, due to the genesis of bedrock [16,17,18], the climate [19,20,21], and the sedimentation cycle of transgression and regression [22,23,24], the mineral composition of Quaternary marine clays in different deltas or local deltas is obviously different. The difference of mineral composition is the main reason for the difference of the Atterberg limits water content of marine clay. Meanwhile, the dynamic characteristics of marine clay under cyclic loading are affected by many factors [25,26], such as plasticity index (PI), confining pressure, void ratio, over-consolidation, and initial static shear stresses, etc. The extension parameter of the Atterberg limit water content, PI, directly determines the classification and physical properties of soils [27]. Additionally, the PI value is mainly influenced by the mineral composition and sediment fabric, which was also found to affect the dynamic properties of marine clay in laboratory dynamic testing [28].

Clay minerals in cohesive soils have frequently been included in research on dynamic properties. Marcuson and Wahls [29] studied the effects of consolidation time on dynamic shear modulus in remolded cohesive soils samples with kaolinite and calcium-based montmorillonite (Ca-montmorillonite). Subsequently, Fahoum et al. [30] and Park and Kim [31] used various artificial clay minerals to predict the dynamic properties of cohesive soil in their studies, which indicated that clay soils with a higher plastic mineral content provided better dynamic properties such as cyclic strength. Recent researches [32,33,34,35] summarized and suggested that a) a critical level of clay mineral content does exist; b) that clay minerals exhibit different dynamic property trends before and after this critical point; yet c) this critical point disappears when the clay particles consist in highly plastic minerals. The reason for this phenomenon is explained by the different microscopic fabric between clay minerals and coarse particles in the soil [36]. The above research has demonstrated that clay minerals have an important effect on the dynamic properties of cohesive soils, and also proved that various artificial clay minerals could be used as substitutes for clay particles in cohesive soils to study the influence of clay mineral composition on dynamic properties.

Although many studies of the dynamic properties achieved by adding artificial clay minerals to clays were conducted, a number of specific problems pertaining to dynamic properties were identified in marine clay—as a type of clay—comprising artificial clay minerals. These issues required urgent solutions which were sought in the present study.

• Previous research on the effects of mineral composition on the dynamic properties of cohesive soils aimed to identify the influence of mineral composition in sand–clay cohesive soils on their dynamic properties. However, little data exist to quantify the effect of clay minerals in marine clay on the latter’s dynamic properties under large strain. According to Boulanger and Idriss [37,38], large strain and excess pore water pressure rapidly developed in sand–clay mixture with clay minerals, which was contrary to the gradual development of marine clay. This different development between sand–clay cohesive soil and marine clay was due to the failure of sand–clay mixture from excess pore water pressure, while the failure of marine clay arose from the development of strain and eventual fabric collapse. Therefore, we should re-study the dynamic properties of marine clay under large strain by focusing on mineral composition, especially clay minerals, and the fabric formed by clay minerals.
• Natural marine clay is generally composed of a variety of non-clay minerals (such as quartz and albite) and clay minerals (such as montmorillonite and kaolinite). Unlike other cohesive soils, the non-clay mineral particle size of marine clay is generally small and similar to that of clay mineral particles [39]. However, few studies [40,41] to date have investigated the dynamic properties of non-clay minerals with similar particle size to clay particles in marine clay. In addition, the difference in particle size between coarse quartz particles and fine clay particles in marine clay was found significantly to affect the mechanical properties of marine clay, (e.g., cyclic strength [42] and peak strength [43]). The mineral composition of natural marine clay is furthermore complex, and its content in various minerals cannot be controlled artificially. It is therefore difficult to investigate the influence of mineral content on dynamic properties. Studying the effects of mineral content on dynamic properties would require overcoming difficulties in achieving sample uniformity within laboratory dynamic testing. These challenging problems result from differences in the deposition rate from different minerals [44] and from the effect of consolidation time under high cementation conditions [45]. These research shortcomings and complexities of marine clays indicate that the mineral composition and particle size of natural marine clay in the relevant local area should imperatively be considered when studying the influence of mineral composition on the large strain dynamic properties of marine clay.

In addition, clay minerals significantly impact on the microstructure and fabric of different clay minerals specimens. Some previous studies [46,47] found that the influence of mineral composition on mechanical properties, especially dynamic properties, could not be ignored for cohesive soil. Sun et al. [48] proved that the microstructure and fabric of natural marine clay with the same initial and loading states correlated with their mechanical properties by performing test using a field emission scanning electron microscope. Meanwhile, Cuisinier et al. [49] demonstrated the alkaline solution weakened the shear strength behavior of compacted artificial bentonite–argillite mixture by combining scanning electron microscopy (SEM) and mercury intrusion porosimetry (MIP) testing. However, these studies still do not consider the mineral composition as a variable, especially the content of clay minerals, when systematically studying the influence of microstructure and fabric on the dynamic properties of artificial marine clays.

Therefore, to investigate the effects of clay mineral composition on the dynamic properties and sediment fabric of marine clay under large strain, laboratory dynamic triaxial testing was conducted with clay mineral content as the primary research parameter, and the Atterberg limits and PI as auxiliary parameters. Based on the mineral composition of natural marine clays in two of the largest estuarine deltas (Pearl River Delta and Han River Delta) in Guangdong province, South China, four types of raw mineral powder (quartz, albite, Na-montmorillonite, and kaolinite) with similar particle sizes were used to produce the artificial marine clays. The research focused on the stiffness degradation and energy dissipation of different clay minerals. Subsequently, the sediment fabric of microstructure and microporosity in artificial marine clay specimens were examined using low-vacuum environmental scanning electron microscopy (LVESEM) testing and mercury intrusion porosimetry (MIP) testing. It was anticipated that the test results would help establish a research method to quantify the role of clay minerals in the dynamic properties and fabric of marine clay. The conclusions were proposed to help improve the understanding and application of mineralogy and engineering geology in studying the mechanical properties of marine clay.

2. Materials and Methods

2.1. Mineral Composition of Natural and Artificial Marine Clay

2.1.1. Geological Conditions and Mineral Composition of Natural Marine Clay

Since the Pliocene in the Neogene, the second Himalayan movement caused several northeast to southwest orientated fault zones under the two estuary (Pearl River and Han River) Deltas, which resulted in obstructing both the Pearl and Han Rivers in Guangdong Province, South China [50]. The existence of fault zones in close proximity of the South China Sea resulted in the more significant formation of Quaternary marine sediments along the delta front to the outside of the most extended shell sand bar, than continental sedimentation formation. Both deltas were formed during the Mindel-Riss and Riss-Wurm interglacial periods. Marine clay formed as a result of transgression during the Riss-Wurm interglacial, Atlantic, and Sub-Atlantic periods [51]. During these periods, three marine clay layers were formed from three sedimentary cycle of the Quaternary deposits in Pearl River Delta. However, due to only weak regression during the Sub-boreal period, which may have been negligible, continuous transgression occurred during the Atlantic and Sub-Atlantic periods, eventually leading to the formation of two sedimentary cycle of Quaternary deposits in Han River Delta [52].

In order to analyze the mineral composition of both estuarine deltas, three marine clay specimens were sampled from them and mineral composition test results were measured by X-ray diffraction. The basic physical properties of these three marine clays are listed in

Table 1. The basic physical properties in marine clay of two deltas in the South China Sea.

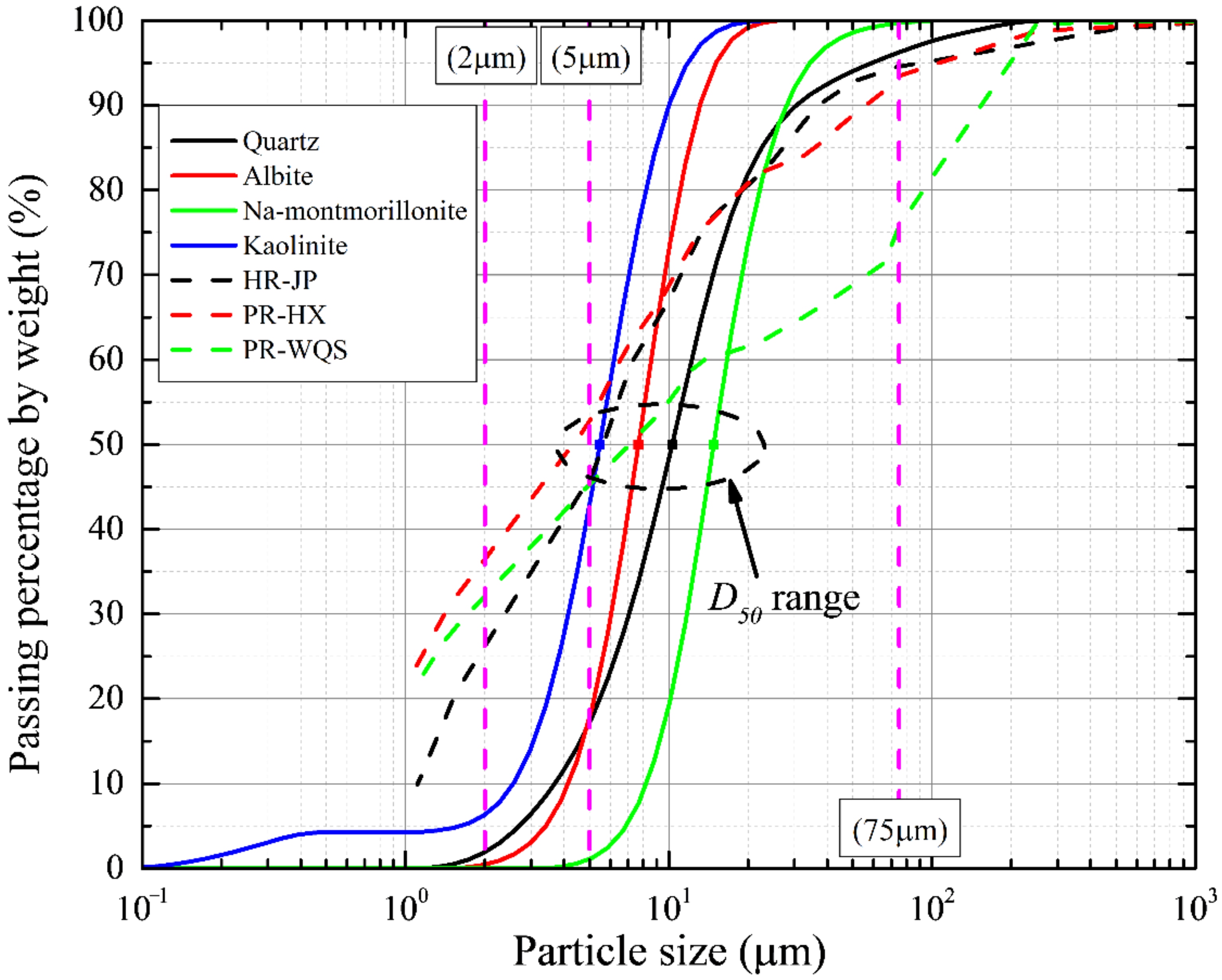
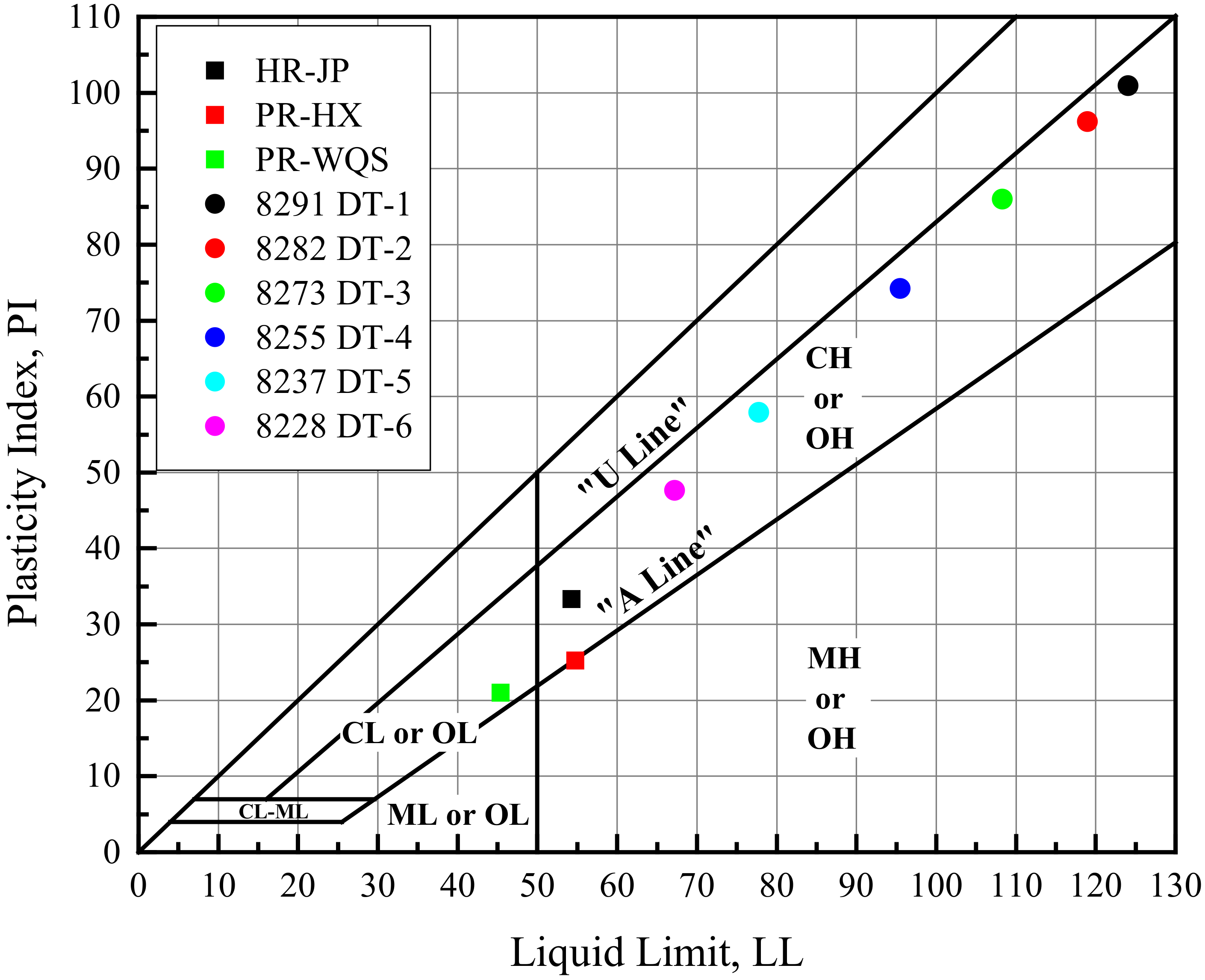
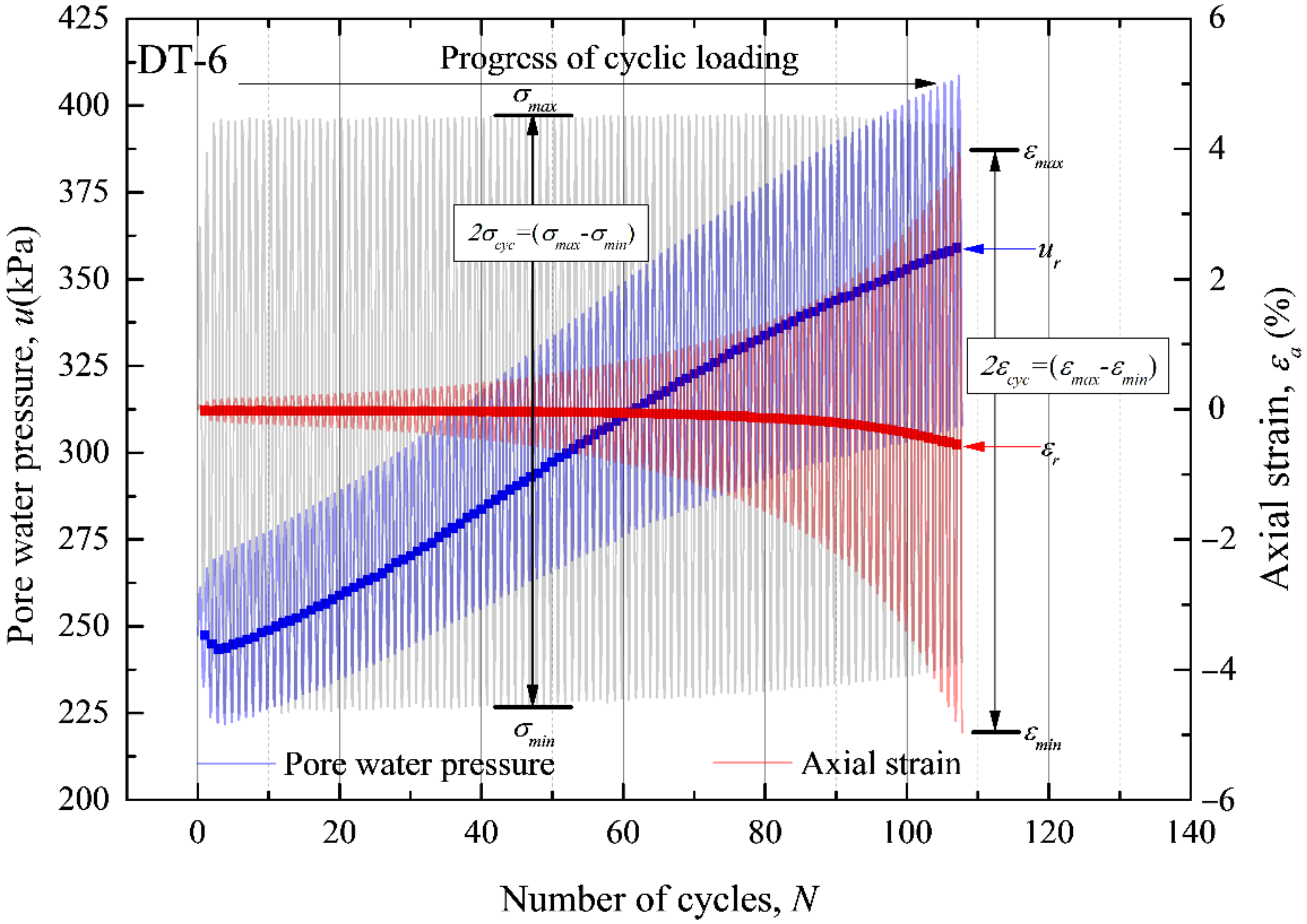
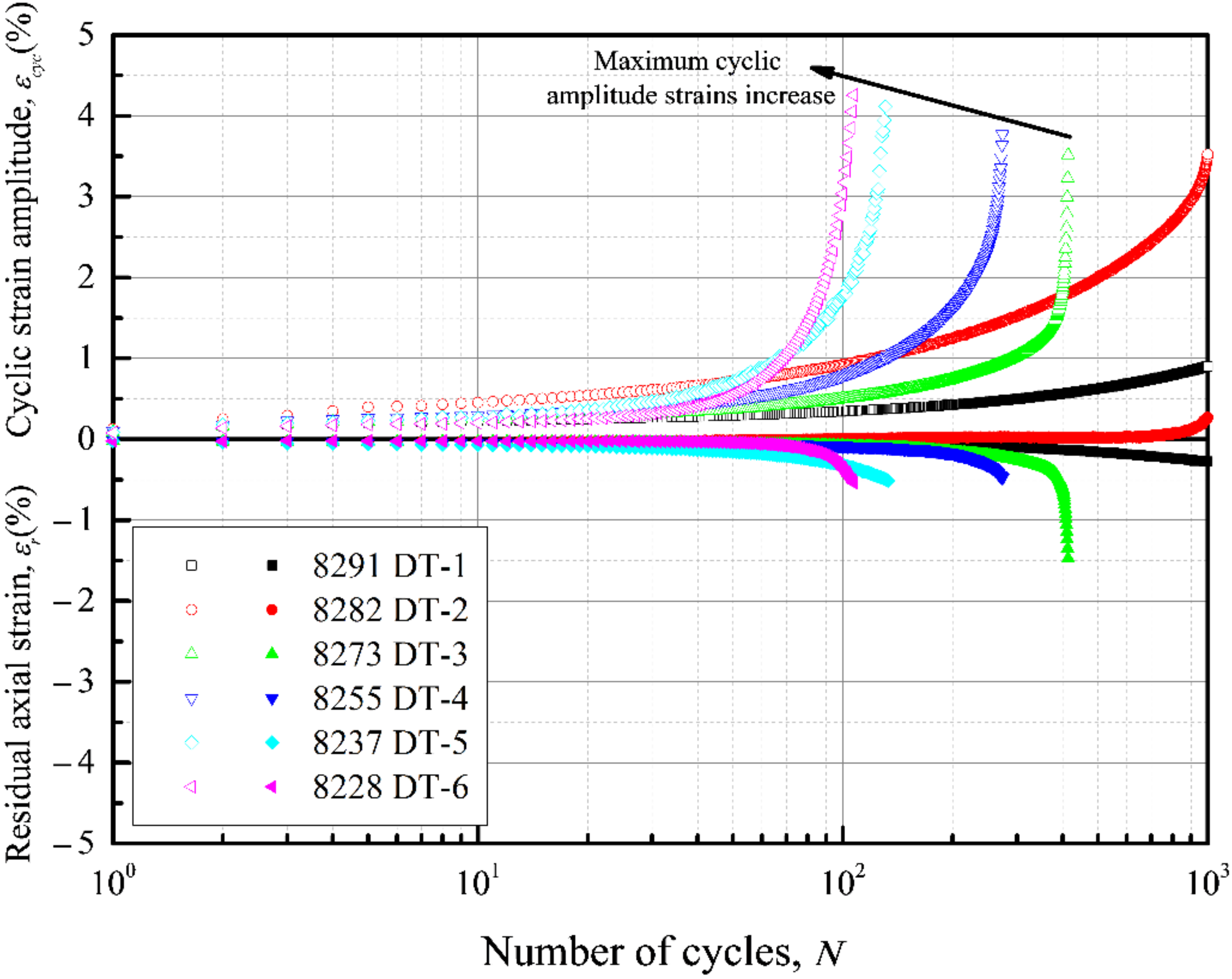
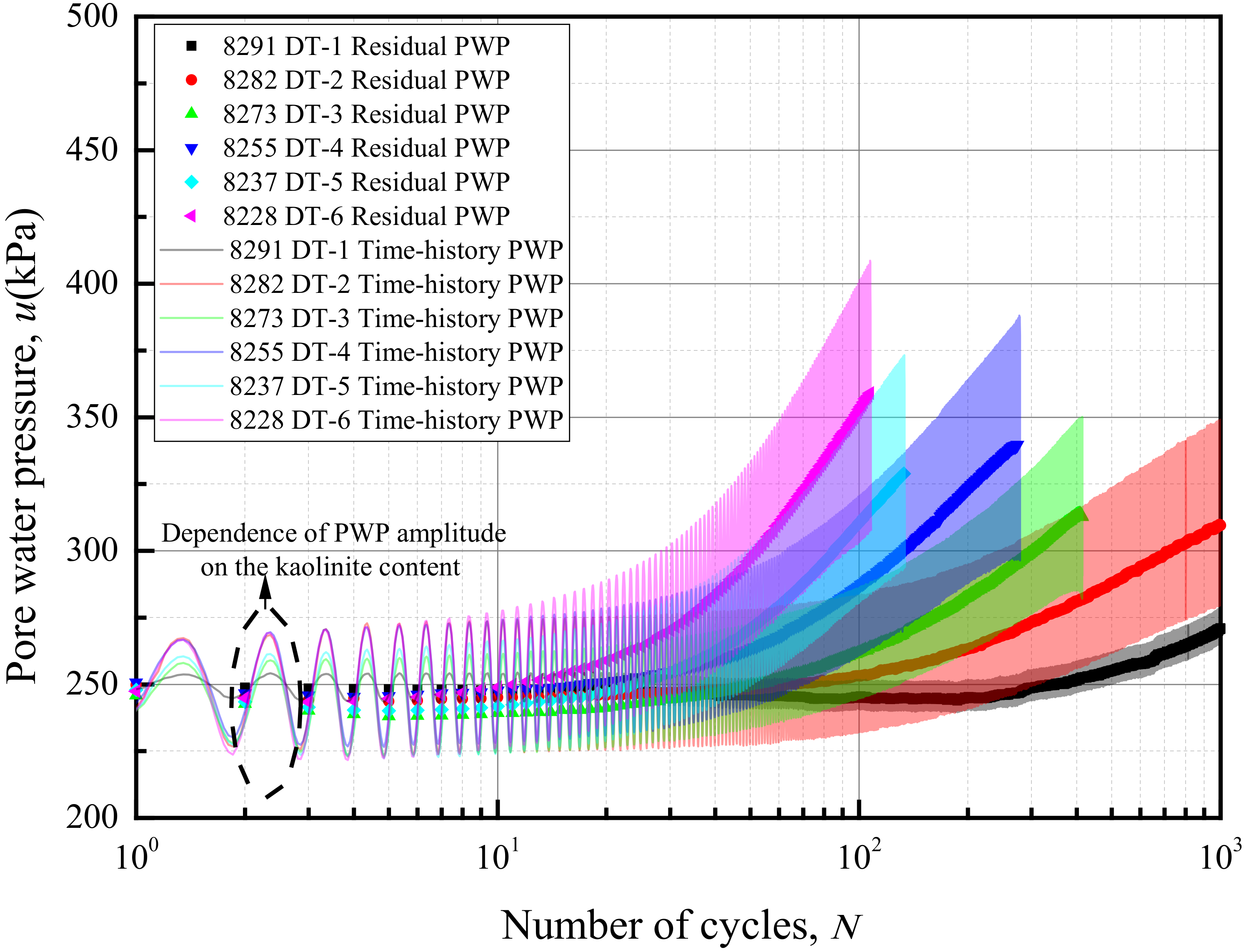
Sample Name 1	Specific Gravity ${\mathit{G}}_{\mathit{s}}$	Natural Void Ratio $\mathit{e}$	Plastic Limit PL (%)	Liquid Limit LL (%)	Plasticity Index PI (%)	Indexes of Unconsolidated Direct Shear
						c (kPa)	$\mathit{\phi }$$(°)$
HR-JP	2.67	1.771	21.0	54.3	33.3	11.1	5.3
PR-HX	2.73	1.584	29.6	54.8	25.2	12.4	2.3
PR-WQS	2.77	1.612	24.4	45.4	21.0	4.5	3.8

¹ HR and PR represent the Han River Delta and the Pearl River Delta, respectively. JP, HX, and WQS represent the names of sampling locations.

. The corresponding mineral compositions are shown in

Table 2. The mass ratio of sedimentary mineral composition in marine clay of two deltas in the South China Sea.

Sample Name	Depth (m)	Quartz (%)	Albite (%)	Montmorillonite (%)	Kaolinite (%)	Illite (%)	Chlorite (%)	Calcite (%)	Pyrite (%)	Geological Age
HR-JP	8.2~8.7	20.1	11.5	-	20.8	23.9	23.7	-	-	Sub-Atlantic period ($Q_4^3$)
PR-HX	22.1~22.5	24.8	-	-	23.3	23.4	26.3	-	2.2	Atlantic period ($Q_4^{2-1}$)
PR-WQS	7.8~8.3	34.1	-	-	19.3	17.5	24.1	5.0	-	Sub-Atlantic period ($Q_4^3$)

. These results were also compared to those of earlier studies of the mineral composition of marine clay found in Pearl River Delta [53] and in Han River Delta [54], reported in

Table 3. The mass ratio of sedimentary minerals composition in marine clay of the Pearl River Delta in the Jinwan (JW) District of Zhuhai [53] and the Han River Delta in the Chenghai (CH) District of Shantou [54].

Sampling Location	Sample Name	Depth (m)	Quartz (%)	Albite (%)	Montmorillonite (%)	Kaolinite (%)	Illite (%)	Halite (%)	Calcite (%)	Pyrite (%)	Other Minerals (%)	Geological Age
Pearl River Delta	PR-JW (1-1)	3.0	41.2	7.4	7.4	22.2	19.8	-	-	-	2.0	Sub-Atlantic period ($Q_4^3$)
	PR-JW (1-8)	19.0	41.8	5.9	8.5	18.8	17.6	-	-	2.6	4.8	Atlantic period ($Q_4^{2-1}$)
	PR-JW (2-1)	4.5	33.6	6.6	14.0	18.9	18.8	2.5	3.3	1.4	0.9	Sub-Atlantic period ($Q_4^3$)
	PR-JW (2-8)	18.5	40.4	5.1	11.8	16.0	17.7	2.4	4.2	2.3	0.1	Atlantic period ($Q_4^{2-1}$)
Han River Delta	HR-CH (39-1)	4.0	25.6	7.9	19.8	15.5	13.4	17.6	-	-	0.2	Sub-Atlantic period ($Q_4^3$)
	HR-CH (39-4)	19.5	29.5	9.8	-	20.6	24.1	15.9	-	-	0.1	Atlantic period ($Q_4^{2-1}$)

. The above tables show the mineral composition and geological age of the marine clays taken by drilling and sampling. The locations of the above sampling operations are shown in Figure 1.

Since all sampling locations were in the front delta area outside the most extensive shell sand bar, borehole analysis revealed these marine clays to be sediments formed by the transgression of the Quaternary Holocene period. It is well documented that the main sedimentary minerals in marine clay are non-clay minerals of quartz and albite, and clay minerals of montmorillonite, kaolinite, illite, and chlorite, along with small numbers of other minerals. For non-clay minerals, the ratio of quartz to albite ranged between 3:1 and 7:1, while for clay minerals, the ratios between the clay minerals varied among the diverse samples from the two deltas. To study the effects of clay mineral composition on the dynamic properties of artificial marine clay, the mineral composition of the natural marine clay in two estuarine deltas in the South China Sea was investigated. The mineral composition of natural marine clay in these two estuarine deltas was hence taken as the basis of and background for the study of dynamic properties.

2.1.2. Mineral Composition of Artificial Marine Clay

Based on results of the above-mentioned mineral component analysis of marine clay, samples were obtained by mixing corresponding proportions of raw minerals for further laboratory dynamic testing and sediment fabric measurement. Four raw minerals were selected as the raw materials to create the artificial marine clay. Firstly, the non-clay minerals were selected from the main components: quartz and albite. Secondly, the clay minerals were selected from Na-montmorillonite and kaolinite, which are the main clay mineral components in natural marine clays [39]. In his study of clay mineralogy, Grim [55] found that these two clay minerals displayed extreme characteristics in terms of isomorphous substitution, specific surface area, and plasticity. According to earlier mineral analysis studies in the field [56], these four minerals were identified as the most common ones in natural marine clay. The raw minerals extracted from mining and their main parameters and mineral composition are shown in

Table 4. The basic physical properties of raw minerals.

Raw Mineral	Specific Gravity ${\mathit{G}}_{\mathit{s}}$	Plastic Limit PL (%)	Liquid limit LL (%)	Plasticity Index 1 PI (%)	Specific Surface Area 2 ${\mathit{S}}_{\mathit{s}} ({\mathbf{m}}^2/\mathbf{g})$	Mineral Composition 3 (%)
Quartz	2.656	9.1	15.7	6.6	2.66	Quartz 97.0, Mica 3.0
Albite	2.659	6.8	12.6	5.8	5.47	Albite 91.4, Anorthite 8.5
Na-montmorillonite	2.888	42.0	173.0	131.0	336.94	Na-montmorillonite 90.0, Quartz 8.3, Calcite 1.7
Kaolinite	2.500	36.8	64.6	27.8	11.81	Kaolinite 98.2, Plagioclase 1.8

¹ The Atterberg limit of non-clay minerals including the plastic limit and the liquid limit is due to the long-range interparticle attractive force, i.e., van der Waals forces [39]. The plasticity index is equal to the liquid limit minus the plastic limit. ² The specific surface area of raw minerals is determined by using ethylene glycol monomethyl ether [57]. ³ The mineral composition of raw materials is determined by the X-ray diffraction based on the Normalized Reference Intensity Ratio Method [58].

.

Using a laser-scattering particle-size distribution analyzer, the particle size distribution of four types of raw minerals and three types of natural marine clays presented in Table 1 is shown in Figure 2. By screening out particles larger than 75 μm, the D50 (mean particle size) of raw minerals was explicitly controlled from 5 μm to 15 μm, including 10.31 μm for quartz, 7.67 μm for albite, 14.81 μm for Na-montmorillonite, and 5.47 μm for kaolinite. The mean particle sizes of the four raw minerals were consistent with the particle size of natural marine clays (HR-JP, PR-HX, and PR-WQS). The samples of the four minerals with similar mean particle sizes presented three advantages: (a) When all particle sizes were less than 75 μm, the artificial marine clay was classified as fine-grained soil; (b) If the size of particles approached 75 μm, the fine-grained soil would exhibit a rapid shaking reaction, thereby causing water slowly to appear on the surface of the specimen in liquefaction-like form during sample preparation and testing [59]. The mean particle sizes of typical natural marine clay in both deltas were furthermore primarily measured around 5 μm as shown in Figure 2. Therefore, the mean particle size of the four minerals was controlled to remain close to 5 μm rather than 75 μm. (c) If the particle size of each raw mineral presented different orders of magnitude, then particle size did become a relevant factor influencing the dynamic properties of fine-grained soil as mentioned in the Introduction of this paper. For these three reasons, the particle size of the four raw minerals was limited to a consistent narrow range.

2.2. Laboratory Dynamic Triaxial Test

2.2.1. Specimen Preparation

On the basis of the mineral composition of natural marine clays, all artificial marine clays were made up of four raw minerals. The artificial marine clay was produced by mixing components according to specific mass ratios. The mass ratio of quartz to albite was fixed at 8:2 in non-clay minerals, while the mass ratio of Na-montmorillonite to kaolinite was adjusted to between 9:1 and 2:8 in clay minerals. The abbreviations for mass ratio of raw minerals (quartz: albite: Na-montmorillonite: kaolinite) were defined as the name of the corresponding artificial marine clay specimen. For example, the ratio of quartz, albite, Na-montmorillonite, and kaolinite was 8:2:9:1, hence the name of the associated specimen in this paper was 8291. The specimens were remolded into eight layers using a moist tamping method. This sample preparation method was used in preference to the slurry deposition method commonly used for marine clay to avoid the delamination caused by different mineral deposition rates. All samples intended for laboratory dynamic triaxial testing were 39.1 mm (diameter) × 80 mm ± 0.5 mm (height). Lastly, six test specimens were produced, the names and physical parameters of which are shown in

Table 5. The parameters of laboratory dynamic triaxial testing of artificial marine clays.

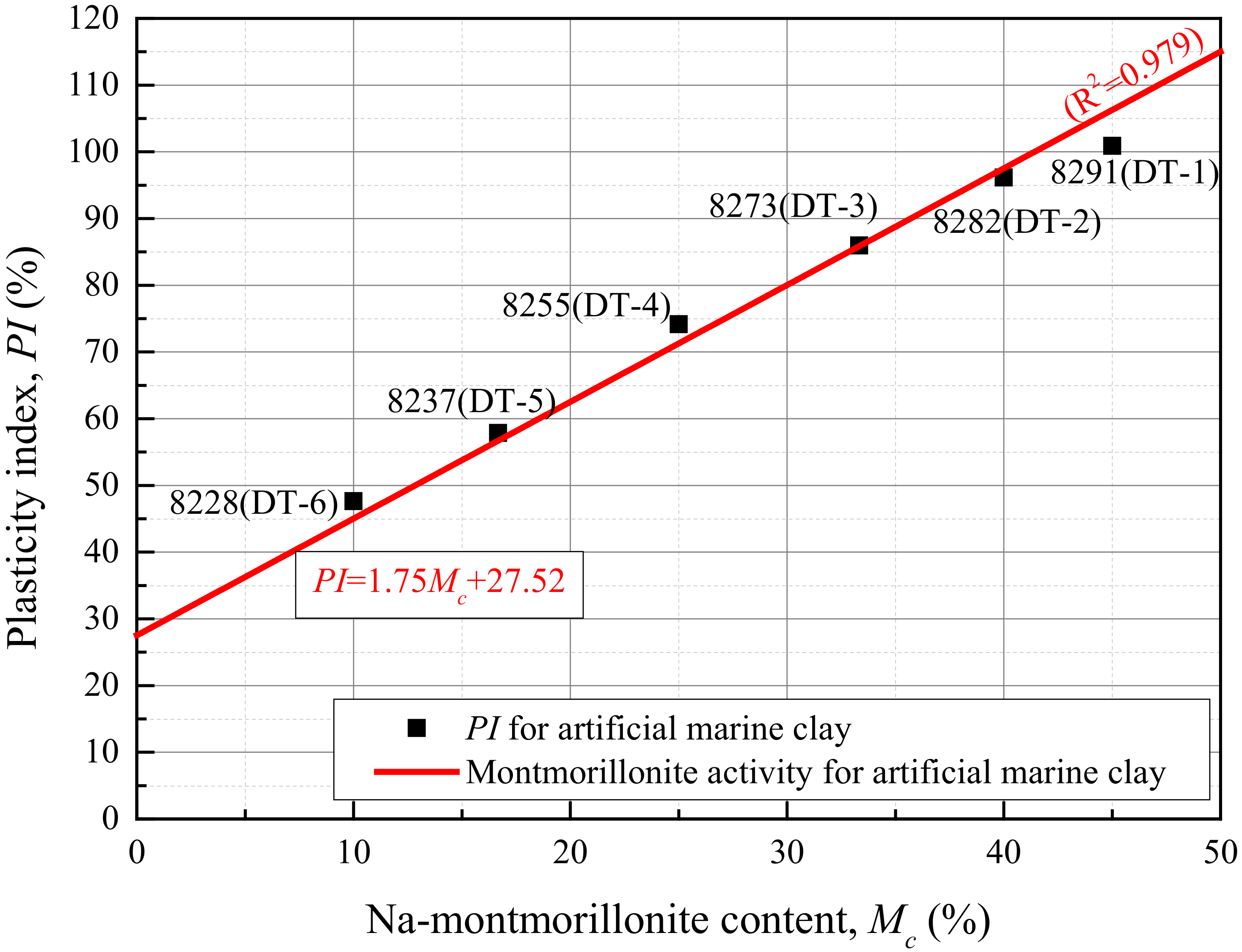
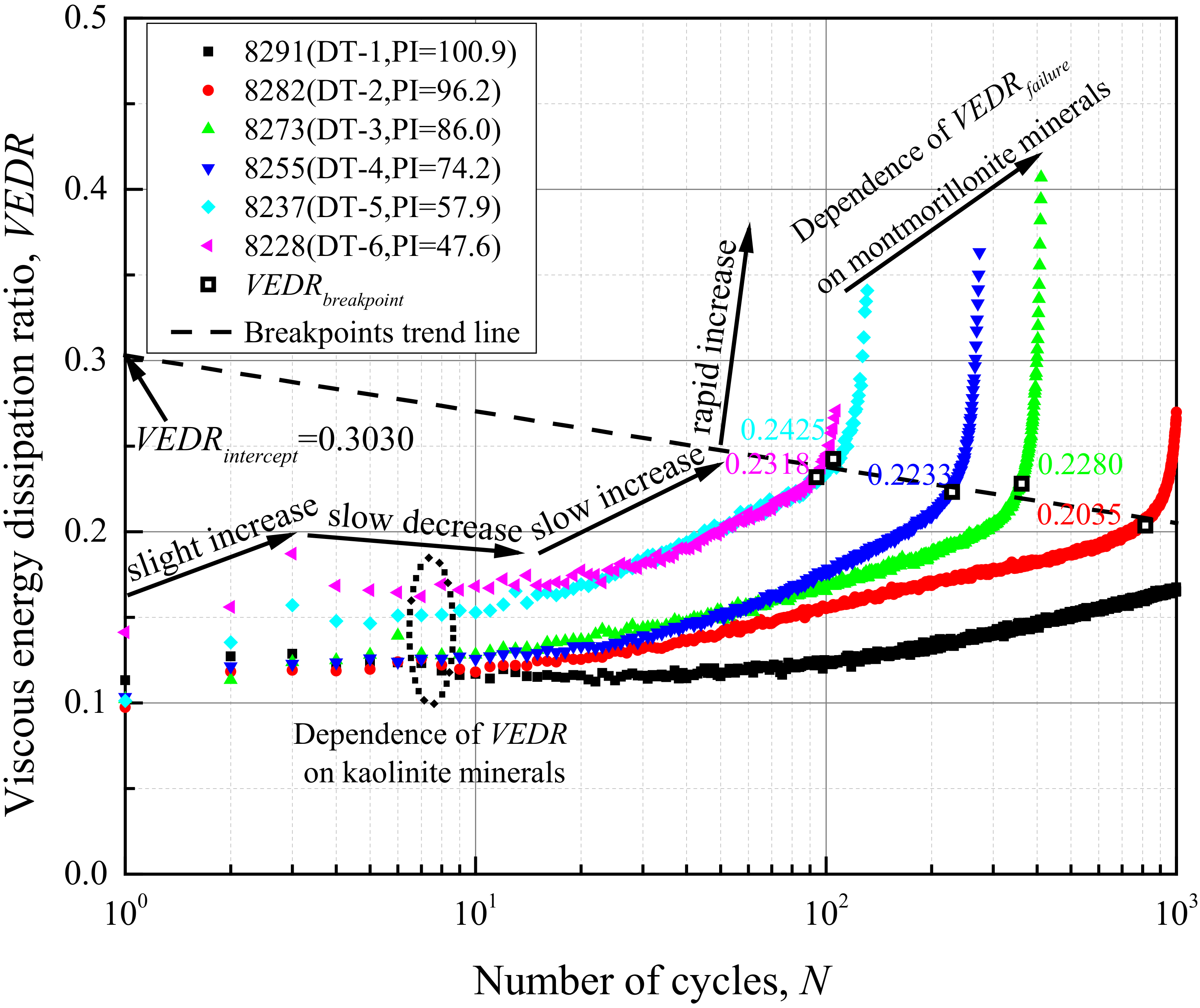
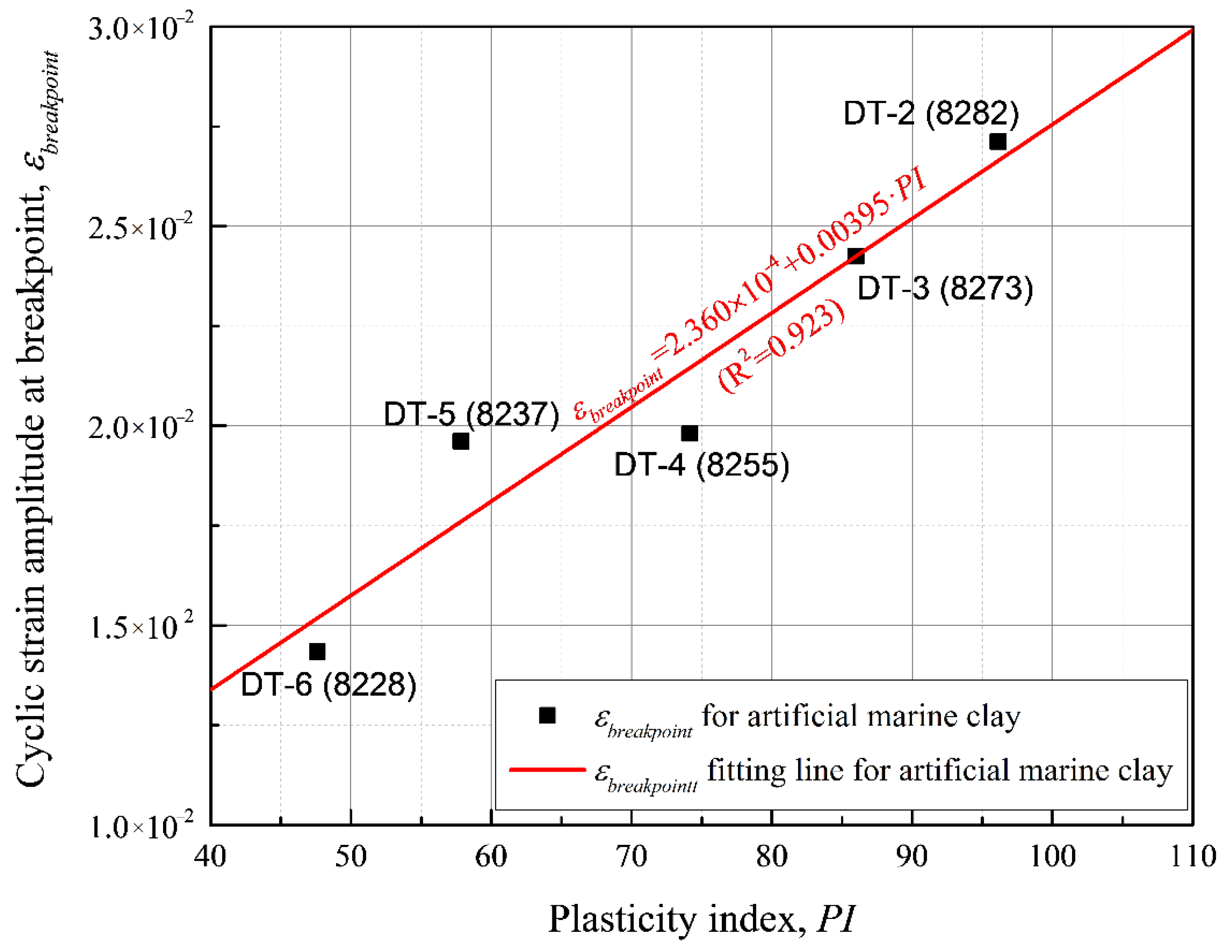
Test Specimen	Mass Ratio of Raw Minerals (Quartz: Albite: Na-Montmorillonite: Kaolinite)	Specific Gravity ${\mathit{G}}_{\mathit{s}}$	Saturated Water Content ${\mathit{w}}_{\mathit{i}\mathit{n}\mathit{i}\mathit{t}\mathit{i}\mathit{a}\mathit{l}}$ (%)	Plastic Limit PL (%)	Liquid Limit LL (%)	Plasticity Index PI (%)	Liquidity Index 1 LI	Cyclic Stress Ratio CSR	Consolidation Pressure			Quality of Specimen		Terminated Cycle ${\mathit{N}}_{\mathit{f}}$	Maximum Cyclic Strain Amplitude 2 ${\mathit{\epsilon }}_{\mathit{c}\mathit{y}\mathit{c},\mathbf{max}}$ (%)	VEDRbreakpoint Cycle 3 Nbreakpoint
									Axial Pressure ${\mathit{\sigma }}_{\mathit{a}}$ (kPa)	Radial Pressure ${\mathit{\sigma }}_{\mathit{r}}$ (kPa)	Back Pressure ${\mathit{\sigma }}_{\mathit{B}}$ (kPa)	Volume Change ${\mathit{\epsilon }}_{\mathit{v}\mathit{o}\mathit{l}}$ (ml)	Relative Void Ratio Change $\mathbf{\Delta }\mathit{e}/{\mathit{e}}_{\mathit{o}}$
DT-1	8:2:9:1 (8291) 4	2.75	55.8	23.2	124.1	100.9	0.32	0.284	448.8	448.4	250.3	26.2	0.45	1000	0.91	-
DT-2	8:2:8:2 (8282)	2.73	56.2	22.8	119.0	96.2	0.35	0.282	449.2	449.0	249.6	19.2	0.33	1000	3.53	815
DT-3	8:2:6.7:3.3 (8273)	2.71	56.7	22.3	108.3	86.0	0.40	0.268	448.2	449.4	245.8	16.8	0.29	414	3.52	362
DT-4	8:2:5:5 (8255)	2.68	57.4	21.3	95.5	74.2	0.49	0.282	452.0	451.4	250.7	19.2	0.33	274	3.77	229
DT-5	8:2:3.3:6.7(8237)	2.64	58.1	19.9	77.8	57.9	0.66	0.269	452.3	451.6	245.0	17.7	0.30	133	4.12	105
DT-6	8:2:2:8 (8228)	2.62	58.7	19.6	67.1	47.6	0.82	0.281	448.9	449.6	247.4	20.5	0.35	107	4.26	94

¹ The liquid limit index of the remolded sample is calculated at the void ratio of 1.537. ² Maximum cyclic strain amplitude (${\epsilon }_{cyc}=\left({\epsilon }_{max}-{\epsilon }_{min}\right)/2$) is at the end of the test. ³ N_{VEDRbreakpoint} is the number of cycles at VEDR_breakpoint. ⁴ The abbreviation for specimen is in parentheses.

. It should be noted that since the void ratio significantly influences the mechanical properties and dynamic characteristics of marine clay [60], all saturated specimens comprised the same void ratio (1.537), whilst retaining different raw mineral volume fractions in accordance with their variable mass ratios.

In addition, a higher content of Na-montmorillonite was found to slightly increase the plastic limit, significantly raise the liquid limit, and was accompanied by a surge in the plasticity index, as shown in Table 5. The Montmorillonite activity [61] was introduced to reflect the linear effect of Na-montmorillonite content (Mc) on plasticity, as shown in Figure 3. When the Na-Montmorillonite content was nil, the mass ratio (quartz: albite: Na-montmorillonite: kaolinite) of mineral composition was 8:2:0:10. The artificial marine clay was composed of only non-clay minerals and kaolinite, and PI = 27.65. In order to express the natural marine clay and artificial marine clay from a geotechnical point of view, a plasticity chart [62] was produced and is shown in Figure 4, which demonstrates that HR-JP of natural marine clays and all artificial marine clays belonged to the category of fat clay, abbreviated CH. PR-HX is on the edge of “A line” and classified as elastic silt, abbreviated MH. PR-WQS is classified as lean clay with sand, abbreviated CL, due to the existence of about 25% coarse-grained particle from particle size distribution in Figure 2.

2.2.2. Experimental Procedure

In order to analyze the influence of clay mineral composition on the dynamic properties of marine clay under large strain, a series of consolidated undrained cyclic triaxial tests were conducted on soil specimens with different mineral compositions, using the stress-controlled DDS-70 microprocessor-controlled electromagnetic cyclic triaxial testing system (Binta Instrument Technology Co., Ltd., Beijing, China). The experimental apparatus and typical specimen diagram are shown in Figure 5. Existing studies showed that during hydration under high cementation conditions, the dynamic characteristics of marine clay were affected by the consolidation time [28,45]. Meanwhile, the Quaternary marine clay generally showed slight over-consolidation [1,63]. For these reasons, all specimens with saturation coefficient B greater than 0.97 after subsequent vacuum saturation and back pressure saturation were subjected to strict control of the consolidation time during the corresponding process. After 24 hours’ consolidation under a back pressure of 200 kPa (the mean principal effective stress was 250 kPa), the primary consolidation was completed. The back pressure was then raised to 250 kPa for a further 24 h (the mean principal effective stress was 200 kPa). The resulting specimens showed the same consolidation time with an over-consolidation ratio of 1.25. As indicated in Table 5, cyclic triaxial tests were conducted on specimens DT-1 to DT-6 under a virtually identical cyclic stress ratio (CSR, namely the ratio of cyclic shear stress amplitude to the mean effective principal stress, ${\tau }_{\mathrm{cyc}}/p{\prime }_0$), from 0.268 to 0.284. This CSR range ensured that all specimens underwent at least 100 cycles by the end of the test. During the experiment, the cyclic loading waveform was sinusoidal, and the loading frequency was 0.1 Hz. The test was terminated when a single amplitude strain reached 5% or the number of cycles reached 1000. Figure 6 below shows the DT-6 results of dynamic triaxial testing of artificial marine clay.

To verify the repeatability of cyclic triaxial testing of artificial marine clays, two series of original and parallel trials were performed on the 8255 series ($CSR\approx 0.215$, test 1 and 2 are not listed in Table 5 as a test series) and 8228 series ($CSR\approx 0.281$) under identical test conditions, as shown in Figure 7. The figures reveal the results of two test components: (a) strain development and (b) hysteresis curve. Strain development included cyclic axial strain amplitude (the maximum and minimum axial strain amplitude at each cycle, ${\epsilon }_{cyc}=({\epsilon }_{\max }-{\epsilon }_{\min })/2$) and residual axial strain (cumulative strain when deviator stress is nil at each cycle, ${\epsilon }_r$). The hysteresis curves represented the results of the 8255 series at the 500th cycle and the 8228 series at its failure cycle, respectively. As the figures illustrate, the differences in strain development and hysteresis curve of representative cycles were minimal in both series. The above results further demonstrated the reliability of cyclic triaxial testing of artificial marine clays.

3. Results

3.1. Cyclic Triaxial Test Results

The results of laboratory large strain dynamic testing of artificial marine clays were generally presented under three categories: (a) strain development; (b) pore water pressure change; and (c) hysteresis curve shape.

3.1.1. Strain

The strain development test results were presented in terms of cyclic axial strain amplitude and residual axial strain, as shown in Figure 8. The cyclic axial strain amplitude was used as an indicator of strain development, which increased with the loading cycle until completion of the test. The terminated cycle and maximum cyclic amplitude strain are presented in Table 5. As the proportion of Na-montmorillonite in the specimens decreased (from DT-3 to DT-6), the maximum cyclic amplitude strain at the failure cycle increased from 3.52% to 4.26% under identical test termination conditions (i.e., with the single amplitude strain of 5%). At the same time, the cyclic amplitude strain curve of the specimens with less Na-montmorillonite content changed from a gradual to an abrupt rise. The mineral composition of Na-montmorillonite was therefore found to hinder the rapid development of strain under unchanged remaining test conditions; increased Na-montmorillonite content was furthermore shown to further limit the development of strain significantly.

3.1.2. Pore Water Pressure

The residual pore water pressure (PWP) and time-history of PWP are recorded in Figure 9. The residual PWP was equal to the PWP at zero deviatoric stress within the cycle. Due to the same back pressure and over-consolidation ratio, PWP of all specimens started from 250 kPa, initially developing in a negative direction and then increasing in a positive direction until the tests were terminated. The time-history PWP curves indicated that the development of pore water pressure was synchronous with the sinusoidal cyclic loading. The samples with high montmorillonite content demonstrated a slower cumulative increase rate in pore water pressure and lower residual pore water pressure at the end of the test. Meanwhile, the specimens with extremely high montmorillonite content, especially DT-1, presented a narrower pore water pressure amplitude (the width of time-history PWP) than low montmorillonite content specimens. Therefore, montmorillonite in mineral composition was also found to play a role in inhibiting the rise of PWP while limiting strain increase. The impeditive development of PWP affected both the cumulative results (residual PWP) and cyclic results (PWP amplitude) as the Na-montmorillonite content increased.

3.1.3. Hysteresis Curve Shape

Although the CSRs of all specimens were similar; their strains exhibited significant differences due to their various mineral compositions. In order to eliminate the differences in stress and strain, the double-normalized hysteresis curve at the failure cycle (or terminated cycle) was used to compare the shapes of the hysteresis curves. In Figure 10a, the evolution of the double-normalized hysteresis curve process is presented and explained by moving the hysteresis curve back to the origin of the X-axis and double-normalizing. The normalized deviatoric stress in the Figure is equal to the deviatoric stress divided by the cyclic axial stress amplitude (${\sigma }_{cyc}=({\sigma }_{\max }-{\sigma }_{\min })/2$). The normalized axial strain is equal to the axial strain after the hysteresis curve has been moved back to the origin ($Movement={\epsilon }_a-({\epsilon }_{\max }+{\epsilon }_{\min })/2$), divided by the cyclic axial strain amplitude. Subsequently, the double-normalized hysteresis curves of artificial marine clays at the failure cycle are presented in Figure 10b. Here, some specimens with high montmorillonite content (DT-1 and DT-2) reveal narrow hysteresis curves resembling a “banana shape”, because they only meet the requirements for 1000 terminated cycles, but not those for large strain failure. In other specimens (DT-3 to DT-6), the samples with high montmorillonite content such as DT-3 and DT-4, comprise a more rounded “olive shape” than the specimens with low montmorillonite content such as DT-5 and DT-6. A corresponding relationship can furthermore be seen in Figure 10b between the shape of the double-normalized hysteresis curve and viscous energy dissipation, which will be discussed in the following Section 4.2.

3.2. Stiffness and Energy Dissipation

Previous research [3,64,65] indicated that the dynamic properties of stiffness degradation and energy performance in artificial marine clays could be further calculated and explored on the basis of test results of strains and hysteresis curves under cyclic loading.

3.2.1. Stiffness Degradation

The cyclic axial strain amplitude (${\epsilon }_{cyc}$) was transformed into cyclic shear strain amplitude (${\gamma }_{cyc}$) by Poisson’s ratio ($\mu$) as shown in Equation (1) below. The shear modulus under the cyclic triaxial test was obtained from the slope of the stress–strain top-line in Equation (2) below and Poisson’s ratio conversion in Equation (3) below. Based on the assumption of undrained conditions, Poisson’s ratio was assumed to be 0.5 in this study.

$${\gamma }_{cyc}=\left(1+\mu \right){\epsilon }_{cyc}$$

(1)

$$E_d=\frac{{\sigma }_{cyc}}{{\epsilon }_{cyc}}=\frac{\left({\sigma }_{\max }-{\sigma }_{\min }\right)/2}{\left({\epsilon }_{\max }-{\epsilon }_{\min }\right)/2}$$

(2)

$$G_d=\frac{E_d}{2\left(1+\mu \right)}$$

(3)

In order furthermore to eliminate the influence of the maximum dynamic shear modulus of various artificial marine clays, the normalized dynamic shear modulus was presented. The maximum dynamic shear moduli of artificial marine clay were determined from the results of resonance column tests [41] and shown in

Table 6. The parameters result of the Martin–Davidenkov model of artificial marine clays.

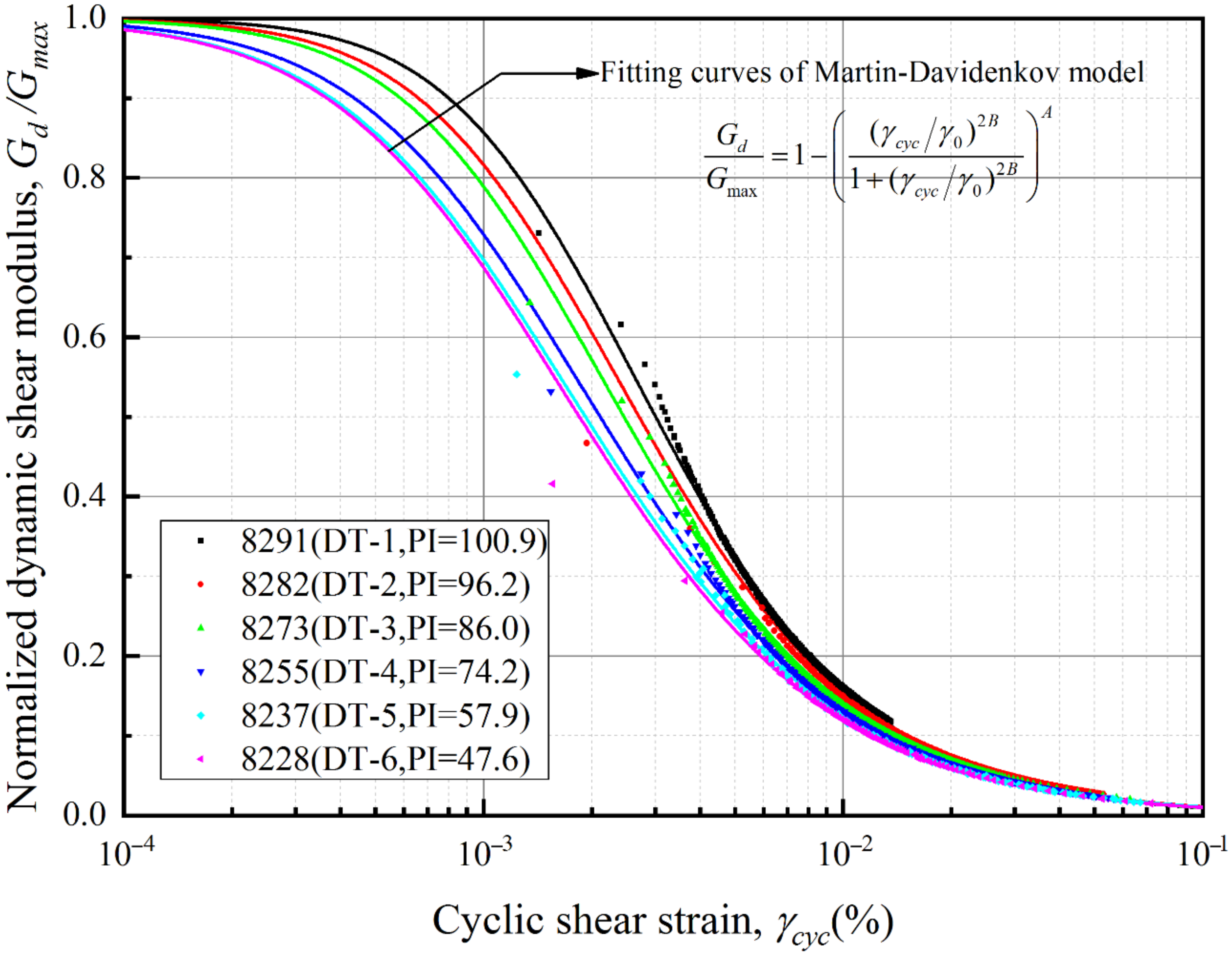
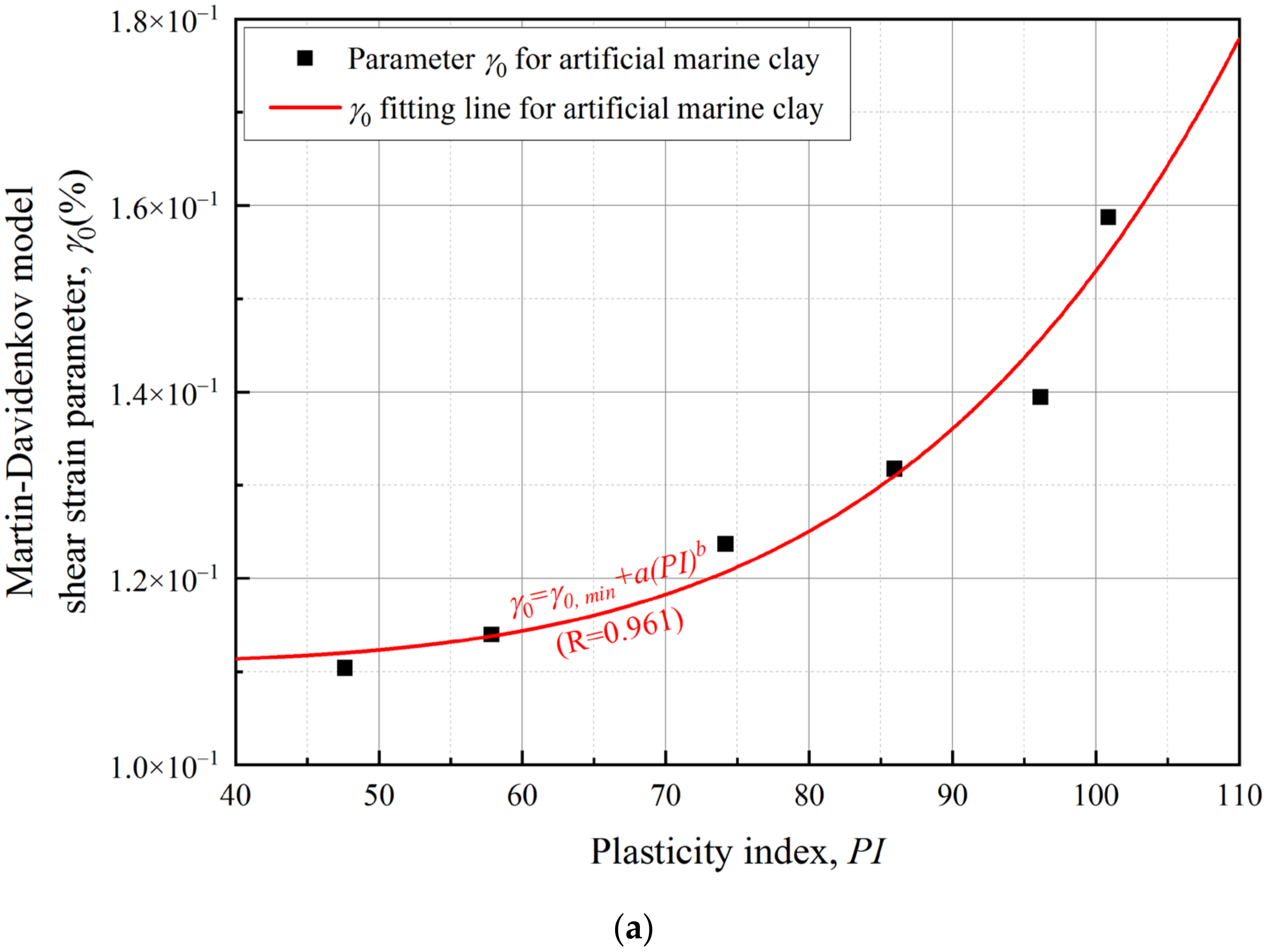
Test Specimen	Plasticity Index ${\mathit{I}}_{\mathit{P}}$	Maximum Dynamic Shear Modulus 1 Gmax (MPa)	Martin–Davidenkov Model Parameters			Correlation Coefficient ${\mathit{R}}^{\mathbf{2}}$
			${\mathit{\gamma }}_{\mathbf{0}}$	$\mathit{A}$	$\mathit{B}$
DT-1	100.9	8.56	1.587 × 10−3	1.889	0.636	0.997
DT-2	96.2	8.08	1.394 × 10−3	1.859	0.599	0.993
DT-3	86.0	8.03	1.318 × 10−3	1.787	0.598	0.997
DT-4	74.2	6.29	1.234 × 10−3	1.594	0.566	0.995
DT-5	57.9	5.71	1.140 × 10−3	1.556	0.554	0.991
DT-6	47.6	4.94	1.104 × 10−3	1.552	0.553	0.999

¹ The maximum dynamic shear modulus of artificial marine clays refers to Shan et al. [41] by resonance column test.

. The relationship between cyclic shear strain amplitude in large-scale strain and normalized shear modulus was obtained, as shown in Figure 11.

With the increased cyclic shear strain, the normalized shear modulus exhibited a tendency towards degradation. The cyclic shear strain ranged from 1.24 × 10⁻³ to 7.17 × 10⁻², a relatively large strain. Lastly, under a cyclic shear strain of 10⁻¹, the shear modulus of all specimens degraded from around 0.6 to nearly zero. The samples with high montmorillonite content displayed greater normalized shear moduli under the same cyclic shear strain. Since stiffness resulted from the transmission of shear waves between particles and intergranular contact, the specimens with high montmorillonite content (high plasticity) displayed greater contact, even once the shear strain had occurred. This conclusion was deemed consistent with the small strain stiffness test results of resonant column testing in artificial marine clays [41]. Meanwhile, combined with the plasticity index of artificial marine clays, the above conclusion, was deemed consistent with the relationship between stiffness degradation and soil plasticity for natural normal and over-consolidated soils studied by Vucetic and Dobry [66].

In addition, the fitting curves of the nonlinear Martin–Davidenkov model [67] was adopted to describe the stiffness degradation, as shown in Figure 11. The Martin–Davidenkov model was expressed as follow:

$$\frac{G_d}{G_{\max }}=1-{\left(\frac{{\left({\gamma }_{cyc}/{\gamma }_0\right)}^{2B}}{1+{\left({\gamma }_{cyc}/{\gamma }_0\right)}^{2B}}\right)}^A$$

(4)

where ${\gamma }_0$, A, and B were fitting parameters related to stiffness degradation, and the corresponding parameter results are presented in Table 6.

The plasticity index (PI) rose with the increase in montmorillonite content within the mineral composition. At that point, all three parameters in the Martin–Davidenkov model showed transformation of power functions (Equations (5)–(7) below) trend increases with the rise of PI, as shown in Figure 12, which was deemed consistent with the above stiffness degradation.

$$\begin{gathered} {\gamma }_0={\gamma }_{0,\min }+a_{\gamma }\cdot {\left(PI\right)}^{b_{\gamma }} \\ ({\gamma }_{0,\min }=1.109\times {10}^{-3}, a_{\gamma }=7.237\times {10}^{-12}, \mathrm{and} b_{\gamma }=4.882) \end{gathered}$$

(5)

$$\begin{gathered} A=A_{\min }+a_A\cdot {\left(PI\right)}^{b_A} \\ (A_{\min }=1.502, a_A=5.706\times {10}^{-8} , \mathrm{and} b_A=3.420) \end{gathered}$$

(6)

$$\begin{gathered} B=B_{\min }+a_B\cdot {\left(PI\right)}^{b_B} \\ (B_{\min }=0.549, a_B=6.532\times {10}^{-11} \mathrm{and} b_B=4.533) \end{gathered}$$

(7)

where ${\gamma }_{0,\min },a_{\gamma }, b_{\gamma }, A_{\min }, a_A,b_A,B_{\min }, a_B, and b_B$ are fitting parameters. When the mass ratio (quartz: albite: Na-montmorillonite: kaolinite) of mineral composition was 8:2:0:10, the lower limit reached by the domain of PI in the three equations was 27.52, as can be seen in Figure 3. At the same time, ${\gamma }_0$, A, and B were 1.110 × 10⁻³, 1.507, and 0.550, respectively, which were all minimum values.

3.2.2. Viscous Energy Dissipation

The area contained within the hysteresis curve is taken as viscous energy dissipation of each cycle has been widely recognized by researchers [68,69,70]. The calculation method of viscous energy dissipation for each cycle is presented in Equation (8). Furthermore, the viscous energy dissipation ratio (VEDR), a non-dimensional energy index to eliminate stress and strain [71,72,73], was introduced to investigate the viscous energy dissipation characteristics of artificial marine clay. VEDR is dimensionless in terms of viscous energy dissipation in each cycle. It is similar to calculating the area ratio between hysteretic curve and circumscribed square in double-normalized hysteresis curves. The expression and schematic diagram of VEDR are shown in Equation (9) and Figure 13 below, respectively.

$$\Delta W_i=A_{Hysteresis}={\displaystyle \sum _{i=1}^{n-1}\frac{\left({\sigma }_{d,i+1}+{\sigma }_{d,i}\right)}{2}\left({\epsilon }_{a,i+1}-{\epsilon }_{a,i}\right)}$$

(8)

$$\mathrm{VEDR}=\frac{\Delta W_i}{S_{\mathrm{rectangle}}}=\frac{\Delta W_i}{({\sigma }_{\max ,i}-{\sigma }_{\min ,i})({\epsilon }_{\max ,i}-{\epsilon }_{\min ,i})}$$

(9)

Figure 14 shows the relationship between number of cycles and VEDR for artificial marine clays. The VEDR curves follow a slight increase–slow decrease–slow increase pattern before undergoing a sudden, rapid increase at the obvious breakpoint, except in the case of DT-1. DT-1 is where failure does not occur due to the required single amplitude strain, hence the final stage of rapid increase is not reached. In general, the VEDR curves showed a rising trend, indicating that viscous energy dissipation in artificial marine clay increased overall with cyclic loading. The wave-like formation and rising trend of VEDR curves described above were confirmed to be fully consistent with the research results of Shan et al. [61].

At the same time, the artificial marine clay specimens with various clay mineral contents displayed different VEDRs in the early and failure cycles. In the early cycles, the development of VEDRs was limited by the content in montmorillonite. VEDRs with high montmorillonite content were lower than those with high kaolinite content in the same cycles. In the failure cycles, VEDRs (for DT-3 to DT-6) increased with the rise in montmorillonite content. This indicated that a high montmorillonite content reflected more prominent viscous energy dissipation capability under the same failure strain. However, the VEDRs in the terminal cycles of samples with extremely high montmorillonite content (DT-1 and DT-2) were lower. The differences in shape of the double-normalized hysteretic curves also reflected the energy dissipation status of artificial marine clays. The rounder, olive-shaped double-normalized hysteretic loops reflected greater viscous energy dissipation. In contrast, the double-normalized hysteresis curves of nonfailure specimens with extremely high montmorillonite content were banana-shaped.

Furthermore, the VEDR_breakpoint of artificial marine clays was affected by the montmorillonite content of the clay. Shan et al. [61] indicated that VEDR_breakpoint was the point at which the gradient of the VEDR curve became very steep and marked the energy turning point at a late stage of cyclic loading. The VEDR_breakpoint of artificial marine clay is illustrated in Figure 14. With reduced montmorillonite content and increased kaolinite content, the VEDR_breakpoint rose slowly. Eventually, the intercept of VEDR_breakpoint trend line in artificial marine clay was 0.3030. It should be noted that this intercept of VEDR represents the energy ratio at the point when soil specimens failed after only one cycle and should only correlated with the composition and proportion of non-clay minerals. In order to further illustrate the dynamic characteristics of the VEDR_breakpoint, the linear relationship between cyclic strain amplitude at breakpoint (${\epsilon }_{breakpoint}$) and plasticity index (PI) for artificial marine clays is shown in Figure 15. This provided further evidence that the dissipated viscous energy of high montmorillonite content specimens was inhibited, and the cyclic strain of energy breakpoint was delayed.

4. Microstructure and Fabric

The low-vacuum environmental scanning electron microscopy testing (LVESEM, Quanta 200, Center for Electron Microscopy and Analysis (CEMAS), Columbus, OH, USA) and MIP testing (AutoPore 9510, Micromeritics Instrument Corporation., Norcross, GA, USA) were conducted to investigate artificial marine clay fabric microstructure and microporosity in artificial marine clay specimens. Four out of the six consolidated artificial marine clays (8291, 8282, 8255, and 8228 specimens) were selected to undergo the sediment fabric tests. Freeze-drying pretreatment [74] was carried out on the artificial marine clay specimens after the consolidated treatment before the sediment fabric tests. The LVESEM and MIP test specimens were immersed for about 1 min in a container filled with isopentane as a transition. Then, the specimens were transferred to a container filled with liquid nitrogen (−196 °C) and soaked for about 1 min. After complete freezing, the pore water was extracted using a vacuum pump that provided an absolute pressure of 6 Pa. The dried specimens were then kept in a vacuum dryer pending the sediment fabric tests.

4.1. LVESEM Analysis

The horizontal section of the dried specimens was broken off by hand, and the flat observation area was selected as the test area for the LVESEM experiment. Figure 16 shows the LVESEM test results for artificial marine clay. Based on the SEM petrology atlas [75], the atlas comparison method was used to distinguish the mineral particles and analyze artificial marine clay fabric in the LVESEM images. The LVESEM images of the four artificial marine clay specimens, the consolidated specimens with high montmorillonite content, especially specimen 8291, demonstrated pronounced flocculated and aggregated structures with edge-to-face and edge-to-edge contacts at the same initial void ratio. At the same time, the consolidated specimens with low montmorillonite content, especially specimen 8228, displayed dispersed and deflocculated structures with face-to-face association. As suggested by Gumaste et al. [44], the reason proposed for this sediment fabric phenomenon was that montmorillonite comprise a larger specific surface area and greater capacity for isomorphous substitution than kaolinite. This was attributed to the fact that montmorillonite particles show greater Coulomb attraction and London–van der Waals forces to overcome diffuse double-layer models of repulsive forces, and eventually form a flocculated sediment fabric.

Chen et al. [76] proposed that the unloaded flocculated structures in the sediment fabric tended to show greater random particle orientation and deformability and were thus more sensitive to load. As a result, pore variations of the specimens with higher montmorillonite content were more significant than those with lower montmorillonite content after consolidation under the same effective stress. For example, although samples 8291, 8282, 8255, and 8228 shared the same initial void ratio prior to consolidation, their respective pore area percentages after consolidation were 55.8%, 56.7%, 57.8%, and 61.4% according to LVESEM images from the Particles (Pores) and Cracks Analysis System (PCAS, Nanjing University, Nanjing, Jiangsu, China) [77] which can be processed into binarized images and help calculate the proportion of pore spaces. Compared with kaolinite, montmorillonite comprised a thicker adsorbed water film (stern layer) and narrower free water passage (diffusion layer) between weakly adsorbed water layers. The narrow path and low porosity of montmorillonite hindered the development of pore water pressure under cyclic loading. Research by Pillai et al. [78] furthermore indicated that dispersed microfabric was found to offer reduced resistance under cyclic loading.

As marine clay with lower void ratio was shown to have a higher dynamic shear modulus [79], the low porosity in specimens with high montmorillonite content offered a reasonable explanation for the high stiffness under the same strain conditions from Figure 11. From the perspective of energy dissipation, viscous energy dissipation in cohesionless particles with liquefaction potential is mainly provided by the sliding and rolling occurring between particles [80]. Similarly, in artificial marine clays, the advantage of montmorillonite compared to kaolinite in terms of specific surface area and capacity for isomorphous substitution may result in a significant increase in intergranular contact between particle–particle, particle–aggregate, and aggregate–aggregate. Therefore, this increased intergranular contact increases the difficult of the sliding and rolling between montmorillonite particles in the consolidated flocculated low-porosity specimens under the same cyclic loading. Lastly, the specimens with high montmorillonite content were shown to experience a more prolonged rise in viscous energy before failure on the basis criterion of single amplitude strain, resulting in greater VEDR at the failure cycle (VEDR_failure). At the same time, the VEDR of high-montmorillonite content specimens remained low, and the cyclic strain amplitudes at breakpoint were delayed.

4.2. MIP Analysis

Dried specimens weighing between 0.8 g and 1 g were tested in the automatic mercury porosimeter. Since mercury is a non-wetting liquid when in contact with mineral particles, the relationship between mercury intrusion pressure and pore diameter could be derived from the Washburn equation [81]. On the basis of Diamond’s [82] experimental study of mercury intrusion into clay with kaolinite and illite, the contact angle between mercury and clay minerals was determined as 147 degrees, and the surface tension coefficient as 0.485 N·m⁻¹. At the same time, with the increased mercury intrusion pressure, the pressure-associated pore diameter decreased continuously. The results of MIP tests were therefore plotted in terms of the variation of cumulative (V_cumulative) and incremental (V_incremental) intrusion volumes of mercury in the specimen with respect to pore diameter (D_i) as shown in Figure 17 and Figure 18, respectively. The cumulative intrusion volume of mercury ($V_{cumulative}={\displaystyle \sum }_i\Delta V_i$) reflected the cumulative mercury content of the intrusion curve under different pore diameters. The incremental intrusion volume of mercury ($V_{incremental}=-\Delta V_i/\Delta log{D}_i$) expressed the characteristics of pore distribution. The MIP test results are listed in

Table 7. The result of the fabric in artificial marine clays by LVESEM test and MIP test.

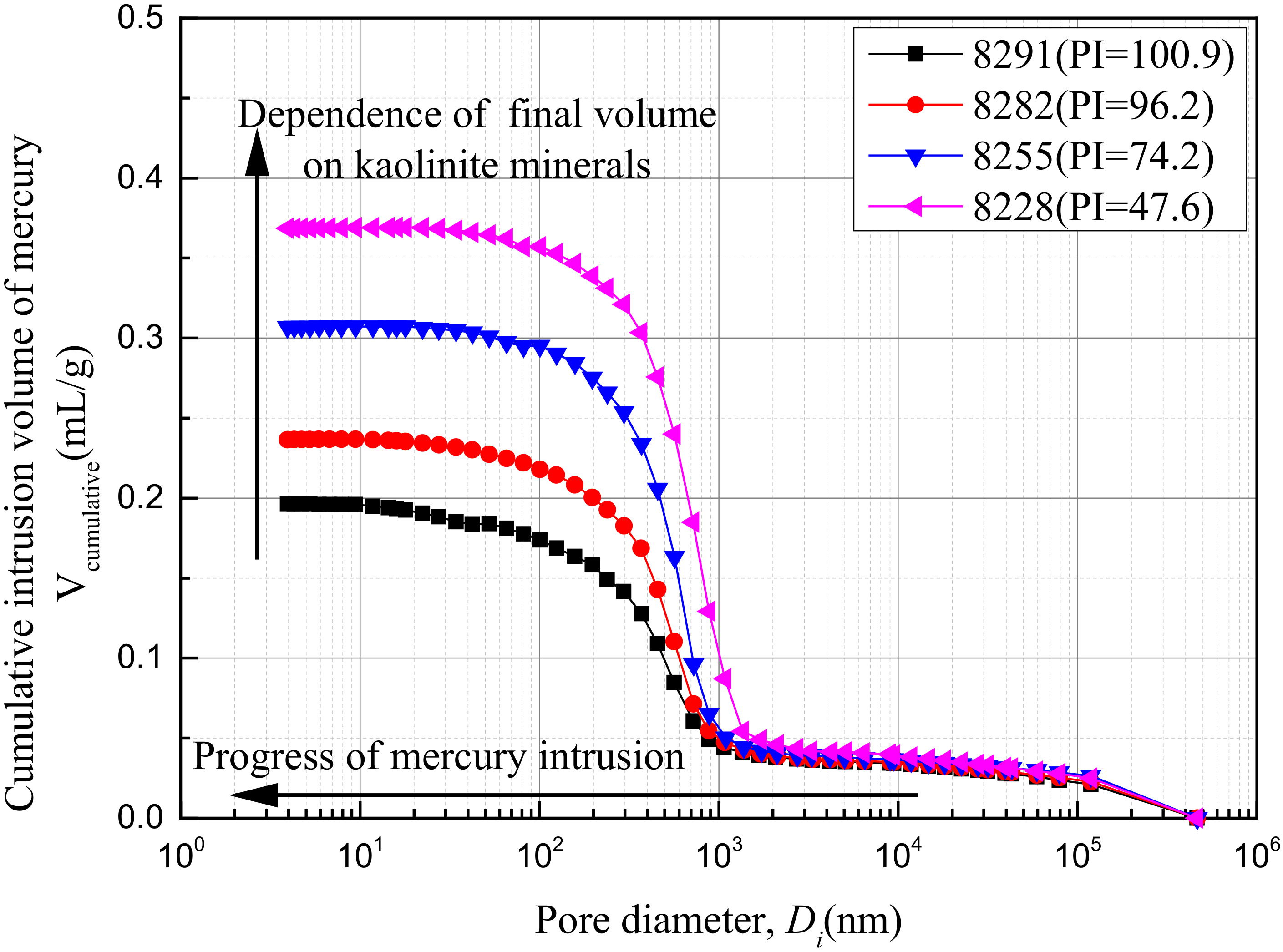
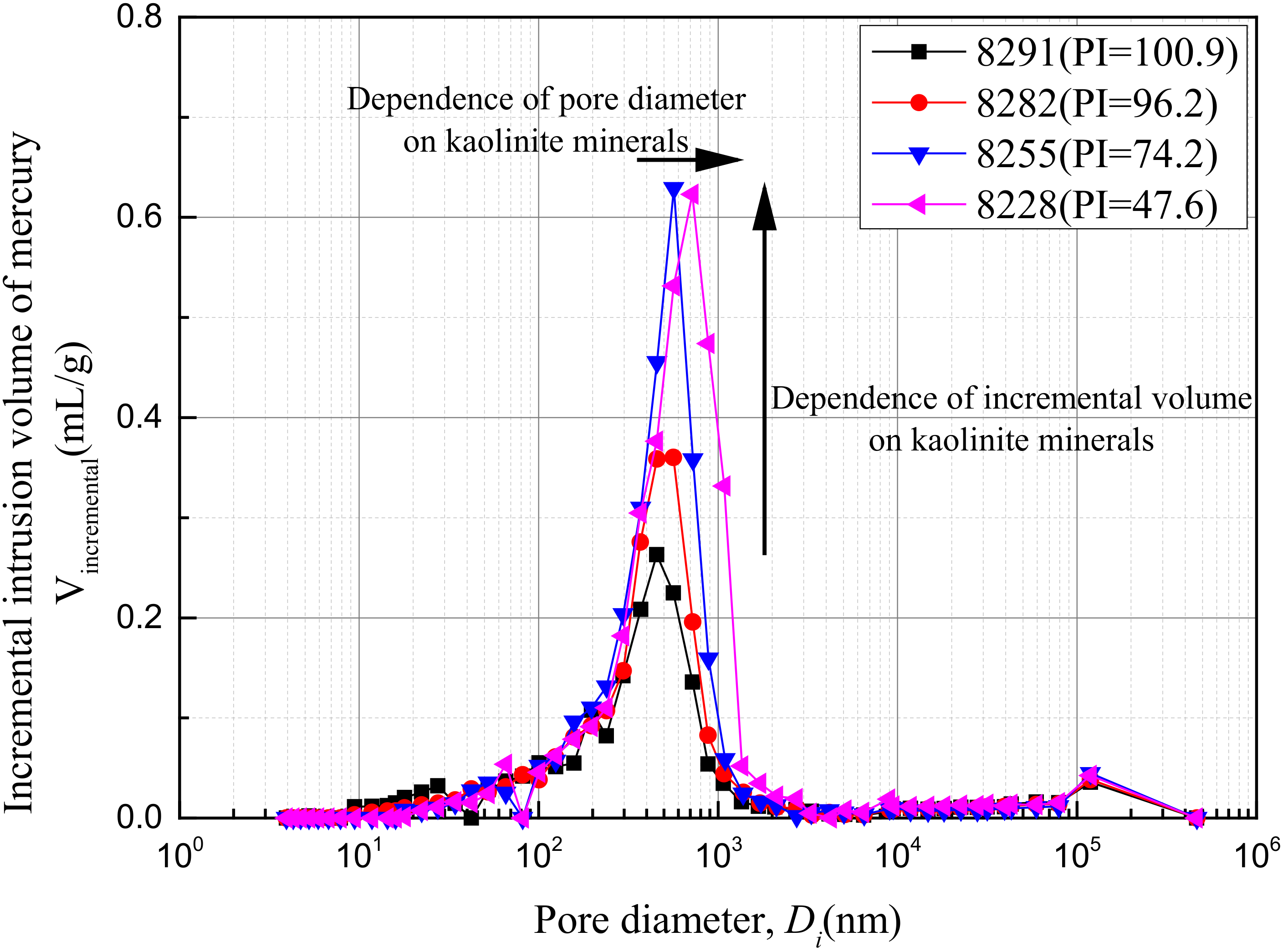
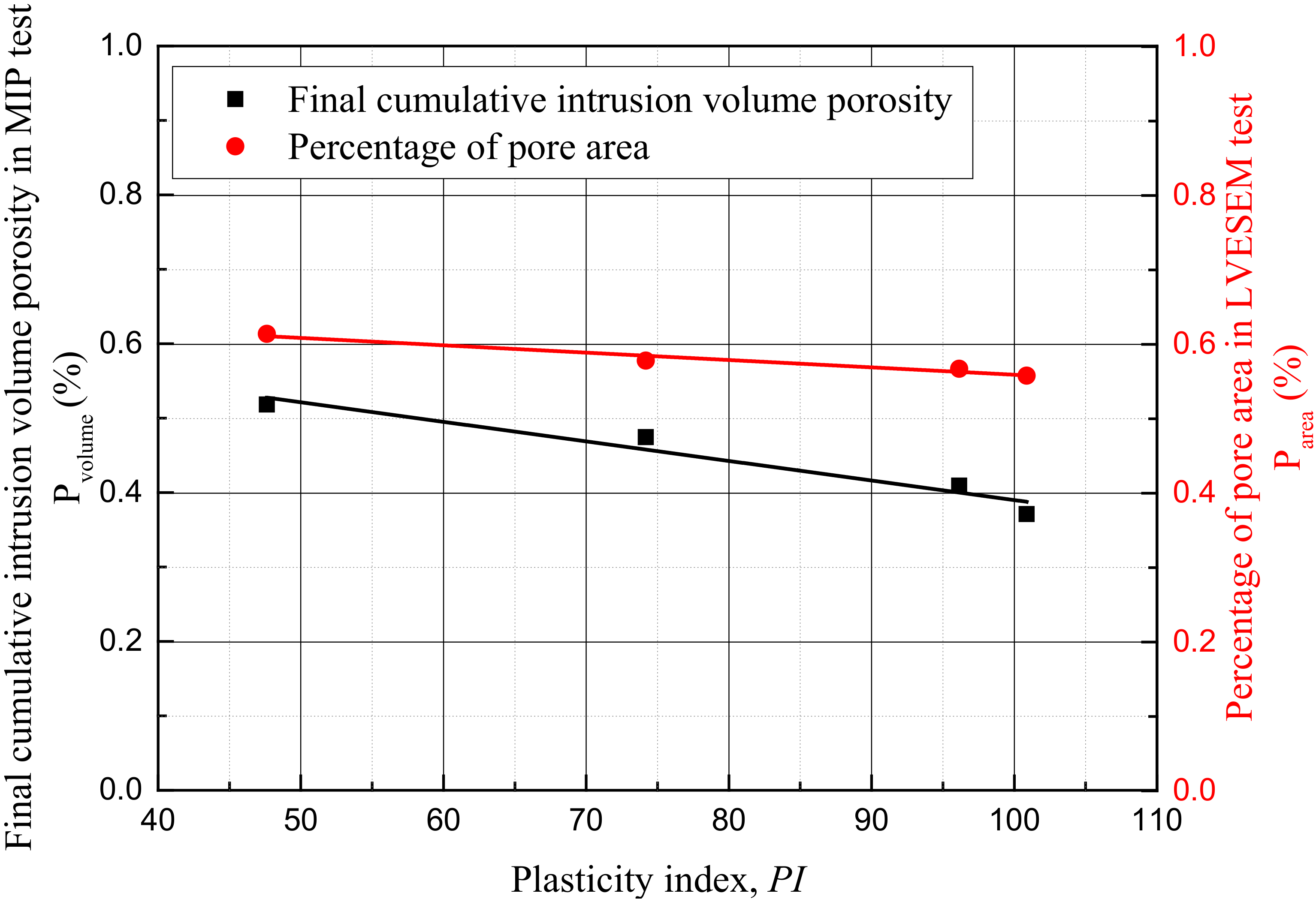
Test Specimen	Plasticity Index ${\mathit{I}}_{\mathit{P}}$	Percentage of Pore Area 1 Parea (%)	Final Cumulative Intrusion Volume of Mercury Vcumulative (mL/g)	Intra-Aggregate Pore Diameter Dintra-aggregate (nm)	Incremental Intrusion Volume of Mercury at Intra-Aggregate Pore Vincremental (mL/g)
8291	100.9	55.8	0.196	456	0.263
8282	96.2	56.7	0.237	564	0.360
8255	57.9	57.8	0.307	566	0.629
8228	47.6	61.4	0.369	718	0.623

¹ The percentage of pore area of artificial marine clays is calculated by Particles (Pores) and Cracks Analysis System (PCAS) [77].

.

Figure 17 shows how the cumulative intrusion curves of the specimens with high montmorillonite content always remain below those with low montmorillonite content. This study result proved that the total pore volume of high montmorillonite specimens such as samples 8291 and 8282, is lower than that of low montmorillonite specimens, as samples 8255 and 8228. This conclusion was demonstrably consistent with the pore areas percentage findings in LVESEM. The relationships between PI and final cumulative intrusion volume porosity in MIP test results and percentage of pore areas in LVESEM test results are shown in Figure 19. With the increase in plasticity, the pore volumes and pore areas of artificial marine clay decreased gradually. However, the fitting line of pore volume is steeper than that of pore area in Figure 19. It should be remembered that cumulative intrusion volume porosity is a typical three-dimensional pore space, while percentage of pore area is a two-dimensional pore space on the observed section. Therefore, the pore volume is more sensitive than pore area to the influence of plasticity index.

From Figure 18, it can be seen that the incremental mercury intrusion volumes in all artificial marine clays showed as a unimodal curve. Garcia-Bengochea et al. [83] proposed the existence of bimodality between inter-aggregate pore and intra-aggregate pore in natural fine-grained soil. However, Delage and Lefebvre [84] reported the results of the Champlain experiment involving scanning reconstituted clay after consolidation by electron microscopy (SEM) and performing an MIP test. They found that the consolidation behavior resulted in the collapse of the larger inter-aggregate pore while the finer intra-aggregate pore remained intact. The inter-aggregate pore was unmistakably seen to have disappeared, while the size of intra-aggregate pore had remained between 466 and 718 nm in the consolidated artificial marine clay. As shown in Table 7, the diameters of intra-aggregate pore and incremental intrusion volumes of the specimens with high montmorillonite content (samples 8291 and 8282) were furthermore found to be lower than those of the specimens with low montmorillonite content (samples 8255 and 8228). These findings indicated that montmorillonite not only constituted the principal determining factor of (intra-aggregate) pore size of the finer artificial marine clay, but also contributed to a more uniform pore distribution within the specimens.

The MIP test results and LVESEM test results in microstructure and microporosity provided mutual confirmation. These tests result fully reflected the sediment fabric of artificial marine clay observed from two experimental perspectives. Meanwhile, the sediment fabric of artificial marine clay comprising various clay minerals significantly influenced their dynamic properties. This further proved that the sediment fabric that resulted from clay mineral composition was primarily responsible for the variations in dynamic properties, and that the plasticity index could only be used as a reference parameter.

5. Conclusions

According to the geological conditions and mineral composition analysis results of marine clay from two typical estuarine deltas in Guangdong Province, South China, artificial marine clays composed of different clay mineral contents were remolded. Under identical laboratory dynamic triaxial testing conditions, the dynamic properties of artificial marine clays at large strain were investigated with particular consideration of the effects of changes in montmorillonite and kaolinite content in clay minerals. Meanwhile, low-vacuum environmental scanning electron microscopy (LVESEM) test and mercury intrusion porosimetry (MIP) tests were carried out on artificial marine clays to explore the sediment fabric of microstructure and microporosity.

Based on observations from the laboratory dynamic triaxial testing results on artificial marine clays, the dynamic properties of the specimens with high montmorillonite content were: (a) a smoother strain increase rate and smaller maximum cyclic strain amplitude; (b) an inhibited increase in pore water pressure including a slower cumulative increase rate in pore water pressure, reduced residual pore water pressure, and narrower pore water pressure amplitude; (c) a more rounded double-normalized hysteresis curve at the failure cycle. Artificial marine clays with high montmorillonite content were found to present very high Atterberg limits and plasticity indices, which was attributed to the fact that strong and loose-adsorbed water (stern layer) was more easily adsorbed on clay surfaces by montmorillonite in the plastic state. It was therefore deemed unconducive to the development of strain caused by aggregate particles sliding and rolling and the rise of free water-induced pore water pressure.

Accordingly, both the stiffness degradation curve and the viscous energy dissipation ratio curve were affected by clay mineral composition. The specimens with high montmorillonite content displayed greater normalized shear moduli under the same cyclic shear strain and experienced a longer period of increased viscous energy before failure. The breakpoint of viscous energy dissipation with high montmorillonite content occurred at greater cyclic strain amplitude. Moreover, due to the influence of specific surface area and isomorphous substitution, the flocculated fabric of the high montmorillonite content specimens and the dispersed fabric of the low montmorillonite content specimens were presented under a low-vacuum environmental scanning electron microscopy test and mercury intrusion porosimetry test. After the same initial void ratio and effective stress consolidation, the flocculated low porosity of the high montmorillonite specimens ensured the opportunity for contact among aggregates under an identical cyclic strain, which provided favorable conditions to improve stiffness. Furthermore, montmorillonite minerals were found to impede sliding and rolling between particles. This reaction is the reason for the slow increase of viscous energy before failure and the hysteretic strain at the breakpoint of viscous energy dissipation in high montmorillonite specimens.

It should be noted that previous research [28,66,85] primarily focused on the influence of the plasticity index on the dynamic properties in marine clay when discussing mineral composition. In the present authors’ view, the plasticity index should be considered as an extension parameter based on Atterberg’s limit water content according to differing mineral compositions. Although soil plasticity variations are reflected by strong and loose absorbed water and are important indicators in practical engineering, they are unable to reflect the actual component of marine clays. Recent studies [35,40] have shown that even if cohesive soils share a similar plasticity index, their dynamic characteristics are quite different. The results of the present study have shown that the composition of clay mineral does indeed influence the dynamic properties of high plasticity marine clay under large strain due to differences in microstructure and fabric. Thus, this research on clay mineralogy may provide guidance for future engineering geology studies.