Three-Dimensional Modelling of Non-Linear Wave-Induced Seabed Response around Offshore Open-Ended Pile
Abstract
:1. Introduction
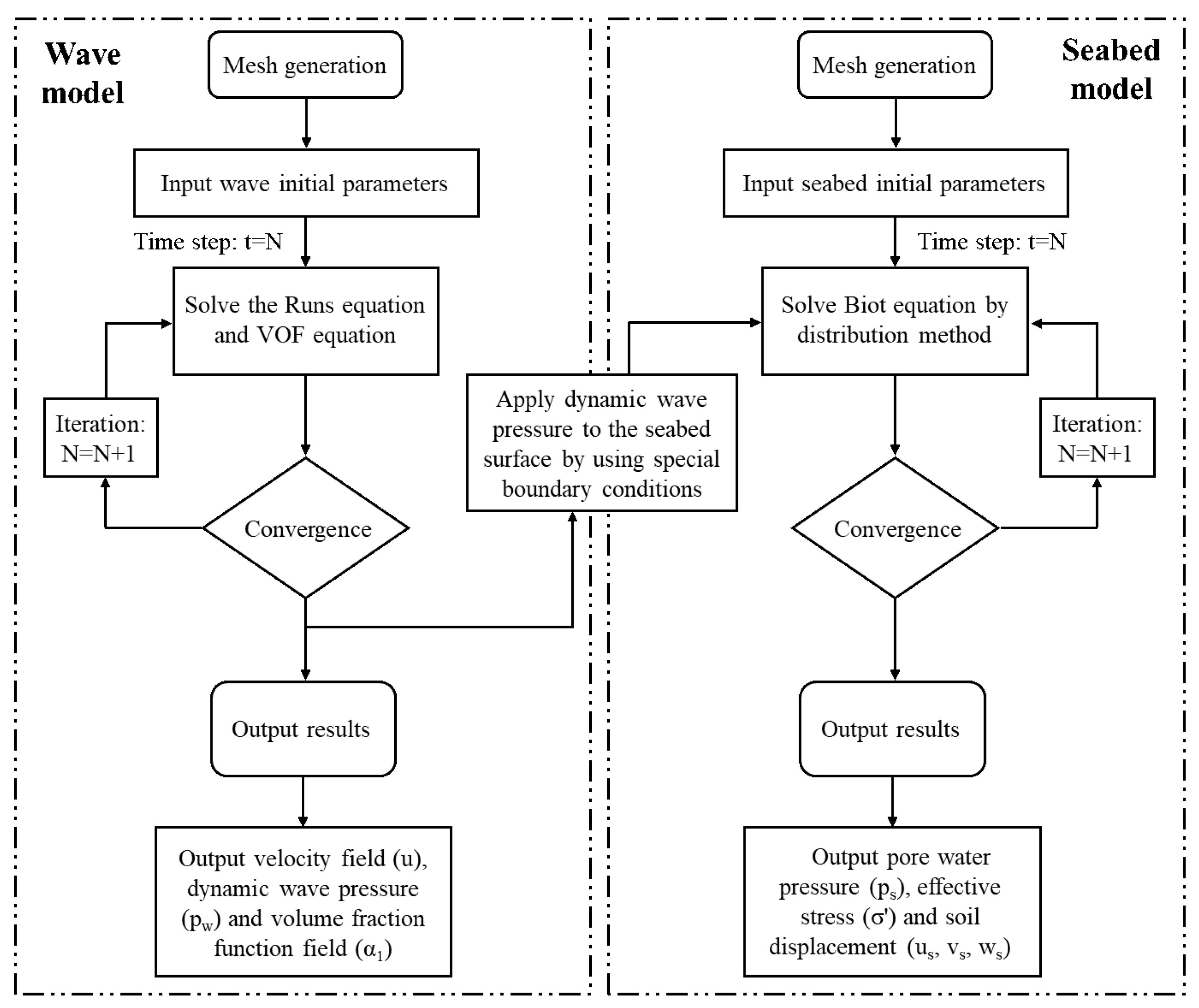
2. Coupled Numerical Model: PORO–FSSI–FOAM
2.1. Wave Model
2.2. Seabed Model
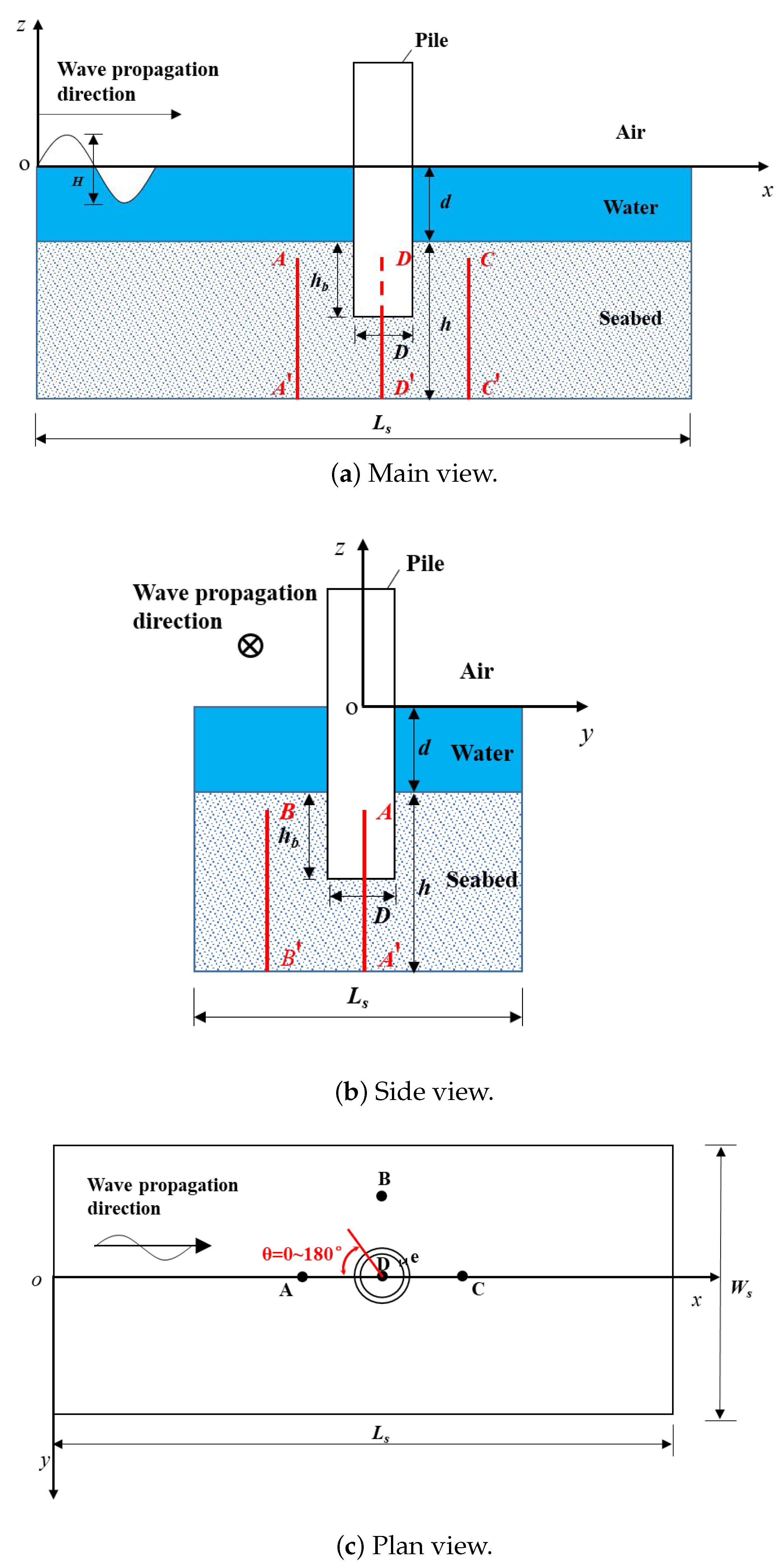
2.3. Computational Domains
2.4. Numerical Scheme
2.5. Boundary Conditions
- Wave model: at x = 0, the velocity profile U and the volume fraction are imposed based on fifth-order wave theory [29] in this work; at x = , an active wave absorption technique works by constantly adjusting the boundary conditions with a correction velocity and a corrected phase fraction for removing the wave reflection.
- Seabed model: at z = , we have ; an impermeable boundary condition, , is applied at z = ; similarly, a fixed wall boundary condition, , is adopted at the lateral sides of the computational domain; in terms of the boundary between the pile and the seabed, we assume that the soil skeleton and the structure move synchronously, i.e., .
2.6. Integration of Wave and Seabed Models
3. Model Validation
3.1. Wave Model Verification
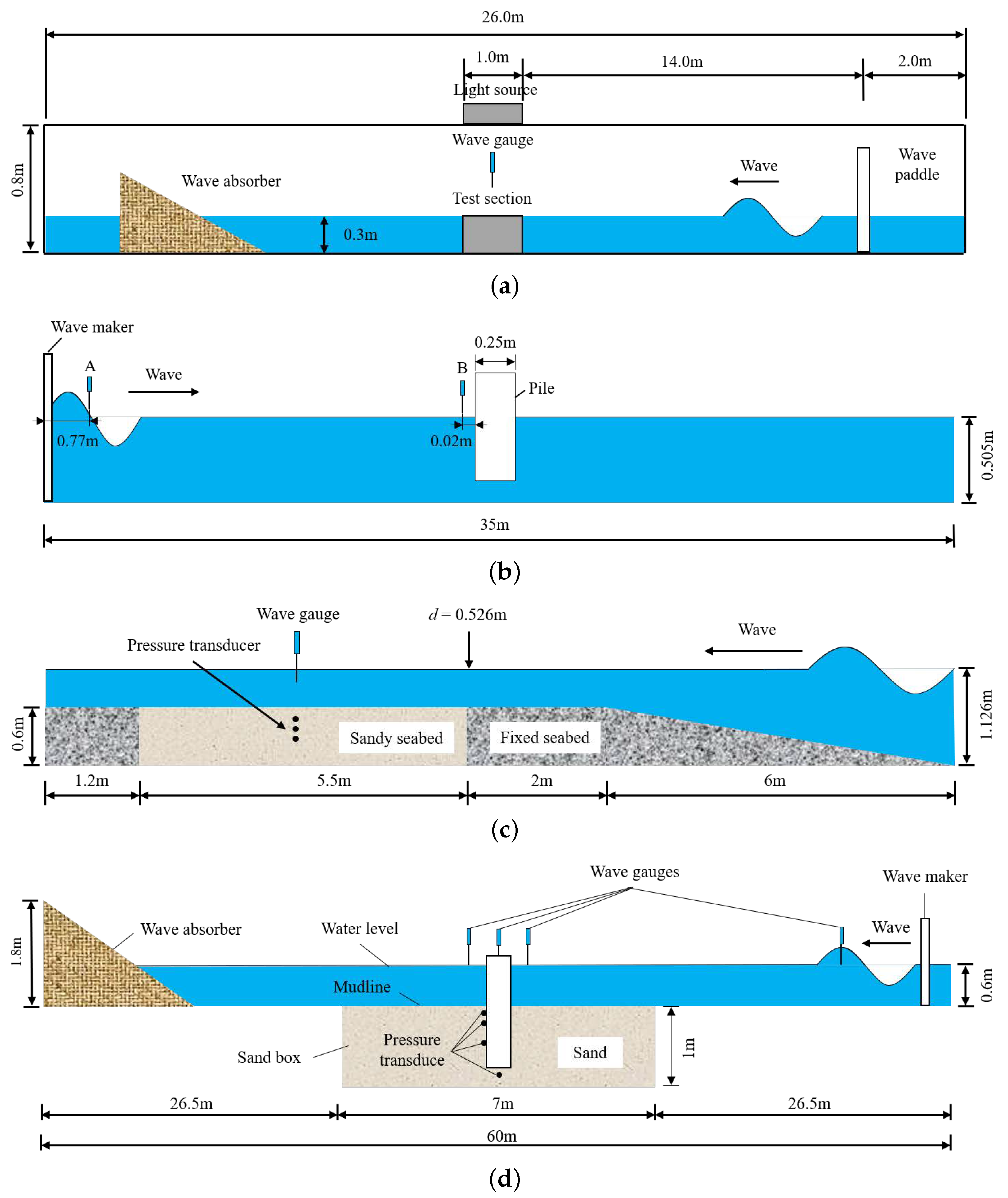
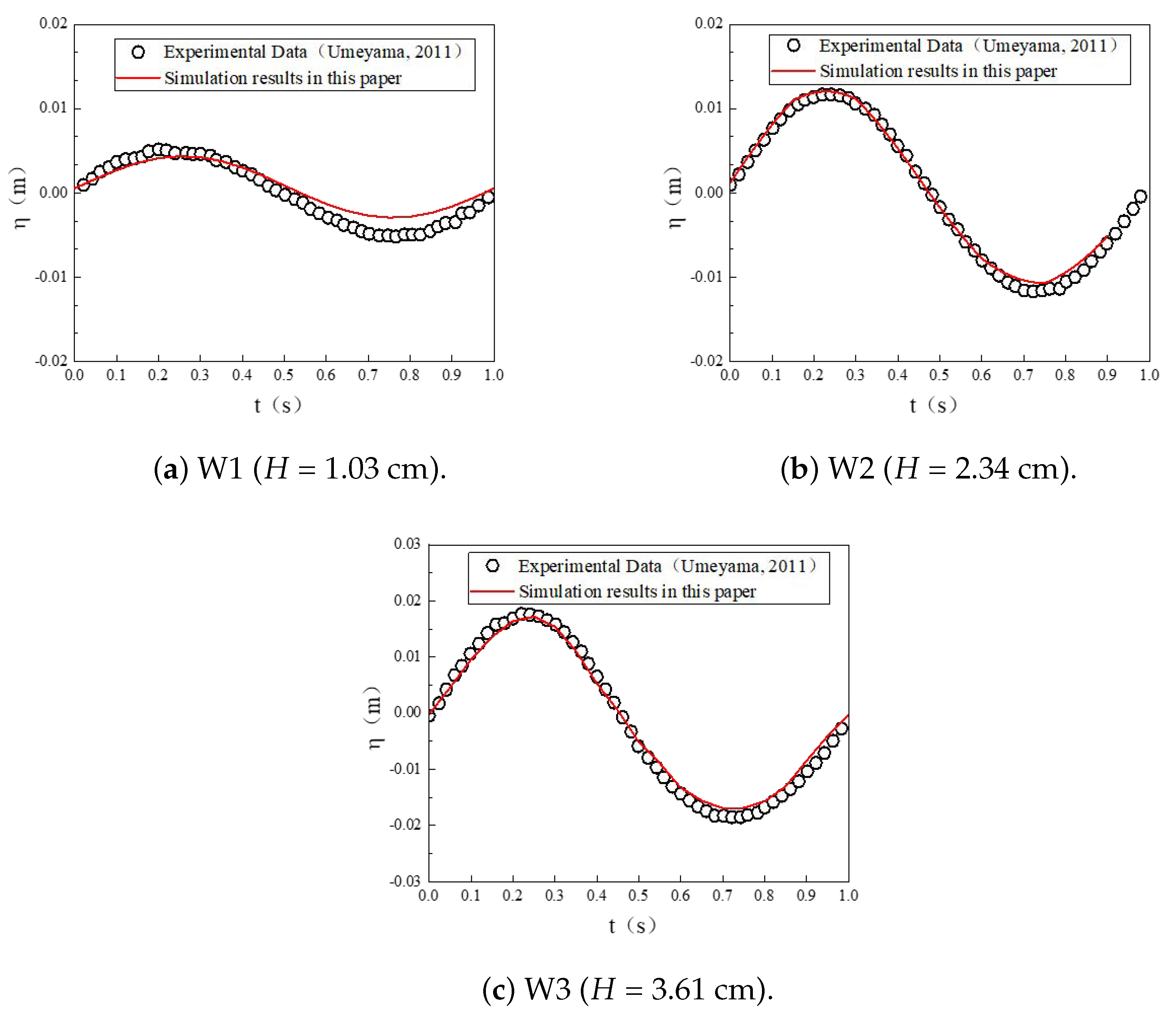
3.1.1. Verification of Wave Model without a Structure
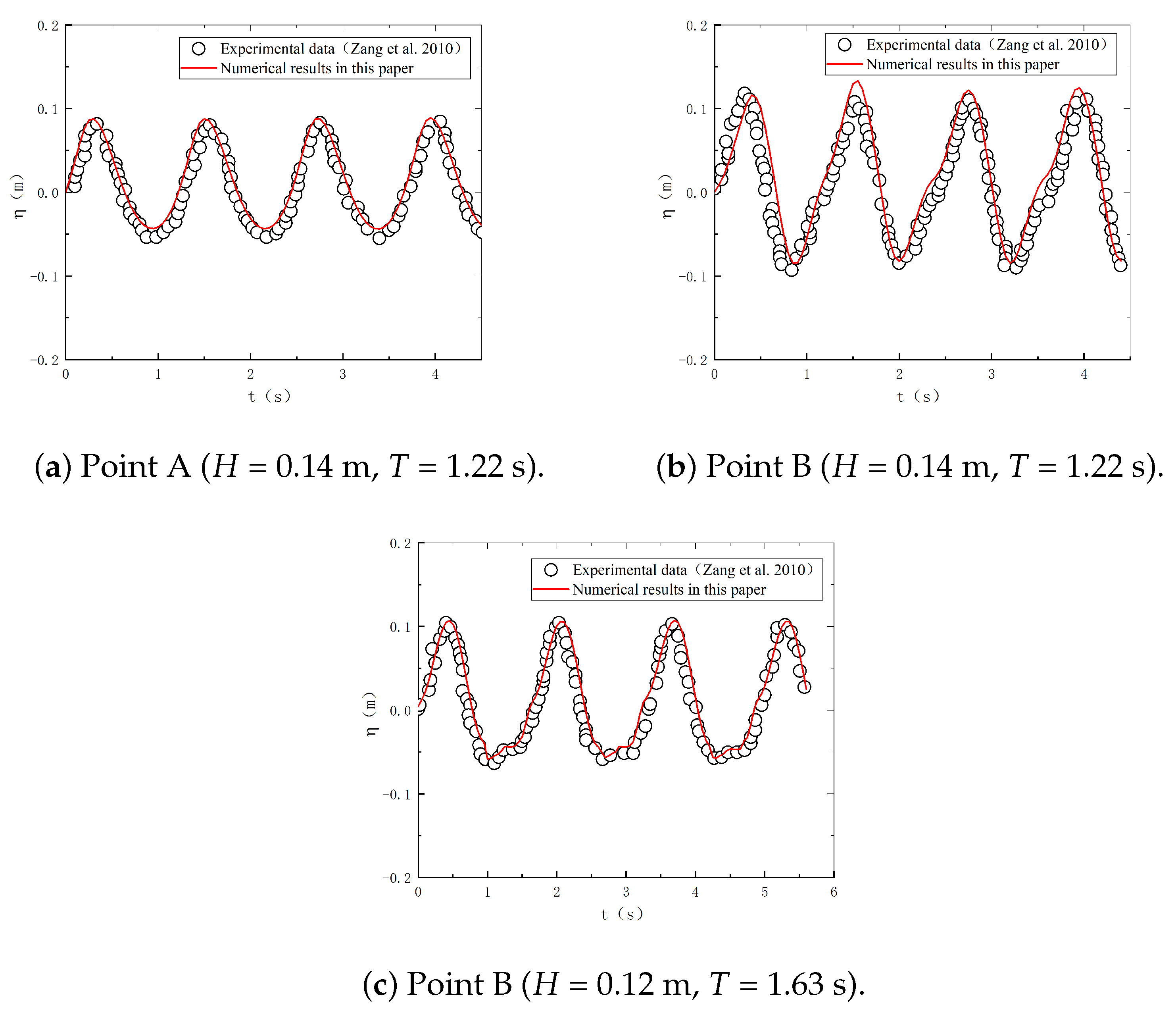
3.1.2. Verification of Wave Model with a Structure
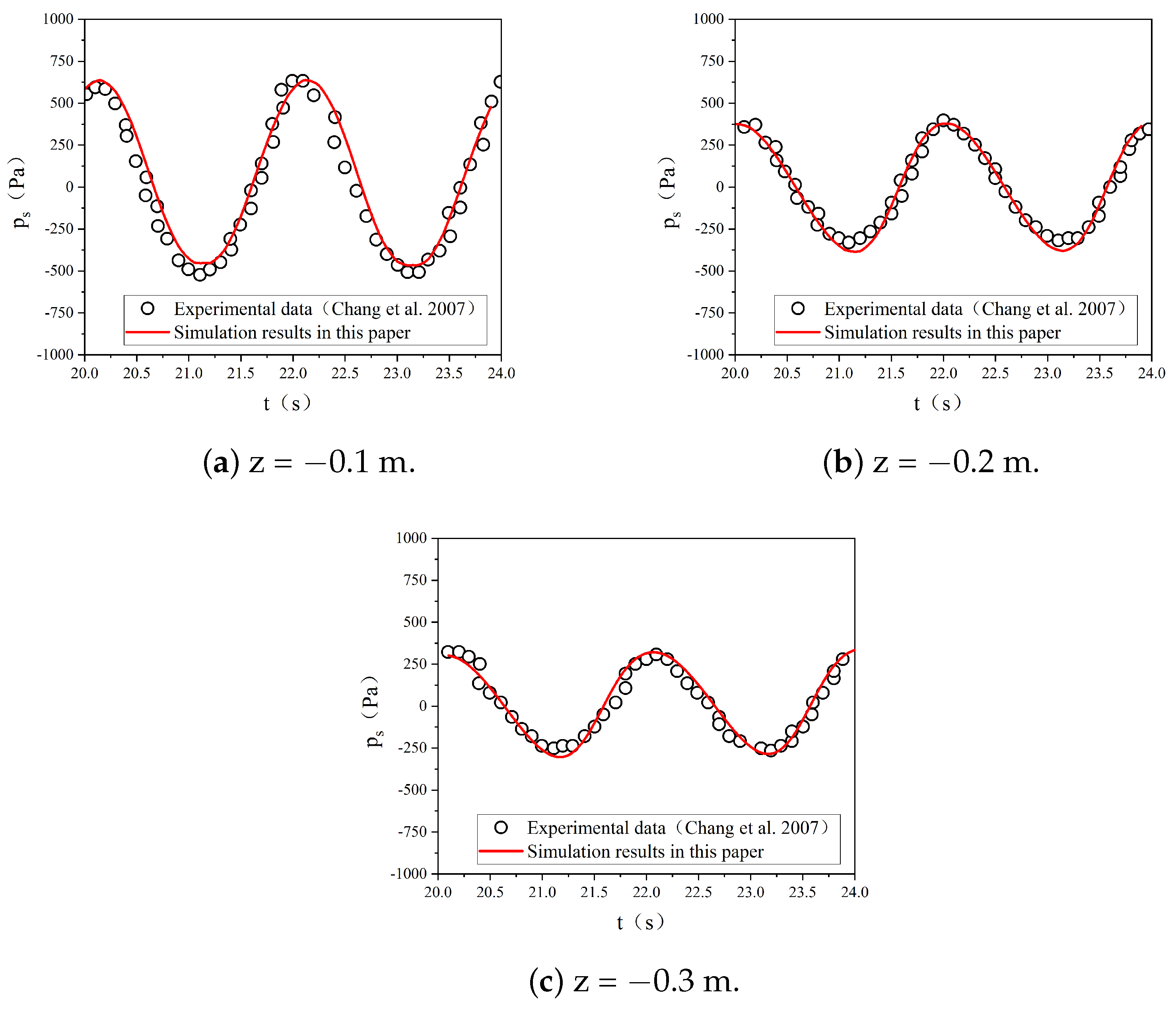
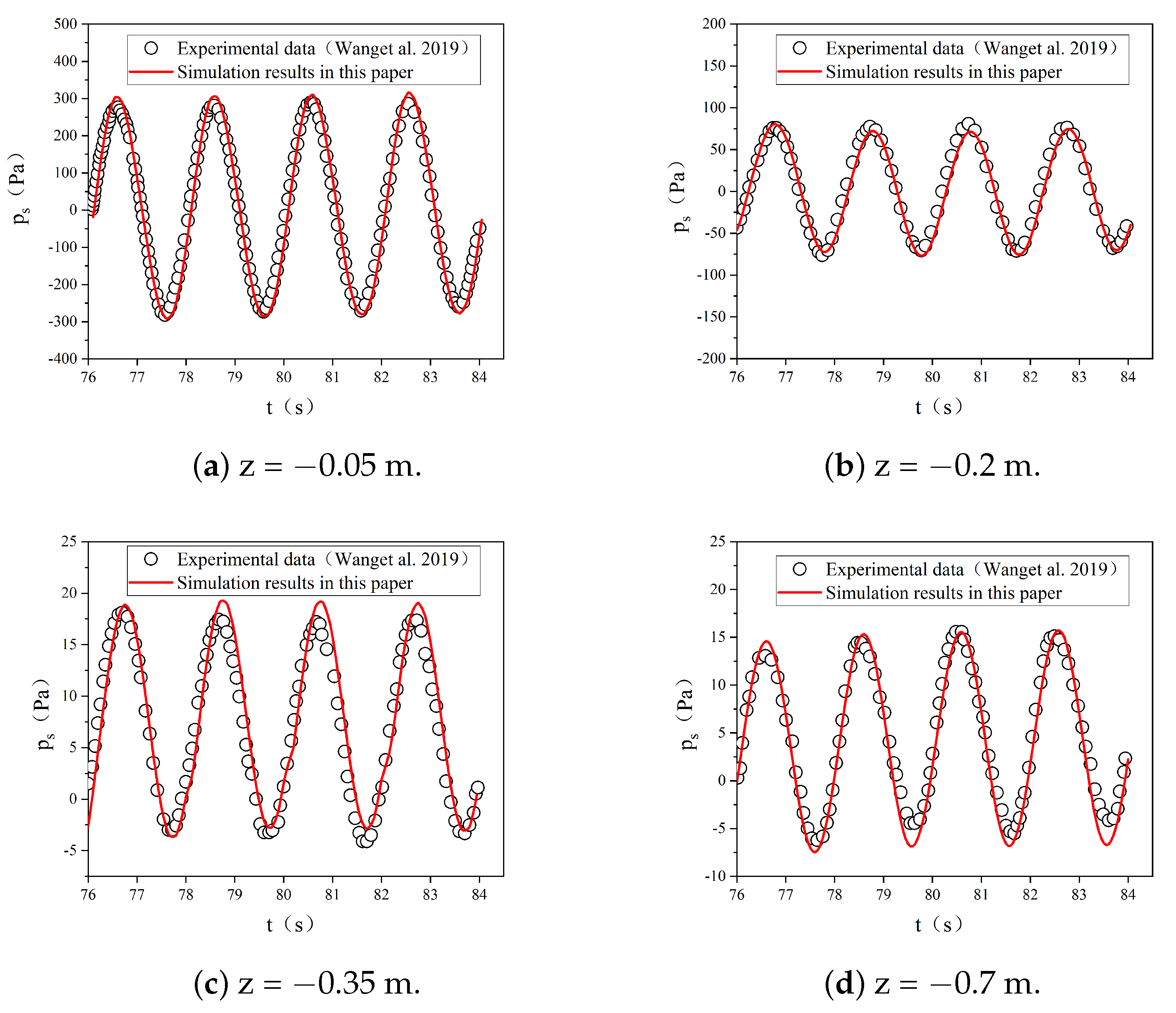
3.2. Seabed Model Verification
3.2.1. Validation of Seabed Model without a Structure
3.2.2. Verification of Seabed Model with a Structure
4. Results And Discussion
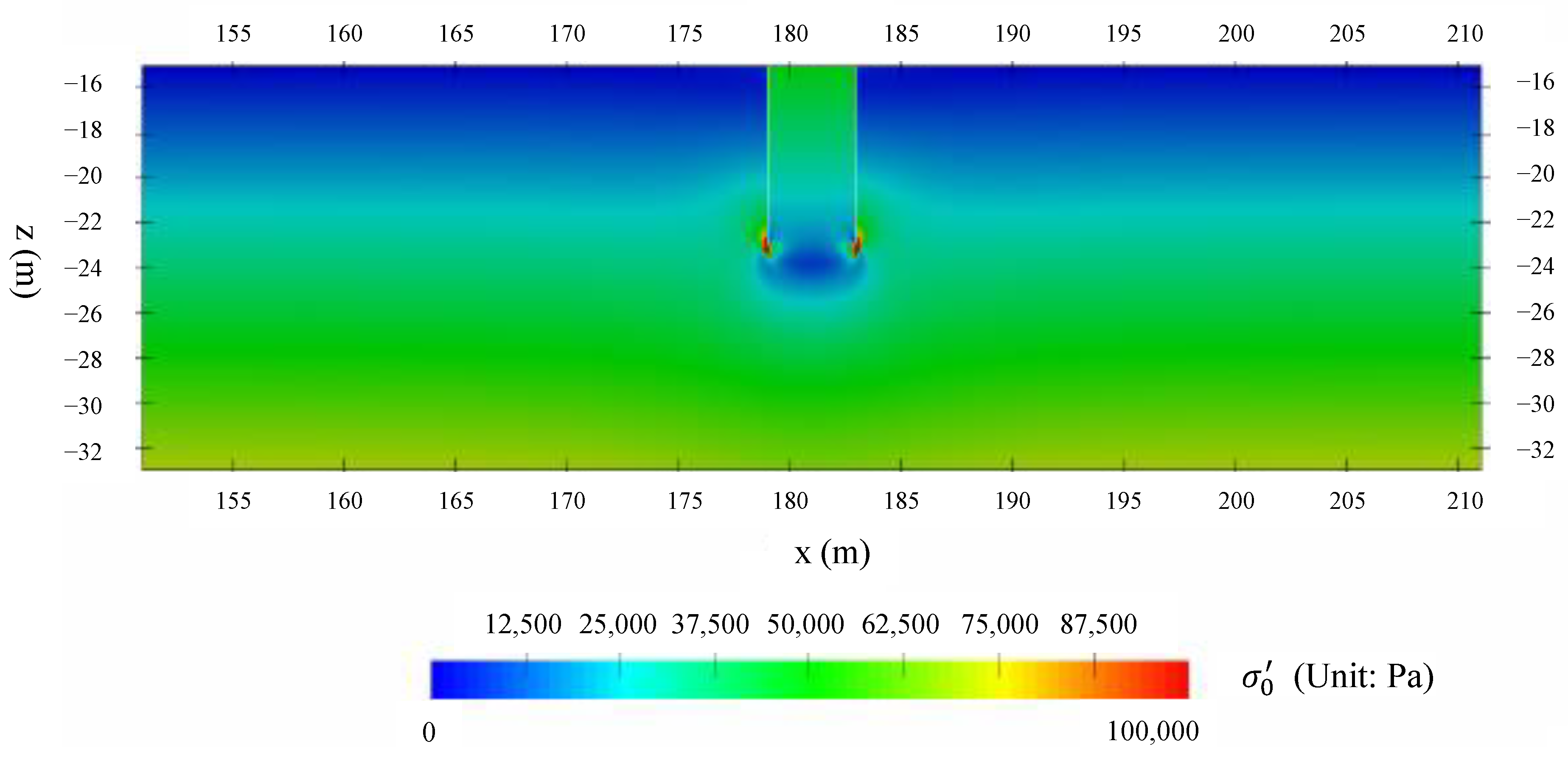
4.1. Seabed Consolidation
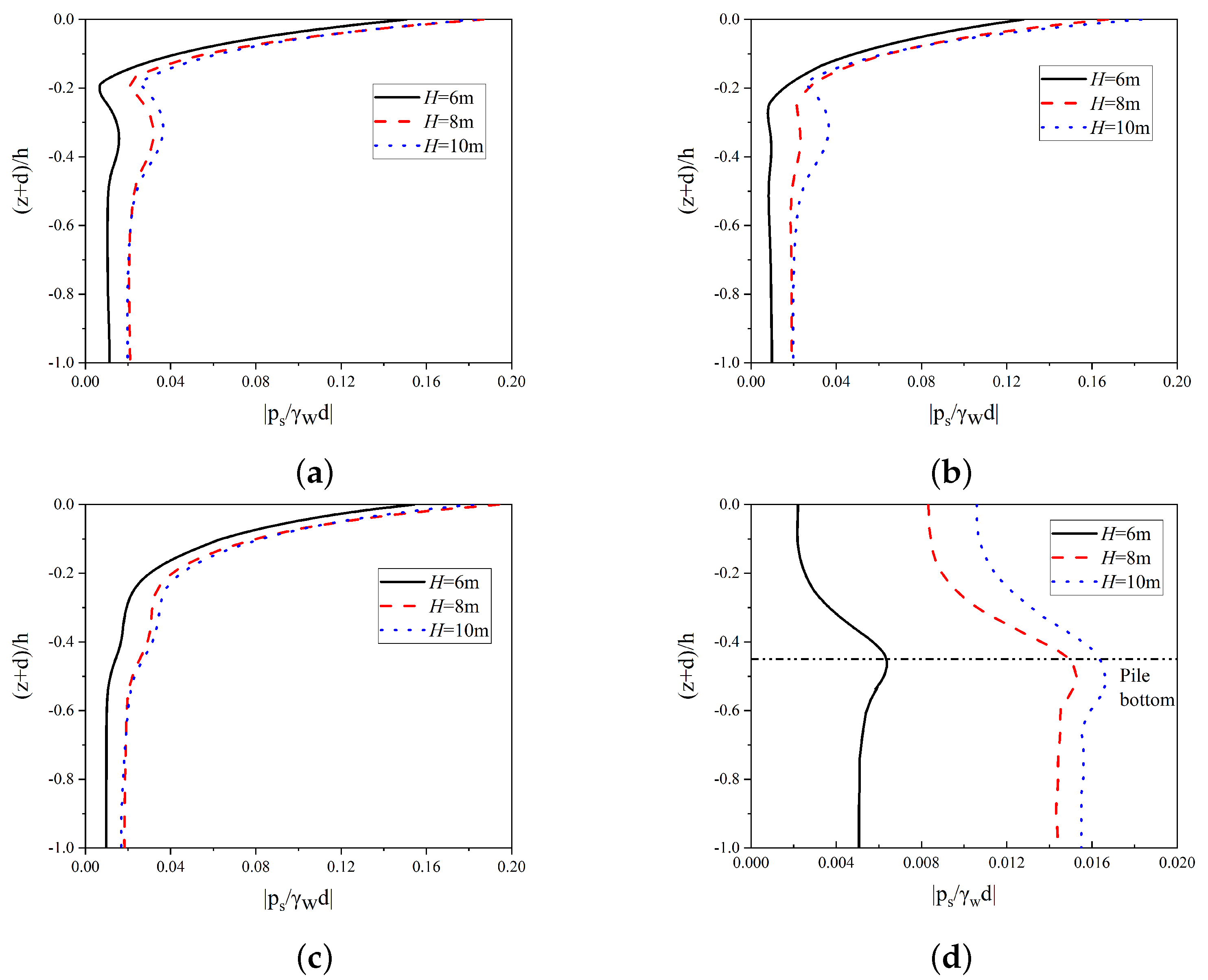
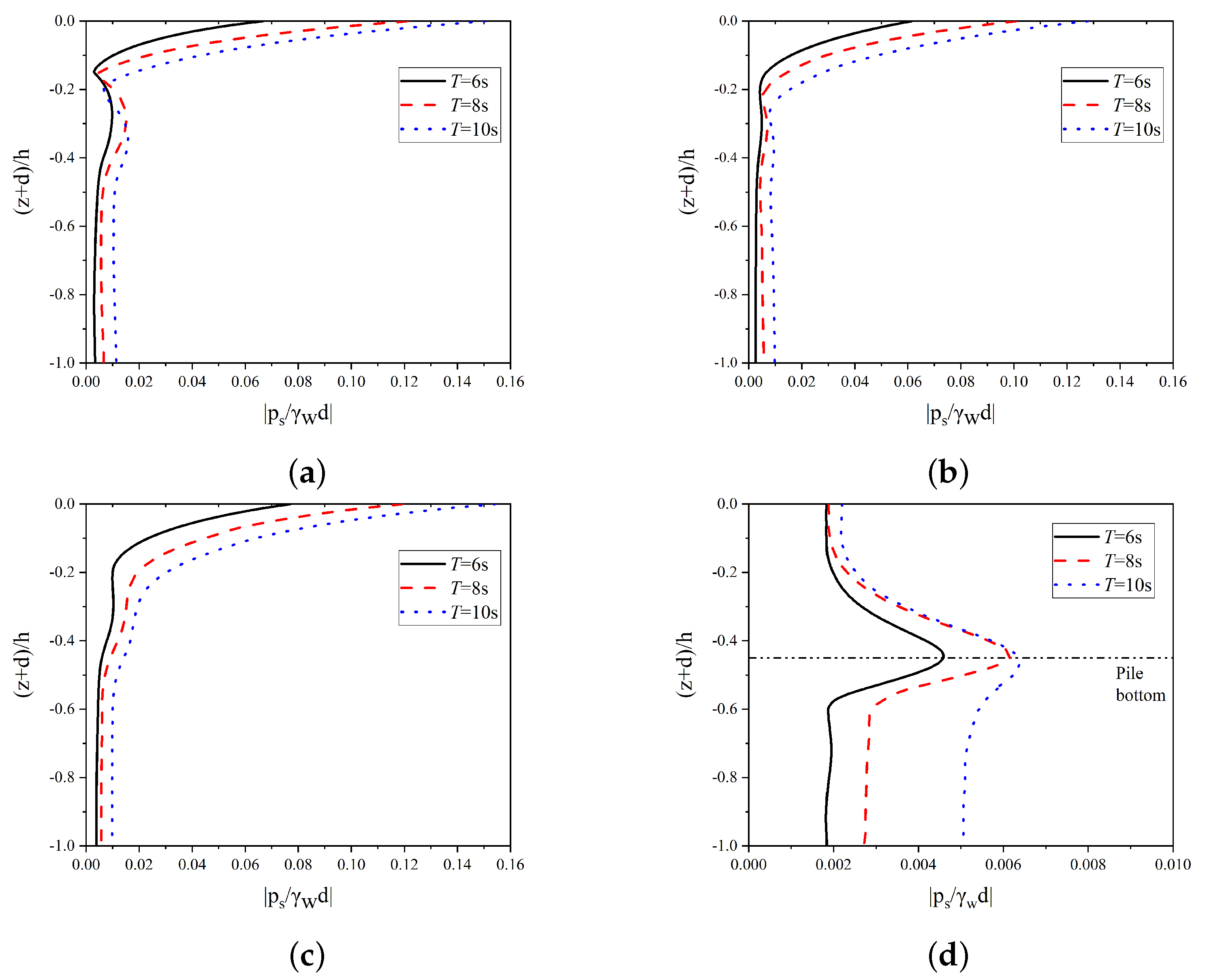
4.2. Influence of Wave Characteristics on the Transient Soil Response around the Open-Ended Pile
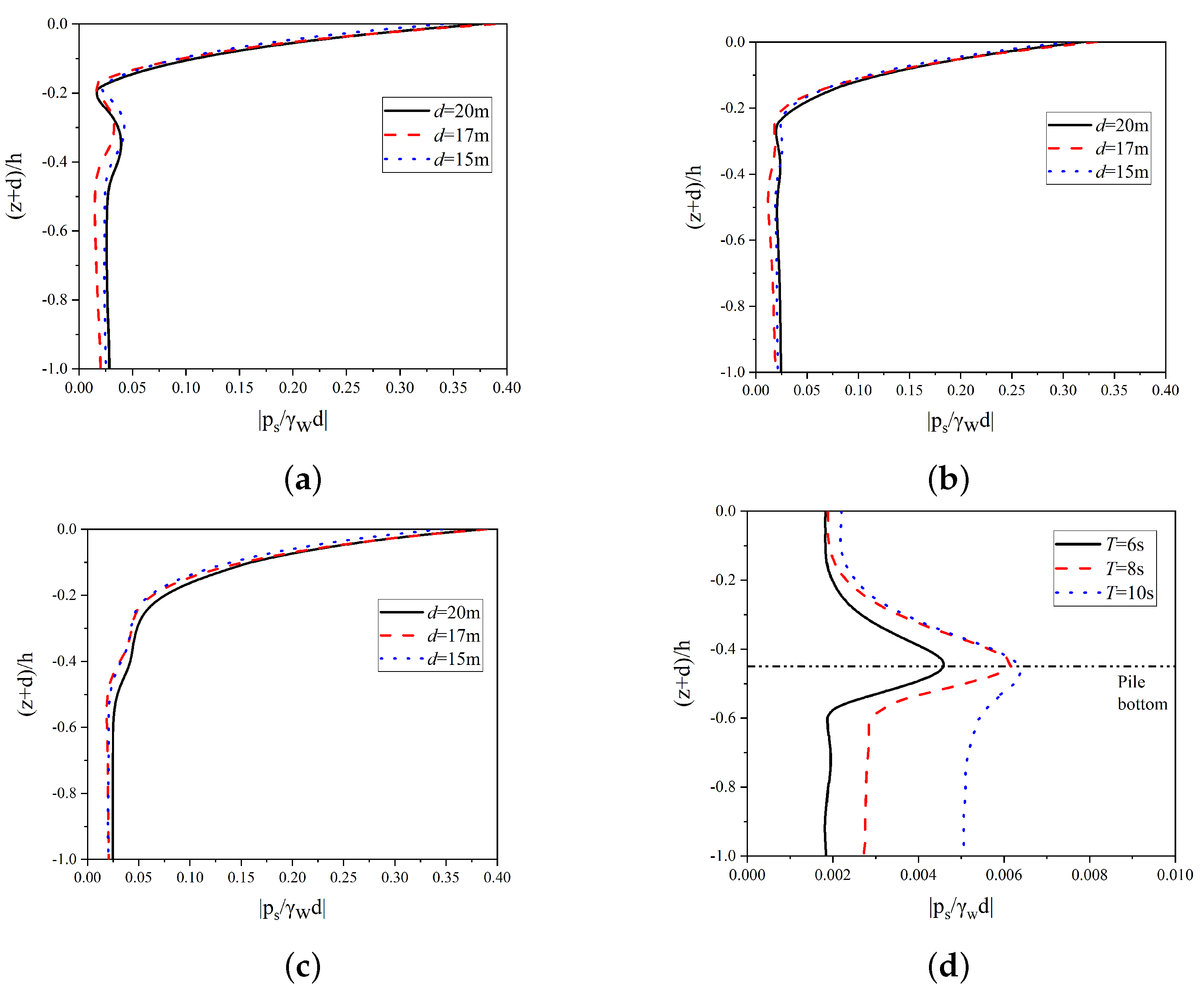
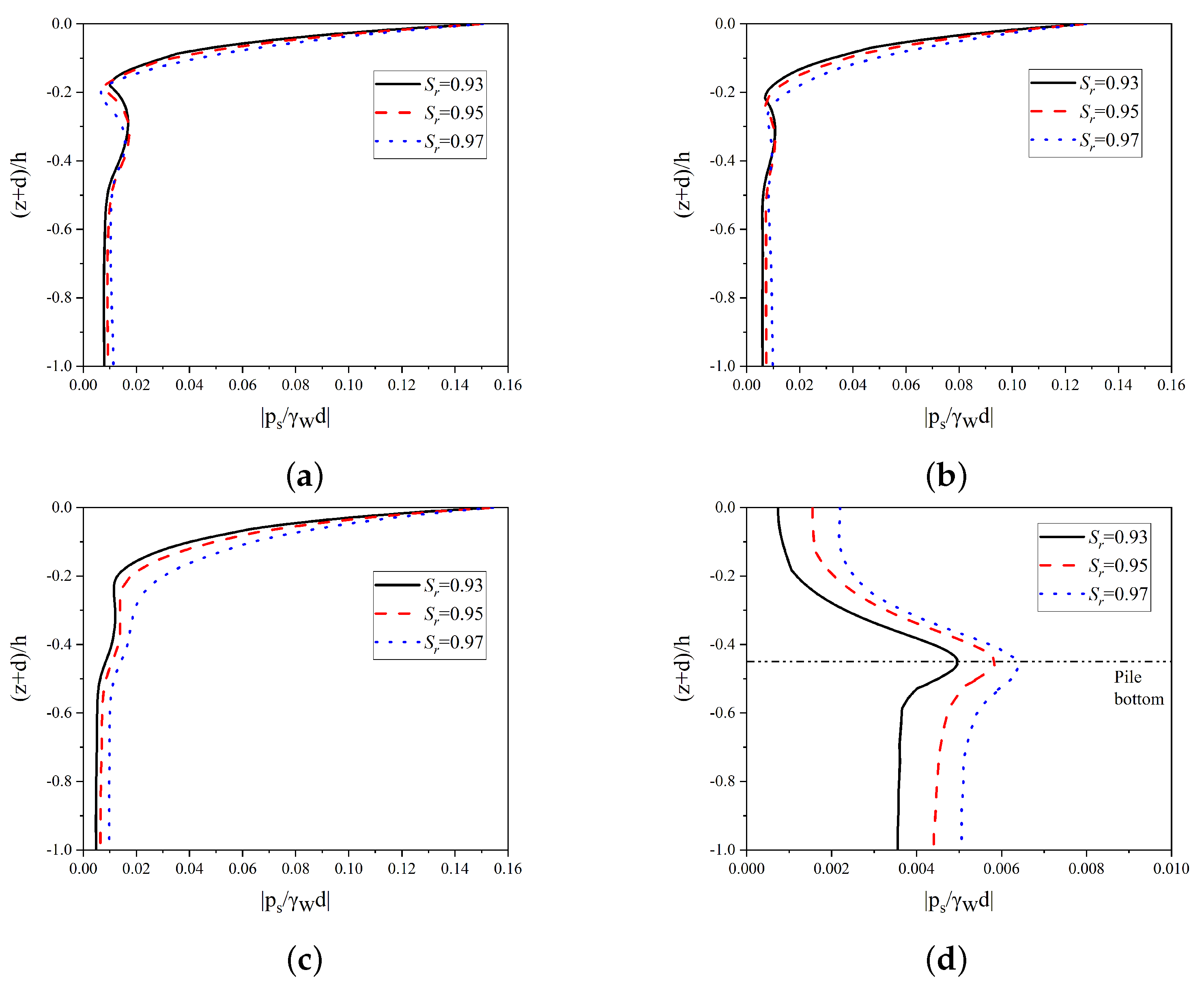
4.3. Influence of Seabed Characteristics on Transient Soil Response around the Open-Ended Pile
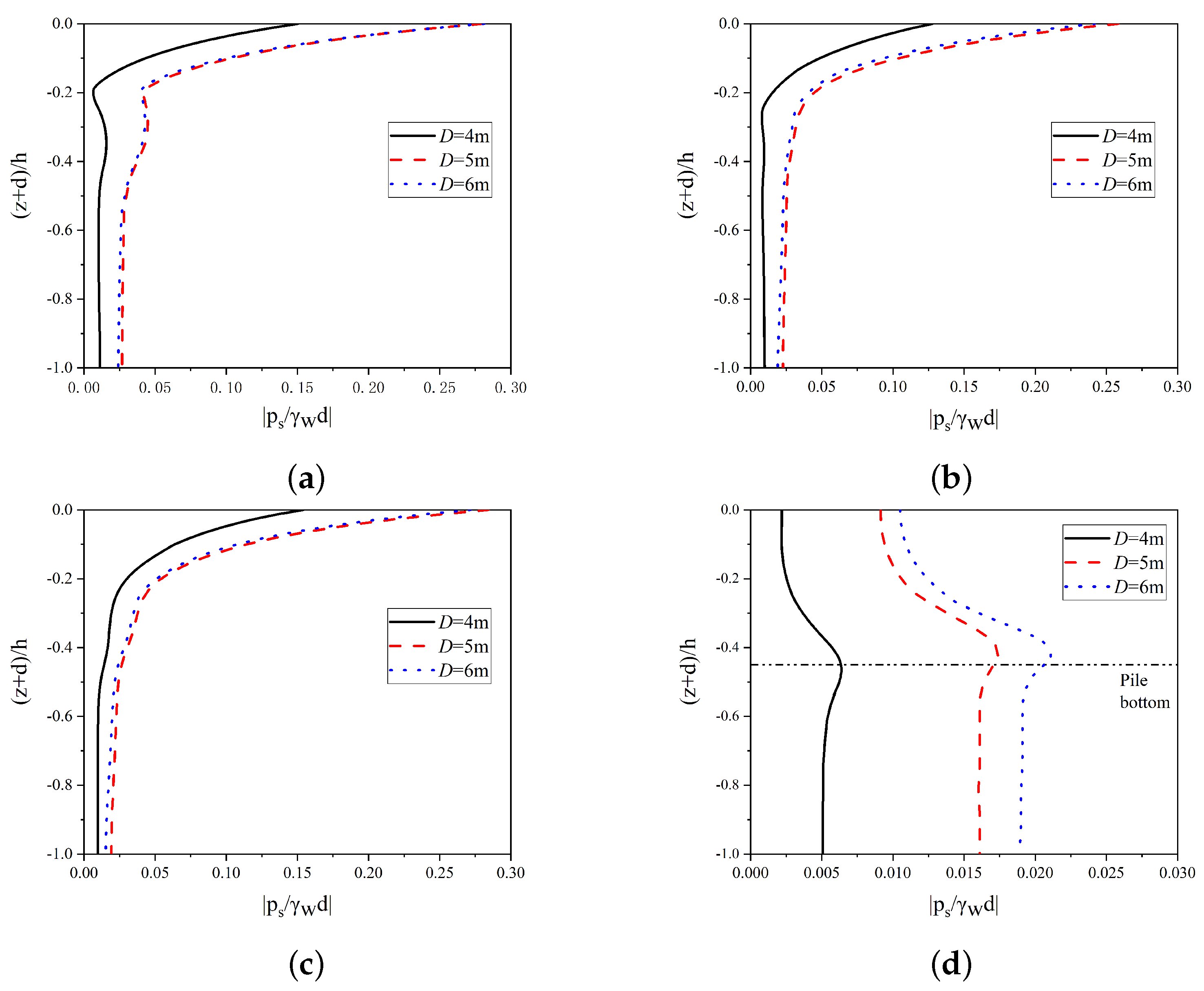
4.4. Influence of Pile Characteristics on Transient Soil Response around the Open-Ended Pile
4.5. Influence of Environmental and Structural Characteristics on Transient Soil Liquefaction around the Open-Ended Pile
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sumer, B.M. Liquefaction around Marine Structures; World Scientific: Hackensack, NJ, USA, 2014. [Google Scholar]
- Sumer, B.M.; Fredsøe, J. The Mechanics of Scour in the Marine Environment; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2002. [Google Scholar]
- Jeng, D.S. Mechanics of Wave-Seabed-Structure Interactions: Modelling, Processes and Applications; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Li, Y.; Ong, M.C.; Tang, T. Numerical analysis of wave-induced poro-elastic seabed response around a hexagonal gravity-based offshore foundation. Coast. Eng. 2018, 136, 81–95. [Google Scholar] [CrossRef]
- Celli, D.; Li, Y.; Ong, M.C.; Di Risio, M. Random wave-induced momentary liquefaction around rubble mound breakwaters with submerged berms. J. Mar. Sci. Eng. 2020, 8, 338. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 26, 155–164. [Google Scholar] [CrossRef]
- Chang, K.T.; Jeng, D.S. Numerical study for wave-induced seabed response around offshore wind turbine foundation in Donghai offshore wind farm, Shanghai, China. Ocean Eng. 2014, 85, 32–43. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Q.; Wu, Z.; Zhang, J.; Sui, T.; Wen, Y. Numerical study on effects of the embedded monopile foundation on local wave-induced porous seabed response. Math. Probl. Eng. 2015, 184621. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Sui, T.; Zheng, J.; Xie, M.; Nguyen, V.T. Modelling wave-induced 3D non-homogeneous seabed response. Appl. Ocean Res. 2016, 61, 101–114. [Google Scholar] [CrossRef]
- Wang, S.; Wang, P.; Zhai, H.; Zhang, Q.; Chen, L.; Duan, L.; Liu, Y.; Jeng, D.S. Experimental study for wave-induced pore water pressures in a porous seabed around a mono-pile. J. Mar. Sci. Eng. 2019, 7, 237. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.G.; Gao, F.P. Physical modelling of local scour development around a large-diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Zhai, H.; Wang, P.; Jeng, D.S.; Zhang, Q.; Wang, S.; Duan, L.; Liu, Y. Physical modeling of combined waves and current propagating around a partially embedded monopile in a porous seabed. Ocean Eng. 2020, 205, 107307. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhai, H.; Wang, P.; Wang, S.; Duan, L.; Chen, L.; Liu, Y.; Jeng, D.S. Experimental study on irregular wave-induced pore water pressures in a porous seabed around a mono-pile. Appl. Ocean Res. 2020, 95, 102041. [Google Scholar] [CrossRef]
- Li, C.; Gao, F.; Yang, L. Breaking-wave induced transient pore pressure in a sandy seabed: Flume modeling and observations. J. Mar. Sci. Eng. 2021, 9, 160. [Google Scholar] [CrossRef]
- Li, X.; Gao, F.; Yang, B.; Zang, J. Wave-induced pore pressure response and soil liquefaction around pile foundation. Int. J. Offshore Polar Eng. 2011, 21, 233–239. [Google Scholar]
- Sui, T.; Zhang, C.; Guo, Y.; Zheng, J.; Jeng, D.S.; Zhang, J.; Zhang, W. Three-dimensional numerical model for wave-induced seabed response around mono-pile. Ships Offshore Struct. 2016, 11, 667–678. [Google Scholar] [CrossRef] [Green Version]
- Sui, T.; Zheng, J.; Zhang, C.; Jeng, D.S.; Zhang, J.; Guo, Y.; He, R. Consolidation of unsaturated seabed around an inserted pile foundation and its effects on the wave-induced momentary liquefaction. Ocean Eng. 2017, 131, 308–321. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Pokrajac, D.; Guo, Y.; Jeng, D.s.; Tang, T.; Rey, N.; Zheng, J.; Zhang, J. Investigation of nonlinear wave-induced seabed response around mono-pile foundation. Coast. Eng. 2017, 121, 197–211. [Google Scholar] [CrossRef] [Green Version]
- Duan, L.; Jeng, D.S.; Wang, D. PORO–FSSI–FOAM: Seabed response around a mono-pile under natural loadings. Ocean Eng. 2019, 184, 239–254. [Google Scholar] [CrossRef]
- Abdelkader, A.; El Naggar, M.H. Hybrid foundation system for offshore wind turbine. Geotech. Geol. Eng. 2018, 36, 2921–2937. [Google Scholar] [CrossRef]
- Jeng, D.S.; Ye, J.H.; Zhang, J.S.; Liu, P.L.-F. An integrated model for the wave-induced seabed response around marine structures: Model verifications and applications. Coast. Eng. 2013, 72, 1–19. [Google Scholar] [CrossRef]
- Liang, Z.; Jeng, D.S. PORO–FSSI–FOAM model for seafloor liquefaction around a pipeline under combined random wave and current loading. Appl. Ocean Res. 2021, 107, 102497. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorption for Navier-Stokes models: Application to OpenFOAM. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Higuera, P.; Buldakov, E.; Stagonas, D. Simulation of Steep Waves Interacting with a Cylinder by Coupling CFD and Lagrangian Models. Int. J. Offshore Polar Eng. 2021, 31, 87–94. [Google Scholar] [CrossRef]
- Verruijt, A. Flow Through Porous Media; Chapter Elastic Storage of Aquifers; Academic Press: London, UK, 1969; pp. 331–376. [Google Scholar]
- Ye, J.; Jeng, D.S. Response of seabed to natural loadin: Waves and current. J. Eng. Mech. 2012, 138, 601–613. [Google Scholar] [CrossRef]
- Chakrabarti, S.K. Offshore Structure Modeling; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 1994. [Google Scholar]
- Greenshields, C.J.; OpenFOAM v9 User Guide. The OpenFOAM Foundation. 2017. Available online: https://cfd.direct/openfoam/user-guide (accessed on 12 October 2021).
- Skjelbreia, L.; Hendrickson, J.A. Fifth order gravity wave theory. Proceedings of 7th International Conference on Coastal Engineering, Mexico City, Mexico, 29 January 1960; pp. 184–196. [Google Scholar]
- Umeyama, M. Coupled PIV and PTV measurements of particle velocities and trajectories for surface waves following a steady current. J. Waterw. Port, Coast. Ocean Eng. 2011, 137, 85–94. [Google Scholar] [CrossRef]
- Zang, J.; Taylor, P.H.; Morgan, G.; Stringer, R.; Orszaghova, J.; Grice, J.; Tello, M. Steep wave and breaking wave impact on offshore wind turbine foundations–ringing re-visited. In Proceedings of the 25th International Workshop on Water Waves and Floating Bodies, Harbin, China, 9–12 May 2010; pp. 9–12. [Google Scholar]
- Chang, S.C.; Lin, J.G.; Chien, L.K.; Chiu, Y.F. An experimental study on non-linear progressive wave-induced dynamic stresses in seabed. Ocean Eng. 2007, 34, 2311–2329. [Google Scholar] [CrossRef]
- Yamamoto, T.; Koning, H.; Sellmeijer, H.; Hijum, E.V. On the response of a poro-elastic bed to water waves. J. Fluid Mech. 1978, 87, 193–206. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Jeng, D.S.; Liao, C.C.; Zhu, J.F. Three-dimensional modeling of wave-induced residual seabed response around a mono-pile foundation. Coast. Eng. 2017, 128, 1–21. [Google Scholar] [CrossRef]
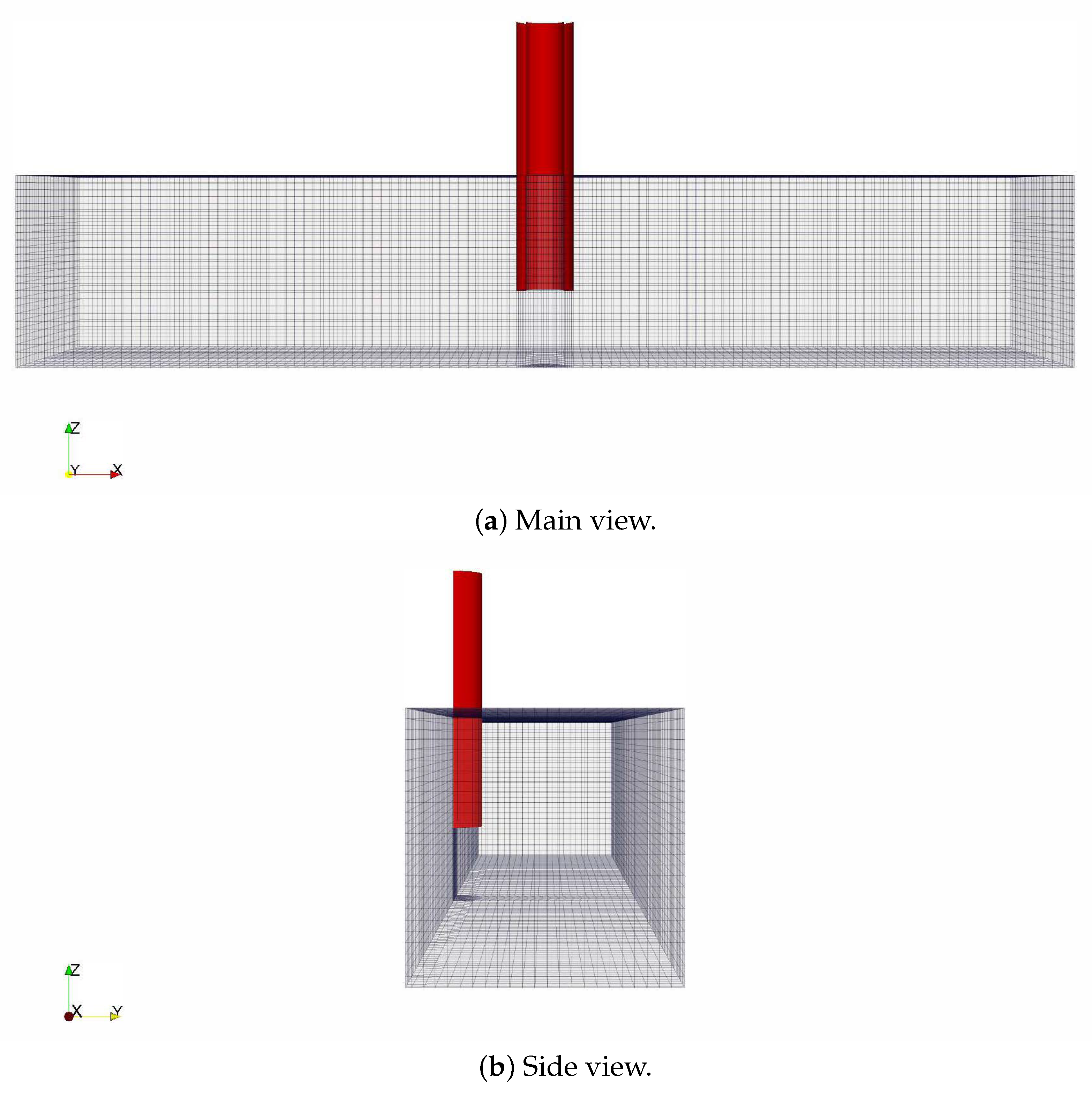
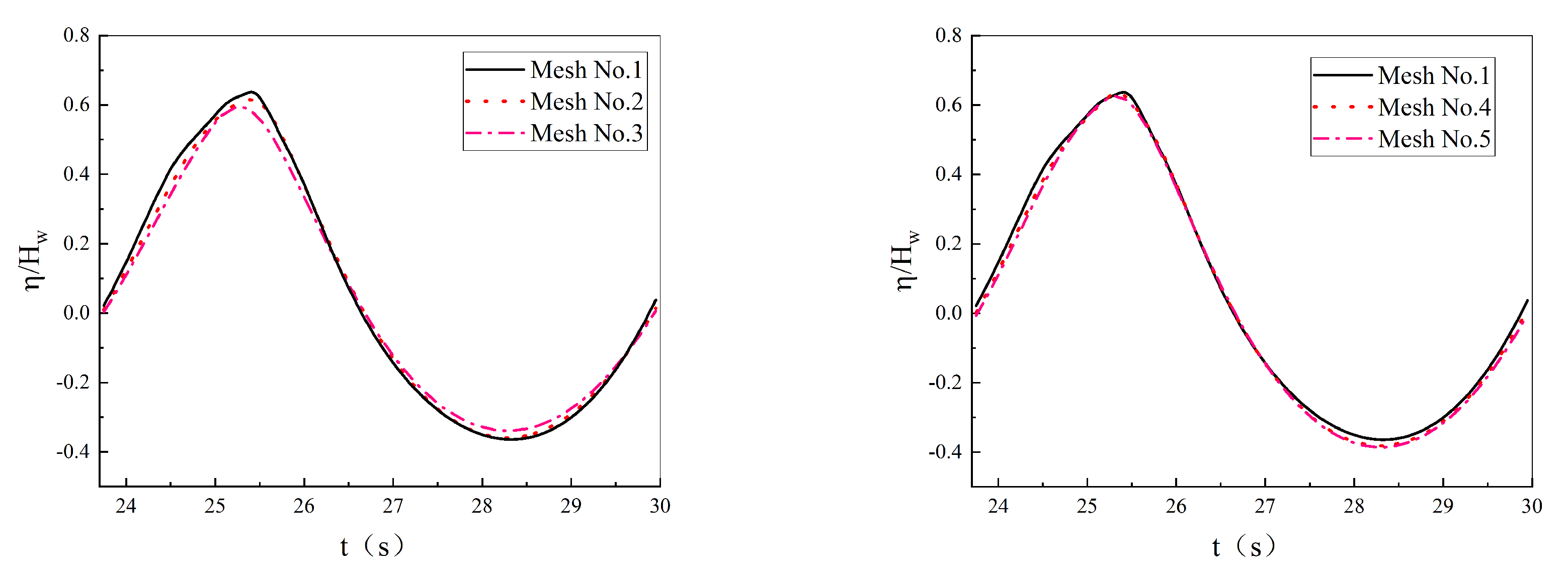
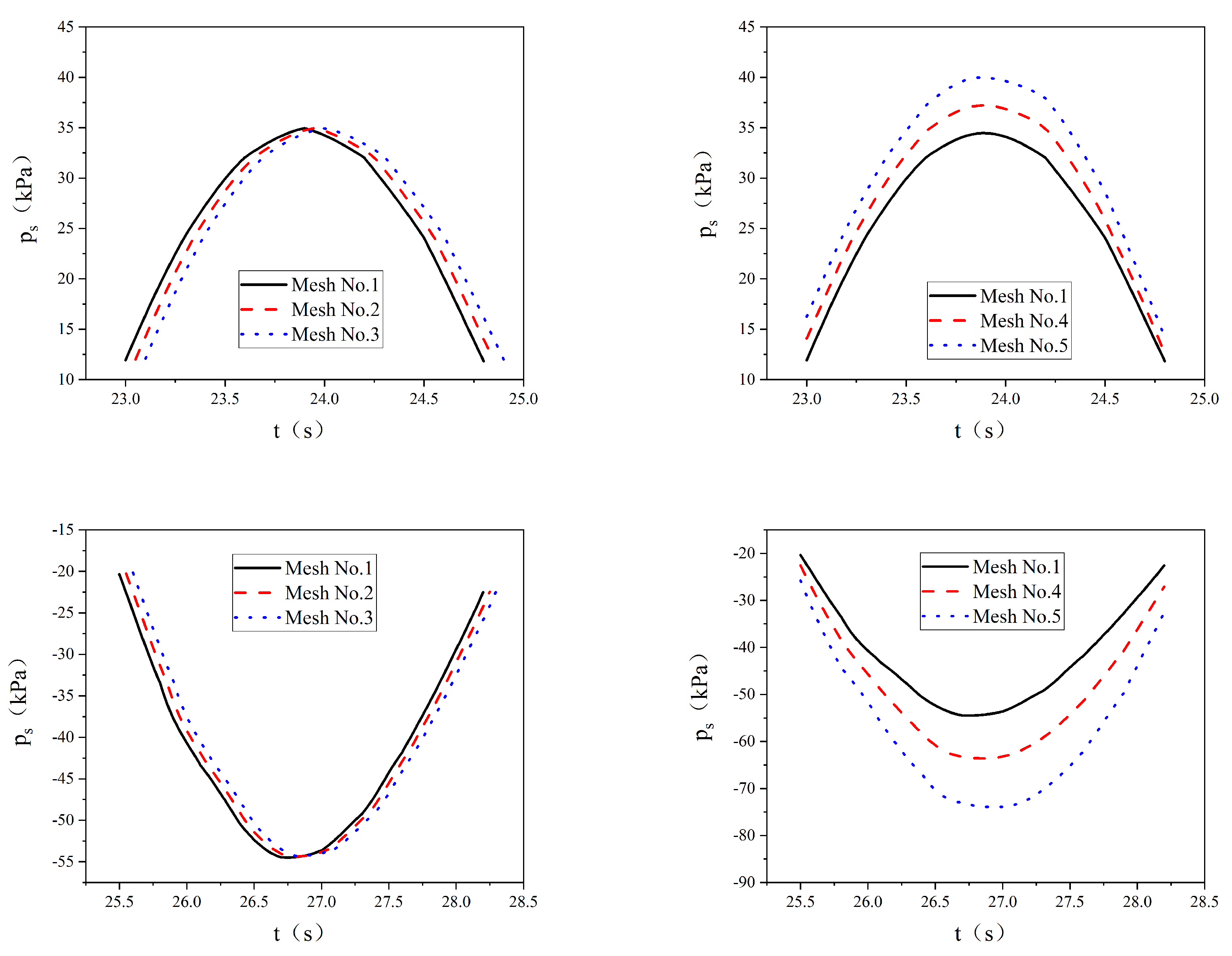



| Mesh No. | = | Mesh Number | |
|---|---|---|---|
| 1 | H/10 | 5090160 | |
| 2 | H/10 | 2282880 | |
| 3 | H/10 | 586224 | |
| 4 | H/15 | 76335240 | |
| 5 | H/20 | 10180320 |
| Mesh No. | = | Mesh Number | |
|---|---|---|---|
| 1 | h/10 | 5256620 | |
| 2 | h/10 | 4715440 | |
| 3 | h/10 | 1211160 | |
| 4 | h/15 | 10513240 | |
| 5 | h/20 | 15769860 |
| No. | H [m] | T [s] | d [m] | D [m] | |
|---|---|---|---|---|---|
| Umeyama [30] | |||||
| W1 | 0.0103 | 1 | 0.3 | [-] | |
| W2 | 0.0234 | 1 | 0.3 | [-] | |
| W3 | 0.0361 | 1 | 0.3 | [-] | |
| Zang et al. [31] | |||||
| R2 | 0.14 | 1.22 | 0.505 | 0.25 | |
| R3 | 0.12 | 1.63 | 0.505 | 0.25 |
| H [m] | T [s] | d [m] | h [m] | [-] | G [N/m2] | [-] | [m/s] | |
|---|---|---|---|---|---|---|---|---|
| Chang et al. [32] | ||||||||
| 0.25 | 2 | 0.562 | 0.6 | 1 | 10 | 0.12 | 2.11 × 10 | |
| Wang et al. [10] | ||||||||
| 0.1 | 1.4 & 2 | 0.6 | 1 | 1 | 8.85 × 10 | 0.3 | 2.382 × 10 |
| Parameter | Value | Unit | |
|---|---|---|---|
| Wave | Regular wave height (H) | 6, 8, 10 | m |
| Regular wave period (T) | 6, 8, 10 | s | |
| Water depth (d) | 15, 17, 20 | m | |
| Seabed | Seabed thickness (h) | 18 | m |
| Degree of saturation () | 0.93, 0.95, 0.97 | - | |
| Shear modulus (G) | 10 | N/m | |
| Poisson’s ratio () | 0.33 | - | |
| Porosity () | 0.425 | - | |
| Soil permeability () | 10, 5 × 10, 10 | m/s | |
| Open-ended pile | Pile diameter (D) | 4, 5, 6 | m |
| Buried depth () | 8 | m | |
| Pipe wall (e) | 0.04 | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Chen, S.; Li, X.; Liang, Z. Three-Dimensional Modelling of Non-Linear Wave-Induced Seabed Response around Offshore Open-Ended Pile. J. Mar. Sci. Eng. 2021, 9, 1238. https://doi.org/10.3390/jmse9111238
Liu J, Chen S, Li X, Liang Z. Three-Dimensional Modelling of Non-Linear Wave-Induced Seabed Response around Offshore Open-Ended Pile. Journal of Marine Science and Engineering. 2021; 9(11):1238. https://doi.org/10.3390/jmse9111238
Chicago/Turabian StyleLiu, Junwei, Shuiyue Chen, Xin Li, and Zuodong Liang. 2021. "Three-Dimensional Modelling of Non-Linear Wave-Induced Seabed Response around Offshore Open-Ended Pile" Journal of Marine Science and Engineering 9, no. 11: 1238. https://doi.org/10.3390/jmse9111238
APA StyleLiu, J., Chen, S., Li, X., & Liang, Z. (2021). Three-Dimensional Modelling of Non-Linear Wave-Induced Seabed Response around Offshore Open-Ended Pile. Journal of Marine Science and Engineering, 9(11), 1238. https://doi.org/10.3390/jmse9111238







