Abstract
The latest container vessel grounding in the Suez Canal, which occurred on 23 March 2021 (the Ever Given), raised many questions regarding the safety of navigation. The sudden concern about safety is due to fears that traffic flow through the Suez Canal could be blocked for longer periods of time. Besides external forces imposed by wind, in this case bank effect had a significant influence on the ship’s grounding. Bank effect occurs due to restricted water flow caused by narrow waterways. Many fairway design standards consider sloped banks such as those of the Suez Canal as unsubstantial in bank-effect forces. This paper analyses the impact of sloped banks on container ship trajectory and proposes minimal distances that may decrease bank-effect forces in order to reduce the risk of vessel grounding and increase the safety of navigation. However, this type of accident has happened before and may occur again due to a small sailing distance from the bank in cases where vessel speed is increased.
1. Introduction
The grounding of container vessel Ever Given raised concerns of possible Suez Canal blockage. The Suez Canal is one of the main fairways between the Indian Ocean and the Mediterranean Sea/Atlantic Ocean. According to Suez Canal Authorities [1], 18,880 vessels transited the Suez Canal carrying over 1,207,087,000 tons of cargo in 2019. The daily average was 51.7 ships per day and 3,307,000 tons of cargo. Container vessels comprise 28% of all vessels in transit. According to reports [2], the Suez Canal has a good safety record and in 2020 had 75 incidents reported, with grounding being the most common type of accident. In the past 10 years, every third accident was related to grounding.
Detailed information about accidents is scarce and most available information is in the form of media reports where the initial causes are not stated. One accident that was investigated was the grounding of container vessel APL Danube [3]. The vessel (length 299.95 m) grounded on 19 April 2019 at southbound transit due to bank effect according to an investigation. The vessel veered off from the middle of the canal close to the eastern bank, where the bow was then pushed away from the bank. The rudder was turned towards the bank to counter bow movement, but this was ineffective due to low water flow. Besides bank effect, investigation determined that crew members did not detect that the vessel was closing toward the bank.
The latest grounding of Ever Given received the most attention due to a period of blockage of the Suez Canal. An investigation will be carried out, with the only existing information about the accident being AIS (automatic identification system) track data. The vessel track published by Maritime Casualty Specialists [4] was one of the first videos that showed the vessel’s track and speed from AIS data. The track shows that the vessel was pushed by a southerly wind onto the western channel bank. In order to obtain better responsivity, the vessel speed was increased to about 13.5 knots in the final moments. That high speed, in combination with the proximity to the bank, caused bank effect, and the vessel consequently grounded. However, this is yet to be confirmed by official accident investigation, which will provide more detailed information.
While previous groundings were caused by the same effect, this accident showed that vessel navigational safety may be in danger in some cases. Sloped banks are considered less influential than vertical embankments, however these real situations and research data show that sloped bank effect may have a significant external influence on vessel trajectory.
2. Bank Effect and Channel Design Standards
Bank effect occurs due to asymmetric flow around the vessel hull when sailing near a bank, which results in a force acting on the vessel and a yawing moment pushing the bow away from the bank. The magnitude of this effect depends on bank shape, water depth, vessel distance from the bank, vessel properties and speed [5]. A decreased distance between vessel and bank influences manoeuvring performance considerably and makes it difficult to steer [6]. Besides distance, bank effect is pronounced with increased vessel speed [7]. The influence of sloped banks was researched in a towing tank using a vessel model, which showed that sailing above sloped banks generated larger forces than vertical banks [8].
Fairway design guidelines recognize and consider bank effect in horizontal fairway dimensions. Harbour Approach Channels Design Guidelines Report No. 121-2014 [9] by PIANC (Permanent International Association of Navigation Congresses) defines horizontal fairway dimensions as the sum of the basic manoeuvre lane, additional width due to external forces and additional bank clearance on both fairway sides. The additional fairway width is determined by the fairway location (inner protected or outer unprotected channel), ship speed and bank type. The clearance is greater if the vessel speed is higher and the bank is steeper. Recommendation for Maritime Works ROM 3.1-99 [10] by Puertos Del Estado includes bank effect in fairway width as additional banks’ safety distance and bank safety margin. The bank safety margin is a method for the calculation of error margin, and is added to the additional distance to compensate for bank effect. The sum of these two elements provides total additional fairway width to account for bank effect. The necessary fairway width is determined based on slope type and vessel speed. In the previous method, vertical banks have a larger recommended additional width than sloped banks. Technical Standards and Commentaries for Port and Harbour Facilities in Japan, by the Japanese Ministry of Land, Infrastructure, Transport and Tourism (MLIT) [11], only provide the additional width due to bank effect for vertical banks. Data are given by vessel type, which is determined in towing tanks and represents the distance from the bank where a small rudder action (up to 5°) can overcome bank forces.
These methods all state that vertical banks have far greater vessel bank distance than sloped banks. Design standards recommendations are shown in Table 1, and the recommended additional fairway width due to bank effect for vertical banks is greater than for sloped banks. This comparison may lead to the conclusion that current recommendations are not appropriate and do not ensure an adequate level of safety in navigation, because the effect of the sloped banks may be also significant.

Table 1.
Comparison of recommended fairway design standards for vessel–bank distances.
3. The Bank Effect of Sloped Banks
As the latest event of grounding showed, sloped banks may have a significant effect on vessel trajectory. Figure 1 indicates that the Suez Canal has slopes with 1:4 gradient (the slope length is four times larger than the slope height) and an approximate surface width of 313 m. However, at a depth of 24 m the width is approximately 121 m. A container ship of 400 m length and 59 m width at static draft of 15.7 has approximately 180 m of canal width. This gives around 60.5 m of free space on each side of the vessel before grounding. That distance can be even smaller due to higher dynamic draft caused by the squat effect. However, this horizontal distance is not only used for avoiding bank effect, but also must allow additional distance for other external forces (such as drift due to wind), steering drift and other factors that cause vessels to veer off from their trajectory. While the dimensions of the Suez Canal have increased over time, the breadth of container vessels also increased significantly with increases in their capacity (Figure 1).
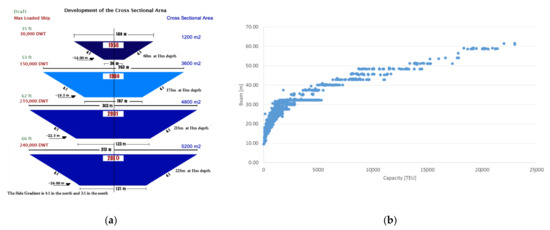
Figure 1.
Development of the Suez Canal cross section (a) [12] and growth of container vessels size in TEU capacity and beam (b) [13].
The research analysing the effect of sloped banks suggests that the generated forces are significant. A study [5] that included container vessel models sailing near different bank types in towing tanks showed greater forces at sloped banks compared with vertical banks. The vessel model represents a 350 m long and 42.9 m wide container vessel. The model was towed at different speeds, at different drafts and at different distances from the banks. Figure 2 shows the sway force of a 1:3 slope ratio bank and vertical banks at different speeds and different distances from the bank. It can be seen that sway force is greater with higher vessel speed and bank slope. Additionally, the maximum sway force occurs at a shorter distance from sloped banks than vertical banks. This indicates that when the vessel is over the bank, the under-keel clearance decreases in comparison with vertical banks, where that phenomena does not occur. This conclusion is in accordance with research [14] suggesting yawing moment increases substantially with decreasing under-keel clearance.
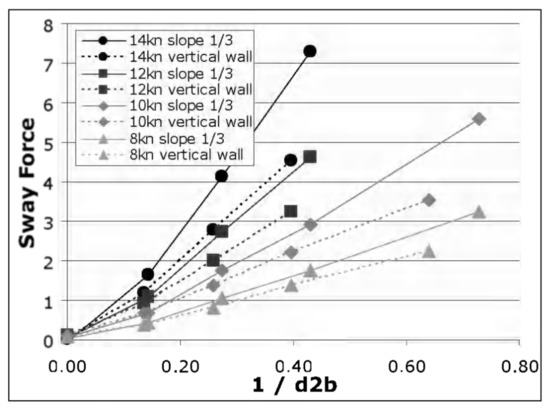
Figure 2.
Sway force (scaled to model) induced by different bank types at different vessel speeds and distances from the bank [5].
Similar results were obtained in [15] using a real-time navigational simulator for container vessels in different types of banks, vessel speeds and distances from the bank. The results suggest the same pattern of sway force and proposed minimum distances from the bank to avoid vessel grounding.
4. Simulation of Sloped Bank Effect on Large Container Vessels
The analysed recommendations suggest that sloped banks may have less influence on vessel trajectory than vertical banks. However, real events prove that significant bank effects may occur when sailing near sloped banks. To confirm the sloped bank effect, simulation tests were conducted using the Transas NaviSailor NTPro 5000 v5.35 real-time simulator. Previously, the ship-handling simulator has proved to be a suitable tool for basic and advanced ship-handling operations and for advanced manoeuvres required in search and rescue operations [16], and for the analysis of accidents at sea [17] or incidents (near misses) [18], including the impact of AIS spoofing on nautical safety [19]. More recently, the simulator has increasingly been used for seafarer competency research [20,21]; port, waterway and canal planning [22] and pilot training [23]. This simulator is certified by a DNV certificate [24] which confirms that simulations, vessel models and generated data are tested and certified as reliable. During simulation, the additional forces caused by banks are calculated as hydrodynamic components of vector forces and moments affecting the vessel. The principal parameters in vessel/channel interaction are vessel breadth; draft and length ratios; distance between vessel and channel boundaries; vessel speed; angle between vessel centreline and channel line of the wall; vessel rate of turn; and channel width, depth and slope angle. The effect of these parameters on vessel hydrodynamic forces is calculated based on an analysis of various model-testing results [25]. However, to validate the results, simulated data will be compared with towing tank results [5] (Figure 2).
During simulations, the following vessel models and conditions were used. The model represented a container vessel 347 m long and 43 m wide with 14 m of draft. The summer deadweight of the vessel was 104,696 tons with a block coefficient of 0.65. The fairway was sloped in a ratio of 1:4 to simulate the Suez Canal banks and the canal depth was adjusted to 1.2 and 1.5 vessel drafts. The fairway was simulated on one side because the vessel only approached one side of the channel, with the other side too far away to produce a significant effect. Weather and sea conditions, along with sea current, were set to zero.
Simulations were repeated several times for the same settings to obtain stabilised data. The distance from the bank (d) (distance between ship and closest horizontal bank point) was set from 50 m to 10 m, at a frequency of approach of 10 m. Three sailing speeds were tested: 10, 7.5 and 5 knots. The steering was set to track control interconnected auto-pilot on “Precise” mode in order to simulate the return of the ship to its original route, as in-course control setting ensures that a vessel can continue to sail in the same course but on a parallel route. This eliminates human error in steering and enables uniformity of simulations. To confirm that the ship deviated from its route, simulations with rudder in midship were also conducted.
Figure 3 shows the vessel trajectory at a speed of 10 knots, using distances from the bank of 50 m (Figure 3a), 30 m (Figure 3b) and 10 m (Figure 3c). It can be seen that if there is no rudder action the bank effect will push the vessel bow away from the bank regardless of the distance from the bank.
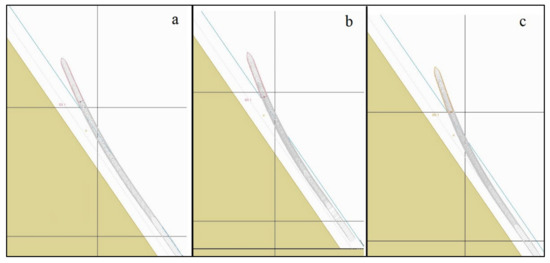
Figure 3.
Ship trajectory under 1:4 ratio sloped bank effect and speed 10 knots when rudder is set to midship: (a) 50 m distance from slope; (b) 30 m distance from slope; (c) 10 m distance from slope.
More than 100 simulations were conducted and the lateral force and cross-track error were measured. The data provide information regarding the influence of the sloped bank effect on vessel trajectory and at what distance a vessel should sail in order to avoid grounding due to bank-effect-induced trajectory oscillation.
Figure 4 displays simulated sloped bank force data. The full line represents the force for a depth draft ratio of 1.2 and the dotted line represents the force for a depth draft ratio of 1.5. It can be seen that increments of vessel speed increased the acting force, resulting in larger oscillations of vessel trajectory. Simulated force was then compared with bank force in Figure 2 [5] gathered from the towing tank test that validated and confirmed the simulated data were reliable and accurate.
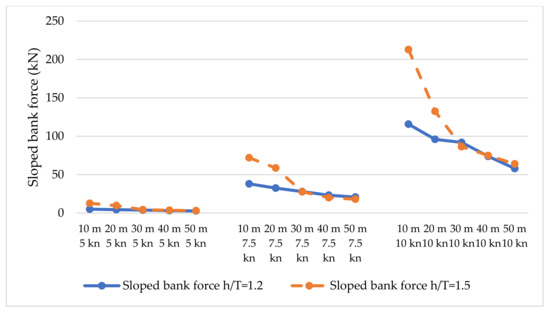
Figure 4.
Sloped bank force acting on vessel when sailing at different speeds and distances from a sloped bank (h-depth; T-draft).
The difference between two depth-draft ratios is occurred due to vessel movement over a sloped bank (Figure 5). Larger depth-draft ratio allows larger fairway width and the vessel may move more over the bank.
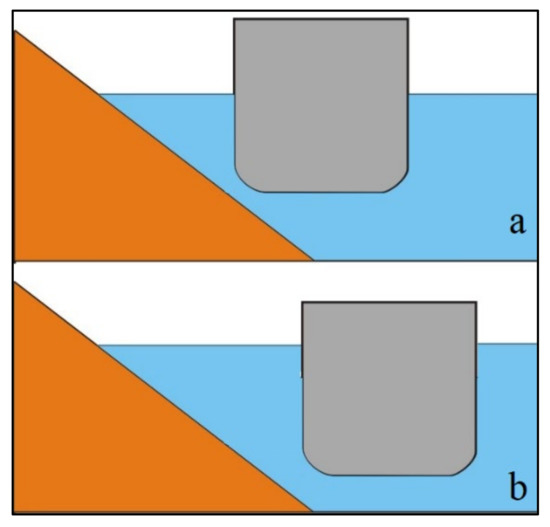
Figure 5.
Vessel movement over a sloped bank: (a) vessel depth–draft ratio 1.5; (b) vessel depth–draft ratio 1.2.
Figure 6 represents the maximum cross-track error caused by the sloped bank effect and rudder action. As expected, the greater cross-track error was obtained at the highest sailing speed. However, the data show that for lateral force the greatest offset and force will occur at a 1.5 depth draft ratio. This occurs due to increased vessel movement inside the bank. With a higher depth–draft ratio (Figure 5a), the vessel can move over the sloped part of the bank more than it can with a lower depth–draft ratio (Figure 5b), and thus the bank force and effect on trajectory are increased.
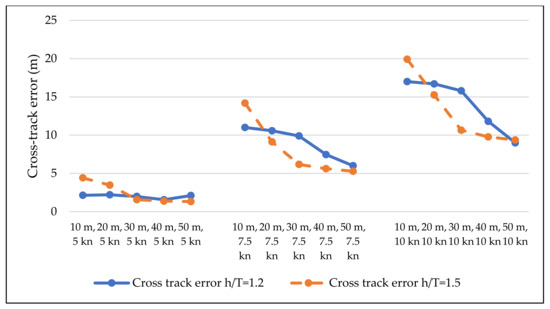
Figure 6.
Maximum recorded cross-track error of a vessel when sailing at different speeds and distances from a sloped bank.
The simulated data can provide recommendations for ship bank distance in order to avoid significant bank effects. For the analysed bank type and vessel, the recommended distances from the sloped bank are shown in Table 2.

Table 2.
Suggested additional fairway distances to accommodate bank effect.
The distances in Table 2 are relative to vessel breadth and may be used for larger similar vessel types. If we compare these data to the situation in the Suez Canal, which has banks with a slope ratio of 1:4, the following is obtained. A container vessel that is 59 m wide and with a draft of 15.7 m has 180 m of underwater fairway width. Based on the canal depth and vessel draft, the ratio is 1.5. At an approximate distance of 50 m from the bank (when the vessel is sailing approximately at the centre of the canal) and sailing at 7.5 knots, the vessel needs 0.2 B (breadth) distance from the bank, which in this instance is approximately 12 m. Additionally, if the vessel comes closer to the bank at a distance of 20 m, then the required vessel bank distance is equal to the minimum vessel bank distance, and this may lead to bank-effect-induced grounding (depending on the action taken). In this instance, the minimum required distance to avoid significant influence of bank effect at speed 7.5 knots and 1:4 slope ratio bank is 20 m. The vessel, when sailing at the centre of the canal, has only 43.5 m at either side to correct its trajectory oscillation and consequently avoid grounding. This implies that when other external forces act (e.g., wind force), the vessel has only 43.5 m in width to correct its trajectory and with greater cross-track error the bank force is even stronger, which makes the vessel harder to control.
5. Discussion
This research was conducted using real-time navigational simulation. This simulator was originally used as a teaching aid. However, as the models were upgraded, it has increasingly been used as a research tool. The simulator’s models have been developed by real ship data or ship models in towing tanks. In most cases, the mathematical models are based on model tests carried out in towing tanks [26]. Since the models used in simulation are based on model test data, many research and fairway tests are conducted using navigational simulators in order to reduce costs and time. Navigational simulation is also the only tool to test new fairways before they are built. The continuous development and improvement of mathematical-physical models, together with increasing computing power and photo-realistic displays, make simulations paramount to any other approach, as long as the flaws, drawbacks and imperfections of this virtual reality are known to the involved parties and are considered in the evaluation phase of the results [27,28]. The results of similar studies have proved that the simulator is a suitable tool, capable of supporting designs and verifying designs in sea-traffic engineering [29]. This is proof that the real-time simulation method is highly applicable when the effectiveness of safety improvement planning of port and harbour facilities must be assessed [30].
In the present study, the simulation was conducted using only one bank since the main goal was to investigate the influence of sloped-bank-induced yawing and cross-track error. This effect occurs when a vessel veers off the middle of a canal and comes too close to one bank. In such instances, only one bank induces a force on the vessel hull since the other side of the bank is too far away to induce significant counter-reacting forces. When these forces are present, the vessel trajectory will start to oscillate between both banks and in extreme cases may result in grounding.
The results obtained from simulation showed that a sloped bank generates sufficient force to induce significant yawing moment and route oscillation. Similar research showed that 1:3 and 1:5 sloped banks and larger under-keel clearance generate similar yaw moments as vertical banks [31]. One study [26] showed that the magnitude of a lateral force at the forward perpendicular, either an attraction or a repulsion force, will increase with the forward speed of the ship, when the ship sails closer to the bank, or in a more confined cross section. Similar results were obtained in research using a fixed water depth, where larger bank angles led to greater transverse force and yaw moment [32].
6. Conclusions
Bank effect is generally considered to be a force that significantly occurs when sailing near vertical banks, and sloped banks were previously considered non-influential in terms of bank effect. However, sloped banks are superior to vertical banks and provide more sea area for vessels. The latest research in towing tanks and navigational simulators suggests that sloped banks also generate significant bank effect. This is even more important because sloped banks are often found in narrow channels and canals and, in combination with low depth and larger speed, could lead to grounding. Modern vessel size is increasing and fairways are lagging behind, which may lead to greater pressure to achieve economic results. The present research shows that in one of the most important fairways, a large 20,000 TEU container vessel has approximately only 50 m of manoeuvring space at each side of the fairway before bank effect significantly influences its trajectory and the vessel grounds. Grounding due to bank effect has happened before and the latest occurrence due to high speed and hard grounding shows that the safety of navigation is in danger and relies only on the diligence of crew and pilot in keeping the vessel in the centre of the fairway. Grounding can be prevented by upgrading the education of vessel bridge teams and pilots in terms of improving training methods and familiarity with the bank effect forces that influence vessel trajectory. Consideration should also be given to upgrading vessel wheelhouse posters in order to provide more information, even in electronic form, as well as Pilot/Master information exchange cards.
Author Contributions
Conceptualization, M.B. and V.P.; methodology, M.B.; validation, M.B., R.M. and D.M.; data curation, M.B.; writing—original draft preparation, V.P.; writing—review and editing, V.P., R.M. and D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
There are no conflict of interest.
References
- Suez Canal Authority. Annual Report 2019; Planning & Research Department, Information Center, Suez Canal Traffic Statistics: Ismailia, Egypt, 2019.
- Allianz Global Corporate & Speciality. Safety and Shipping Review 2020; Alliant Global Corporate and Speciality: Berchem, Belgium, 2020. [Google Scholar]
- Transport Malta. Marine Safety Investigation Report, APL Danube, Report No. 08/2020; Marine Safety Investigation Unit: Furjana, Malta, 2020.
- Marine Casualty Specialists. Available online: http://www.maricaspe.com/ (accessed on 10 May 2021).
- Lataire, E.; Vantorre, M.; Laforce, E.; Eloot, K.; Delefortrie, G. Navigation in Confined Waters: Influence of Bank Characteristics on Ship-Bank Interaction. In Proceedings of the International Conference on Marine Research and Transportation, ICMRT, Naples, Italy, 28–30 June 2007. [Google Scholar]
- Serban, P.S.; Panaitescu, V.N. Simulation of ship to shore interaction in shallow and narrow waters. Sci. Bull. Mircea Cel Batran Nav. Acad. 2015, 18, 112. [Google Scholar]
- Sian, A.Y.; Maimun, A.; Priyanto, A.; Ahmed, Y.M. Assessment of Ship-Bank Interactions on LNG Tanker in Shallow Water. J. Technol. 2014, 66, 141–144. [Google Scholar] [CrossRef][Green Version]
- Eloot, K.; Vantorre, M. Ship behaviour in shallow and confined water: An overview of hydrodynamic effects through EFD. In Proceedings of the AVT-Specialists’ Meeting on Assessment of Stability and Control Prediction Methods for Air and Sea Vehicles, Portsdown, UK, 11 October 2011. [Google Scholar]
- Permanent International Association of Navigation Congresses (PIANC). Harbour Approach Channels Design Guidelines; Report No. 121–2014; PIANC MarCom Working Group 30: Brussels, Belgium, 2014. [Google Scholar]
- Del Estado, P. Recommendations for Maritime Works (Spain) ROM 3.1-99: Designing Maritime Configuration of Ports, Approach Channels and Floatation Areas. Spain CEDEX. 1999. Available online: https://www.puertos.es/es-es/BibliotecaV2/ROM%203.1-99%20(EN).pdf (accessed on 14 November 2021).
- Ministry of Land, Infrastructure, Transport and Tourism (MLIT). Technical Standards and Commentaries for Port and Harbour Facilities in Japan; OCDI: Tokyo, Japan, 2009. Available online: https://ocdi.or.jp/tec_st/tec_pdf/tech_00H.pdf (accessed on 14 November 2021).
- Suez Canal Authority. Available online: https://www.suezcanal.gov.eg/English/About/SuezCanal/Pages/CanalCharacteristics.aspx (accessed on 10 May 2021).
- Container-Ship Size: What Dimensions Can We Expect to See? Available online: https://piernext.portdebarcelona.cat/en/mobility/container-ship-size/ (accessed on 10 August 2021).
- Vantorre, M.; Delefortrie, G.; Eloot, K.; Laforce, E. Experimental investigation of ship-bank interaction forces. In Proceedings of the International Conference MARSIM, Kanazawa, Japan, 25–28 August 2003. [Google Scholar]
- Baric, M.; Mohovic, R.; Mohovic, D. Determining Restricted Fairway Additional Width due to Bank Effect for Fine Form Vessels. J. Navig. 2019, 72, 1435–1448. [Google Scholar] [CrossRef]
- Kim, I.; Chae, C.; Lee, S. Simulation Study of the IAMSAR Standard Recovery Maneuvers for the Improvement of Serviceability. J. Mar. Sci. Eng. 2020, 8, 445. [Google Scholar] [CrossRef]
- Hörteborn, A.; Ringsberg, J.W. A method for risk analysis of ship collisions with stationary infrastructure using AIS data and a ship manoeuvring simulator. Ocean Eng. 2021, 235, 109396. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. A ship domain-based model of collision risk for near-miss detection and Collision Alert Systems. Reliab. Eng. Syst. Saf. 2021, 214, 107766. [Google Scholar] [CrossRef]
- Androjna, A.; Perkovič, M.; Pavic, I.; Mišković, J. AIS Data Vulnerability Indicated by a Spoofing Case-Study. Appl. Sci. 2021, 11, 5015. [Google Scholar] [CrossRef]
- Park, D.J.; Yim, J.B.; Yang, H.S.; Lee, C.K. Navigators’ Errors in a Ship Collision via Simulation Experiment in South Korea. Symmetry 2020, 12, 529. [Google Scholar] [CrossRef]
- Yim, J.-B.; Park, D.-J.; Youn, I.-H. Development of navigator behavior models for the evaluation of collision avoidance behavior in the collision-prone navigation environment. Appl. Sci. 2019, 9, 3114. [Google Scholar] [CrossRef]
- Łazuga, K.; Minh, Q.N.; Gucma, L. Cost-Effective Design of Port Approaches Using Simulation Methods Based on the Example of a Modernized Port in the Ustka. J. Mar. Sci. Eng. 2021, 9, 211. [Google Scholar] [CrossRef]
- Žagar, D.; Svetina, M.; Košir, A.; Dimc, F. Human factor in navigation: Overview of cognitive load measurement during simulated navigational tasks. J. Mar. Sci. Eng. 2020, 8, 775. [Google Scholar] [CrossRef]
- DNV Statement of Compliance. Bridge Operation Simulator, Navi-Trainer NTPro 5000, Class A Standard for Certification of Maritime Simulators No. 2. Sandefjord. 2012. Available online: https://www.transas.com.ua/certificates-sim/SIM%20-%20002%20121218%20DNV.pdf (accessed on 14 November 2021).
- Transas MIP Ltd. Description of Transas Ship Motion Mathematical Model; Version 2.11; Transas MIP Ltd.: Cork, Ireland, 2012; pp. 62–63. [Google Scholar]
- Lataire, E. Experiment Based Mathematical Modelling of Ship-Bank Interaction. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2014. [Google Scholar]
- Böttner, C.-U. Ship handling simulation in approach channel and harbour design. In Proceedings of the 34th PIANC World Congress: Connecting Maritime Hubs Globally, Panama City, FL, USA, 7–11 May 2018. [Google Scholar]
- Senčila, V.; Zažeckis, R.; Jankauskas, A.; Eitutis, R. The Use of a full mission bridge simulator ensuring navigational safety during the Klaipeda Seaport development. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 417–424. [Google Scholar] [CrossRef]
- Czaplewski, K.; Zwolan, P. Using the software of Navi-Trainer PRO 5000 simulator for assessment of the designed navigational infrastructure. Pol. Nav. Acad. Annu. Navig. 2011, 18, 55–68. [Google Scholar]
- Perkovic, M.; Brcko, T.; Luin, B.; Vidmar, P. Ship handling challenges when vessels are outgrowing ports. In Proceedings of the 19TH INTERNATIONAL NAVIGATION SIMULATOR LECTURERS’ CONFERENCE, Western Cape, South Africa, 5 September 2016. [Google Scholar]
- Duffy, J.T. Modelling of Ship-Bank Interaction and Ship Squat for Ship-Handling Simulation. Ph.D. Thesis, University of Tasmania, Hobar, Australia, 2008; p. 103. [Google Scholar]
- Luo, W.; Yang, B.; Sun, Y. Hydrodynamic Analysis of KVLCC2 Ship Sailing near Inclined Banks. Math. Probl. Eng. 2021, 1, 6655971. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).