Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method
Abstract
:1. Introduction
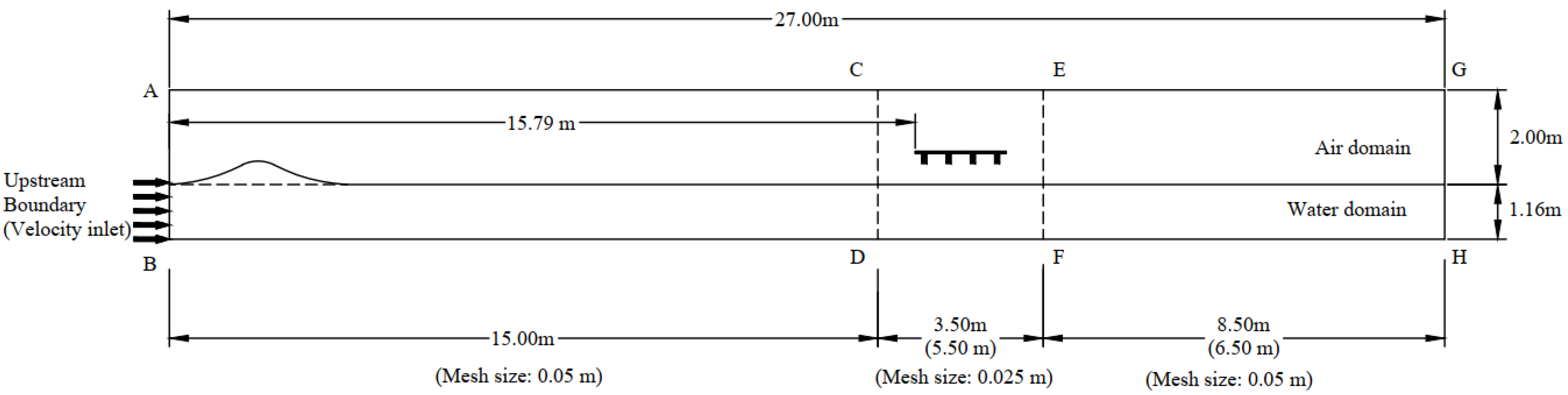
2. Numerical Modeling
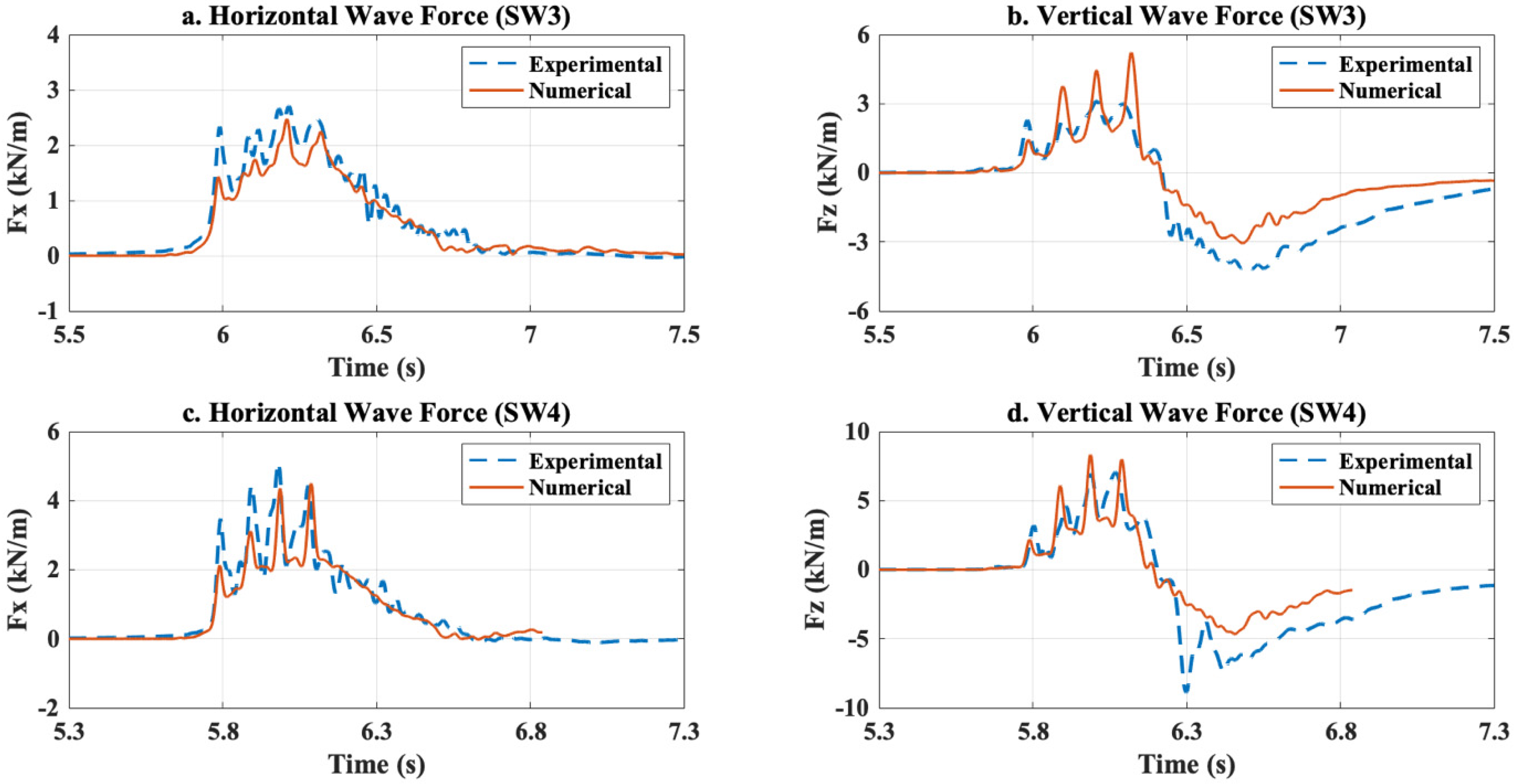
2.1. Governing Equations and Validation
2.2. Parametric Investigation
3. Effect of Number of Girders
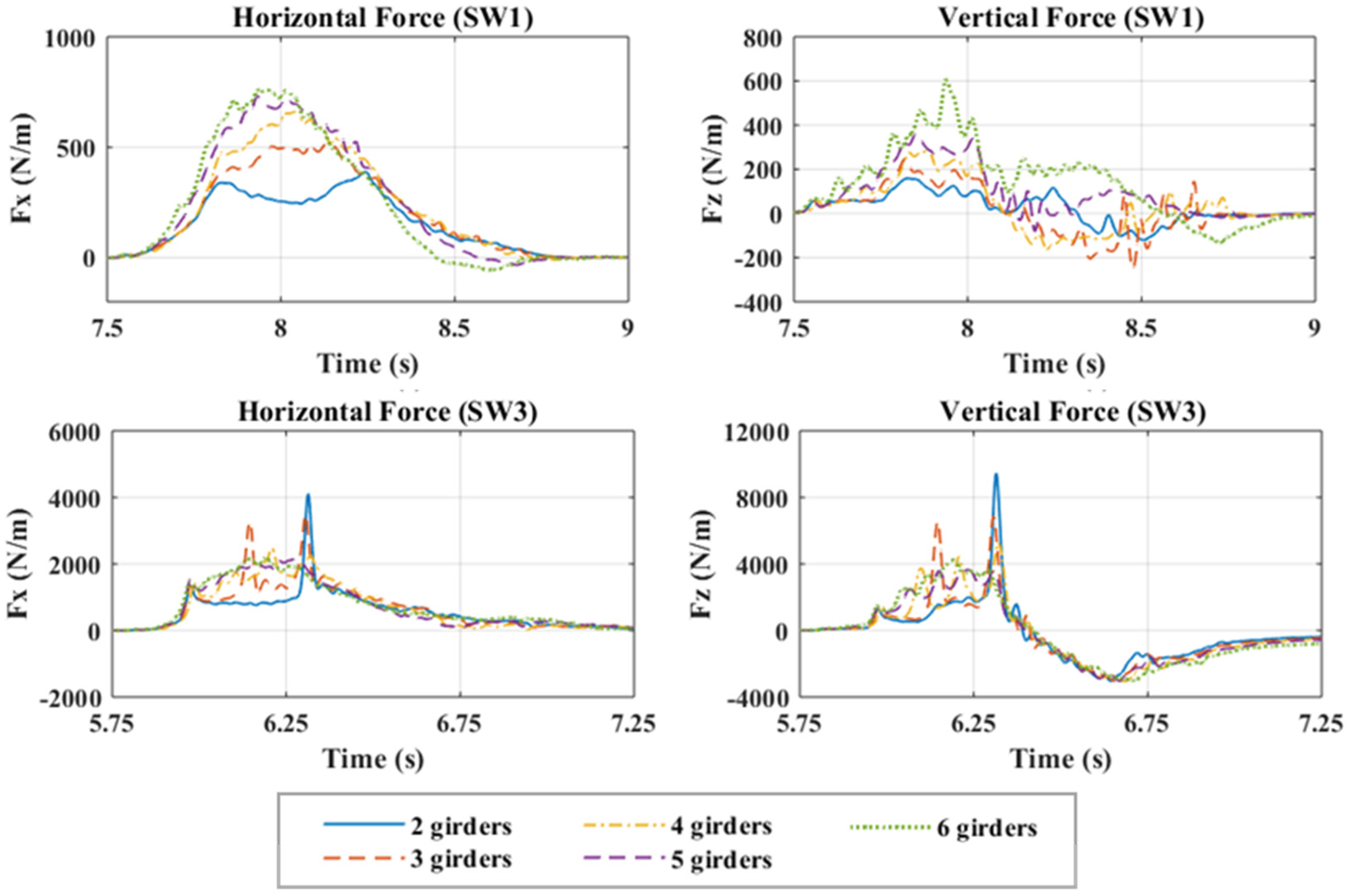
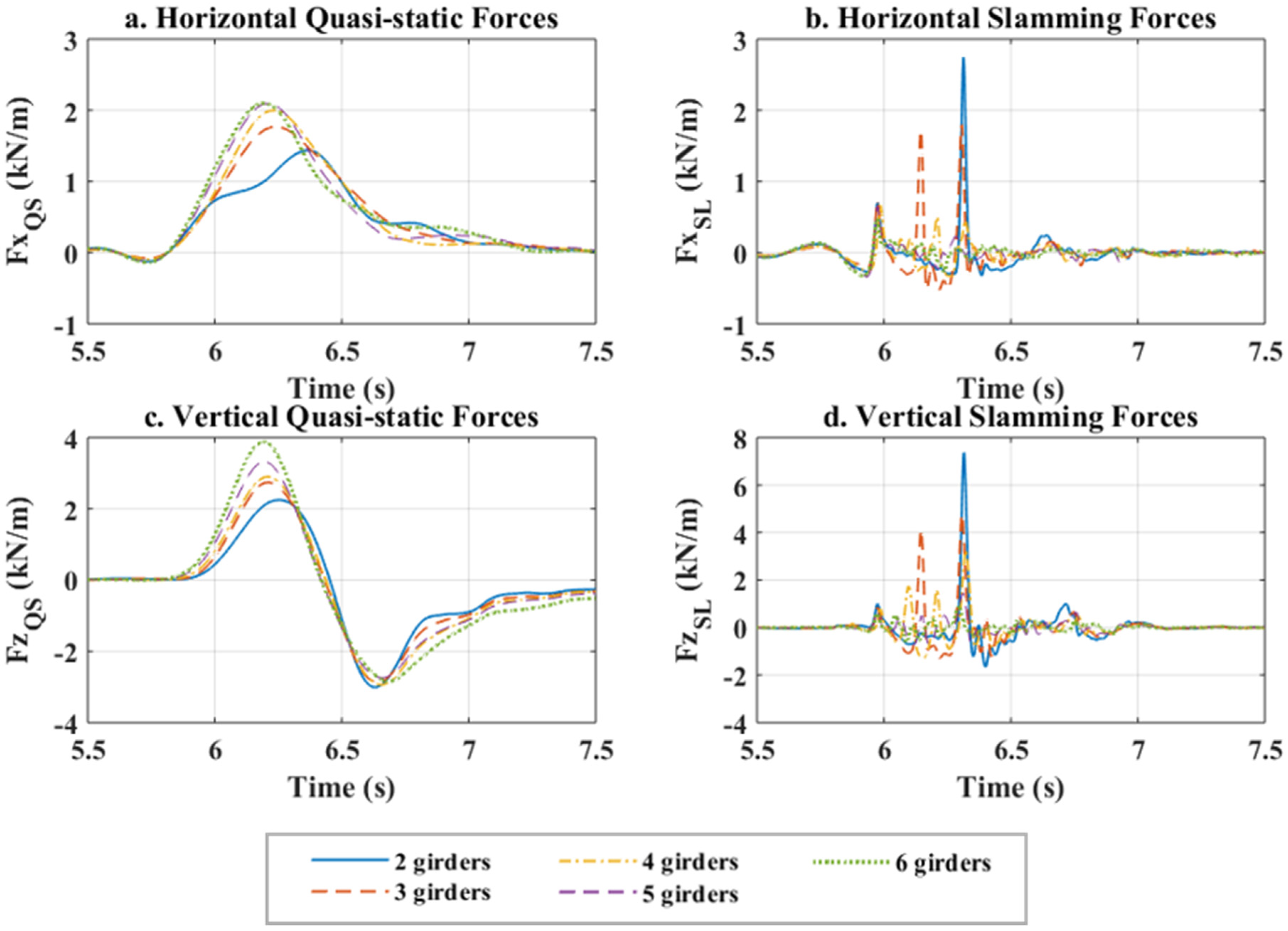
3.1. Horizontal and Vertical Forces
- For large wave heights the magnitudes of the slamming components are twice as large as the quasi-static components for the two-girder case, meaning that they will have a governing effect on the total forces. However, for the decks with the largest Ng (e.g., 5, 6) the quasi-static components are larger than the slamming ones (due to the simultaneous reduction of and the increase of , as Ng increases)
- For small wave heights the quasi-static component has a governing role over the total forces, irrespective of the number of girders.
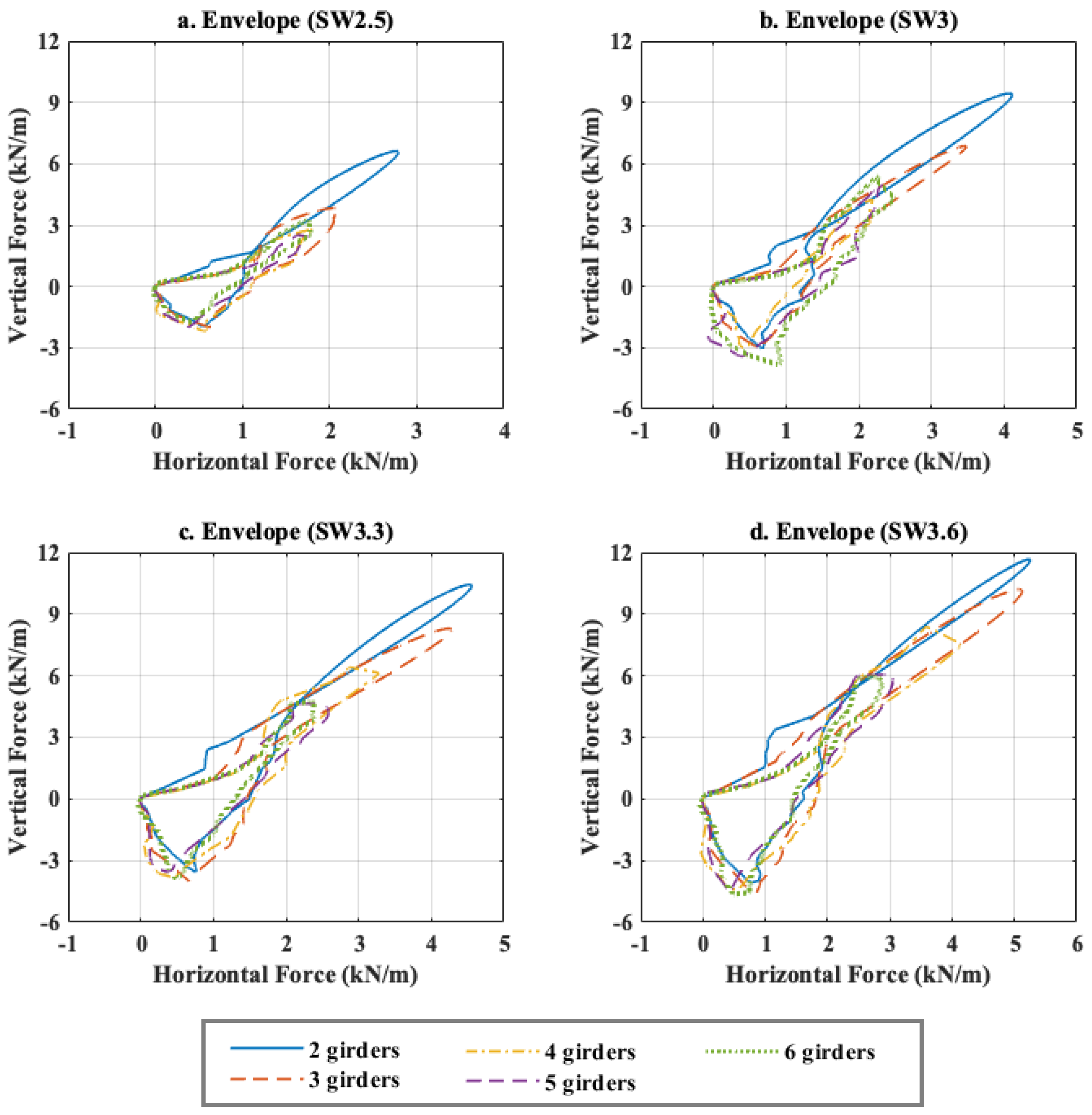
3.2. Demand Diagrams
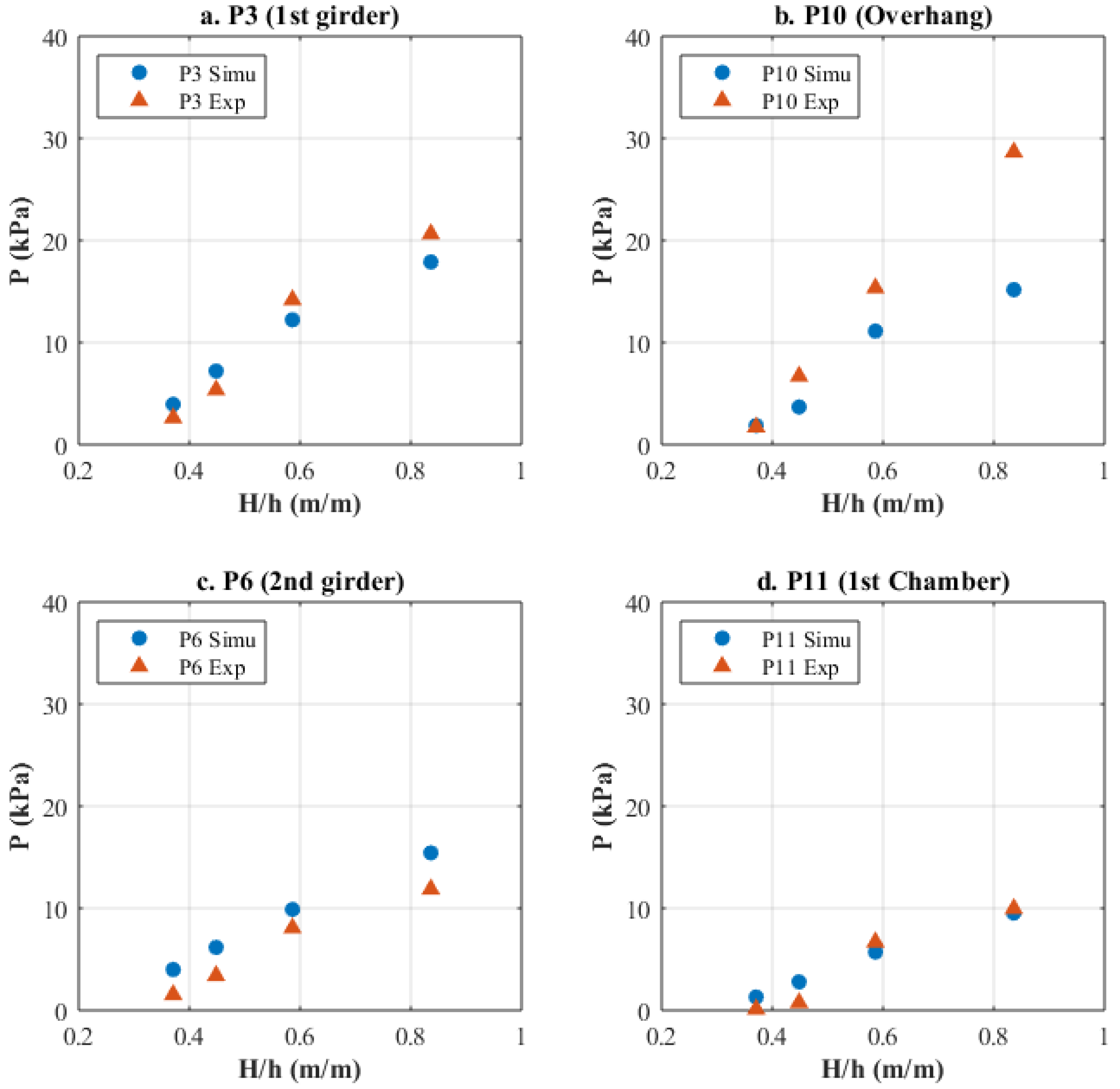
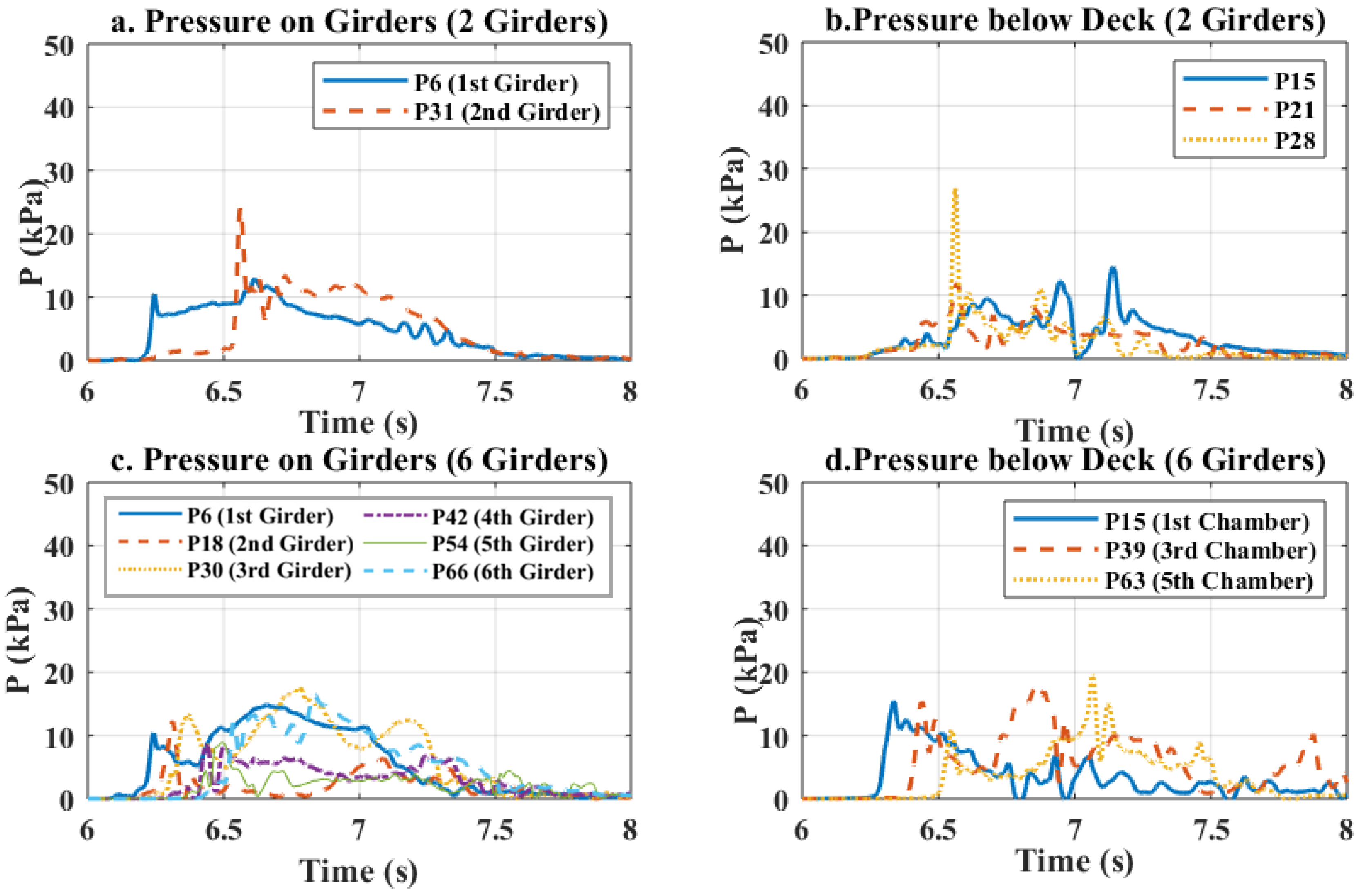
3.3. Pressures and Fluid Velocities
- In the case of the two-girder deck the long-duration pressures on the offshore and onshore girder are quite similar, however, the onshore girder (downstream) witnesses a much larger impulsive component. Similarly, the uplift pressures below the deck have a major impulsive peak at the location close to the onshore side (P28), while the peak does not exist at the remaining locations below the deck.
- On the other hand, in the case of the six-girder deck the maximums of the pressure histories are much smaller, with only some small-to-negligible impulsive peaks.
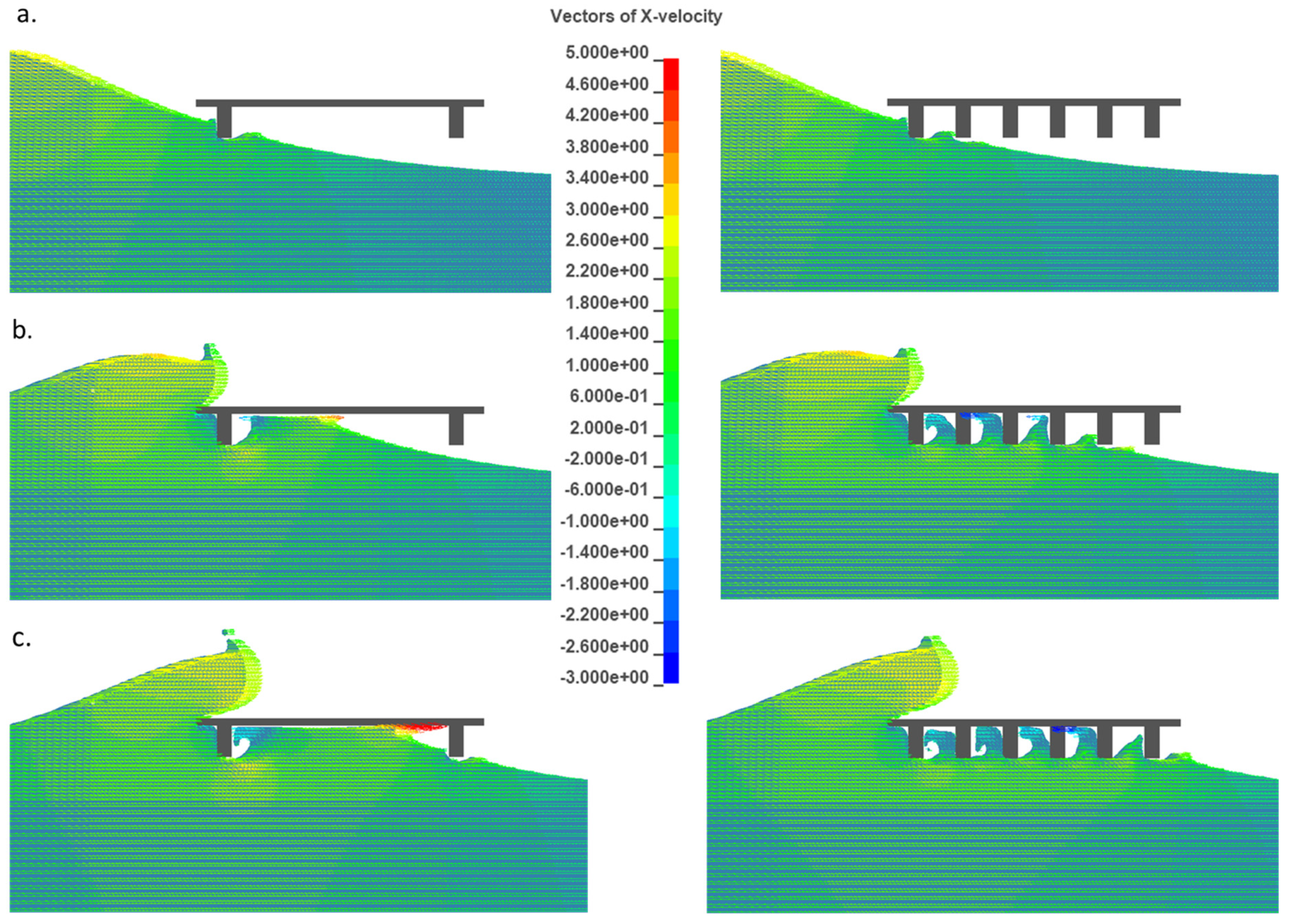
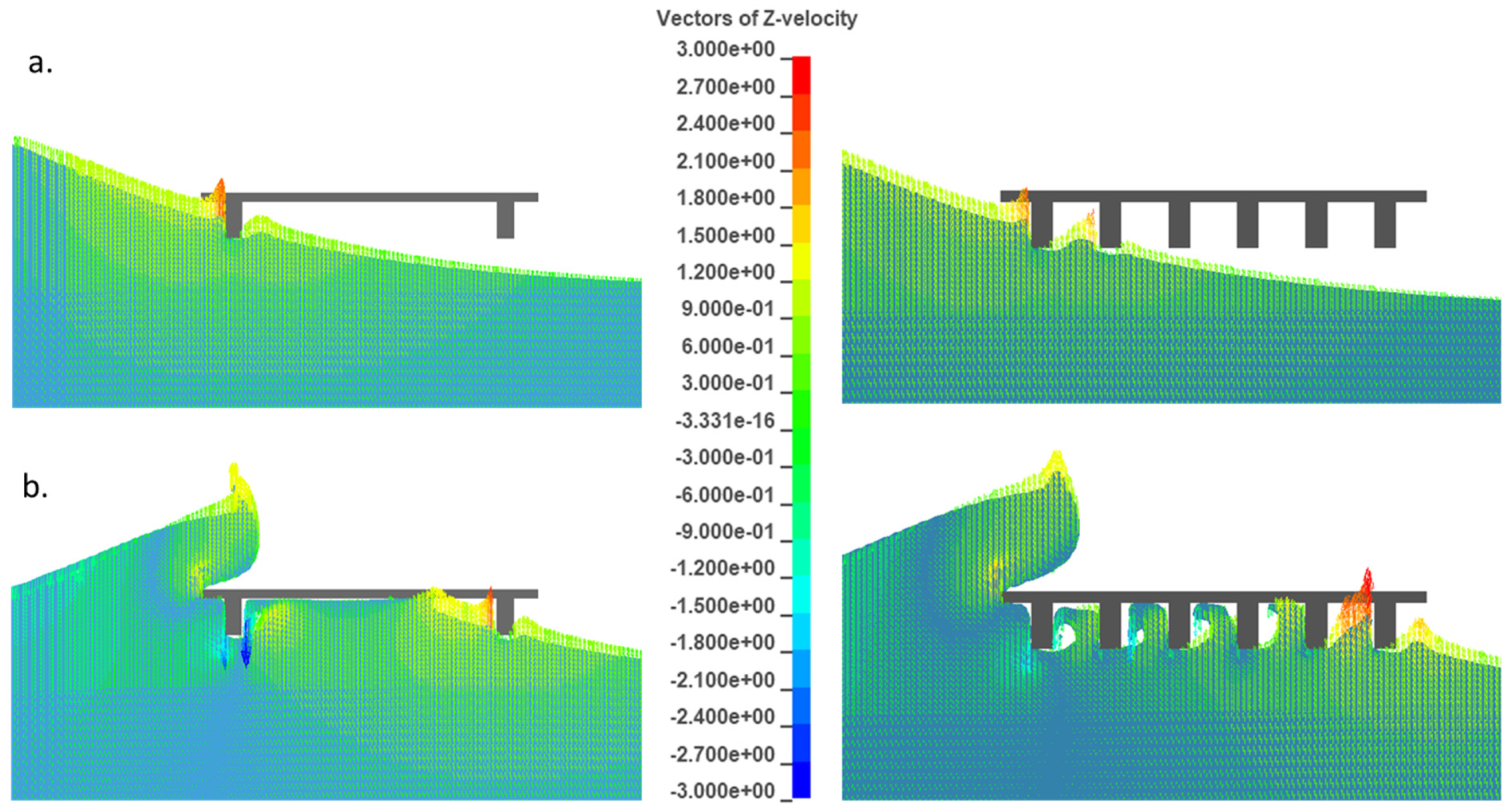
- In the two-girder case, the wave impacts first the upstream (offshore) girder, then it reaches the bottom of the deck—at a location close to the mid-width—and after that it accelerates and impacts the downstream girder and deck slab with much larger horizontal and vertical velocities. These large velocities are the reason for the generation of the impulsive pressures and slamming component of the total horizontal and uplift forces.
- On the other hand, in the case of the six-girder bridge, the wave does not accelerate and the horizontal velocities remain low when the wave reaches the downstream girder. However, in the vertical direction, although the wave accelerates and impacts the last chamber next to the downstream girder with a large velocity, this impact happens on a small area, while at the same instant the velocities in the remaining chambers are in the negative direction (pointing downwards), meaning that those chambers do not contribute significantly to the total uplift. In contrast, at the same instant in the two-girder case the wave impacts violently on a larger area close to the downstream side of the deck (since it is not limited by the presence of additional girders) while the majority of the remaining area below the deck is witnessing pure buoyancy, resulting in larger total uplift forces than the six-girder deck.
4. Effect of Bridge Width
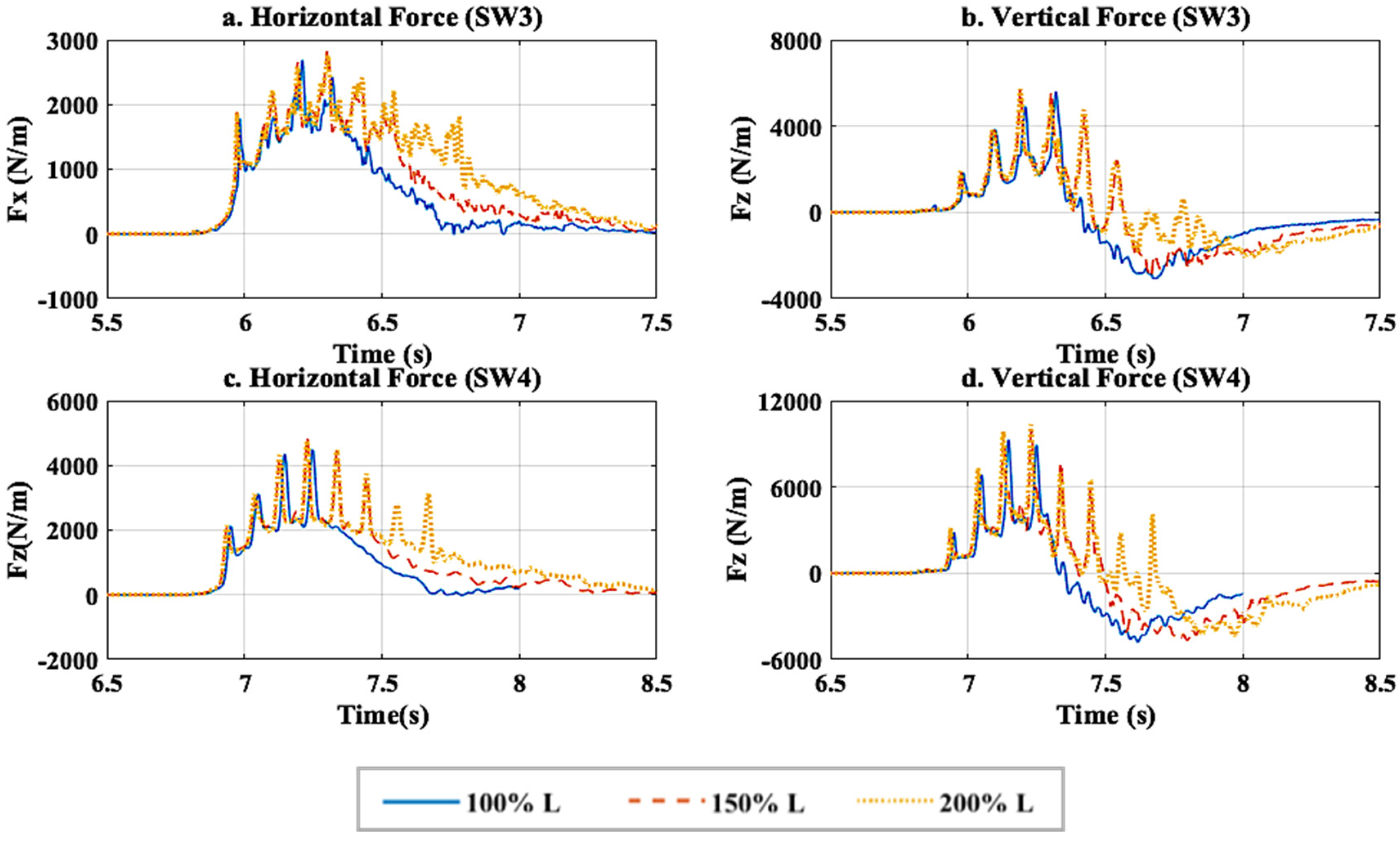
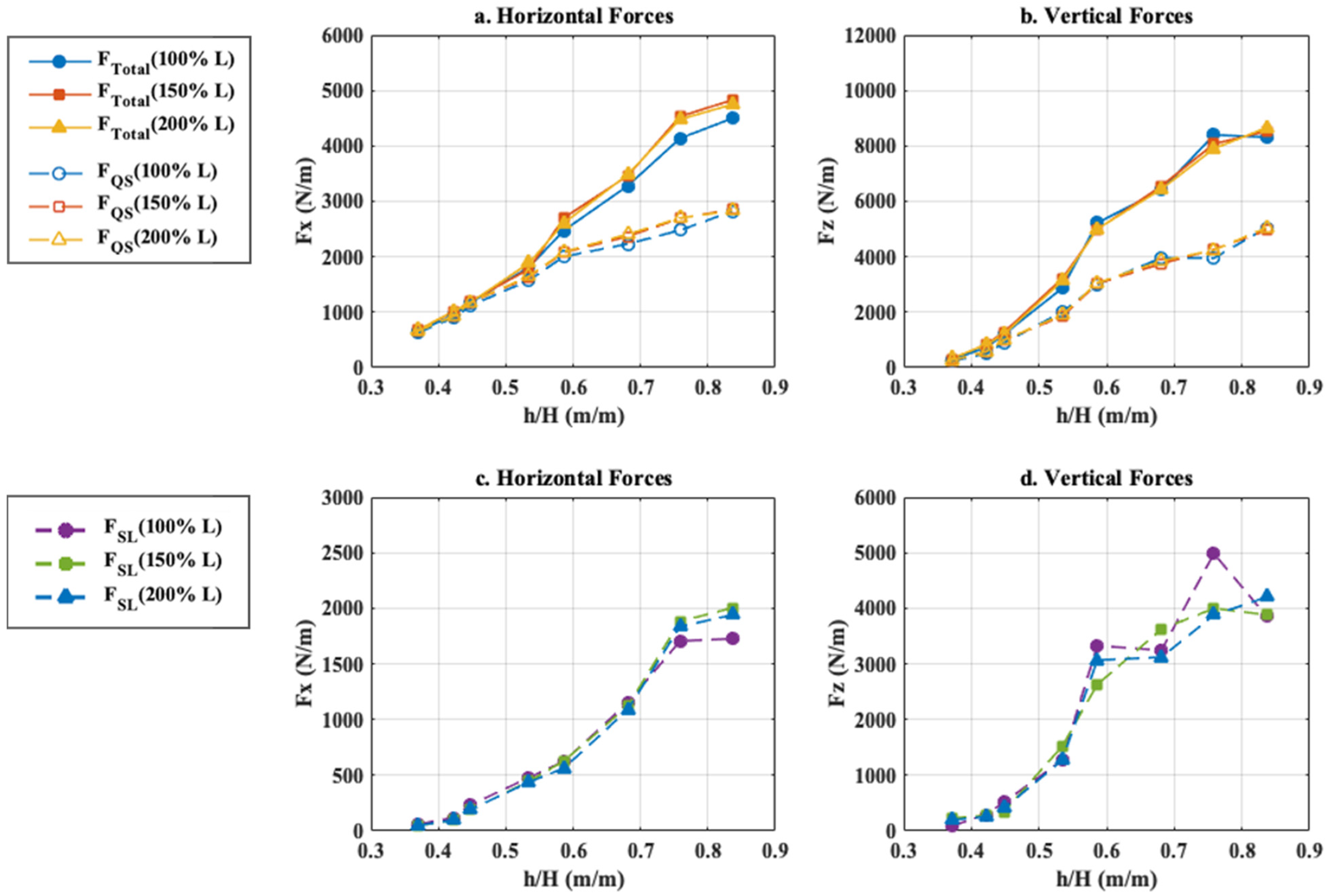
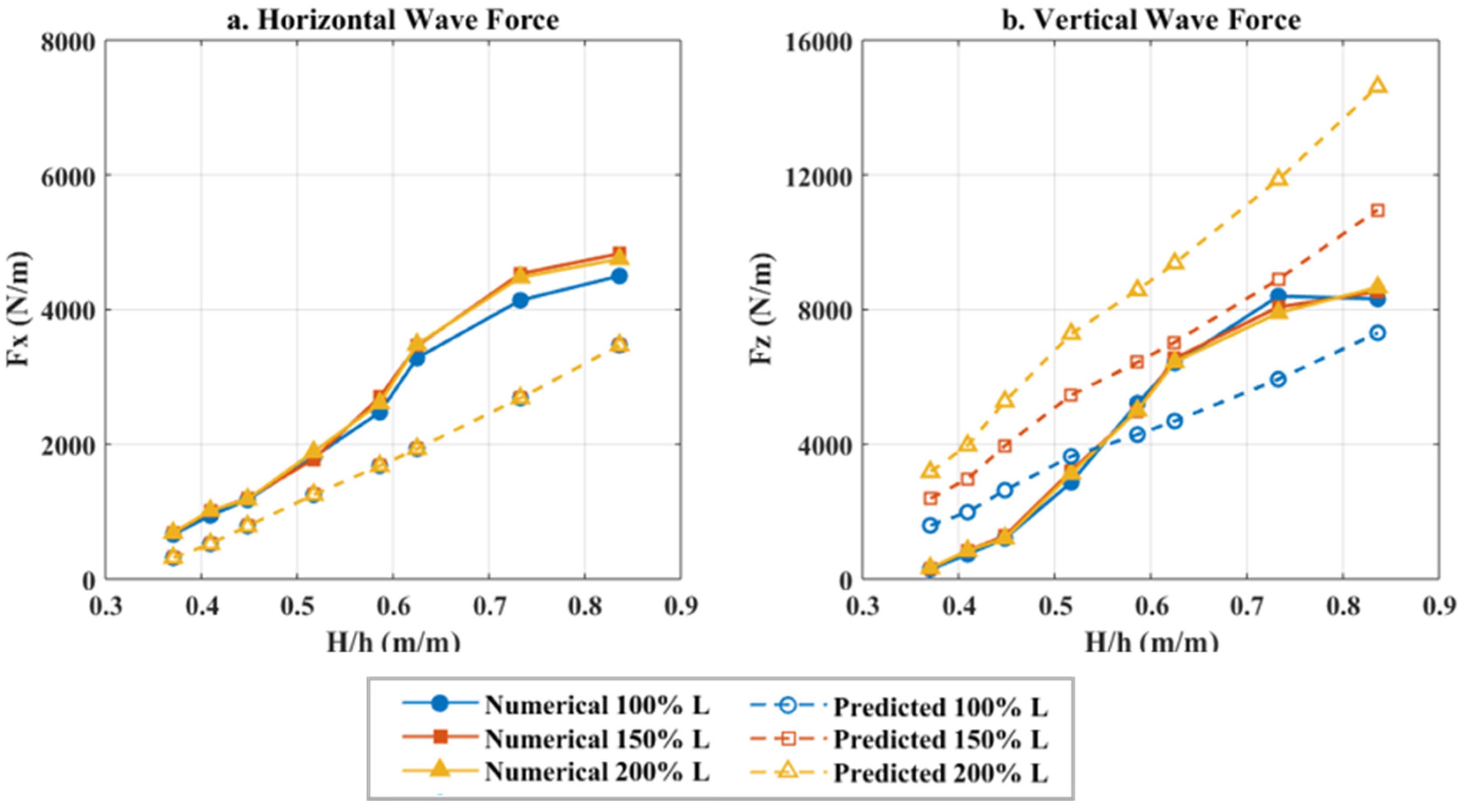
4.1. Horizontal and Vertical Forces
4.2. Wave Impact Process
5. New Predictive Equations for Wave Loads
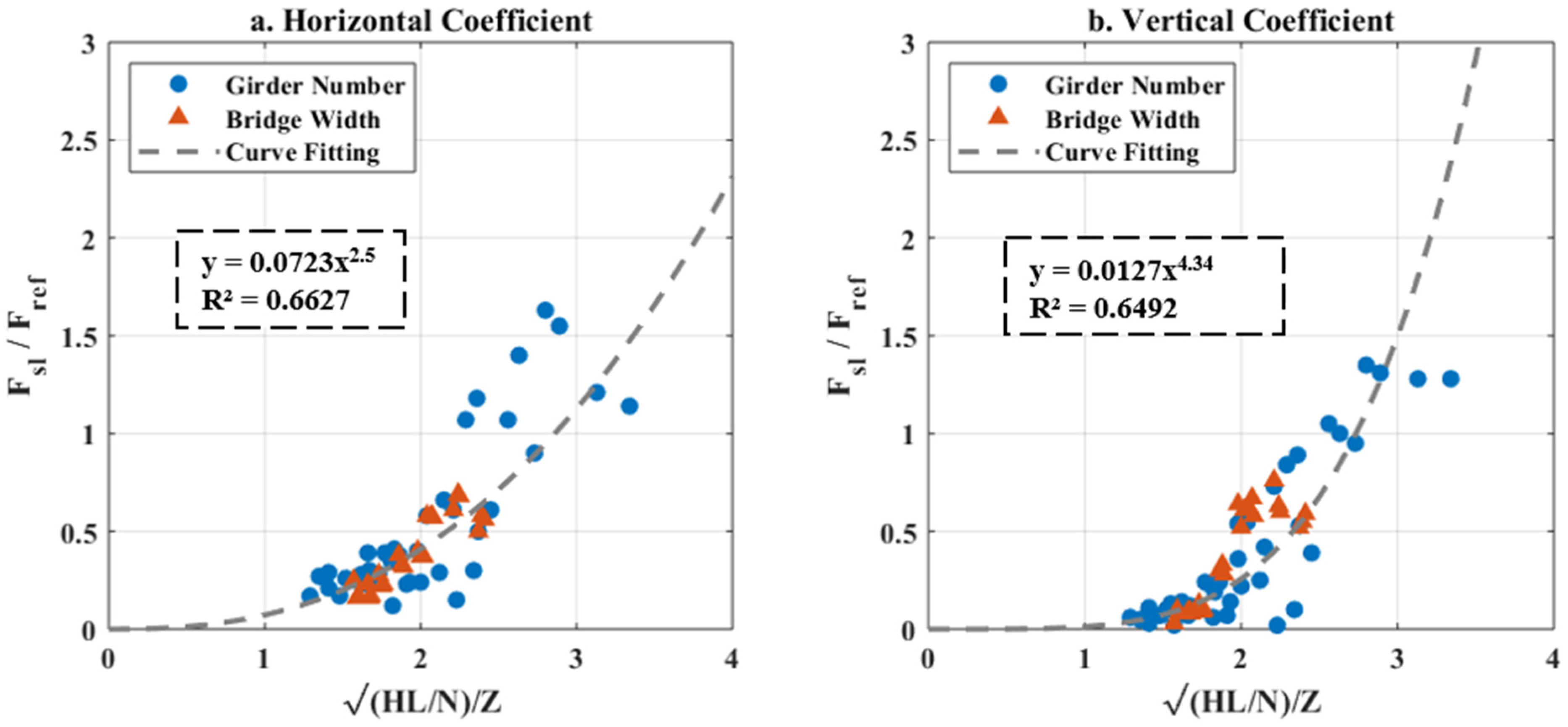
5.1. Motivation
5.2. Formulation
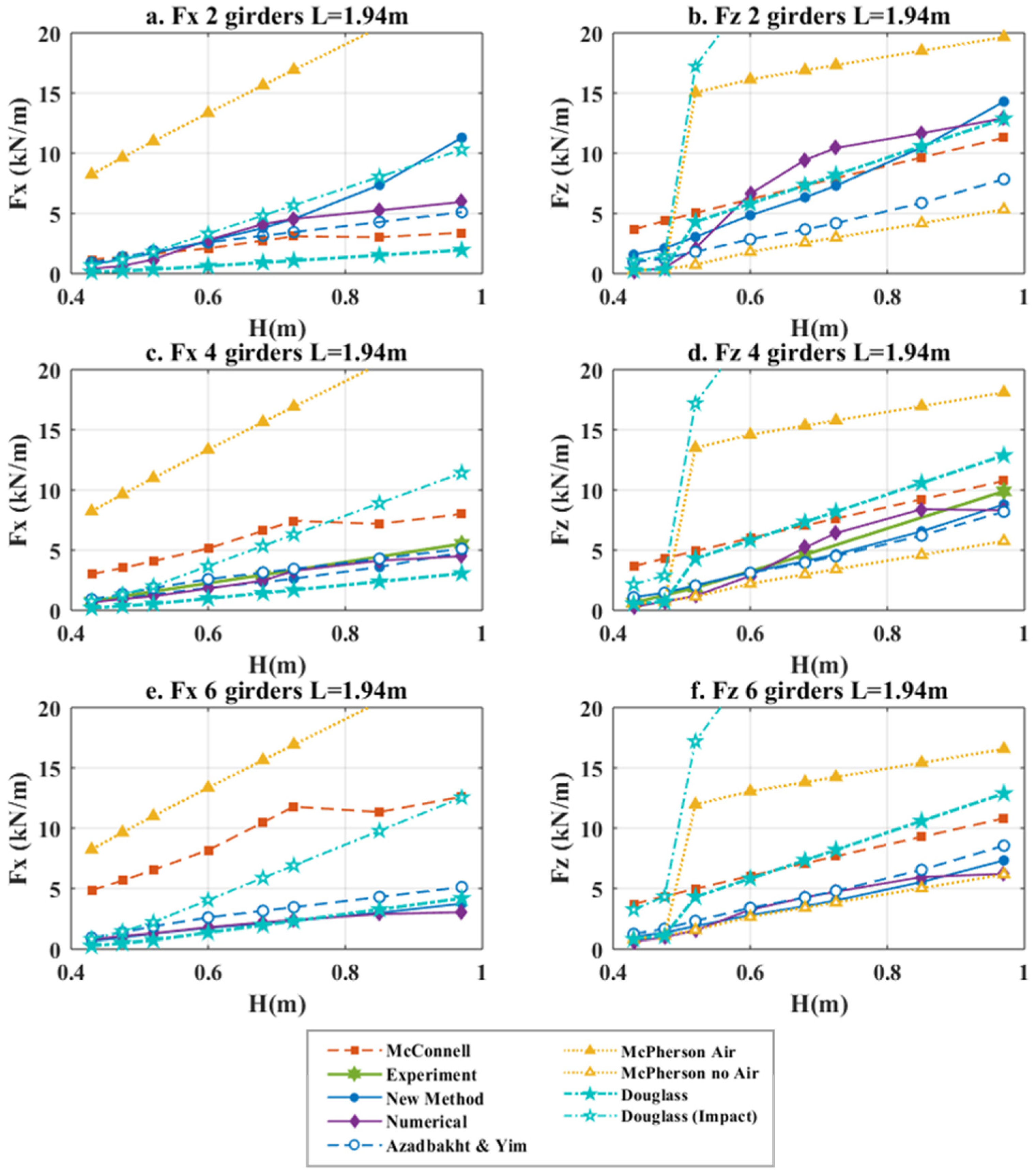
5.3. Accuracy of New Method and Comparison with Existing Equations
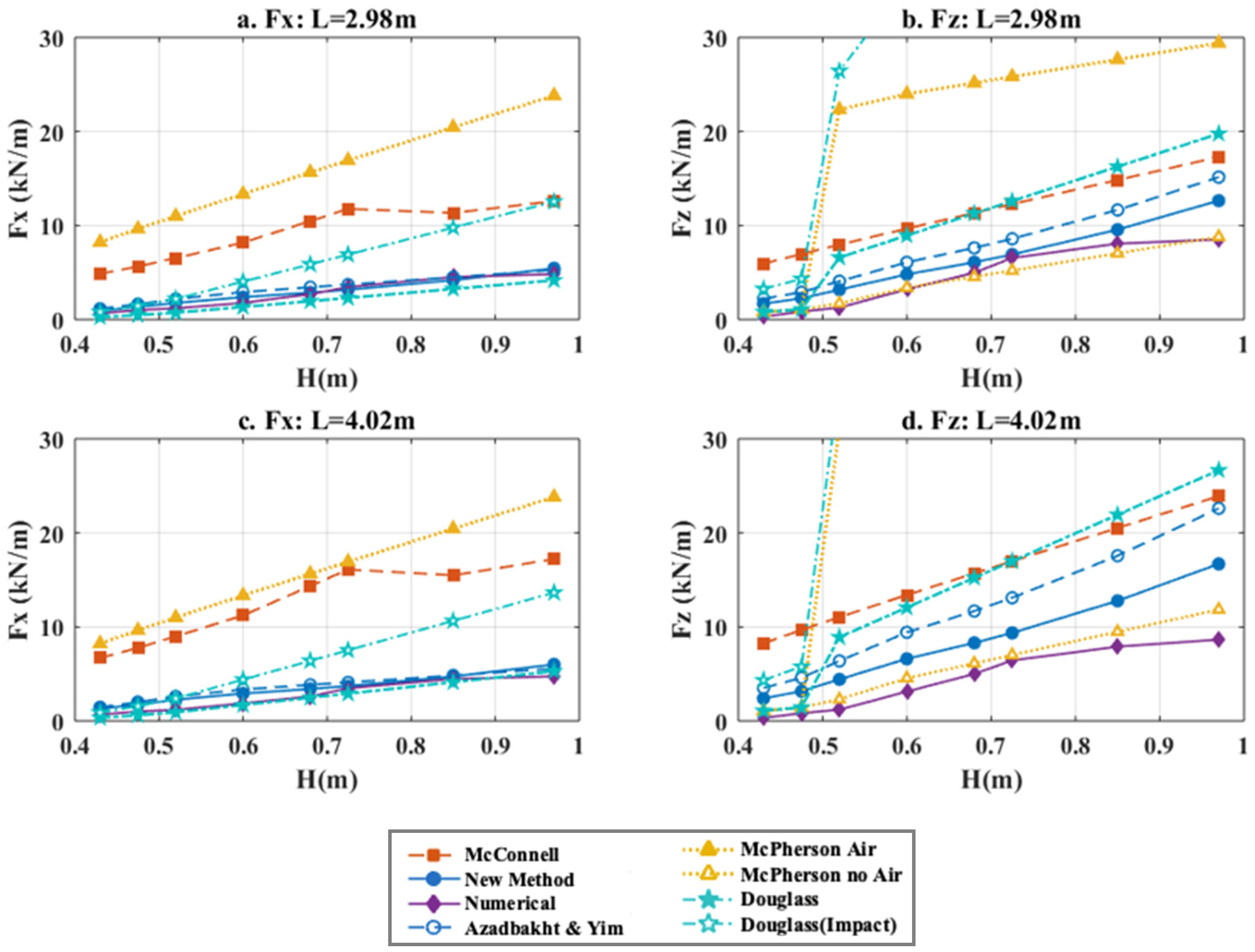
- The predictive equations of McConnell et al. [6], i.e., Equations (A1) and (A2), divided the wave forces into several components, including the ones applied on the internal and the seaward (upstream) structural elements, and considering both the slab and the girders (beams) of jetties. The force on each component is a function of a reference hydrostatic force, without the explicit consideration of the impulsive component. The total wave forces are the summation of the wave forces on each structural element, which means that this set of equations considers the geometry of the deck.
- Douglass et al. [7] proposed predictive equations for the total applied wave forces on a coastal deck (see Equations (A3)–(A6)). These forces are calculated based on (i) a reference hydrostatic force and (ii) different coefficients that can be used to estimate either the “slowly-varying” forces or the total ones that include the impact component as well. Interestingly, the impact coefficient of the uplift forces was suggested to be three times larger than “slowly-varying” coefficient, revealing the high magnitude of the impact forces. Moreover, the equation for the uplift force is a function of the bridge width, while the horizontal force is a function of the number of girders Ng. In the horizontal force equation the internal girders are contributing to the total force with a reduced coefficient of 0.4 relative to the offshore external girder (coefficient = 1).
- McPherson [8] developed a different set of equations for the total wave loads applied on coastal bridge decks. In contrast to the equation of [7], the horizontal force was not a function of the internal girders, but just the external offshore and onshore girders, meaning the Ng did not influence the predicted force. On the other hand, the uplift wave force was distributed into the hydrostatic force (), buoyancy force (), the weight of overtopping water () and the air-entrapment force (). In this method all the internal chambers were assumed to be filled with air up to 50% of their individual volume, which means that the total uplift was dependent on the volume of the chamber and consequently on the number of girders Ng.
6. Summary and Conclusions
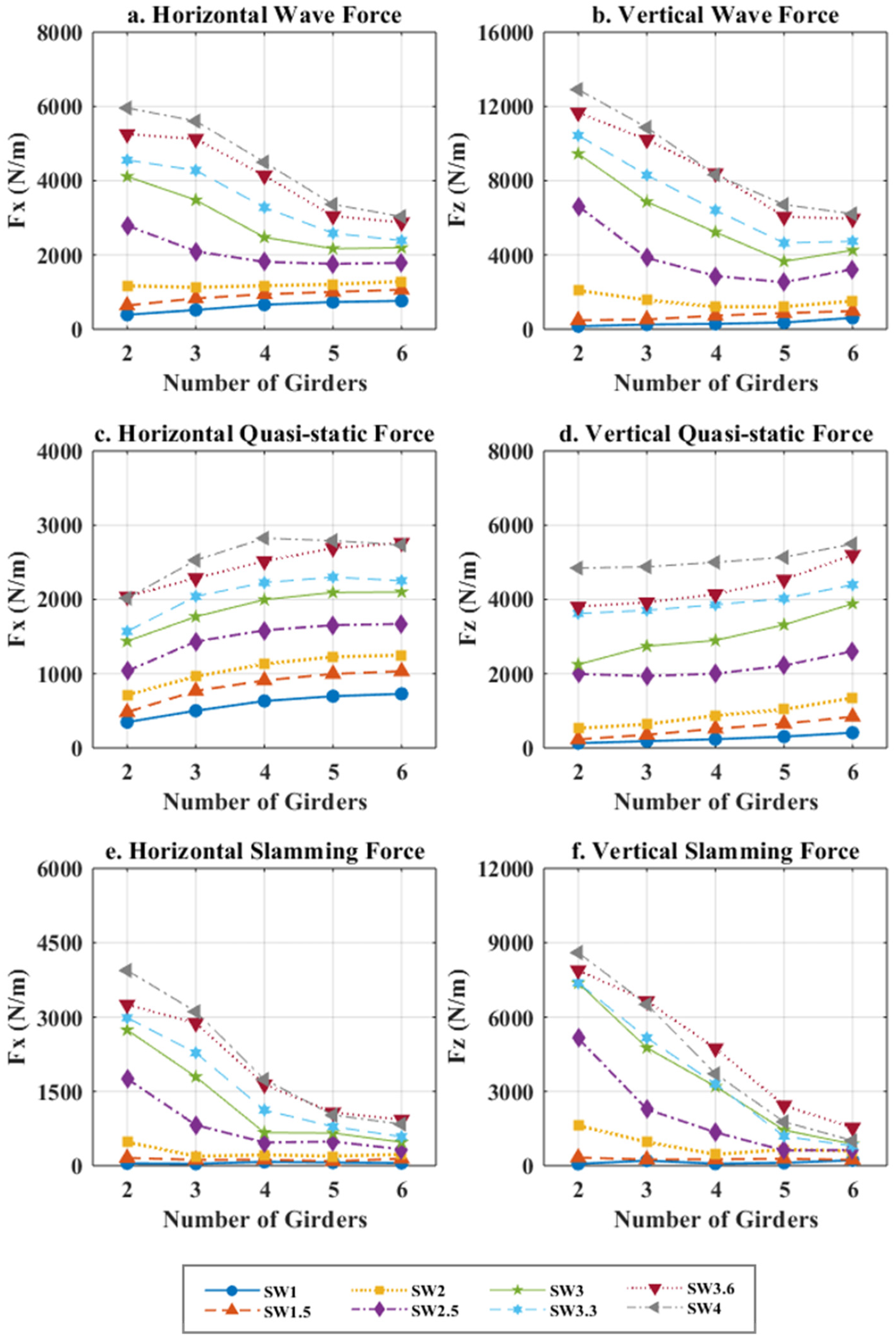
- The effect of Ng on the total forces is dependent on the wave height H. For small H, the maximum horizontal and vertical forces increase with Ng at a relatively small rate, while for medium-to-large H the increase of the Ng causes major reductions of the forces at a much larger rate. In fact, the five-girder deck has to withstand about 50% and 33% of the horizontal and uplift forces applied on the two-girder deck.
- For both the horizontal and uplift direction the Ng has an opposite effect on the quasi-static and slamming forces, which could potentially explain the complex role of Ng observed in previous studies [40,50,51]. In fact, as Ng increases, the maximum values of the quasi-static forces increase nonlinearly with a slow rate, while the slamming forces decrease dramatically. Depending on the deck geometry, the latter forces can be twice as large as the former ones for the big waves and negligible for the small ones, which means that the effect of Ng on the total forces is governed by its effect on (i) the slamming forces when the wave height is large and Ng is small, (ii) the quasi-static ones when the wave is small, and (iii) both components for all other cases.
- The main reason for the generation of larger horizontal and uplift forces on the decks with a small Ng (i.e., 2, 3) is the fact that the fluid particles accelerate after the initial impact on the offshore girder and propagate inside a long chamber that allows the fluid to increase its velocity further. This results in a more violent slamming on the onshore girder and deck slab that generates large impulsive pressures and forces. For a large Ng (e.g., 5, 6), the multiple girders and chambers (i) prevent the fluid from accelerating, (ii) cause the formation of unsynchronized eddies in each chamber that dissipate energy, and (iii) result in multiple but smaller loads on the deck due to the out-of-phase application of pressures on the consecutive structural elements.
- The increase of the bridge width (from L to 1.5 L and 2 L) increases the number of peaks in the force histories due to the additional girders and chambers, and tends to elongate the inundation process and duration of the applied forces. However, it has a minor-to-negligible effect on the maximum horizontal and uplift force. In the vertical direction, this can be attributed to the fact the maximum uplift tends to occur when the wave has inundated the three chambers (less than 100% L), and after that the wave overtops the deck counter-acting any uplift pressures that might be generated in the additional chambers of the wider decks. Moreover, for very wide decks the wave cannot inundate the whole deck width, meaning that the maximum inundation and respective forces are limited by the wavelength.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mondal, G.; Rai, D.C. Performance of Harbour Structures in Andaman Islands during 2004 Sumatra earthquake. Eng. Struct. 2008, 30, 174–182. [Google Scholar] [CrossRef]
- Padgett, J.; DesRoches, R.; Nielson, B.; Yashinsky, M.; Kwon, O.S.; Burdette, N.; Tavera, E. Bridge Damage and Repair Costs from Hurricane Katrina. J. Bridge Eng. 2008, 13, 6–14. [Google Scholar] [CrossRef] [Green Version]
- Maruyama, Y.; Kitamura, K.; Yamazaki, F. Estimation of Tsunami-Inundated Areas in Asahi City, Chiba Prefecture, after the 2011 Tohoku-Oki Earthquake. Earthq. Spectra. 2013, 29, S201–S217. [Google Scholar] [CrossRef] [Green Version]
- Maruyama, K.; Tanaka, Y.; Kosa, K.; Hosoda, A.; Arikawa, T. Evaluation of Tsunami Force Acting on Bridge Girders. In Proceedings of the 13th East Asia-Pacific Conference on Structural Engineering and Construction, Sapporo, Japan, 11–13 September 2013. [Google Scholar]
- Williams, J.H.; Wilson, T.M.; Horspool, N.; Paulik, R.; Wotherspoon, L.; Lane, E.M.; Hughes, M.W. Assessing Transportation Vulnerability to Tsunamis: Utilising Post-Event Field Data from the 2011 Tōhoku Tsunami, Japan, and the 2015 Illapel Tsunami, Chile. Nat. Hazards Earth Syst. Sci. 2020, 20, 451–470. [Google Scholar] [CrossRef] [Green Version]
- McConnell, K.; Allsop, W.; Cruickshank, I. Piers, Jetties, and Related Structures Exposed to Waves: Guidelines for Hydraulic Loadings; Thomas Telford Ltd.: London, UK, 2004. [Google Scholar]
- Douglass, S.L.; Chen, Q.; Olsen, J.M.; Edge, B.L.; Brown, D. Wave Forces on Bridge Decks; Department of Transportation, Federal Highway Administration, Office of Bridge Technology: Washington, DC, USA, 2006.
- McPherson, R.L. Hurricane-Induced Wave and Surge Forces on Bridge Decks. Master’s Thesis, Texas A.&M. University, College Station, TX, USA, 2008. [Google Scholar]
- Azadbakht, M.; Yim, S.C. Simulation and Estimation of Tsunami Loads on Bridge Superstructures. J. Waterw. Port Coast. Ocean Eng. 2015, 141, 04014031. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.; Lomonaco, P. Tsunami Loads on a Representative Coastal Bridge Deck: Experimental Study and Validation of Design Equations. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Ghamry, E.; Osman, A. Wave Forces on a Dock. Technical Rep. No. HEL-9-1, Hydraulic Engineering Laboratory, University of California, Berkeley, CA, USA. 1963. Available online: https://trid.trb.org/view/9928 (accessed on 5 October 2021).
- French, J.A. Wave Uplift Pressures on Horizontal Platforms. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1970. [Google Scholar]
- Overbeek, J.; Klabbers, I.M. Design of Jetty Decks for Extreme Vertical Wave Loads. In Proceedings of the Ports Conference, Norfolk, VA, USA, 29 April–2 May 2001. [Google Scholar]
- Wang, H. Water Wave Pressure on Horizontal Plate. J. Hydr. Div. 1970, 96, 1997–2017. [Google Scholar] [CrossRef]
- Robertson, I.N.; Riggs, H.R.; Yim, S.C.; Young, Y.L. Lessons from Hurricane Katrina Storm Surge on Bridges and Buildings. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 463–483. [Google Scholar] [CrossRef]
- Bradner, C. Large-Scale Laboratory Observations of Wave Forces on a Highway Bridge Superstructure. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2008. [Google Scholar]
- Guo, A.; Fang, Q.; Li, H. Analytical Solution of Hurricane Wave Forces Acting on Submerged Bridge Decks. Ocean Eng. 2015, 108, 519–528. [Google Scholar] [CrossRef]
- Nakamura, T.; Sawa, Y.; Mizutani, N. Study on the Evaluation of Temporal Change in Horizontal and Vertical Tsunami Forces Acting on a Bridge Superstructure. Coast. Eng. J. 2016, 58, 1640020. [Google Scholar] [CrossRef] [Green Version]
- Istrati, D. Large-Scale Experiments of Tsunami Inundation of Bridges Including Fluid-Structure-Interaction. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2017. Available online: https://scholarworks.unr.edu//handle/11714/2030 (accessed on 1 January 2021).
- Istrati, D.; Buckle, I.; Itani, A.; Lomonaco, P.; Yim, S. Large-Scale FSI Experiments on Tsunami-Induced Forces in Bridges. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017; Available online: https://www.wcee.nicee.org/wcee/article/16WCEE/WCEE2017-2579.pdf (accessed on 24 October 2021).
- Huang, B.; Zhu, B.; Cui, S.; Duan, L.; Zhang, J. Experimental and Numerical Modelling of Wave Forces on Coastal Bridge Superstructures with Box Girders, Part I: Regular Waves. Ocean Eng. 2018, 149, 53–77. [Google Scholar] [CrossRef]
- Denson, K.H. Wave Forces on Causeway-Type Coastal Bridges. NASA STI/Recon Technical Report, N. 79 1978. Available online: https://ui.adsabs.harvard.edu/abs/1978STIN...7920293D/abstract (accessed on 5 October 2021).
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Agrawal, A.; Qu, K.; Tang, H.S. Numerical Investigation of Connection Forces of a Coastal Bridge Deck Impacted by Solitary Waves. J. Bridge Eng. 2018, 23, 04017108. [Google Scholar] [CrossRef]
- AASHTO. Guide Specifications for Bridges Vulnerable to Coastal Storms, American Association of State Highway and Transportation Officials (AASHTO); American Association of State Highway and Transportation Officials: Washington, DC, USA, 2008. [Google Scholar]
- Istrati, D.; Buckle, I. Role of Trapped Air on the Tsunami-Induced Transient Loads and Response Of coastal Bridges. Geosciences 2019, 9, 191. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Yang, W.; Li, Q.; Li, A. CFD Investigation of the Cap Effects on Wave Loads on Piles for the Pile-Cap Foundation. Ocean Eng. 2019, 183, 249–261. [Google Scholar] [CrossRef]
- Xu, B.; Wei, K.; Qin, S.; Hong, J. Experimental Study of Wave Loads on Elevated Pile Cap of Pile Group Foundation for Sea-crossing Bridges. Ocean Eng. 2020, 197, 106896. [Google Scholar] [CrossRef]
- Do, T.A.; Nguyen, T.H.; Nguyen, H.M.; Tran, N.D.; Nguyen, L.N. Evaluation of Dynamic Impact of Flow with Bridge Pier Using Smoothed Particle Hydrodynamics Method. Prog. Comput. Fluid Dyn. 2020, 20, 332–348. Available online: http://www.inderscience.com/offer.php?id=111401 (accessed on 15 July 2021). [CrossRef]
- Qeshta, I.M.; Hashemi, M.J.; Gravina, R.; Setunge, S. Review of Resilience Assessment of Coastal Bridges to Extreme Wave-Induced Loads. Eng. Struct. 2019, 185, 332–352. [Google Scholar] [CrossRef]
- Webb, B.M.; Cleary, J.C. Drag-Induced Displacement of a Simply Supported Bridge Span during Hurricane Katrina. J. Perform. Constr. Facil. 2019, 33, 04019040. [Google Scholar] [CrossRef]
- Lomonaco, P.; Istrati, D.; Maddux, T.; Buckle, I.; Yim, S.; Xiang, T. Large-Scale Testing of Tsunami Impact Forces on Bridges. In Proceedings of the 6th International Conference on the Application of Physical Modelling in Coastal and Port Engineering and Science (Coastlab16), Ottawa, OTT, Canada, 10–13 May 2016. [Google Scholar] [CrossRef]
- Huang, W.; Xiao, H. Numerical Modeling of Dynamic Wave Force Acting on Escambia Bay Bridge Deck During Hurricane Ivan. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 164–175. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I. Effect of Fluid-Structure Interaction on Connection Forces in Bridges due to Tsunami Loads. In Proceedings of the 30th US-Japan Bridge Engineering Workshop, Washington, DC, USA, 21–23 October 2014; Available online: https://www.pwri.go.jp/eng/ujnr/tc/g/pdf/30/30-10-2_Buckle.pdf (accessed on 20 October 2021).
- Xu, G.; Cai, C.S. Numerical Simulations of Lateral Restraining Stiffness Effect on Bridge Deck–Wave Interaction under Solitary Waves. Eng. Struct. 2015, 101, 337–351. [Google Scholar] [CrossRef]
- Matamoros, A.; Testik, F.; Nasouri, R.; Montoya, A. Coastal Bridges under Hurricane Stresses along the Texas and Louisiana Coast, Transportation Consortium of South-Central States, December 2018. Available online: https://digitalcommons.lsu.edu/transet_pubs/29/ (accessed on 10 June 2021).
- Greco, F.; Lonetti, P.; Blasi, P.N. Vulnerability Analysis of Bridge Superstructures under Extreme Fluid Actions. J. Fluids Struct. 2020, 93, 102843. [Google Scholar] [CrossRef]
- Wei, Z.P.; Dalrymple, R.A. Numerical Study on Mitigating Tsunami Force on Bridges by an SPH Model. J. Ocean Eng. Mar. Energy 2016, 2, 365–380. [Google Scholar] [CrossRef] [Green Version]
- Aristodemo, F.; Tripepi, G.; Meringolo, D.D.; Veltri, P. Solitary Wave-Induced Forces on Horizontal Circular Cylinders: Laboratory Experiments and SPH Simulations. Coast. Eng. 2017, 129, 17–35. [Google Scholar] [CrossRef]
- Sarfaraz, M.; Pak, A. SPH Numerical Simulation of Tsunami Wave Forces Impinged on Bridge Superstructures. Coast Eng. 2017, 121, 145–157. [Google Scholar] [CrossRef]
- Zhu, M.J.; Elkhetali, I.; Scott, M.H. Validation of OpenSees for Tsunami Loading on Bridge Superstructures. J. Bridge Eng. 2018, 23, 04018015. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Bozorgnia, M.; Lee, J.J. Computational Fluid Dynamic Analysis of Highway Bridges Exposed to Hurricane Waves. In Proceedings of the 33rd Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012; Coastal Engineering Research Council, ASCE: Reston, VA, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Crowley, R.; Robeck, C.; Dompe, P. A Three-Dimensional Computational Analysis of Bridges Subjected to Monochromatic Wave Attack. J. Fluids Struct. 2018, 79, 76–93. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S.; Itani, A. Tsunami Induced Forces in Bridges: Large-Scale Experiments and the Role of Air-Entrapment. Coast. Eng. Proc. 2017, 35, 30. [Google Scholar] [CrossRef] [Green Version]
- Motley, M.R.; Wong, H.K.; Qin, X.; Winter, A.O.; Eberhard, M.O. Tsunami-Induced Forces on Skewed Bridges. J. Waterw. Port Coast. Ocean. Eng. 2016, 142, 04015025. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I. Tsunami Loads on Straight and Skewed Bridges—Part 1: Experimental Investigation and Design Recommendations, No. FHWA-OR-RD-21-12; Oregon Department of Transportation. Research Section: Salem, OR, USA, 2021. Available online: https://rosap.ntl.bts.gov/view/dot/55988 (accessed on 1 June 2021).
- Istrati, D.; Buckle, I. Tsunami Loads on Straight and Skewed Bridges—Part 2: Numerical Investigation and Design Recommendations, No. FHWA-OR-RD-21-13; Oregon Department of Transportation. Research Section: Salem, OR, USA, 2021. Available online: https://rosap.ntl.bts.gov/view/dot/55947 (accessed on 1 June 2021).
- Istrati, D.; Hasanpour, A.; Buckle, I. Numerical Investigation of Tsunami-Borne Debris Damming Loads on a Coastal Bridge. In Proceedings of the 17th World Conference of Earthquake Engineering, Sendai, Japan, 27 September–2 October 2021. [Google Scholar]
- Hayatdavoodi, M.; Seiffert, B.; Ertekin, R.C. Experiments and Computations of Solitary-Wave Forces on a Coastal-Bridge Deck. Part II: Deck with Girders. Coast. Eng. 2014, 88, 210–228. [Google Scholar] [CrossRef]
- Moideen, R.; Behera, M.R.; Kamath, A.; Bihs, H. Effect of Girder Spacing and Depth on the Solitary Wave Impact on Coastal Bridge Deck for Different Airgaps. J. Mar. Sci. Eng. 2019, 7, 140. [Google Scholar] [CrossRef] [Green Version]
- Hallquist, J.O. LS-DYNA Theory Manual. Liverm. Softw. Technol. Corp. 2006, 3, 25–31. [Google Scholar]
- Souli, M.; Benson, D.J. Arbitrary Lagrangian Eulerian and Fluid-Structure Interaction: Numerical Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Takahashi, S.; Tanimoto, K.; Miyanaga, S. Uplift Wave Forces due to Compression of Enclosed Air Layer and Their Similitude Low. Coast. Eng. Jpn. 1985, 28, 191–206. [Google Scholar] [CrossRef]
- Cuomo, G.; Shimosako, K.I.; Takahashi, S. Wave-in-Deck Loads on Coastal Bridges and the Role of Air. Coast. Eng. 2009, 56, 793–809. [Google Scholar] [CrossRef]
- Hayatdavoodi, M.; Treichel, K.; Ertekin, R.C. Parametric study of Nonlinear Wave Loads on Submerged Decks in Shallow Water. J. Fluids Struct. 2019, 86, 266–289. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunamis-The Propagation of Long Waves on to a Shelf. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1979. [Google Scholar]
- AASHTO. LRFD Bridge Design Specifications, 8th ed.; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2007. [Google Scholar]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S.; Itani, A. Large-Scale Experiments of Tsunami Impact Forces on Bridges: The Role of Fluid-Structure Interaction and Air-Venting. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]




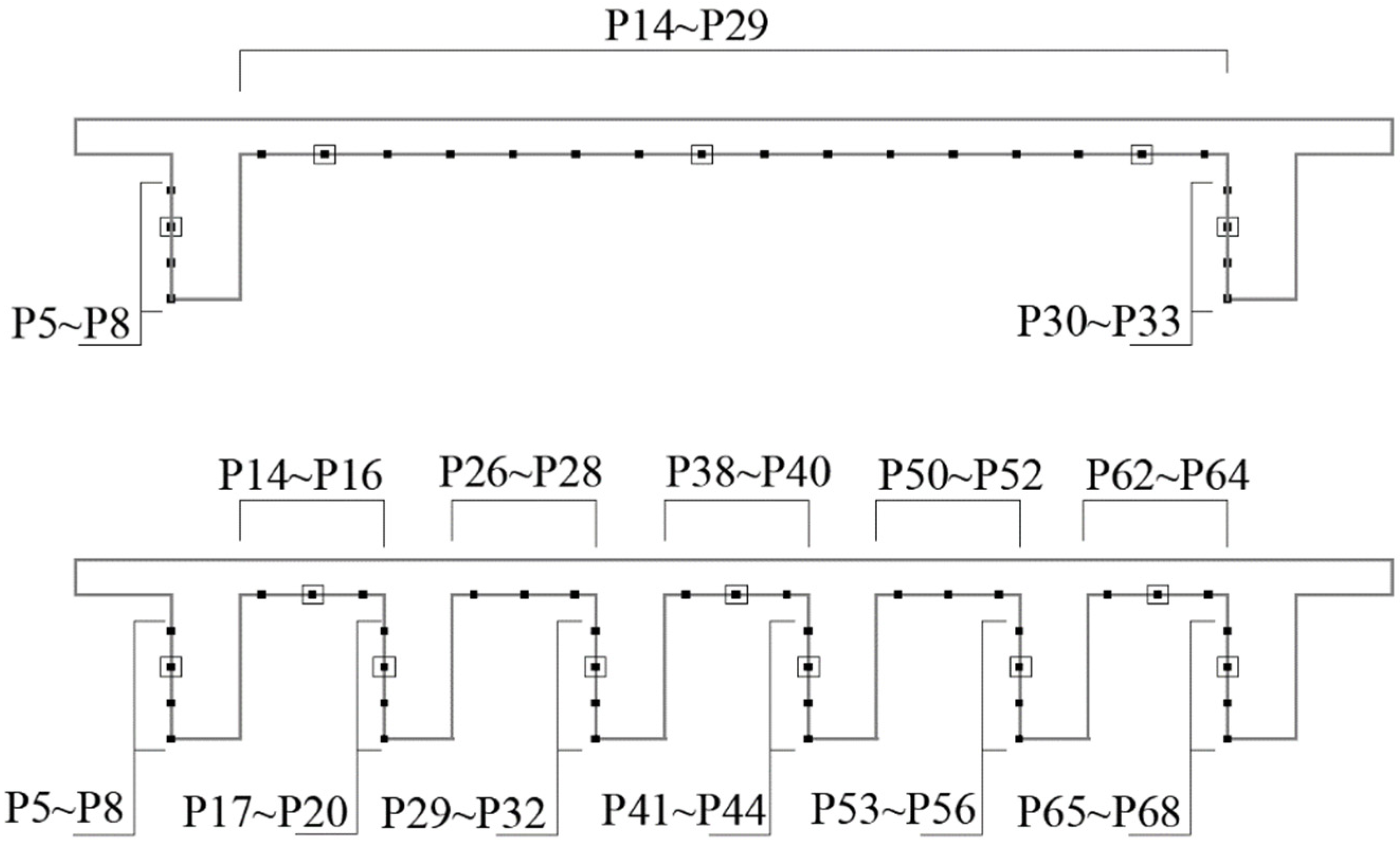



| Comparison A (L = 1.94 m) | Comparison B | |
|---|---|---|
| Number of Girders (Ng) | Girder Spacing S (m) | Bridge Width L |
| 2 | 1.46 | = 1.94 m) |
| 3 | 0.68 | = 2.97 m) |
| 4 | 0.42 | = 4.01 m) |
| 5 | 0.29 | |
| 6 | 0.21 | |
| Case # | Impact Wave Height H (m) | Normalized Wave Height (H/h) |
|---|---|---|
| SW1 | 0.430 | 0.37 |
| SW1.5 | 0.475 | 0.41 |
| SW2 | 0.520 | 0.45 |
| SW2.5 | 0.600 | 0.52 |
| SW3 | 0.680 | 0.59 |
| SW3.3 | 0.725 | 0.63 |
| SW3.6 | 0.850 | 0.73 |
| SW4 | 0.970 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. https://doi.org/10.3390/jmse9121342
Xiang T, Istrati D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. Journal of Marine Science and Engineering. 2021; 9(12):1342. https://doi.org/10.3390/jmse9121342
Chicago/Turabian StyleXiang, Tao, and Denis Istrati. 2021. "Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method" Journal of Marine Science and Engineering 9, no. 12: 1342. https://doi.org/10.3390/jmse9121342
APA StyleXiang, T., & Istrati, D. (2021). Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. Journal of Marine Science and Engineering, 9(12), 1342. https://doi.org/10.3390/jmse9121342







