Emergence of Solitons from Irregular Waves in Deep Water
Abstract
:1. Introduction
2. Brief Introduction of Solitons
3. High-Order Spectral Model
4. Numerical Flume Set-Up and Validation
5. Results and Discussion
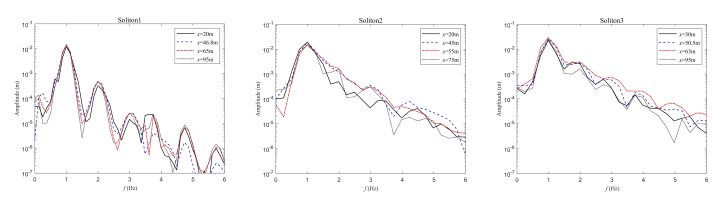
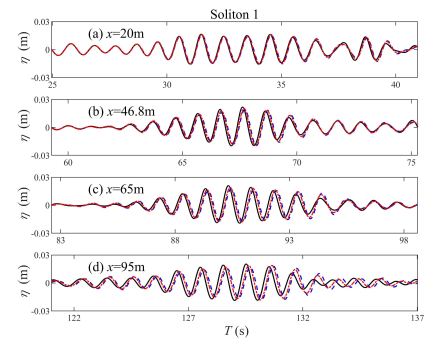
5.1. Identification of Solitons
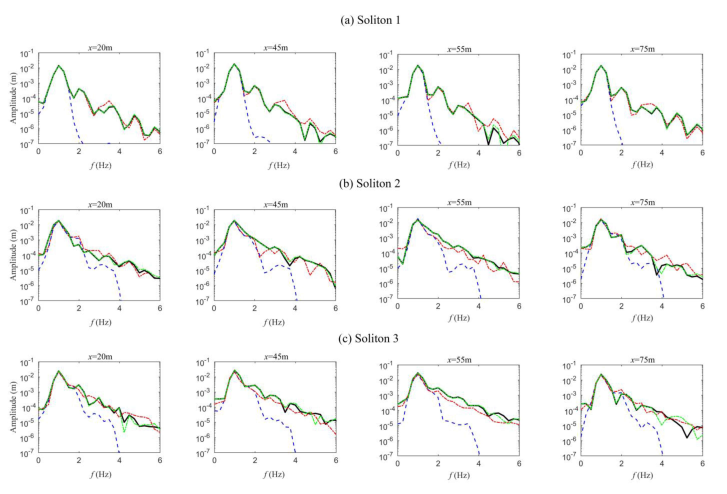
5.2. Persistence Distance of Solitons
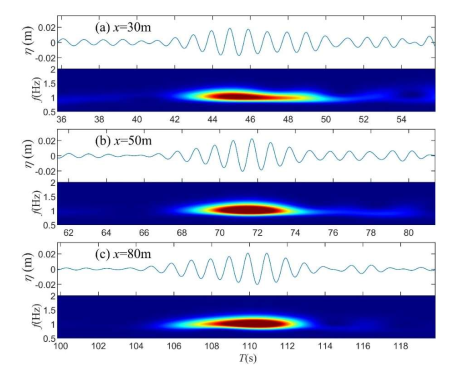
5.3. Formation of Solitons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic Rogue Waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Nikolkina, I.; Didenkulova, I. Rogue waves in 2006–2010. Nat. Hazards Earth Syst. Sci. 2011, 11, 2913–2924. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B/Fluids 2003, 22, 603–634. [Google Scholar] [CrossRef] [Green Version]
- Lighthill, M.J. Contributions to the Theory of Waves in Non-linear Dispersive Systems. IMA J. Appl. Math. 1965, 1, 269–306. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Feir, J.E. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Zakharov, V. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Benney, D.J.; Newell, A.C. The Propagation of Nonlinear Wave Envelopes. J. Math. Phys. 1967, 46, 133–139. [Google Scholar] [CrossRef]
- Chu, V.H.; Mei, C.C. On slowly-varying Stokes waves. J. Fluid Mech. 1970, 41, 873–887. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, V.E.; Shabat, A.B. Exact Theory of Two-dimensional Self-focusing and One-dimensional Self-modulation of Waves in Nonlinear Media. Sov. J. Exp. Theor. Phys. 1972, 34, 62. [Google Scholar]
- Chabchoub, A.; Onorato, M.; Akhmediev, N. Hydrodynamic Envelope Solitons and Breathers. In Rogue and Shock Waves in Nonlinear Dispersive Media; Onorato, M., Resitori, S., Baronio, F., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 55–87. ISBN 978-3-319-39214-1. [Google Scholar]
- Slunyaev, A.V. Analysis of the Nonlinear Spectrum of Intense Sea Wave with the Purpose of Extreme Wave Prediction. Radiophys. Quantum Electron. 2018, 61, 1–21. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Korneev, V.I. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 1986, 69, 1089–1093. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Taki, M. Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 2009, 373, 675–678. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Mussot, A.; Chabchoub, A.; Dias, F. Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 2019, 1, 675–689. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Chekhovskoy, I.S.; Fedoruk, M.P. Nonlinear Fourier transform for characterization of the coherent structures in optical microresonators. Opt. Lett. 2020, 45, 3059–3062. [Google Scholar] [CrossRef]
- Chekhovskoy, I.S.; Shtyrina, O.V.; Fedoruk, M.P.; Medvedev, S.B.; Turitsyn, S.K. Nonlinear Fourier Transform for Analysis of Coherent Structures in Dissipative Systems. Phys. Rev. Lett. 2019, 122, 153901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suret, P.; Tikan, A.; Bonnefoy, F.; Copie, F.; Ducrozet, G.; Gelash, A.; Prabhudesai, G.; Michel, G.; Cazaubiel, A.; Falcon, E.; et al. Nonlinear Spectral Synthesis of Soliton Gas in Deep-Water Surface Gravity Waves. Phys. Rev. Lett. 2020, 125, 264101. [Google Scholar] [CrossRef]
- Sun, Y.-H. Soliton synchronization in the focusing nonlinear Schrödinger equation. Phys. Rev. E 2016, 93, 052222. [Google Scholar] [CrossRef]
- Bonnefoy, F.; Tikan, A.; Copie, F.; Suret, P.; Ducrozet, G.; Prabhudesai, G.; Michel, G.; Cazaubiel, A.; Falcon, E.; El, G.; et al. From modulational instability to focusing dam breaks in water waves. Phys. Rev. Fluids 2020, 5, 034802. [Google Scholar] [CrossRef] [Green Version]
- Clamond, D.; Grue, J. Interaction between envelope solitons as a model for freak wave formations. Part I: Long time interaction. Comptes Rendus Mécanique 2002, 330, 575–580. [Google Scholar] [CrossRef]
- Dyachenko, A.I.; Zakharov, V.E. On the formation of freak waves on the surface of deep water. JETP Lett. 2008, 88, 307–311. [Google Scholar] [CrossRef]
- Slunyaev, A.V. Numerical simulation of “limiting” envelope solitons of gravity waves on deep water. J. Exp. Theor. Phys. 2009, 109, 676–686. [Google Scholar] [CrossRef]
- Slunyaev, A.; Clauss, G.F.; Klein, M.; Onorato, M. Simulations and experiments of short intense envelope solitons of surface water waves. Phys. Fluids 2013, 25, 067105. [Google Scholar] [CrossRef] [Green Version]
- Slunyaev, A.; Klein, M.; Clauss, G.F. Laboratory and numerical study of intense envelope solitons of water waves: Generation, reflection from a wall, and collisions. Phys. Fluids 2017, 29, 47103. [Google Scholar] [CrossRef] [Green Version]
- Ducrozet, G.; Slunyaev, A.V.; Stepanyants, Y.A. Transformation of envelope solitons on a bottom step. Phys. Fluids 2021, 33, 066606. [Google Scholar] [CrossRef]
- Viotti, C.; Dutykh, D.; Dudley, J.; Dias, F. Emergence of coherent wave groups in deep-water random sea. Phys. Rev. E 2013, 87, 063001. [Google Scholar] [CrossRef] [Green Version]
- Cazaubiel, A.; Michel, G.; Lepot, S.; Semin, B.; Aumaître, S.; Berhanu, M.; Bonnefoy, F.; Falcon, E. Coexistence of solitons and extreme events in deep water surface waves. Phys. Rev. Fluids 2018, 3, 114802. [Google Scholar] [CrossRef] [Green Version]
- West, B.J.; Brueckner, K.A.; Janda, R.S.; Milder, D.M.; Milton, R.L. A new numerical method for surface hydrodynamics. J. Geophys. Res. Ocean. 1987, 92, 11803–11824. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Le Touzé, D.; Ferrant, P. A modified High-Order Spectral method for wavemaker modeling in a numerical wave tank. Eur. J. Mech. B/Fluids 2012, 34, 19–34. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Le Touzé, D.; Ferrant, P. HOS-ocean: Open-source solver for nonlinear waves in open ocean based on High-Order Spectral method. Comput. Phys. Commun. 2016, 203, 245–254. [Google Scholar] [CrossRef] [Green Version]
- Dommermuth, D.G.; Yue, D.K.P. A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 1987, 184, 267–288. [Google Scholar] [CrossRef]
- Gouin, M.; Ducrozet, G.; Ferrant, P. Development and validation of a non-linear spectral model for water waves over variable depth. Eur. J. Mech. B/Fluids 2016, 57, 115–128. [Google Scholar] [CrossRef] [Green Version]
- Bonnefoy, F.; Le Touzé, D.; Ferrant, P. Generation of fully-nonlinear prescribed wave fields using a high-order spectral model. In Proceedings of the International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004; Volume 1, pp. 257–263. [Google Scholar]
- Bonnefoy, F.; Le Touzé, D.; Ferrant, P. A fully-spectral 3D time-domain model for second-order simulation of wavetank experiments. Part A: Formulation, implementation and numerical properties. Appl. Ocean Res. 2006, 28, 33–43. [Google Scholar] [CrossRef]
- Li, J.-X.; Li, P.-F.; Liu, S.-X. Observations of freak waves in random wave field in 2D experimental wave flume. China Ocean Eng. 2013, 27, 659–670. [Google Scholar] [CrossRef]
- Huang, N.E.; Long, S.R.; Tung, C.-C.; Donelan, M.A.; Yuan, Y.; Lai, R.J. The local properties of ocean surface waves by the phase-Time method. Geophys. Res. Lett. 1992, 19, 685–688. [Google Scholar] [CrossRef]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Feir, J.E. Discussion: Some results from wave pulse experiments. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 299, 54–58. [Google Scholar] [CrossRef]
- Lo, E.; Mei, C.C. A numerical study of water-wave modulation based on a higher-order nonlinear Schrödinger equation. J. Fluid Mech. 1985, 150, 395–416. [Google Scholar] [CrossRef]
- Michel, G.; Bonnefoy, F.; Ducrozet, G.; Prabhudesai, G.; Cazaubiel, A.; Copie, F.; Tikan, A.; Suret, P.; Randoux, S.; Falcon, E. Emergence of Peregrine solitons in integrable turbulence of deep water gravity waves. Phys. Rev. Fluids 2020, 5, 082801. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Gibson, R.; Swan, C. The evolution of large ocean waves: The role of local and rapid spectral changes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 21–48. [Google Scholar] [CrossRef]
- Ma, Y.; Dong, G.; Liu, S.; Zang, J.; Li, J.; Sun, Y. Laboratory Study of Unidirectional Focusing Waves in Intermediate Depth Water. J. Eng. Mech. 2010, 136, 78–90. [Google Scholar] [CrossRef]
- Dong, G.; Liao, B.; Ma, Y.; Perlin, M. Experimental investigation of the Peregrine Breather of gravity waves on finite water depth. Phys. Rev. Fluids 2018, 3, 064801. [Google Scholar] [CrossRef]
- Donelan, M.A.; Drennan, W.M.; Magnusson, A.K. Nonstationary Analysis of the Directional Properties of Propagating Waves. J. Phys. Oceanogr. 1996, 26, 1901–1914. [Google Scholar] [CrossRef] [Green Version]




| Hs (m) | Tp (s) | kph | ε = kpHs/2 | γ | Δf/fp | |
|---|---|---|---|---|---|---|
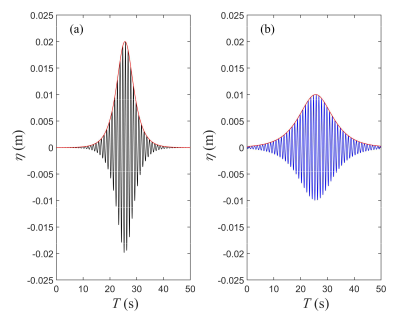
| Case A | 0.064 | 1.0 | 4.82 | 0.12 | 3.3 | 0.10 |
| Case B | 0.03 | 1.0 | 4.82 | 0.06 | 7.0 | 0.07 |
| M = 1 | M = 2 | M = 3 | M = 6 | ||
|---|---|---|---|---|---|
| Soliton 1 | Asol (m) | 0.0196 | 0.0207 | 0.0225 | 0.0225 |
| L/Lp | 45.8 | 49.8 | 67.3 | 67.3 | |
| Soliton 2 | Asol (m) | 0.0268 | 0.0277 | 0.0285 | 0.0285 |
| L/Lp | 13.2 | 14.5 | 15.6 | 15.6 | |
| Soliton 3 | Asol (m) | 0.0293 | 0.0334 | 0.0404 | 0.0404 |
| L/Lp | 20.9 | 22.7 | 32.2 | 32.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, W.; Ma, Y.; Dong, G.; Zhang, J.; Ma, X. Emergence of Solitons from Irregular Waves in Deep Water. J. Mar. Sci. Eng. 2021, 9, 1369. https://doi.org/10.3390/jmse9121369
Xia W, Ma Y, Dong G, Zhang J, Ma X. Emergence of Solitons from Irregular Waves in Deep Water. Journal of Marine Science and Engineering. 2021; 9(12):1369. https://doi.org/10.3390/jmse9121369
Chicago/Turabian StyleXia, Weida, Yuxiang Ma, Guohai Dong, Jie Zhang, and Xiaozhou Ma. 2021. "Emergence of Solitons from Irregular Waves in Deep Water" Journal of Marine Science and Engineering 9, no. 12: 1369. https://doi.org/10.3390/jmse9121369
APA StyleXia, W., Ma, Y., Dong, G., Zhang, J., & Ma, X. (2021). Emergence of Solitons from Irregular Waves in Deep Water. Journal of Marine Science and Engineering, 9(12), 1369. https://doi.org/10.3390/jmse9121369






