Geoacoustic Estimation of the Seafloor Sound Speed Profile in Deep Passive Margin Setting Using Standard Multichannel Seismic Data
Abstract
:1. Introduction
1.1. Methods for Estimating the Sound Speed in the Seafloor
1.2. Sound Speed Models of the Sub-Bottom Layers
1.3. The Study Site
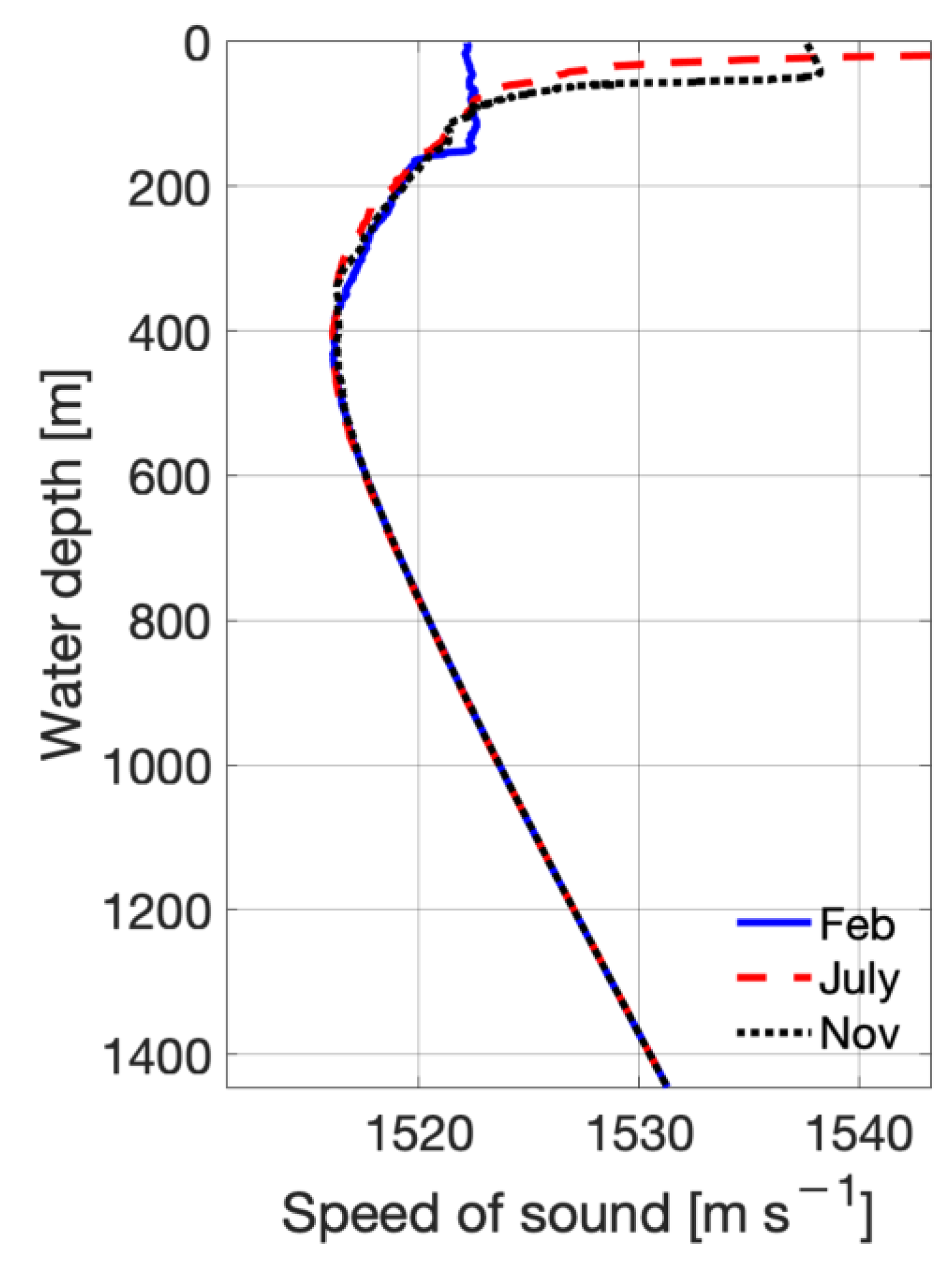
2. The Experimental Data
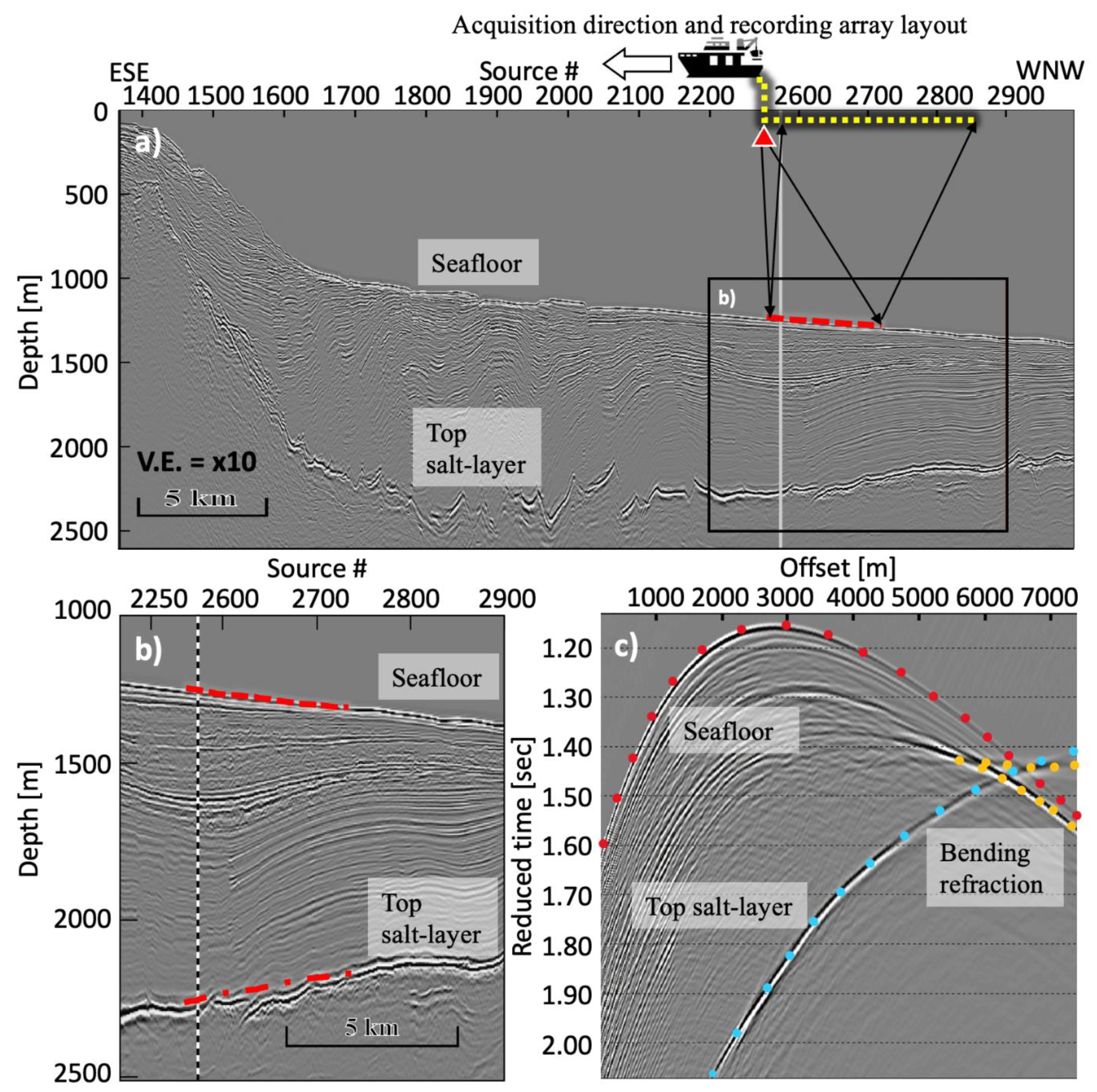
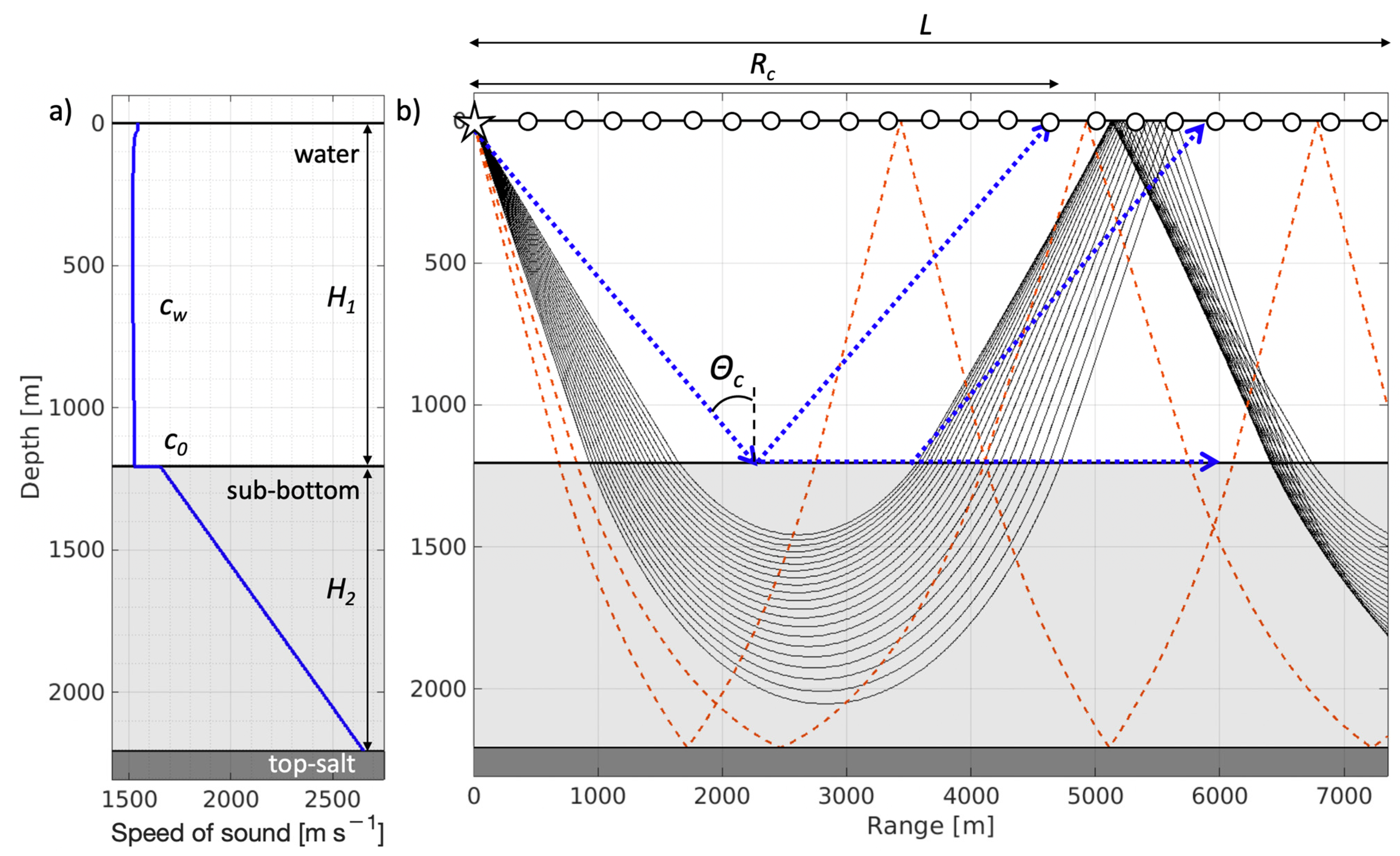
2.1. Methodology for Seafloor Sound Speed Estimation Based on Travel Times Matching
2.2. Constant Sound Speed in the Water Layer
2.3. Constant Sound Speed in the Water and a Constant Velocity Gradient in the Sub-Bottom Layer
2.4. Stratified Water and a Constant Velocity Gradient in the Sub-Bottom Layer
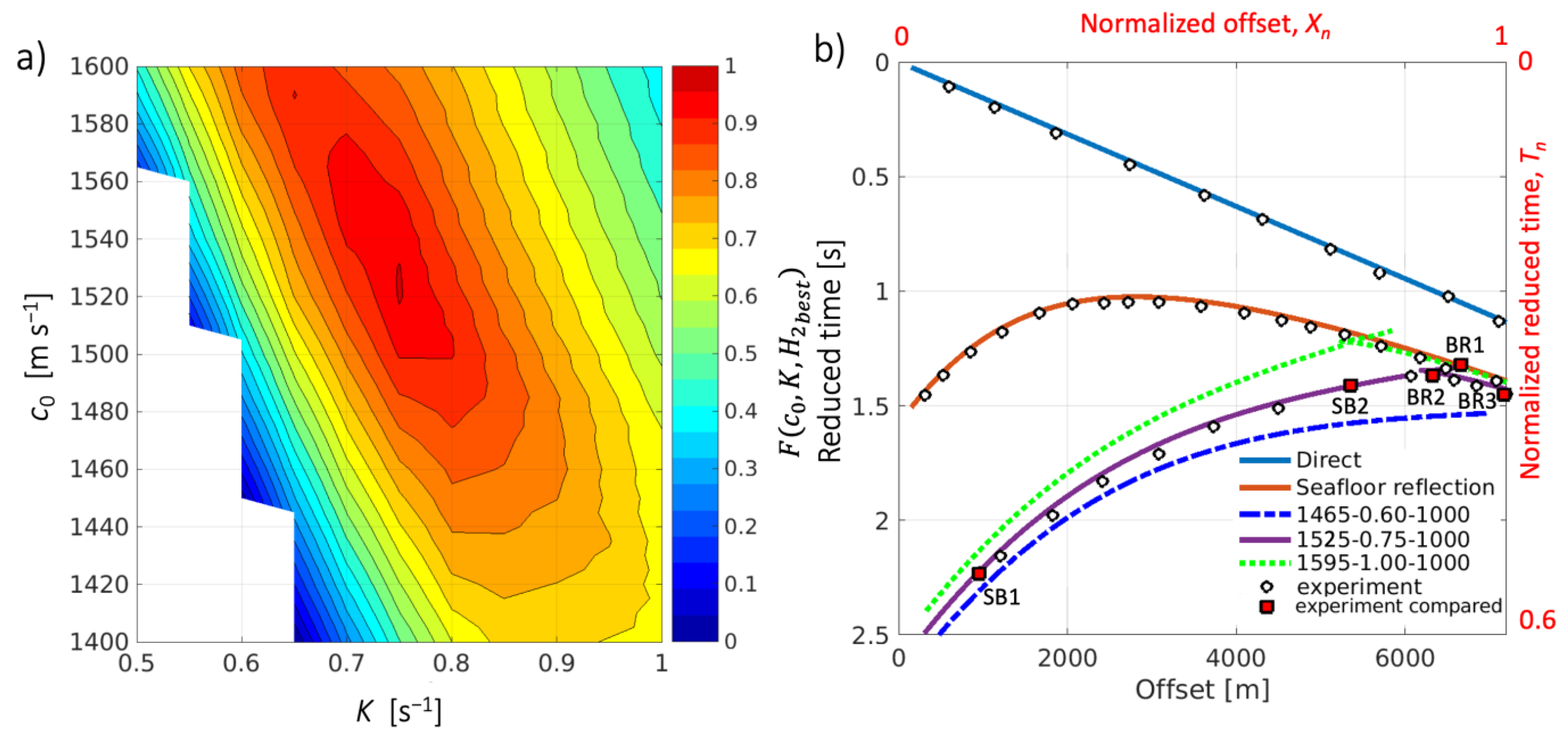
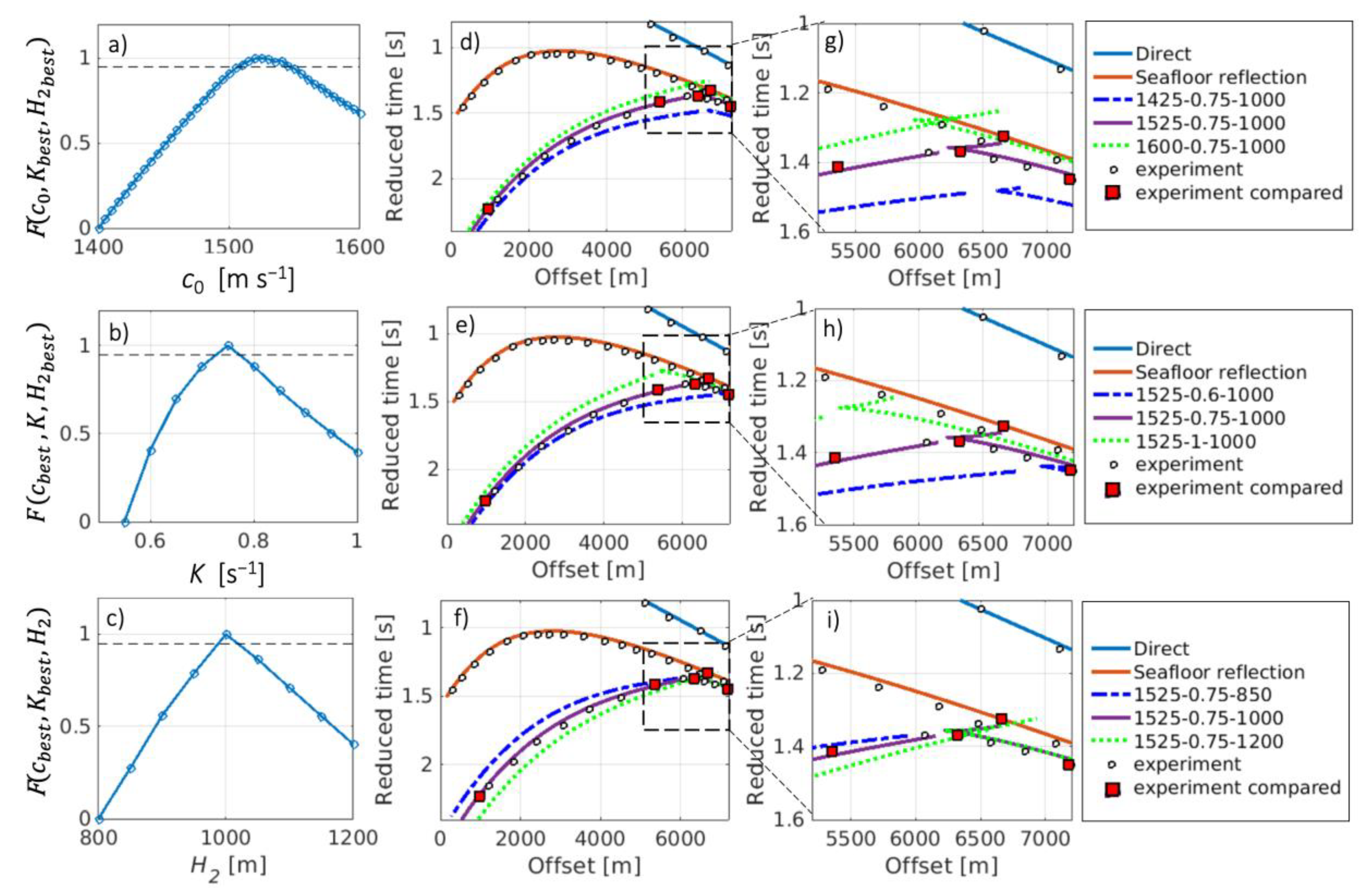
2.5. The Geoacoustic Inversion Procedure
2.6. Validating the Sound-Speed Estimations through Caustic Amplitude Modeling
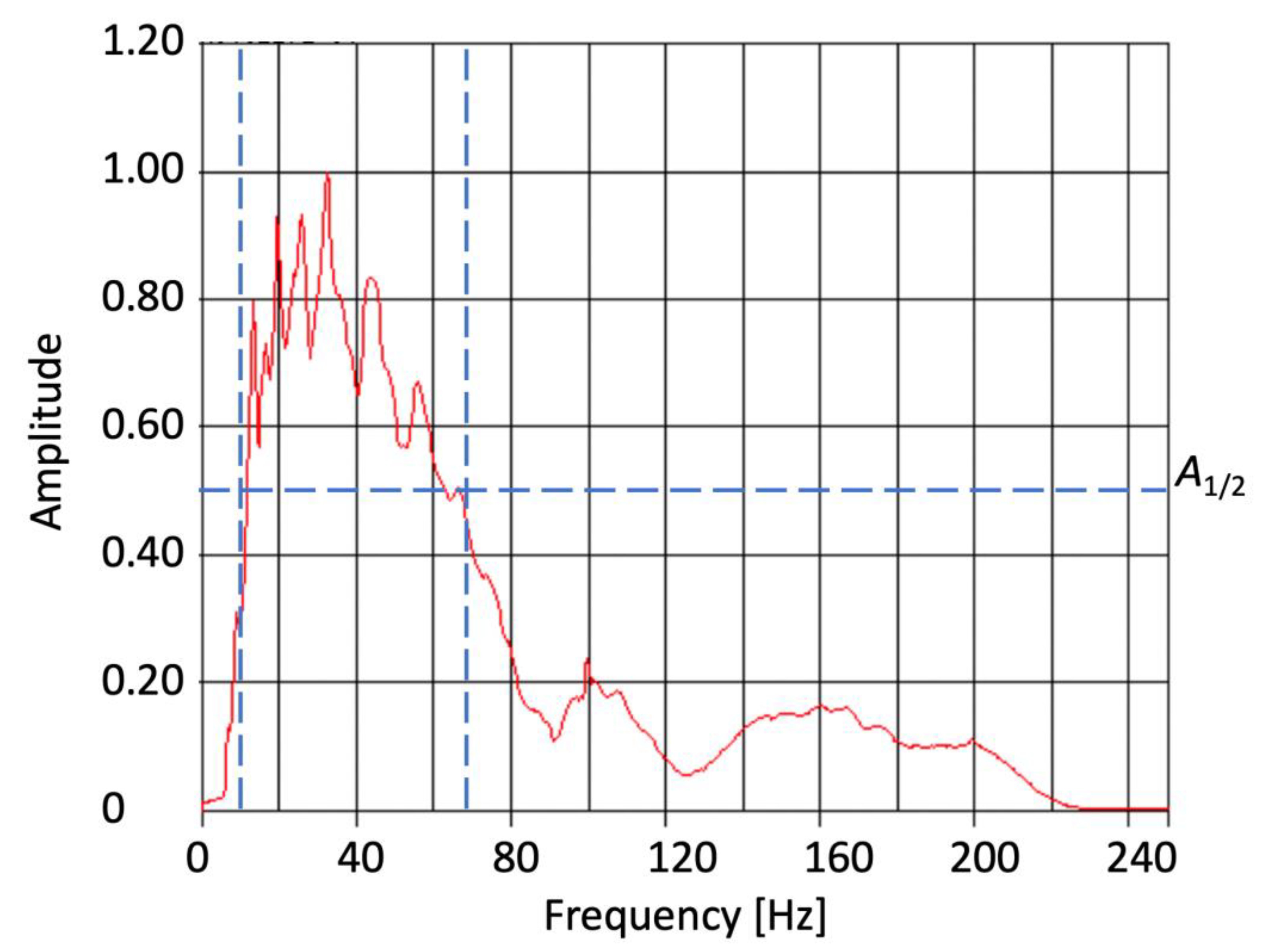
2.7. The Ricker Wavelet
2.8. Modeling of a Synthetic Source Gather
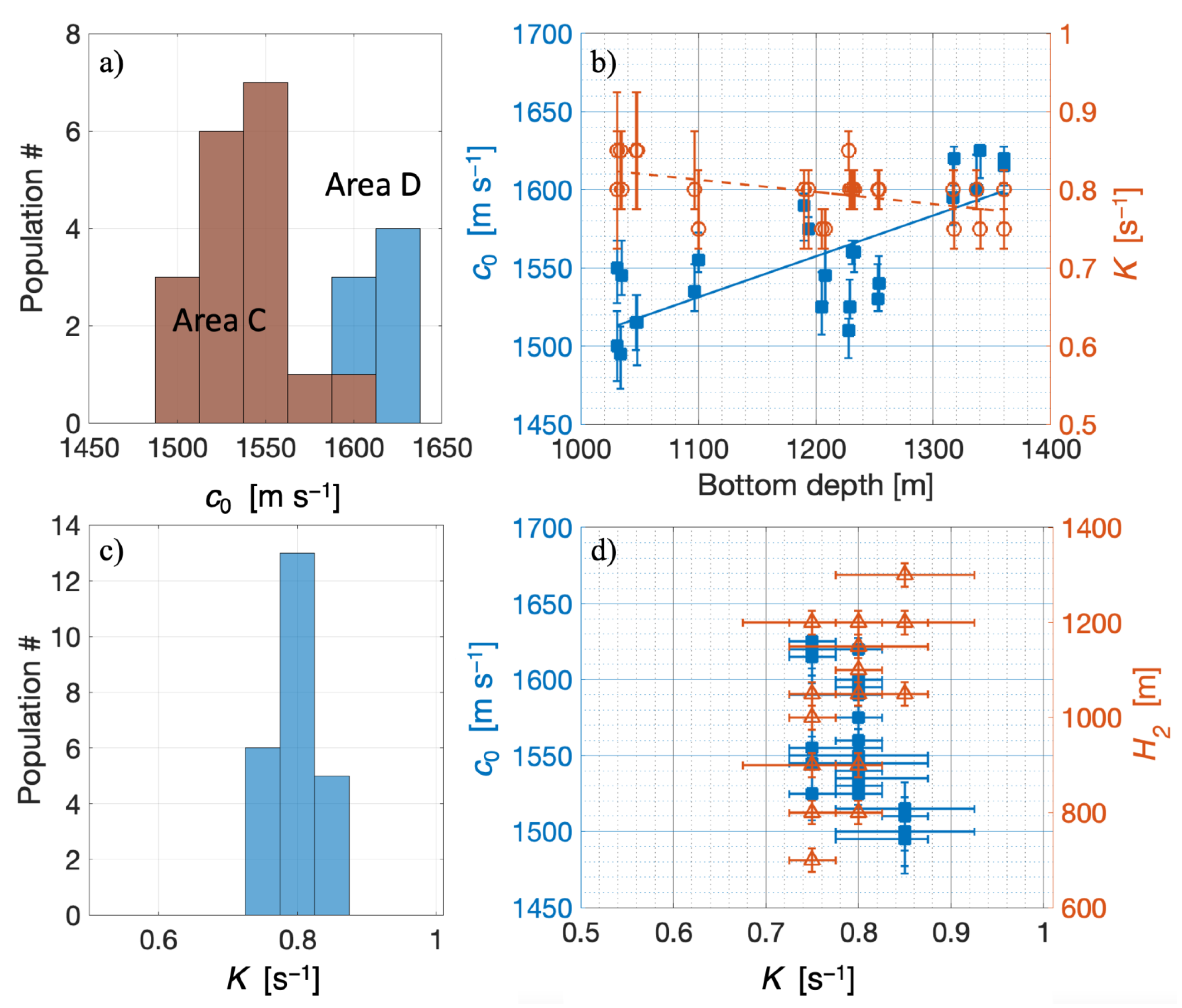
3. Inversion Results
4. Discussion
4.1. Advantages and Constraints of Our Estimation Methodology
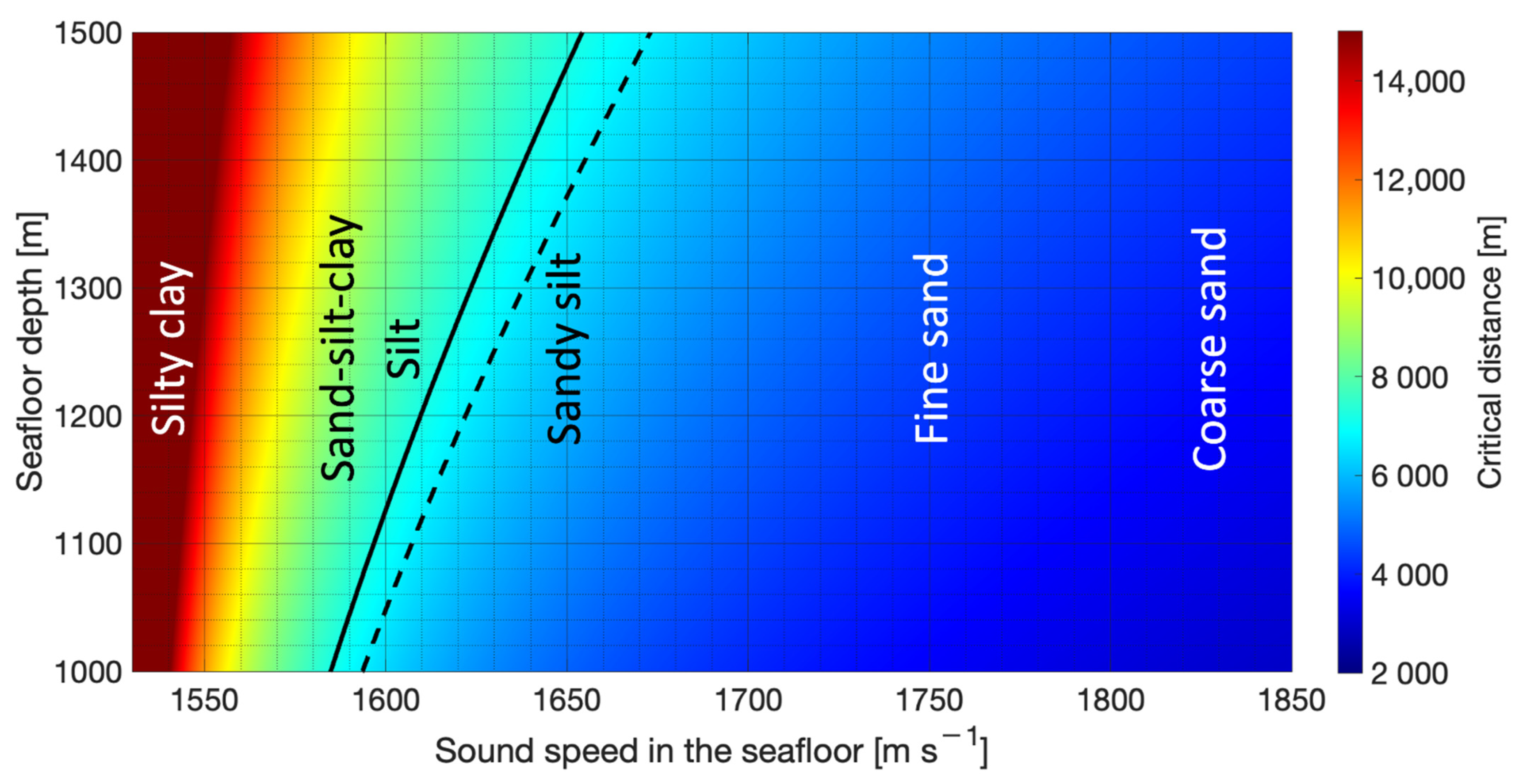
4.2. Effect of Sediment Porosity on Sound Speed and Density
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rajan, S.D.; Frisk, G.V. Seasonal variations of the sediment compressional wave-speed profile in the Gulf of Mexico. J. Acoust. Soc. Am. 1992, 91, 127–135. [Google Scholar] [CrossRef]
- Fu, S.S.; Wilkens, R.H.; Frazer, L.N. Acoustic lance: New in situ seafloor velocity profiles. J. Acoust. Soc. Am. 1996, 99, 234–242. [Google Scholar] [CrossRef]
- Katsnelson, B.; Katsman, R.; Lunkov, A.; Ostrovsky, I. Acoustical methodology for determination of gas content in aquatic sediments, with application to Lake Kinneret, Israel, as a case study. Limnol. Oceanogr. Methods 2017, 15, 531–541. [Google Scholar] [CrossRef]
- Katsnelson, B.; Lunkov, A.; Ostrovsky, I.; Uzhansky, E. Estimation of gassy sediment parameters from measurements of angular and frequency dependencies of reflection coefficient. Proc. Meet. Acoust. 2018, 33, 005004. [Google Scholar] [CrossRef]
- Katsnelson, B.; Lunkov, A.; Ostrovsky, I.; Uzhansky, E. Characterization of gassy layer of sediment in shallow water using acoustical method. Lake Kinneret as a case study. Environ. Sci. Technol. Sumbitted.
- Lunkov, A.A.; Katsnelson, B.G. Using discrete low-frequency components of shipping noise for gassy sediment characterization in shallow water. J. Acoust. Soc. Am. 2020, 147, EL428–EL433. [Google Scholar] [CrossRef]
- Uzhansky, E.; Katsnelson, B.; Lunkov, A.; Ostrovsky, I. Spatial and temporal variability of free gas content in shallow sediments: Lake Kinneret as a case study. Geo-Marine Lett. 2020, 40, 491–505. [Google Scholar] [CrossRef]
- Haque, K.F.; Kabir, K.H.; Abdelgawad, A. Advancement of routing protocols and applications of Underwater Wireless Sensor Network (UWSN)-A survey. J. Sens. Actuator Netw. 2020, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- Alfouzan, F.A. Energy-efficient collision avoidance mac protocols for underwater sensor networks: Survey and challenges. J. Mar. Sci. Eng. 2021, 9, 741. [Google Scholar] [CrossRef]
- Hamilton, E.L.; Bachman, R.T. Sound velocity and related properties of marine sediments. J. Acoust. Soc. Am. 1982, 72, 1891–1904. [Google Scholar] [CrossRef]
- Birch, F. Seismology and Earth Structure, 1952. Available online: https://csim.kaust.edu.sa/files/ErSE210/Refraction.pdf (accessed on 2 November 2021).
- Kim, D.-C.; Kim, G.-Y.; Jung, J.-H.; Seo, Y.-K.; Wilkens, R.H.; Yoo, D.-G.; Lee, G.-H.; Kim, J.-C.; Yi, H.-I.; Cifci, G. Laboratory/In Situ Sound Velocities of Shelf Sediments in the South Sea of Korea. Fish. Aquat. Sci. 2008, 11, 103–112. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Stoll, R.D. Marine sediment acoustics. J. Acoust. Soc. Am. 1985, 77, 1789–1799. [Google Scholar] [CrossRef]
- Chotiros, N.P.; Isakson, M.J. A broadband model of sandy ocean sediments: Biot-Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am. 2004, 116, 2011–2022. [Google Scholar] [CrossRef] [Green Version]
- Buckingham, M.J. On pore-fluid viscosity and the wave properties of saturated granular materials including marine sediments. J. Acoust. Soc. Am. 2007, 122, 1486–1501. [Google Scholar] [CrossRef] [Green Version]
- Robb, G.B.N.; Best, A.I.; Dix, J.K.; White, P.R.; Leighton, T.G.; Bull, J.M.; Harris, A. Measurement of the in situ compressional wave properties of marine sediments. IEEE J. Ocean. Eng. 2007, 32, 484–496. [Google Scholar] [CrossRef]
- Buckingham, M.J.; Richardson, M.D. On tone-burst measurements of sound speed and attenuation in sandy marine sediments. IEEE J. Ocean. Eng. 2002, 27, 429–453. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Tang, D.; Williams, K.L. Direct measurement of sediment sound speed in Shallow Water’06. J. Acoust. Soc. Am. 2008, 124, EL116–EL121. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Kim, G.; Seo, Y.; Ha, D.; Ha, I.; Yoon, Y.; Kim, J. Automated Velocity Measurement Technique for Unconsolidated Marine Sediment. Sea 1999, 4, 400–404. [Google Scholar]
- Akal, T. The relationship between the physical properties of underwater sediments that affect bottom reflection. Mar. Geol. 1972, 13, 251–266. [Google Scholar] [CrossRef]
- Ostrovsky, I.; Tegowski, J. Hydroacoustic analysis of spatial and temporal variability of bottom sediment characteristics in Lake Kinneret in relation to water level fluctuation. Geo-Marine Lett. 2010, 30, 261–269. [Google Scholar] [CrossRef]
- van Walree, P.A.; Tęgowski, J.; Laban, C.; Simons, D.G. Acoustic seafloor discrimination with echo shape parameters: A comparison with the ground truth. Cont. Shelf Res. 2005, 25, 2273–2293. [Google Scholar] [CrossRef]
- Godin, O.A.; Chapman, N.R.; Laidlaw, M.C.A.; Hannay, D.E. Head wave data inversion for geoacoustic parameters of the ocean bottom off Vancouver Island. J. Acoust. Soc. Am. 1999, 106, 2540–2551. [Google Scholar] [CrossRef]
- Holland, C.W.; Osler, J. High-resolution geoacoustic inversion in shallow water: A joint time- and frequency-domain technique. J. Acoust. Soc. Am. 2000, 107, 1263–1279. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, F. Geoacoustic inversion for sediments in the South China Sea based on a hybrid inversion scheme. Chin. J. Oceanol. Limnol. 2010, 28, 990–995. [Google Scholar] [CrossRef]
- Baggeroer, A.B.; Kuperman, W.A.; Mikhalevsky, P.N. An overview of matched field methods in ocean acoustics. IEEE J. Ocean. Eng. 1993, 18, 401–424. [Google Scholar] [CrossRef]
- Siderius, M.; Harrison, C.H.; Porter, M.B. A passive fathometer technique for imaging seabed layering using ambient noise. J. Acoust. Soc. Am. 2006, 120, 1315–1323. [Google Scholar] [CrossRef] [Green Version]
- Godin, O.A.; Katsnelson, B.G.; Qin, J.; Brown, M.G.; Zabotin, N.A.; Zang, X. Application of time reversal to passive acoustic remote sensing of the ocean. Acoust. Phys. 2017, 63, 309–320. [Google Scholar] [CrossRef]
- Qin, J.X.; Katsnelson, B.; Godin, O.; Li, Z.L. Geoacoustic Inversion Using Time Reversal of Ocean Noise. Chin. Phys. Lett. 2017, 34, 094301. [Google Scholar] [CrossRef]
- Tõth, Z.; Spiess, V.; Mogollõn, J.M.; Jensen, J.B. Estimating the free gas content in Baltic Sea sediments using compressional wave velocity from marine seismic data. J. Geophys. Res. 2014, 119, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Cerveny, V.; Ravindra, R. Theory of Seismic Head Waves; University of Toronto Press: Toronto, ON, Canada, 1971; ISBN 9789896540821. [Google Scholar]
- Hall, M.V. Measurement of seabed sound speeds from head waves in shallow water. IEEE J. Ocean. Eng. 1996, 21, 413–422. [Google Scholar] [CrossRef]
- Ewing, J.I.; Purdy, G.M. Upper crustal velocity structure in the ROSE area of trh east pacific rise. J. Geophys. Res. 1982, 87, 8397. [Google Scholar] [CrossRef]
- Stephen, R.A. Travel-time curves for a simple sea floor model. Mar. Geophys. Res. 1982, 5, 315–326. [Google Scholar] [CrossRef]
- Brekhovskikh, L.; Lysanov, Y. Fundamentals of Ocean Acoustics; Springer: Berlin, Germany, 1991; ISBN 3540113053. [Google Scholar]
- Holland, C.W.; Hollett, R.; Troiano, L. Measurement technique for bottom scattering in shallow water. J. Acoust. Soc. Am. 2000, 108, 997. [Google Scholar] [CrossRef]
- Holland, C.W.; Neumann, P. Sub-bottom scattering: A modeling approach. J. Acoust. Soc. Am. 1998, 104, 1363–1373. [Google Scholar] [CrossRef]
- Jensen, F.; Kuperman, W.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: Berlin, Germany, 2011; ISBN 9781441986771. [Google Scholar]
- Al-Chalabi, M. Parameter nonuniqueness in velocity versus depth functions. Geophysics 1997, 62, 970–979. [Google Scholar] [CrossRef]
- Dix, C.H. Seismic velocities from surface measurements. Geophysics 1955, 20, 68–86. [Google Scholar] [CrossRef]
- Slotnick, M.M. On seismic computations, with applications, I. Geophysics 1936, 1, 9–22. [Google Scholar] [CrossRef]
- Hamilton, E.L. Sound velocity gradients in marine sediments. J. Acoust. Soc. Am. 1979, 65, 909–922. [Google Scholar] [CrossRef]
- Ravve, I.; Koren, Z. Exponential asymptotically bounded velocity model: Part I—Effective models and velocity transformations. Geophysics 2006, 71, T53–T65. [Google Scholar] [CrossRef]
- Hamilton, E.L. Geoacoustic modeling of the sea floor. J. Acoust. Soc. Am. 1980, 68, 1313–1340. [Google Scholar] [CrossRef]
- Al-Chalabi, M. Instantaneous slowness versus depth functions. Geophysics 1997, 62, 270–273. [Google Scholar] [CrossRef]
- Garfunkel, Z. Origin of the Eastern Mediterranean basin: A reevaluation. Tectonophysics 2004, 391, 11–34. [Google Scholar] [CrossRef]
- Meilijson, A.; Hilgen, F.; Sepúlveda, J.; Steinberg, J.; Fairbank, V.; Flecker, R.; Waldmann, N.D.; Spaulding, S.A.; Bialik, O.M.; Boudinot, F.G.; et al. Chronology with a pinch of salt: Integrated stratigraphy of Messinian evaporites in the deep Eastern Mediterranean reveals long-lasting halite deposition during Atlantic connectivity. Earth-Sci. Rev. 2019, 194, 374–398. [Google Scholar] [CrossRef]
- Zucker, E.; Gvirtzman, Z.; Granjeon, D.; Garcia-Castellanos, D.; Enzel, Y. The accretion of the Levant continental shelf alongside the Nile Delta by immense margin-parallel sediment transport. Mar. Pet. Geol. 2021, 126, 104876. [Google Scholar] [CrossRef]
- Tibor, G.; Ben-Avraham, Z.; Steckler, M.; Fligelman, H. Late Tertiary subsidence history of the southern Levant Margin, eastern Mediterranean Sea, and its implications to the understanding of the Messinian Event. J. Geophys. Res. 1992, 97, 17593–17614. [Google Scholar] [CrossRef]
- Buchbinder, B.; Zilberman, E. Sequence stratigraphy of Miocene-Pliocene carbonate-siliciclastic shelf deposits in the eastern Mediterranean margin (Israel): Effects of eustasy and tectonics. Sediment. Geol. 1997, 112, 7–32. [Google Scholar] [CrossRef]
- Hecht, A.; Pinardi, N.; Robinson, A.R. Currents, Water Masses, Eddies and Jets in the Mediterranean Levantine Basin. J. Phys. Oceanogr. 1988, 18, 1320–1353. [Google Scholar] [CrossRef] [Green Version]
- Uzhansky, E.; Gadol, O.; Lang, G.; Katsnelson, B.; Copel, S.; Kazaz, T.; Makovsky, Y. Using a kilometers-long horizontal multichannel array for estimating seafloor sound speed in a passive margin setting. Proc. Meet. Acoust. 2021, 44, 005002. [Google Scholar]
- Reich, T.; Ben-Ezra, T.; Belkin, N.; Tsemel, A.; Aharonovich, D.; Roth-Rosenberg, D.; Givati, S.; Bialik, O.; Herut, B.; Berman-Frank, I.; et al. Seasonal dynamics of phytoplankton and bacterioplankton at the ultra-oligotrophic southeastern Mediterranean Sea. bioRxiv 2021. [Google Scholar] [CrossRef]
- Chen, C.T.; Millero, F.J. Speed of sound in seawater at high pressures. J. Acoust. Soc. Am. 1977, 62, 1129–1135. [Google Scholar] [CrossRef]
- Nettleton, L.L. Geophysical Prospecting for Oil; McGraw Hill Education: New York, NY, USA, 1940. [Google Scholar]
- Porter, M.B. The BELLHOP Manual and User’s Guide: Preliminary Draft; Heat, Light, and Sound Research, Inc: La Jolla, CA, USA, 2011; pp. 1–57. [Google Scholar]
- Collins, M.D.; Lingevitch, J.F.; Calvo, D.C. Fast and Accurate Seismic Computations in Laterally Varying Environments. IEEE Access 2021, 9, 103258–103265. [Google Scholar] [CrossRef]
- Collins, M.D.; Siegmann, W.L. Parabolic Equation Techniques for Seismology, Seismo-Acoustics, and Arctic Acoustics. J. Theor. Comput. Acoust. 2021, 29, 1–21. [Google Scholar] [CrossRef]
- Ricker, N. Wavelet functions and their polynomials. Geophysics 1944, 9, 314–323. [Google Scholar] [CrossRef]
- Ricker, N. The form and laws of propagation of seismic wavelets. Geophysics 1953, 18, 10–40. [Google Scholar] [CrossRef]
- Hosken, J.W.J. Ricker wavelets in their various guises. First Break 1988, 6. [Google Scholar] [CrossRef]
- Wang, Y. Frequencies of the Ricker wavelet. Geophysics 2015, 80, A31–A37. [Google Scholar] [CrossRef] [Green Version]
- Collins, M.D. User’s Guide for RAM Versions; Naval Research Laboratory: Washington, DC, USA, 1999. [Google Scholar]
- Collins, M.D. The stabilized self-starter. J. Acoust. Soc. Am. 1999, 106, 1724–1726. [Google Scholar] [CrossRef]
- Dragoset, B. Introduction to air guns and air-gun arrays. Lead. Edge 2000, 19, 892–897. [Google Scholar] [CrossRef]
- Caldwell, J.; Dragoset, W. A Brief Overview of Seismic air-gun arrays. Lead. Edge 2000, 19, 898–902. [Google Scholar] [CrossRef] [Green Version]
- Faust, L.Y. A velocity function including lithologic variation. Geophysics 1953, 18, 271–288. [Google Scholar] [CrossRef]
- Robein, E. Velocities, Time-Imaging and Depth-Imaging in Reflection Seismics: Principles and Methods; EAGE Publications: Houten, The Netherlands, 2003. [Google Scholar]
- Brekhovskikh, L. Waves in Layered Media; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Landa, E.; Thore, P.; Sorin, V.; Koren, Z. Interpretation of velocity estimates from coherency inversion. Geophysics 1991, 56, 1377–1383. [Google Scholar] [CrossRef]



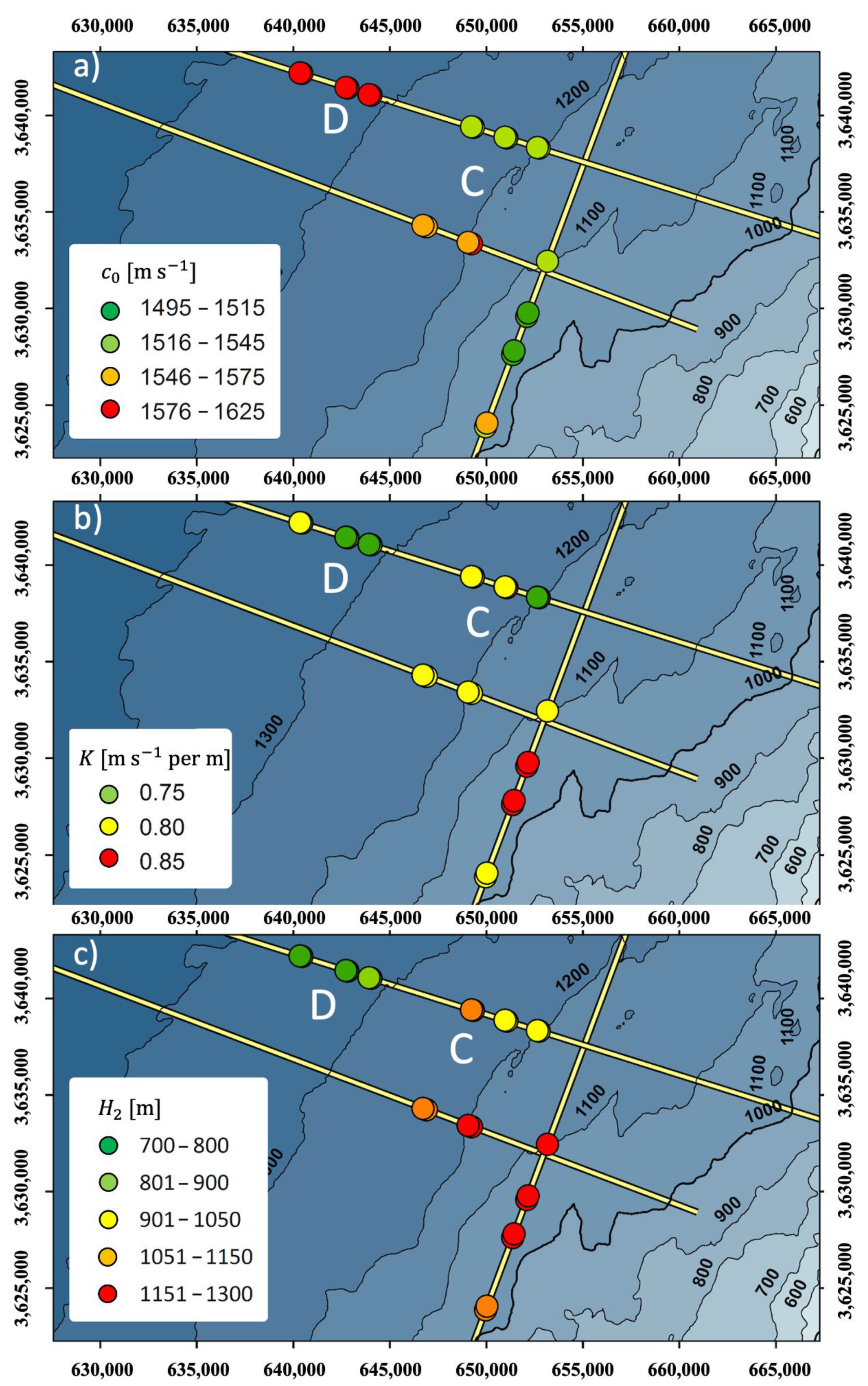
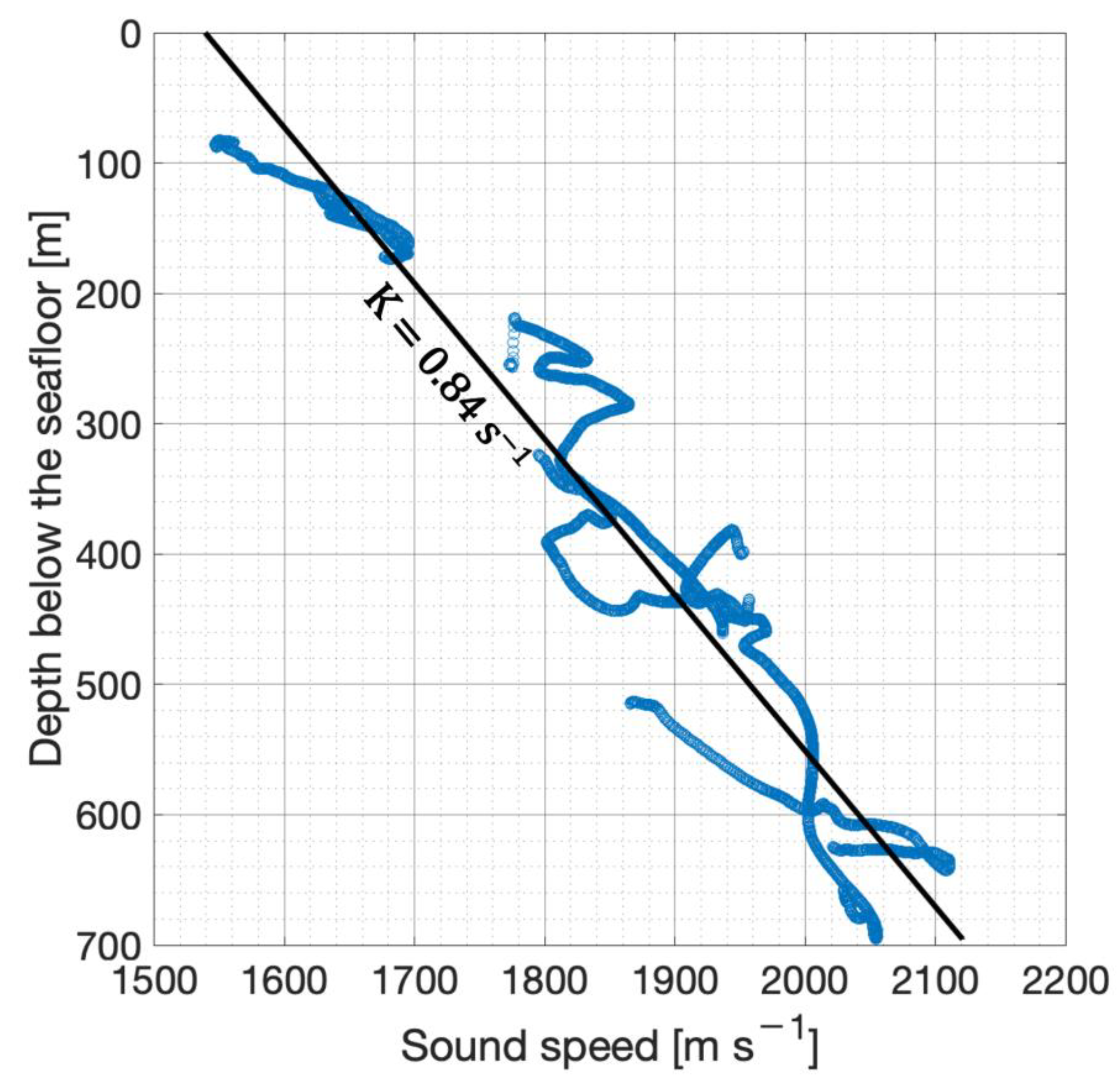

| Line Name | FFID # | x [m] | y [m] | [m] | [m s−1] | [m s−1] | [s−1] | [s−1] | [m] |
|---|---|---|---|---|---|---|---|---|---|
| EMED-00-003 | 2670 | 649,974 | 3,623,866 | 1035 | 1545 | 1535–1565 | 0.8 | 0.8–0.85 | 1150 |
| 2674 | 650,043 | 3,624,054 | 1031 | 1550 | 1530–1565 | 0.8 | 0.75–0.85 | 1150 | |
| 2750 | 651,373 | 3,627,613 | 1031 | 1500 | 1480–1520 | 0.85 | 0.8–0.9 | 1200 | |
| 2754 | 651,441 | 3,627,801 | 1034 | 1495 | 1475–1510 | 0.85 | 0.8–0.85 | 1200 | |
| 2792 | 652,106 | 3,629,580 | 1047 | 1515 | 1500–1530 | 0.85 | 0.8–0.9 | 1300 | |
| 2796 | 652,173 | 3,629,769 | 1048 | 1515 | 1490–1530 | 0.85 | 0.8–0.9 | 1300 | |
| 2853 | 653,171 | 3,632,438 | 1097 | 1535 | 1525–1550 | 0.8 | 0.8–0.85 | 1200 | |
| 2857 | 653,239 | 3,266,326 | 1100 | 1555 | 1550–1570 | 0.75 | 0.75–0.8 | 1200 | |
| EMED-00-054 | 351 | 649,245 | 3,633,347 | 1190 | 1590 | 1570–1595 | 0.8 | 0.75–0.8 | 1200 |
| 355 | 649,059 | 3,633,419 | 1194 | 1575 | 1565–1580 | 0.8 | 0.75–0.8 | 1200 | |
| 401 | 646,906 | 3,634,230 | 1231 | 1560 | 1555–1565 | 0.8 | 0.8–0.8 | 1100 | |
| 405 | 646,720 | 3,634,302 | 1233 | 1560 | 1550–1565 | 0.8 | 0.8–0.8 | 1100 | |
| ISEM-2073-108 | 2290 | 652,744 | 3,638,304 | 1205 | 1525 | 1510–1545 | 0.75 | 0.75–0.75 | 1000 |
| 2294 | 652,650 | 3,638,335 | 1208 | 1545 | 1530–1560 | 0.75 | 0.75–0.75 | 1050 | |
| 2360 | 651,076 | 3,638,831 | 1228 | 1510 | 1495–1515 | 0.85 | 0.85–0.85 | 1050 | |
| 2364 | 650,980 | 3,638,859 | 1229 | 1525 | 1520–1540 | 0.8 | 0.8–0.8 | 1050 | |
| 2433 | 649,333 | 3,639,371 | 1253 | 1530 | 1525–1550 | 0.8 | 0.8–0.8 | 1100 | |
| 2437 | 649,238 | 3,639,400 | 1254 | 1540 | 1525–1555 | 0.8 | 0.8–0.8 | 1100 | |
| ISEM-2073-109 | 2650 | 644,018 | 3,641,039 | 1317 | 1595 | 1580–1620 | 0.8 | 0.8–0.8 | 900 |
| 2654 | 643,922 | 3,641,067 | 1318 | 1620 | 1605–1625 | 0.75 | 0.75–0.8 | 900 | |
| 2700 | 642,825 | 3,641,410 | 1337 | 1600 | 1595–1620 | 0.8 | 0.8–0.8 | 800 | |
| 2704 | 642,730 | 3,641,441 | 1340 | 1625 | 1610–1625 | 0.75 | 0.75–0.75 | 800 | |
| 2800 | 640,444 | 3,642,168 | 1360 | 1615 | 1600–1625 | 0.75 | 0.75–0.75 | 700 | |
| 2804 | 640,348 | 3,642,197 | 1360 | 1620 | 1605–1625 | 0.8 | 0.8–0.8 | 800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzhansky, E.; Gadol, O.; Lang, G.; Katsnelson, B.; Copel, S.; Kazaz, T.; Makovsky, Y. Geoacoustic Estimation of the Seafloor Sound Speed Profile in Deep Passive Margin Setting Using Standard Multichannel Seismic Data. J. Mar. Sci. Eng. 2021, 9, 1423. https://doi.org/10.3390/jmse9121423
Uzhansky E, Gadol O, Lang G, Katsnelson B, Copel S, Kazaz T, Makovsky Y. Geoacoustic Estimation of the Seafloor Sound Speed Profile in Deep Passive Margin Setting Using Standard Multichannel Seismic Data. Journal of Marine Science and Engineering. 2021; 9(12):1423. https://doi.org/10.3390/jmse9121423
Chicago/Turabian StyleUzhansky, Ernst, Omri Gadol, Guy Lang, Boris Katsnelson, Shelly Copel, Tom Kazaz, and Yizhaq Makovsky. 2021. "Geoacoustic Estimation of the Seafloor Sound Speed Profile in Deep Passive Margin Setting Using Standard Multichannel Seismic Data" Journal of Marine Science and Engineering 9, no. 12: 1423. https://doi.org/10.3390/jmse9121423
APA StyleUzhansky, E., Gadol, O., Lang, G., Katsnelson, B., Copel, S., Kazaz, T., & Makovsky, Y. (2021). Geoacoustic Estimation of the Seafloor Sound Speed Profile in Deep Passive Margin Setting Using Standard Multichannel Seismic Data. Journal of Marine Science and Engineering, 9(12), 1423. https://doi.org/10.3390/jmse9121423







