Fatigue Characteristic of Designed T-Type Specimen under Two-Step Repeating Variable Amplitude Load with Low-Amplitude Load below the Fatigue Limit
Abstract
:1. Introduction
2. Experimental Setup
2.1. Material
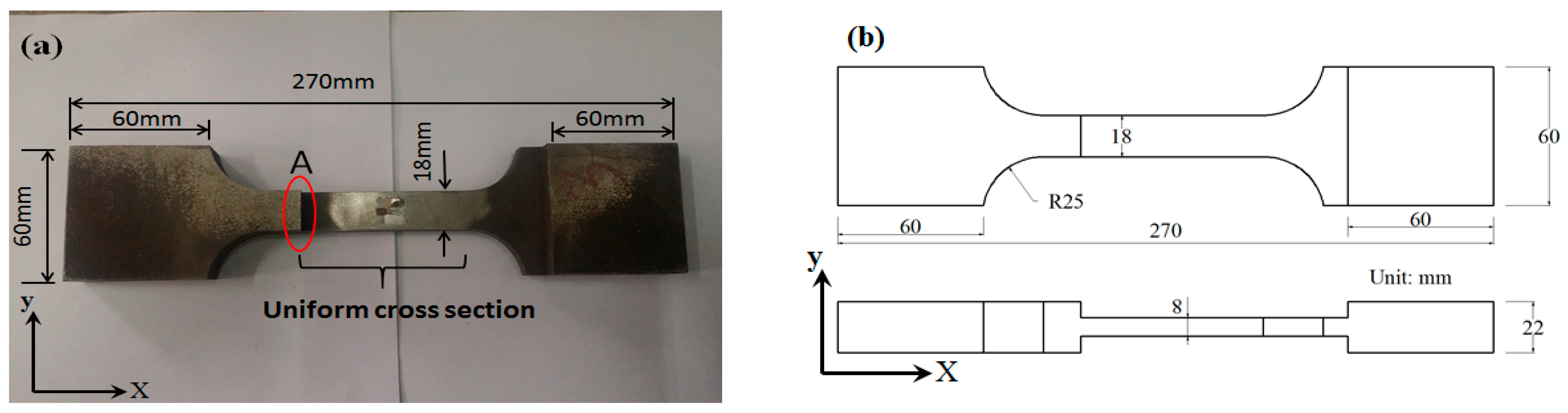
2.2. Designed T-Type Specimen
2.3. Strain Measurement
2.4. Fatigue Test
2.4.1. Constant Amplitude Fatigue Tests
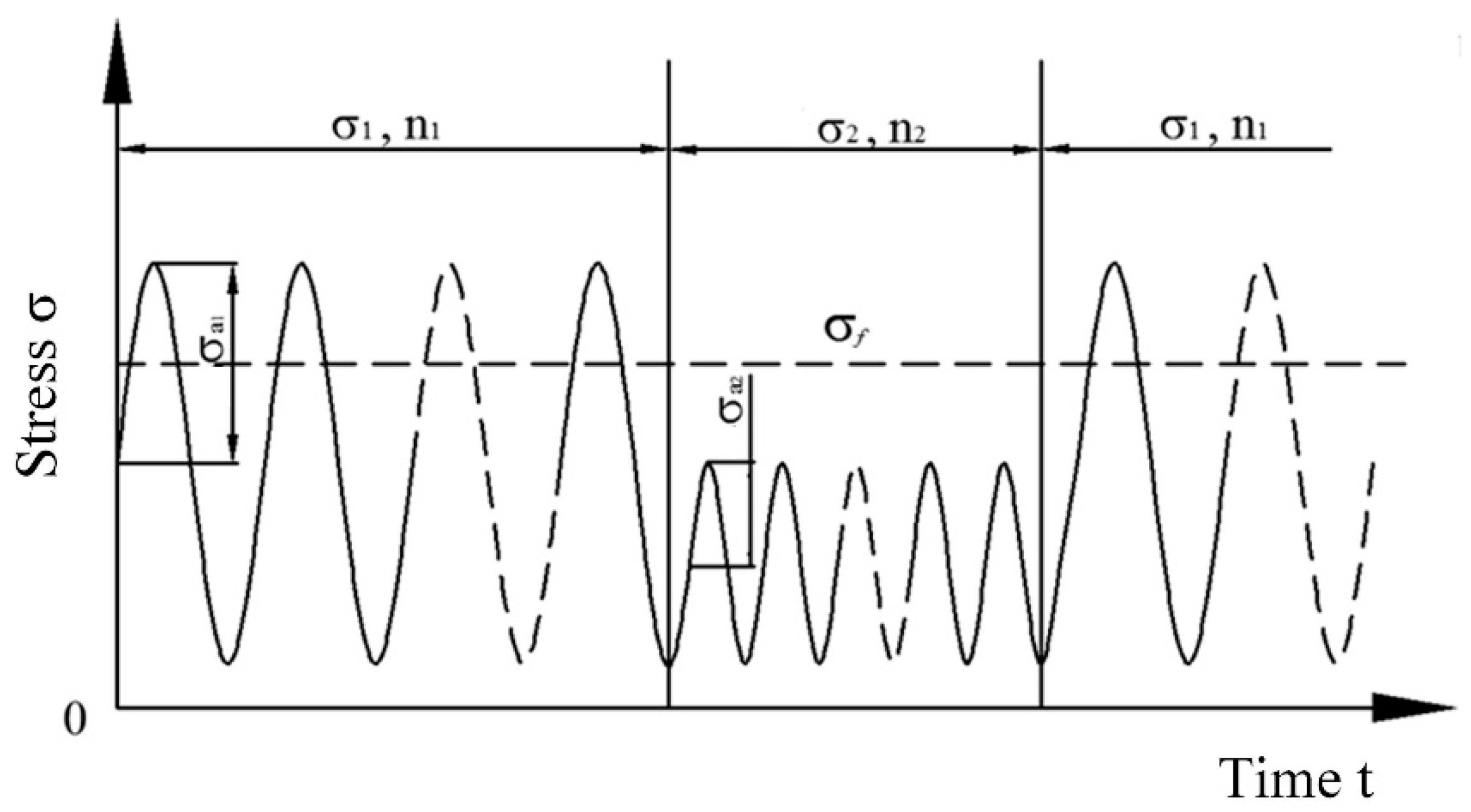
2.4.2. Variable Amplitude Loading Tests
3. Results and Discussion
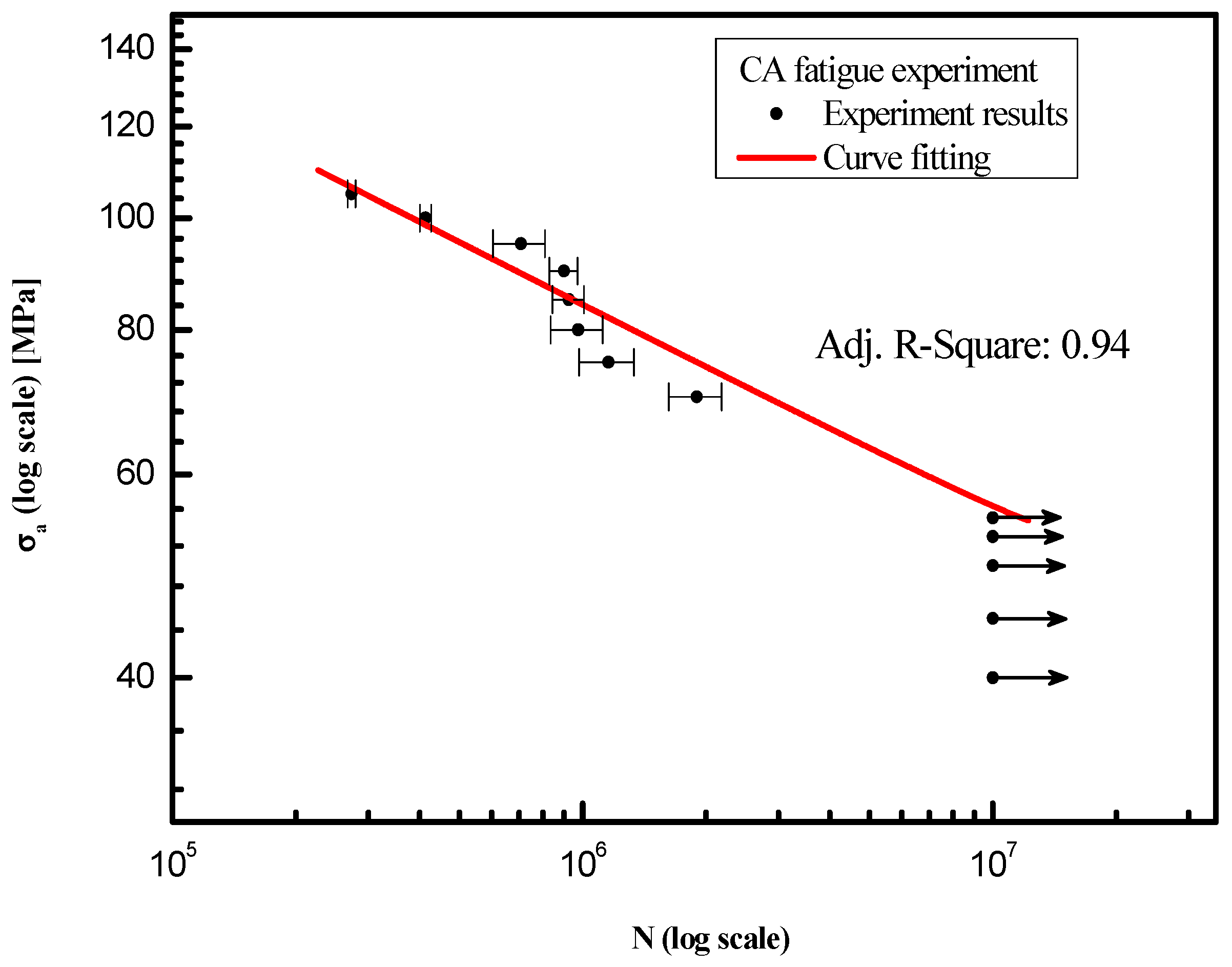
3.1. Constant Amplitude Test Results
3.2. Variable Amplitude Fatigue Experiment Results
4. Damage Accumulation of Variable Fatigue Experiment Analysis
5. Non-Linear Damage Evaluation
6. Conclusions
- (1)
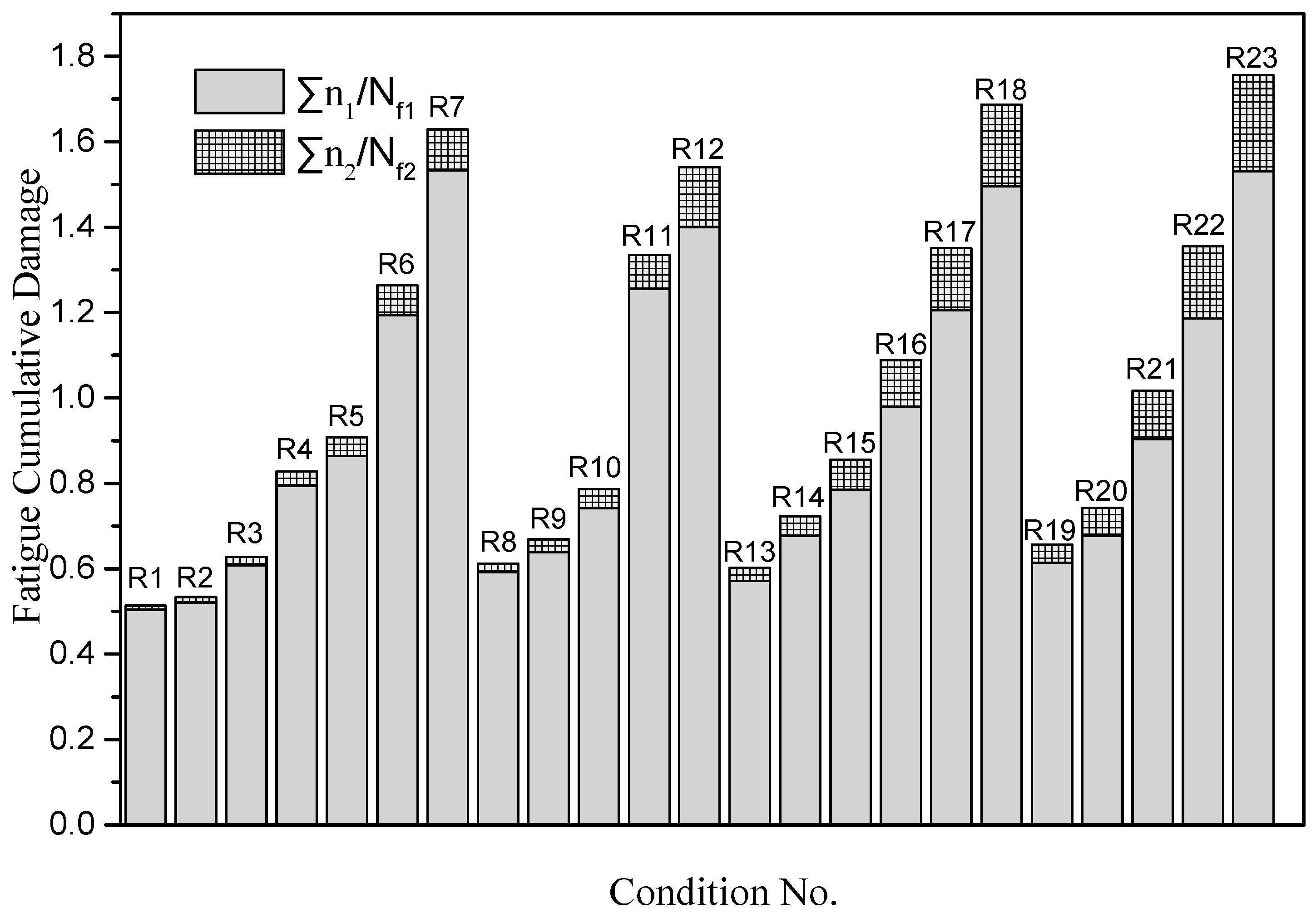
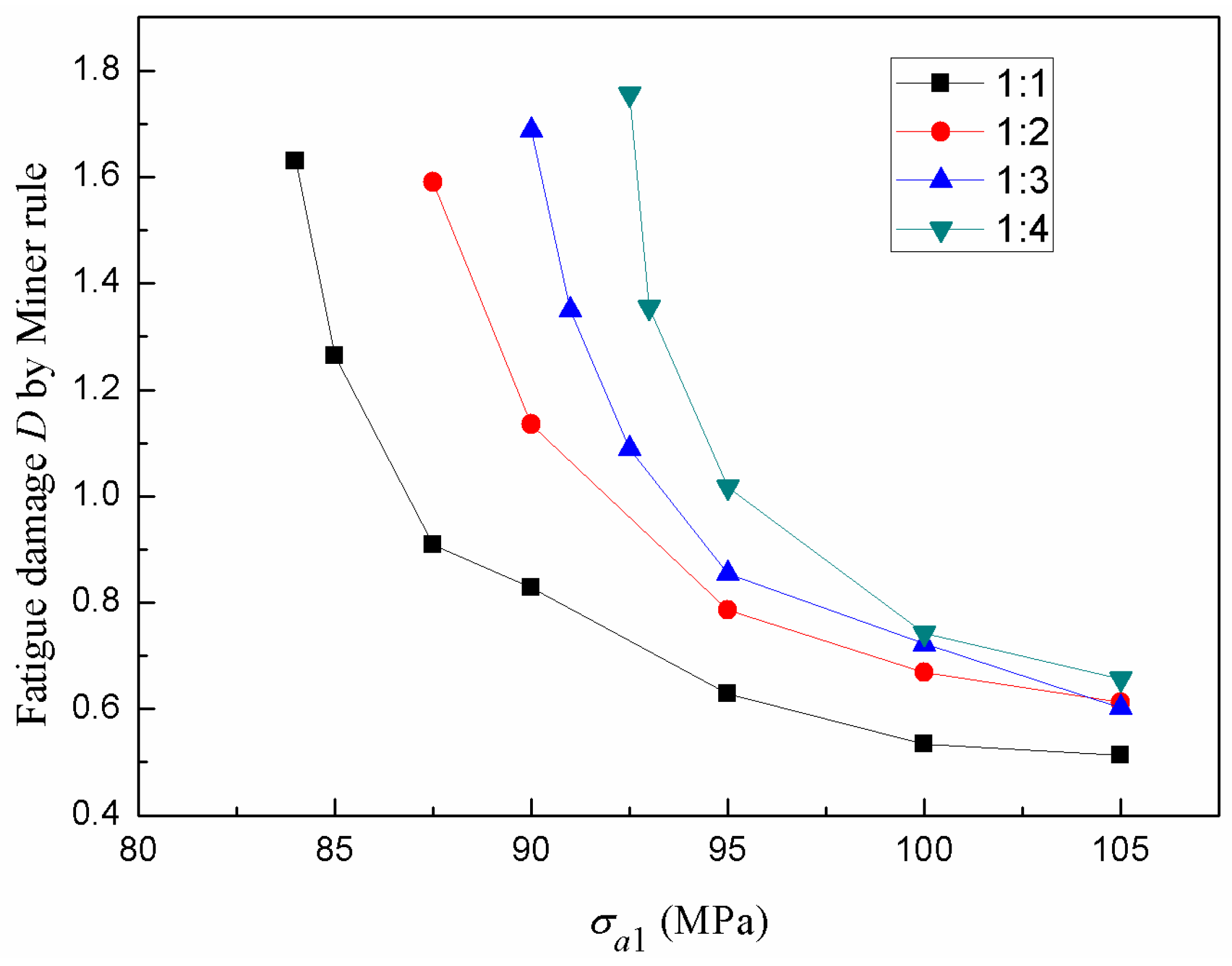
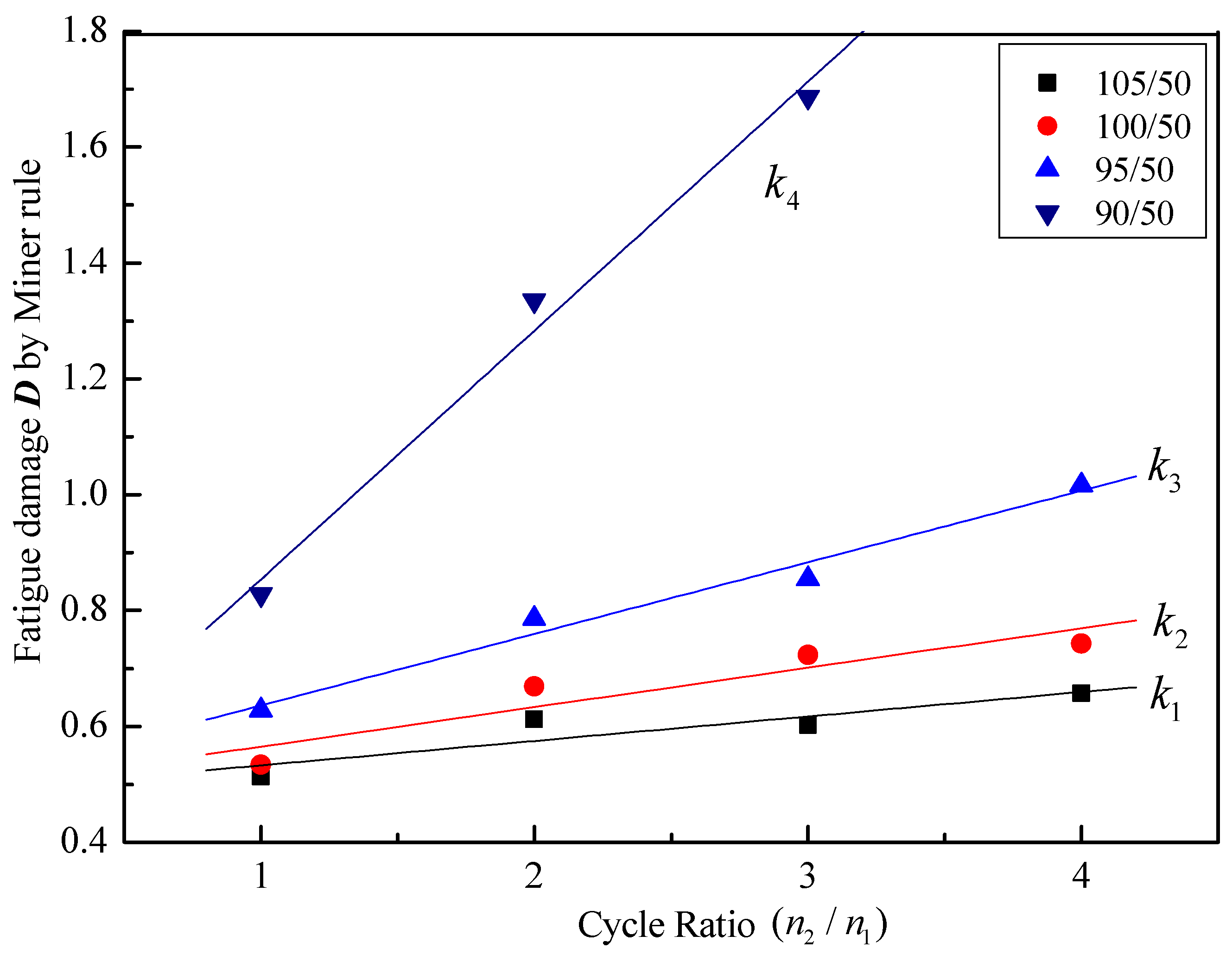
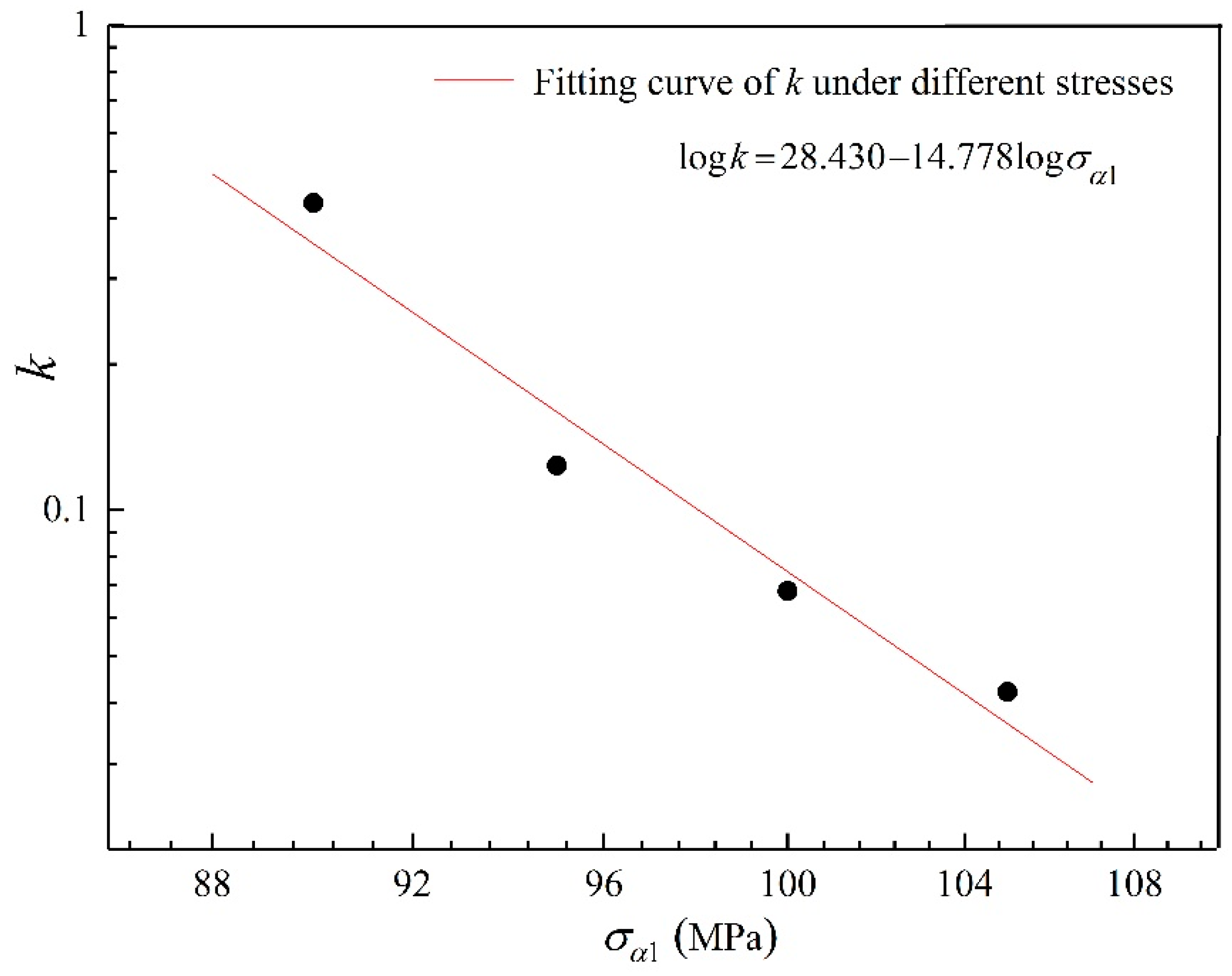
- For the fatigue performance of designed T-type specimens under two-step VA load, the fatigue cumulative damage values calculated by linear Miner rule are not 1. Compared with the cumulative damage caused by high cyclic stress, the cumulative damage caused by low stress below CAFL is relatively small. It is found that the cumulative damage decreases with the increase of the high stress under the same cycle ratio. While under the same high-low load stress ratio, the cumulative fatigue damage increases with the linear increase of the cycle ratio of the low stress to the high stress, and logarithmic curve between the slope k and high stress above CAFL is linear.
- (2)
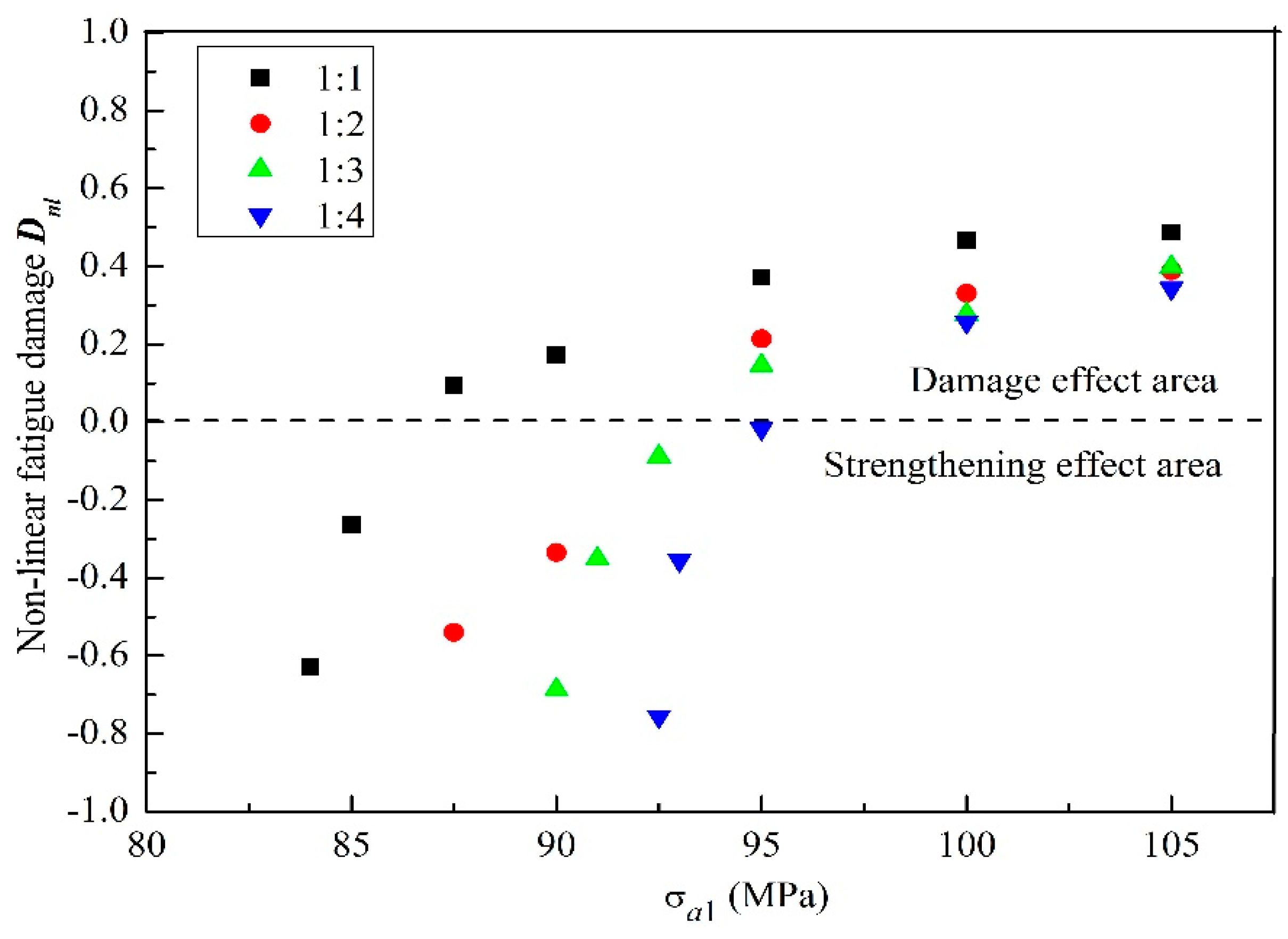
- Nonlinear cumulative damage Dnl is used to evaluate the load interaction between low and high cyclic stress. It is found that the load interaction shows different damage or strengthening effects with the change of low-high load cycle ratio and high cyclic stress. The area of strengthening effect occurs at high cyclic stress and low load cycle ratio.
- (3)
- From Figure 11, it can be seen that the linear slope of fatigue cumulative damage with the cycle ratio n2/n1 increases with the decrease of high stress in the loading block. The slopes k3 and k4 represent the linear slope of fatigue cumulative damage with the cycle ratio n2/n1 under high-low stress of 95/50 and 90/50 MPa, respectively. The reason is that the high stress in the loading block is closer to the low stress 50 MPa, the fatigue damage caused by both the high and the low stresses is much smaller. When the cycles of low stress take a larger percentage, i.e., a larger ratio of n2/n1, the strengthening effects are more obvious. As shown in Figure 13, two of the three points at the high stress of 90 MPa are in the strengthening effect area, and only one of the four points at the high stress of 95 MPa is in the strengthening effect area. All of the four points at the high stress of 100 MPa or 105 MPa are in the damage effect area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gan, J.; Sun, D.; Wang, Z.; Luo, P.; Wu, W. The effect of shot peening on fatigue life of Q345D T-welded joint. J. Constr. Steel Res. 2016, 126, 74–82. [Google Scholar] [CrossRef]
- Li, Z.; Mao, W.; Ringsberg, J.W.; Johnson, E.; Storhaug, G. A comparative study of fatigue assessments of container ship structures using various direct calculation approaches. Ocean. Eng. 2014, 82, 65–74. [Google Scholar] [CrossRef]
- Beretta, S.; Carboni, M. Variable amplitude fatigue crack growth in a mild steel for railway axles: Experiments and predictive models. Eng. Fract. Mech. 2011, 78, 848–862. [Google Scholar] [CrossRef]
- Warhadpande, A.; Jalalahmadi, B.; Slack, T.S.; Sadeghi, F. A new finite element fatigue modeling approach for life scatter in tensile steel specimens. Int. J. Fatigue 2010, 32, 685–697. [Google Scholar] [CrossRef]
- Sun, D.; Gan, J.; Wang, Z.; Luo, P.; Wu, W. Experimental and analytical investigation of fatigue crack propagation of T-welded joints considering the effect of boundary condition. Fatigue Fract. Eng. Mater. Struct. 2016, 40, 894–908. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 67, A159–A164. [Google Scholar]
- Zhang, Y.-H.; Maddox, S. Investigation of fatigue damage to welded joints under variable amplitude loading spectra. Int. J. Fatigue 2009, 31, 138–152. [Google Scholar] [CrossRef]
- Stäcker, C.; Sander, M. Experimental, analytical and numerical analyses of constant and variable amplitude loadings in the very high cycle fatigue regime. Appl. Fract. Mech. 2017, 92, 394–409. [Google Scholar] [CrossRef]
- Tilly, G. Fatigue of land-based structures. Int. J. Fatigue 1985, 7, 67–78. [Google Scholar] [CrossRef]
- Dahle, T. Spectrum fatigue life of welded specimen in relation to the linear damage rule. In Fatigue Under Spectrum Loading and in Corrosive Environments; Blom, A.F., Ed.; EMAS Publishing: Birchwood Park Warrington, UK, 1993; pp. 133–147. [Google Scholar]
- Tubby, P.J.; Razmjoo, G.R.; Gurney, T.R.; Priddle, E.K. Fatigue of Welded Joints Under Variable Amplitude Loading, In: OTO 94 804; HSE Books: Sudbury, ON, Canada, 1996. [Google Scholar]
- Gurney, T.R. Exploratory Investigation of the Significance of the Low Stresses in a Fatigue Loading Spectrum; TWI Member Report 718/2000; TWI Ltd: Cambridge, UK, December 2000. [Google Scholar]
- Berger, C.; Eulitz, K.G.; Heuler, P.; Kotte, K.L.; Naundorf, H.; Schuetz, W.; Sonsino, C.M.; Wimmer, A.; Zenner, H. Betriebsfestigkeit in Germany—An overview. Int. J. Fatigue 2002, 24, 603–625. [Google Scholar] [CrossRef]
- Dattoma, V.; Giancane, S.; Nobile, R.; Panella, F. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model. Int. J. Fatigue 2006, 28, 89–95. [Google Scholar] [CrossRef]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Bolchoun, A.; Baumgartner, J.; Kaufmann, H. A new method for fatigue life evaluation under out-of-phase variable amplitude loadings and its application to thin-walled magnesium welds. Int. J. Fatigue 2017, 101, 159–168. [Google Scholar] [CrossRef]
- Marco, S.M.; Starkey, W.L. A concept of fatigue damage. Trans. ASME 1954, 76, 627–632. [Google Scholar]
- Hell, M.; Wagener, R.; Kaufmann, H.; Melz, T. Fatigue life design of components under variable amplitude loading with respect to cyclic material behaviour. Procedia Eng. 2015, 101, 194–202. [Google Scholar] [CrossRef]
- Gatts, R.R. Cumulative fatigue damage with random loading. ASME J. Basic Eng. 1962, 84, 403–409. [Google Scholar] [CrossRef]
- He, L.; Akebono, H.; Kato, M.; Sugeta, A. Fatigue life prediction method for AISI 316 stainless steel under variable-amplitude loading considering low-amplitude loading below the endurance limit in the ultrahigh cycle regime. Int. J. Fatigue 2017, 101, 18–26. [Google Scholar] [CrossRef]
- Gan, J.; Zhao, K.; Wang, Z.; Wang, X.; Wu, W. Fatigue damage of designed T-type specimen under different proportion re-peating Two-Step variable amplitude loads. Eng. Fract. Mech. 2019, 221, 106684. [Google Scholar] [CrossRef]
- Xi, L.; Zheng, S. Strengthening of transmission gear under low-amplitude loads. Mat. Sci. Eng. A-Struct. 2008, 488, 55–63. [Google Scholar] [CrossRef]
- Xi, L.; Songlin, Z. Changes in mechanical properties of vehicle components after strengthening under low-amplitude loads below the fatigue limit. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 847–855. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chang, K.-H.; Van Do, V.N. Modeling the high cycle fatigue behavior of T-joint fillet welds considering weld-induced residual stresses based on continuum damage mechanics. Eng. Struct. 2016, 125, 205–216. [Google Scholar] [CrossRef]
- Ciavarella, M.; D’Antuono, P.; Demelio, G. A simple finding on variable amplitude (Gassner) fatigue SN curves obtained using Miner’s rule for unnotched or notched specimen. Eng. Fract. Mech. 2017, 176, 178–185. [Google Scholar] [CrossRef]
- Keating, P.B.; Fisher, J.W. Evaluation of Fatigue Tests and Design Criteria on Welded Details; NCHRP Report 286; Transportation Research Board: Washington, DC, WA, USA, 1986; pp. 163–172. [Google Scholar]
- Keating, P.B.; Fisher, J.W. Full-scale welded details under random variable amplitude loading. In Fatigue of Welded Constructions; Maddox, S.J., Ed.; Elsevier: Brighton, UK, 1987. [Google Scholar]
- Dahle, T. Long-life spectrum fatigue tests of welded joints. Int. J. Fatigue 1994, 16, 392–396. [Google Scholar] [CrossRef]
- Marquis, G. Long Life Spectrum Fatigue Of Carbon And Stainless Steel Welds. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 739–753. [Google Scholar] [CrossRef]
- Hobbacher, A.F. Recommendations for fatigue design of welded joints and components. In Recommendations for Fatigue Design of Welded Joints and Components; Springer Nature: London, UK, 2016. [Google Scholar]
- Lv, Z.; Huang, H.-Z.; Zhu, S.-P.; Gao, H.; Zuo, F. A modified nonlinear fatigue damage accumulation model. Int. J. Damage Mech. 2014, 24, 168–181. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, S.M.; Kim, Y.N.; Kim, S.G.; Lee, K.E.; Kim, G.R. A comparative study for the fatigue assessment of a ship structure by use of hot spot stress and structural stress approaches. Ocean. Eng. 2009, 36, 1067–1072. [Google Scholar] [CrossRef]
- Erny, C.; Thévenet, D.; Cognard, J.-Y.; Körner, M. Fatigue life prediction of welded ship details. Mar. Struct. 2012, 25, 13–32. [Google Scholar] [CrossRef]
- Li, Z.; Ringsberg, J.W.; Storhaug, G. Time-domain fatigue assessment of ship side-shell structures. Int. J. Fatigue 2013, 55, 276–290. [Google Scholar] [CrossRef]
- Xu, X.; Augello, R.; Yang, H. The generation and validation of a CUF-based FEA model with laser-based experiments. Mech. Adv. Mater. Struct. 2019, 1–8. [Google Scholar] [CrossRef]
- Xu, X.; Yang, H.; Augello, R.; Carrera, E. Optimized free-form surface modeling of point clouds from laser-based measurement. Mech. Adv. Mater. Struct. 2019, 1–9. [Google Scholar] [CrossRef]
- Carrera, E.; Pagani, A.; Augello, R. On the role of large cross-sectional deformations in the nonlinear analysis of composite thin-walled structures. Arch. Appl. Mech. 2020, 1–17. [Google Scholar] [CrossRef]
- Carrera, E.; Pagani, A.; Augello, R. Evaluation of geometrically nonlinear effects due to large cross-sectional deformations of compact and shell-like structures. Mech. Adv. Mater. Struct. 2018, 27, 1269–1277. [Google Scholar] [CrossRef]
- Sun, D.; Gan, J.; Wang, Z.; Wu, W.-G. Experimental study on fatigue characteristics of T-welded joint under repeating two-step load. In Proceedings of the International Offshore and Polar Engineering Conference, ISOPE-1-17-236, 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- CCS. Metallic Materials—Tensile Testing. China Classification of Society; Standards Press of China: Beijing, China, 2016. [Google Scholar]
- Gao, X.; Gan, J.; Sun, D.; Wu, W. Experimental study on fatigue characteristics of typical welded joints of river-sea-going ship. In Proceedings of the International Offshore and Polar Engineering Conference, ISOPE-1-17-358, 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Dong, P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- BSI. BS 7608: 2014+A1: 2015 Guide to Fatigue Design and Assessment of Steel Products; British Standards Institution: London, UK, 2015. [Google Scholar]





| Q345D | Element | C | Mn | Si | S | P | Ni | Cr | Mo | V | Cu | Fe |
| Wt.-% | 0.15 | 1.39 | 0.28 | 0.003 | 0.015 | 0.01 | 0.05 | 0.007 | 0.004 | 0.04 | Balance |
| Ultimate tensile strength, [MPa] | 539 |
| Monotonic yield strength, [MPa] | 384 |
| Young’s modulus, E [GPa] | 206 |
| Poisson’s coefficient, | 0.26 |
| elongation, [%] | 30.5 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 105 | 100 | 95 | 90 | 85 | 80 | 75 | 70 | 55 | 53 | 50 | 45 | 40 | |
| R | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Specimen No. | σa [MPa] | R | Average Cycles to Failure | Three Repeated Fatigue Experiment Results | ||
|---|---|---|---|---|---|---|
| C1 | 105 | 0.1 | 273,187 | 267,358 | 270,591 | 281,612 |
| C2 | 100 | 0.1 | 413,863 | 395,732 | 419,934 | 425,923 |
| C3 | 95 | 0.1 | 706,895 | 575,216 | 719,683 | 825,786 |
| C4 | 90 | 0.1 | 896,437 | 804,140 | 908,442 | 976,729 |
| C5 | 85 | 0.1 | 925,700 | 1,035,762 | 898,867 | 842,471 |
| C6 | 80 | 0.1 | 975,620 | 841,147 | 914,587 | 1,171,126 |
| C7 | 75 | 0.1 | 1,156,460 | 1,400,569 | 1,075,784 | 993,027 |
| C8 | 70 | 0.1 | 1,933,942 | 1,829,748 | 1,656,775 | 2,315,303 |
| C9 | 55 | 0.1 | 107+ | 107+ | 107+ | 107+ |
| C10 | 53 | 0.1 | 107+ | 107+ | 107+ | 107+ |
| C11 | 50 | 0.1 | 107+ | 107+ | 107+ | 107+ |
| C12 | 45 | 0.1 | 107+ | 107+ | 107+ | 107+ |
| C13 | 40 | 0.1 | 107+ | 107+ | 107+ | 107+ |
| Stress (MPa) σa1/σa2 | Specimen No. under Different Load Block (n1/n2) | |||
|---|---|---|---|---|
| 20,000/20,000 (1:1) | 20,000/40,000 (1:2) | 20,000/60,000 (1:3) | 20,000/80,000 (1:4) | |
| 105/50 | R1 | R8 | R13 | R19 |
| 100/50 | R2 | R9 | R14 | R20 |
| 95/50 | R3 | R10 | R15 | R21 |
| 93/50 | - | - | - | R22 |
| 92.5/50 | - | - | R16 | R23 |
| 91/50 | - | - | R17 | - |
| 90/50 | R4 | R11 | R18 | - |
| 87.5/50 | R5 | R12 | - | - |
| 85/50 | R6 | - | - | - |
| 84/50 | R7 | - | - | - |
| Specimen No. | First Step | Second Step | |||
|---|---|---|---|---|---|
| Nf1 (Cycle) | Nf2 (Cycle) | ||||
| R1 | 293,018 | 16,000,000 | 147,790 | 145,000 | 292,790 |
| R2 | 383,800 | 16,000,000 | 200,000 | 204,431 | 404,431 |
| R3 | 509,075 | 16,000,000 | 310,000 | 315,434 | 625,434 |
| R4 | 689,256 | 16,000,000 | 547,533 | 540,000 | 1,087,500 |
| R5 | 804,793 | 16,000,000 | 695,000 | 702,573 | 1,397,573 |
| R6 | 945,578 | 16,000,000 | 1,128,637 | 1,120,000 | 2,248,637 |
| R7 | 1,007,230 | 16,000,000 | 1,544,489 | 1,530,000 | 3,174,489 |
| R8 | 293,018 | 16,000,000 | 173,321 | 320,000 | 493,321 |
| R9 | 383,800 | 16,000,000 | 245,315 | 480,000 | 725,315 |
| R10 | 509,075 | 16,000,000 | 377,466 | 720,000 | 1,097,466 |
| R11 | 689,256 | 16,000,000 | 640,000 | 1,276,359 | 1,916,359 |
| R12 | 804,793 | 16,000,000 | 1,126,710 | 2,240,000 | 3,366,710 |
| R13 | 293,018 | 16,000,000 | 167,548 | 480,000 | 657,548 |
| R14 | 383,800 | 16,000,000 | 260,000 | 723,971 | 983,971 |
| R15 | 509,075 | 16,000,000 | 400,000 | 1,109,637 | 1,509,637 |
| R16 | 591,961 | 16,000,000 | 580,000 | 1,743,492 | 2,323,492 |
| R17 | 647,055 | 16,000,000 | 780,000 | 2,326,483 | 3,106,483 |
| R18 | 689,256 | 16,000,000 | 1,031,126 | 3,060,000 | 4,091,126 |
| R19 | 293,018 | 16,000,000 | 180,000 | 677,563 | 837,563 |
| R20 | 383,800 | 16,000,000 | 260,000 | 1,042,741 | 1,302,741 |
| R21 | 509,075 | 16,000,000 | 460,000 | 1,811,567 | 2,271,567 |
| R22 | 573,166 | 16,000,000 | 680,000 | 2,705,437 | 3,385,437 |
| R23 | 591,961 | 16,000,000 | 906,292 | 3,600,000 | 4,506,292 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, J.; Sun, D.; Deng, H.; Wang, Z.; Wang, X.; Yao, L.; Wu, W. Fatigue Characteristic of Designed T-Type Specimen under Two-Step Repeating Variable Amplitude Load with Low-Amplitude Load below the Fatigue Limit. J. Mar. Sci. Eng. 2021, 9, 107. https://doi.org/10.3390/jmse9020107
Gan J, Sun D, Deng H, Wang Z, Wang X, Yao L, Wu W. Fatigue Characteristic of Designed T-Type Specimen under Two-Step Repeating Variable Amplitude Load with Low-Amplitude Load below the Fatigue Limit. Journal of Marine Science and Engineering. 2021; 9(2):107. https://doi.org/10.3390/jmse9020107
Chicago/Turabian StyleGan, Jin, Di Sun, Hui Deng, Zhou Wang, Xiaoli Wang, Li Yao, and Weiguo Wu. 2021. "Fatigue Characteristic of Designed T-Type Specimen under Two-Step Repeating Variable Amplitude Load with Low-Amplitude Load below the Fatigue Limit" Journal of Marine Science and Engineering 9, no. 2: 107. https://doi.org/10.3390/jmse9020107
APA StyleGan, J., Sun, D., Deng, H., Wang, Z., Wang, X., Yao, L., & Wu, W. (2021). Fatigue Characteristic of Designed T-Type Specimen under Two-Step Repeating Variable Amplitude Load with Low-Amplitude Load below the Fatigue Limit. Journal of Marine Science and Engineering, 9(2), 107. https://doi.org/10.3390/jmse9020107








