An Interpretable Aid Decision-Making Model for Flag State Control Ship Detention Based on SMOTE and XGBoost
Abstract
:1. Introduction
2. Literature Review
2.1. Flag Ship Control (FSC) Ship Detention Analysis
2.2. Extreme Gradient Boosting (XGBoost) Algorithm Applications
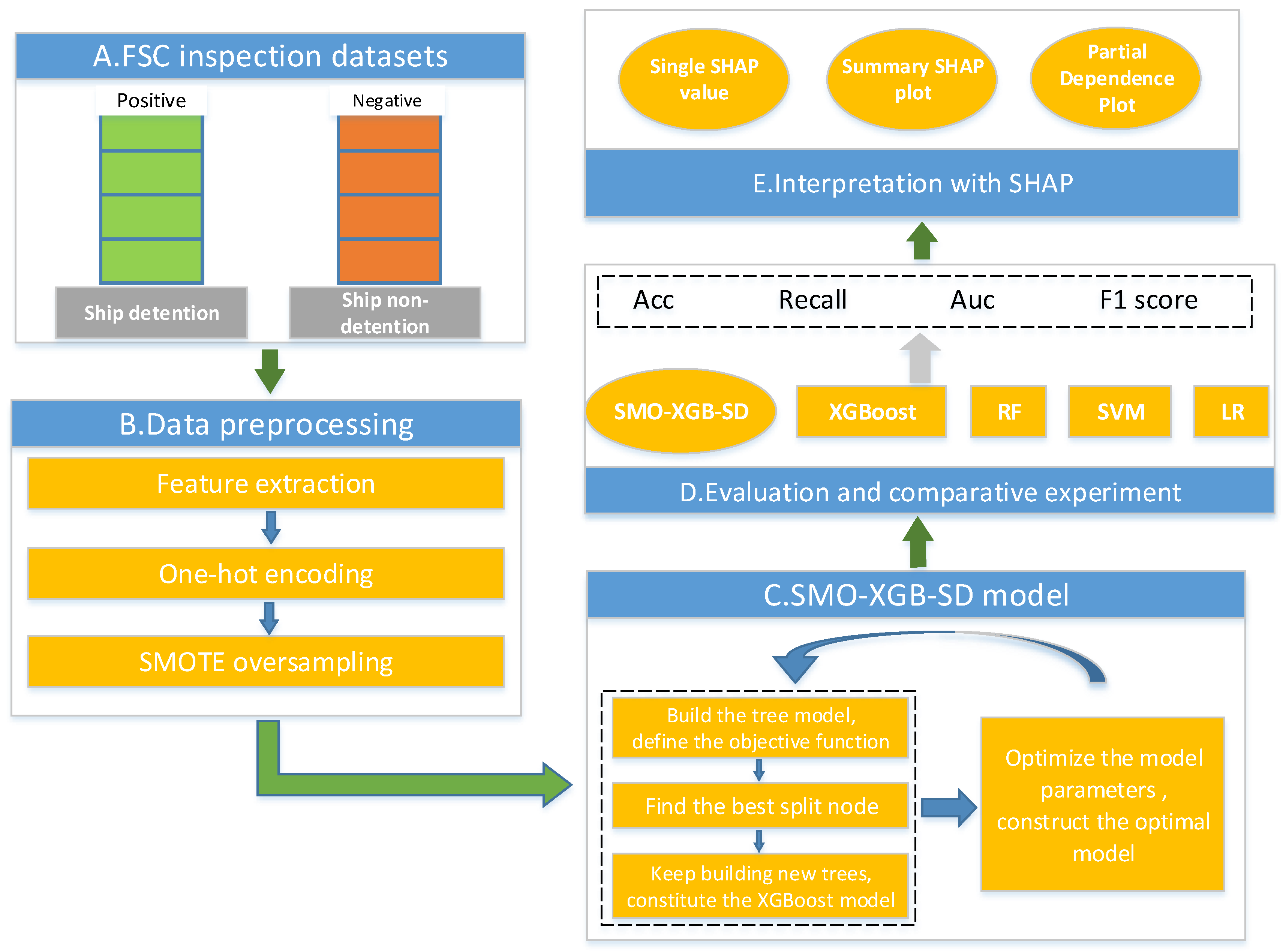
3. Overall Framework
4. Materials and Methods
4.1. Original FSC Inspection Datasets
4.2. Synthetic Minority Oversampling Technique (SMOTE)
4.3. One-Hot Encoding
4.4. XGBoost Classification Machine Learning Algorithm
4.5. Evaluation Metrics
4.6. Shapley Additive Explanations (SHAP) Method
5. Results and Discussion
5.1. Data Preprocessing and Oversampling Analysis
5.2. Comparison with Other Classification Algorithms
5.3. Interpretation with SHAP Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gan, G.; Lee, H.; Chung, C.; Chen, S. Performance evaluation of the security management of Changjiang maritime safety administrations: Application with undesirable outputs in data development analysis. J. Mar. Sci. Technol. Jpn. 2017, 25, 213–219. [Google Scholar] [CrossRef]
- Guan, Z.; Zhang, J. Concretely Strengthen the Safety Management of Passenger Rolling Ship Transportation in Bohai Bay. Mar. Technol. 2005. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Regulations of the People’s Republic of China on Ship Safety Supervision. Available online: http://www.mot.gov.cn/zhengcejiedu/chuanboaqjdgz/xiangguanzhengce/201707/t20170727_2661551.html (accessed on 12 December 2020).
- Kim, G.; Gong, G. Forecasting Model for Korean Ships’ Detention in Port State Control. J. Korean Inst. Navig. Port. Res. 2008, 32, 729–736. [Google Scholar] [CrossRef]
- Sun, L. The Study on Ship’s Detain Decision for China’s PSC; Dalian Maritime University: Dalian, China, 2011. [Google Scholar]
- Yang, Z.; Yang, Z.; Yin, J. Realising advanced risk-based port state control inspection using data-driven Bayesian networks. Transp. Res. Part A Policy Pract. 2018, 110, 38–56. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Y. Detain risk of ship’s port state control inspection based on Bayesian networks. J. Ningbo Univ. Nat. Sci. Eng. Ed. 2020, 33, 111–115. [Google Scholar]
- Zhang, Q. Evaluation of Ship Safety Based on Flag State Inspection Result; Dalian Maritime University: Dalian, China, 2014. [Google Scholar]
- Hao, Y.; Huang, Q. Association Among Safety Defects for Inland Ship. Navig. China 2016, 39, 77–81. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Xu, L.; Wan, Z.; Fei, Y.; Zheng, T. Identification of key factors of ship detention under Port State Control. Mar. Policy 2019, 102, 21–27. [Google Scholar] [CrossRef]
- Tsou, M. Big data analysis of port state control ship detention database. J. Mar. Eng. Technol. 2018, 18, 113–121. [Google Scholar] [CrossRef]
- Cariou, P.; Mejia, M.Q.; Wolff, F. An econometric analysis of deficiencies noted in port state control inspections. Marit. Policy Manag. 2007, 34, 243–258. [Google Scholar] [CrossRef]
- Bao, L.S.; Yip, T.L. Culture effects on vessel detention. In Proceedings of the Annual Conference of the International Association of Maritime Economists, Lisbon, Portugal, 7–9 July 2010; pp. 1–22. [Google Scholar]
- Cariou, P.; Mejia, M.Q.; Wolff, F. Evidence on target factors used for port state control inspections. Mar. Policy 2009, 33, 847–859. [Google Scholar] [CrossRef]
- Fu, J.; Chen, X.; Wu, S.; Shi, C.; Zhao, J.; Xian, J. Ship Detention Situation Prediction via Optimized Analytic Hierarchy Process and Naïve Bayes Model. Math. Probl. Eng. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Rocha, W.F.D.C.; Sheen, D.A. Determination of physicochemical properties of petroleum derivatives and biodiesel using GC/MS and chemometric methods with uncertainty estimation. Fuel 2019, 243, 413–422. [Google Scholar] [CrossRef]
- Farid, D.M.; Zhang, L.; Rahman, C.M.; Hossain, M.A.; Strachan, R. Hybrid decision tree and naïve Bayes classifiers for multi-class classification tasks. Expert Syst. Appl. 2014, 41, 1937–1946. [Google Scholar] [CrossRef]
- Han, S.; Wang, Y.; Liao, W.; Duan, X.; Guo, J.; Yu, Y.; Ye, L.; Li, J.; Chen, X.; Chen, H. The distinguishing intrinsic brain circuitry in treatment-naïve first-episode schizophrenia: Ensemble learning classification. Neurocomputing 2019, 365, 44–53. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wires Data Min. Knowl. Discov. 2018, 8. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Tan, Y.; Gan, V.J.L.; Zhang, J. Analyzing the Leading Causes of Traffic Fatalities Using XGBoost and Grid-Based Analysis: A City Management Perspective. IEEE Access 2019, 7, 148059–148072. [Google Scholar] [CrossRef]
- Bi, Y.; Xiang, D.; Ge, Z.; Li, F.; Jia, C.; Song, J. An Interpretable Prediction Model for Identifying N7-Methylguanosine Sites Based on XGBoost and SHAP. Mol. Ther. Nucleic Acids 2020, 22, 362–372. [Google Scholar] [CrossRef] [PubMed]
- Mahmud, S.M.H.; Chen, W.; Jahan, H.; Liu, Y.; Sujan, N.I.; Ahmed, S. iDTi-CSsmoteB: Identification of Drug–Target Interaction Based on Drug Chemical Structure and Protein Sequence Using XGBoost with Over-Sampling Technique SMOTE. IEEE Access 2019, 7, 48699–48714. [Google Scholar] [CrossRef]
- Wang, S.; Liu, S.; Zhang, J.; Che, X.; Yuan, Y.; Wang, Z.; Kong, D. A new method of diesel fuel brands identification: SMOTE oversampling combined with XGBoost ensemble learning. Fuel 2020, 282, 118848. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Shi, H.; Chen, Y.; Chen, X. Summary of research on SMOTE oversampling and its improved algorithms. CAAI Trans. Intell. Syst. 2019, 14, 1073–1083. [Google Scholar] [CrossRef]
- Cassel, M.; Lima, F. Evaluating One-Hot Encoding Finite State Machines for SEU Reliability in SRAM-based FPGAs. In Proceedings of the 12th IEEE International On-Line Testing Symposium (IOLTS’06), Lake Como, Italy, 10–12 July 2006. [Google Scholar]
- Rodríguez, P.; Bautista, M.A.; Gonzàlez, J.; Escalera, S. Beyond one-hot encoding: Lower dimensional target embedding. Image Vis. Comput. 2018, 75, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Jin, M.; Shi, W.; Yuen, K.F.; Xiao, Y.; Li, K.X. Oil tanker risks on the marine environment: An empirical study and policy implications. Mar. Policy 2019, 108, 103655. [Google Scholar] [CrossRef]
- Nobre, J.; Neves, R.F. Combining Principal Component Analysis, Discrete Wavelet Transform and XGBoost to trade in the financial markets. Expert Syst. Appl. 2019, 125, 181–194. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Li, Q. Multi-criteria comprehensive study on predictive algorithm of hourly heating energy consumption for residential buildings. Sustain. Cities Soc. 2019, 49, 101623. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Z.; Yang, J.; Fang, H.; Hu, Y. Prediction of ship collision risk based on CART. IET Intell. Transp. Syst. 2018, 12, 1345–1350. [Google Scholar] [CrossRef]
- Crawford, S.L. Extensions to the CART algorithm. Int. J. Man-Mach. Stud. 1989, 31, 197–217. [Google Scholar] [CrossRef]
- Wang, X.; Lou, X.Y.; Hu, S.Y.; He, S.C. Evaluation of Safe Driving Behavior of Transport Vehicles Based on K-SVM-XGBoost. In Proceedings of the 2020 3rd International Conference on Advanced Electronic Materials, Computers and Software Engineering, Shenzhen, China, 24–26 April 2020; pp. 84–92. [Google Scholar]
- Brown, C.D.; Davis, H.T. Receiver operating characteristics curves and related decision measures: A tutorial. Chemometr. Intell. Lab. 2006, 80, 24–38. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, UK, 2017; pp. 4765–4774. [Google Scholar]









| NO. | MMSI | Ship’s Name | Port of Registry | Date of Inspection | Port of Inspection | Inspection Authority | Number of Deficiencies | Ship Detention Result | Deficiency Code | Defect Description |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 412400000 | SHIP A1 | Anqing | 23 June 2017 | Anqing | Anqing Port Marine Department | 8 | No | 9999 | Other: Port of registry and name of vessel not clear |
| 2 | 412400001 | SHIP A2 | Fuling | 16 June 2017 | Fengdu | Chongqing Fengdu Marine Department | 23 | Yes | 1499 | Other: No identification for engine-room valves |
| 3 | 412400002 | SHIP A3 | Fengjie | 15 June 2017 | Wanzhou | Chongqing Wanzhou Marine Department | 9 | Yes | 0741 | Fire hose, fittings and hydrants, hoses, squirts, one hose broken |
| 75439 | 412475438 | SHIP Z1 | Jiujiang | 1 July 2017 | Yueyang | Yueyang Linxiang Marine Department | 8 | No | 0899 | Other: No plugging equipment |
| 75440 | 412475439 | SHIP Z2 | Jiujiang | 1 July 2017 | Yueyang | Yueyang Linxiang Marine Department | 8 | No | 0830 | Pipes and wires: Engine room piping coloring does not meet the requirements |
| 75441 | 412475440 | SHIP Z3 | Jiujiang | 1 July 2017 | Yueyang | Yueyang Linxiang Marine Department | 8 | No | 9910 | National flag: defaced |
| Feature | Value | Description | Feature | Value | Description |
|---|---|---|---|---|---|
| Location (port) of registry | AH | Anhui Province | Inspection authority (continued) | WHan | Wuhan Maritime Safety Administration |
| CQ | Chongqing Province | SX | Sanxia Maritime Safety Administration | ||
| HEE | Henan Province | LZ | Luzhou Maritime Safety Administration | ||
| HB | Hubei Province | Number of deficiencies | 0–50 | The value range of the number of deficiencies | |
| SH | Shanghai | Deficiency code | 0100 | Ship certificate and related documents | |
| SC | Sichuan Province | 0200 | Crew certificate and watchkeeping | ||
| JX | Jiangxi Province | 0600 | Lifesaving equipment | ||
| JS | Jiangsu Province | 0700 | Fire equipment | ||
| SD | Shandong Province | 0800 | Accident prevention | ||
| ZJ | Zhejiang Province | 0900 | Structure, stability, and related equipment | ||
| YN | Yunnan Province | 1000 | Warning signs | ||
| LN | Liaoning Province | 1100 | Goods | ||
| GZ | Guizhou Province | 1200 | Load line | ||
| Date of inspection | 1 | Spring | 1300 | Mooring equipment | |
| 2 | Summer | 1400 | Main power and auxiliary equipment | ||
| 3 | Fall | 1500 | Navigation safety | ||
| 4 | Winter | 1600 | Radio | ||
| Inspection authority | CQ | Chongqing Maritime Safety Administration | 1700 | Dangerous goods safety and pollution prevention | |
| YB | Yibin Maritime Safety Administration | 1800 | Oil tankers, chemical tankers, and liquefied gas tankers | ||
| WH | Wuhu Maritime Safety Administration | 1900 | Pollution prevention | ||
| HS | Huangshi Maritime Safety Administration | 2000 | Operational inspection | ||
| JZ | Jingzhou Maritime Safety Administration | 2500 | ISM/NSM | ||
| YC | Yichang Maritime Safety Administration | 2600 | Bulk carrier additional safety measures | ||
| JJ | Jiujiang Maritime Safety Administration | 2700 | Ro-ro ship additional safety measures | ||
| YY | Yueyang Maritime Safety Administration | 2800 | High-speed passenger ship additional safety measures | ||
| AQ | Anqing Maritime Safety Administration | 9900 | Others |
| XGBoost | SMO-XGB-SD | RF | SVM | LR |
|---|---|---|---|---|
| booster = ‘gbtree’ n_estimators = 110, max_depth = 3, learning_rate = 0.3 | booster = ‘gbtree’ n_estimators = 110, max_depth = 3, learning_rate = 0.3 | n_estimators = 10, max_depth = 4 | C = 2, kernel = ‘rbf’, probability = True | C = 10, penalty = ‘l2′, solver = ‘liblinear’ |
| Models | XGBoost | SMO-XGB-SD | RF | SVM | LR |
|---|---|---|---|---|---|
| Acc | 0.978 | 0.993 | 0.976 | 0.976 | 0.971 |
| P | 0.780 | 0.980 | 0.910 | 0.910 | 0.520 |
| Recall | 0.350 | 0.830 | 0.170 | 0.270 | 0.110 |
| F1 score | 0.480 | 0.880 | 0.280 | 0.410 | 0.180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Hao, Y.; Wang, X. An Interpretable Aid Decision-Making Model for Flag State Control Ship Detention Based on SMOTE and XGBoost. J. Mar. Sci. Eng. 2021, 9, 156. https://doi.org/10.3390/jmse9020156
He J, Hao Y, Wang X. An Interpretable Aid Decision-Making Model for Flag State Control Ship Detention Based on SMOTE and XGBoost. Journal of Marine Science and Engineering. 2021; 9(2):156. https://doi.org/10.3390/jmse9020156
Chicago/Turabian StyleHe, Jian, Yong Hao, and Xiaoqiong Wang. 2021. "An Interpretable Aid Decision-Making Model for Flag State Control Ship Detention Based on SMOTE and XGBoost" Journal of Marine Science and Engineering 9, no. 2: 156. https://doi.org/10.3390/jmse9020156
APA StyleHe, J., Hao, Y., & Wang, X. (2021). An Interpretable Aid Decision-Making Model for Flag State Control Ship Detention Based on SMOTE and XGBoost. Journal of Marine Science and Engineering, 9(2), 156. https://doi.org/10.3390/jmse9020156






