A Unifying Task Priority Approach for Autonomous Underwater Vehicles Integrating Homing and Docking Maneuvers
Abstract
:1. Introduction
2. General Notations and Model Definition
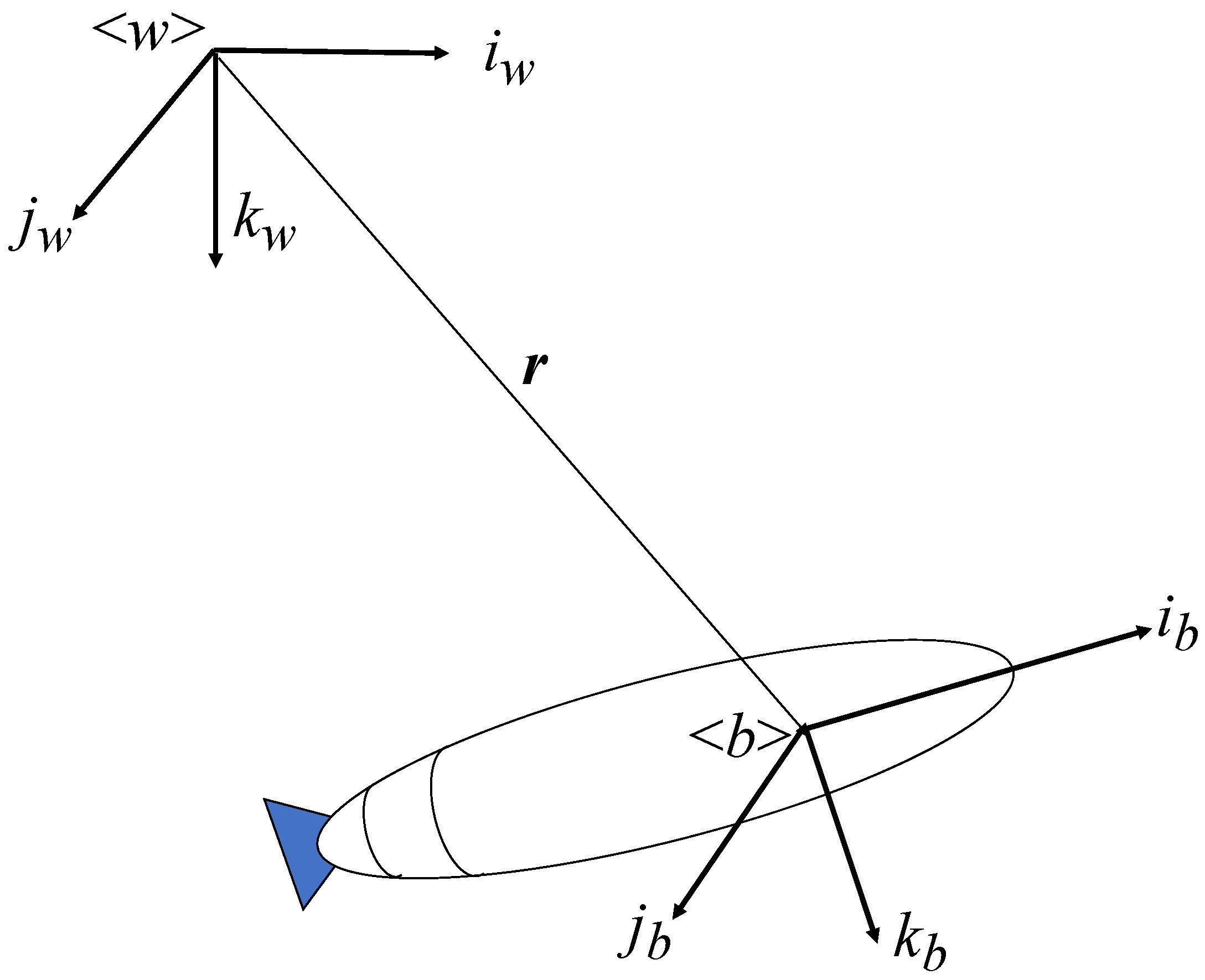
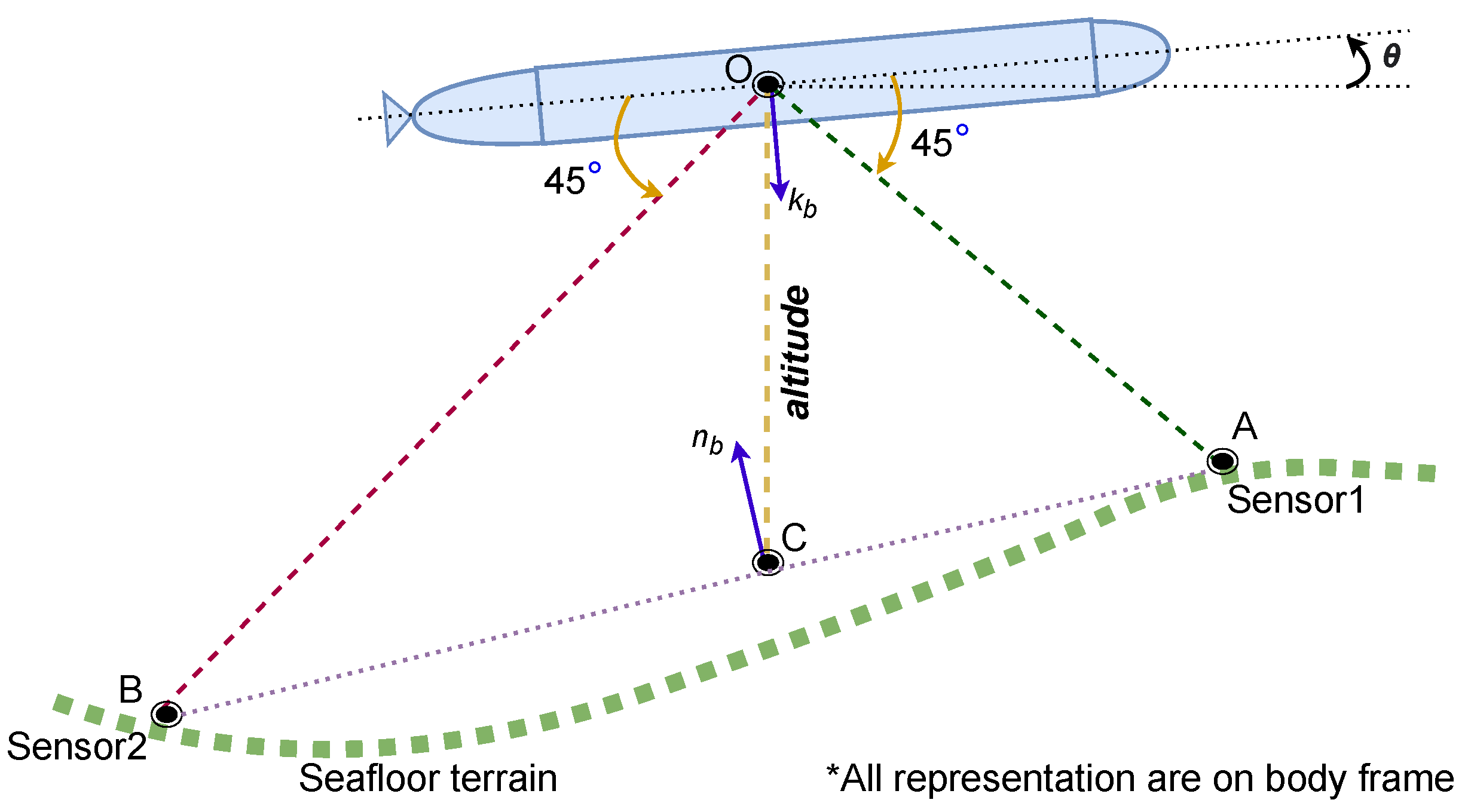
2.1. Frames and Transformations
2.2. AUV Kinematic and Dynamic Model
2.2.1. Kinematic Model
2.2.2. Dynamic Model
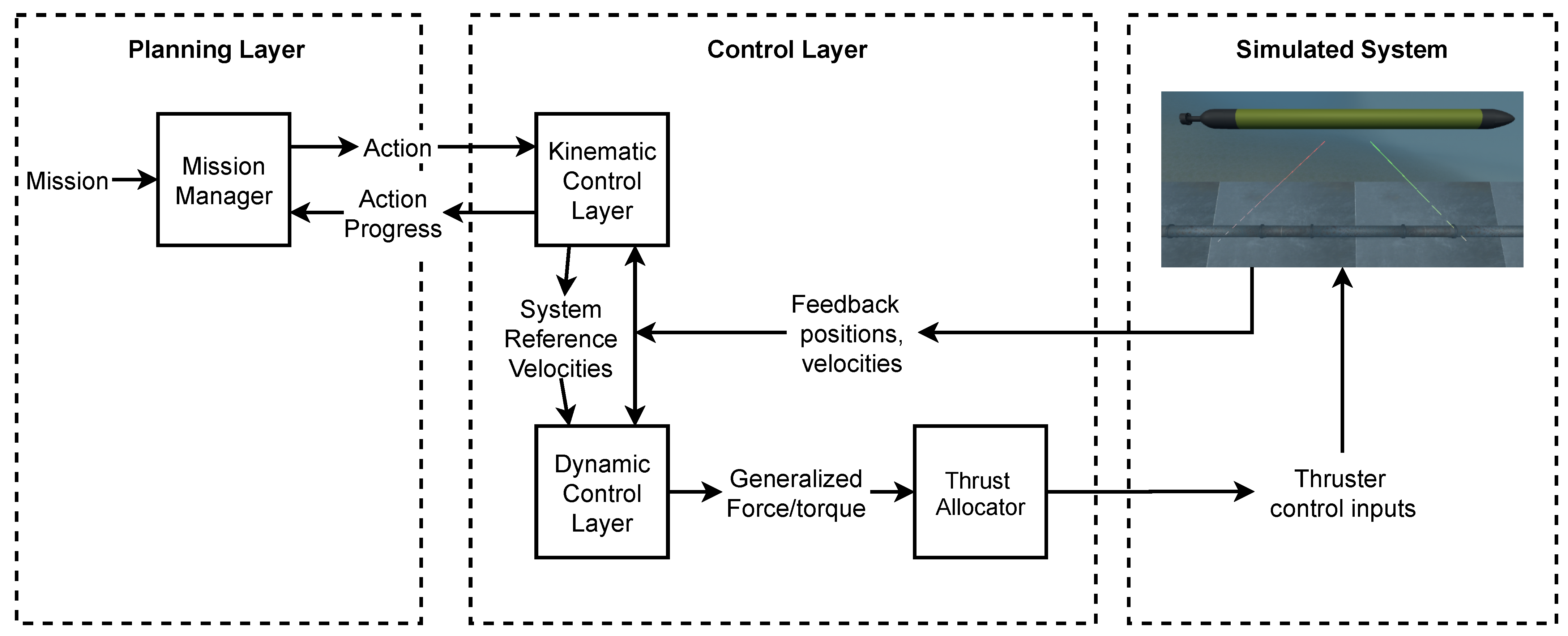
3. Control Architecture
3.1. Task Priority Framework and Definitions
- is the collection of reference rates of the scalar task for priority level k;
- is the Jacobian relation that connects the time derivative of the kth task vector with the system velocity vector ; and
- is the diagonal matrix constituting the activation functions.
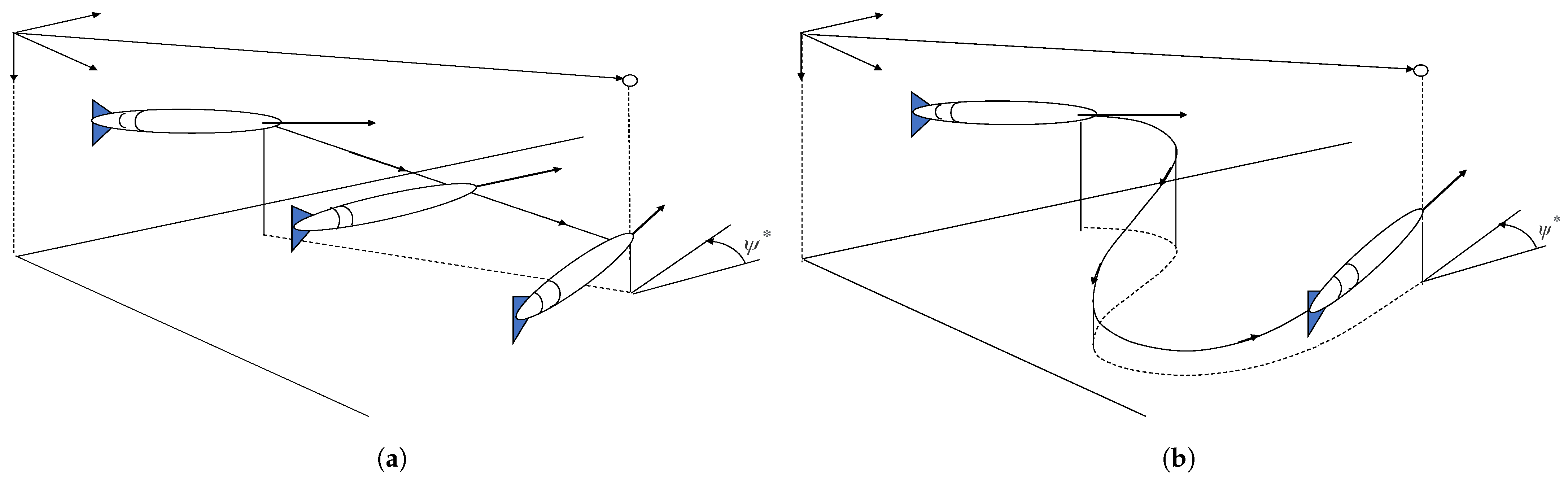
3.2. A Task Priority Approach Integrating Homing and Docking Maneuvers
3.3. Description of Tasks within an Action
4. Simulation Results
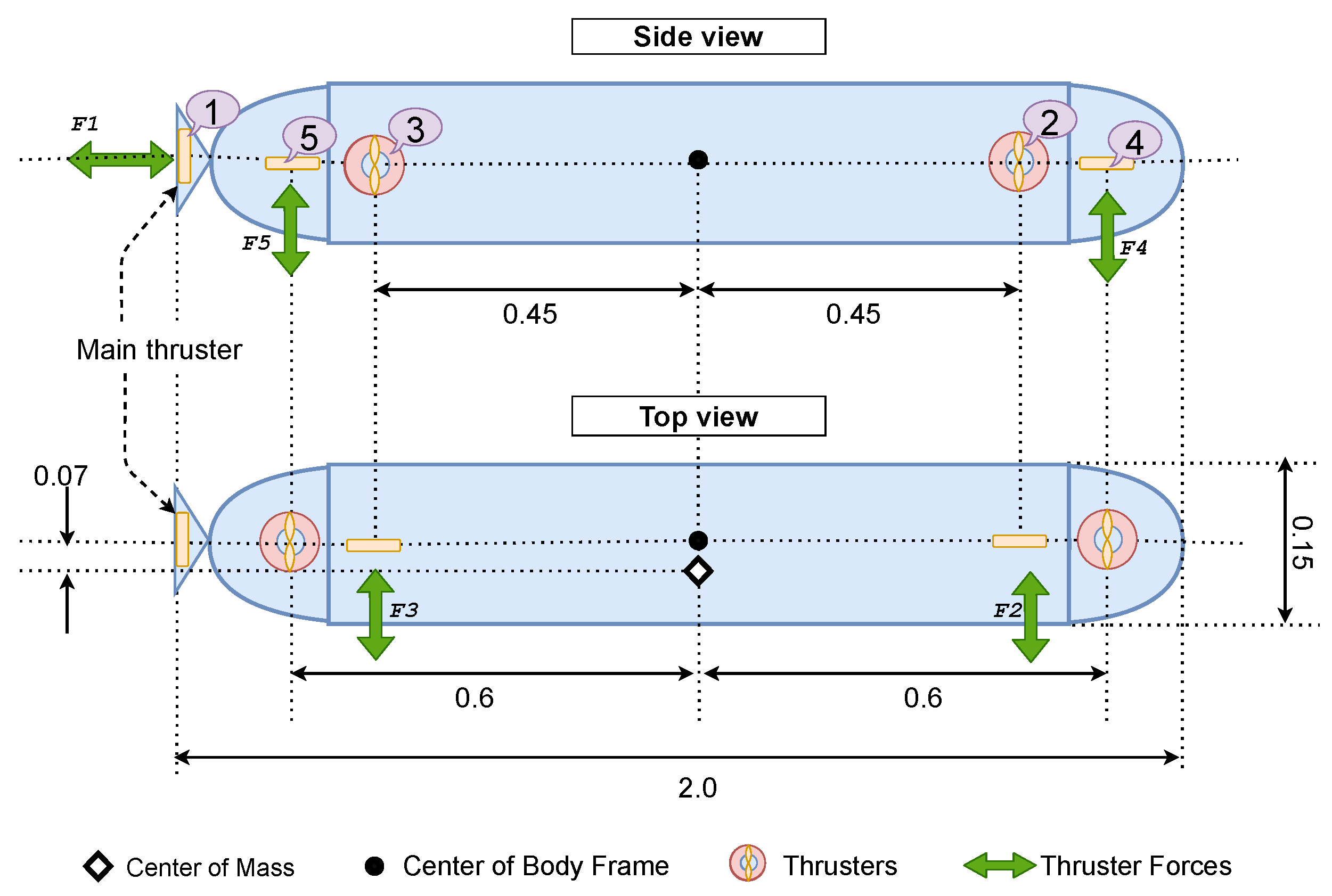
4.1. Simulation Setup
4.2. Free Space Parking and Docking Tests
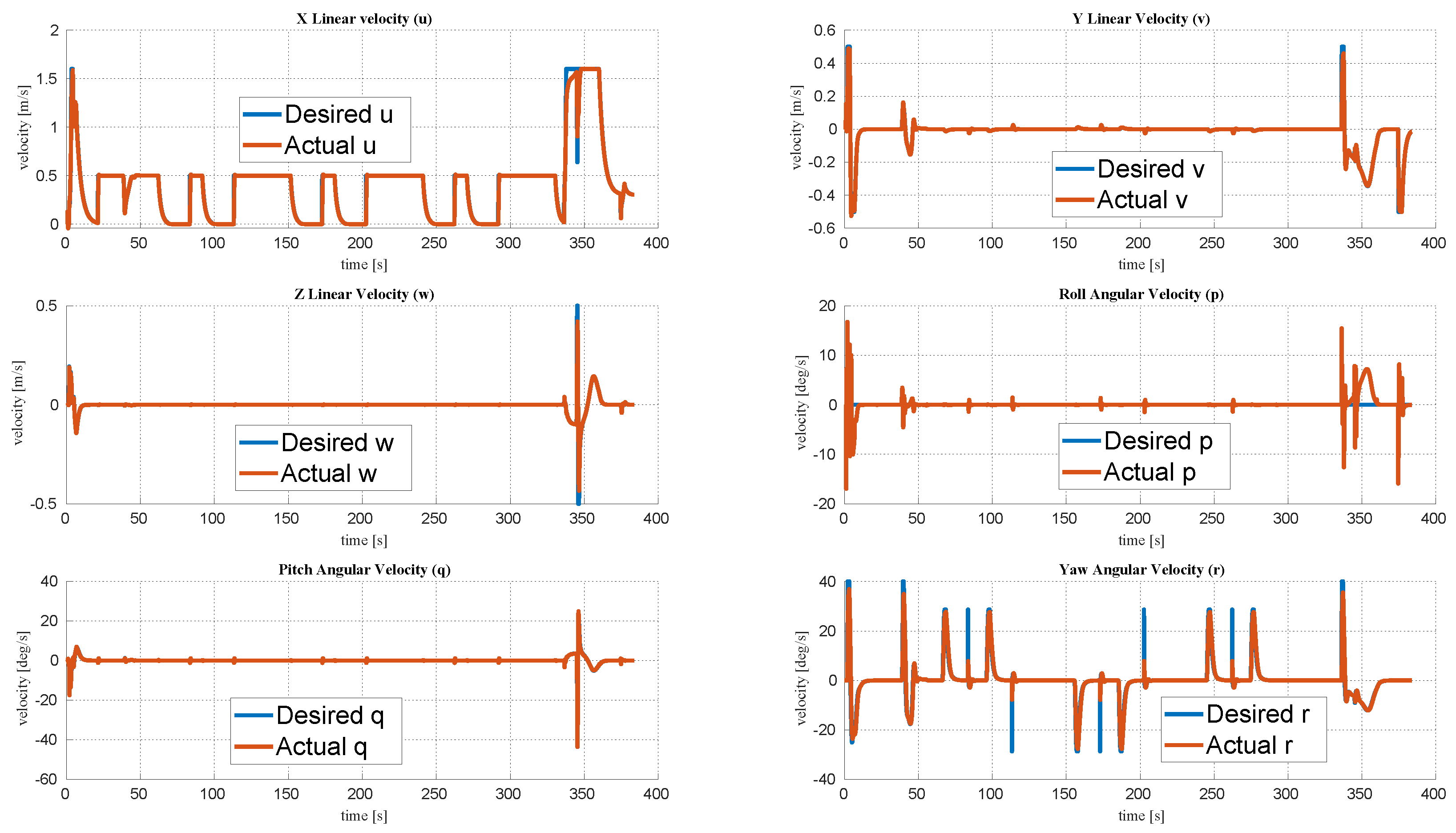
4.3. Vehicle Performing a Complete Mission
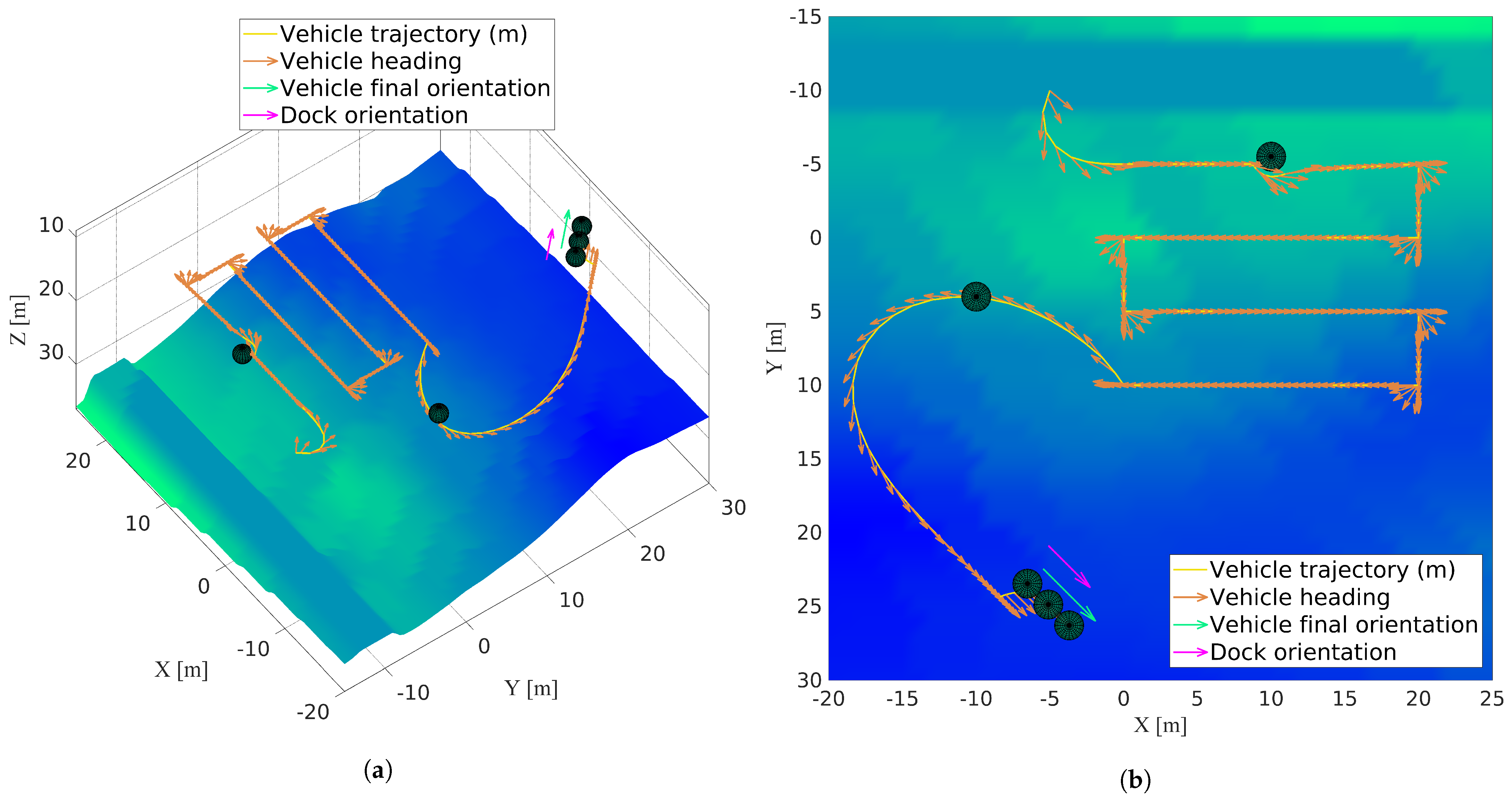
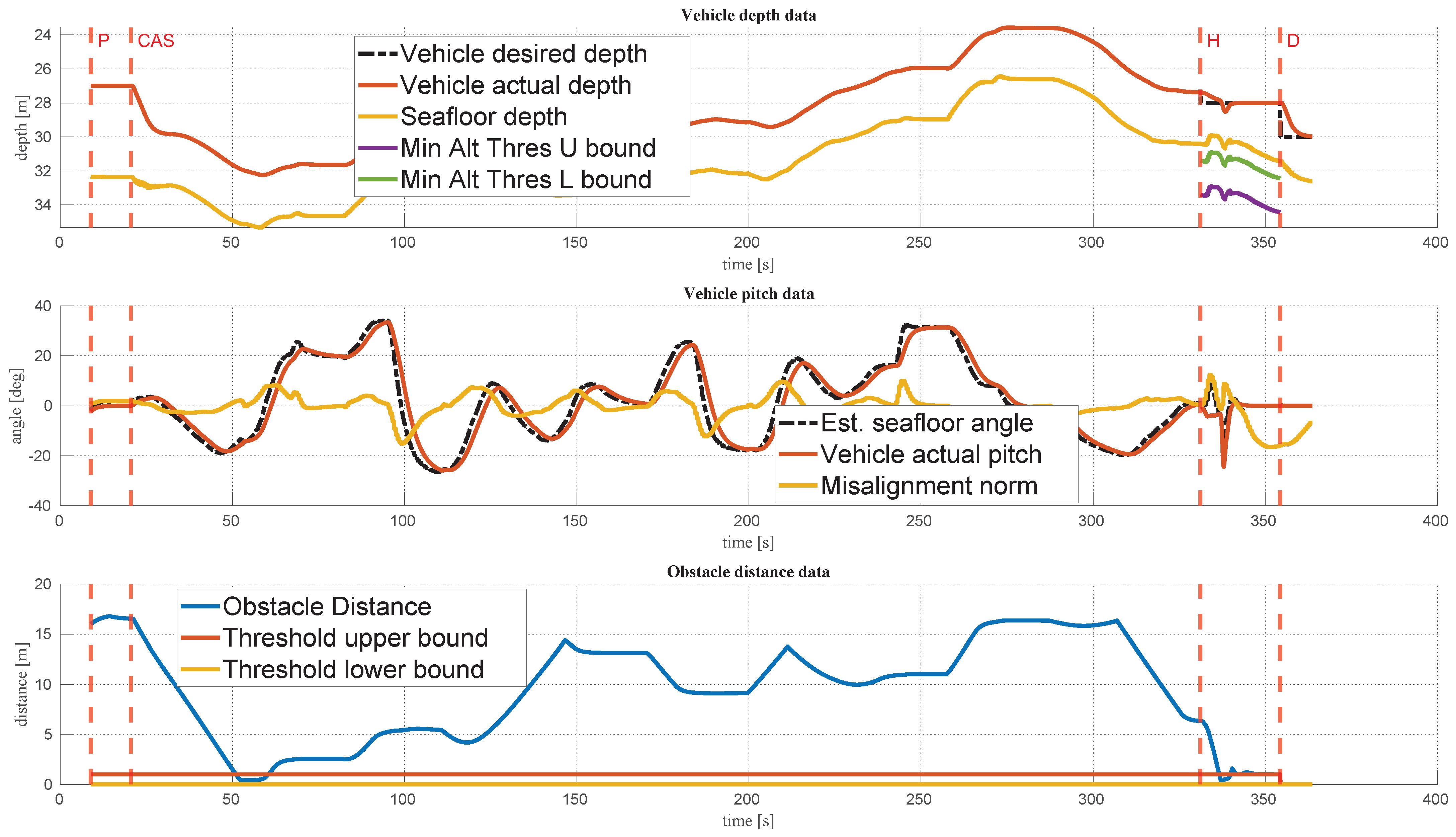
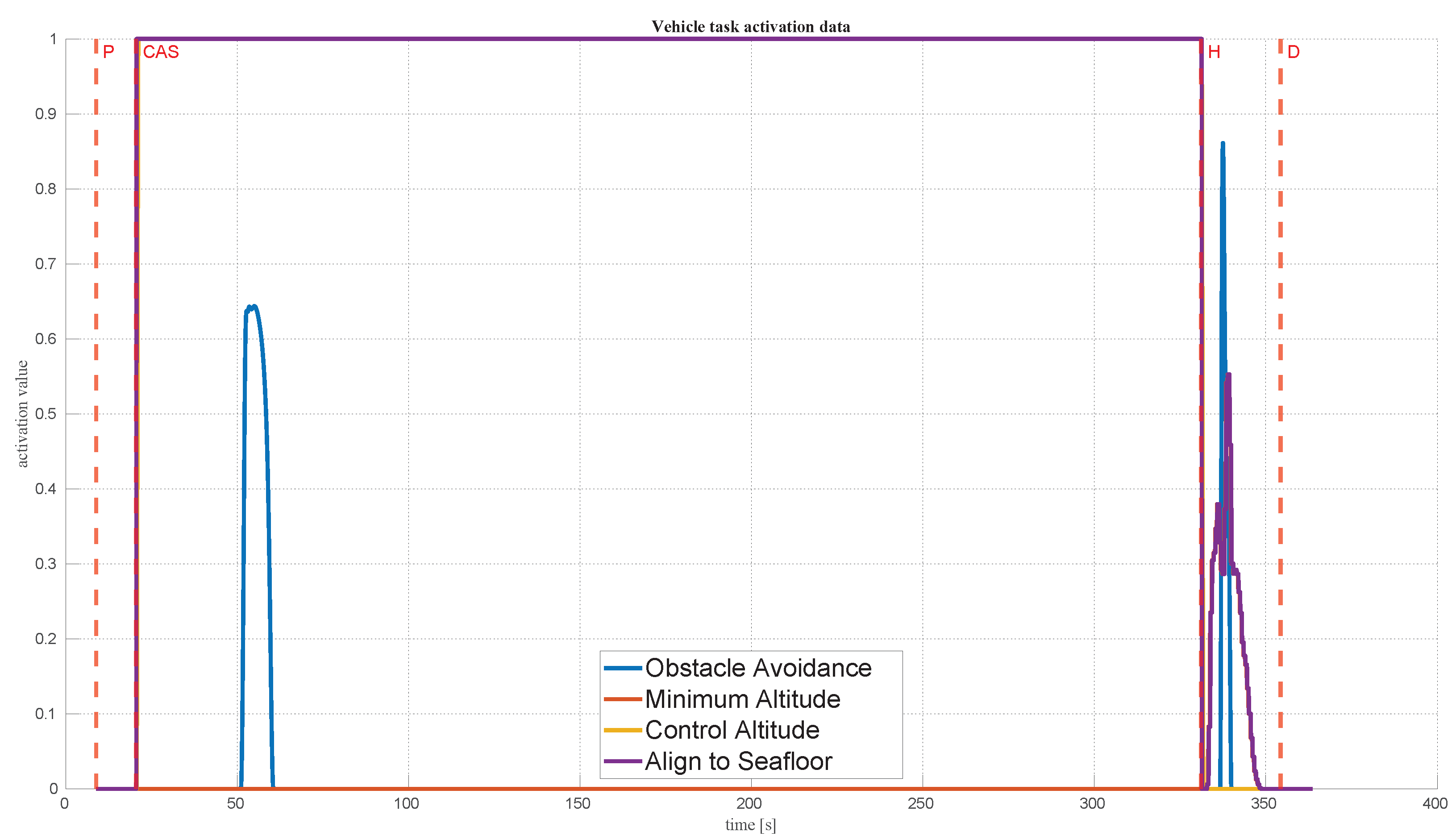
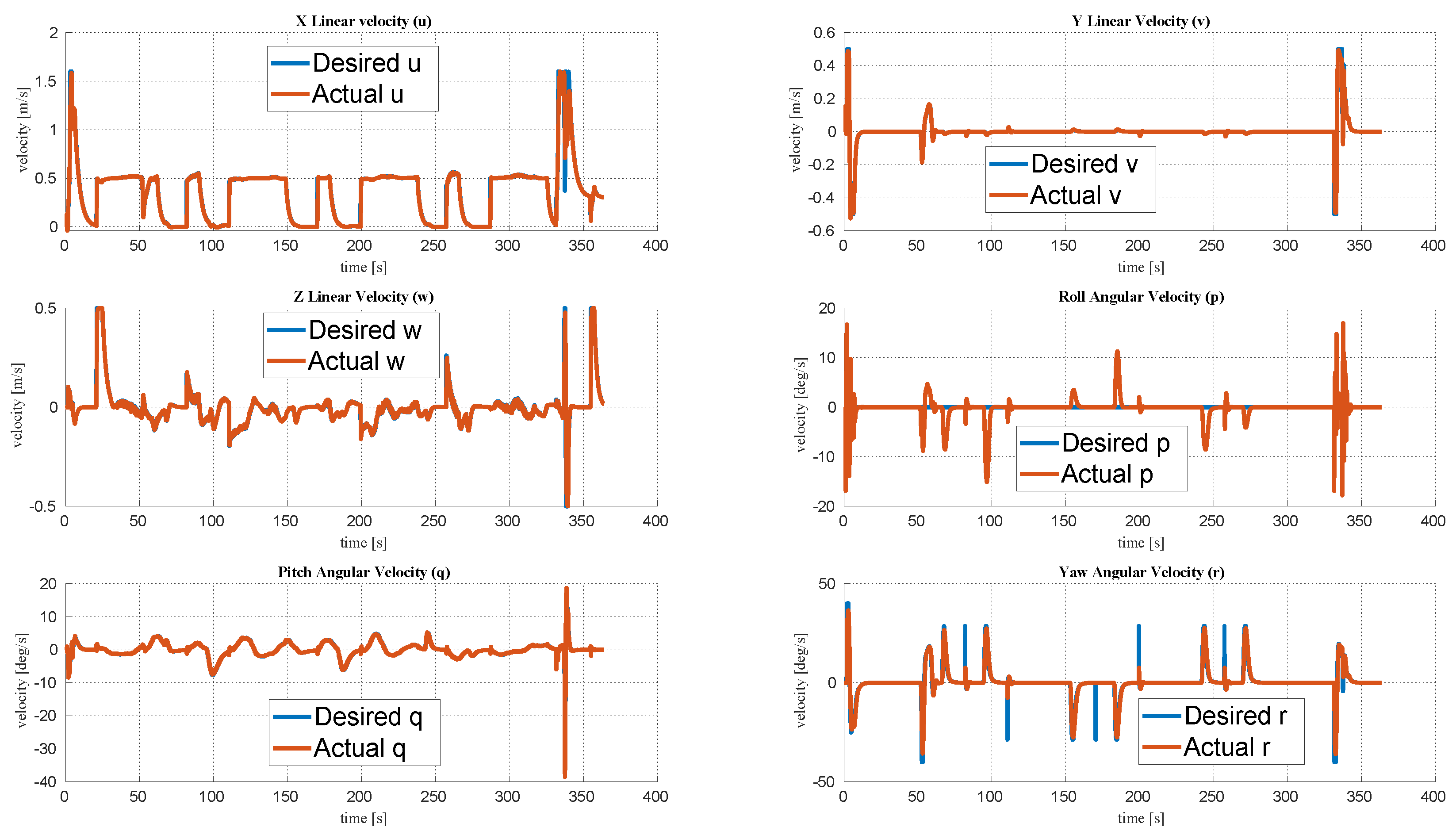
4.3.1. Constant Depth Mission with Docking to a Moving Docking Station Close to the Surface
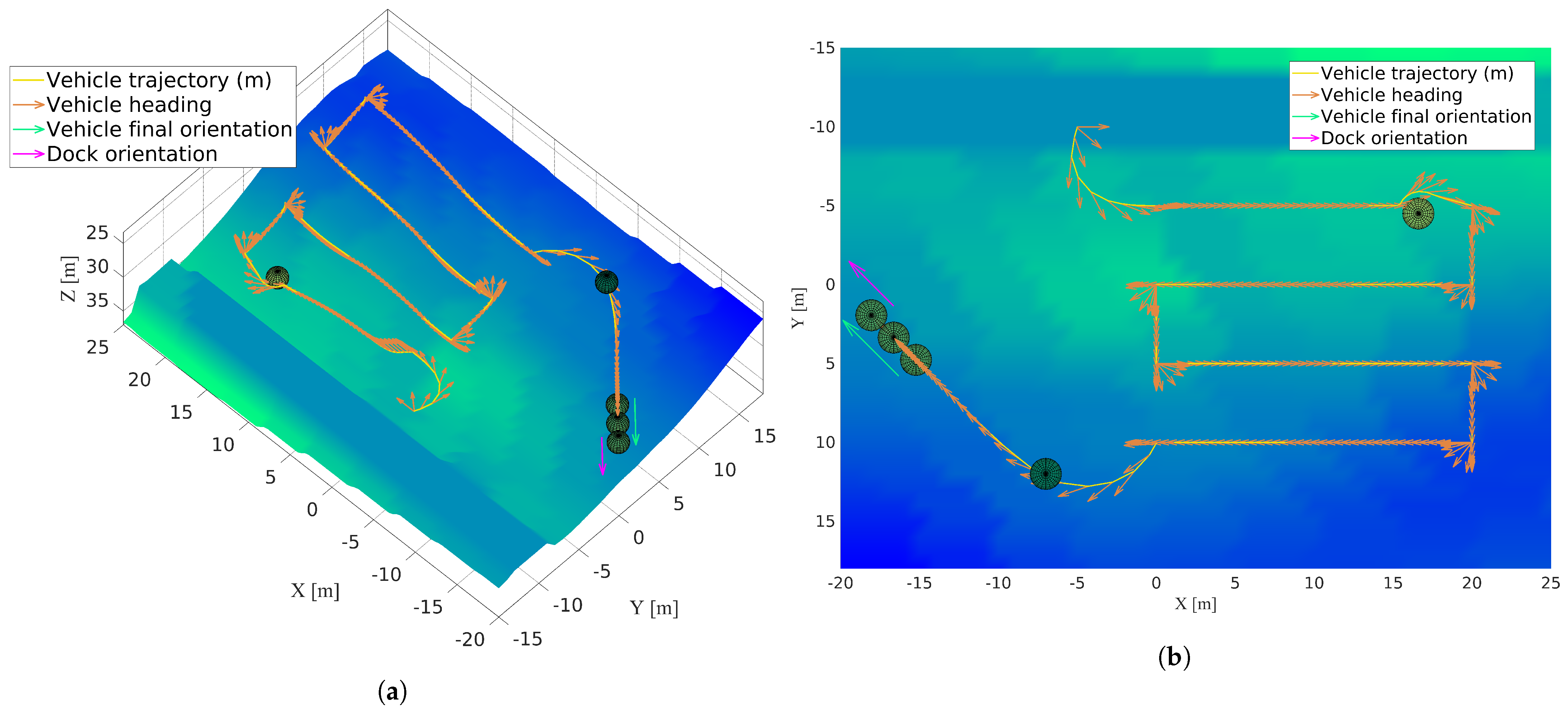
4.3.2. Constant Altitude Mission with Terrain Following and Docking to a Moving Docking Station Situated Close to the Seafloor
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wynn, R.B.; Huvenne, V.A.I.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, J.W.; Healey, A.J. The Present State of Autonomous Underwater Vehicle (AUV) Applications and Technologies. Mar. Technol. Soc. J. 2008, 42, 44–51. [Google Scholar] [CrossRef]
- Joye, S.B. Deepwater Horizon, 5 years on. Science 2015, 349, 592–593. [Google Scholar] [CrossRef]
- Anderson, B.; Crowell, J. Workhorse AUV—A cost-sensible new Autonomous Underwater Vehicle for Surveys/Soundings, Search & Rescue, and Research. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005. [Google Scholar] [CrossRef]
- Marani, G.; Choi, S.K.; Yuh, J. Underwater autonomous manipulation for intervention missions AUVs. Ocean Eng. 2009, 36, 15–23. [Google Scholar] [CrossRef]
- Palomeras, N.; Vallicrosa, G.; Mallios, A.; Bosch, J.; Vidal, E.; Hurtos, N.; Carreras, M.; Ridao, P. AUV homing and docking for remote operations. Ocean Eng. 2018, 154, 106–120. [Google Scholar] [CrossRef]
- Song, Z.; Marburg, A.; Manalang, D. Resident Subsea Robotic Systems: A Review. Mar. Technol. Soc. J. 2020, 54. [Google Scholar] [CrossRef]
- Martin, A.Y. Unmanned Maritime Vehicles: Technology Evolution and Implications. Mar. Technol. Soc. J. 2013, 47. [Google Scholar] [CrossRef]
- Newell, T. Technical Building Blocks for a Resident Subsea Vehicle. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Curtin, T.; Manalang, D. Resident Autonomous Underwater Vehicles: Docking Revisited. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Manalang, D.; Delaney, J.; Marburg, A.; Nawaz, A. Resident AUV Workshop 2018: Applications and a Path Forward. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Jacobs, T. Robotic Roustabouts for Tomorrow’s Subsea Fields. J. Pet. Technol. 2014, 66, 50–55. [Google Scholar] [CrossRef]
- Gilmour, B.; Niccum, G.; O’Donnell, T. Field resident AUV systems—Chevron’s long-term goal for AUV development. In Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles (AUV), Southampton, UK, 24–27 September 2012. [Google Scholar] [CrossRef]
- Zagatti, R.; Juliano, D.R.; Doak, R.; Souza, G.M.; de Paula Nardy, L.; Lepikson, H.A.; Gaudig, C.; Kirchner, F. FlatFish Resident AUV: Leading the Autonomy Era for Subsea Oil and Gas Operations. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Matsuda, T.; Maki, T.; Masuda, K.; Sakamaki, T. Resident autonomous underwater vehicle: Underwater system for prolonged and continuous monitoring based at a seafloor station. Robot. Auton. Syst. 2019, 120, 103231. [Google Scholar] [CrossRef]
- Furuholmen, M.; Hanssen, A.; Carter, R.; Hatlen, K.; Siesjo, J. Resident Autonomous Underwater Vehicle Systems—A Review of Drivers, Applications, and Integration Options for the Subsea Oil and Gas Market. In Proceedings of the Offshore Mediterranean Conference, Ravenna, Italy, 20–22 March 2013. [Google Scholar]
- Sarda, E.I.; Dhanak, M.R. A USV-Based Automated Launch and Recovery System for AUVs. IEEE J. Ocean. Eng. 2016, 42, 37–55. [Google Scholar] [CrossRef]
- Ahmad, S.M.; Sutton, R.; Burns, R. Retrieval of an Autonomous Underwater Vehicle: An Interception Approach. Underw. Technol. Int. J. Soc. Underw. 2003, 25, 185–197. [Google Scholar] [CrossRef]
- Hardy, T.; Barlow, G. Unmanned Underwater Vehicle (UUV) deployment and retrieval considerations for submarines. In Proceedings of the International Naval Engineering Conference and Exhibition, Hamburg, Germany, 1–3 April 2008. [Google Scholar]
- Renilson, M. A simplified concept for recovering a UUV to a submarine. Underw. Technol. Int. J. Soc. Underw. 2014, 32, 193–197. [Google Scholar] [CrossRef] [Green Version]
- Stuart, H.; Wang, S.; Khatib, O.; Cutkosky, M.R. The Ocean One hands: An adaptive design for robust marine manipulation. Int. J. Robot. Res. 2017, 36, 150–166. [Google Scholar] [CrossRef]
- Simetti, E. Autonomous Underwater Intervention. Curr. Robot. Rep. 2020, 1, 117–122. [Google Scholar] [CrossRef]
- Stokey, R.; Purcell, M.; Forrester, N.; Austin, T.; Goldsborough, R.; Allen, B.; von Alt, C. A docking system for REMUS, an autonomous underwater vehicle. In Proceedings of the OCEANS’97. MTS/IEEE Conference Proceedings, Halifax, NS, Canada, 6–9 October 1997; Volume 2, pp. 1132–1136. [Google Scholar]
- Vu, M.T.; Choi, H.S.; Nhat, T.Q.M.; Nguyen, N.D.; Lee, S.D.; Le, T.H.; Sur, J. Docking assessment algorithm for autonomous underwater vehicles. Appl. Ocean Res. 2020, 100, 102180. [Google Scholar] [CrossRef]
- Maire, F.D.; Prasser, D.; Dunbabin, M.; Dawson, M. A vision based target detection system for docking of an autonomous underwater vehicle. In Proceedings of the 2009 Australasion Conference on Robotics and Automation, Sydney, Australia, 2–4 December 2009. [Google Scholar]
- Cowen, S.; Briest, S.; Dombrowski, J. Underwater docking of autonomous undersea vehicles using optical terminal guidance. In Proceedings of the OCEANS’97, MTS/IEEE Conference Proceedings, Halifax, NS, Canada, 6–9 October 1997; Volume 2, pp. 1143–1147. [Google Scholar]
- Trslić, P.; Weir, A.; Riordan, J.; Omerdic, E.; Toal, D.; Dooly, G. Vision-Based Localization System Suited to Resident Underwater Vehicles. Sensors 2020, 20, 529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brignone, L.; Perrier, M.; Viala, C. A fully autonomous docking strategy for intervention AUVs. In Proceedings of the OCEANS 2007-Europe, Aberdeen, Scotland, 18–21 June 2007; pp. 1–6. [Google Scholar]
- Vandavasi, B.N.J.; Arunachalam, U.; Narayanaswamy, V.; Raju, R.; Vittal, D.P.; Muthiah, R.; Gidugu, A.R. Concept and testing of an electromagnetic homing guidance system for autonomous underwater vehicles. Appl. Ocean Res. 2018, 73, 149–159. [Google Scholar] [CrossRef]
- Woo, J.; Kim, N. Vector Field based Guidance Method for Docking of an Unmanned Surface Vehicle. In Proceedings of the Twelfth ISOPE Pacific/Asia Offshore Mechanics Symposium, Gold Coast, Australia, 4–7 October 2016. [Google Scholar]
- Sujit, P.B.; Healey, A.J.; Sousa, J.B. AUV docking on a moving submarine using a K-R navigation function. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, D.; Chen, T.; Zhou, J.; Wei, S.; Wang, Y. Modeling, strategy and control of UUV for autonomous underwater docking recovery to moving platform. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017. [Google Scholar] [CrossRef]
- Breivik, M.; Loberg, J.E. A Virtual Target-Based Underway Docking Procedure for Unmanned Surface Vehicles. IFAC Proc. Vol. 2011, 44, 13630–13635. [Google Scholar] [CrossRef] [Green Version]
- Siciliano, B.; Slotine, J.J.E. A general framework for managing multiple tasks in highly redundant robotic systems. In Proceedings of the Fifth International Conference on Advanced Robotics ’Robots in Unstructured Environments, Pisa, Italy, 19–22 July 1991. [Google Scholar] [CrossRef]
- Lee, J.; Mansard, N.; Park, J. Intermediate Desired Value Approach for Task Transition of Robots in Kinematic Control. IEEE Trans. Robot. 2012, 28, 1260–1277. [Google Scholar] [CrossRef]
- Moe, S.; Antonelli, G.; Teel, A.R.; Pettersen, K.Y.; Schrimpf, J. Set-Based Tasks within the Singularity-Robust Multiple Task-Priority Inverse Kinematics Framework: General Formulation, Stability Analysis, and Experimental Results. Front. Robot. AI 2016, 3. [Google Scholar] [CrossRef]
- Simetti, E.; Casalino, G.; Wanderlingh, F.; Aicardi, M. Task priority control of underwater intervention systems: Theory and applications. Ocean Eng. 2018, 164, 40–54. [Google Scholar] [CrossRef]
- Cieślak, P.; Simoni, R.; Ridao Rodríguez, P.; Youakim, D. Practical formulation of obstacle avoidance in the Task-Priority framework for use in robotic inspection and intervention scenarios. Robot. Auton. Syst. 2020, 124, 103396. [Google Scholar] [CrossRef]
- Simetti, E.; Casalino, G. A Novel Practical Technique to Integrate Inequality Control Objectives and Task Transitions in Priority Based Control. J. Intell. Robot. Syst. 2016, 84, 877–902. [Google Scholar] [CrossRef]
- Simetti, E.; Wanderlingh, F.; Torelli, S.; Bibuli, M.; Odetti, A.; Bruzzone, G.; Rizzini, D.L.; Aleotti, J.; Palli, G.; Moriello, L.; et al. Autonomous Underwater Intervention: Experimental Results of the MARIS Project. IEEE J. Ocean. Eng. 2018, 43, 620–639. [Google Scholar] [CrossRef]
- Di Lillo, P.; Simetti, E.; Wanderlingh, F.; Casalino, G.; Antonelli, G. Underwater Intervention With Remote Supervision via Satellite Communication: Developed Control Architecture and Experimental Results Within the Dexrov Project. IEEE Trans. Control Syst. Technol. 2020, 29, 102–123. [Google Scholar] [CrossRef]
- Di Vito, D.; De Palma, D.; Simetti, E.; Indiveri, G.; Antonelli, G. Experimental validation of the modeling and control of a multibody underwater vehicle manipulator system for sea mining exploration. J. Field Robot. 2020. [Google Scholar] [CrossRef]
- Simetti, E.; Campos, R.; Di Vito, D.; Quintana, J.; Antonelli, G.; Garcia, R.; Turetta, A. Sea Mining Exploration with an UVMS: Experimental Validation of the Control and Perception Framework. IEEE/ASME Trans. Mechatronics 2020, 1. [Google Scholar] [CrossRef]
- Simetti, E.; Casalino, G. Manipulation and Transportation With Cooperative Underwater Vehicle Manipulator Systems. IEEE J. Ocean. Eng. 2016, 42, 782–799. [Google Scholar] [CrossRef]
- Simetti, E.; Casalino, G.; Wanderlingh, F.; Aicardi, M. A task priority approach to cooperative mobile manipulation: Theory and experiments. Robot. Auton. Syst. 2019, 122, 103287. [Google Scholar] [CrossRef]
- Aicardi, M.; Cannata, G.; Casalino, G.; Indiveri, G. Guidance of 3d underwater nonholonomic vehicle via projection on holonomic solutions. Underw. Veh. Technol. 2000, 12, 11–16. [Google Scholar]
- Aicardi, M.; Casalino, G.; Indiveri, G. Closed loop control of 3D underactuated vehicles via velocity field tracking. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Proceedings (Cat. No.01TH8556), Como, Italy, 8–12 July 2001; Volume 1. [Google Scholar] [CrossRef]
- SNAME. Nomenclature for Treating the Motion of a Submerged Body through a Fluid; Technical and Research Bulletin No. 1-5; SNAME: New York, NY, USA, 1950; pp. 1–15. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Fossen, T.I.; Fjellstad, O.E. Nonlinear modelling of marine vehicles in 6 degrees of freedom. Math. Model. Syst. 1995, 1, 17–27. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley Online Library: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- Antonelli, G.; Indiveri, G.; Chiaverini, S. Prioritized closed-loop inverse kinematic algorithms for redundant robotic systems with velocity saturations. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2015; pp. 5892–5897. [Google Scholar] [CrossRef]
- Lekkas, A.; Fossen, T.I. Line-of-Sight Guidance for Path Following of Marine Vehicles. In Advanced in Marine Robotics; LAP LAMBERT Academic Publishing, 2013; pp. 63–92. Available online: https://www.lap-publishing.com/catalog/details/store/gb/book/978-3-659-41689-7/advanced-in-marine-robotics (accessed on 3 February 2021).
| 1 |








| Task | Task Type | |||||
|---|---|---|---|---|---|---|
| Minimum Altitude | I | 1 | 1 | 1 | ||
| Obstacle Avoidance | I | 2 | 2 | 2 | ||
| Horizontal Alignment | I | 3 | ||||
| Vehicle Altitude | E | 3 | ||||
| Vehicle Depth | E | 3 | ||||
| Seafloor Alignment | E | 4 | 4 | 1 | ||
| Field Velocity | E | 5 | ||||
| Follow 2D Path | E | 5 | 5 | |||
| Velocity Alignment | E | 6 | 6 | 6 | ||
| Hold Position | E | 2 | ||||
| Survey Leg Alignment | E | 3 | ||||
| Terminal Dock | E | 1 | ||||
| Dock Attitude | E | 2 |
| System Parameter | Value | Model Parameter | Value |
|---|---|---|---|
| DOF | 5 | Type | Torpedo |
| Length | 2 m | G | 9.810 |
| Width | 0.15 m | 1023.6 | |
| Weight | 31 kg | CG | [0.000, 0.000, 0.070] |
| Main Propulsion | Central thruster | CB | [0.000, 0.000, 0.000] |
| Propellers | 5 | Added Mass | diag [−0.47, −22.7, −22.7, −0.1, −3.64, −3.64] |
| Linear Drag | diag [1.079, 10.21, 10.21, 0.5, 1.061, 1.061] | ||
| Quadratic Drag | diag [0.794, 102.1, 102.1, 20.48, 15.191, 15.191] | ||
| Thruster distance | [−1.0, 0.45, −0.45, 0.6, −0.6] |
| Parameter | Value |
|---|---|
| Vehicle initial pose / Home (m, deg) | [−5, −10, 18, 0, 0, 40] |
| Waypoint 1 pose (m, deg) | [0, −5, 20, 0, 0, 0] |
| Waypoint 2 pose (m, deg) | [20, −5, 20, 0, 0, 90] |
| Waypoint 3 pose (m, deg) | [20, 0, 20, 0, 0, 180] |
| Waypoint 4 pose (m, deg) | [0, 0, 20, 0, 0, 90] |
| Waypoint 5 pose (m, deg) | [0, 5, 20, 0, 0, 0] |
| Waypoint 6 pose (m, deg) | [20, 5, 20, 0, 0, 90] |
| Waypoint 7 pose (m, deg) | [20, 10, 20, 0, 0, 180] |
| Waypoint 8 pose (m, deg) | [0, 10, 20, 0, 0, 180] |
| Dock velocity (m/s) (in the dock frame) | [0.3, 0, 0] |
| Ocean current velocity (m/s) (in the world frame) | [0, 0.2, 0] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomas, C.; Simetti, E.; Casalino, G. A Unifying Task Priority Approach for Autonomous Underwater Vehicles Integrating Homing and Docking Maneuvers. J. Mar. Sci. Eng. 2021, 9, 162. https://doi.org/10.3390/jmse9020162
Thomas C, Simetti E, Casalino G. A Unifying Task Priority Approach for Autonomous Underwater Vehicles Integrating Homing and Docking Maneuvers. Journal of Marine Science and Engineering. 2021; 9(2):162. https://doi.org/10.3390/jmse9020162
Chicago/Turabian StyleThomas, Cris, Enrico Simetti, and Giuseppe Casalino. 2021. "A Unifying Task Priority Approach for Autonomous Underwater Vehicles Integrating Homing and Docking Maneuvers" Journal of Marine Science and Engineering 9, no. 2: 162. https://doi.org/10.3390/jmse9020162
APA StyleThomas, C., Simetti, E., & Casalino, G. (2021). A Unifying Task Priority Approach for Autonomous Underwater Vehicles Integrating Homing and Docking Maneuvers. Journal of Marine Science and Engineering, 9(2), 162. https://doi.org/10.3390/jmse9020162







