Dynamic Evacuation Planning on Cruise Ships Based on an Improved Ant Colony System (IACS)
Abstract
1. Introduction
2. Establishment of an Algorithm Model
2.1. ACS
2.2. Mathematical Modeling
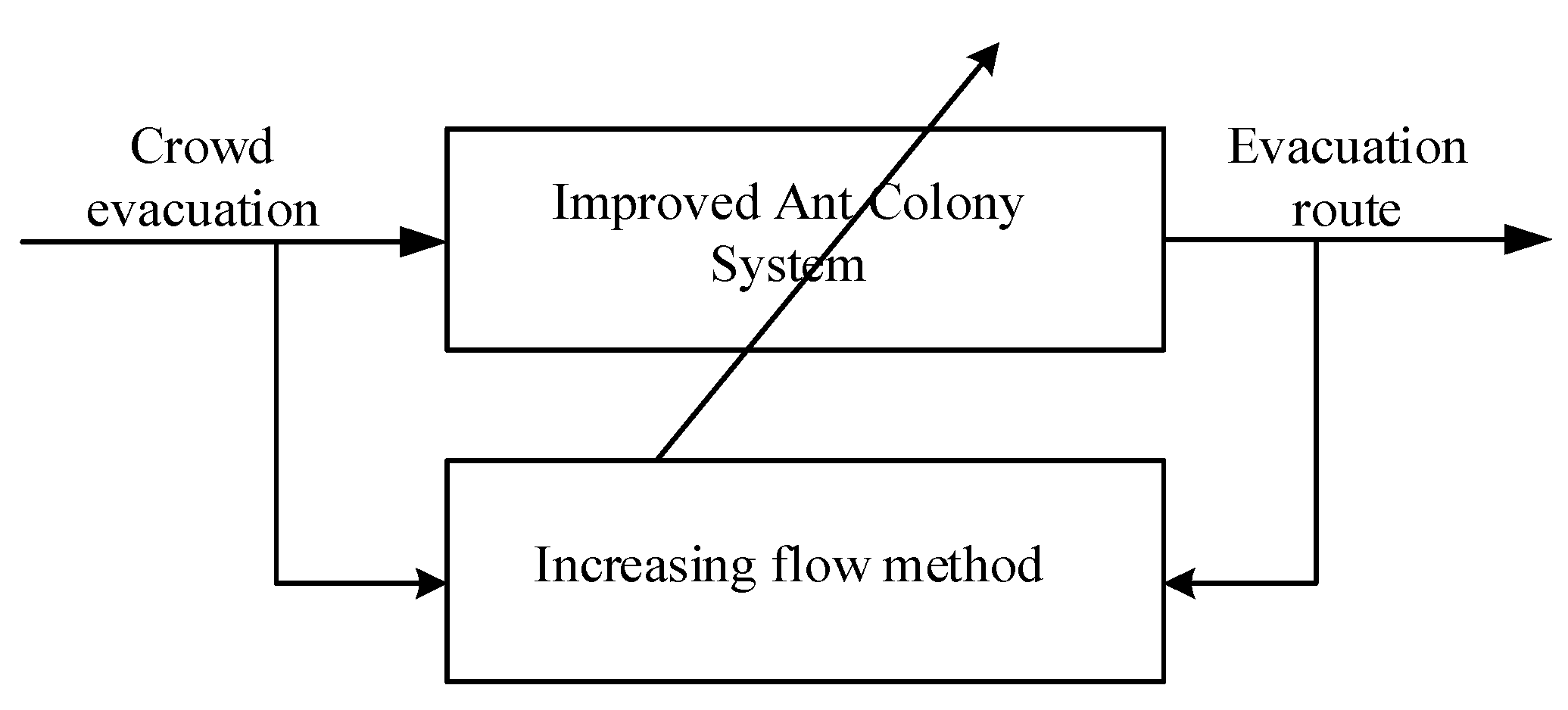
2.3. Proposed the IACS
- If the capacity is sufficiently large to meet the cardinal number, then the flow of will increase the cardinal number when a group of people move from nodes i to j.
- If the capacity is sufficiently small to meet the cardinal number, then part of the people will be allocated to other paths until the end of the evacuation with the maximum capacity of when a group of people move from nodes i to j.where represents the number of people passing by in unit time from nodes i to j.
- Initialize the parameters, number of ant colonies m, expected heuristic factor , maximum number of iterations , pheromone volatilization factor , random number , and number of ants placing pheromone after each iteration ;
- Start the iteration and initialize the position of the ants according to the position of the actual crowd;
- Calculate the next node j selected by the current crowd and the probability of selecting this node using Formulas (5) and (6);
- Increase the flow according to Formulas (13)–(15) and form a complete path set by minimizing the total evacuation time;
- Update the local pheromones in Formulas (8) and (9) ;
- Evaluate whether the number of iterations reaches the maximum number . If yes, then end the iterations and output the optimal path set; otherwise, update the global pheromones according to Formulas (16) and (17) and return to Step 2;
- End the algorithm and output the results.
3. Definition of Problems
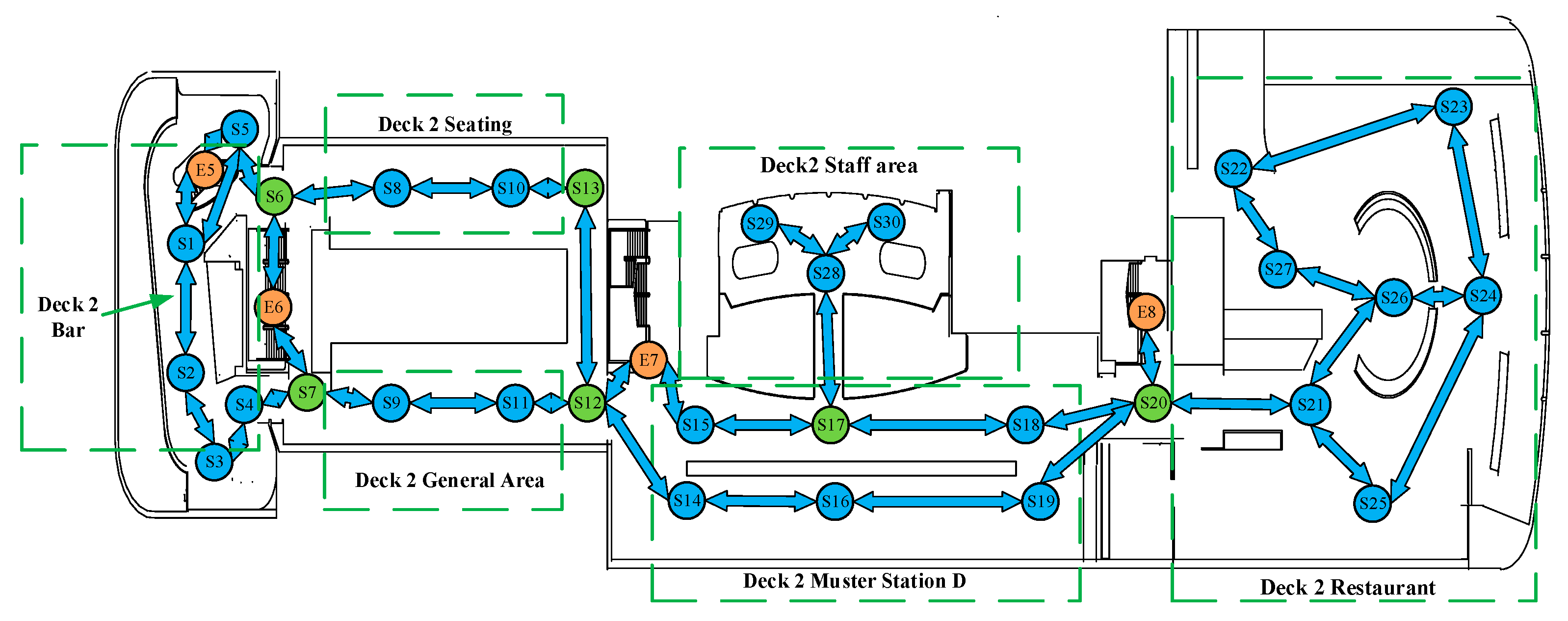
3.1. Establishment of a Ship Node Network
- The departure points are set in person activity areas, such as guest rooms, staff areas, and cockpit and so on, and transfer nodes are set at turns or corridor intersections;
- Considering the actual layout of the cruise ship, muster station D contains many nodes.
3.2. Edge Maximum Capacity
3.3. Problem Description
- Everyone can reach the safe area;
- Do not consider family group behavior;
- Ship motion, heeling, and trimming are not considered;
- Does not consider the effects of smoke, heat and toxic fire products on passenger/crew performance.
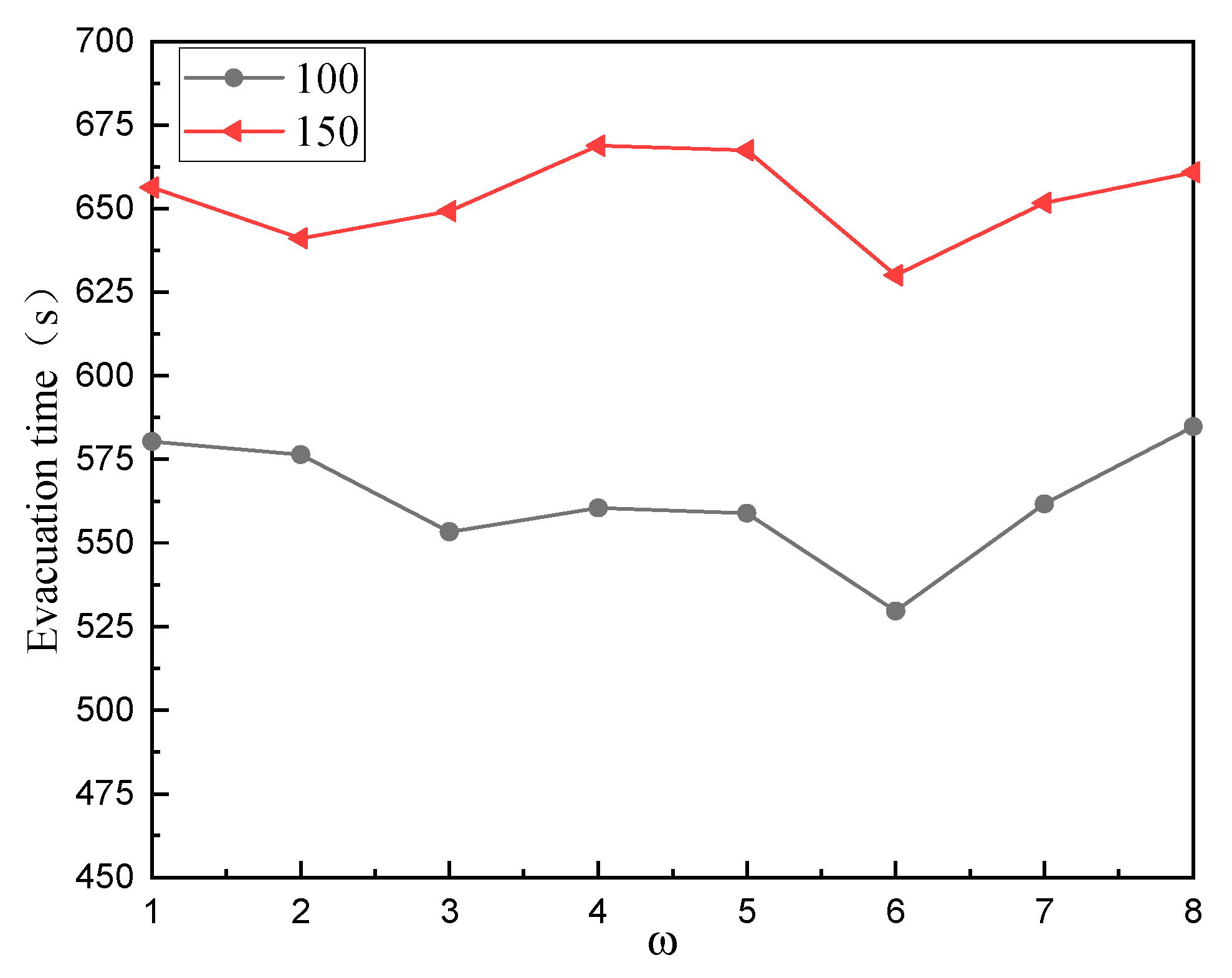
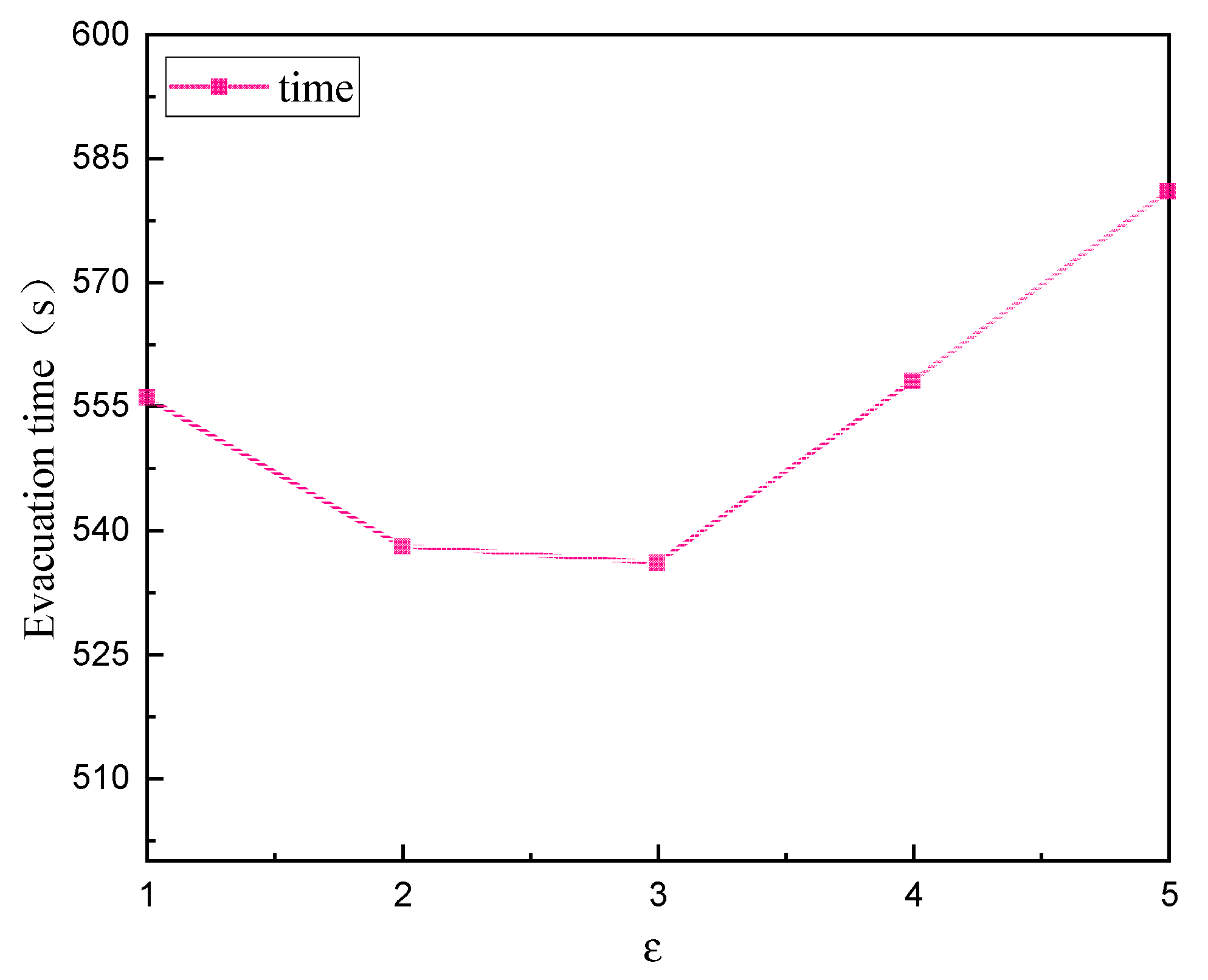
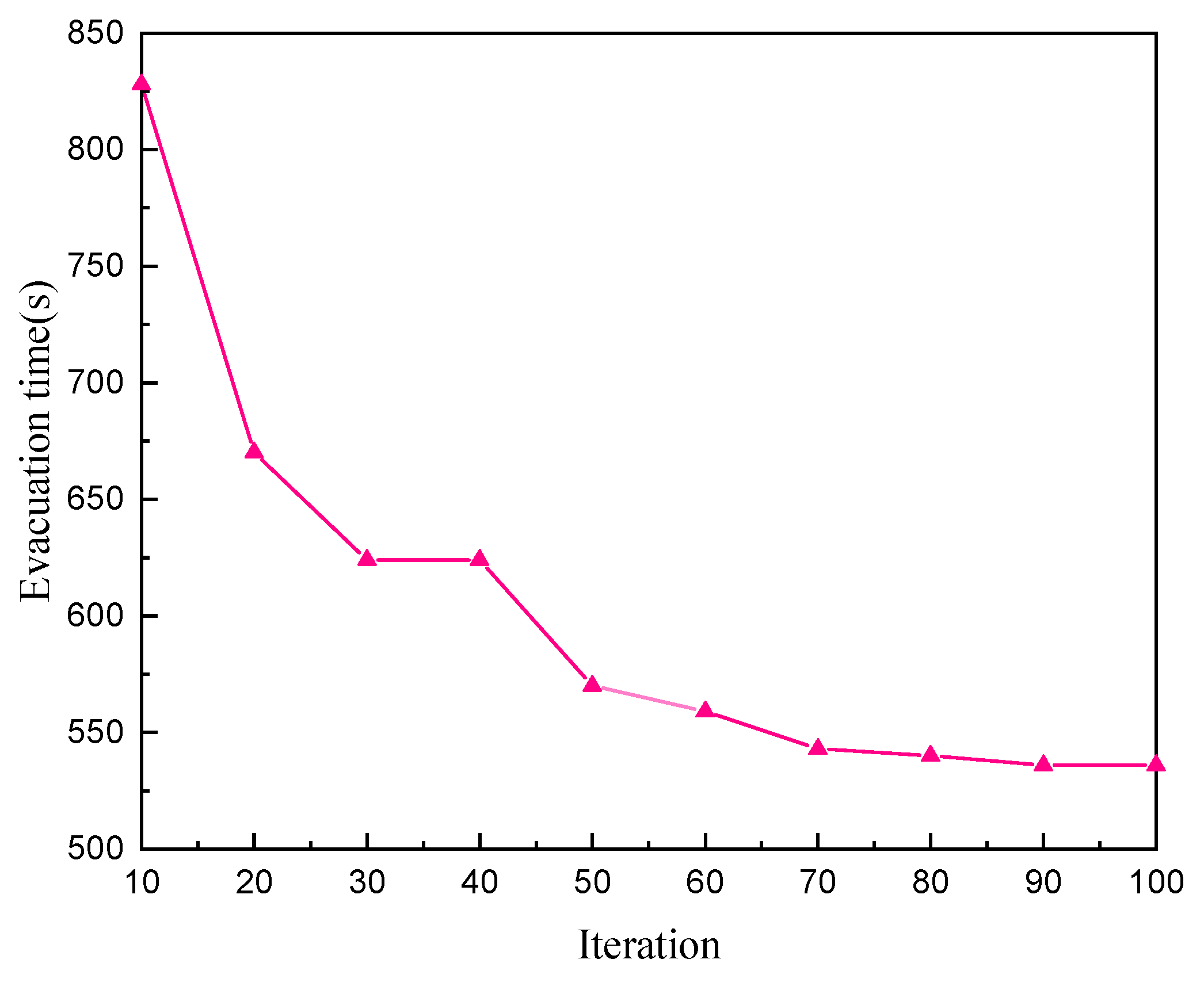
4. Results with Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, M.; Cai, W.; Zhao, H. Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model. Symmetry 2019, 11, 1166. [Google Scholar] [CrossRef]
- Park, Y.S.; Park, S.W.; Cho, I.S. A Basic Study on Prediction Module Development of Collision Risk based on Ship’s Operator’s Consciousness. J. Navig. Port. Res. 2018, 39, 199–207. [Google Scholar] [CrossRef]
- Park, Y.S.; Kim, J.S.; Park, J.S. A Study on the Future Traffic Volume Estimation for Kwangyang Port Using the Consideration Factors of Marine Traffic Engineering. J. Navig. Port. Res. 2007, 31, 447–454. [Google Scholar] [CrossRef][Green Version]
- Xie, Q.; Li, S.; Ma, C.; Wang, J.; Liu, J.; Wang, Y. Uncertainty analysis of passenger evacuation time for ships’ safe return to port in fires using polynomial chaos expansion with Gauss quadrature. Appl. Ocean. Res. 2020, 101, 102190. [Google Scholar] [CrossRef]
- Grandison, A.; Deere, S.; Lawrence, P.; Galea, E.R. The use of confidence intervals to determine convergence of the total evacuation time for stochastic evacuation models. Ocean. Eng. 2017, 146, 234–245. [Google Scholar] [CrossRef]
- Aydogdu, Y.V.; Aksoy, S. A study on quantitative benefits of port community systems. Marit. Policy Manag. 2015, 42, 1–10. [Google Scholar] [CrossRef]
- Vanem, E.; Skjong, R. Designing for safety in passenger ships utilizing advanced evacuation analyses—A risk based approach. Safety Sci. 2006, 44, 111–135. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.; Park, J.H.; Park, B.J. The current status and future issues in human evacuation from ships. Safety Sci. 2003, 41, 861–876. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, Q.S. The adaptive cruise control vehicles in the cellular automata model. Phys. Lett. A 2006, 359, 99–102. [Google Scholar] [CrossRef]
- Pelechano, N.; Malkawi, A. Evacuation simulation models: Challenges in modeling high rise building evacuation with cellular automata approaches. Automat. Constr. 2008, 17, 377–385. [Google Scholar] [CrossRef]
- Xia, C.; Wang, H.; Zhang, A.; Zhang, W. A high-performance cellular automata model for urban simulation based on vectorization and parallel computing technology. Int. J. Geograp. Inf. Sci. 2018, 32, 399–424. [Google Scholar] [CrossRef]
- Uno, K.; Kashiyama, K. Development of simulation system for the disaster evacuation based on multi-agent model using GIS. Tsinghua Sci. Technol. 2008, 13, 348–353. [Google Scholar] [CrossRef]
- Zhou, M.; Dong, H.; Zhao, Y.; Ioannou, P.A.; Wang, F.Y. Optimization of crowd evacuation with leaders in urban rail transit stations. IEEE Trans. Intel. Transp. 2019, 20, 4476–4487. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, C.; Wen, J.; Li, W.; Liu, R.; Xu, H. Integrating multi-agent evacuation simulation and multi-criteria evaluation for spatial allocation of urban emergency shelters. Int. J. Geogr. Inf. Sci. 2018, 32, 1884–1910. [Google Scholar] [CrossRef]
- Wang, C.; Wang, K.; Tao, J.; Zhou, Y. Research on Real-Time Optimal Path Planning Model and Algorithm for Ship Block Transportation in Shipyard. J. Mar. Sci. Eng. 2020, 8, 991. [Google Scholar] [CrossRef]
- Zhou, J.W.; Liu, M.R.; Kong, L.J.; Kuang, H. Paired behavior effect on pedestrian evacuation dynamics. Acta Phys. Sin. 2009, 58, 3001–3007. [Google Scholar]
- Kinsey, M.J.; Gwynne, S.M.V.; Kuligowski, E.D.; Kinateder, M. Cognitive biases within decision making during fire evacuations. Fire Technol. 2019, 55, 465–485. [Google Scholar] [CrossRef]
- Aydogdu, Y.V. A comparison of maritime risk perception and accident statistics in the Istanbul Straight. J. Navig. 2014, 67, 129. [Google Scholar] [CrossRef]
- Jeong, J.S.; Kim, S.Y. A Design of Communication Network Architecture for E-Navigation Services. J. Navig. Port. Res. 2008, 32, 37–45. [Google Scholar] [CrossRef]
- Jeong, J.S.; Sakaguchi, K.; Araki, K.; Takada, J.I. Generalization of MUSIC using extended array mode vector for joint estimation of instantaneous DOA and angular spread. IEICE Trans. Commun. 2001, 84, 1781–1789. [Google Scholar]
- Li, Y.; Cai, W.; Kana, A.A. Design of level of service on facilities for crowd evacuation using genetic algorithm optimization. Safety Sci. 2019, 120, 237–247. [Google Scholar] [CrossRef]
- Dulebenets, M.A.; Pasha, J.; Abioye, O.F.; Kavoosi, M.; Ozguven, E.E.; Moses, R.; Sando, T. Exact and heuristic solution algorithms for efficient emergency evacuation in areas with vulnerable populations. Int. J. Disaster Risk Reduct. 2019, 39, 101114. [Google Scholar] [CrossRef]
- Ni, W.; Li, W.; Wang, H.; Xiong, C.; Guo, D. Capacity-constrained contraflow adaption for lane reconfiguration in evacuation planning. J. Adv. Transport. 2018, 2018. [Google Scholar] [CrossRef]
- Goerigk, M.; Deghdak, K.; Heßler, P. A comprehensive evacuation planning model and genetic solution algorithm. Transport. Res. E-log. 2014, 71, 82–97. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, F.; Ma, Y.; Pota, H.R.; Shen, W. Evacuation path optimization based on quantum ant colony algorithm. Adv. Eng. Inform. 2016, 30, 259–267. [Google Scholar] [CrossRef]
- Batmetan, J.R.; Santoso, A. A multiple-objective ant colony algorithm for optimizing disaster relief logistics. Adv. Sci. Lett. 2017, 23, 2344–2347. [Google Scholar] [CrossRef]
- Forcael, E.; González, V.; Orozco, F.; Vargas, S.; Pantoja, A.; Moscoso, P. Ant colony optimization model for tsunamis evacuation routes. Comput. Aided Civ. Inf. 2014, 29, 723–737. [Google Scholar] [CrossRef]
- Lim, G.J.; Zangeneh, S.; Baharnemati, M.R.; Assavapokee, T. A capacitated network flow optimization approach for short notice evacuation planning. Eur. J. Oper. Res. 2012, 223, 234–245. [Google Scholar] [CrossRef]
- Cova, T.J.; Johnson, J.P. A network flow model for lane-based evacuation routing. Transport. Res. A Pol. 2003, 37, 579–604. [Google Scholar] [CrossRef]
- Chen, P.H.; Feng, F. A fast flow control algorithm for real-time emergency evacuation in large indoor areas. Fire Saf. J. 2009, 44, 732–740. [Google Scholar] [CrossRef]
- Russo, F.; Rindone, C. Planning in road evacuation: Classification of exogenous activities. WIT Trans. Built Environ. 2011, 116, 639–651. [Google Scholar]
- Gai, W.M.; Du, Y.; Deng, Y.F. Evacuation risk assessment of regional evacuation for major accidents and its application in emergency planning: A case study. Saf. Sci. 2018, 106, 203–218. [Google Scholar] [CrossRef]
- Di Gangi, M.; Velonà, P. Multimodal mesoscopic approach in modeling pedestrian evacuation. Transport. Res. Rec. 2009, 2090, 51–58. [Google Scholar] [CrossRef]
- Russo, F.; Vitetta, A. Risk evaluation in a transportation system. Int. J. Sustain. Dev. Plan. 2006, 1, 170–191. [Google Scholar] [CrossRef]
- Yoo, B.; Choi, S.D. Emergency evacuation plan for hazardous chemicals leakage accidents using GIS-based risk analysis techniques in South Korea. Int. J. Environ. Res. Public Health 2019, 16, 1948. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Zhang, X. Study on rapid evacuation in high-rise buildings. Eng. Sci. Technol. 2017, 20, 1203–1210. [Google Scholar] [CrossRef]
- Seike, M.; Kawabata, N.; Hasegawa, M. Experiments of evacuation speed in smoke-filled tunnel. Tunn. Undergr. Space Tech. 2016, 53, 61–67. [Google Scholar] [CrossRef]
- Huang, Z.M.; Chen, W.N.; Li, Q.; Luo, X.N.; Yuan, H.Q.; Zhang, J. Ant Colony Evacuation Planner: An Ant Colony System With Incremental Flow Assignment for Multipath Crowd Evacuation. IEEE Trans. Cybern. 2020, 2168–2275. [Google Scholar] [CrossRef]
- Gajpal, Y.; Abad, P.L. Multi-ant colony system (MACS) for a vehicle routing problem with backhauls. Eur. J. Oper. Res. 2009, 196, 102–117. [Google Scholar] [CrossRef]
- Wang, T.I.; Wang, K.T.; Huang, Y.M. Using a style-based ant colony system for adaptive learning. Expert Syst. Appl. 2008, 34, 2449–2464. [Google Scholar] [CrossRef]
- Xiong, S. Hierarchical multi-objective evacuation routing in stadium using ant colony optimization approach. J. Transp. Geogr. 2011, 19, 443–451. [Google Scholar]
- Lui, C.H.; Fong, N.K.; Lorente, S.; Bejan, A.; Chow, W.K. Constructal design of pedestrian evacuation from an area. J. Appl. Phys. 2013, 113, 034904. [Google Scholar] [CrossRef]
- Russo, F.; Vitetta, A. Safety of users in road evacuation: General methodology and main results. WIT Trans. Built Environ. 2007, 96, 763–772. [Google Scholar]
- Russo, F.; Chilà, G. Safety of users in road evacuation: RP vs. SP surveys in demand analysis. WIT Trans. Built Environ. 2008, 101, 703–713. [Google Scholar]
- Russo, F.; Rindone, C.; Trecozzi, M.R. The role of training in evacuation. WIT Trans. Inf. Commun. 2012, 44, 491–502. [Google Scholar]
- Guan, J.; Wang, K.; Chen, F. Self-organization Phenomena in an Evacuation Flow. J. Cell. Autom. 2016, 11, 461–473. [Google Scholar]
- Lovreglio, R.; Ronchi, E.; Borri, D. The validation of evacuation simulation models through the analysis of behavioural uncertainty. Reliab. Eng. Syst. Saf. 2014, 131, 166–174. [Google Scholar] [CrossRef]
- Galea, E.R.; Deere, S.; Brown, R.; Filippidis, L. An experimental validation of an evacuation model using data sets generated from two large passenger ships. J. Ship Res. 2013, 57, 155–170. [Google Scholar] [CrossRef]


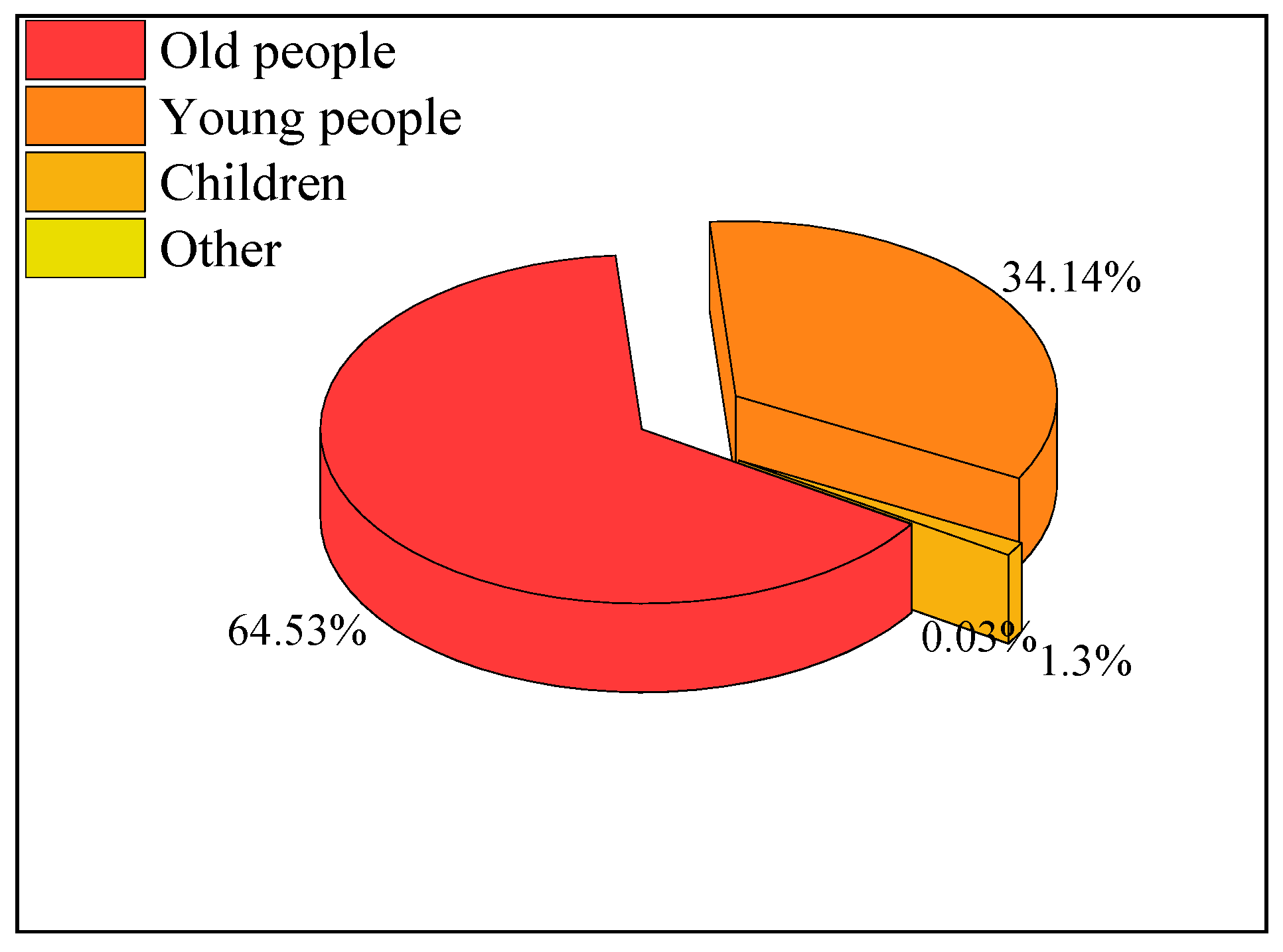





| Stairs | Function | From | To | Wide | High | Long |
|---|---|---|---|---|---|---|
| Stair 1 and Stair 5 | connect deck 1 and deck 2 | Deck 1 | landing | 1 | 1.5 | 2 |
| landing | Deck 2 | 1 | 1.5 | 2 | ||
| Stair 2 and Stair 6 | connect deck 1 and deck 2 | Deck 1 | landing | 1.35 | 1.5 | 1.9 |
| landing | Deck 2 | 1.35 | 1.5 | 1.9 | ||
| Stair 3 and Stair 7 | connect deck 1 and deck 2 | Deck 1 | landing | 1.35 | 1.5 | 1.9 |
| landing | Deck 2 | 1.35 | 1.5 | 1.9 | ||
| Stair 4 and Stair 8 | connect deck 1 and deck 2, | Deck 1 | landing | 1.35 | 1.5 | 1.9 |
| landing | Deck 2 | 1.35 | 1.5 | 1.9 | ||
| Stair 6 and Stair 9 | Deck 2 and Deck 3 | Deck 2 | landing | 1.35 | 1.5 | 1.9 |
| landing | Deck3 | 1.35 | 1.5 | 1.9 | ||
| Stair 7 and Stair 10 | Deck 2 and Deck 3 | Deck 2 | landing | 1.2 | 1.5 | 1.9 |
| landing | Deck 3 | 1.2 | 1.5 | 1.9 |
| Range (Person/min/ft) | Median (Person/m/s) |
|---|---|
| 0–7 | 0.191 |
| 7–10 | 0.465 |
| 10–15 | 0.684 |
| 15–20 | 0.957 |
| 20–25 | 1.230 |
| ≥25 | 1.367 |
| Symbol | Attribute | Value |
|---|---|---|
| m | number of ants | 400 |
| expected heuristic factor | 2 | |
| maximum number of iterations | 100 | |
| parameters of the allocation flow method | 3 | |
| pheromone volatilization factor | 0.5 | |
| random number | 0.5 | |
| number of ants placing pheromone after each iteration | 6 |
| Maximum Number of Iterations | ACS(s) | IACS(s) |
|---|---|---|
| 100 | 796 | 536 |
| 150 | 1265 | 921 |
| 200 | 2330 | 1550 |
| 250 | 2812 | 1746 |
| 300 | 3169 | 2304 |
| People ID | Staring Node | Muster Station | Path Collection |
|---|---|---|---|
| 1 | T5 | Muster station D | T5→T6→E10→E7→S15 |
| 2 | S1 | Muster station C | S1→E5→E1→F5→F6→F31 |
| 3 | F25 | Muster station A | F25→F20→F21→F19→F16→F18 |
| 4 | T1 | Muster station C | T1→T2→E9→E6→E2→F6→F31 |
| 5 | S9 | Muster station D | S9→S11→S12→S14 |
| 6 | S3 | Muster station B | S3→S4→S7→E6→E2→F7→F34 |
| 7 | S23 | Muster station A | S23→S22→S27→S26→S21→S20→S19 |
| 8 | F3 | Muster station B | F3→F4→F7→F34 |
| 9 | S8 | Muster station D | S8→S10→S13→S12→S14 |
| 10 | F5 | Muster station C | F5→F6→F31 |
| 11 | T8 | Muster station D | T8→T7→T6→E10→E7→S15 |
| 12 | T4 | Muster station C | T4→T3→T2→E9→E6→E2→F6→F31 |
| 13 | T11 | Muster station D | T11→T10→E9→E6→E2→F6→F31 |
| 14 | F2 | Muster station B | F2→F3→F4→F7→F34 |
| 15 | F1 | Muster station C | F1→F5→F6→F31 |
| 16 | S8 | Muster station D | S8→S10→S13→S12→S14 |
| 17 | S25 | Muster station D | S25→S21→S20→S19 |
| 18 | S1 | Muster station C | S1→E5→E1→F5→F6→F31 |
| 19 | S26 | Muster station D | S26→S27→S21→S18 |
| 20 | F5 | Muster station C | F5→F6→F31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhang, H.; Xie, J.; Zhao, Q. Dynamic Evacuation Planning on Cruise Ships Based on an Improved Ant Colony System (IACS). J. Mar. Sci. Eng. 2021, 9, 220. https://doi.org/10.3390/jmse9020220
Liu L, Zhang H, Xie J, Zhao Q. Dynamic Evacuation Planning on Cruise Ships Based on an Improved Ant Colony System (IACS). Journal of Marine Science and Engineering. 2021; 9(2):220. https://doi.org/10.3390/jmse9020220
Chicago/Turabian StyleLiu, Linfan, Huajun Zhang, Jupeng Xie, and Qin Zhao. 2021. "Dynamic Evacuation Planning on Cruise Ships Based on an Improved Ant Colony System (IACS)" Journal of Marine Science and Engineering 9, no. 2: 220. https://doi.org/10.3390/jmse9020220
APA StyleLiu, L., Zhang, H., Xie, J., & Zhao, Q. (2021). Dynamic Evacuation Planning on Cruise Ships Based on an Improved Ant Colony System (IACS). Journal of Marine Science and Engineering, 9(2), 220. https://doi.org/10.3390/jmse9020220








