Mooring Analysis of a Floating OWC Wave Energy Converter
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Campaign
2.2. Numerical Simulation Setup
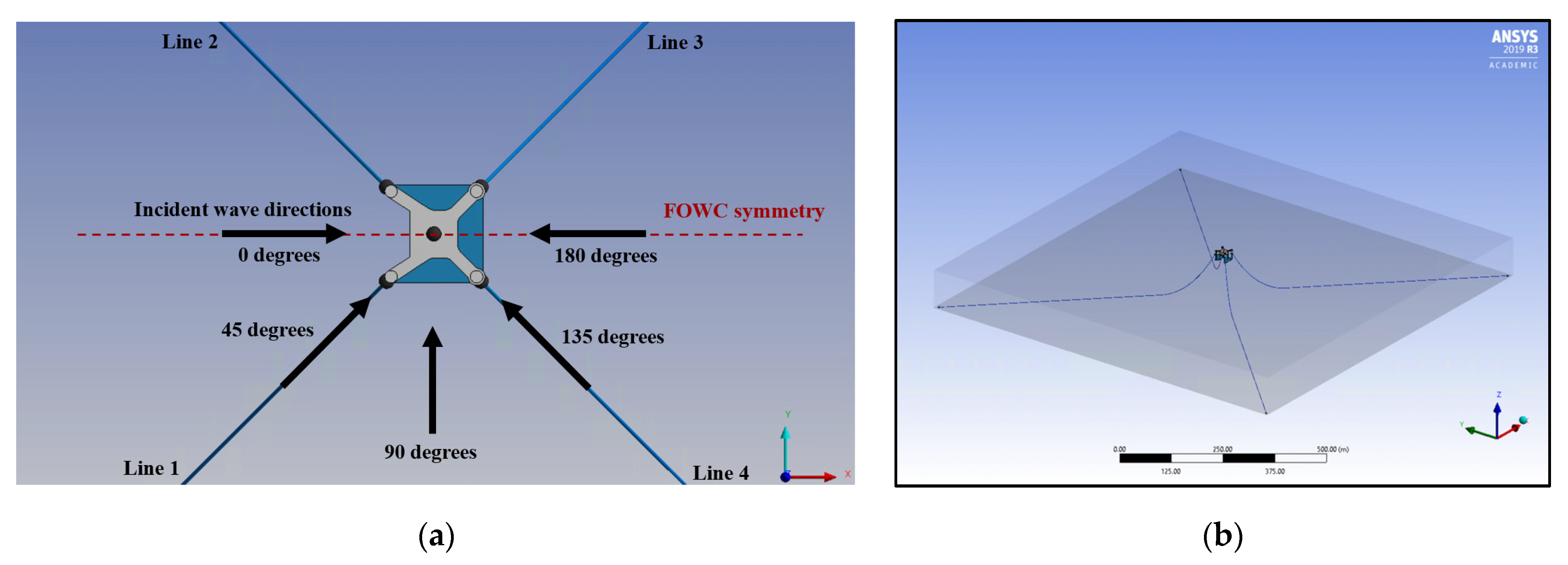
2.2.1. Geometry and Numerical Domain
2.2.2. Additional Viscous Damping
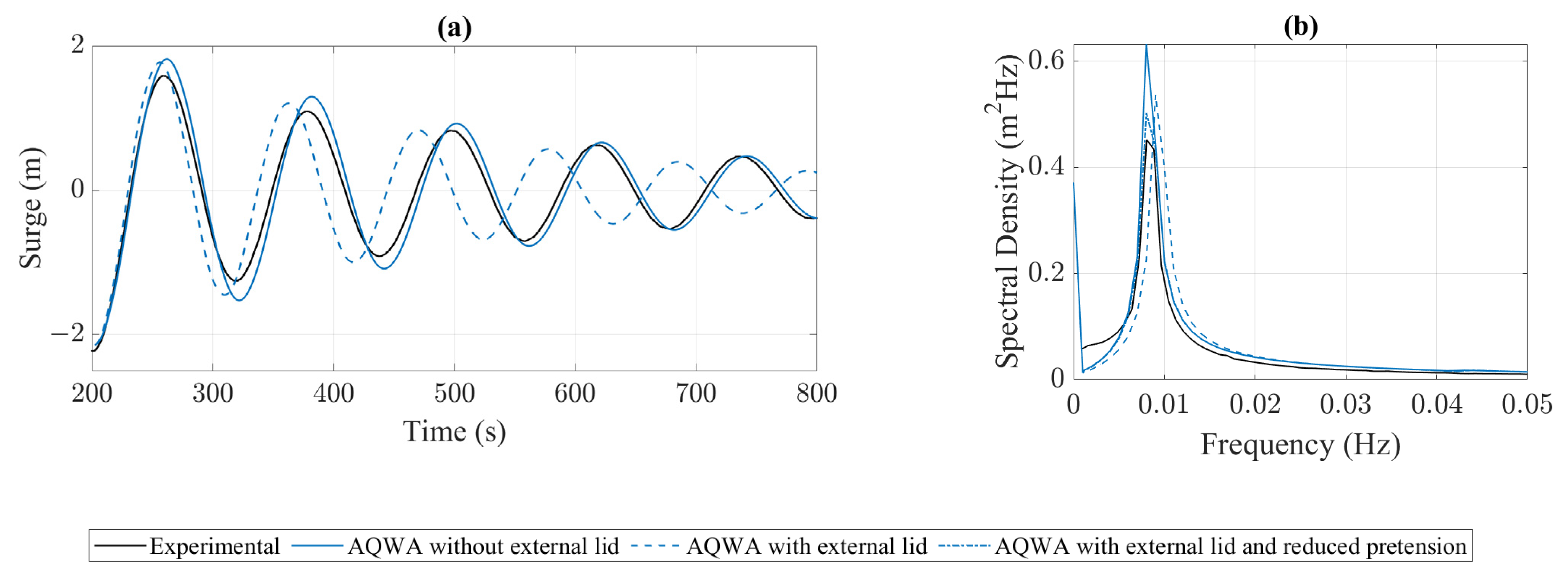
2.2.3. Moonpool Damping Lid
3. Results and Discussion
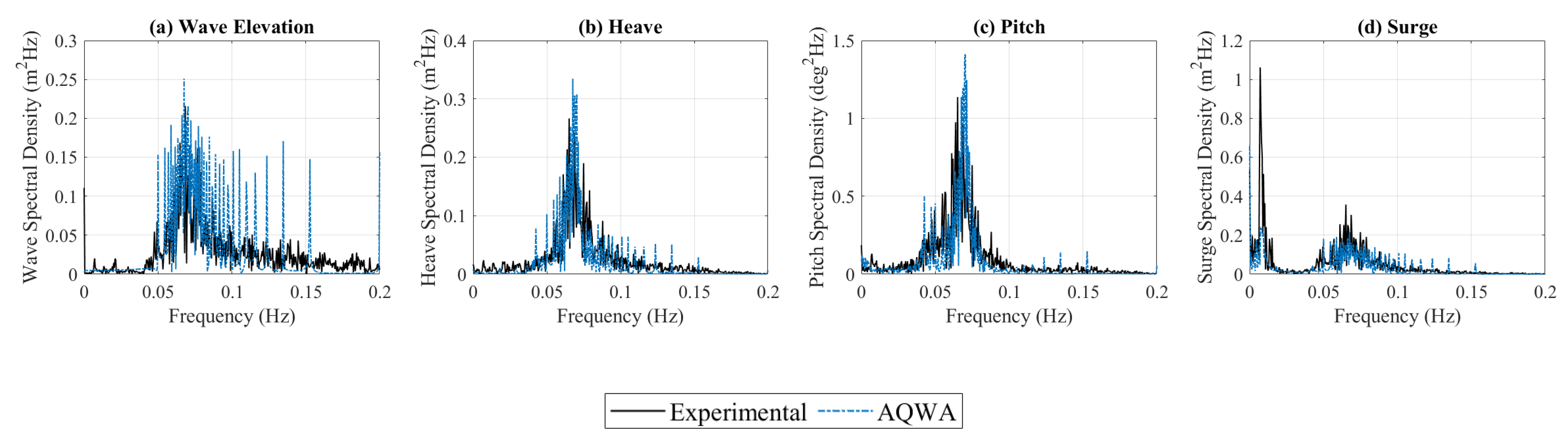
3.1. Numerical Model Validations
3.2. Mooring Analysis
3.2.1. Effect of Wave Height and Incident Wave Direction
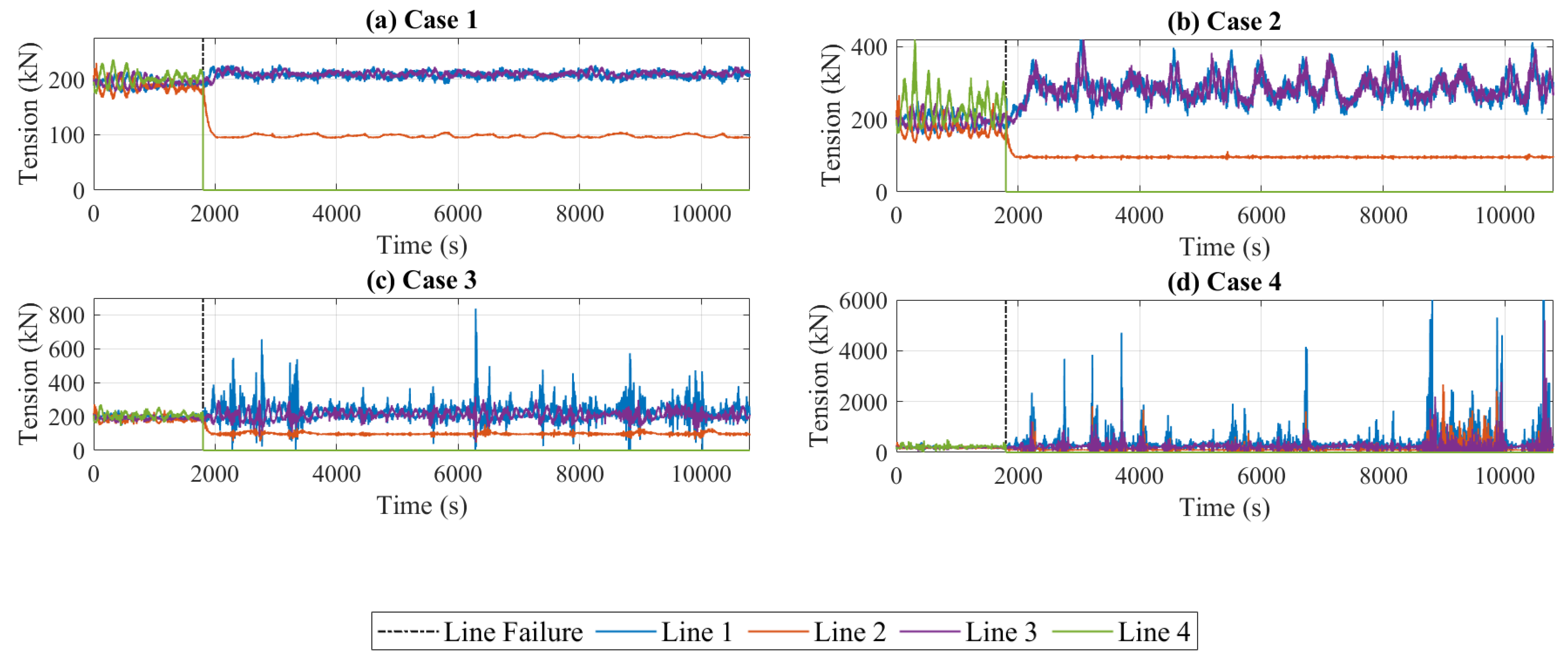
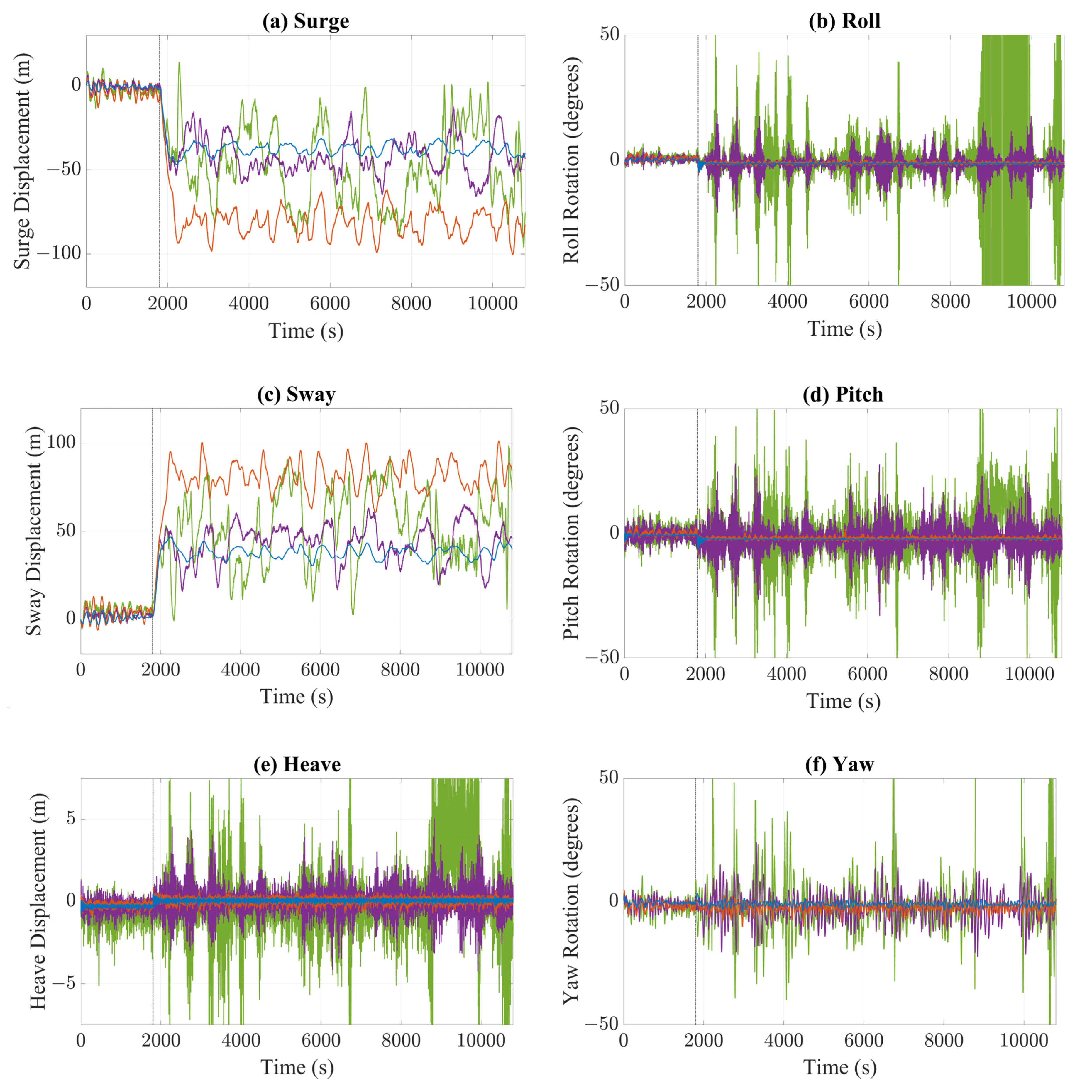
3.2.2. Effect of Mooring Line Failure
4. Conclusions and Recommendations
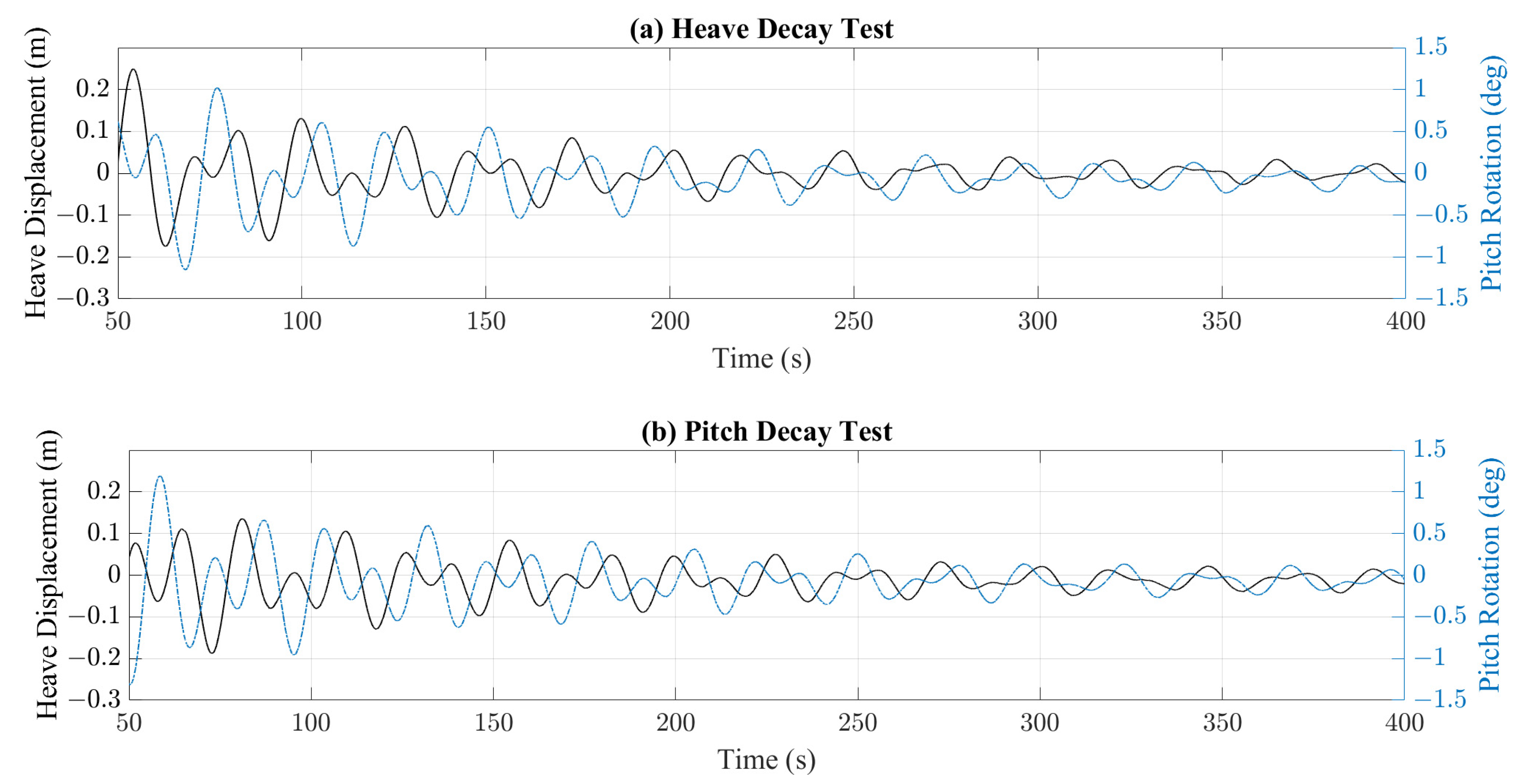
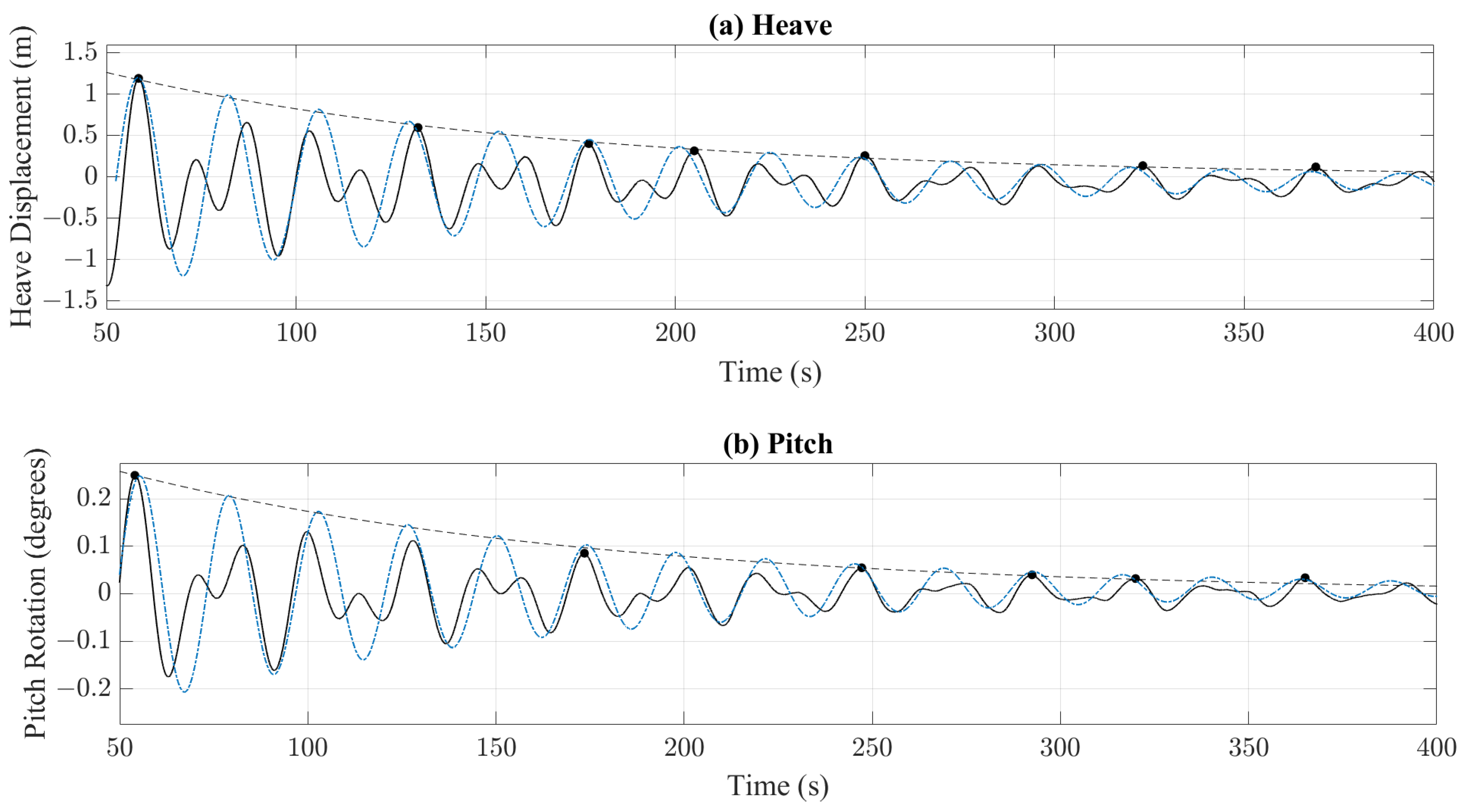
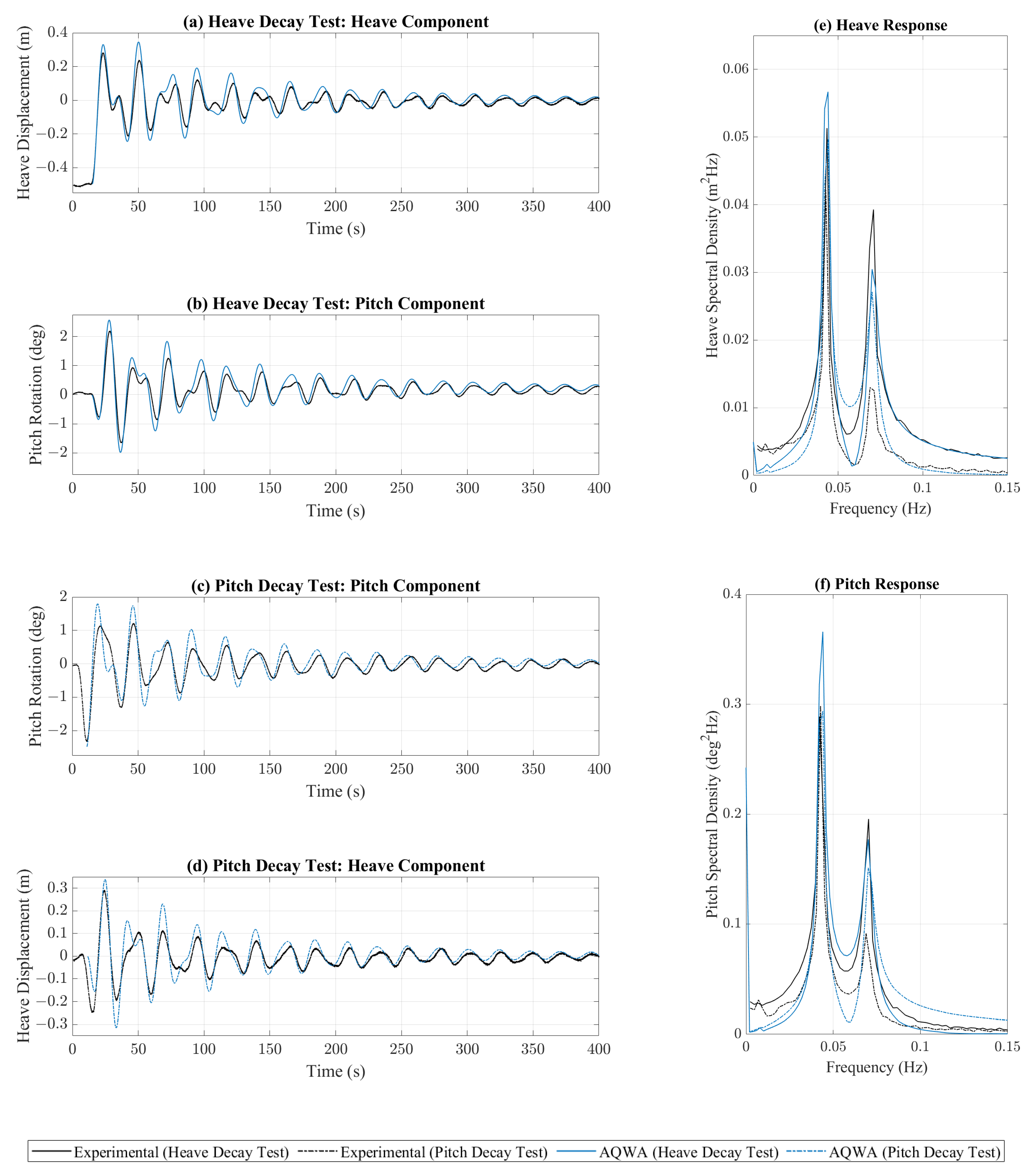
- The lack of viscosity led to overpredictions of the heave and pitch motions around the resonant frequencies. With the addition of an external viscous damping factor, derived experimentally, the solver was able to replicate the free decay tests with considerable accuracy in both magnitude and the period of oscillation.
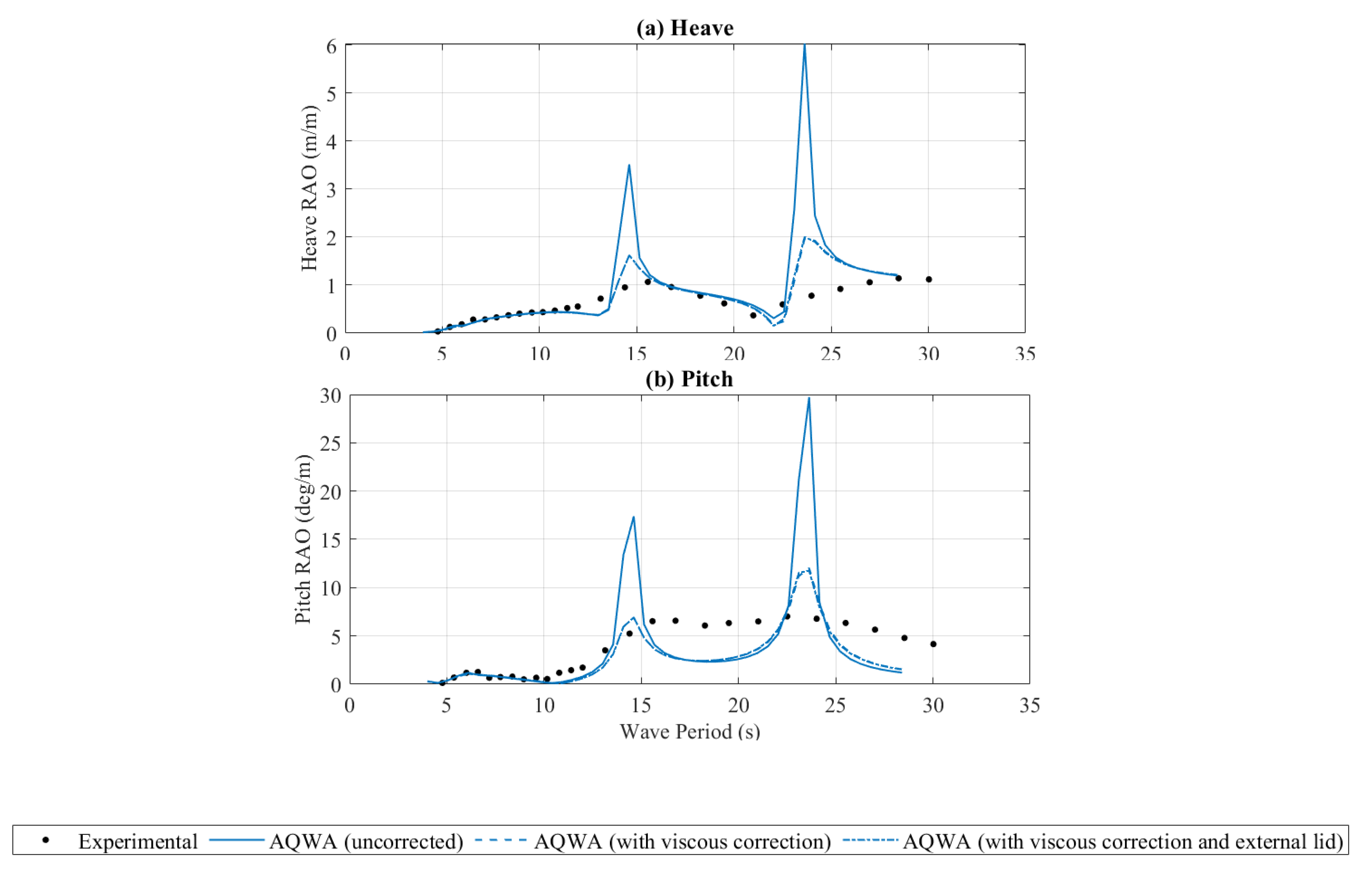
- The validation of the device motions in regular sea states and RAOs showed a close correlation for shorter wave periods. For longer wave periods, the accuracy of the experimental results was found to be likely affected by reflected waves in the testing facility. In irregular sea states, good agreeance was observed for the motions corresponding to the wave frequencies. In all cases, the numerical results slightly overpredicted the response around the resonant frequencies, suggesting that the additional viscous damping could be increased.
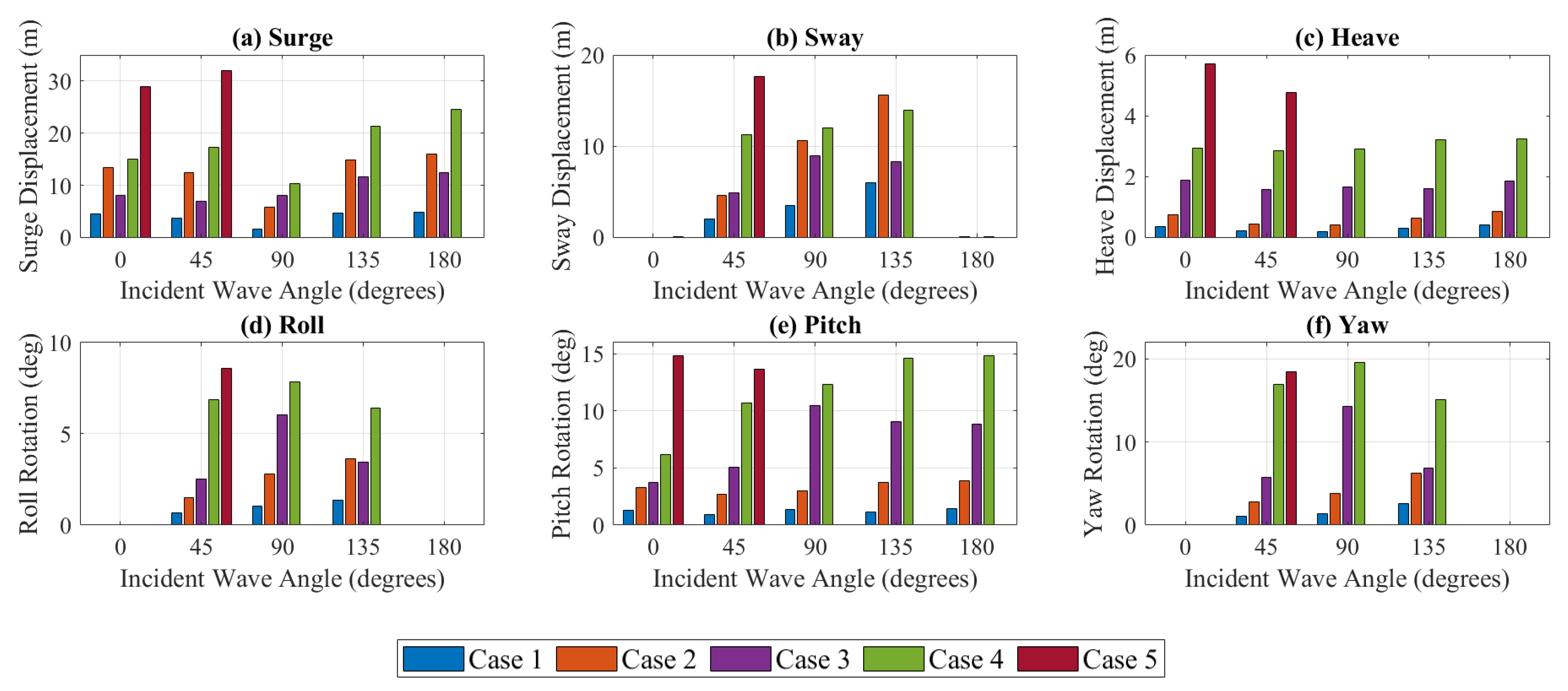
- In the catenary mooring study, wave direction was observed to have a minimal effect on heave and pitch motions and a more prominent effect on sway, roll, and yaw motions. The surge motion was consistent across all directions, excluding beam seas (90°), which showed less response.
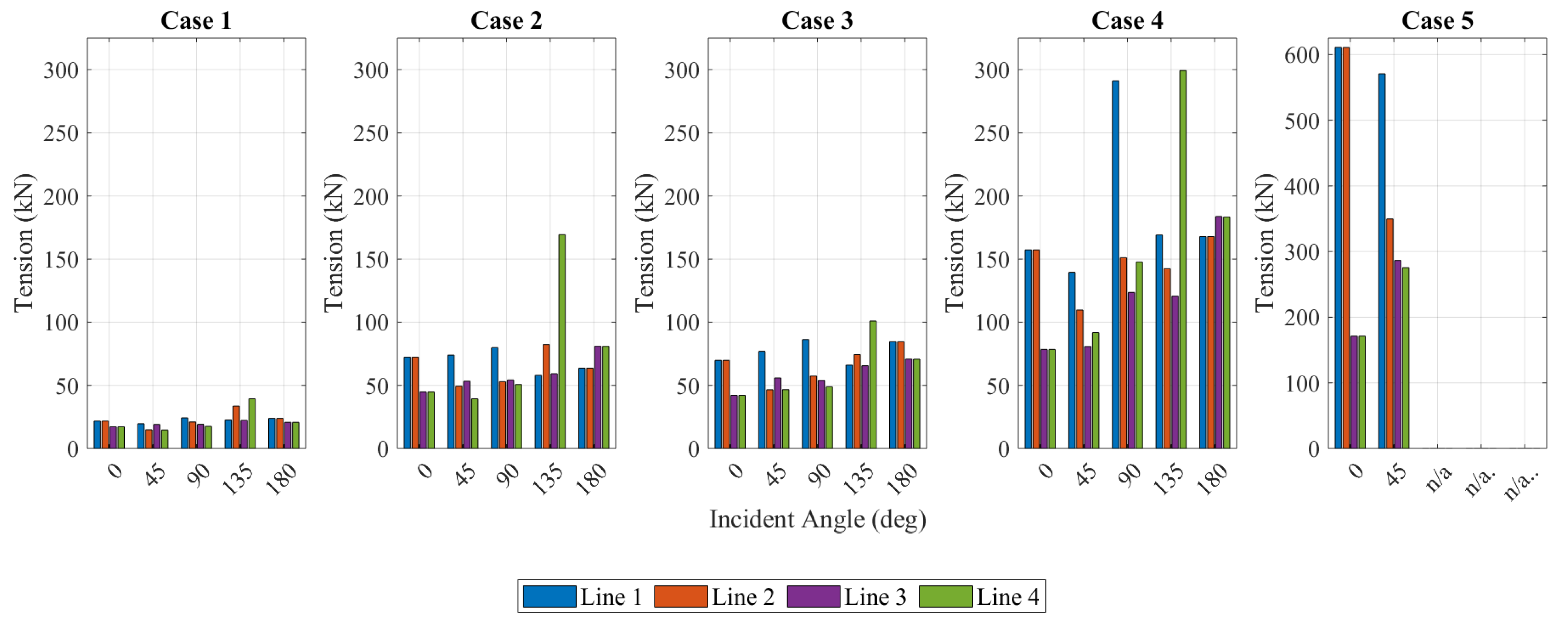
- For all cases tested, the highest tensions were experienced in the mooring line/s on the forward side of the device, relative to the incoming waves. For devices located in areas with a predominant swell direction, mooring design should consider a heavier chain on the forward lines and a lighter chain on the rear, as a cost reduction strategy. Future design iterations should also consider an increased number of incident wave angles, in conjunction with coupled loading from wind and current forces.
- The mooring line tensions were observed to exceed the minimum breaking limit for a sea state of Hs = 9 m and Tp = 12 s. Following the simulated loss of Line 4 under a 135° incident wave, the device showed good recovery for operational to moderate sea states but experienced a catastrophic loss of positive stability in Hs = 6 m and Tp = 12 s. This indicates that a heavier mooring line or alternative configuration must be considered if the expected wave conditions are within this scale.
- Larger horizontal motions were evident in the moderate sea state when compared to the rough sea state, despite the increase in significant wave height. It is suggested that this is the consequence of the shorter wave period in the moderate sea state. To determine the validity of this assumption, a moderate sea state with a longer period should be analysed and compared with the original results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Commonwealth Scientific and Industrial Research Organisation. Ocean Renewable Energy: An Analysis of Ocean Energy in Australia. Available online: https://publications.csiro.au/rpr/download?pid=csiro:EP113441&dsid=DS2 (accessed on 12 April 2020).
- Drew, B.; Plummer, A.; Sahinkaya, M. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Mueller, M.; Wallace, R. Enabling science and technology for marine renewable energy. Energy Policy 2008, 36, 4376–4382. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Review on Power Performance and Efficiency of Wave Energy Converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef] [Green Version]
- Pecher, A.; Kofoed, J. Handbook of Ocean Wave Energy; Ocean Engineering & Oceanography; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bosma, B.; Brekken, T.; Lomonaco, P.; McKee, A.; Paasch, B.; Batten, B. Physical Model Testing and System Identification of a Cylindrical OWC Device. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; Available online: https://www.researchgate.net/publication/319406355_Physical_Model_Testing_and_System_Identification_of_a_Cylindrical_OWC_Device (accessed on 30 September 2020).
- Bailey, H.; Robertson, B.; Buckham, B. Wave-to-wire simulation of a floating oscillating water column wave energy converter. Ocean Eng. 2016, 125, 248–260. [Google Scholar] [CrossRef]
- Gomes, R.; Henriques, J.; Gato, L.; Falcão, A. Wave power extraction of a heaving floating oscillating water column in a wave channel. Renew. Energy 2016, 99, 1262–1275. [Google Scholar] [CrossRef]
- Ma, Y.; Ai, S.; Yang, L.; Zhang, A.; Liu, S.; Zhou, B. Hydrodynamic Performance of a Pitching Float Wave Energy Converter. Energies 2020, 13, 1801. [Google Scholar] [CrossRef] [Green Version]
- Bhinder, M.; Murphy, J. Evaluation of the Viscous Drag for a Domed Cylindrical Moored Wave Energy Converter. J. Mar. Sci. Eng. 2019, 7, 120. [Google Scholar] [CrossRef] [Green Version]
- Beatty, S.; Hall, M.; Buckham, B.; Wild, P.; Bocking, B. Experimental and numerical comparisons of self-reacting point absorber wave energy converters in regular waves. Ocean Eng. 2015, 104, 370–386. [Google Scholar] [CrossRef]
- Yang, S.-H.; Ringsberg, J.W.; Johnson, E.; Hu, Z.; Bergdahl, L.; Duan, F. Experimental and numerical investigation of a taut-moored wave energy converter: A validation of simulated buoy motions. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018, 232, 97–115. [Google Scholar] [CrossRef]
- Zheng, S.; Zhu, G.; Simmonds, D.; Greaves, D.; Iglesias, G. Wave power extraction from a tubular structure integrated oscillating water column. Renew. Energy 2020, 150, 342–355. [Google Scholar] [CrossRef]
- Malta, E.; Gonc¸alves, R.; Matsumoto, F.; Pereira, F.; Fujarra, A.; Nishimoto, K. Damping Coefficient Analyses for Floating Offshore Structures. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 1. [Google Scholar]
- Dinoi, P. Analysis of Wave Resonant Effects in-between Offshore Vessels Arranged Side-By-Side. Ph.D. Thesis, Universidad Politécnica de Madrid (UPM), Madrid, Spain, 2016. Available online: http://oa.upm.es/43593/1/PASQUALE_DINOI.pdf (accessed on 29 March 2020).
- Lee, H.; Poguluri, S.K.; Bae, Y.H. Performance Analysis of Multiple Wave Energy Converters Placed on a Floating Platform in the Frequency Domain. Energies 2018, 11, 406. [Google Scholar] [CrossRef] [Green Version]
- Ravinthrakumar, S.; Kristiansen, T.; Molin, B.; Ommani, B. Coupled vessel and moonpool responses in regular and ir-regular waves. Appl. Ocean Res. 2020, 96, 102010. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Chu, B.; Huang, H. On natural frequencies of three-dimensional moonpool of vessels in the fixed and free-floating conditions. Ocean Eng. 2020, 195, 106656. [Google Scholar] [CrossRef]
- Ravinthrakumar, S.; Kristiansen, T.; Molin, B.; Ommani, B. A two-dimensional numerical and experimental study of pis-ton and sloshing resonance in moonpools with recess. J. Fluid Mech. 2019, 877, 142–166. [Google Scholar] [CrossRef]
- Heo, J.-K.; Park, J.-C.; Koo, W.-C.; Kim, M.-H. Influences of Vorticity to Vertical Motion of Two-Dimensional Moonpool under Forced Heave Motion. Math. Probl. Eng. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Fitzgerald, J.; Bergdahl, L. Including moorings in the assessment of a generic offshore wave energy converter: A frequency domain approach. Mar. Struct. 2008, 21, 23–46. [Google Scholar] [CrossRef]
- Harris, R.; Johanning, L.; Wolfram, J. Mooring systems for wave energy converters: A review of design issues and choices. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 159–168. Available online: https://www.researchgate.net/publication/283549804_Mooring_systems_for_wave_energy_converters_A_review_of_design_issues_and_choices (accessed on 25 March 2020).
- ANSYS. AQWA Reference Manual, 14.5 ed.; SAS IP: Canonsburg, PA, USA, 2012; pp. 54–55. [Google Scholar]
- Khanam, S.; Abdussamie, N.; Ojeda, R. Numerical prediction of wave excitation forces on a fixed tension leg platform concept for offshore wind turbines. In Proceedings of the Australasian Coasts and Ports 2019 Conference, Hobart, Australia, 10–13 September 2019. [Google Scholar]
- Journee, J.; Massie, W. Offshore Hydromechanics, 1st ed.; Delft University of Technology: Delft, The Netherlands, 2001; pp. 222–224. Available online: https://ocw.tudelft.nl/wp-content/uploads/OffshoreHydromechanics_Journee_Massie.pdf (accessed on 17 June 2020).
- Chakrabarti, S. Offshore Structure Modelling; World Scientific Publishing Co.: London, UK, 1994; pp. 447–449. [Google Scholar]
- International Towing Tank Conference. Single Significant Amplitude and Confidence Intervals for Stochastic Processes. 2020. Available online: https://www.ittc.info/media/7999/75-02-01-08.pdf (accessed on 4 October 2020).
- Emami, A.; Gharabaghi, A. Pitch Motion Response of an Equipped Semi-Submersible Platform with Tuned Sloshing Dampers. Int. J. Offsh. Polar Eng. 2020, 3, 47–54. Available online: http://ijcoe.org/article-1-133-en.pdf (accessed on 25 October 2020).
- Gao, S.; Tao, L.-B.; Kou, Y.-F.; Lu, C.; Sun, J.-L. Numerical and Experimental Study on Hydrodynamic Performance of A Novel Semi-Submersible Concept. China Ocean Eng. 2018, 32, 144–156. [Google Scholar] [CrossRef]
- Huijs, F.; De Bruijn, R.; Savenije, F. Concept Design Verification of a Semi-submersible Floating Wind Turbine Using Coupled Simulations. Energy Procedia 2014, 53, 2–12. [Google Scholar] [CrossRef] [Green Version]
- Singh, U.; Abdussamie, N.; Hore, J. Hydrodynamic performance of a floating offshore OWC wave energy converter: An experimental study. Renew. Sustain. Energy Rev. 2020, 117, 109501. [Google Scholar] [CrossRef]
- Murfet, T.; Abdussamie, N. Loads and Response of a Tension Leg Platform Wind Turbine with Non-Rotating Blades: An Experimental Study. J. Mar. Sci. Eng. 2019, 7, 56. [Google Scholar] [CrossRef] [Green Version]
- American Petroleum Institute. Design and Analysis of Station-Keeping Systems for Floating Structures (API-RP-2SK), 3rd ed.; American Petroleum Institute: Washington, DC, USA, 2005. [Google Scholar]
- Ramnas Bruk. Ramnas Bruk Product Catalogue [Brochure]. 2012. Available online: https://ramnas.com/wp-content/uploads/2012/11/Ramnas-Technical-Broschure.pdf (accessed on 16 September 2020).
- Thomsen, J.B.; Ferri, F.; Kofoed, J.P.; Black, K. Cost Optimization of Mooring Solutions for Large Floating Wave Energy Converters. Energies 2018, 11, 159. [Google Scholar] [CrossRef] [Green Version]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990; pp. 257–281. [Google Scholar]
- DNVGL Position Mooring (DNVGL-OS-E301). 2018. Available online: http://rules.dnvgl.com/docs/pdf/dnvgl/os/2018-07/dnvgl-os-e301.pdf (accessed on 16 September 2020).
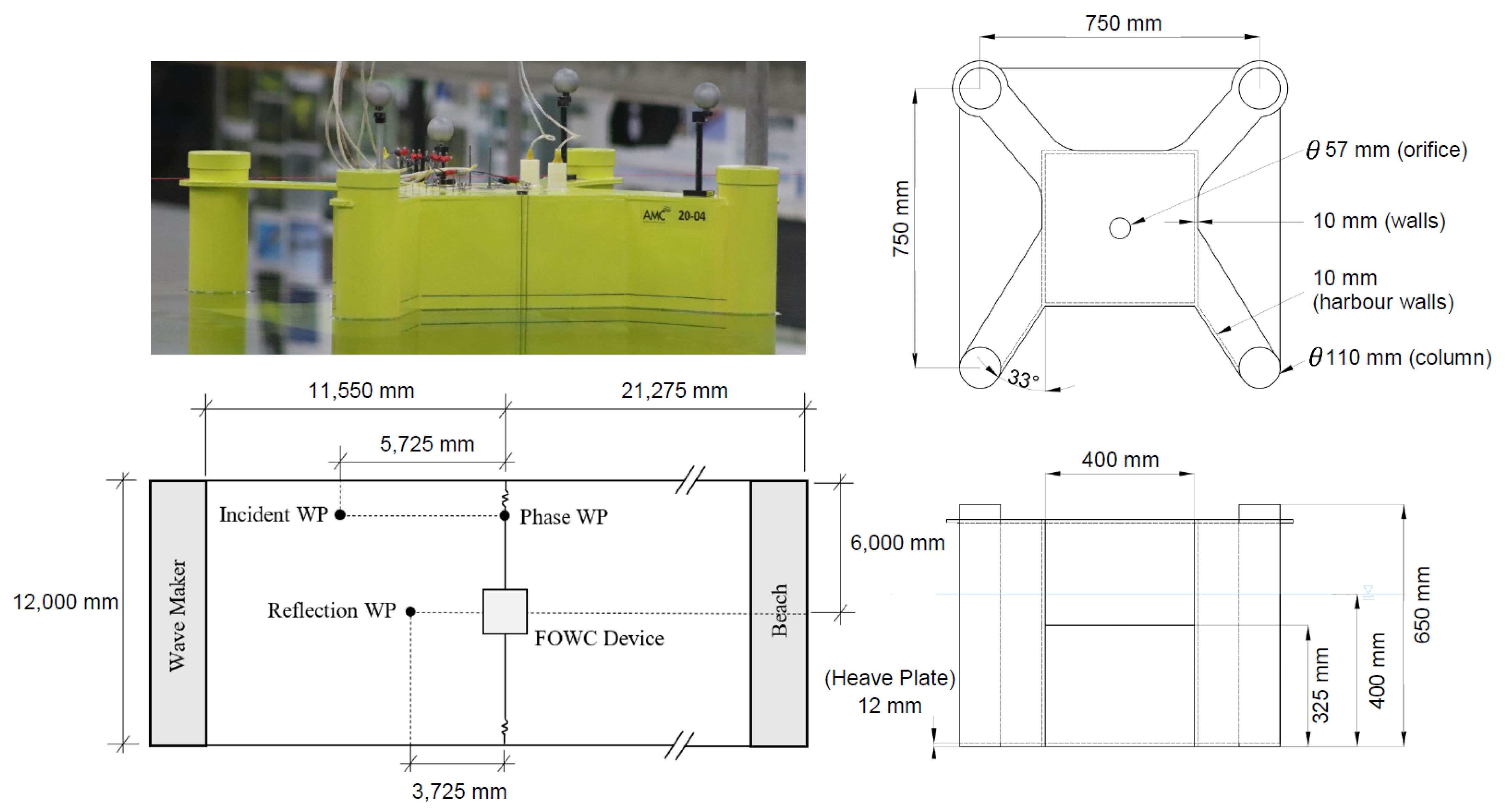
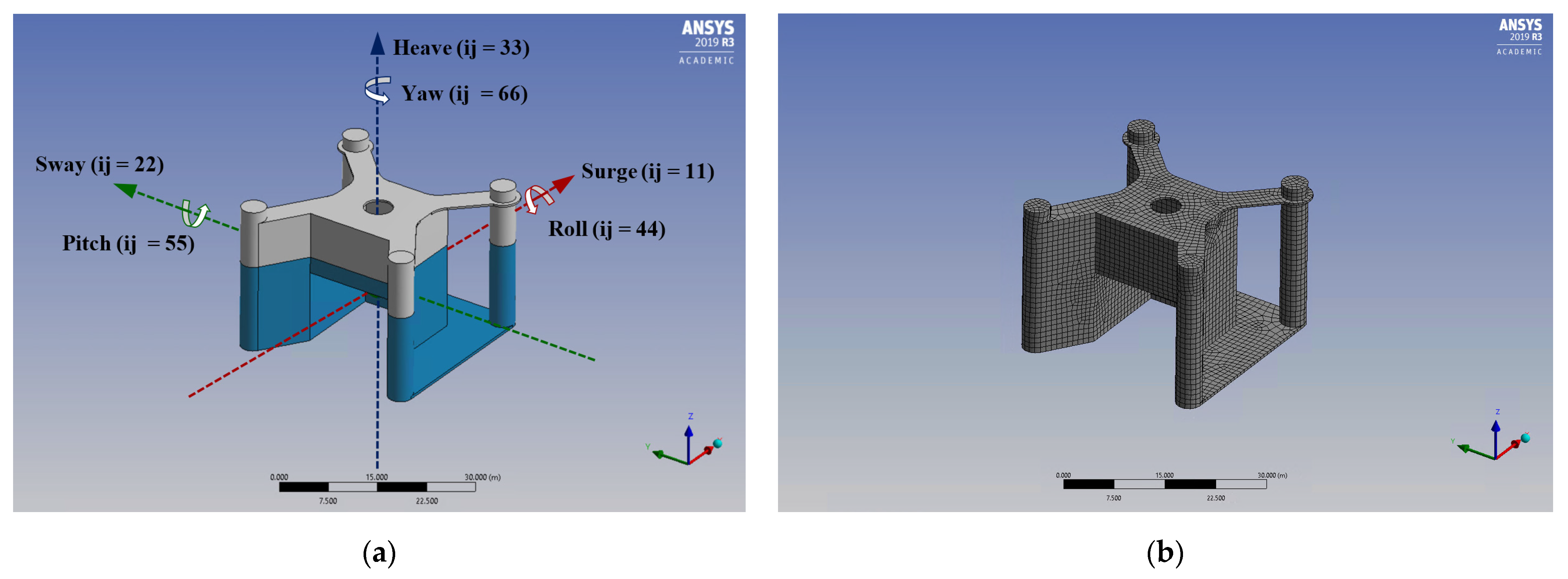


| Description | Model Scale (1:36) | Designed Full Scale | Units | |
|---|---|---|---|---|
| FOWC structure | Mass displacement | 27.0695 | 1.263 × 106 | Kg |
| LCG (from heave plate aft edge) | 0.420 | 15.12 | M | |
| VCG (from keel) | 0.246 | 8.856 | M | |
| Draft | 0.400 | 14.4 | M | |
| Mass Moments of Inertia (Ixx, Iyy, Izz) | 3.719, 3.683, 4.881 | 0.225 × 109, 0.223 × 109, 0.295 × 109 | kg·m2 | |
| Soft moorings | Spring stiffness | 647.8 | 839632 | N/m |
| Pre-tension | 29.43 | 1.37 × 106 | N | |
| AMC MTB | Water depth | 0.893 | 32.15 | m |
| Regular wave conditions | Wave height | 0.039 | 1.404 | m |
| Wave periods | 0.8–5 | 4.8–30 | s | |
| Irregular wave conditions | Significant wave heights | 0.044, 0.094 | 1.584, 3.384 | m |
| Peak periods | 1.502, 2.433 | 9.012, 14.598 | s | |
| Description | Value | Units |
|---|---|---|
| Lid damping factor | 0.0655 | - |
| Gap for external lid | 14.4 | m |
| Degree of Freedom | TN (s) | ζ (%) | External Viscous Force/Moment | |
|---|---|---|---|---|
| Experimental | Numerical | |||
| Heave | 23.742 | 22.71 | 2.99 | 164,240.03 N/m/s |
| Pitch | 23.477 | 22.71 | 3.19 | 7,911,707.55 N·m/rad/s |
| TN (s) | ζ (%) | External Viscous Force (N/m/s) | Mooring Pre-Tension (N) | |
|---|---|---|---|---|
| Experimental | Numerical | |||
| 124.29 | 124.7 | 9.0 | 60153.9 | 2.51 × 106 |
| Condition | Heave (m) | Pitch (Degrees) | Surge (m) | |||
|---|---|---|---|---|---|---|
| Experimental | AQWA | Experimental | AQWA | Experimental | AQWA | |
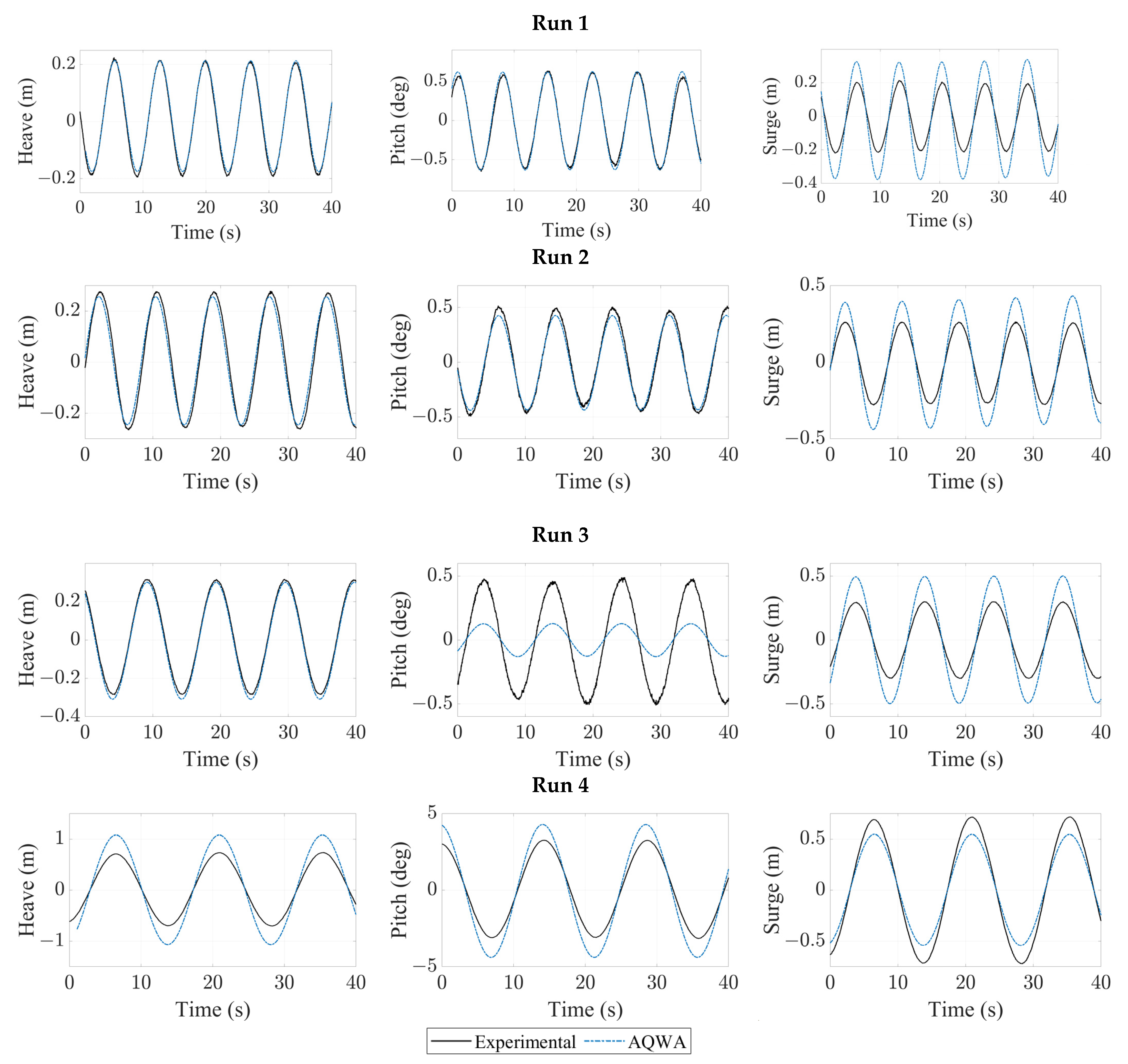
| Run 1 (T = 7.2 s) | 0.214 | 0.213 | 0.601 | 0.623 | 0.204 | 0.328 |
| Run 2 (T = 8.4 s) | 0.278 | 0.256 | 0.500 | 0.428 | 0.257 | 0.408 |
| Run 3 (T = 10.2 s) | 0.283 | 0.308 | 0.482 | 0.128 | 0.296 | 0.494 |
| Run 4 (T = 14.4 s) | 0.704 | 1.073 | 2.930 | 4.333 | 0.708 | 0.539 |
| Condition | Hs (m) | Tp (s) | Heave (m) | Pitch (Degrees) | Surge (m) | |
|---|---|---|---|---|---|---|
| Operational | Experiment | 1.584 | 9.012 | 0.54 | 1.848 | 3.204 |
| AQWA | 1.602 | 8.814 | 0.73 | 3.139 | 3.197 | |
| Elevated | Experiment | 3.384 | 14.598 | 2.700 | 11.311 | 6.768 |
| AQWA | 3.349 | 14.79 | 3.056 | 11.953 | 3.29 |
| Description | Value | Units | Description | Value | Units |
|---|---|---|---|---|---|
| Chain grade | R3 studless | - | Added mass coefficient | 1 | - |
| Chain diameter | 76 | mm | Number of mooring lines | 4 | - |
| Mass/unit length in air | 126 | kg/m | Fairlead locations (x,y,z) | +/– 15.1, +/– 15.1, 0.0 | m |
| Submerged mass/unit length | 100.5 | kg/m | Anchor locations (x,y,z) | +/– 491, +/– 491, –100 | m |
| Minimum breaking load (MBL) | 4.8843 × 106 | N | No. of cable elements | 100 | - |
| Stiffness (EA) | 6.3 × 108 | N | Line length | 715 | m |
| Transverse drag coefficient | 2.4 | - | Safety factor (SF) | 2.0 | - |
| Longitudinal drag coefficient | 1.15 | - |
| Case No. | Description | Input Parameters | Spectral Analysis | Wave Directions (Degrees) | |||
|---|---|---|---|---|---|---|---|
| Hs (m) | Tp (s) | Hs (m) | Tp (s) | Hmax (m) | |||
| 1 | Operational | 1.25 | 8.00 | 1.25 | 8.19 | 2.38 | 0, 45, 90, 135, 180 |
| 2 | Moderate | 2.50 | 8.00 | 2.50 | 8.19 | 4.75 | |
| 3 | Rough | 4.00 | 12.00 | 4.00 | 12.47 | 7.55 | |
| 4 | Very rough | 6.00 | 12.00 | 6.01 | 12.47 | 11.2 | |
| 5 | Survivable | 9.00 | 12.00 | 9.02 | 12.47 | 16.74 | |
| Wave Direction (Degrees) | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| Max. Tension/Line No. | Max. Tension/Line No. | Max. Tension/Line No. | Max. Tension/Line No. | Max. Tension/Line No. | |
| 0 | 219.7/Line 2 | 320.1/Line 1 | 340.76/Line 2 | 621.6/Line 2 | 3411/Line 1 |
| 45 | 222.1/Line 3 | 301.4/Line 1 | 370.2/Line 1 | 517.7/Line 1 | 2933/Line 1 |
| 90 | 227.9/Line 1 | 367.9/Line 1 | 373.2/Line 1 | 2056/Line 1 | 10,450/Line 2 |
| 135 | 242.7/Line 4 | 518.5/Line 4 | 387.7/Line 4 | 1480/Line 1 | 20,511/Line 2 |
| 180 | 221.7/Line 1 | 329.7/Line 3 | 398.8/Line 1 | 750.5/Line 3 | 4995/Line 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pols, A.; Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Mooring Analysis of a Floating OWC Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 228. https://doi.org/10.3390/jmse9020228
Pols A, Gubesch E, Abdussamie N, Penesis I, Chin C. Mooring Analysis of a Floating OWC Wave Energy Converter. Journal of Marine Science and Engineering. 2021; 9(2):228. https://doi.org/10.3390/jmse9020228
Chicago/Turabian StylePols, Alana, Eric Gubesch, Nagi Abdussamie, Irene Penesis, and Christopher Chin. 2021. "Mooring Analysis of a Floating OWC Wave Energy Converter" Journal of Marine Science and Engineering 9, no. 2: 228. https://doi.org/10.3390/jmse9020228
APA StylePols, A., Gubesch, E., Abdussamie, N., Penesis, I., & Chin, C. (2021). Mooring Analysis of a Floating OWC Wave Energy Converter. Journal of Marine Science and Engineering, 9(2), 228. https://doi.org/10.3390/jmse9020228






