Coupled Level-Set and Volume of Fluid (CLSVOF) Solver for Air Lubrication Method of a Flat Plate
Abstract
1. Introduction
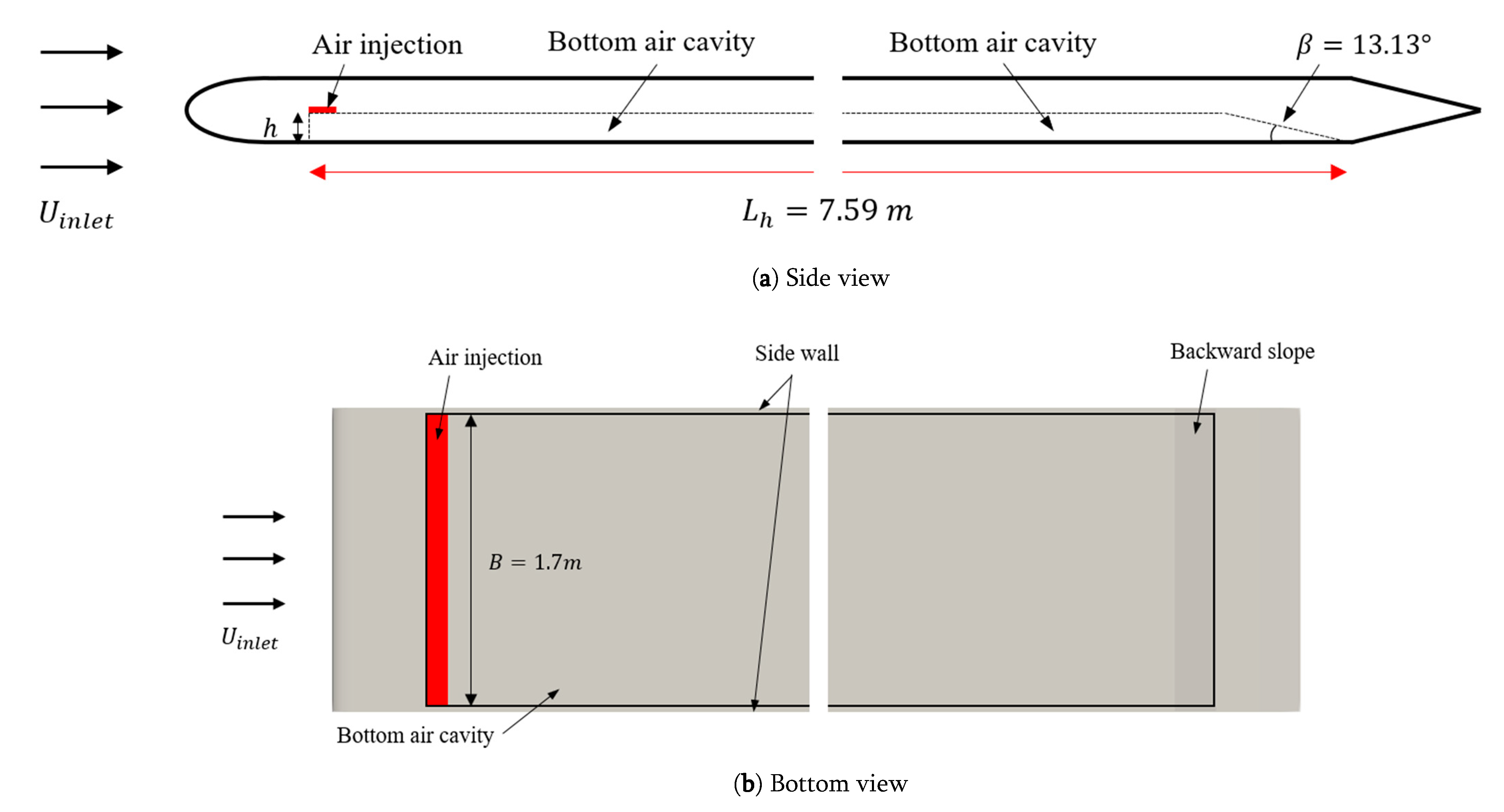
2. Model Description
3. Computational Methods
3.1. Governing Equations
3.2. Interface Capturing Method
3.2.1. VOF Method
3.2.2. CLSVOF Method
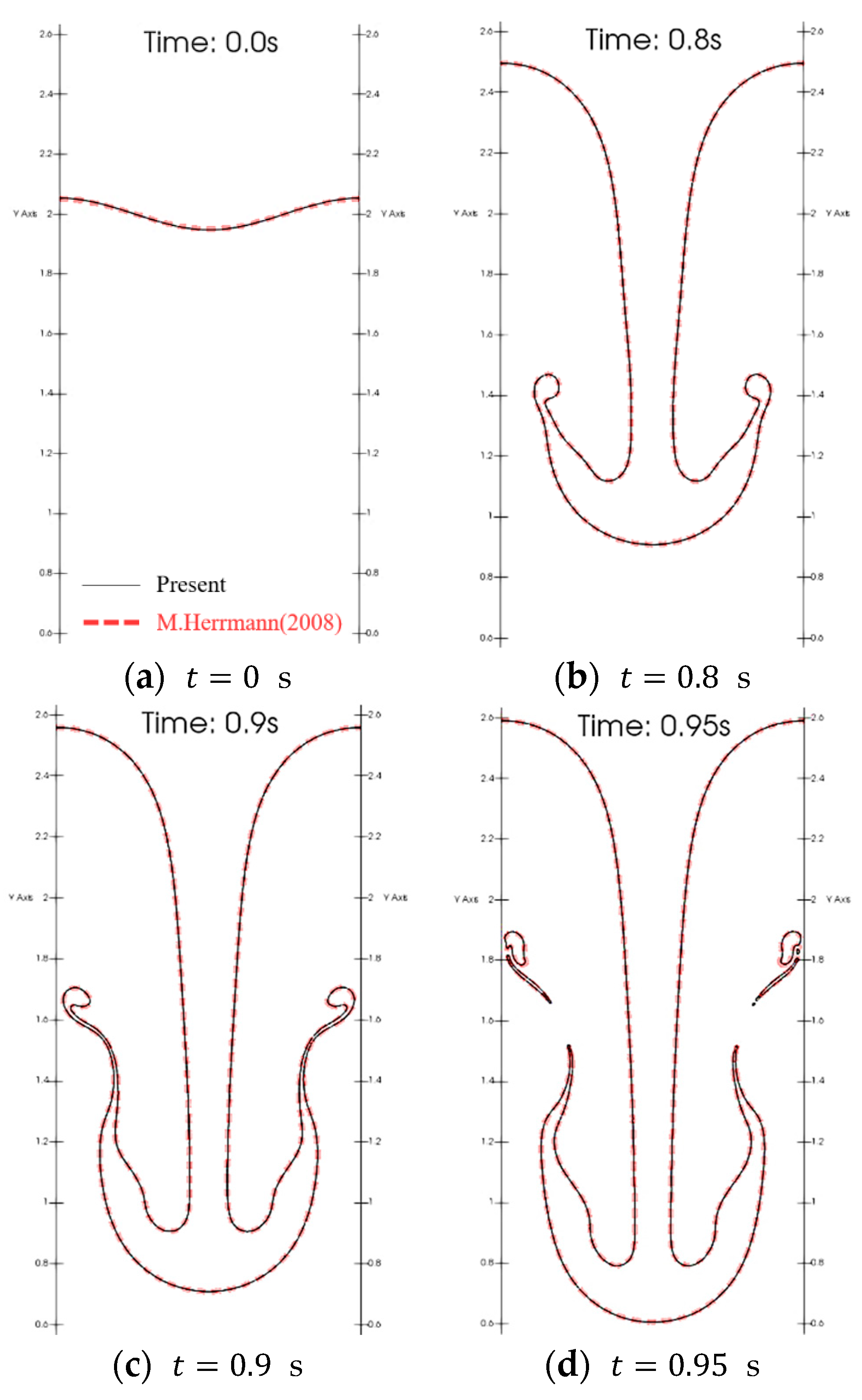
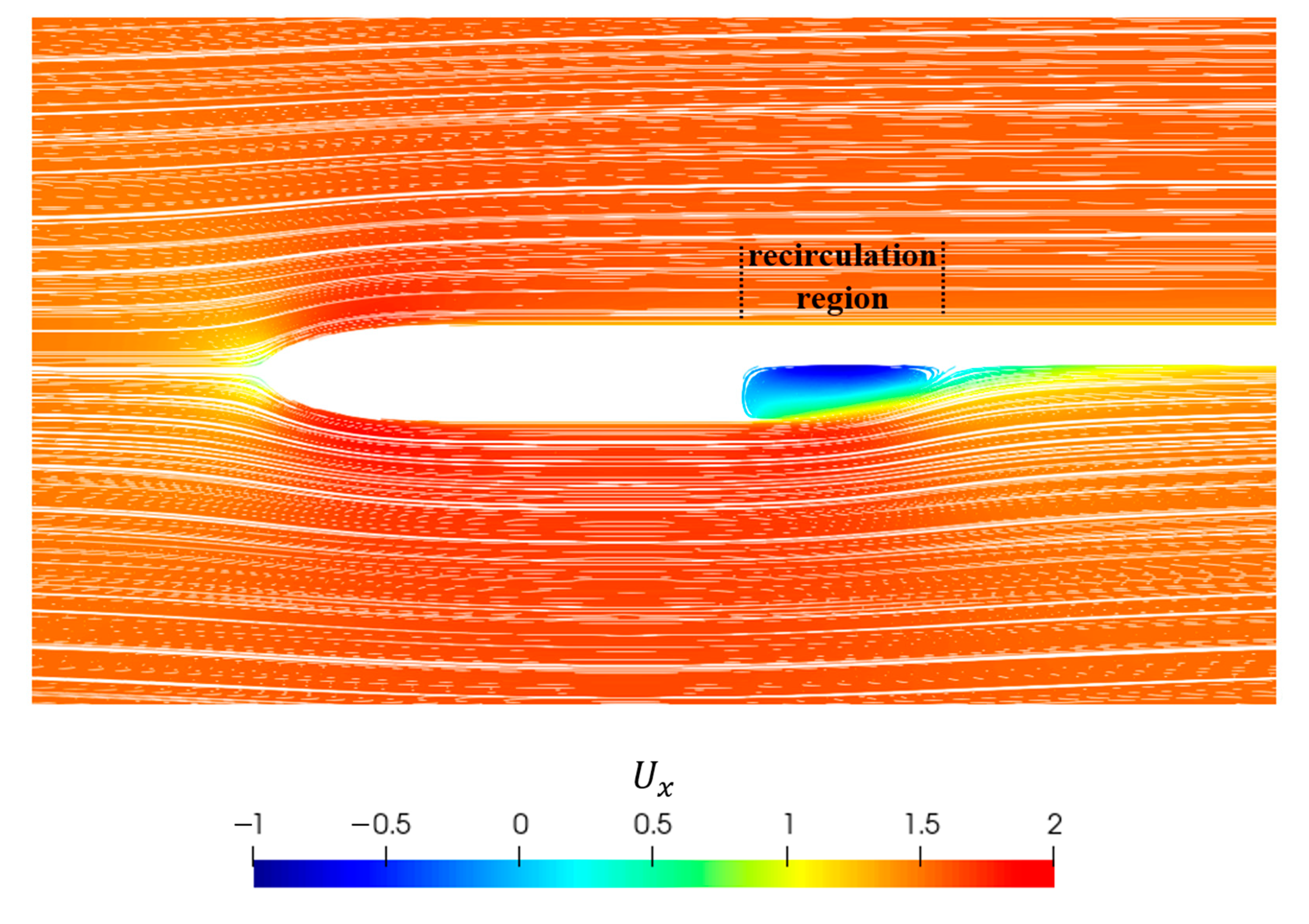
3.2.3. Verification of CLSVOF
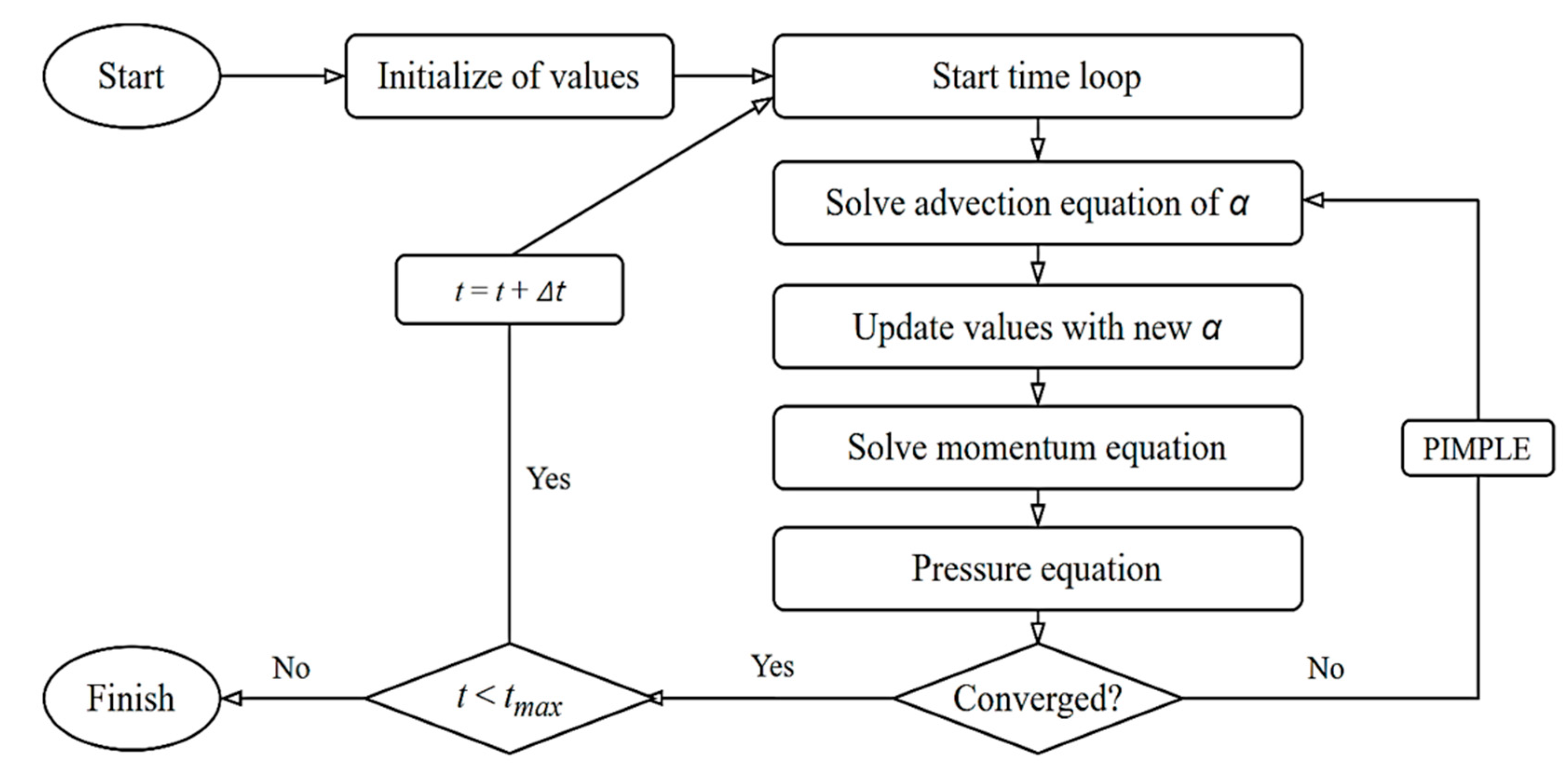
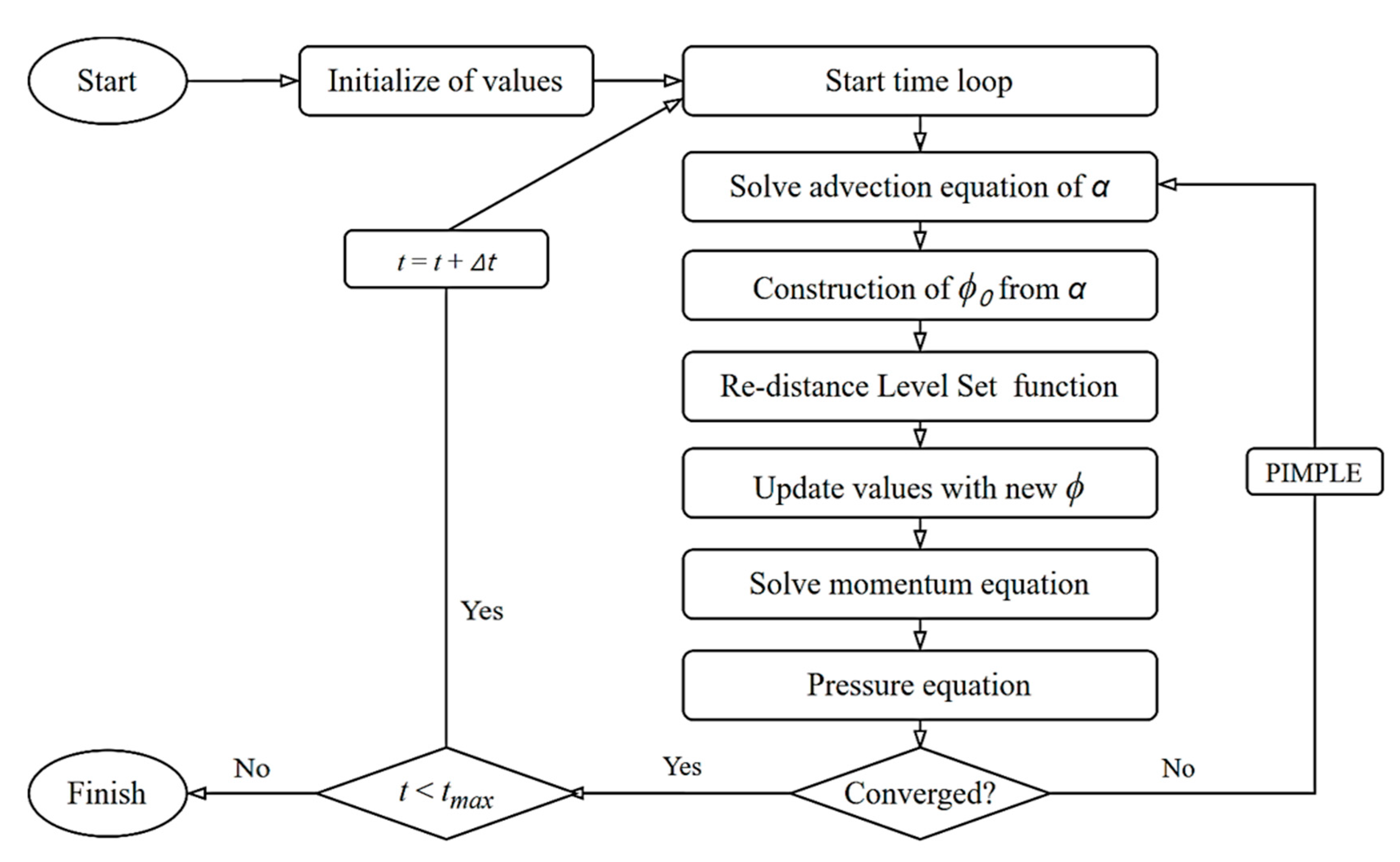
3.3. Numerical Methods
4. Results and Discussion
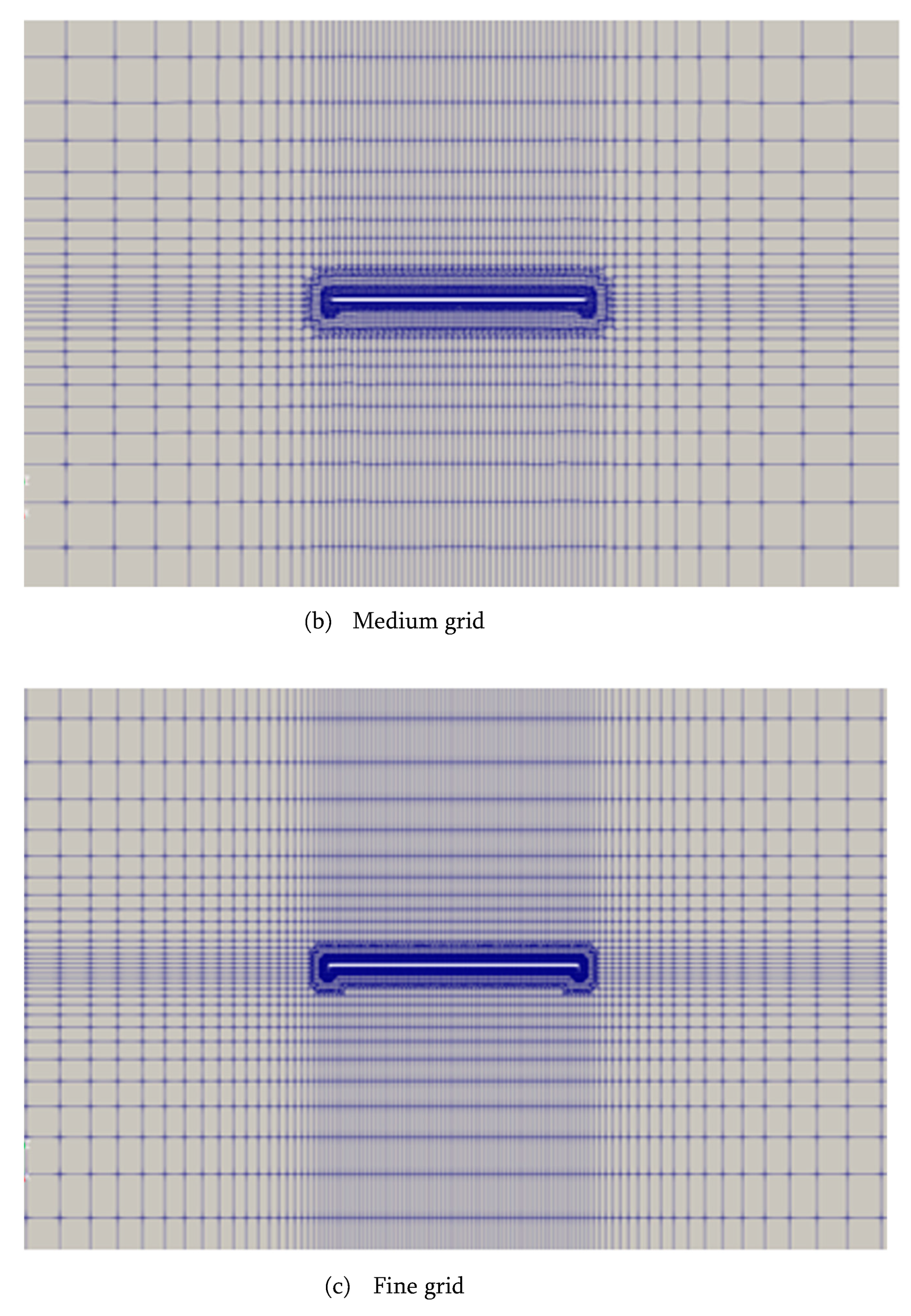
4.1. Domain Extents, Boundary Conditions, and Meshes
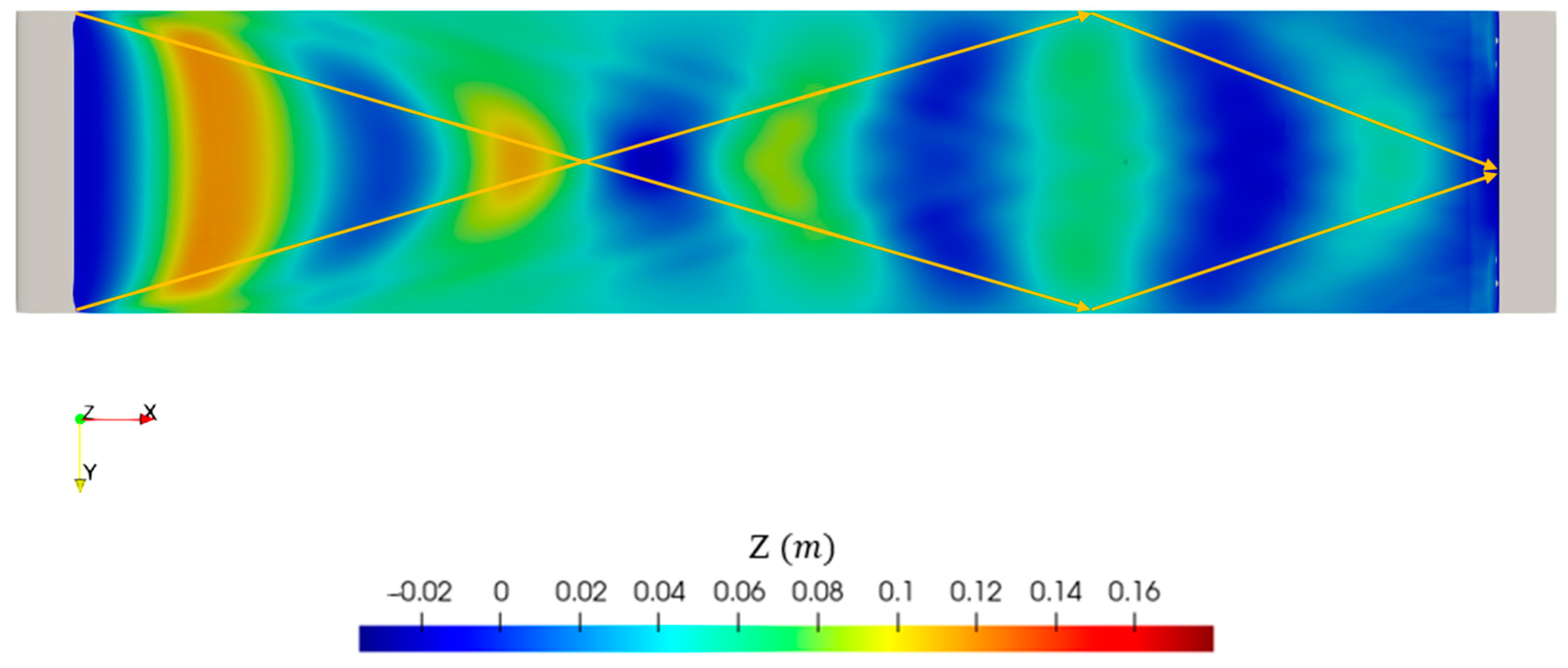
4.2. Grid Uncertainty Assessment
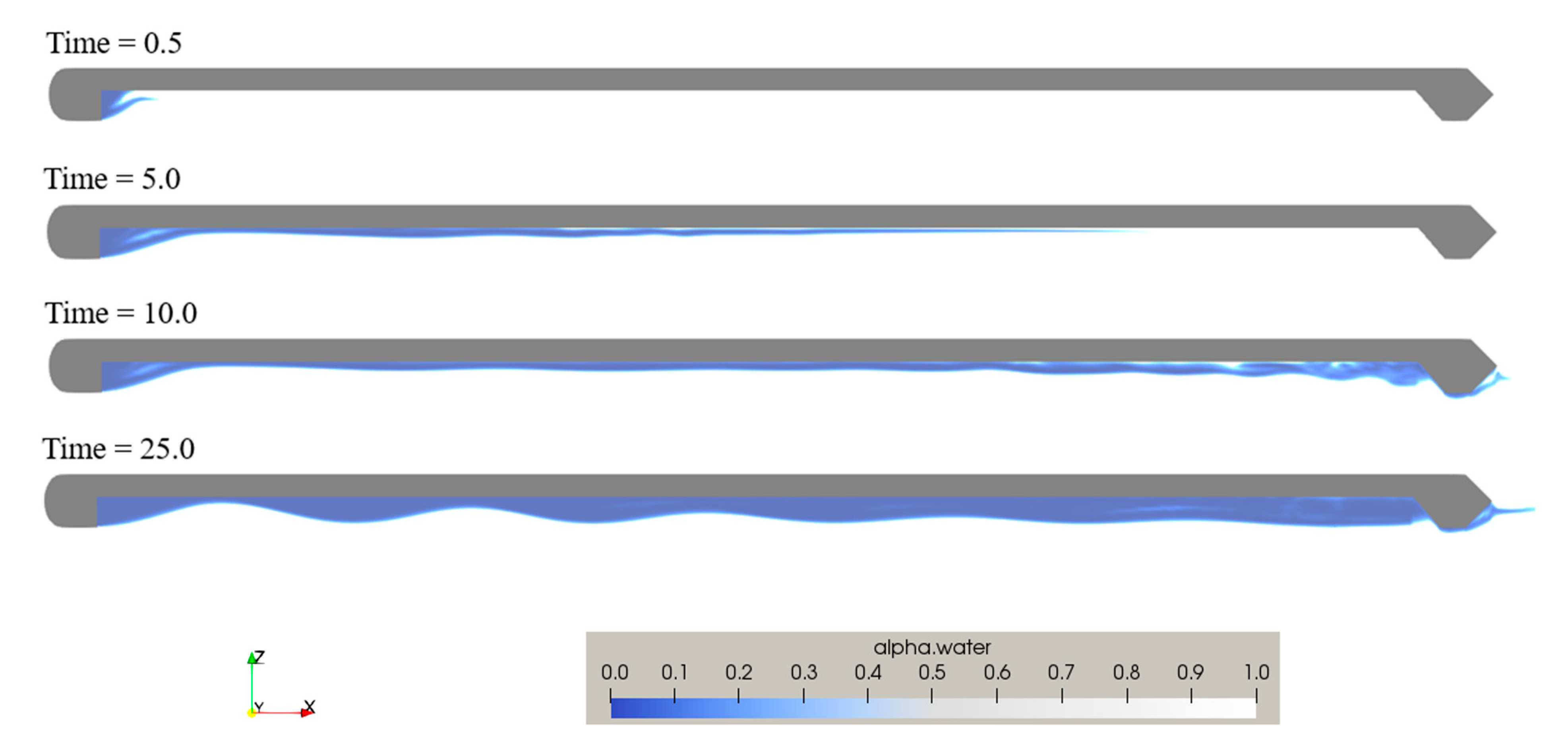
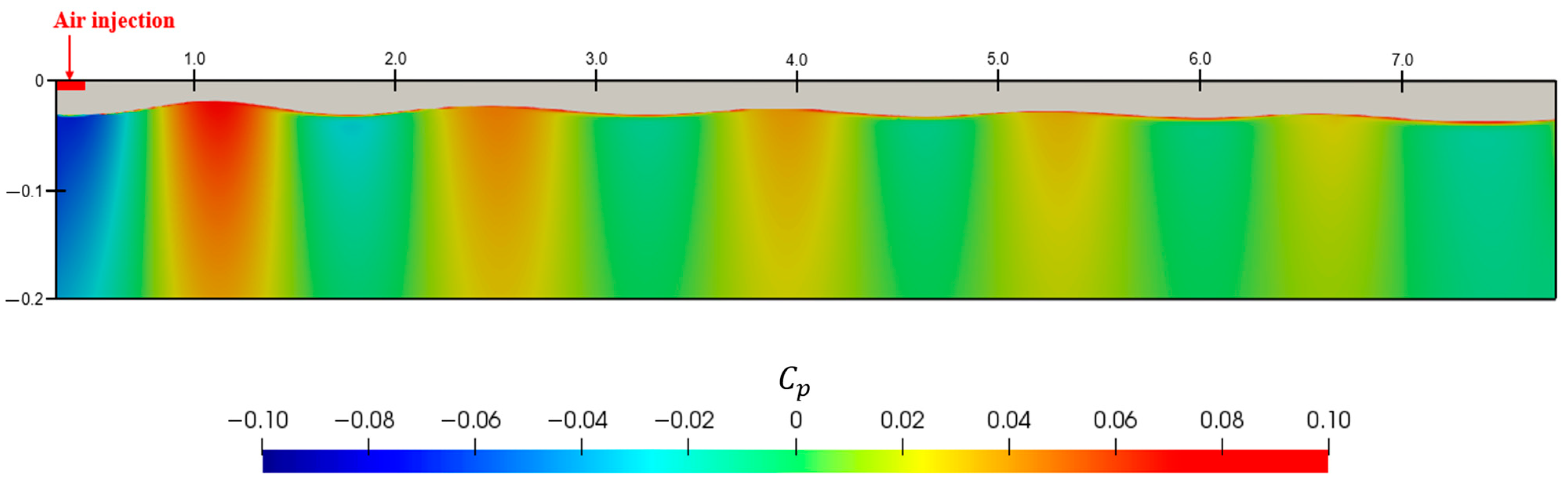
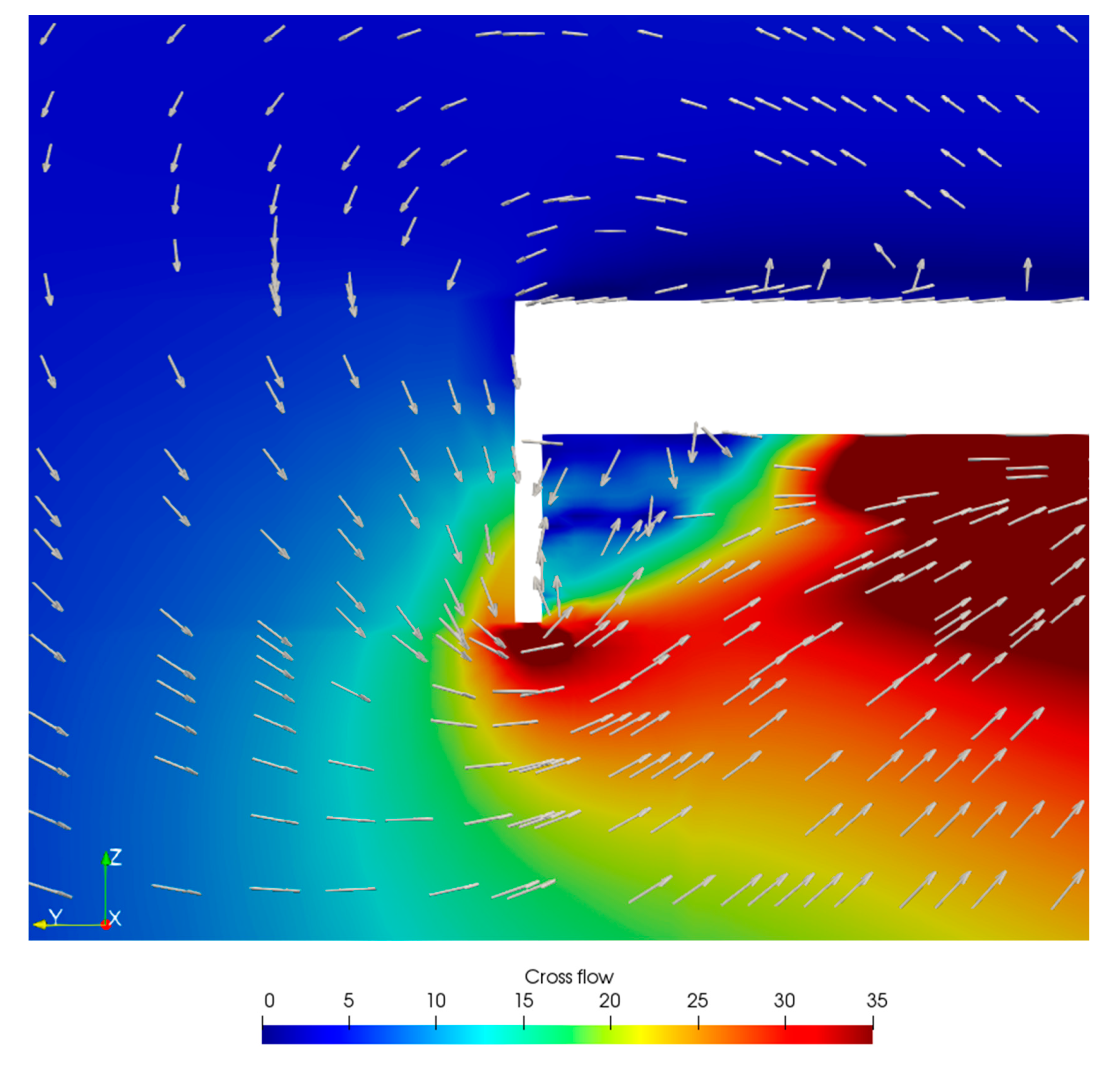
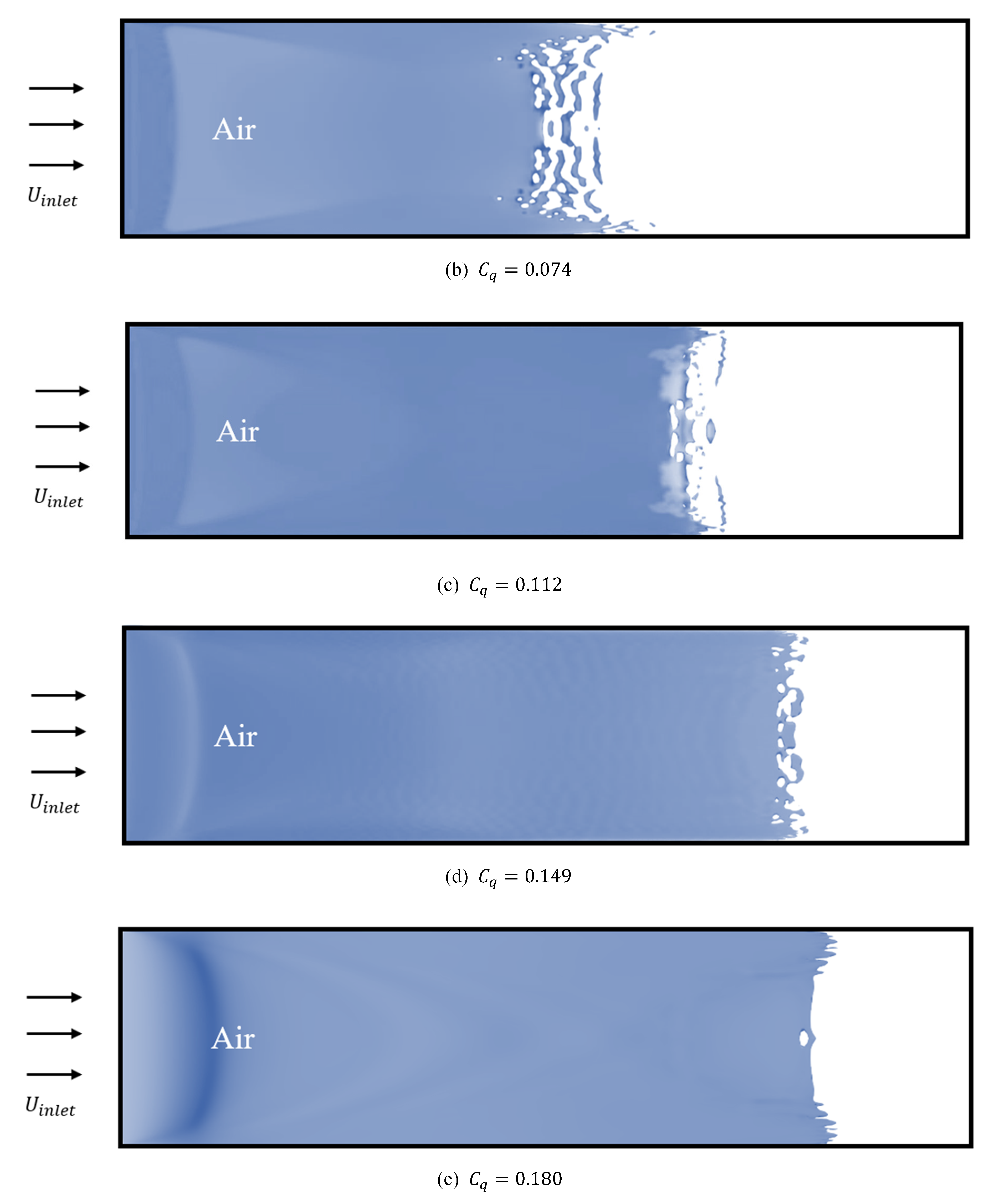
4.3. Air Lubrication Method and Drag Reduction
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nobuaki, S.; Hiroshi, K.; Kunihide, O.; Yasutaka, K.; Björn, W.; Hikaru, K. An overset RaNS prediction and validation of full scale stern wake for 1600TEU container ship and 63,000 DWT bulk carrier with an energy saving device. Appl. Ocean Res. 2020, 105, 102–417. [Google Scholar]
- Park, S.; Oh, G.; Rhee, S.H.; Koo, B.-Y.; Lee, H. Full scale wake prediction of an energy saving device by using computational fluid dynamics. Ocean Eng. 2015, 101, 254–263. [Google Scholar] [CrossRef]
- Zeynep, T.; Noriyuki, S.; Mehmet, A.; Emin, K. An investigation into effects of Gate Rudder system on ship performance as a novel energy-saving and manoeuvring device. Ocean Eng. 2020, 218, 108–250. [Google Scholar]
- Walsh, M. Turbulent Boundary Layer Drag Reduction using Riblets. In Proceedings of the 20th Aerospace Science Meeting, Orlando, FL, USA, 11–14 January 1982. [Google Scholar]
- Gray, J. Studies in Animal Locomotion VI. The Propulsive Powers of the Dolphin. J. Exp. Biol. 1936, 13, 192–199. [Google Scholar]
- Lee, J.; Kim, S.; Kim, B.; Jang, J.; McStay, P. Full scale applications of air lubrication for reduction of ship frictional resistance. In Proceedings of the SNAME Maritime Convention 2017, Houston, TX, USA, 24–28 October 2017. [Google Scholar]
- Mizokami, S.; Kawakita, C.; Kodan, Y. Experimental Study of Air Lubrication Method and Verification of Effects on Actual Hull by Means of Sea Trial. Mitsubishi Heavy Ind. Tech. Rev. 2010, 47, 41–47. [Google Scholar]
- Mäkiharju, S.A.; Marc, P.; Steven, L.C. On the energy economics of air lubrication drag reduction. Int. J. Nav. Arch. 2012, 4, 412–422. [Google Scholar] [CrossRef]
- Du, P.; Wen, J.; Zhang, Z.; Song, D.; Ouahsine, A.; Hu, H. Maintenance of air layer and drag reduction on superhydrophobic surface. Ocean Eng. 2017, 130, 328–335. [Google Scholar] [CrossRef]
- Mäkiharju, S.; Lee, I.; Filip, G. The topology of gas jets injected beneath a surface and subject to liquid cross-flow. J. Fluid Mech. 2017, 818, 141–183. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, I. Optimization of drag reduction effect of air lubrication for a tanker model. Int. J. Naval Arch. Ocean Eng. 2018, 10, 427–438. [Google Scholar] [CrossRef]
- Hao, W.U.; Yongpeng, O.U.; Qing, Y.E. Experimental study of air layer drag reduction on a flat plate and bottom hull of a ship with cavity. Ocean Eng. 2019, 183, 236–248. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Ha, J.-Y.; Paik, K.-J. Numerical study on the extrapolation method for predicting the full-scale resistance of a ship with an air lubrication system. J. Ocean Eng. Technol. 2020, 34, 387–393. [Google Scholar] [CrossRef]
- Kim, H.; Kim, H.; Lee, D. Study on the skin-frictional Drag Reduction Phenomenon by Air Layer using CFD Technique. J. Soc. Naval Arch. Korea 2019, 56, 361–371. [Google Scholar] [CrossRef]
- Bourlioux, A. A coupled level-set volume-of-fluid algorithm for tracking material interfaces. In Proceedings of the 6th International Symposium on Computational Fluid Dynamics, Lake Tahoe, NV, USA, 4–8 September 1995; pp. 15–22. [Google Scholar]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Albadawi, A.; Donoghue, D.B.; Robinson, A.J.; Murray, D.B.; Delauré, Y.M.C. Influence of surface tension implementation in Volume of Fluid and coupled Volume of Fluid with Level Methods for bubble growth and detachment. Int. J. Multiph. Flow 2013, 53, 11–28. [Google Scholar] [CrossRef]
- Dianat, M.; Skarysz, A.; Garmory, A. A coupled level set and volume of fluid method for automotive exterior water management applications. Int. J. Multiph. Flow 2017, 91, 19–38. [Google Scholar] [CrossRef]
- Li, Q.; Ouyang, J.; Yang, B.; Li, X. Numerical simulation of gas-assisted injection molding using CLSVOF method. Appl. Math. Model. 2012, 36, 2262–2274. [Google Scholar] [CrossRef]
- Menter, F. Two Equation Eddy-Viscosity Turbulence Modeling for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Park, S. Development of free-surface decomposition method and its application. J. Adv. Res. Ocean Eng. 2017, 3, 75–82. [Google Scholar]
- Herrmann, M. A balanced force refined level set grid method for two-phase flows on unstructured flow solver grids. J. Comput. Phys. 2008, 227, 2674–2706. [Google Scholar] [CrossRef]
- Park, S.; Seok, W.C.; Park, S.T.; Rhee, S.H.; Choe, Y.; Kim, C.; Kim, J.H.; Ahn, B.K. Compressibility effects on cavity dynamics behind a two-dimensional wedge. J. Mar. Sci. Eng. 2020, 8, 39. [Google Scholar] [CrossRef]
- Weiss, J.; Maruszewski, J.; Smith, W. Implicit Solution of Preconditioned Navier–tokes Equations Using Algebraic Multigrid. AIAA J. 1999, 37, 29–36. [Google Scholar] [CrossRef]
- Song, S.; Park, S. Unresolved CFD and DEM coupled solver for particle-laden flow and its application to single particle settlement. J. Mar. Sci. Eng. 2020, 8, 983. [Google Scholar] [CrossRef]
- Shiri, A.; Anderson, M.; Bensow, R. Hydrodynamics of a Displacement Air Cavity Ship. In Proceedings of the 29th Symposium on Naval Hydrodynamics, Gothenburg, Sweden, 26–31 August 2012. [Google Scholar]





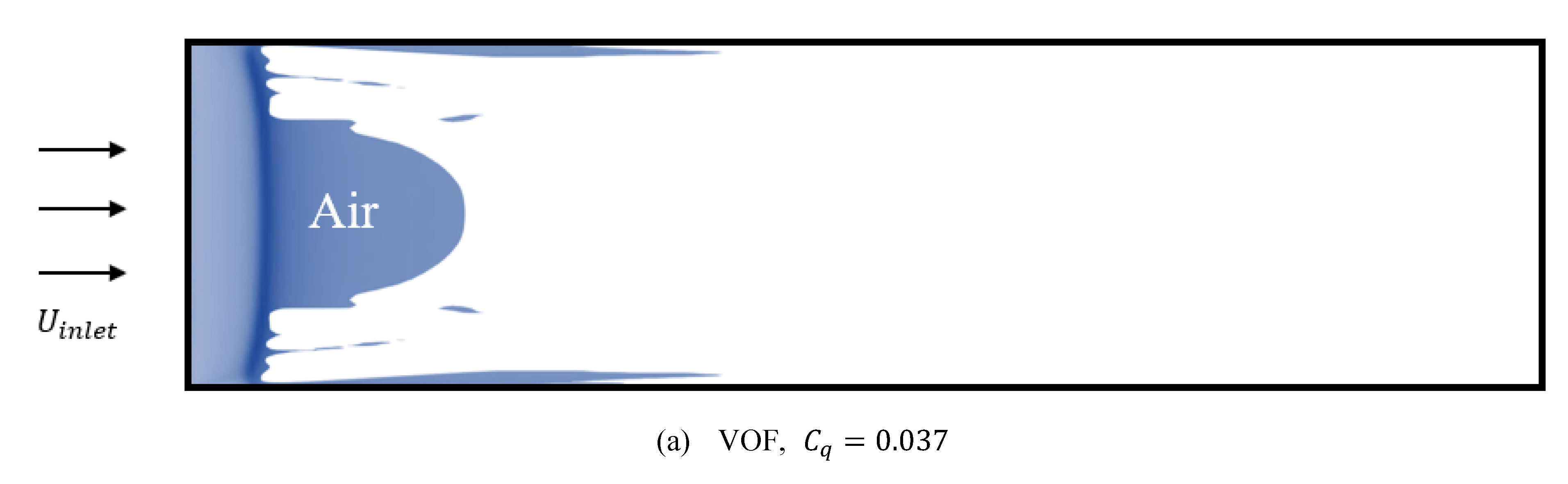
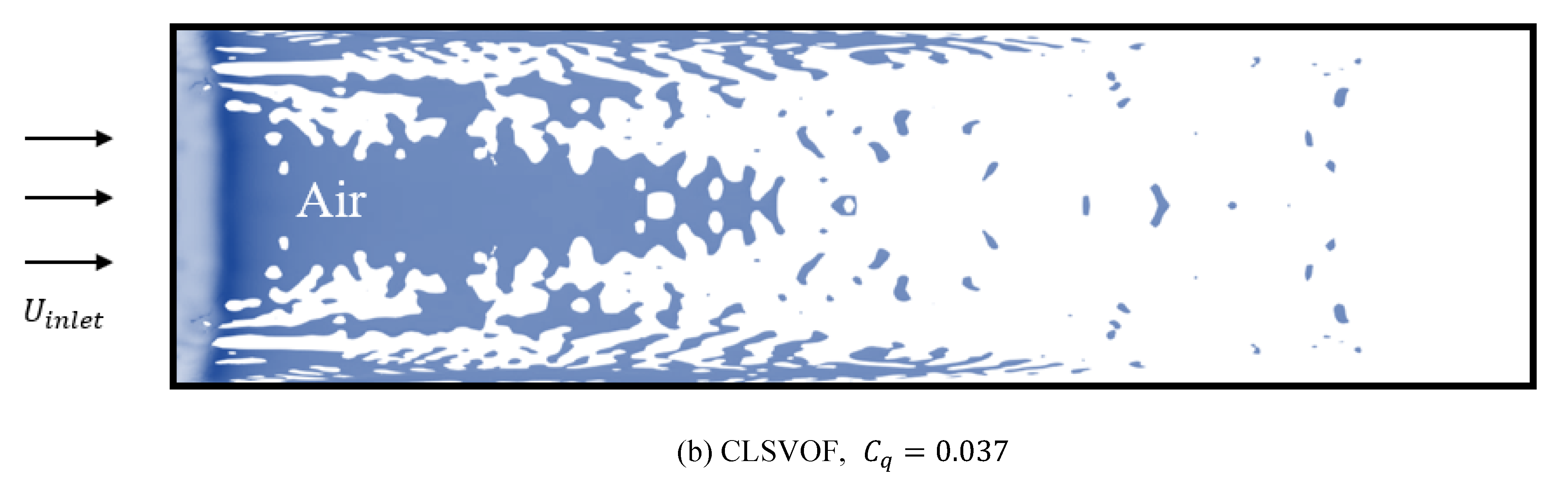

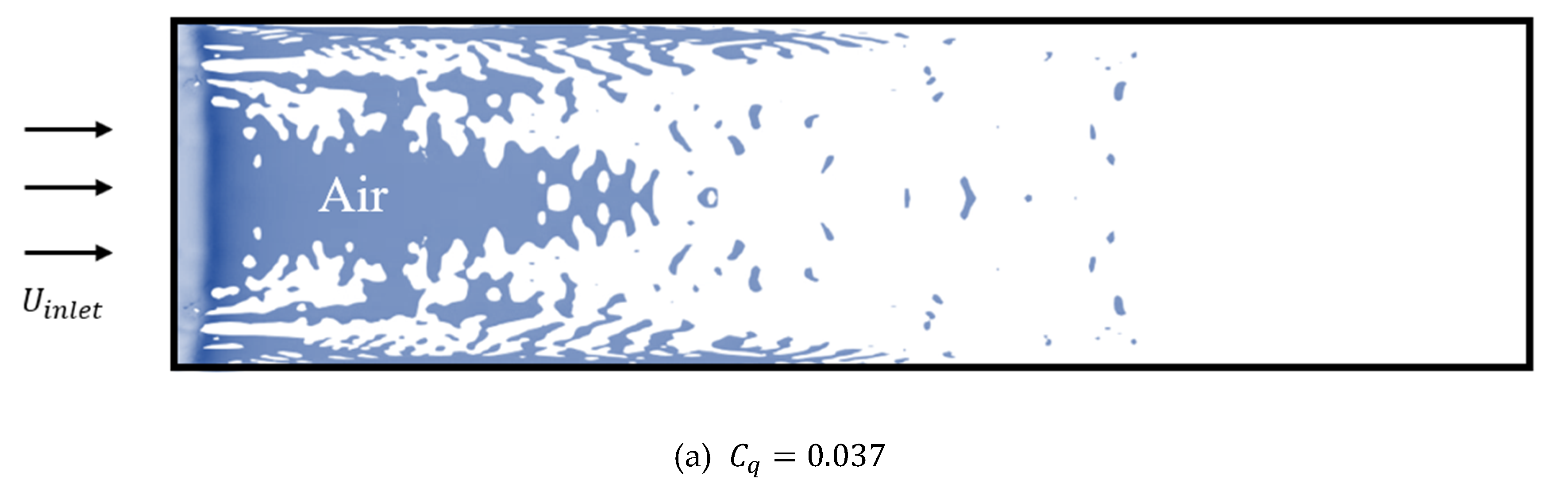
| Case 1 | 0.037 | 0.0152 |
| Case 2 | 0.074 | 0.0304 |
| Case 3 | 0.112 | 0.0461 |
| Case 4 | 0.149 | 0.0614 |
| Case 5 | 0.180 | 0.0742 |
| Grid System | Background Grid Size (m) | Grid Count |
| Coarse | 0.06 | 1,245,645 |
| Medium | 0.042 | 2,822,109 |
| Fine | 0.03 | 4,778,028 |
| Parameter | ||
|---|---|---|
| Fine () | 0.312 | 0.999 |
| Medium () | 0.311 | 0.997 |
| Coarse () | 0.308 | 0.989 |
| 0.333 | 0.25 | |
| −0.001 (−0.32%) | −0.002 (−0.20%) | |
| 0.0015 (0.48%) | 0.00333 (0.33%) | |
| 0.0005 (0.16%) | 0.00133 (0.13%) |
| Present (CLSVOF) | Experiment (Hao et al. [12]) | Difference | |
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Park, S. Coupled Level-Set and Volume of Fluid (CLSVOF) Solver for Air Lubrication Method of a Flat Plate. J. Mar. Sci. Eng. 2021, 9, 231. https://doi.org/10.3390/jmse9020231
Kim H, Park S. Coupled Level-Set and Volume of Fluid (CLSVOF) Solver for Air Lubrication Method of a Flat Plate. Journal of Marine Science and Engineering. 2021; 9(2):231. https://doi.org/10.3390/jmse9020231
Chicago/Turabian StyleKim, Huichan, and Sunho Park. 2021. "Coupled Level-Set and Volume of Fluid (CLSVOF) Solver for Air Lubrication Method of a Flat Plate" Journal of Marine Science and Engineering 9, no. 2: 231. https://doi.org/10.3390/jmse9020231
APA StyleKim, H., & Park, S. (2021). Coupled Level-Set and Volume of Fluid (CLSVOF) Solver for Air Lubrication Method of a Flat Plate. Journal of Marine Science and Engineering, 9(2), 231. https://doi.org/10.3390/jmse9020231







