Multi-Objective Optimization of Jet Pump Based on RBF Neural Network Model
Abstract
:1. Introduction
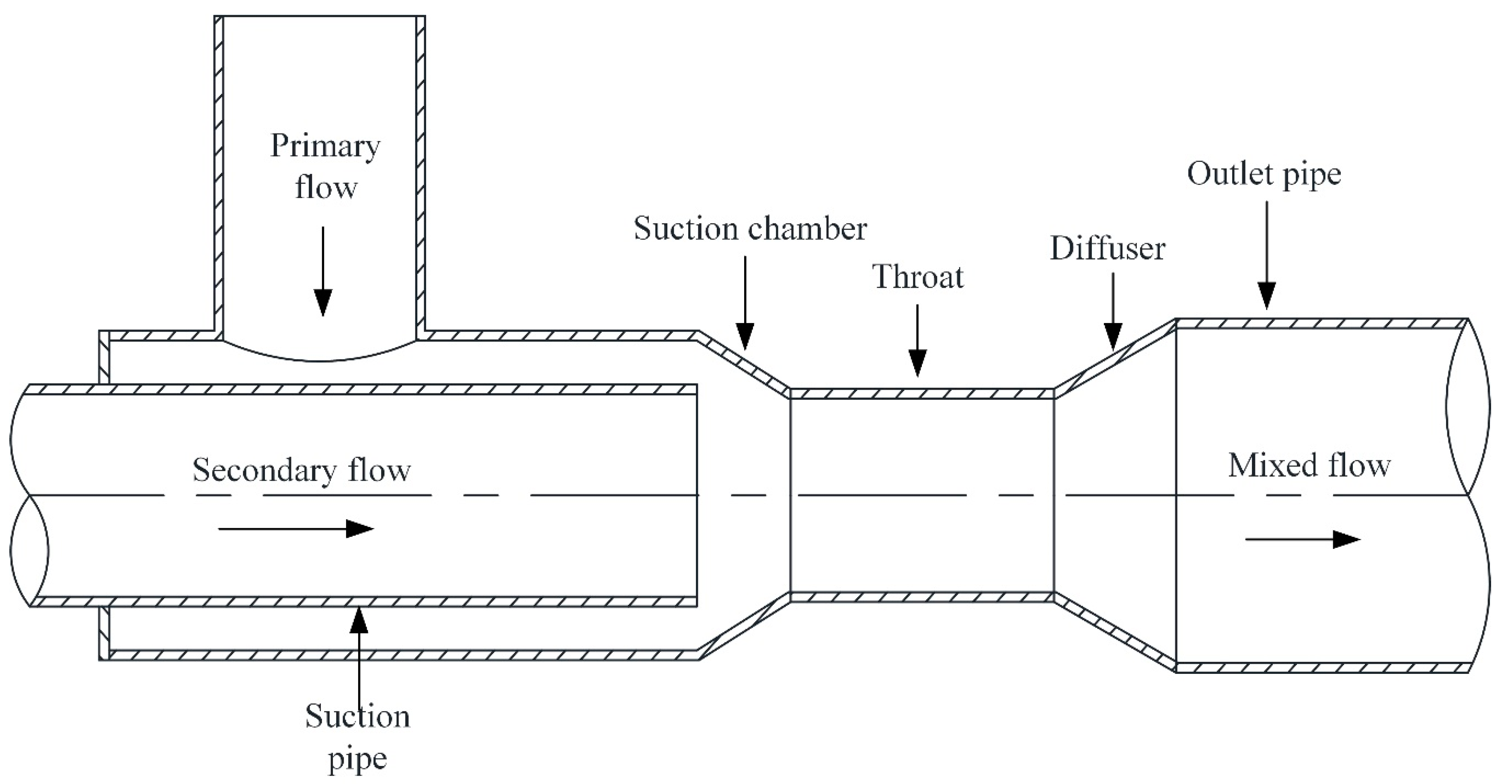
2. Working Principle and Structure of Jet Pump
3. Modeling and Numerical Simulation
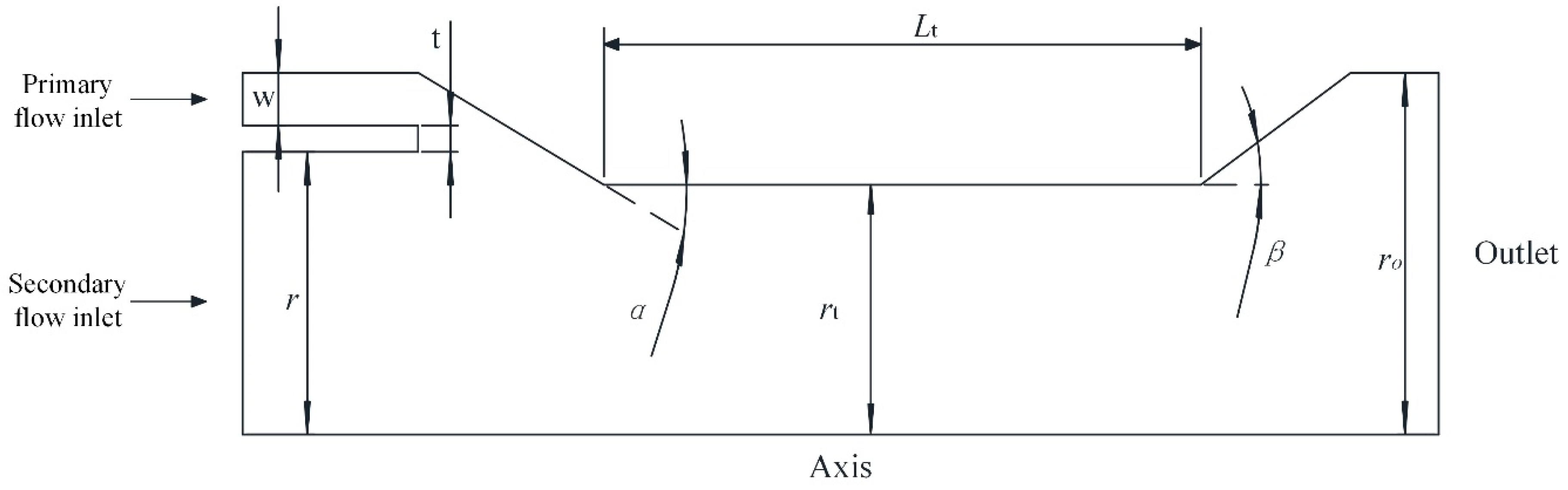
3.1. Modeling
3.2. CFD modeling and Verification
3.2.1. CFD Model
- (1)
- the fluid medium is steady and incompressible;
- (2)
- there is no heat transfer between fluid and the environment;
- (3)
- the influence of the jet pump’s wall roughness is neglected;
- (4)
- the buoyancy influence is neglected.
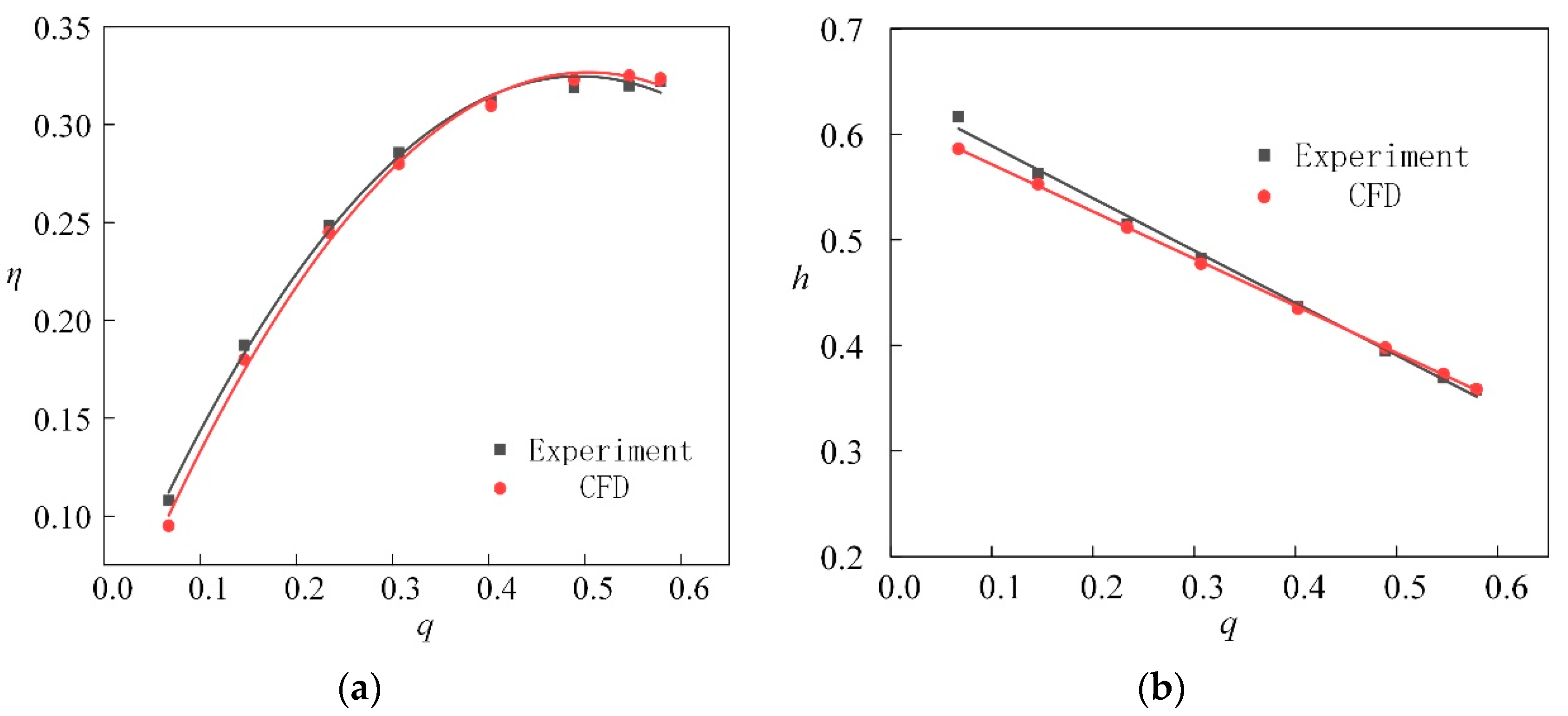
3.2.2. Verification of CFD simulation
4. Hybrid Algorithm and Optimization Process
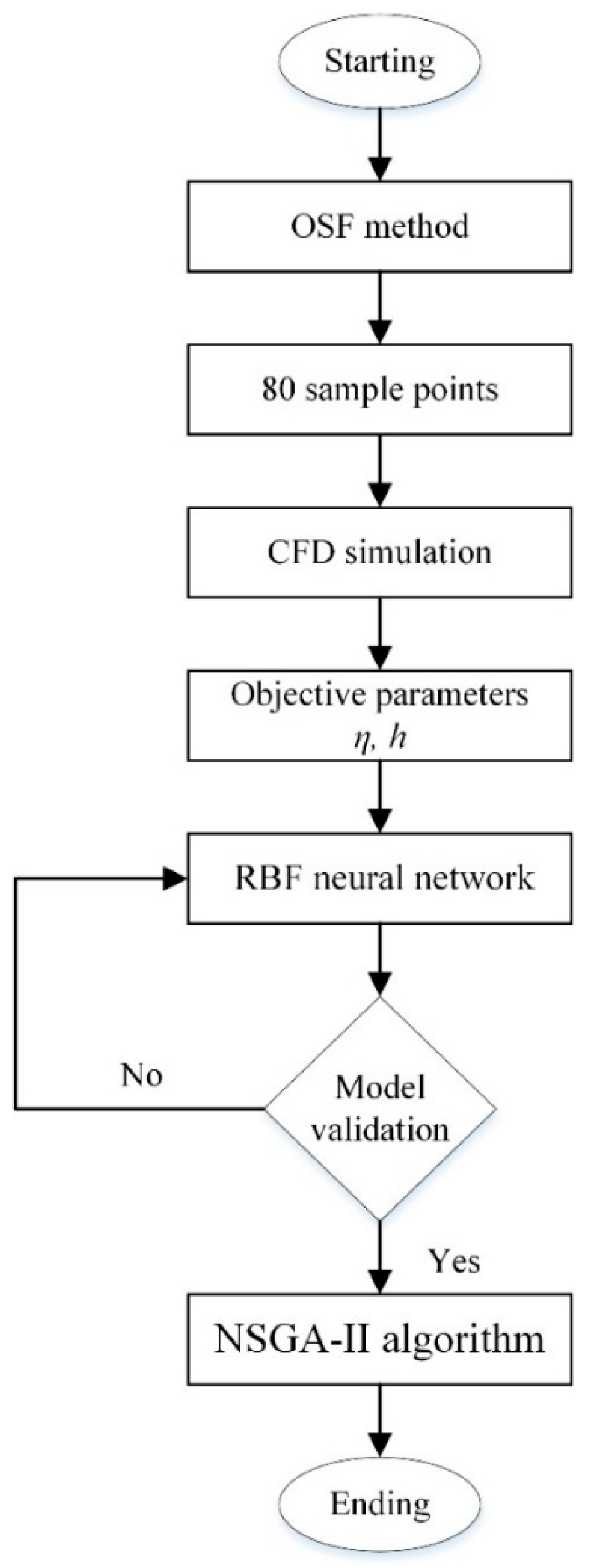
4.1. Optimization Algorithm Design
- Given the space of four design variables, 80 uniformly distributed sample points are generated by the OSF method.
- According to the sampling point, the CFD software Fluent is used to simulate the annular jet pump with different structural parameters. Through numerical simulation, the efficiency and head ratio of the annular jet pump are calculated.
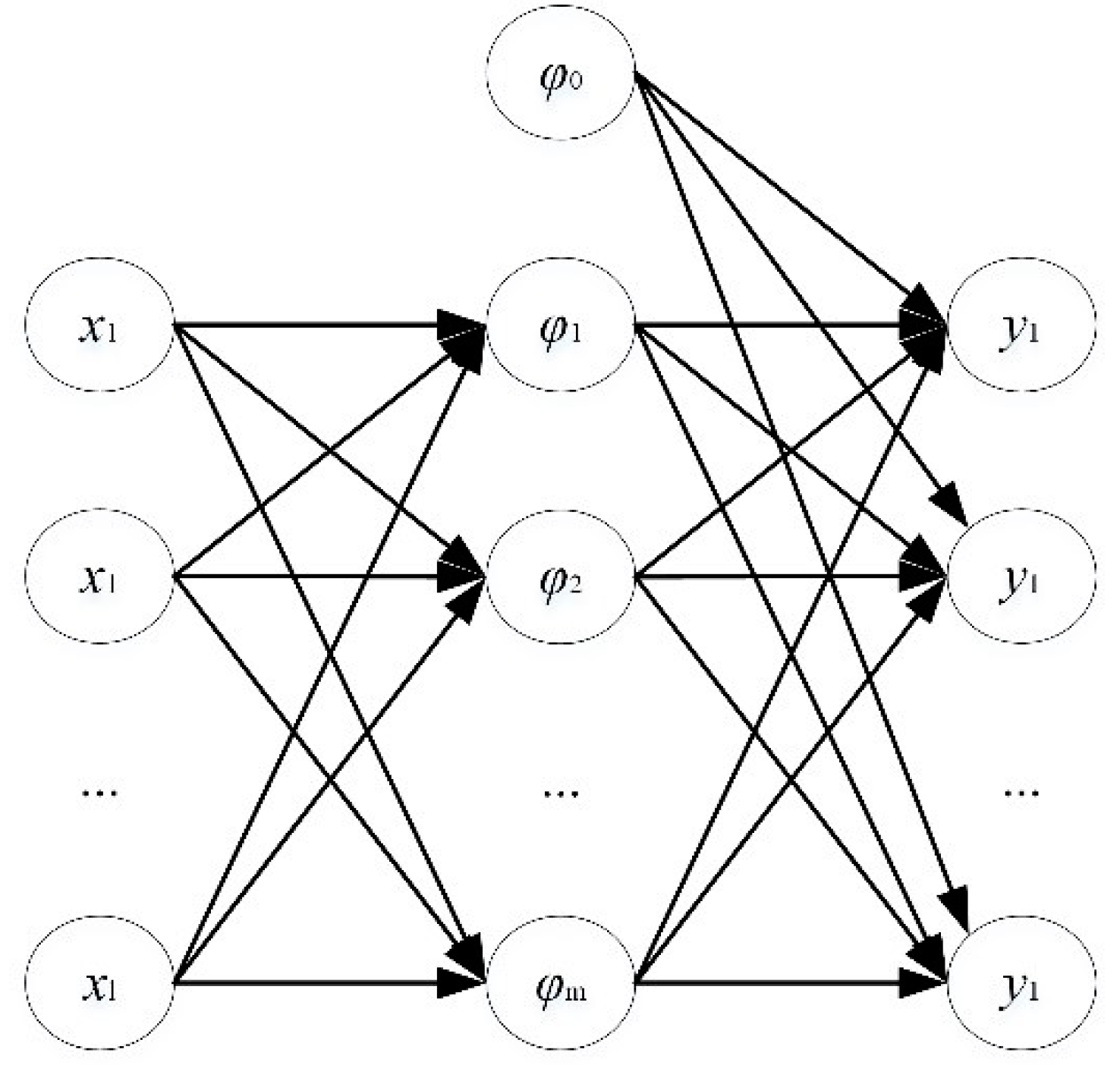
- The neural network model is constructed via the RBF function. The structural parameters of the annular jet pump obtained at the sampling point in step 1 are the input variables, and the efficiency η and head ratio h of the jet pump obtained in step 2 are the output variables.
- The RBF neural network model constructed in step 3 is verified, then the predicted values and simulated values are compared. If the error between the two sets of data is very small, move on to step 5; otherwise, return to step 3 and continue to update the RBF neural network model.
- Based on the RBF neural network model, the NSGA-II optimization algorithm is used to get the optimal solution of the structural parameters of the annular jet pump.
- According to the design parameters of the optimal solution, an optimization model is generated. The CFD simulation and optimization results of the optimization model are verified with each other.
4.2. DOE Method
4.3. Approximate Model
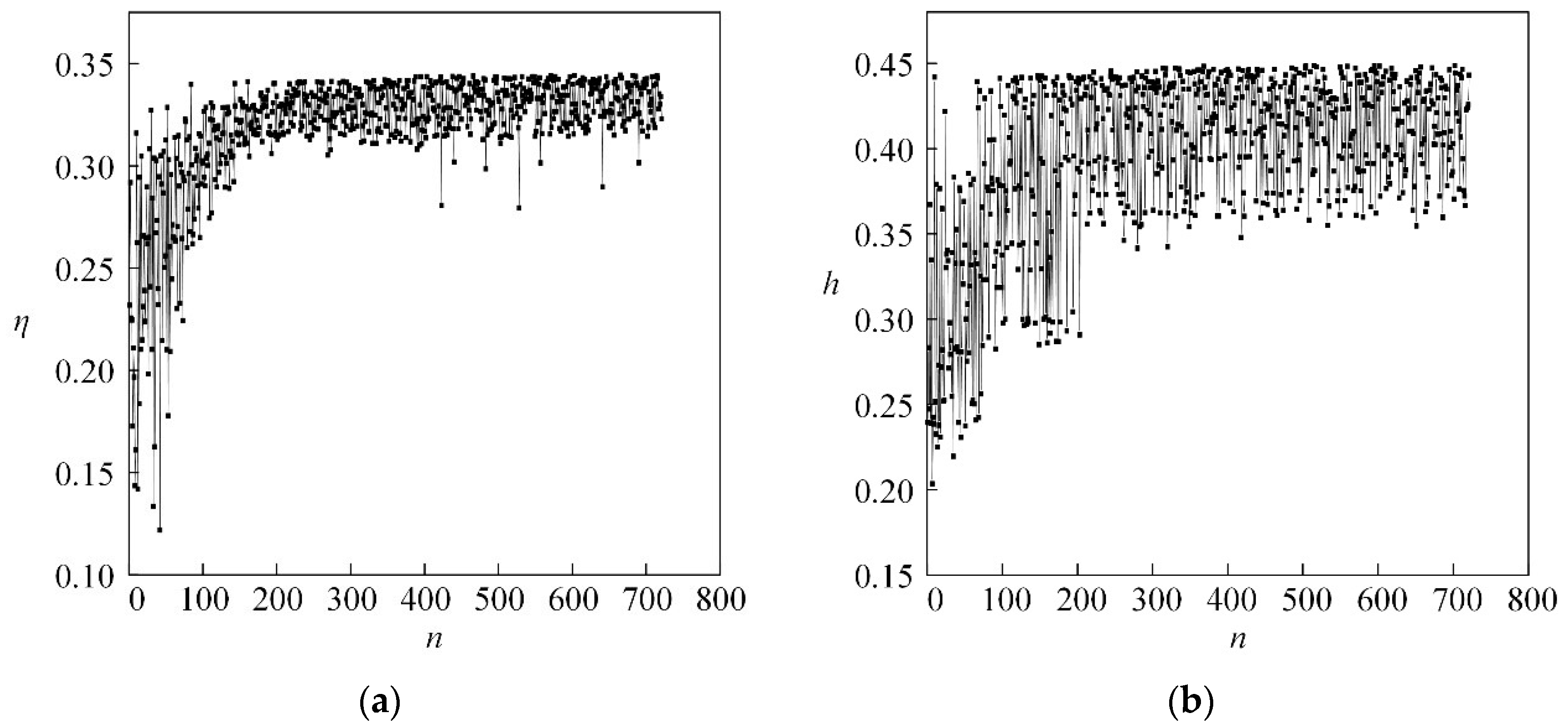
4.4. Establishment of Sample Database
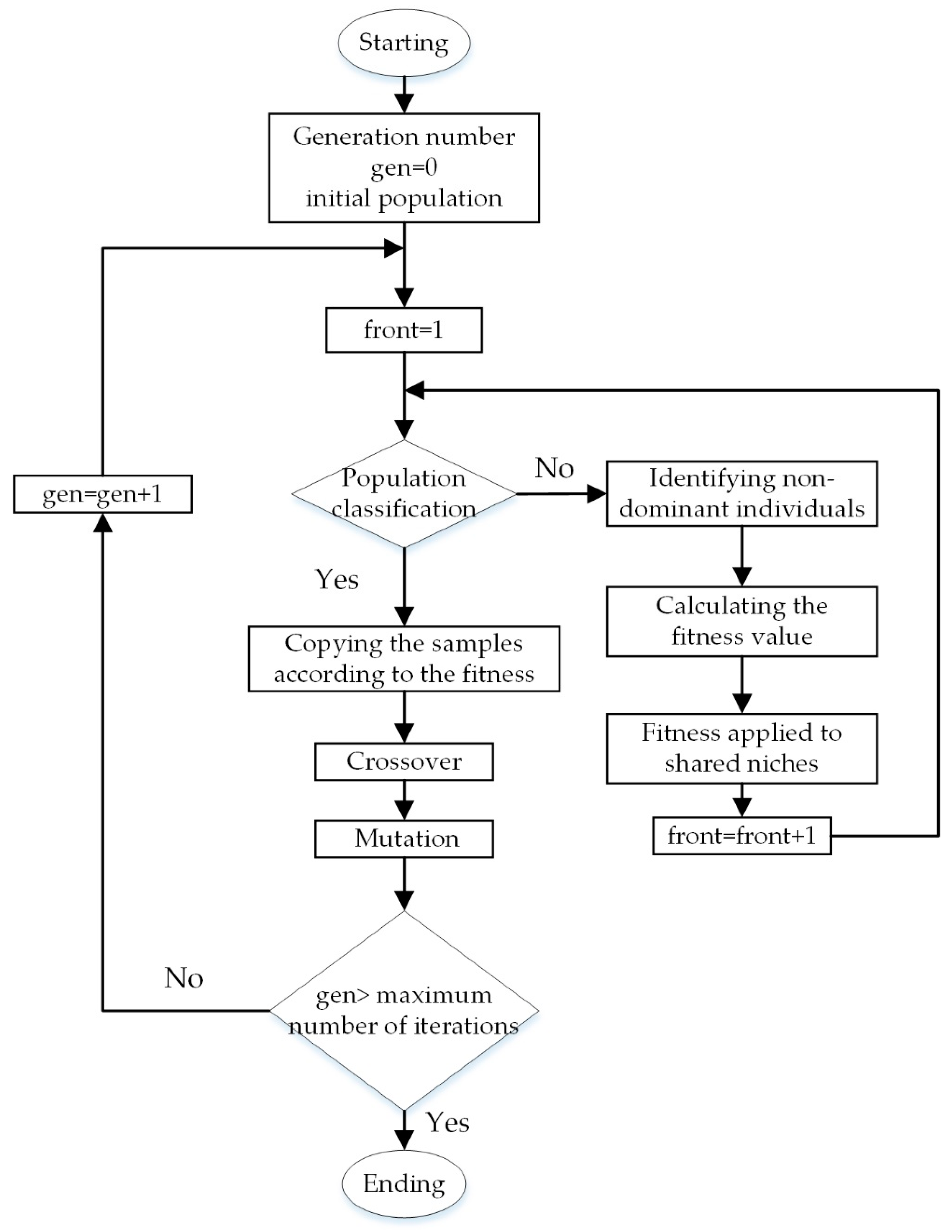
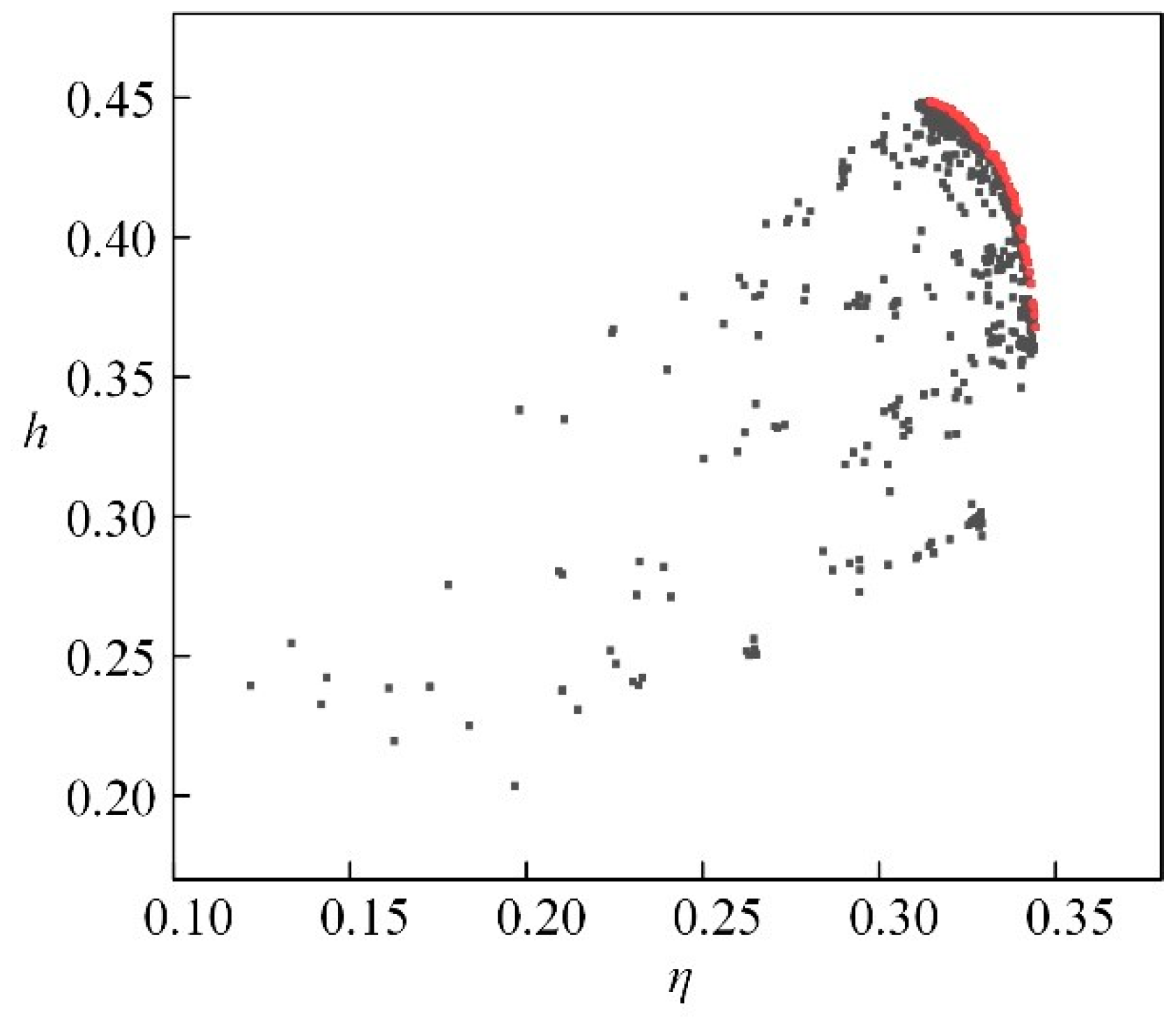
4.5. Multi Objective Optimization Algorithm
5. Results and Discussion
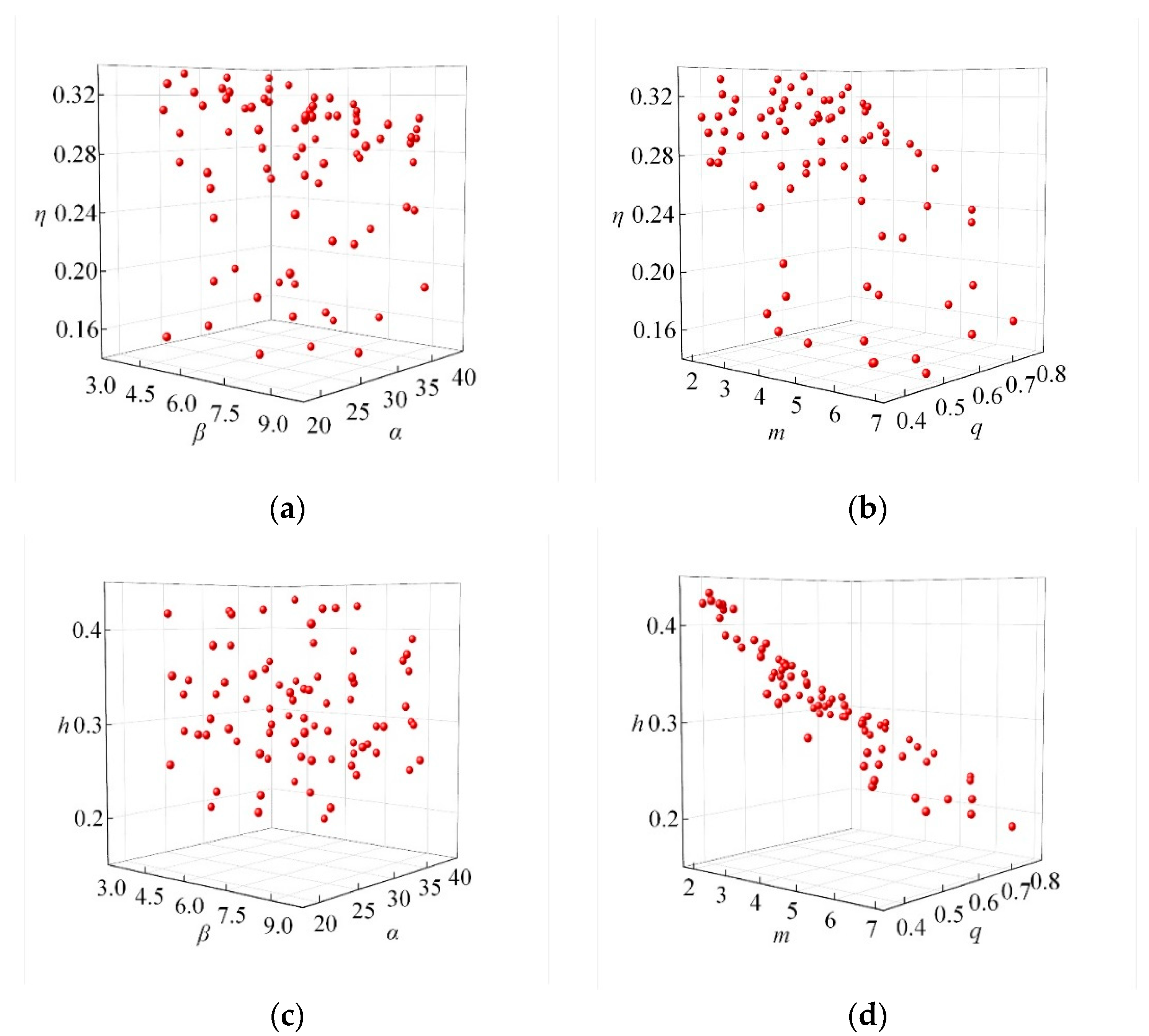
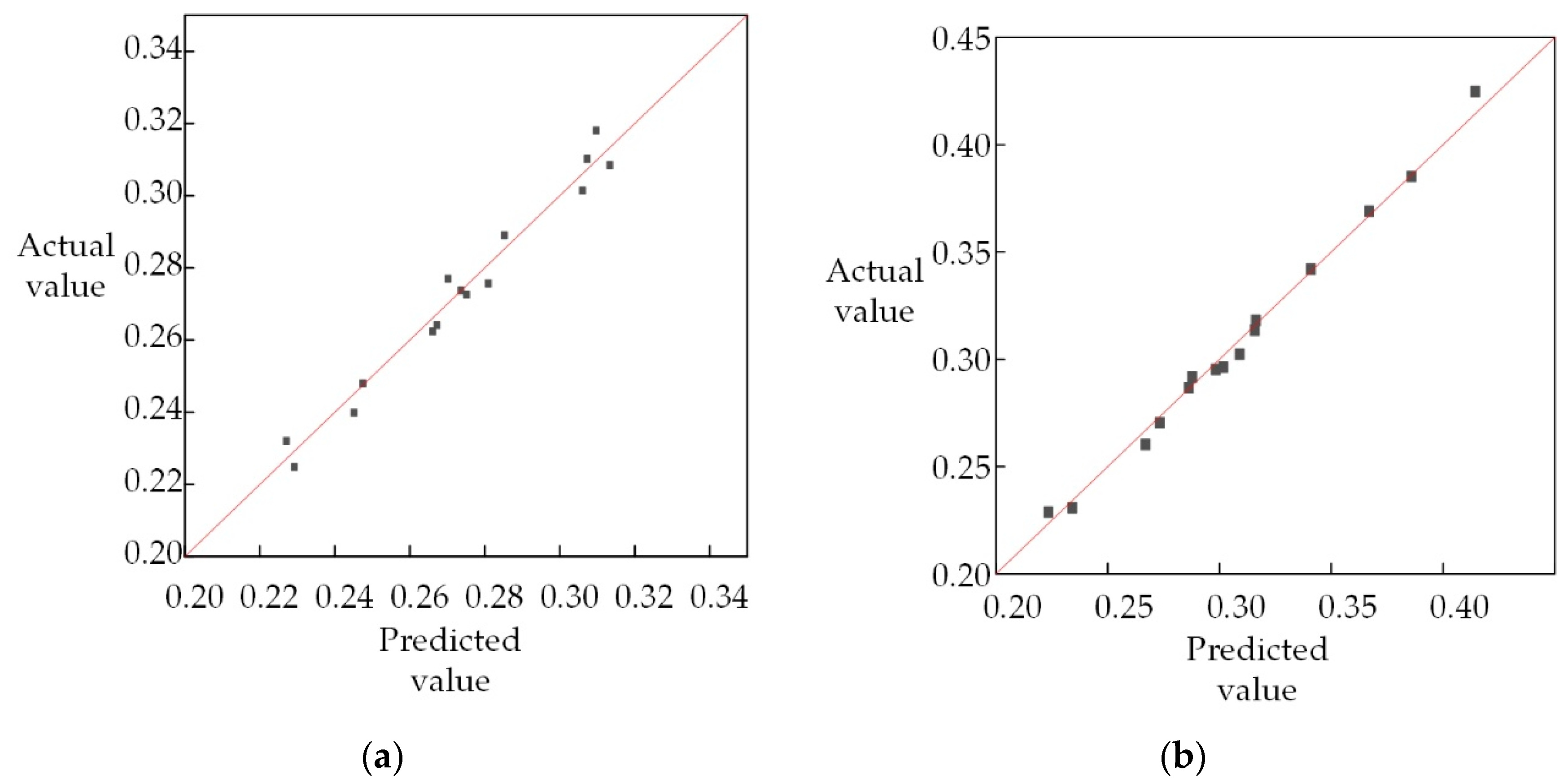
5.1. Error Analysis of RBF Model
5.2. Optimization Results
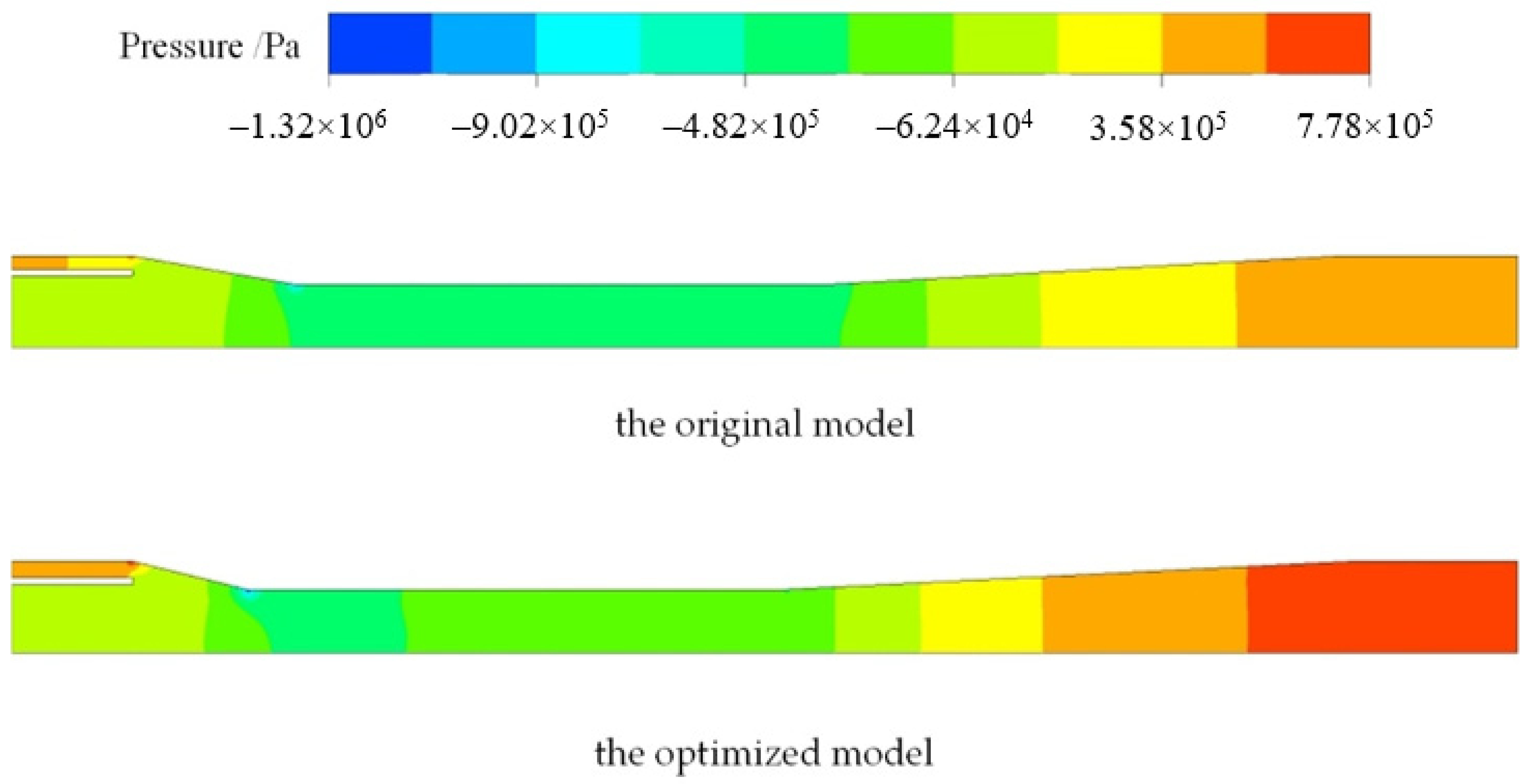
5.3. Analysis of Internal Flow Field Optimization of Jet Pump
6. Conclusions
- (1)
- An RBF neural network approximation model was constructed to analyze the efficiency and head ratio of an annular jet pump. The determination coefficients R2 of the two objectives were greater than 0.97, and the accuracy of the model is reliable.
- (2)
- The NSGA-II algorithm was used to optimize the annular jet pump. In terms of structure, the suction angle increased, the diffusion angle decreased and the flow ratio and area ratio decreased compared with the original model, while in terms of performance, the head ratio increased by 30.46% and efficiency is increased by 7%.
- (3)
- The optimization method based on the RBF neural network model and the NSGA-II optimization algorithm was able obtain the optimal design parameter combination in the global design space of an annular jet pump, which can be applied to other kinds of pumps. However, due to the errors of the CFD and RBF models, this method needs the support of experimental data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| q | m | α(°) | β(°) |
|---|---|---|---|
| 0.5835 | 4.256 | 20.22 | 9.164 |
| 0.7259 | 1.789 | 30.54 | 7.646 |
| 0.538 | 2.454 | 18.84 | 8.178 |
| 0.4013 | 4.078 | 20.5 | 8.936 |
| 0.3899 | 4.876 | 36.1 | 8.026 |
| 0.6462 | 3.019 | 31.92 | 4.228 |
| 0.4297 | 1.959 | 21.34 | 6.734 |
| 0.3842 | 4.349 | 25.24 | 4.988 |
| 0.3671 | 2.649 | 26.08 | 8.556 |
| 0.3614 | 2.491 | 34.44 | 7.722 |
| 0.743 | 2.185 | 36.66 | 4.608 |
| 0.7089 | 3.688 | 24.12 | 4.076 |
| 0.6861 | 1.883 | 37.5 | 9.012 |
| 0.4639 | 2.824 | 29.98 | 4.152 |
| 0.669 | 2.872 | 40 | 8.406 |
| 0.6291 | 6.163 | 35.54 | 5.14 |
| 0.7886 | 5.383 | 23.02 | 5.67 |
| 0.6747 | 1.723 | 30.82 | 5.444 |
| 0.7316 | 2.919 | 20.78 | 5.974 |
| 0.35 | 4.547 | 27.18 | 7.266 |
| 0.6918 | 1.985 | 19.68 | 7.114 |
| 0.612 | 3.995 | 28.58 | 6.126 |
| 0.7544 | 2.529 | 29.14 | 5.898 |
| 0.7658 | 3.835 | 27.46 | 7.494 |
| 0.7829 | 3.915 | 36.94 | 7.038 |
| 0.6348 | 1.812 | 38.32 | 6.582 |
| 0.3728 | 2.28 | 34.98 | 5.292 |
| 0.5551 | 2.155 | 33.04 | 7.95 |
| 0.6804 | 6.347 | 21.9 | 7.494 |
| 0.6576 | 2.012 | 29.42 | 9.772 |
| 0.6063 | 6.953 | 23.3 | 5.368 |
| 0.5038 | 6.737 | 31.08 | 6.886 |
| 0.7772 | 4.447 | 31.36 | 5.216 |
| 0.4753 | 3.419 | 33.6 | 6.506 |
| 0.5949 | 2.968 | 33.32 | 9.62 |
| 0.5722 | 2.313 | 18.28 | 5.518 |
| 0.7601 | 2.691 | 32.76 | 8.784 |
| 0.5095 | 3.482 | 26.64 | 7.798 |
| 0.4468 | 5.992 | 28.58 | 9.088 |
| 0.4867 | 3.019 | 39.16 | 8.482 |
| 0.5494 | 2.382 | 28.02 | 6.05 |
| 0.4639 | 2.067 | 31.64 | 10 |
| 0.7715 | 5.524 | 23.84 | 9.392 |
| 0.612 | 2.248 | 24.96 | 4 |
| 0.4127 | 3.296 | 32.48 | 9.696 |
| 0.7487 | 1.933 | 22.74 | 5.064 |
| 0.407 | 3.18 | 19.4 | 6.658 |
| 0.5835 | 3.76 | 18.56 | 6.81 |
| 0.5323 | 5.249 | 36.38 | 9.468 |
| 0.5209 | 2.735 | 24.68 | 9.848 |
| 0.4354 | 1.835 | 27.74 | 4.76 |
| 0.481 | 1.702 | 33.88 | 6.278 |
| 0.7943 | 2.185 | 37.22 | 6.962 |
| 0.7032 | 7.178 | 32.2 | 7.114 |
| 0.6234 | 4.994 | 28.86 | 8.86 |
| 0.6006 | 4.652 | 37.78 | 7.342 |
| 0.5437 | 3.548 | 22.18 | 4.684 |
| 0.3557 | 4.166 | 34.44 | 4.836 |
| 0.4582 | 5.829 | 38.88 | 5.746 |
| 0.7373 | 3.237 | 19.12 | 8.33 |
| 0.6975 | 3.125 | 25.8 | 9.924 |
| 0.5778 | 1.681 | 23.56 | 5.822 |
| 0.3956 | 1.767 | 29.7 | 8.102 |
| 0.4241 | 1.908 | 21.62 | 9.316 |
| 0.5665 | 1.745 | 25.52 | 8.254 |
| 0.5266 | 3.296 | 38.06 | 4.532 |
| 0.6519 | 2.568 | 26.36 | 7.874 |
| 0.3785 | 2.608 | 27.18 | 6.202 |
| 0.4981 | 6.536 | 22.46 | 7.418 |
| 0.5152 | 5.117 | 30.26 | 4.304 |
| 0.5608 | 2.04 | 34.7 | 4.38 |
| 0.7203 | 4.76 | 35.82 | 9.24 |
| 0.4411 | 1.859 | 38.6 | 8.708 |
| 0.6633 | 2.096 | 19.94 | 9.544 |
| 0.8 | 2.124 | 24.4 | 8.632 |
| 0.7146 | 3.616 | 39.44 | 4.912 |
| 0.4525 | 5.675 | 18 | 5.518 |
| 0.6405 | 2.779 | 35.26 | 6.43 |
| 0.4924 | 2.347 | 39.72 | 6.354 |
| 0.4184 | 2.417 | 21.06 | 4.456 |
References
- Yapıcı, R.; Aldas, K. Optimization of water jet pumps using numerical simulation. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 438–449. [Google Scholar] [CrossRef]
- Meakhail, T.; Teaima, I. Experimental and numerical studies of the effect of area ratio and driving pressure on the performance of water and slurry jet pumps. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2250–2266. [Google Scholar] [CrossRef]
- Long, X.; Xu, M.; Wang, J.; Zou, J.; Bin, J. An experimental study of cavitation damage on tissue of Carassius auratus in a jet fish pump. Ocean Eng. 2019, 174, 43–50. [Google Scholar] [CrossRef]
- Shimizu, Y.; Nakamura, S.; Kuzuhara, S. Studies of the Configuration and Performance of Annular Type Jet Pumps. J. Fluids Eng. 1987, 3, 205–212. [Google Scholar] [CrossRef]
- Kwon, O.B.; Kim, M.K.; Kwon, H.C.; Bae, D.S. Two-dimensional Numerical Simulations on the Performance of an Annular Jet Pump. J. Vis. 2002, 5, 21–28. [Google Scholar] [CrossRef]
- Deng, H.; Liu, X.; Ma, W. Flow Field Analysis for the Diffuser Outlet of Jet Pump Used in the Drain Sand of Petroleum Well. J. Jilin Univ. 2010, 40, 689–693. [Google Scholar] [CrossRef]
- Yang, X.; Long, X.; Yao, X. Numerical investigation on the mixing process in a steam ejector with different nozzle structures. Int. J. Therm. Sci. 2012, 56, 95–106. [Google Scholar] [CrossRef]
- Lyu, Q.; Xiao, Z.; Zeng, Q.; Xiao, L.; Long, X. Implementation of design of experiment for structural optimization of annular jet pumps. J. Mech. Sci. Technol. 2016, 30, 585–592. [Google Scholar] [CrossRef]
- Deng, X.; Dong, J.; Wang, Z.; Tu, J. Numerical analysis of an annular water–air jet pump with self-induced oscillation mixing chamber. J. Comput. Multiph. Flows 2017, 9, 47–53. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Li, M.; Xu, Y.; Wang, B.; Dang, X. Numerical Study on the Working Performance of a Streamlined Annular Jet Pump. Energies 2020, 13, 4411. [Google Scholar] [CrossRef]
- Gao, G.; Xing, Y.; Wang, Y. Effect of Nozzle Throat Geometry on Flow Field in Liquid Gas Jet Pump: A Simulation Study. Chin. J. Vac. Sci. Technol. 2020, 40, 174–179. [Google Scholar] [CrossRef]
- Xu, M.; Yang, X.; Long, X.; Lyu, Q. Large eddy simulation of turbulent flow structure and characteristics in an annular jet pump. J. Hydrodyn. 2017, 2, 702–715. [Google Scholar] [CrossRef]
- Zou, C.H.; Li, H.; Tang, P.; Xu, D.H. Effect of structural forms on the performance of a jet pump for a deep well jet pump. In Proceedings of the Computational Methods and Experimental Measurements XVII, International Conference on Computational Methods and Experimental Measurements 17th, Opatija, Croatia, 5 May 2015. [Google Scholar] [CrossRef] [Green Version]
- Elger, D.; Taylor, S.; Liou, C. Recirculation in an Annular-Type Jet Pump. J. Fluids Eng. 1994, 116, 735–740. [Google Scholar] [CrossRef]
- Keeney, R.; Raifa, H. Decisions with Multiple Objectives: Preferences and Value Tradeoffs. Health Serv. Res. 1978, 13, 1093–1094. [Google Scholar] [CrossRef]
- Marler, R.; Arora, J. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Chen, W.; Wiecek, M.; Zhang, J. Quality utility: A compromise programming approach to robust design. ASME J. Mech. Des. 1999, 121, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Luh, G.; Chueh, C.; Liu, W. MOIA: Multi-objective immune algorithm. Eng. Optim. 2003, 35, 143–164. [Google Scholar] [CrossRef]
- Deb, K.; Jain, S. Multi-Speed Gearbox Design Using Multi-Objective Evolutionary Algorithms. ASME J. Mech. Des. 2003, 125, 609–619. [Google Scholar] [CrossRef] [Green Version]
- Saitou, K.; Cetin, O. Decomposition-Based Assembly Synthesis for Structural Modularity. ASME J. Mech. Des. 2004, 126, 234–243. [Google Scholar] [CrossRef]
- Ma, X.; Li, Y.; Yan, L. Comparsion review of traditional multi-objective optimization methods and multi-objective genetic algorithm. Electr. Drive Autom. 2010, 3, 48–50. [Google Scholar] [CrossRef]
- Barthelemy, J.; Haftka, R. Approximation concepts for optimum structural design—A review. Struct. Multidiscip. Optim. 1993, 5, 129–144. [Google Scholar] [CrossRef]
- Alexandras, A. Stochastic subset optimization incorporating moving least squares response surface methodologies for stochastic sampling. Adv. Eng. Softw. 2012, 44, 3–14. [Google Scholar] [CrossRef]
- Gholap, A.; Khan, J. Design and multi-objective optimization of heat exchangers for refrigerators. Appl. Energy 2007, 84, 1226–1239. [Google Scholar] [CrossRef]
- Verstraete, T.; Alsalihi, Z.; Braembussche, R. Multidisciplinary Optimization of a Radial Compressor for Microgas Turbine Applications. J. Turbomach. 2010, 132, 031004. [Google Scholar] [CrossRef]
- Naseri, M.; Othman, F. Determination of the length of hydraulic jumps using artificial neural networks. Adv. Eng. Softw. 2012, 48, 27–31. [Google Scholar] [CrossRef]
- Frédéric, M.; Luis, A.; Ichiro, H. Efficient preconditioning for image reconstruction with radial basis functions. Adv. Eng. Softw. 2007, 38, 320–327. [Google Scholar] [CrossRef]
- Sun, H.; Schafer, M. Reduced order model assisted evolutionary algorithms for multi-objective flow design optimization. Eng. Optim. 2011, 43, 97–114. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, S.; Wu, J. Multi-objective optimization of double suction centrifugal pump using Kriging metamodels. Adv. Eng. Softw. 2014, 74, 16–26. [Google Scholar] [CrossRef]
- Safikhani, H.; Khalkhali, A.; Farajpoor, M. Pareto Based Multi-Objective Optimization of Centrifugal Pumps Using CFD, Neural Networks and Genetic Algorithms. Eng. Appl. Comp. Fluid. Mech. 2011, 5, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Hu, B.; Feng, Y.; Liu, K. Multi-objective optimization of double vane pump based on radial basis neural network and particle swarm. Trans. Chin. Soc. Agric. Eng. 2019, 35, 25–32. [Google Scholar] [CrossRef]
- Zhao, A.; Lai, Z.; Wu, P. Multi-objective optimization of a low specific speed centrifugal pump using an evolutionary algorithm. Eng. Optim. 2016, 48, 1251–1274. [Google Scholar] [CrossRef]
- Sheha, A.A.A.; Nasr, M.; Hosien, M.A.; Wahba, E.M. Computational and Experimental Study on the Water-Jet Pump Performance. J. Appl. Fluid Mech. 2018, 11, 1013–1020. [Google Scholar] [CrossRef]
- Shih, T.; Liou, W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Infer. 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Amini, A.; Taki, M.; Rohani, A. Applied improved RBF neural network model for predicting the broiler output energies. Appl. Soft Comput. 2020, 87, 106006. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Zu, H.; Zhang, X. An Optimized RBF Neural Network Based on Beetle Antennae Search Algorithm for Modeling the Static Friction in a Robotic Manipulator Joint. Math. Probl. Eng. 2020, 2020, 1024–1034. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Amrit, P.; Sameer, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Kajero, O.; Thorpe, R.; Yao, Y.; Hill, W.; David, S.; Chen, T. Meta-model-based calibration and sensitivity studies of computational fluid dynamics simulation of jet pumps. Chem. Eng. Technol. 2017, 40, 1674–1684. [Google Scholar] [CrossRef]
| Number of Elements | h | e |
|---|---|---|
| coarse | 0.5793 | 0.0924 |
| medium | 0.5798 | 0.0926 |
| fine | 0.5826 | 0.0936 |
| α(°) | β(°) | m | q | |
|---|---|---|---|---|
| Original scheme | 18 | 5.8 | 2.27 | 0.5789 |
| Optimized scheme | 25.02 | 5.1768 | 1.6823 | 0.3702 |
| η | h | |
|---|---|---|
| Original scheme | 0.3325 | 0.3648 |
| Optimized scheme | 0.3558 | 0.4758 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Wang, G.; Zhang, L.; Wang, L.; Yun, F.; Sun, W.; Wang, X.; Chen, X. Multi-Objective Optimization of Jet Pump Based on RBF Neural Network Model. J. Mar. Sci. Eng. 2021, 9, 236. https://doi.org/10.3390/jmse9020236
Xu K, Wang G, Zhang L, Wang L, Yun F, Sun W, Wang X, Chen X. Multi-Objective Optimization of Jet Pump Based on RBF Neural Network Model. Journal of Marine Science and Engineering. 2021; 9(2):236. https://doi.org/10.3390/jmse9020236
Chicago/Turabian StyleXu, Kai, Gang Wang, Luyao Zhang, Liquan Wang, Feihong Yun, Wenhao Sun, Xiangyu Wang, and Xi Chen. 2021. "Multi-Objective Optimization of Jet Pump Based on RBF Neural Network Model" Journal of Marine Science and Engineering 9, no. 2: 236. https://doi.org/10.3390/jmse9020236
APA StyleXu, K., Wang, G., Zhang, L., Wang, L., Yun, F., Sun, W., Wang, X., & Chen, X. (2021). Multi-Objective Optimization of Jet Pump Based on RBF Neural Network Model. Journal of Marine Science and Engineering, 9(2), 236. https://doi.org/10.3390/jmse9020236






