An Integrated Dynamic Model and Optimized Fuzzy Controller for Path Tracking of Deep-Sea Mining Vehicle
Abstract
:1. Introduction
2. Establishment of the MBD Model
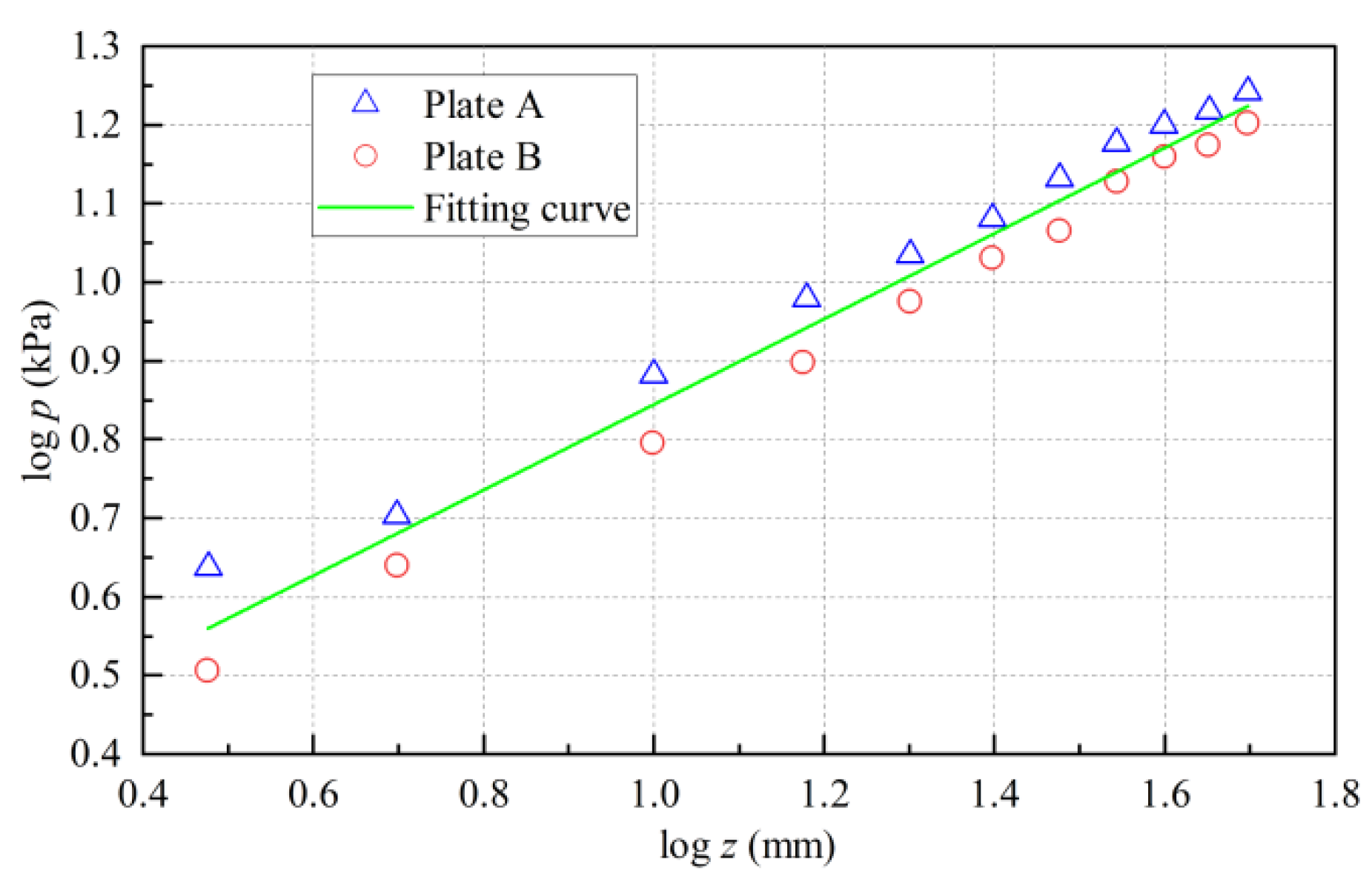
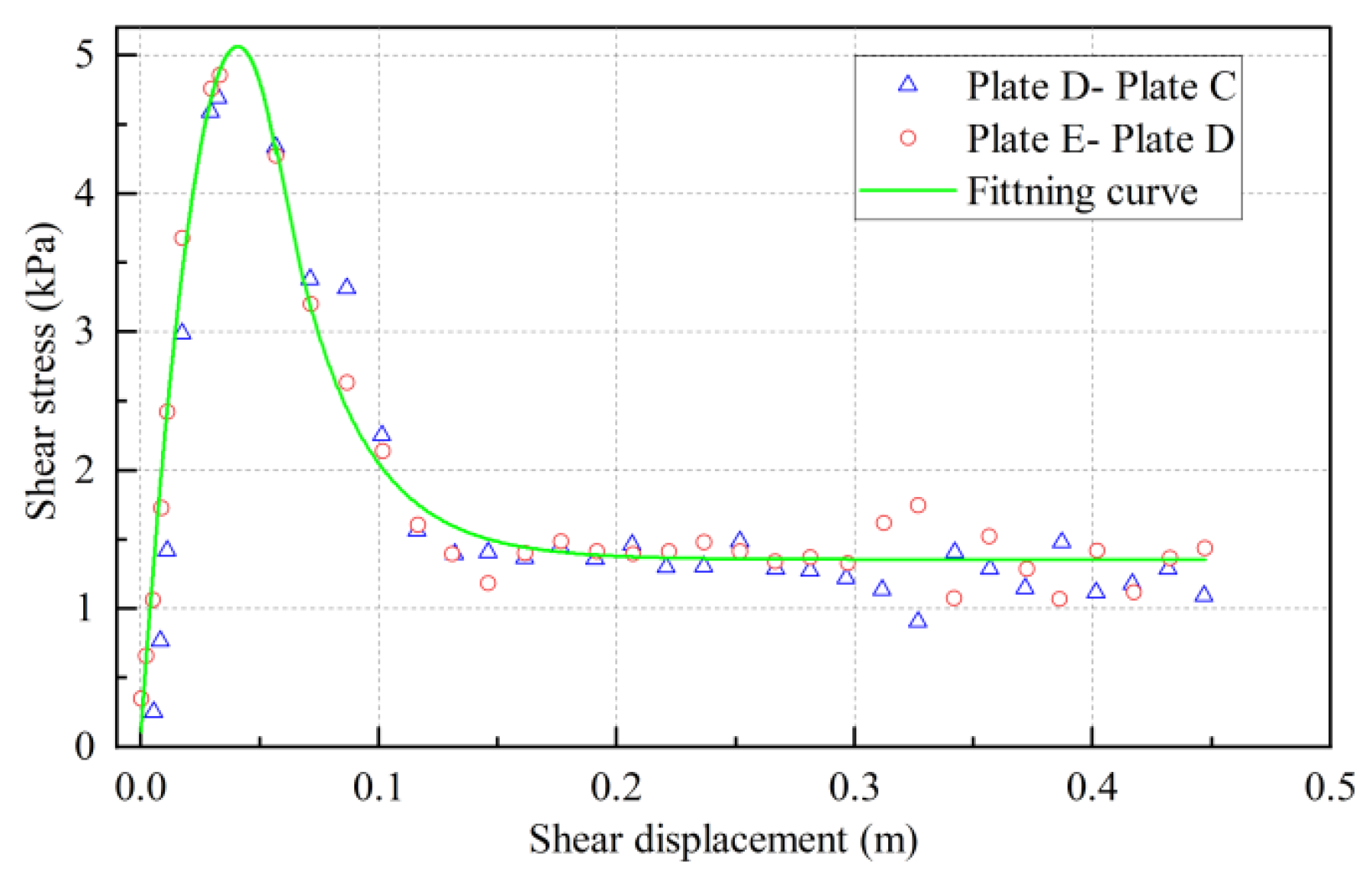
2.1. Vehicle–Sediment Mechanical Interaction
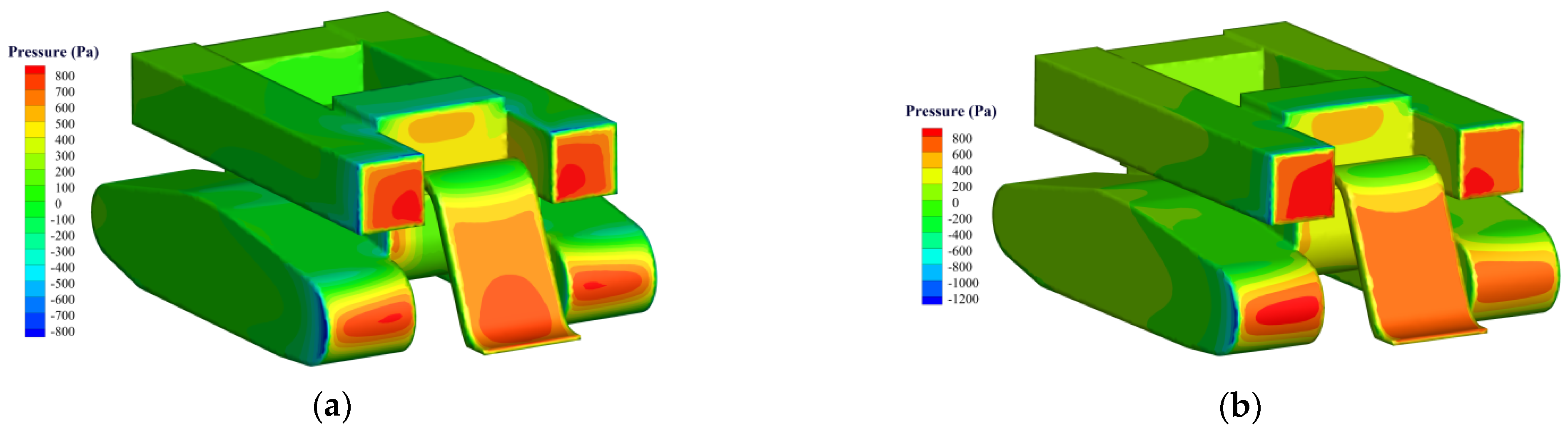
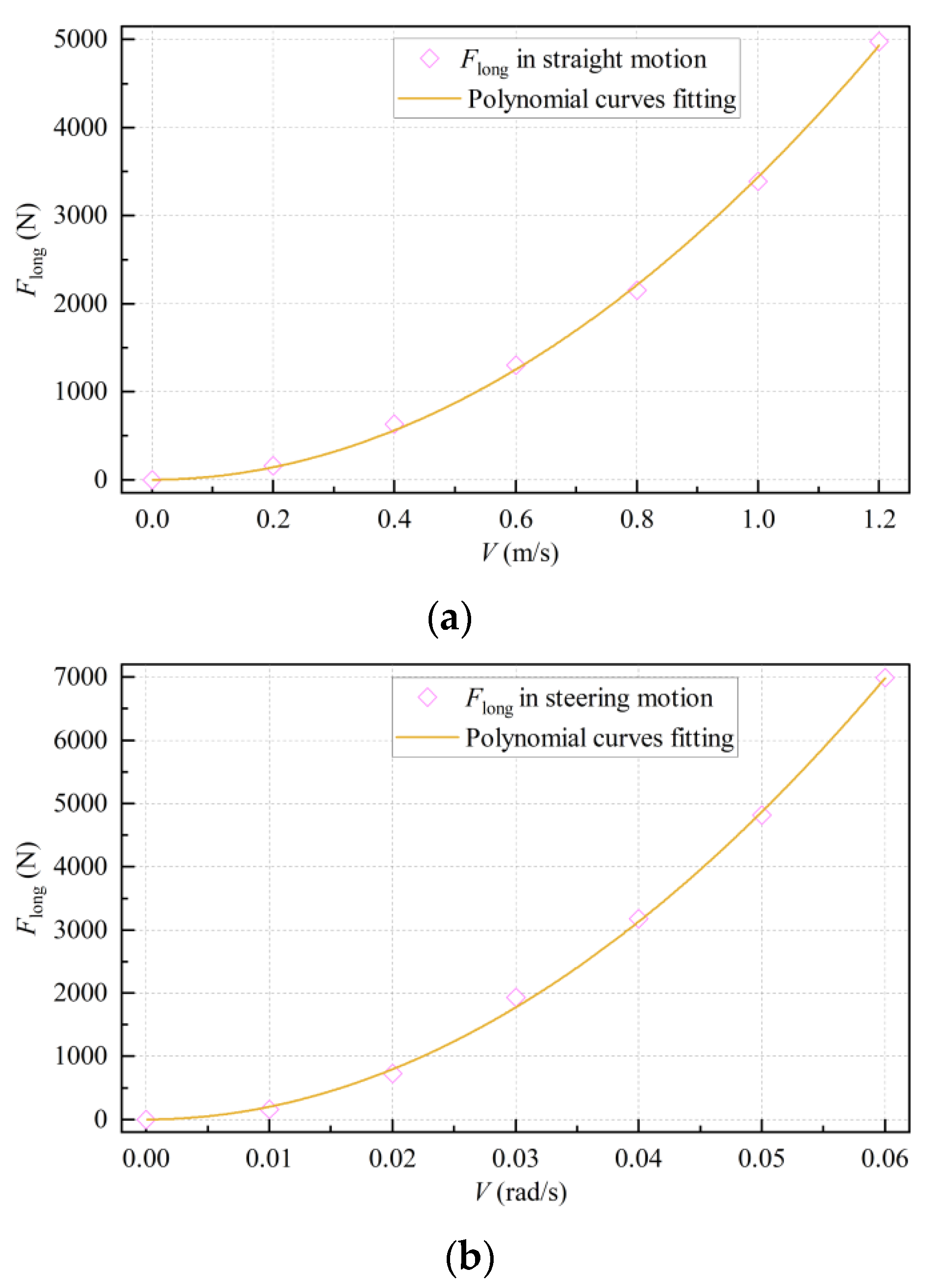
2.2. Spatial Hydrodynamic Distribution
2.2.1. Meshing Method
2.2.2. Simulation Setup Details
2.2.3. Simulation Results
2.3. MBD Model
3. Exploration of the Path-Tracking Controller
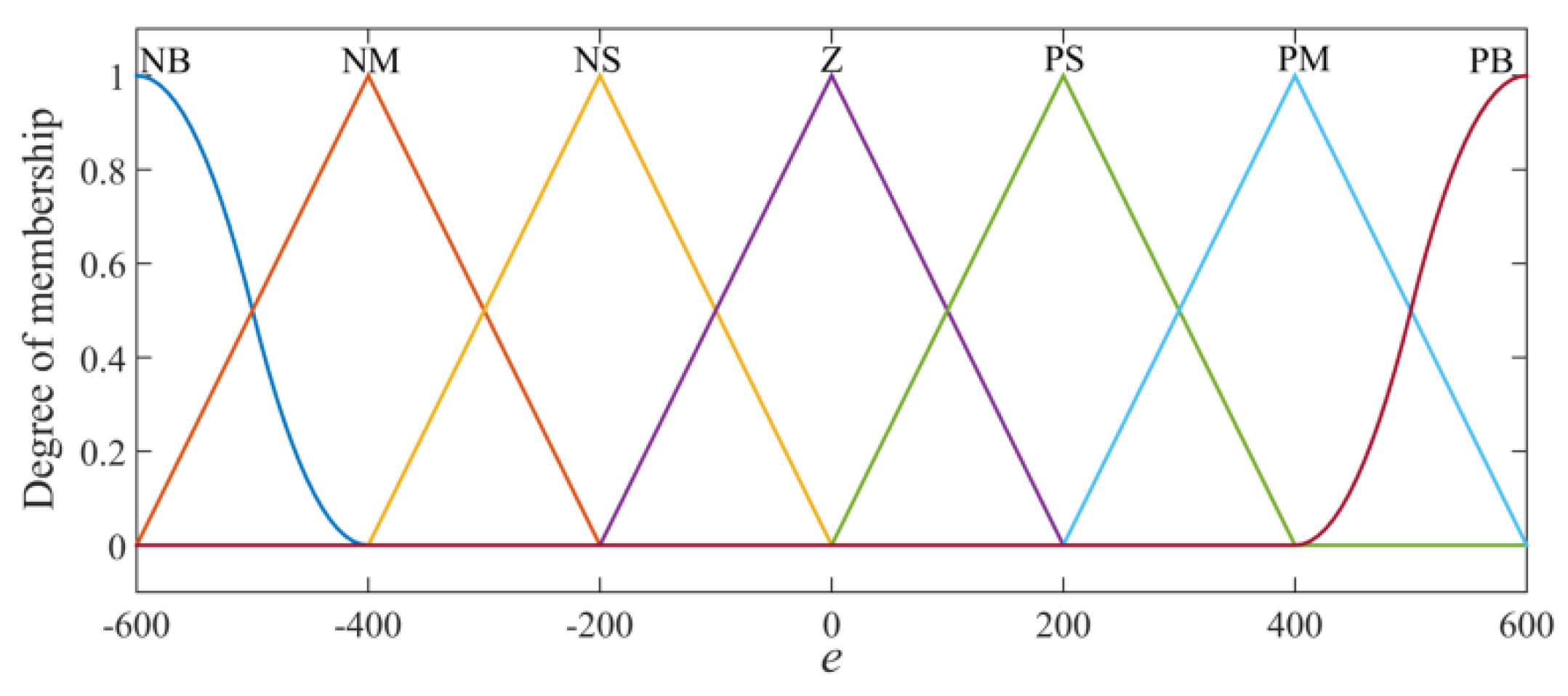
3.1. Design of Fuzzy Controller
3.2. Optimization of Fuzzy Controller
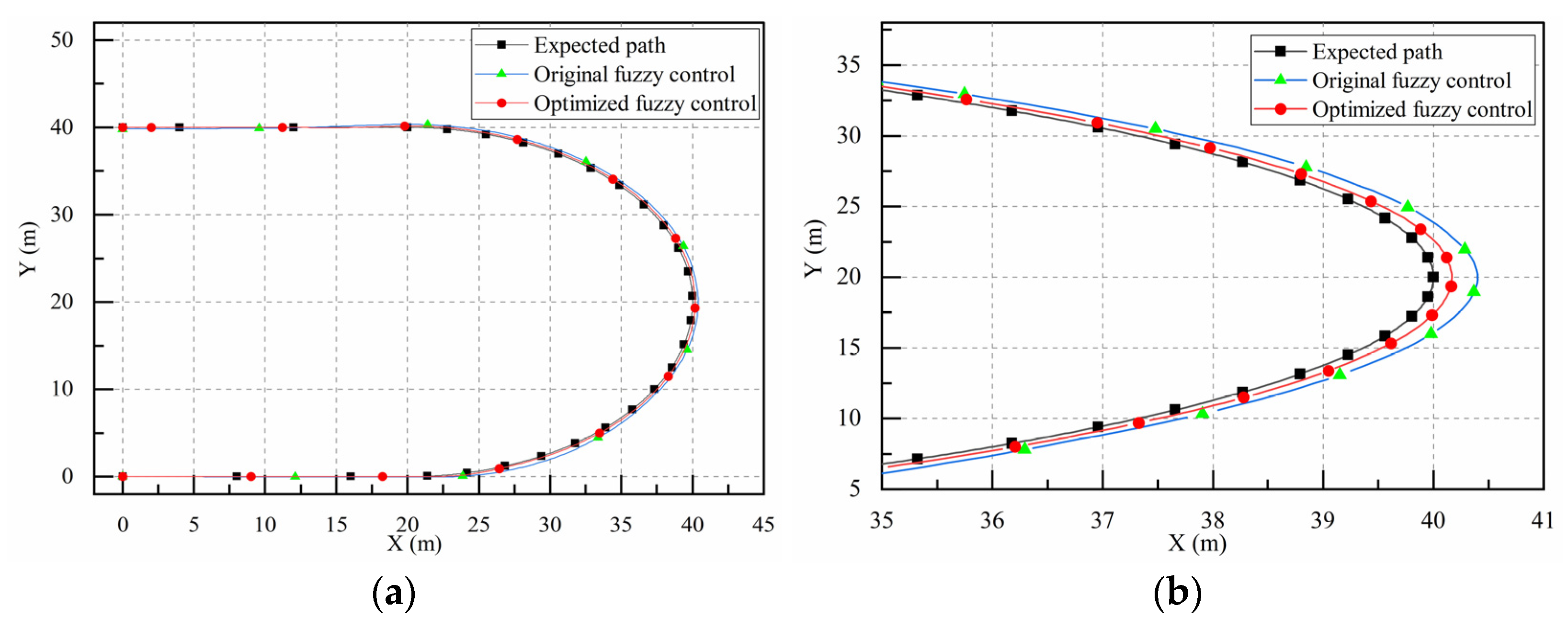
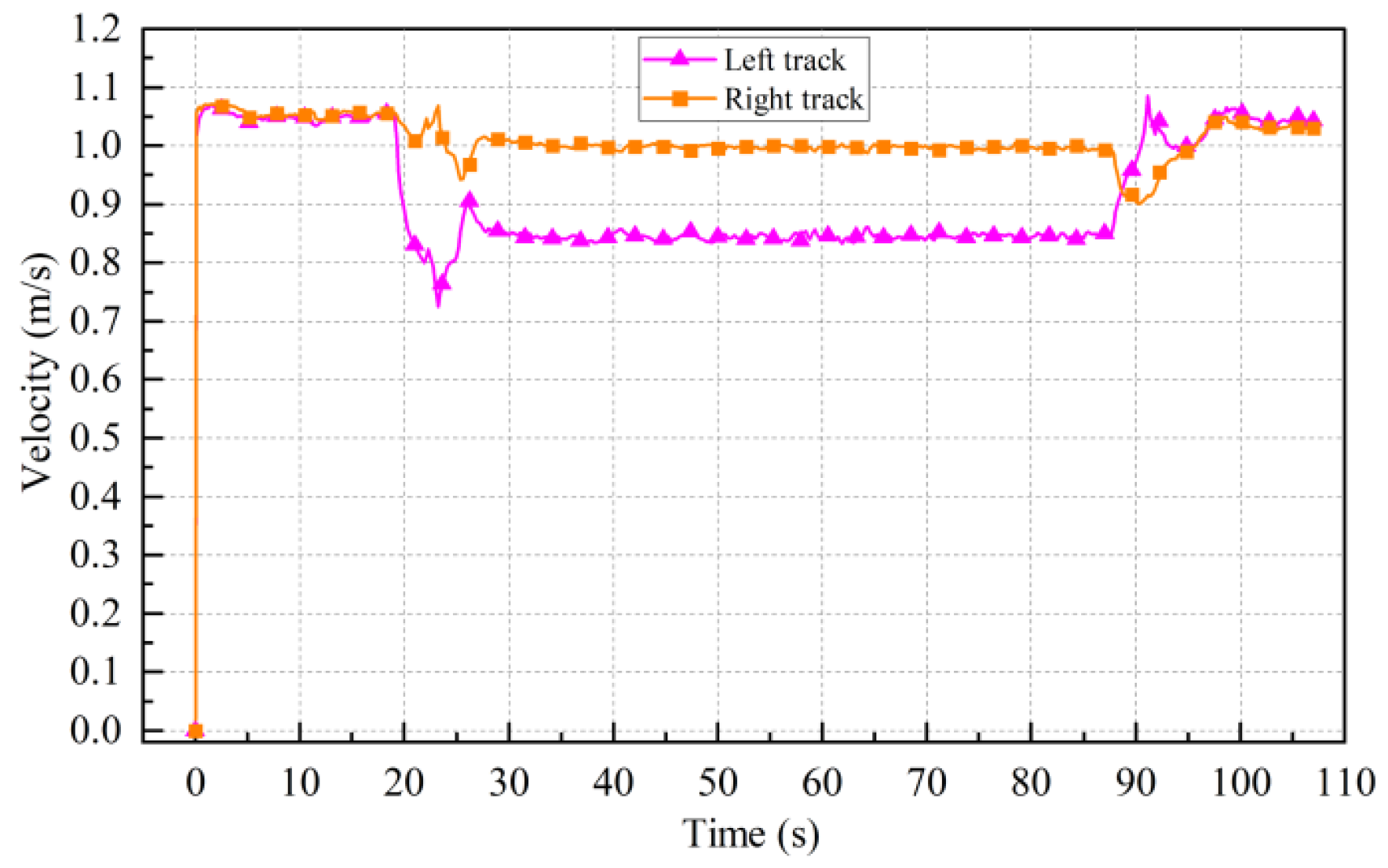
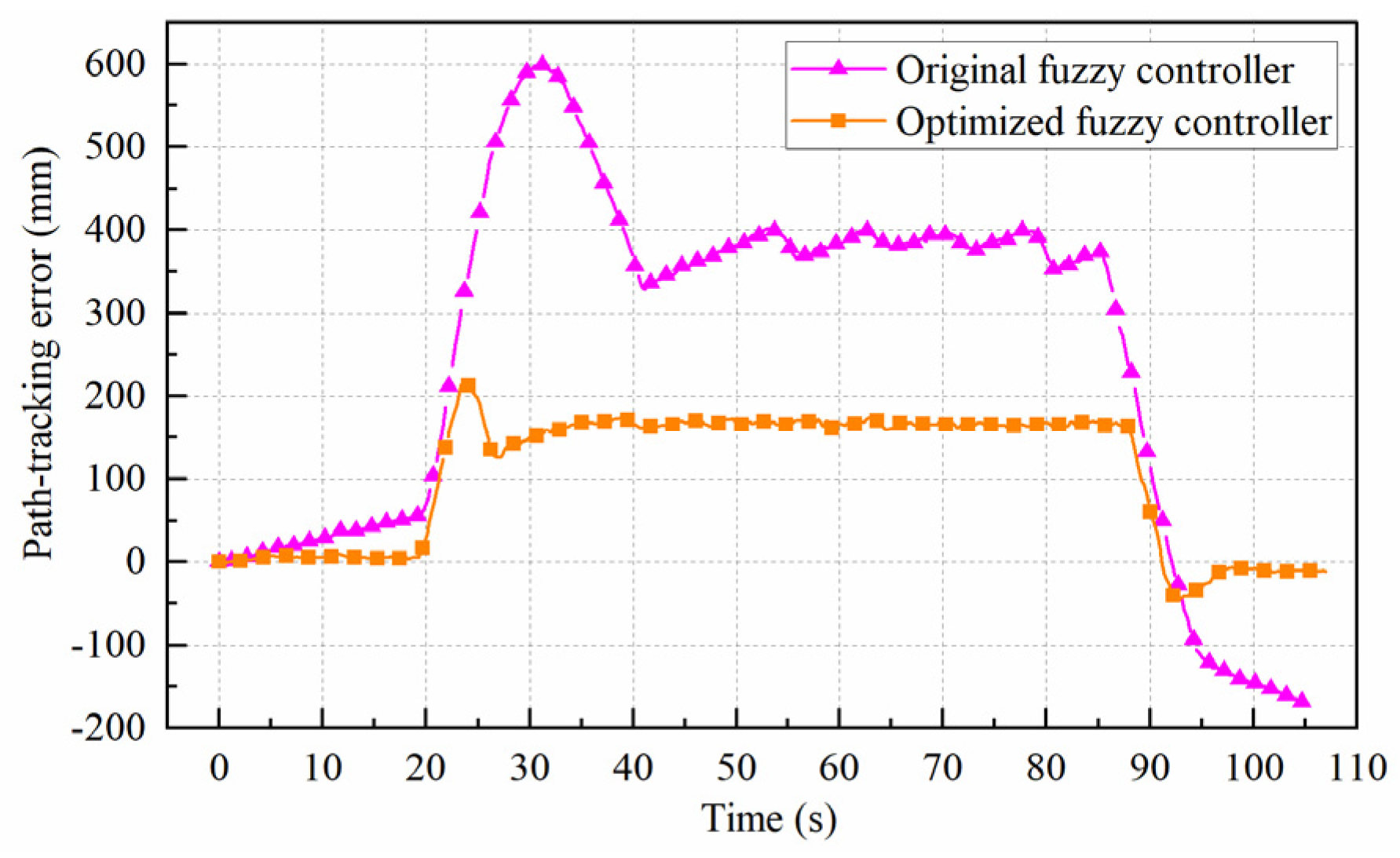
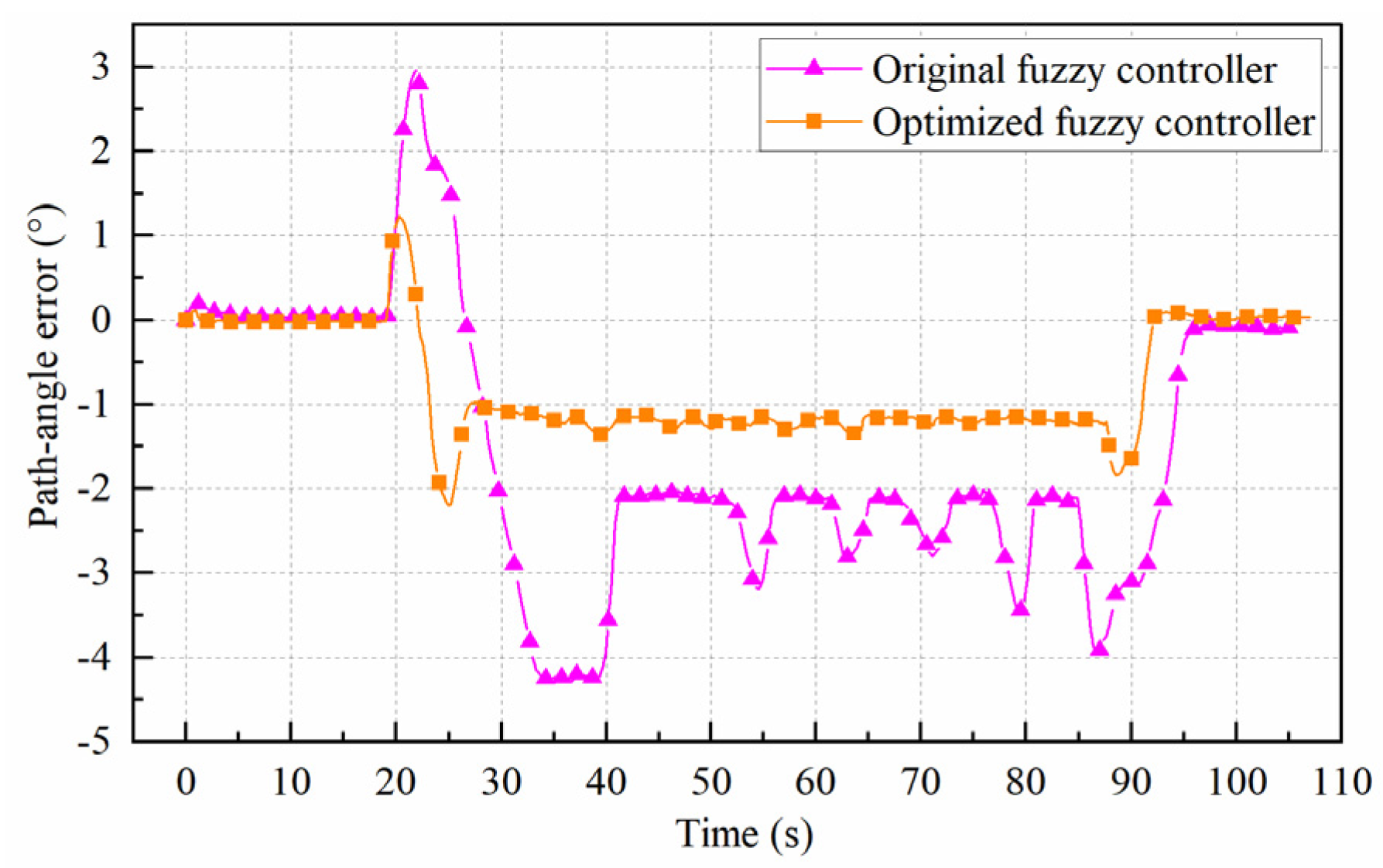
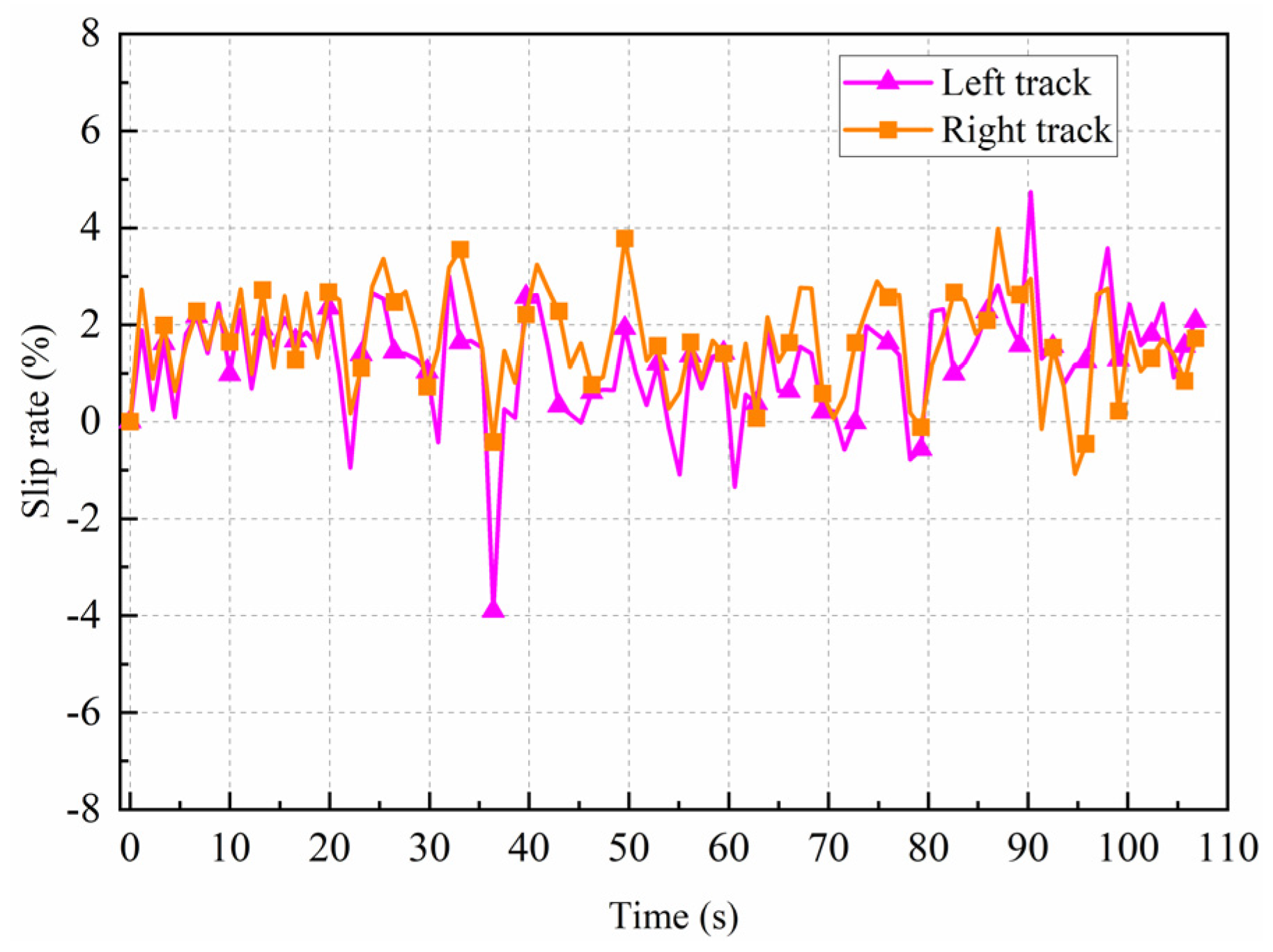
3.3. Simulation Results of Two Controllers
4. Conclusions
- (1)
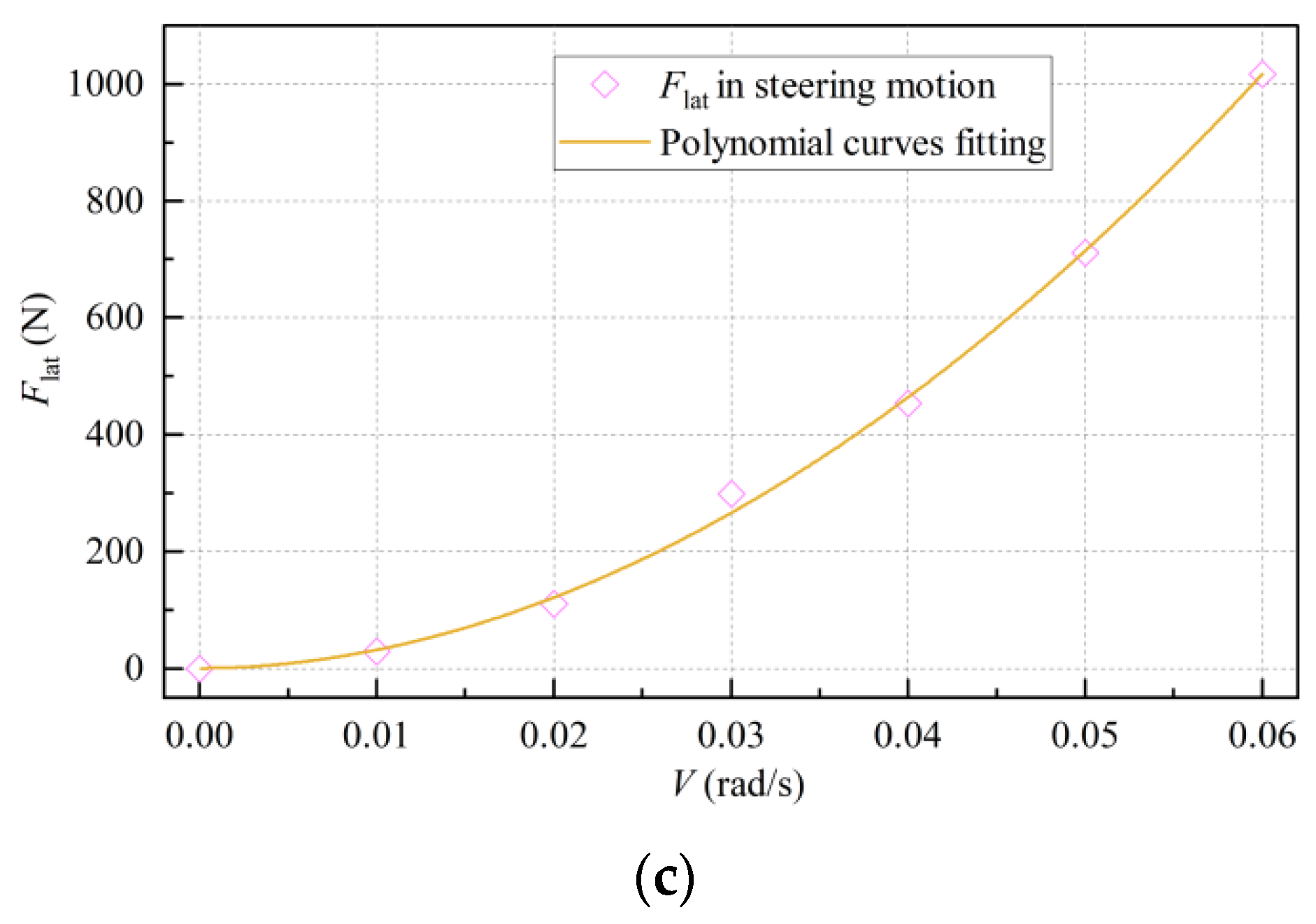
- The related parameters of vehicle–sediment mechanical interaction were calculated by sinkage and shear tests in the laboratory, and the trends of test data were highly consistent with corresponding empirical equations. The longitudinal hydrodynamic resistance and lateral hydrodynamic resistance of the mining vehicle increased exponentially with the increase of speed; simultaneously, the lateral hydrodynamic resistance of straight motion was too small to be ignored.
- (2)
- The MBD model of the deep-sea mining vehicle utilized axis forces and a user subroutine to achieve the integration of the mechanical interaction between vehicle and sediment and the spatial hydrodynamic effects. The central coordinates and actual heading angle of the mining vehicle were sampled in real time to calculate the path-tracking error and path-angle error in different motion states.
- (3)
- The genetic algorithm named MI-LXPM optimized the fuzzy rules of the motion controller. The co-simulation showed that the optimized fuzzy controller had better control accuracy than the original fuzzy controller. The maximum path-tracking error and path-angle error of the optimized fuzzy controller were 214 mm and −2.1°, respectively, but the corresponding values of the original fuzzy controller were 598 mm and −4.3°.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chung, J.S. Deep-Ocean Mining Technology III: Developments. Eighth ISOPE Ocean Mining Symposium; International Society of Offshore and Polar Engineers: Chennai, India, 2009; p. 7. [Google Scholar]
- Hong, S.; Kim, H.W.; Choi, J.S. Transient dynamic analysis of tracked vehicles on extremely soft cohesive soil. In Proceedings of the Fifth (2002) Isope Pacific/Asia Offshore Mechanics Sympopsium, Daejeon, Korea, 17–20 November 2002; pp. 100–107. [Google Scholar]
- Kim, H.W.; Hong, S.; Choi, J.; Yeu, T.K. Dynamic analysis of underwater tracked vehicle on extremely soft soil by using Euler parameters. In Proceedings of the Sixth (2005) Isope Ocean Mining Symposium, Changsha, China, 9–13 October 2005; pp. 141–148. [Google Scholar]
- Kim, H.W.; Hong, S.; Choi, J.S. Comparative study on tracked vehicle dynamics on soft soil: Single-body dynamics vs. multi-body dynamics. In Proceedings of the Fifth (2003) Isope Ocean Mining Symposium, Tsukuba, Japan, 15–19 September 2003; pp. 132–138. [Google Scholar]
- Dai, Y.; Liu, S.-J. An integrated dynamic model of ocean mining system and fast simulation of its longitudinal reciprocating motion. China Ocean Eng. 2013, 27, 231–244. [Google Scholar] [CrossRef]
- Jagadeesh, P.; Murali, K.; Idichandy, V. Experimental investigation of hydrodynamic force coefficients over AUV hull form. Ocean Eng. 2009, 36, 113–118. [Google Scholar] [CrossRef]
- Phillips, A.B.; Turnock, S.R.; Furlong, M. The use of computational fluid dynamics to aid cost-effective hydrodynamic design of autonomous underwater vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2010, 224, 239–254. [Google Scholar] [CrossRef]
- Chin, C.S.; Lin, W.P.; Lin, J.Y. Experimental validation of open-frame ROV model for virtual reality simulation and control. J. Mar. Sci. Technol. 2017, 23, 267–287. [Google Scholar] [CrossRef] [Green Version]
- Vu, M.T.; Choi, H.-S.; Kim, J.-Y.; Tran, N.H. A study on an underwater tracked vehicle with a ladder trencher. Ocean Eng. 2016, 127, 90–102. [Google Scholar] [CrossRef]
- Vu, M.T.; Choi, H.-S.; Ji, D.H.; Jeong, S.-K.; Kim, J.-Y. A study on an up-milling rock crushing tool operation of an underwater tracked vehicle. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 233, 283–300. [Google Scholar] [CrossRef]
- Li, J.; Dai, Y.; Liu, S. Effect of grouser height on tractive performance of tracked mining vehicle. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 2459–2466. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Sun, Y.; Gu, Z. Tractive performance evaluation of seafloor tracked trencher based on laboratory mechanical measurements. Int. J. Nav. Arch. Ocean Eng. 2016, 8, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.-H.; Shin, G.-B.; Chung, C.-K. Experimental study on the soil thrust of underwater tracked vehicles moving on the clay seafloor. Appl. Ocean Res. 2019, 86, 117–127. [Google Scholar] [CrossRef]
- Vu, M.T.; Choi, H.-S.; Nguyen, N.D.; Kim, S.-K. Analytical design of an underwater construction robot on the slope with an up-cutting mode operation of a cutter bar. Appl. Ocean Res. 2019, 86, 289–309. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, C.; Zhang, G.; Xu, H.; Ran, X. Three-Dimensional Path Tracking Control of Autonomous Underwater Vehicle Based on Deep Reinforcement Learning. J. Mar. Sci. Eng. 2019, 7, 443. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; Li, X.; Yin, W.; Pang, L.; Xie, Y.; Huang, Z. Dynamic modelling and motion control research on deep seabed miner. Mar. Georesources Geotechnol. 2020, 1–9. [Google Scholar] [CrossRef]
- Dai, Y.; Su, Q.; Zhang, Y. A new dynamic model and trajectory tracking control strategy for deep ocean mining vehicle. Ocean Eng. 2020, 216, 108162. [Google Scholar] [CrossRef]
- Yeu, T.-K.; Park, S.-J.; Hong, S.; Kim, H.-W.; Choi, J.-S. Path Tracking using Vector Pursuit Algorithm for Tracked Vehicles Driving on the Soft Cohesive Soil. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Korea, 18–21 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2781–2786. [Google Scholar]
- Hong, S.; Choi, J.-S.; Kim, H.-W.; Won, M.-C.; Shin, S.-C.; Rhee, J.-S.; Park, H.-U. A path tracking control algorithm for underwater mining vehicles. J. Mech. Sci. Technol. 2009, 23, 2030–2037. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, J.-W.; Sun, Y.-X.; Hao, S. Path-following control of remotely operated vehicle based on improved hybrid fuzzy PID control. AER Adv. Eng. Res. 2016, 117, 800–806. [Google Scholar]
- Londhe, P.; Mohan, S.; Patre, B.; Waghmare, L. Robust task-space control of an autonomous underwater vehicle-manipulator system by PID-like fuzzy control scheme with disturbance estimator. Ocean Eng. 2017, 139, 1–13. [Google Scholar] [CrossRef]
- Lamraoui, H.C.; Qidan, Z. Path following control of fully-actuated autonomous underwater vehicle in presence of fast-varying disturbances. Appl. Ocean Res. 2019, 86, 40–46. [Google Scholar] [CrossRef]
- Aras, M.S.M.; Abdullah, S.S. Adaptive Simplified Fuzzy Logic Controller for Depth Control of Underwater Remotely Operated Vehicle. Indian J. Geo-Mar. Sci. 2015, 44, 1995–2007. [Google Scholar]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, H.; Zhang, L.; Sun, Y. Research on fuzzy control of path tracking for underwater vehicle based on genetic algorithm optimization. Ocean Eng. 2018, 156, 217–223. [Google Scholar] [CrossRef]
- Londhe, P.S.; Patre, B.M. Adaptive fuzzy sliding mode control for robust trajectory tracking control of an autonomous underwater vehicle. Intell. Serv. Robot. 2018, 12, 87–102. [Google Scholar] [CrossRef]
- Dai, Y.; Zhu, X.; Zhou, H.; Mao, Z.; Wu, W. Trajectory Tracking Control for Seafloor Tracked Vehicle By Adaptive Neural-Fuzzy Inference System Algorithm. Int. J. Comput. Commun. Control. 2018, 13, 465–476. [Google Scholar] [CrossRef] [Green Version]
- Bekker, M.G. Introduction to Terrain-Vehicle Systems; University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Wong, J.; Preston-Thomas, J. On the characterization of the shear stress-displacement relationship of terrain. J. Terramech. 1983, 19, 225–234. [Google Scholar] [CrossRef]
- Benek, J.; Steger, J.; Dougherty, F. A flexible grid embedding technique with application to the Euler equations. In Proceedings of the 6th Computational Fluid Dynamics Conference, Danvers, MA, USA, 13–15 July 1983. [Google Scholar]
- Tang, H.; Jones, S.C.; Sotiropoulos, F. An overset-grid method for 3D unsteady incompressible flows. J. Comput. Phys. 2003, 191, 567–600. [Google Scholar] [CrossRef]
- Hoke, C.; Decker, R.; Cummings, R.; McDaniel, D.; Morton, S. Comparison of Overset Grid and Grid Deformation Techniques Applied to 2-Dimensional NACA Airfoils. In 19th AIAA Computational Fluid Dynamics; American Institute of Aeronautics and Astronautics: San Antonio, TX, USA, 2009. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa Albuquerque: Albuquerque, NM, USA, 1998; Volume 895. [Google Scholar]
- Xiang, X.; Yu, C.; Lapierre, L.; Zhang, J.; Zhang, Q. Survey on Fuzzy-Logic-Based Guidance and Control of Marine Surface Vehicles and Underwater Vehicles. Int. J. Fuzzy Syst. 2018, 20, 572–586. [Google Scholar] [CrossRef]
- Mamdani, E.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Deep, K.; Thakur, M. A new crossover operator for real coded genetic algorithms. Appl. Math. Comput. 2007, 188, 895–911. [Google Scholar] [CrossRef]
- Deep, K.; Singh, K.P.; Kansal, M.; Mohan, C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl. Math. Comput. 2009, 212, 505–518. [Google Scholar] [CrossRef]






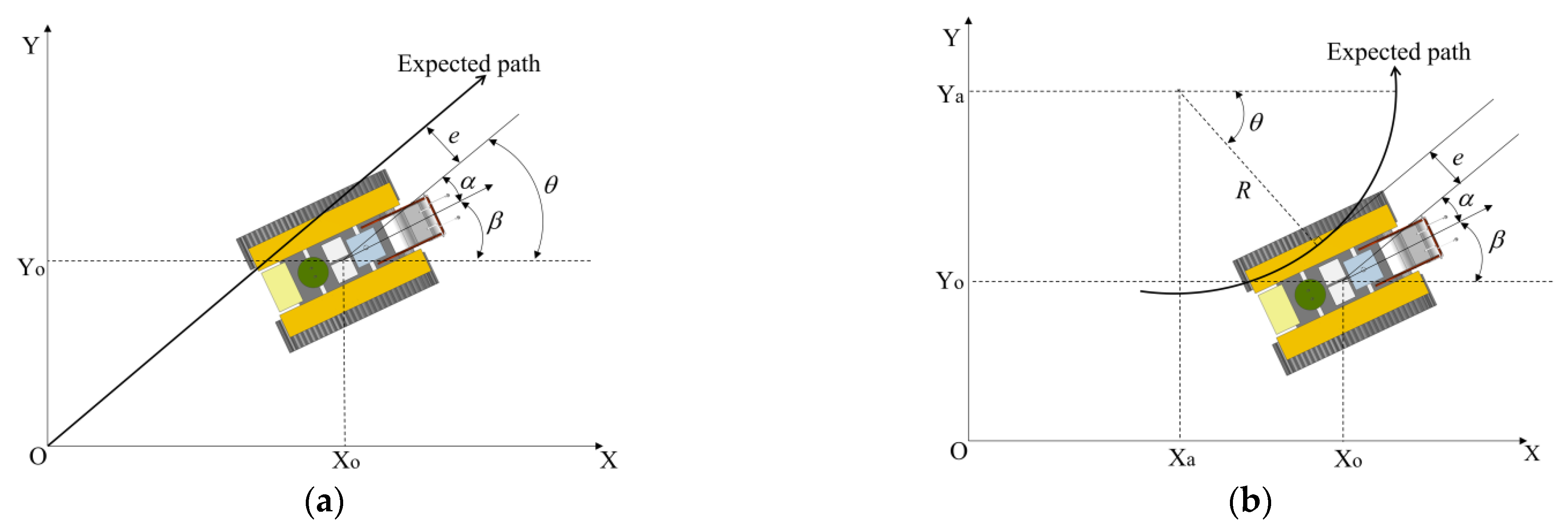



| Data Type | In Situ Test Data | Simulated Sediment Test Data |
|---|---|---|
| Shear strength (kPa) | 4–6.5 | 4.9 |
| Average moisture content (%) | 90–130 | 110 |
| Wet density (g·cm−3) | 1.2–1.5 | 1.3 |
| Dry density (g·cm−3) | 0.54–0.65 | 0.62 |
| Porosity ratio | 3.11–4.13 | 3.28 |
| Mesh | Straight Motion | Steering Motion | ||
|---|---|---|---|---|
| Number of Grids | longitudinal Resistance(N) | Number of Grids | longitudinal Resistance(N) | |
| Coarse | 3.2 million | 3626.37 | 4.4 million | 5016.49 |
| Medium | 4.5 million | 3386.89 | 5.7 million | 4821.83 |
| Fine | 5.6 million | 3327.52 | 6.9 million | 4751.35 |
| Discriminating ratio | 0.248 | 0.362 | ||
| NB | NM | NS | Z | PS | PM | PB | |
|---|---|---|---|---|---|---|---|
| NB | NB | NM | NS | Z | Z | Z | NS |
| NM | NM | Z | Z | PS | PS | PS | Z |
| NS | NS | Z | Z | PM | PM | PS | Z |
| Z | Z | PS | PM | PB | PM | PS | Z |
| PS | Z | PS | PM | PM | Z | Z | NS |
| PM | Z | PS | PS | PS | Z | Z | NM |
| PB | NS | Z | Z | Z | NS | NM | NB |
| NB | NM | NS | Z | PS | PM | PB | |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NM | NS | NS | NS | Z |
| NM | NB | NM | NS | NS | NS | NS | Z |
| NS | NM | NS | NS | Z | Z | Z | Z |
| Z | NM | NM | NS | Z | PS | PM | PM |
| PS | Z | Z | Z | Z | PS | PS | PM |
| PM | Z | PS | PS | PS | PS | PM | PB |
| PB | Z | PS | PS | PS | PM | PB | PB |
| NB | NM | NS | Z | PS | PM | PB | |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NM | Z | Z | NS | NS |
| NM | NM | NS | NS | PS | PS | Z | NS |
| NS | NM | Z | Z | PS | PS | PS | Z |
| Z | Z | PS | PM | PB | PM | PS | Z |
| PS | Z | PS | PS | PS | Z | Z | NM |
| PM | NS | Z | PS | PS | NS | NS | NM |
| PB | NS | NS | Z | Z | NM | NB | NB |
| NB | NM | NS | Z | PS | PM | PB | |
|---|---|---|---|---|---|---|---|
| NB | NB | NB | NM | NS | NS | NS | Z |
| NM | NB | NM | NS | NS | NS | NS | Z |
| NS | NM | NS | NS | Z | Z | Z | Z |
| Z | NM | NM | NS | Z | PS | PM | PM |
| PS | Z | Z | Z | Z | PS | PS | PM |
| PM | Z | PS | PS | PS | PS | PM | PB |
| PB | Z | PS | PS | PS | PM | PB | PB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Xue, C.; Su, Q. An Integrated Dynamic Model and Optimized Fuzzy Controller for Path Tracking of Deep-Sea Mining Vehicle. J. Mar. Sci. Eng. 2021, 9, 249. https://doi.org/10.3390/jmse9030249
Dai Y, Xue C, Su Q. An Integrated Dynamic Model and Optimized Fuzzy Controller for Path Tracking of Deep-Sea Mining Vehicle. Journal of Marine Science and Engineering. 2021; 9(3):249. https://doi.org/10.3390/jmse9030249
Chicago/Turabian StyleDai, Yu, Cong Xue, and Qiao Su. 2021. "An Integrated Dynamic Model and Optimized Fuzzy Controller for Path Tracking of Deep-Sea Mining Vehicle" Journal of Marine Science and Engineering 9, no. 3: 249. https://doi.org/10.3390/jmse9030249
APA StyleDai, Y., Xue, C., & Su, Q. (2021). An Integrated Dynamic Model and Optimized Fuzzy Controller for Path Tracking of Deep-Sea Mining Vehicle. Journal of Marine Science and Engineering, 9(3), 249. https://doi.org/10.3390/jmse9030249







