Region-Searching of Multiple Autonomous Underwater Vehicles: A Distributed Cooperative Path-Maneuvering Control Approach
Abstract
:1. Introduction
2. Problem Statement
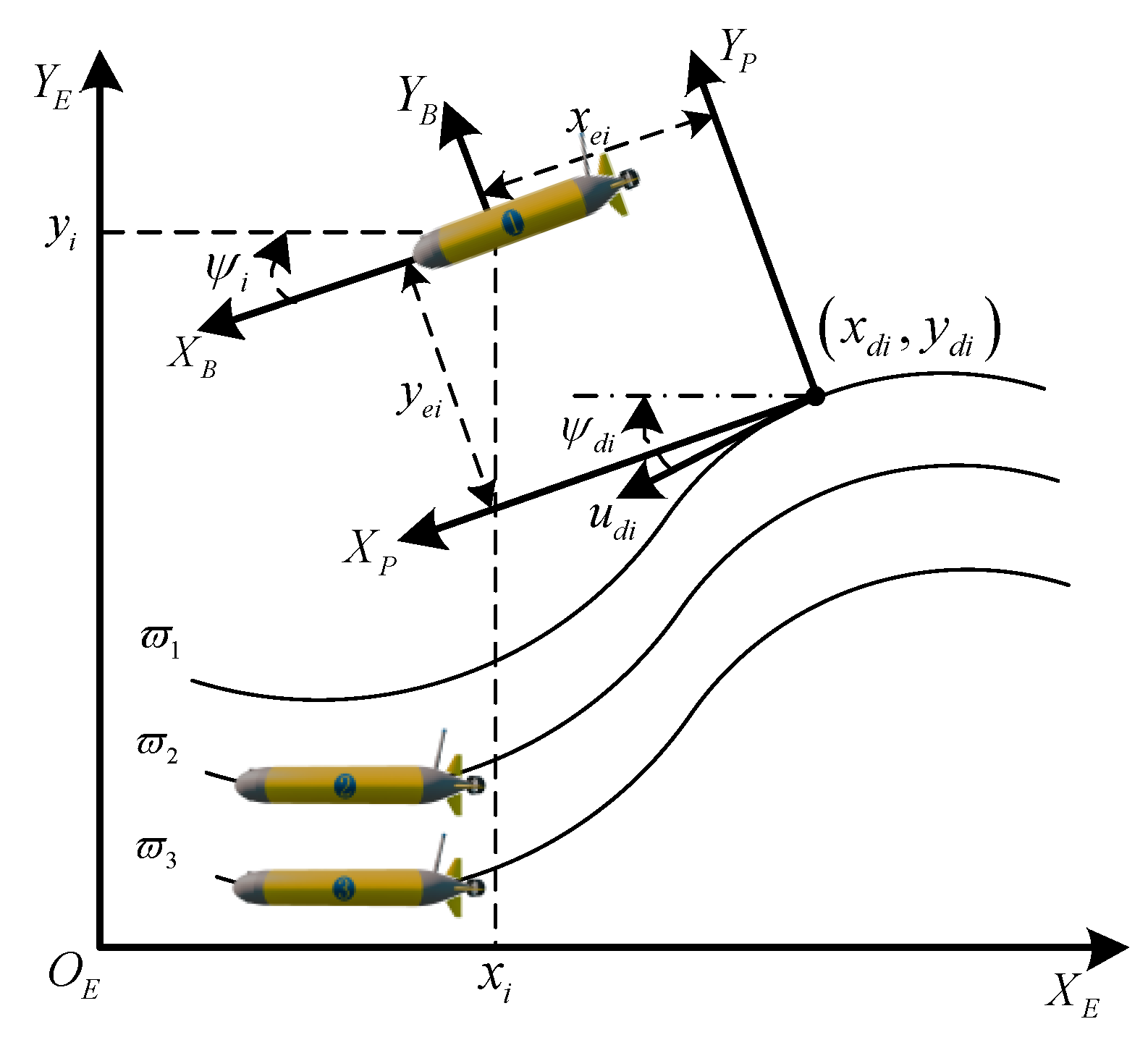
2.1. AUV Model
2.2. Problem Formualtion
3. Distributed Cooperative Path-Maneuvering Control
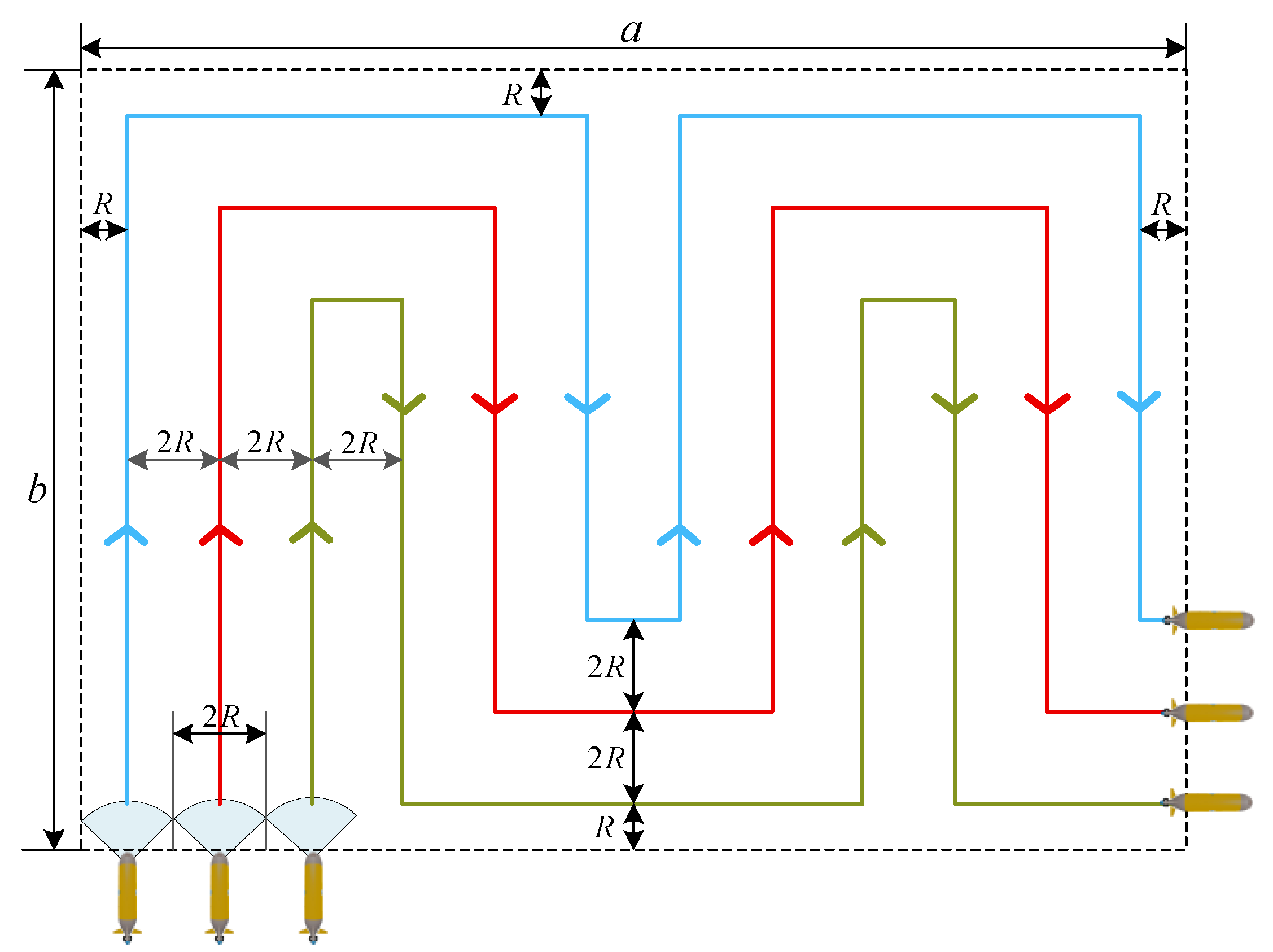
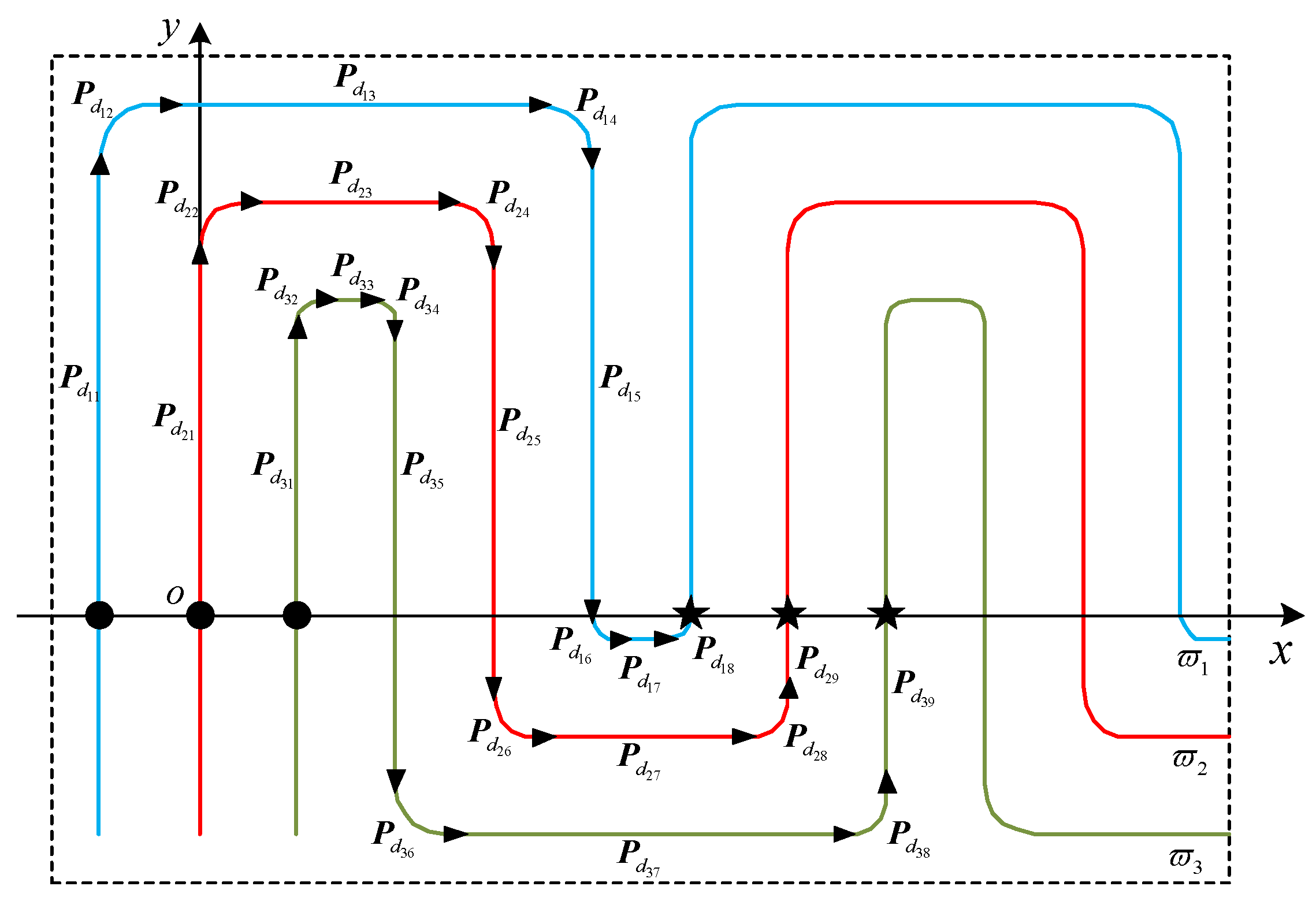
3.1. Coverage Path-Planning Design
3.2. Individual Path-Maneuvering Control Design
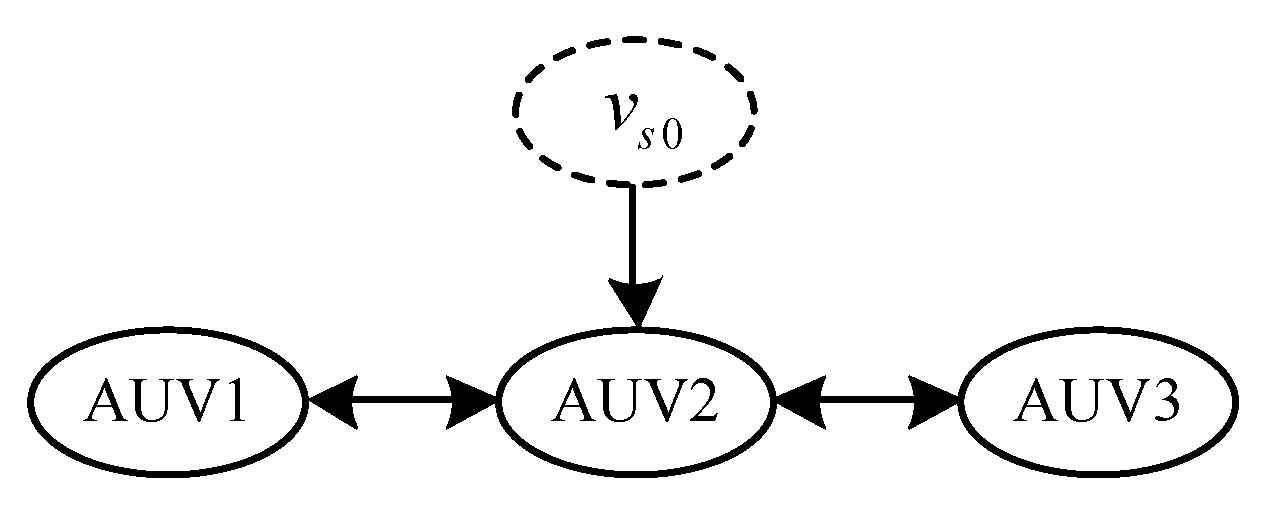
3.3. Path Parameter Synchronization Design
3.4. Stability Analysis
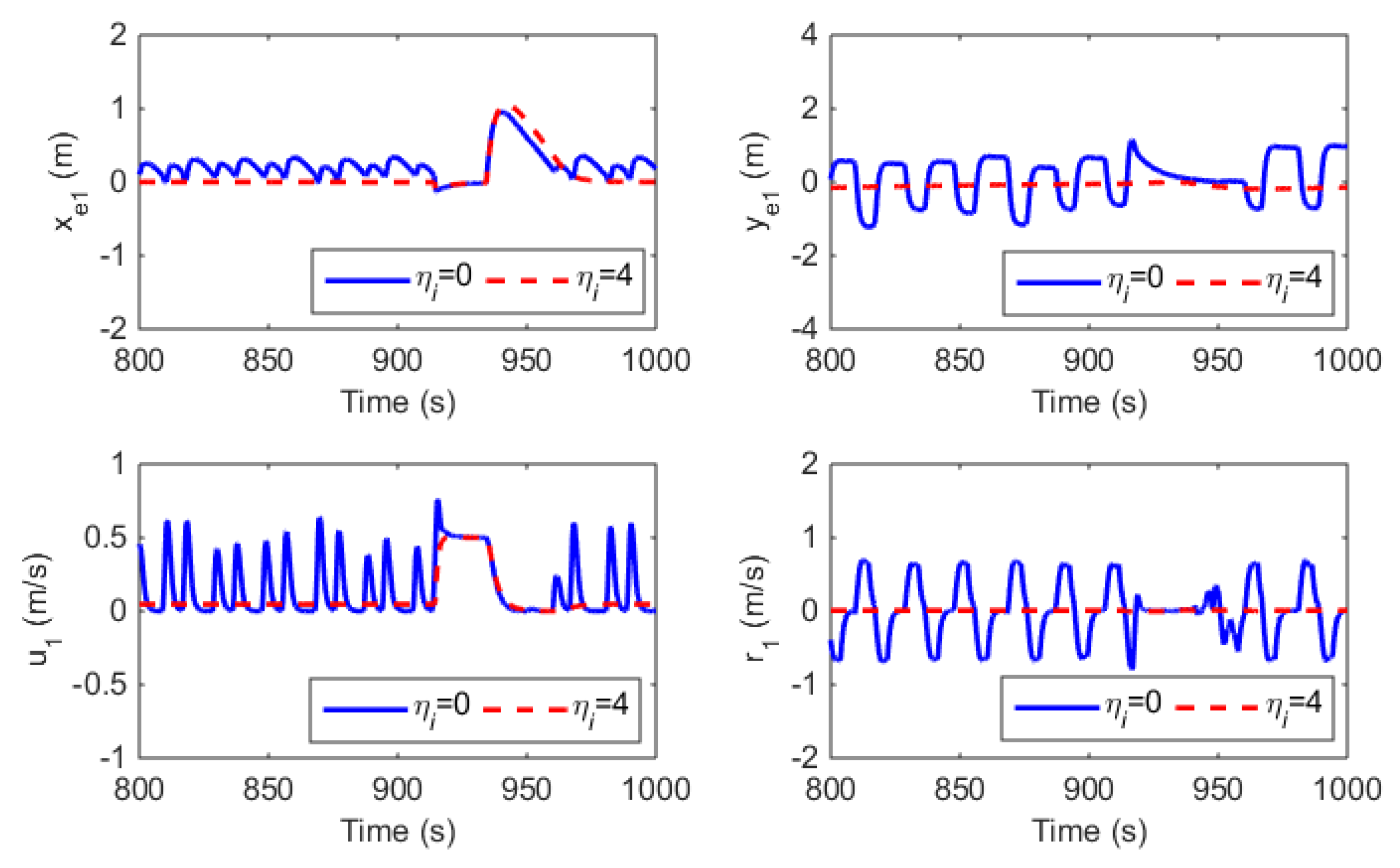
4. Simulation Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bays, M.J.; Shende, A.; Seilwell, J.J. Theory and experimental results for the multiple aspect coverage problem. Ocean Eng. 2012, 54, 51–60. [Google Scholar] [CrossRef]
- Lapierre, L.; Zapata, R.; Lepinay, P. Karst exploration: Unconstrained attitude dynamic control for an AUV. Ocean Eng. 2021, 219, 108321. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Wu, Q. Design for three-dimensional stabilization control of underactuated autonomous underwater vehicles. Ocean Eng. 2018, 150, 327–336. [Google Scholar] [CrossRef]
- Kim, J.; Joe, H.; Yu, S. Time-Delay Controller Design for Position Control of Autonomous Underwater Vehicle Under Disturbances. Trans. Ind. Electron. 2016, 63, 1052–1061. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef] [Green Version]
- Wynn, R.B.; Huvenne, V.A.I.; Le, B. Autonomous underwater vehicles: Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Wu, D.; Liao, Y.; Hu, C. An enhanced fuzzy control strategy for low-level thrusters in marine dynamic positioning systems based on chaotic random distribution harmony search. Int. J. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, D.; Yin, Z. Design of UDE-based dynamic surface control for dynamic positioning of vessels with complex disturbances and input constraints. Ocean Eng. 2021, 220, 108487. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Trajectory tracking control of AUVs via adaptive fast nonsingular integral terminal sliding mode control. IEEE Trans. Ind. Inform. 2020, 16, 1248–1258. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive second-order fast nonsingular terminal sliding mode tracking control for fully actuated autonomous underwater vehicles. IEEE J. Ocean. Eng. 2019, 44, 363–385. [Google Scholar] [CrossRef]
- Wang, N.; Sun, Z.; Jiao, Y. Surge-Heading Guidance Based Finite-Time Path-Following of Underactuated Marine Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 8523–8532. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Hou, Y. Finite-time Unknown Observer Based Coordinated Path-Following Control of Unmanned Underwater Vehicles. J. Frankl. Inst. 2021. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wang, N. Swarm velocity guidance based distributed finite-time coordinated path-following for uncertain under-actuated autonomous surface vehicles. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wang, N. Swarm control with collision avoidance for multiple underactuated surface vehicles. Ocean Eng. 2019, 191, 106516. [Google Scholar] [CrossRef]
- Qu, X.; Liang, X.; Hou, Y. Path-following control of unmanned surface vehicles with unknown dynamics and unmeasured velocities. J. Mar. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Qu, X.; Liang, X.; Hou, Y. Fuzzy State Observer Based Cooperative Path-Following Control of Autonomous Underwater Vehicles with Unknown Dynamics and Ocean Disturbances. Int. J. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wang, N. A Novel Distributed and Self-Organized Swarm Control Framework for Underactuated Unmanned Marine Vehicles. IEEE Access 2019, 7, 112703–112712. [Google Scholar] [CrossRef]
- Hinostroza, M.A.; Xu, H.; Guedes Soares, C. Cooperative operation of autonomous surface vehicles for maintaining formation in complex marine environment. Ocean Eng. 2019, 183, 132–154. [Google Scholar] [CrossRef]
- Loria, A.; Dasdemir, J.; Jarquin, N.A. Leader-Follower formation and tracking control of mobile robots along straight paths. IEEE Trans. Control Syst. Technol. 2016, 24, 727–732. [Google Scholar] [CrossRef] [Green Version]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Tsai, C.C.; Wu, H.L.; Tai, F. Distributed Consensus Formation Control with Collision and Obstacle Avoidance for Uncertain Networked Omnidirectional Multi-Robot Systems Using Fuzzy Wavelet Neural Networks. Int. J. Fuzzy Syst. 2017, 19, 1375–1391. [Google Scholar] [CrossRef]
- Lee, G.; Chwa, D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance. Intell. Serv. Robot. 2018, 11, 127–138. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. Adaptive-observer-based formation tracking of networked uncertain underactuated surface vessels with connectivity preservation and collision avoidance. J. Frankl. Inst. 2019, 356, 7947–7966. [Google Scholar] [CrossRef]
- Fan, J.; Liao, Y.; Li, Y. Formation Control of Multiple Unmanned Surface Vehicles Using the Adaptive Null-Space-Based Behavioral Method. IEEE Access 2019, 7, 87647–87657. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. Cooperative Path Following Ring-Networked Under-Actuated Autonomous Surface Vehicles: Algorithms and Experimental Results. IEEE Trans. Cybern. 2020, 50, 1519–1529. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, D.; Peng, Z. Coordinated path following of multiple underacutated marine surface vehicles along one curve. ISA Trans. 2016, 64, 258–268. [Google Scholar] [CrossRef]
- Almeida, J.; Silvestre, C.; Pascoal, A. Cooperative control of multiple surface vessels in the presence of ocean currents and parametric model uncertainty. Int. J. Robust Nonlinear Control 2010, 20, 1549–1565. [Google Scholar] [CrossRef]
- Qu, X.; Liang, X.; Hou, Y. Finite-time sideslip observer-based synchronized path-following control of multiple unmanned underwater vehicles. Ocean Eng. 2020, 217, 107941. [Google Scholar] [CrossRef]
- Almeida, J.; Silvestre, C.; Pascoal, A. Cooperative control of multiple surface vessels with discrete-time periodic communications. Int. J. Robust Nonlinear Control 2011, 22, 398–419. [Google Scholar] [CrossRef]
- Bibuli, M.; Bruzzone, G.; Caccia, M. Swarm based path-following for cooperative unmanned surface vehicles. J. Eng. Marit. Environ. 2014, 228, 192–207. [Google Scholar] [CrossRef]
- Wang, H.; Wang, D.; Peng, Z. Adaptive dynamic surface control for cooperative path following of underactuated marine surface vehicles via fast learning. IET Control Theory Appl. 2013, 7, 1888–1898. [Google Scholar]
- Xiang, X.; Liu, C.; Lapierre, L. Synchronized path following control of multiple homogenous underactuated UUVs. J. Syst. Sci. Complex. 2012, 25, 71–89. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, P. Coordinated Adaptive Control for Coordinated Path-following Surface Vessels with a Time-invariant Orbital Velocity. IEEE/CAA J. Autom. Sin. 2014, 1, 337–346. [Google Scholar]
- Liang, X.; Qu, X.; Hou, Y. Distributed coordinated tracking control of multiple unmanned surface vehicles under complex marine environments. Ocean Eng. 2020, 205, 107328. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.H.; Jeon, M. A study on path optimization method of an unmanned surface vehicle under environmental loads using genetic algorithm. Ocean Eng. 2017, 142, 616–624. [Google Scholar] [CrossRef]
- Wu, D.; Ma, Z.; Li, A. Identification for fractional order rational models based on particle swarm optimization. Int. J. Comput. Appl. Technol. 2011, 41, 53–59. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Kawabata, K.; Ma, L.; Xue, J. A path generation for automated vehicle based on Bezier curve and via-points. Robot. Auton. Syst. 2015, 74, 243–252. [Google Scholar] [CrossRef]
- Wang, N.; Jin, X.; Er, M.J. A multilayer path planner for a USV under complex marine environments. Ocean Eng. 2019, 184, 1–10. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Hoang, H.V.; Viet-Hung, D.; Laskar, M.N.U. BA*: An online complete coverage algorithm for cleaning robots. Appl. Intell. 2013, 39, 217–235. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Su, S.; Pan, X. Yaw-Guided Trajectory Tracking Control of an Asymmetric Underactuated Surface Vehicle. IEEE Trans. Ind. Inform. 2019, 15, 3502–3513. [Google Scholar] [CrossRef]
- Ceragioli, F.; De, P.C.; Frasca, P. Discontinuities and hysteresis in quantized average consensus. Automatica 2011, 47, 1916–1928. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Qu, X.; Wan, L. Three-dimensional Path Following of an Underactuated AUV Based on Fuzzy Backstepping Sliding Mode Control. Int. J. Fuzzy Syst. 2018, 20, 640–649. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Wang, N. Three-dimensional trajectory tracking of an underactuated AUV based on fuzzy dynamic surface control. IET Intell. Transp. Syst. 2020, 14, 364–370. [Google Scholar] [CrossRef]
- Fossen, T.I. How to incorporate wine, waves and ocean currents in the marine craft equations of motion. In Proceedings of the IFAC Conference on Manoeuvring and Control of Marine Craft, Genoa, Italy, 19–21 September 2012; pp. 126–131. [Google Scholar]
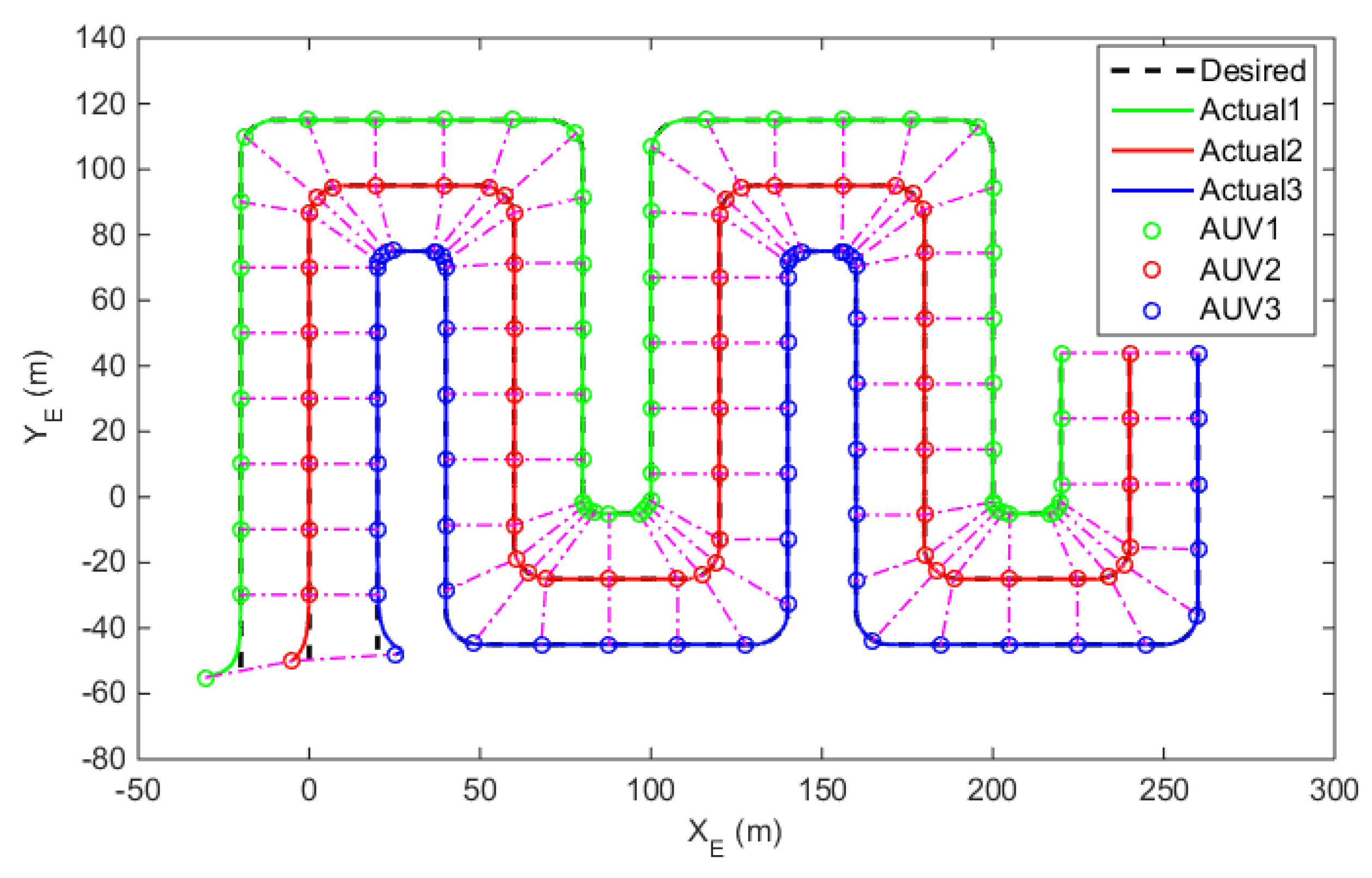
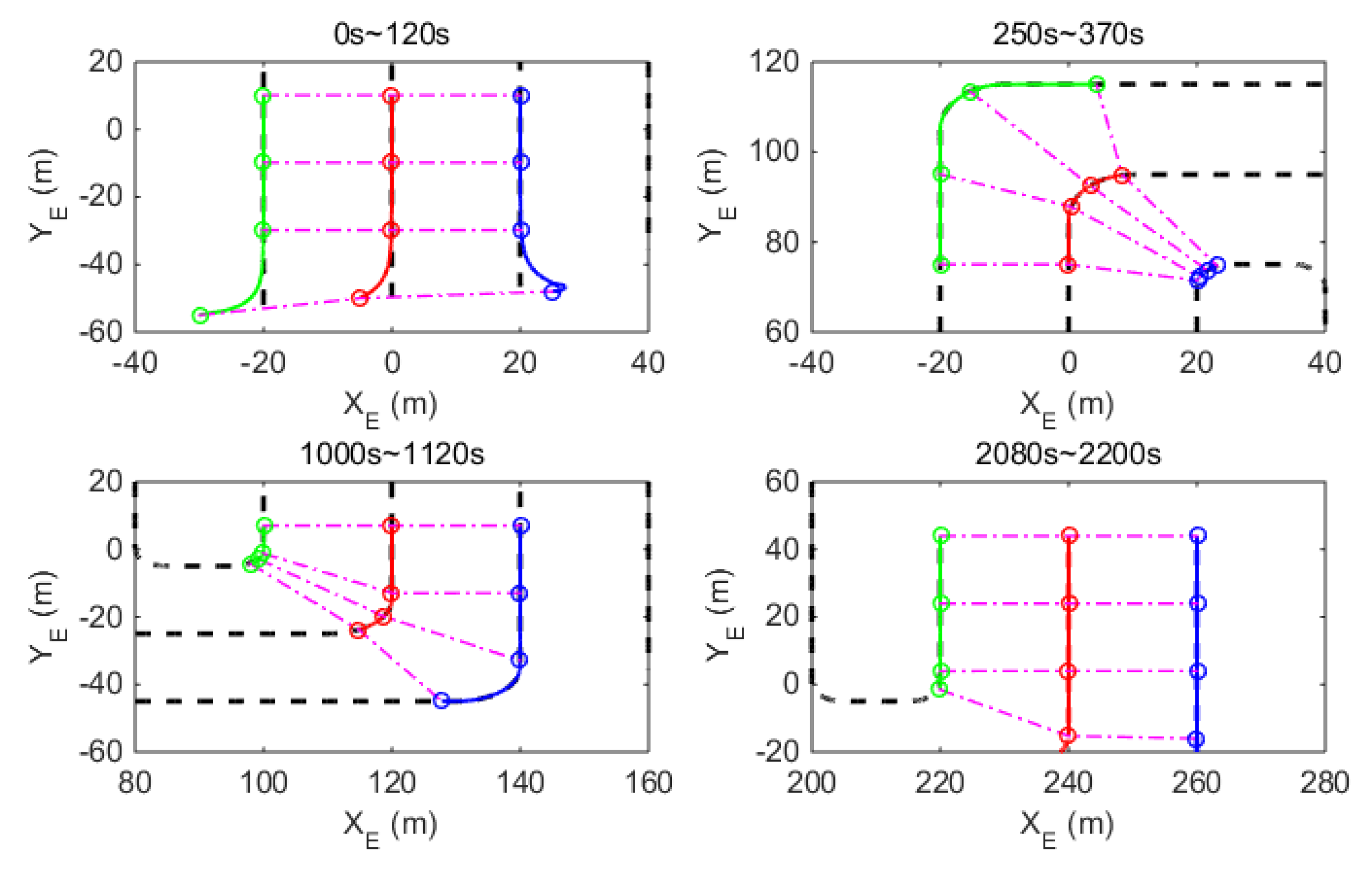
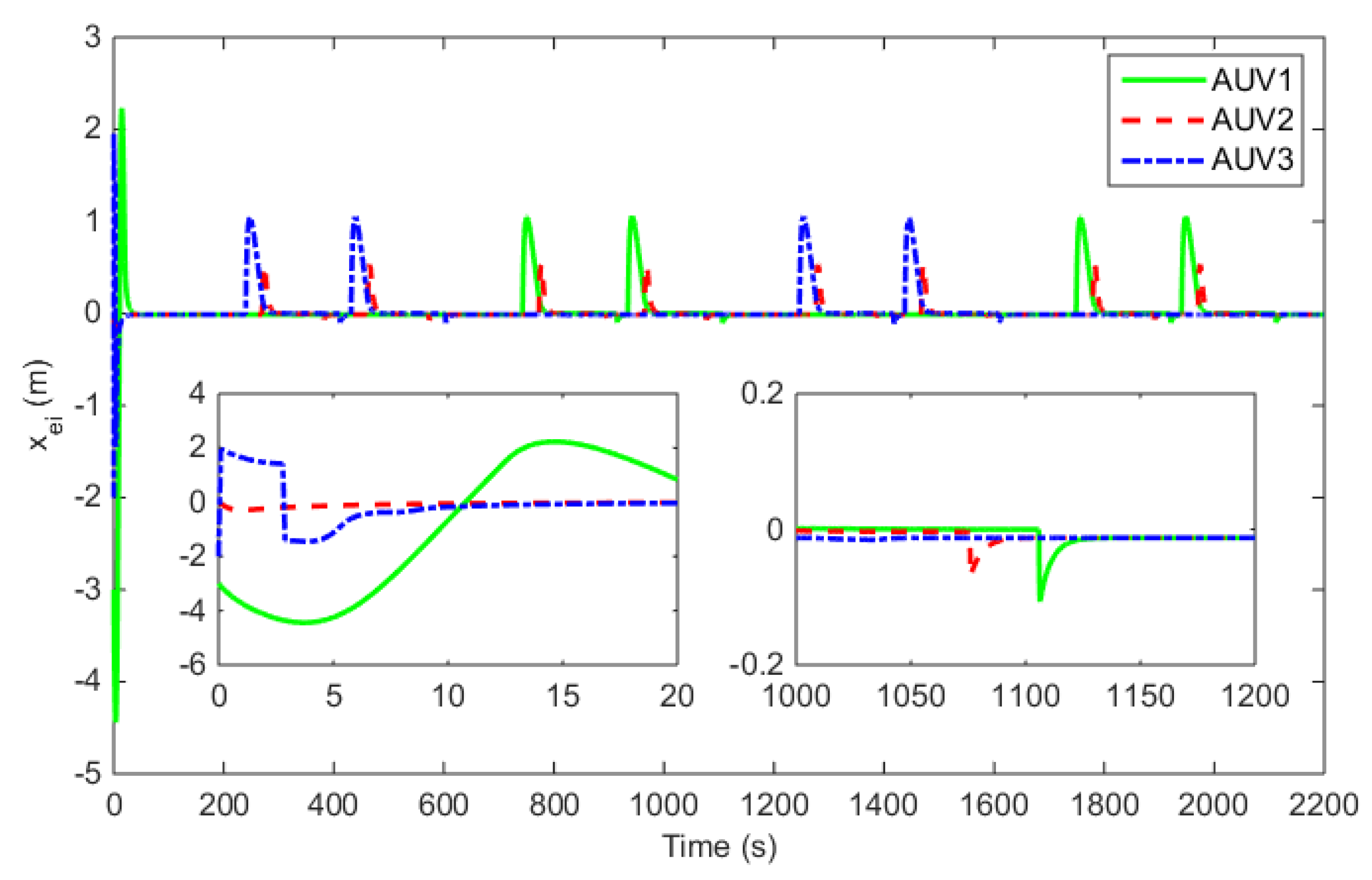
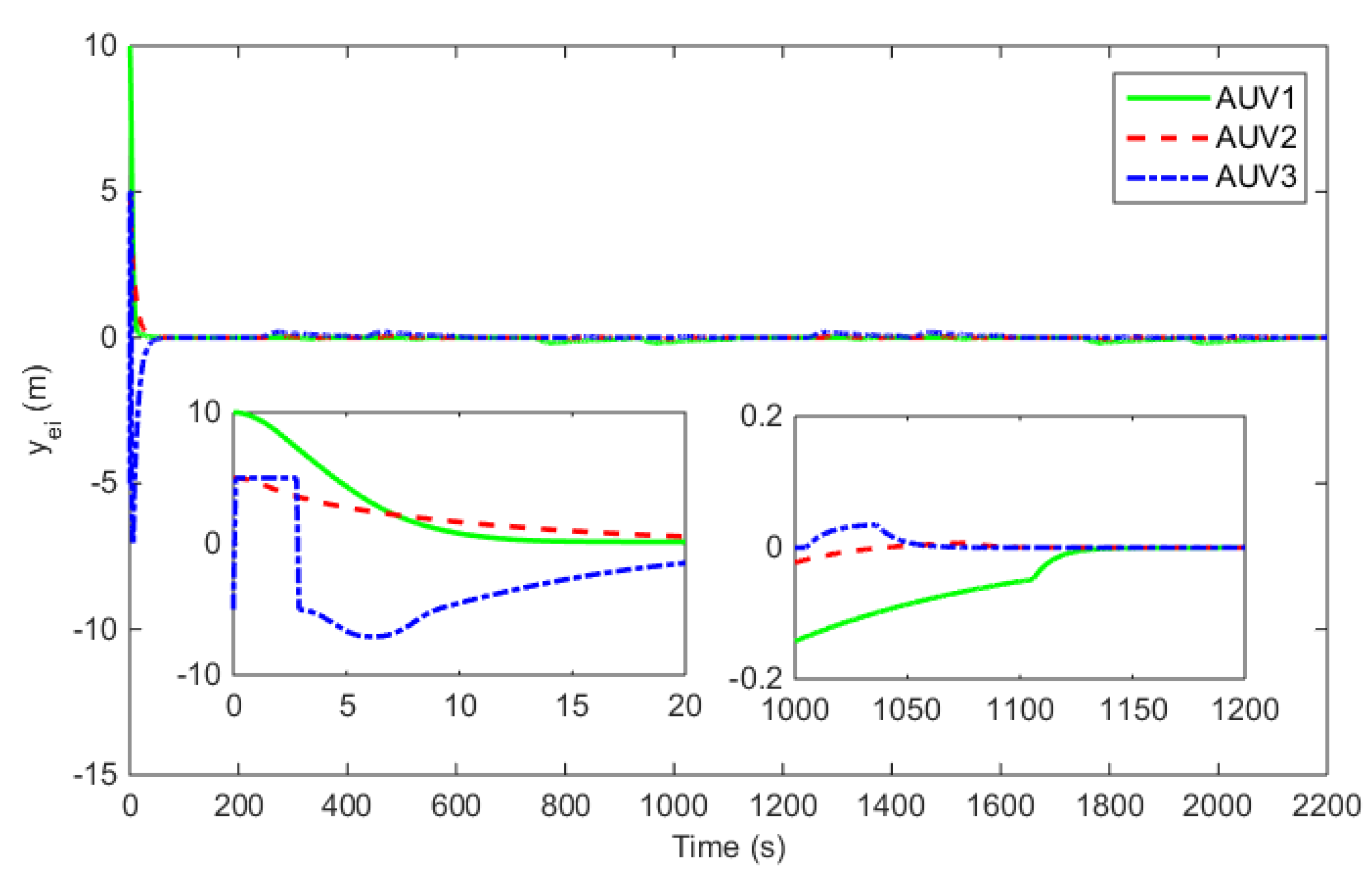
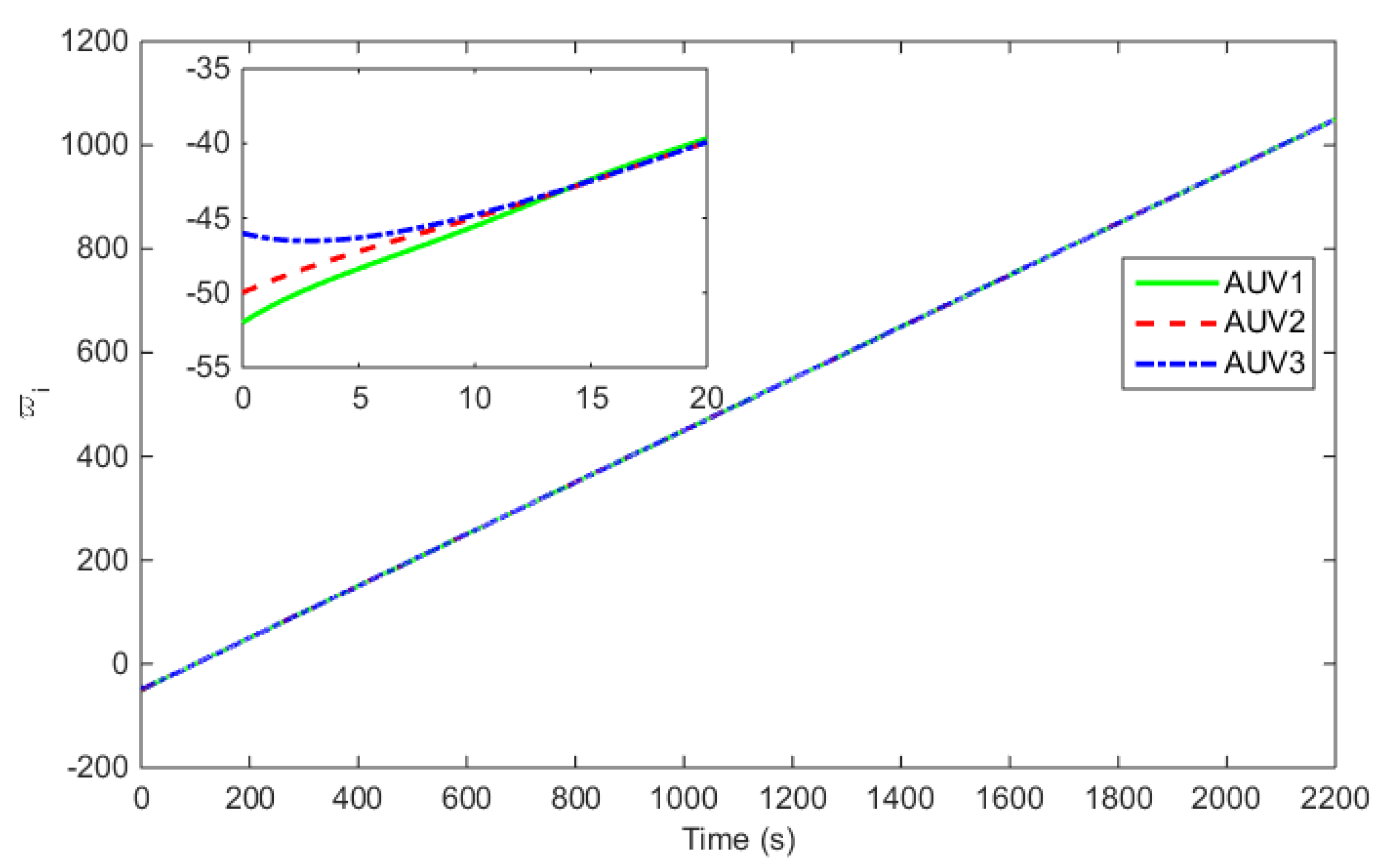

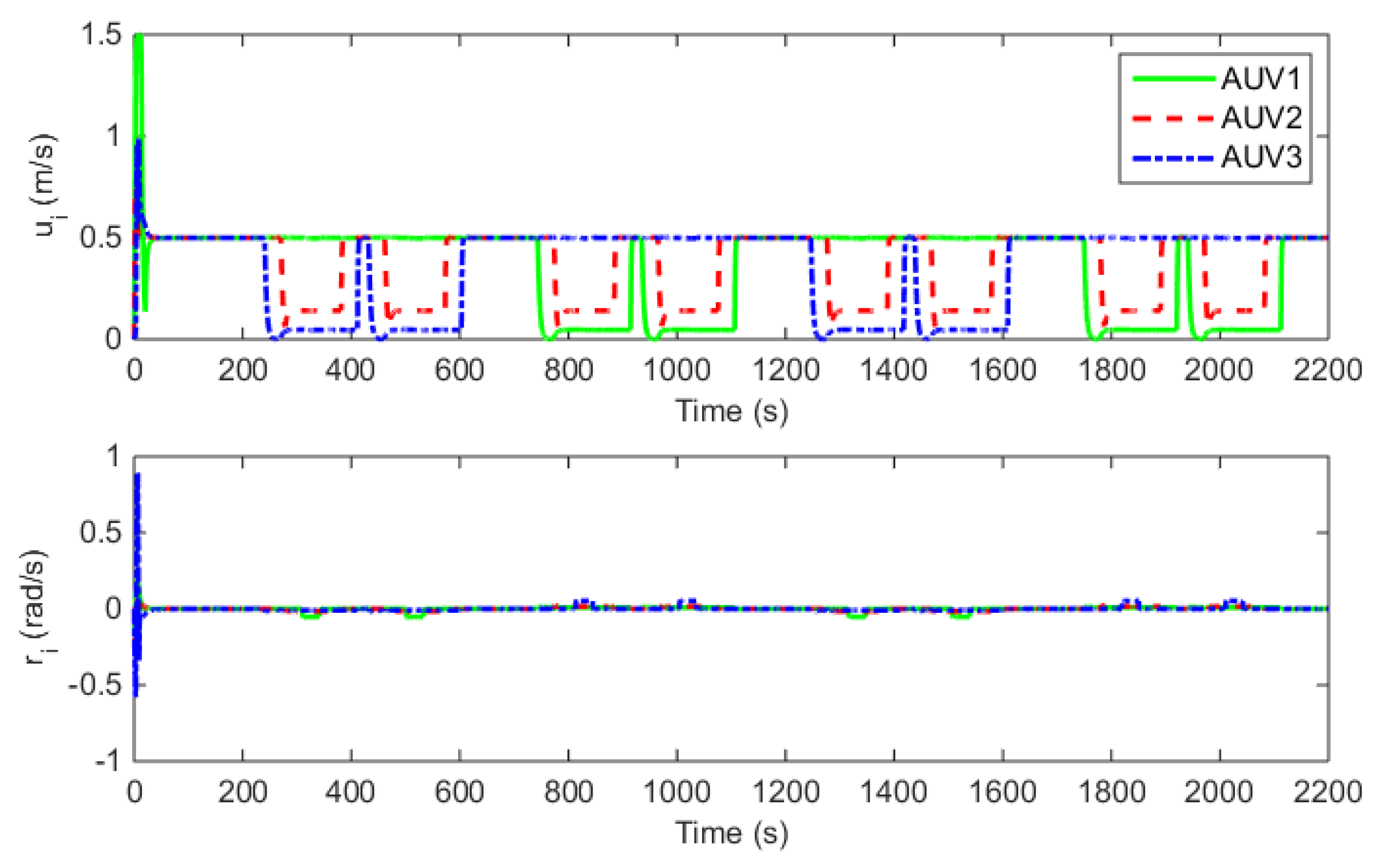
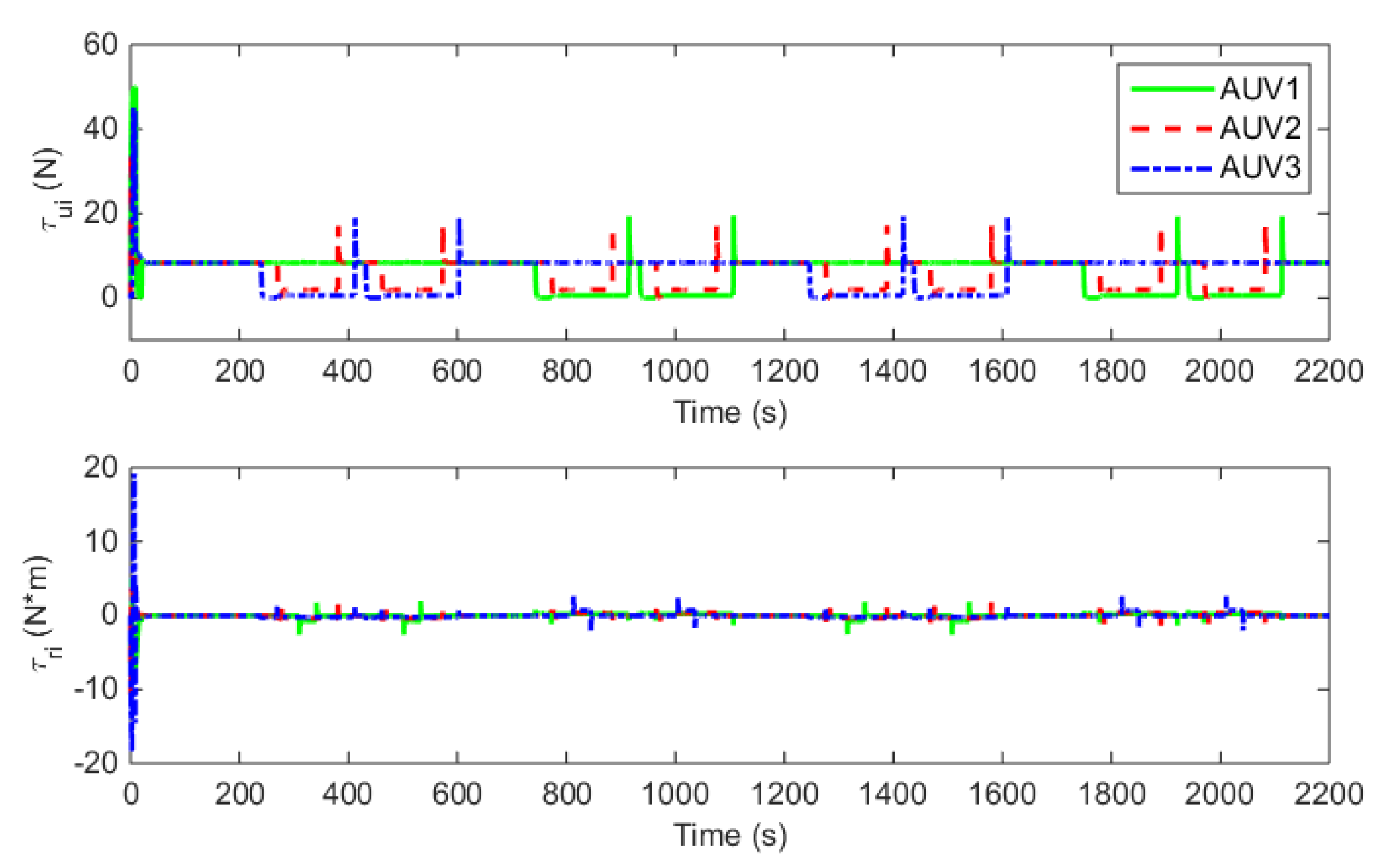
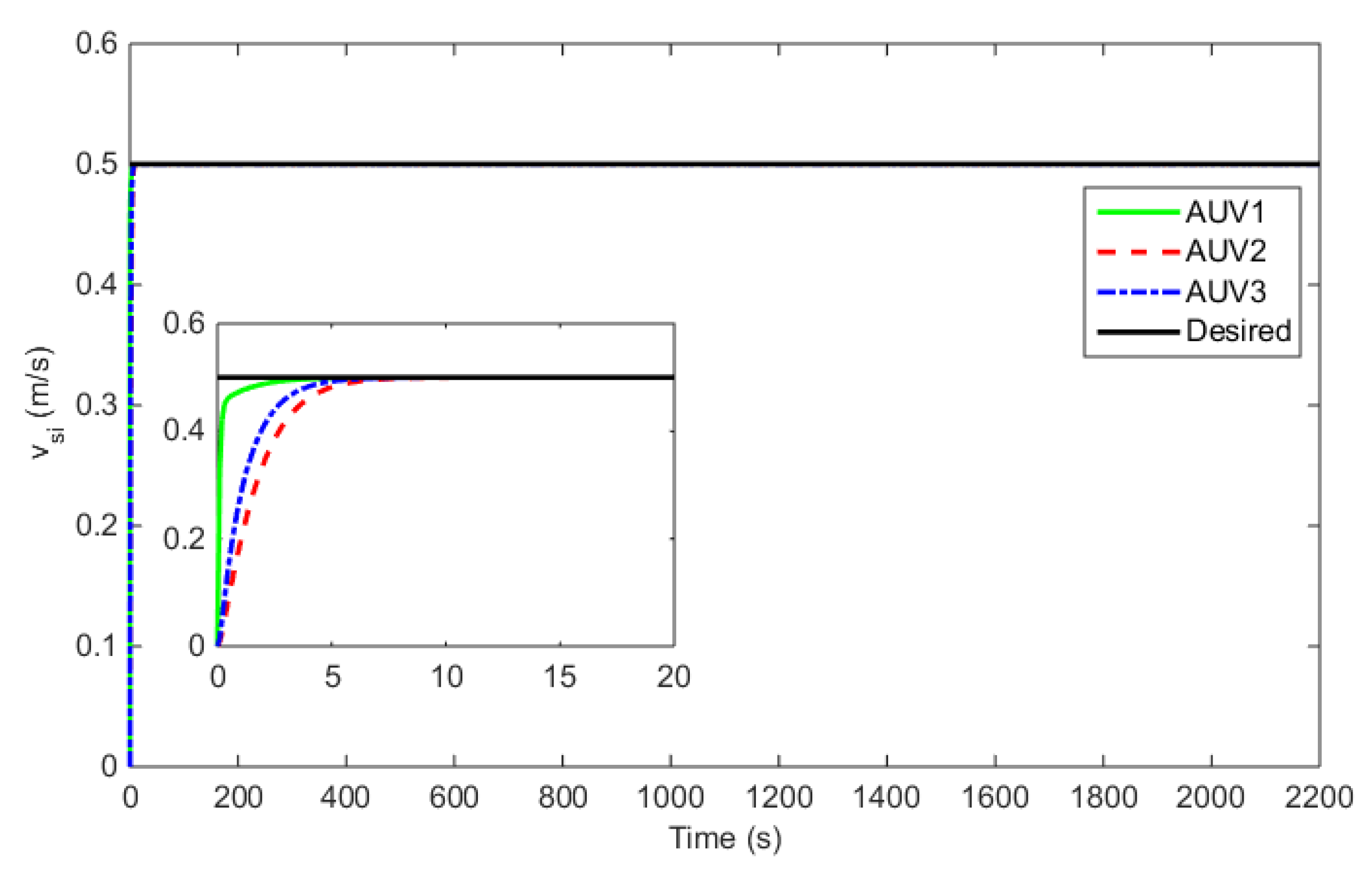
| Para. | Value | Para. | Value | Para. | Value |
|---|---|---|---|---|---|
| 47.52 | |||||
| Index | Items |
|---|---|
| Multiple paths | , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . |
| Control laws | , , , , , , , , , , , . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Qu, X.; Zhang, Z.; Liang, X. Region-Searching of Multiple Autonomous Underwater Vehicles: A Distributed Cooperative Path-Maneuvering Control Approach. J. Mar. Sci. Eng. 2021, 9, 355. https://doi.org/10.3390/jmse9040355
Chen T, Qu X, Zhang Z, Liang X. Region-Searching of Multiple Autonomous Underwater Vehicles: A Distributed Cooperative Path-Maneuvering Control Approach. Journal of Marine Science and Engineering. 2021; 9(4):355. https://doi.org/10.3390/jmse9040355
Chicago/Turabian StyleChen, Tao, Xingru Qu, Zhao Zhang, and Xiao Liang. 2021. "Region-Searching of Multiple Autonomous Underwater Vehicles: A Distributed Cooperative Path-Maneuvering Control Approach" Journal of Marine Science and Engineering 9, no. 4: 355. https://doi.org/10.3390/jmse9040355
APA StyleChen, T., Qu, X., Zhang, Z., & Liang, X. (2021). Region-Searching of Multiple Autonomous Underwater Vehicles: A Distributed Cooperative Path-Maneuvering Control Approach. Journal of Marine Science and Engineering, 9(4), 355. https://doi.org/10.3390/jmse9040355







