Simulating the Coastal Ocean Circulation Near the Cape Peninsula Using a Coupled Numerical Model
Abstract
1. Introduction
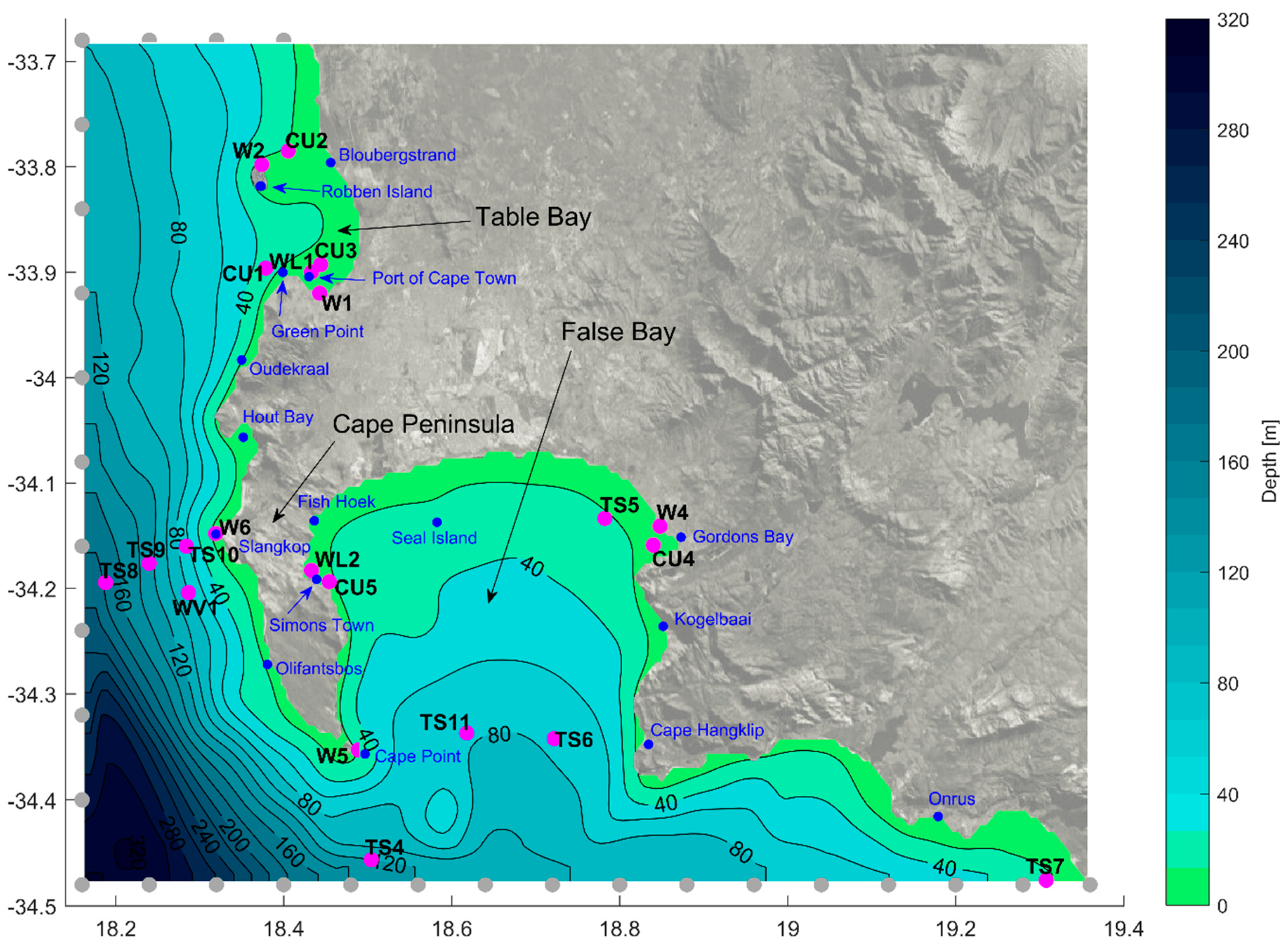
1.1. Geographical Context
1.2. Synoptic Weather Influences
1.3. Existing Knowledge of the Circulation
1.3.1. Table Bay
1.3.2. Western Peninsula
1.3.3. False Bay
1.4. The Case for a Coastal Model
2. Data and Methods
2.1. Numerical Models
2.1.1. Model Grid
2.1.2. Bathymetry
2.1.3. Open Boundary Conditions
2.1.4. Atmospheric and Tidal Forcing
2.2. HRM Calibration and Validation
2.2.1. Calibration Data
2.2.2. Validation Data
3. Results and Discussion
3.1. Atmospheric Forcing Validation
3.2. HRM Calibration Settings
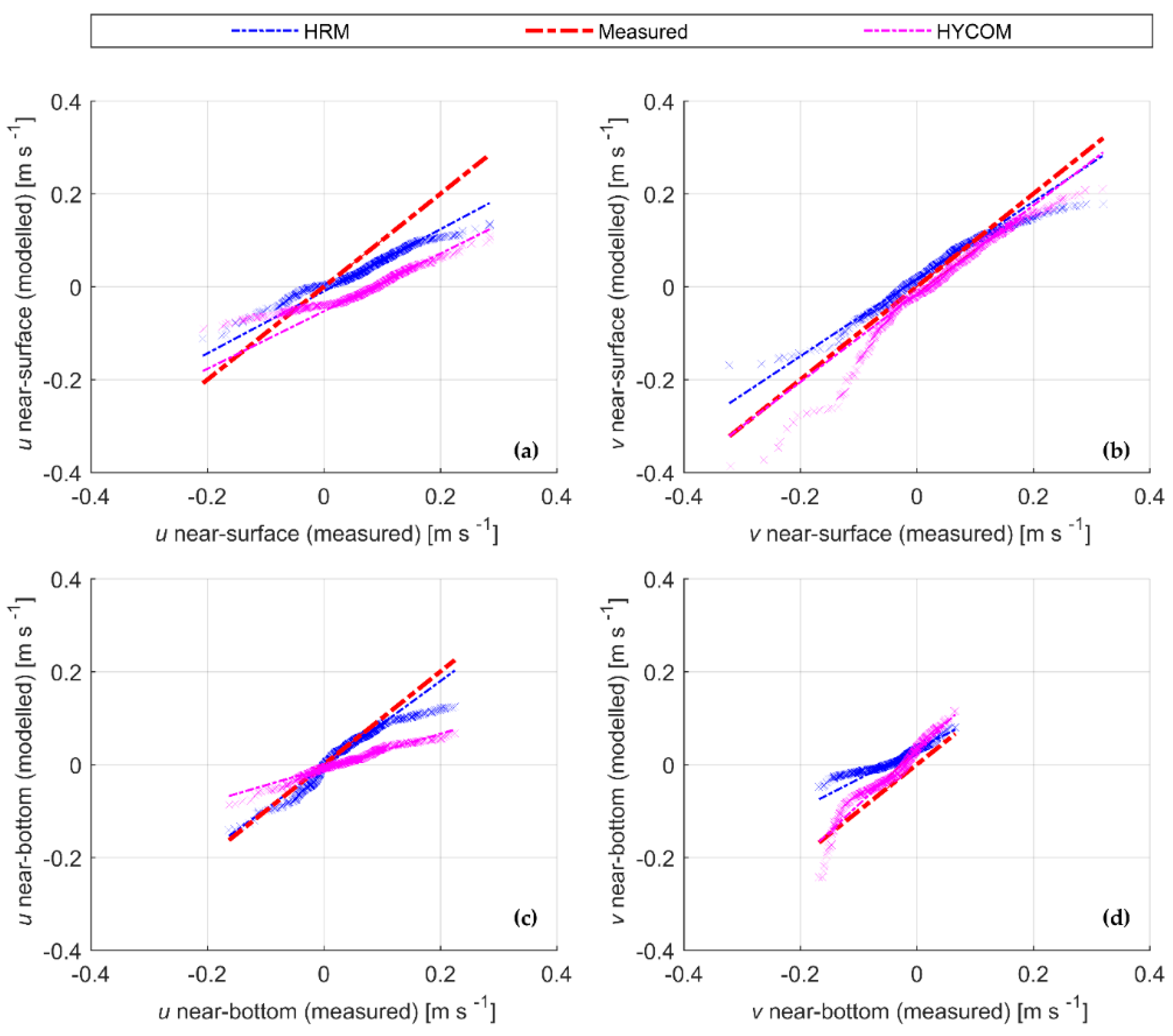
3.3. HRM Calibration Performance
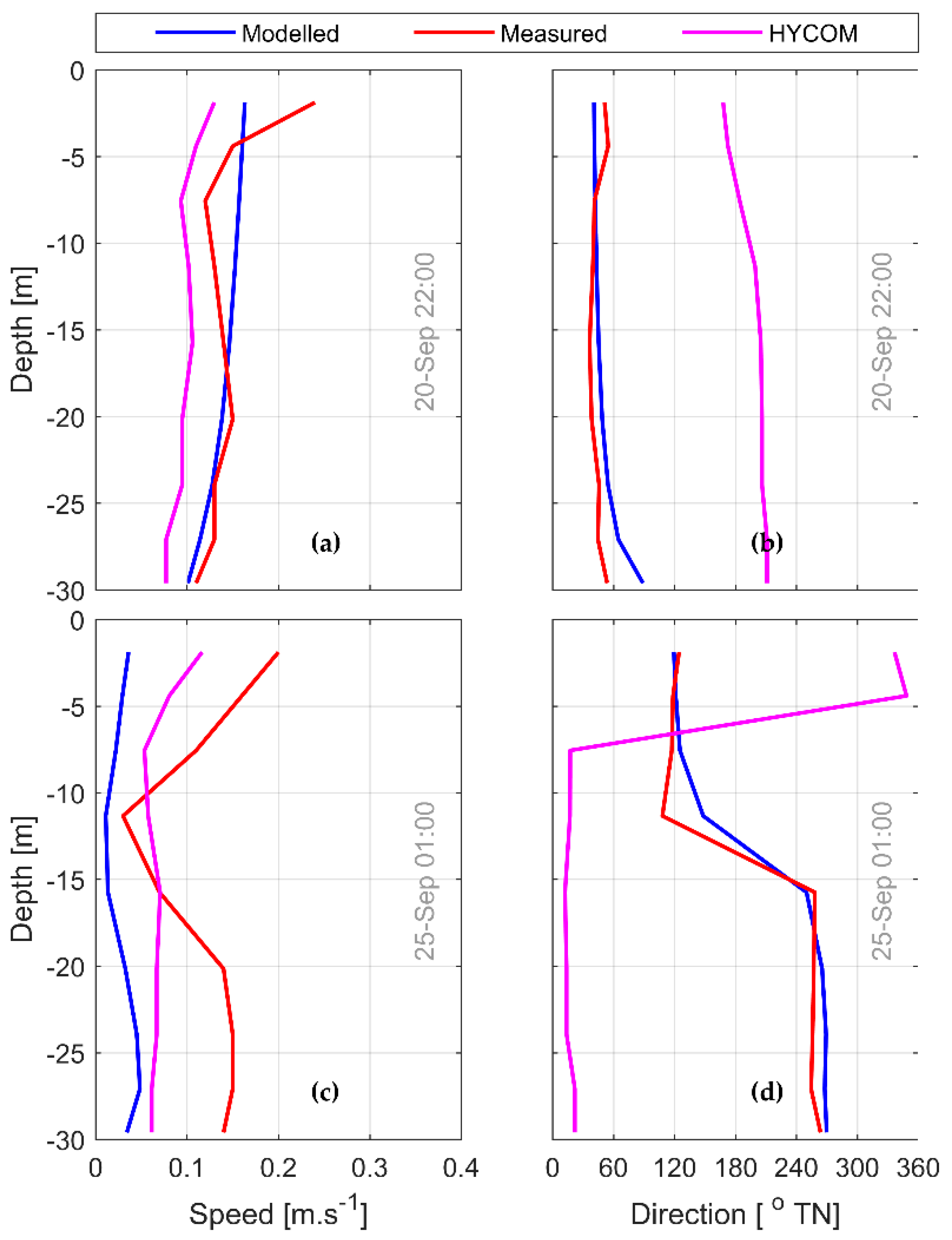
3.4. HRM Validation Performance
3.5. Circulation and Density Dynamics
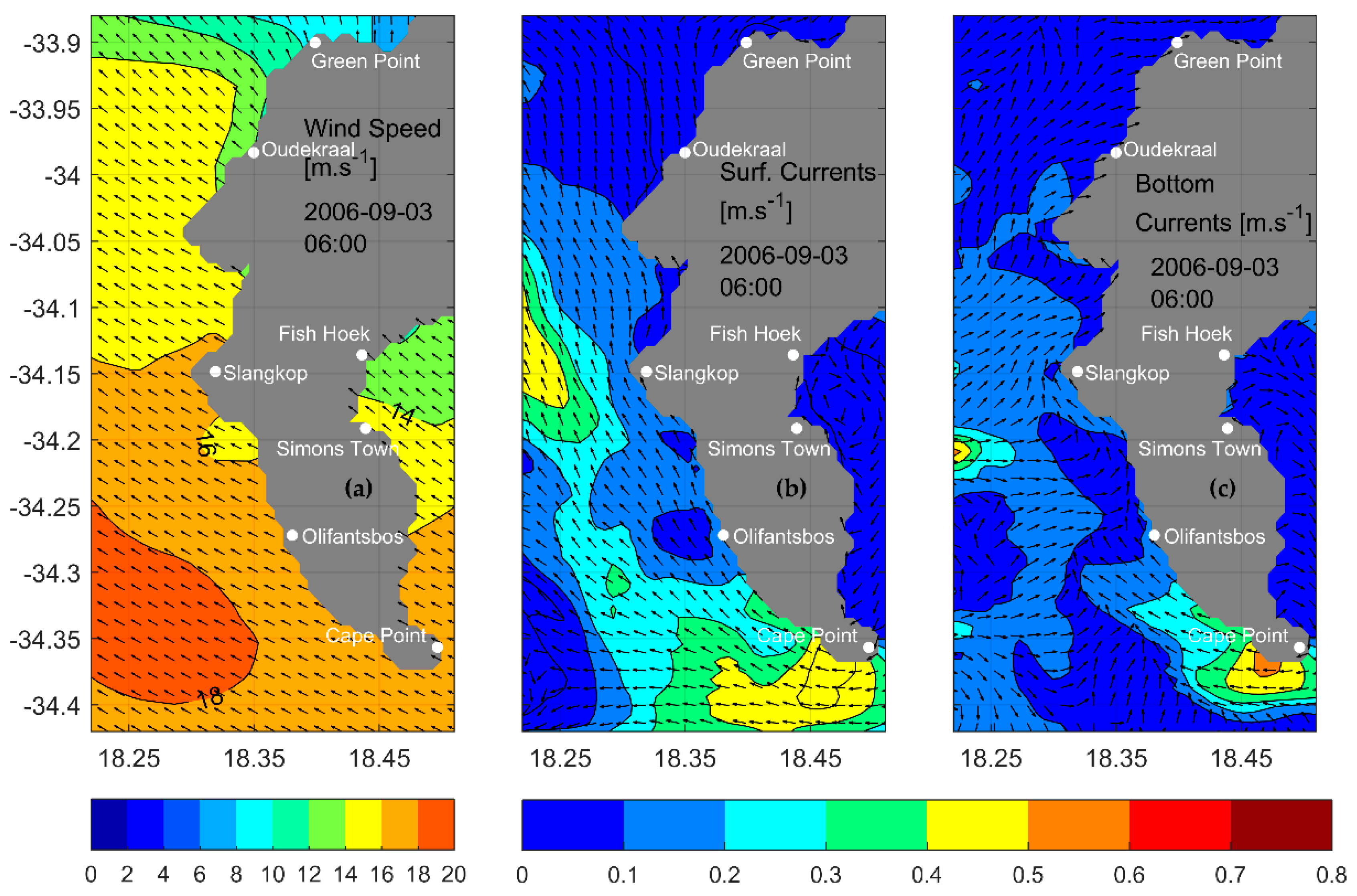
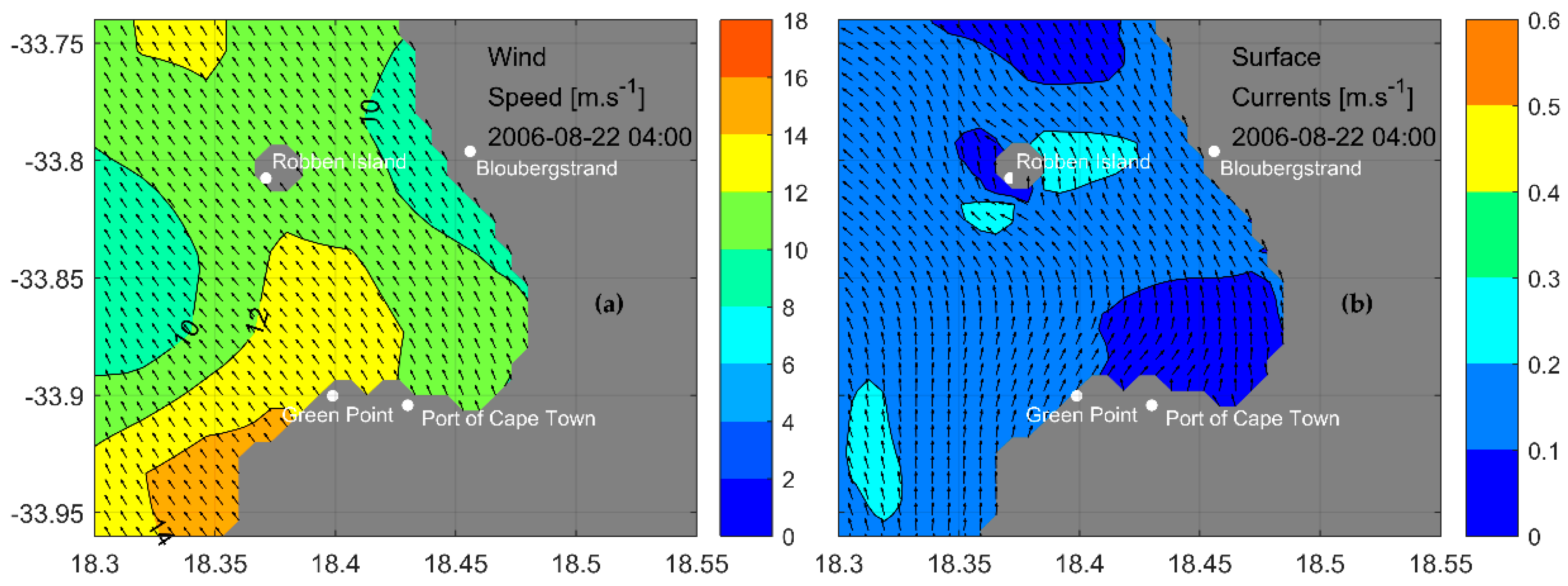
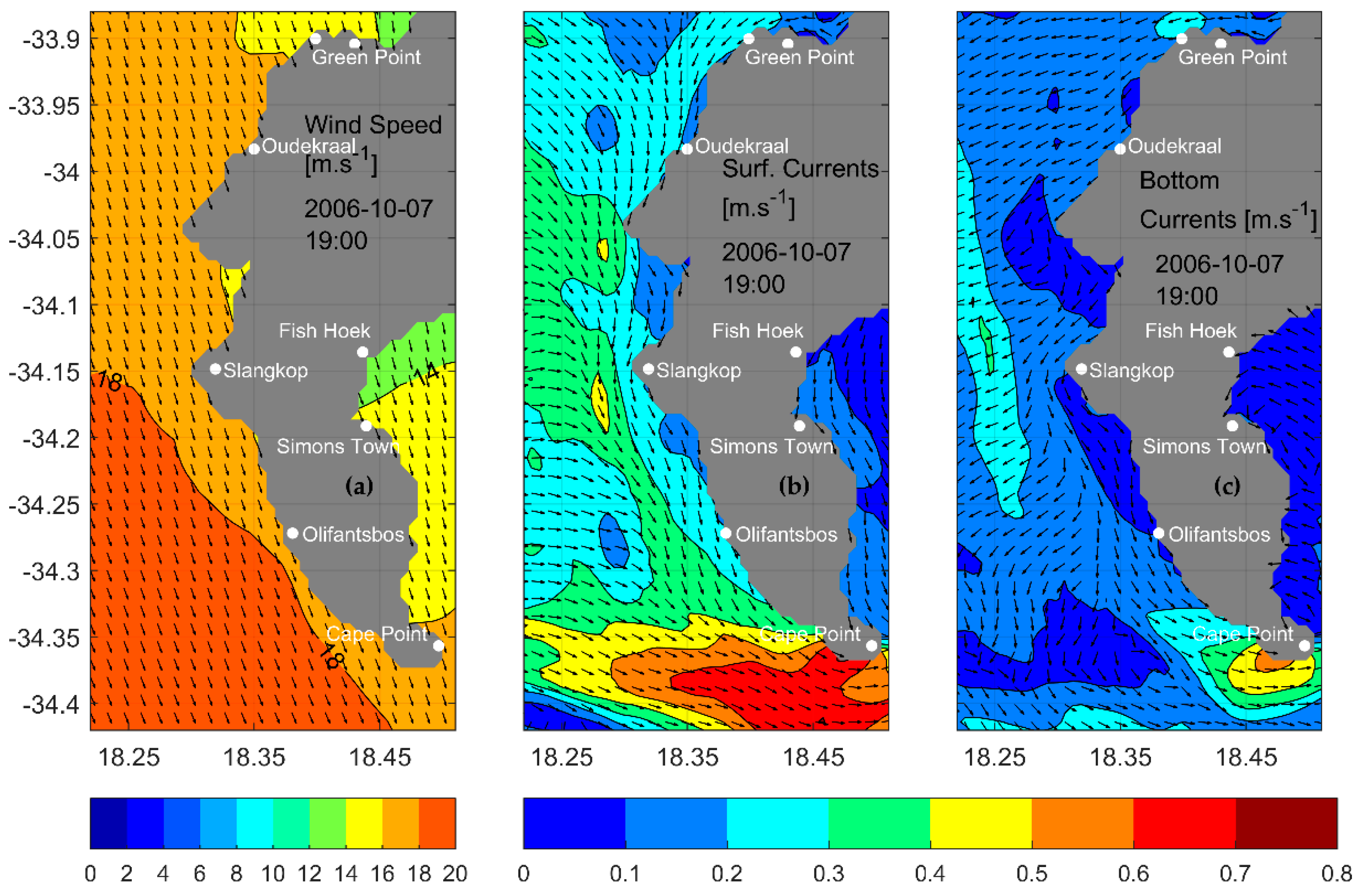
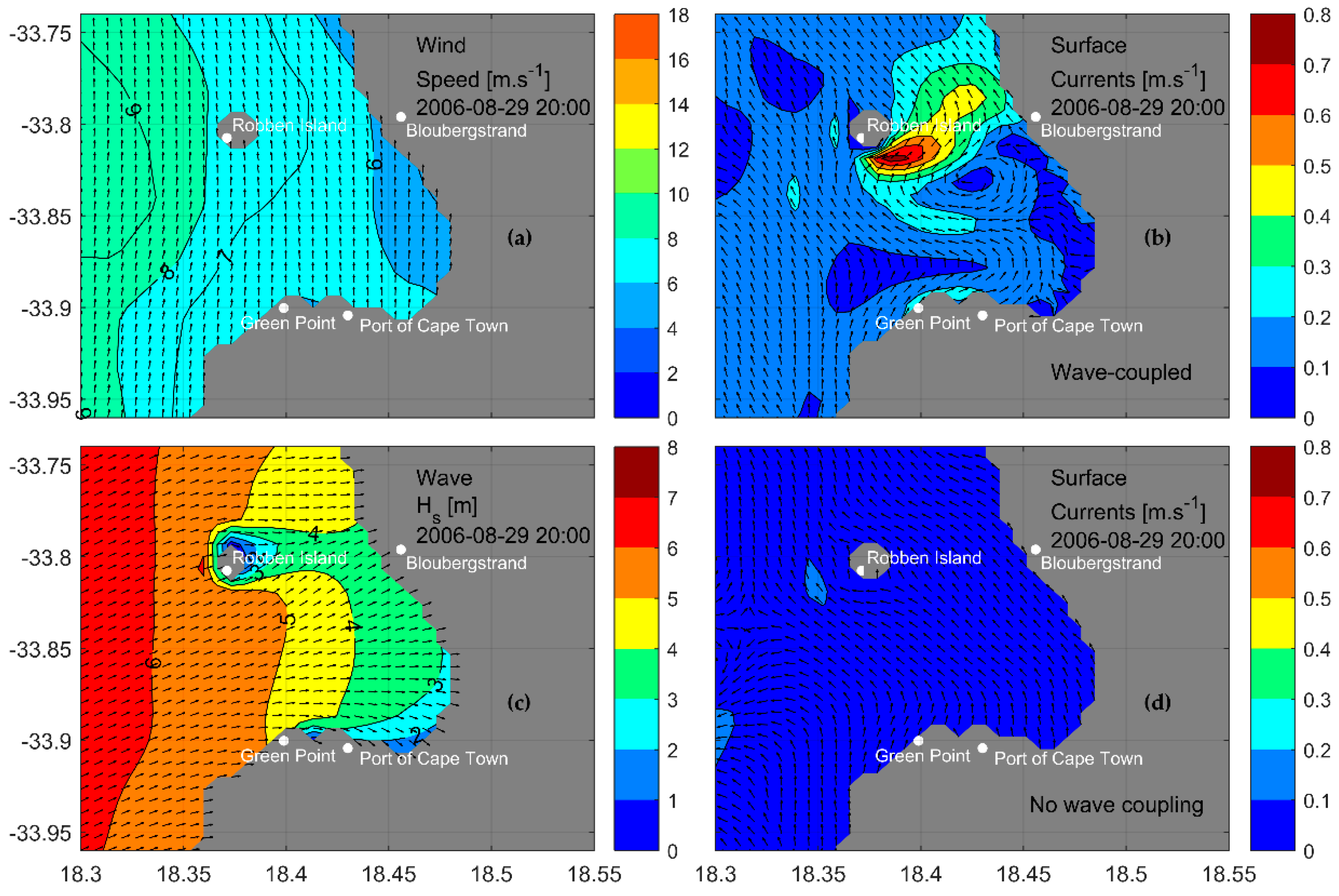
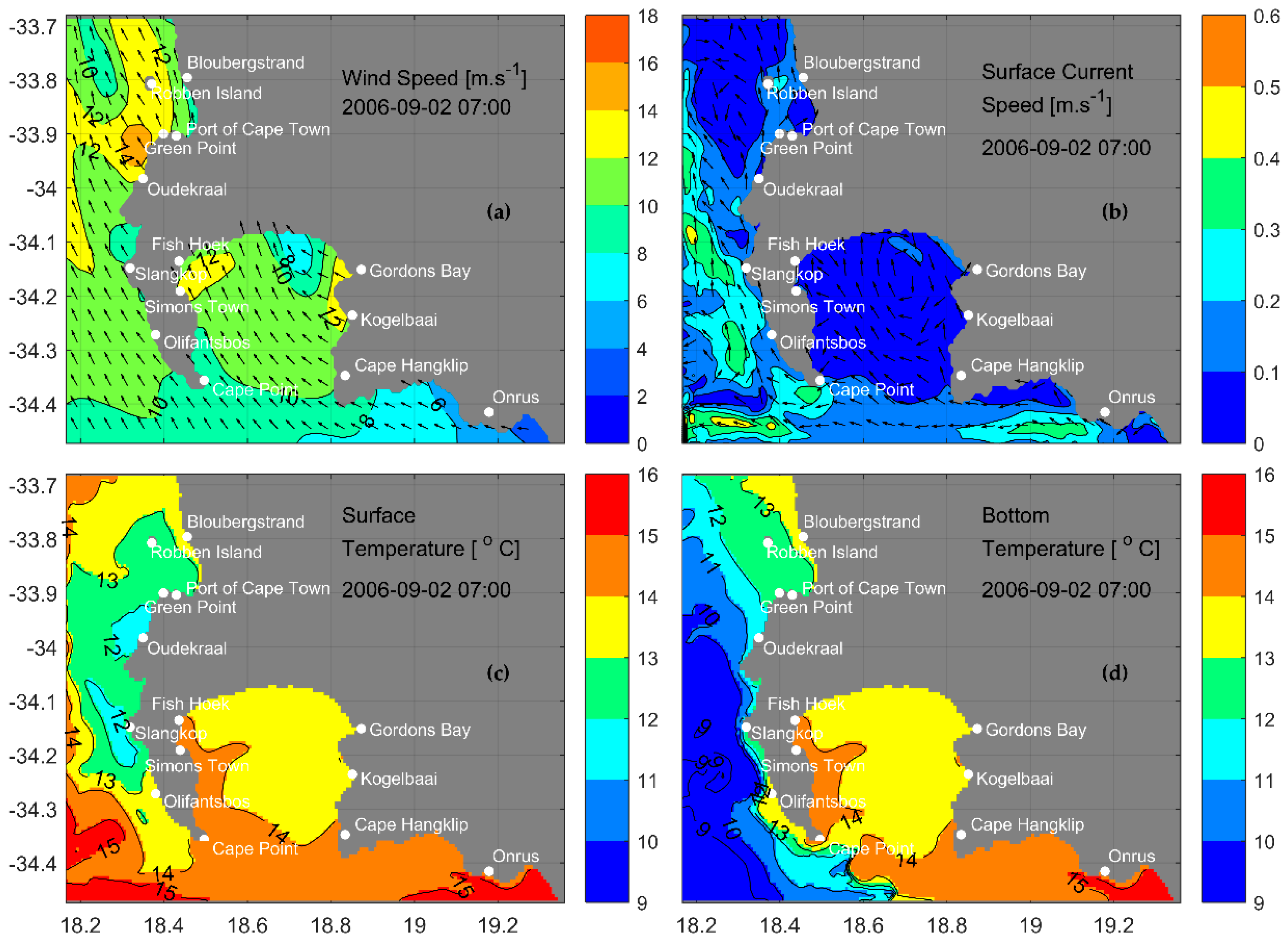
3.5.1. Flow under South Easterly Wind Events
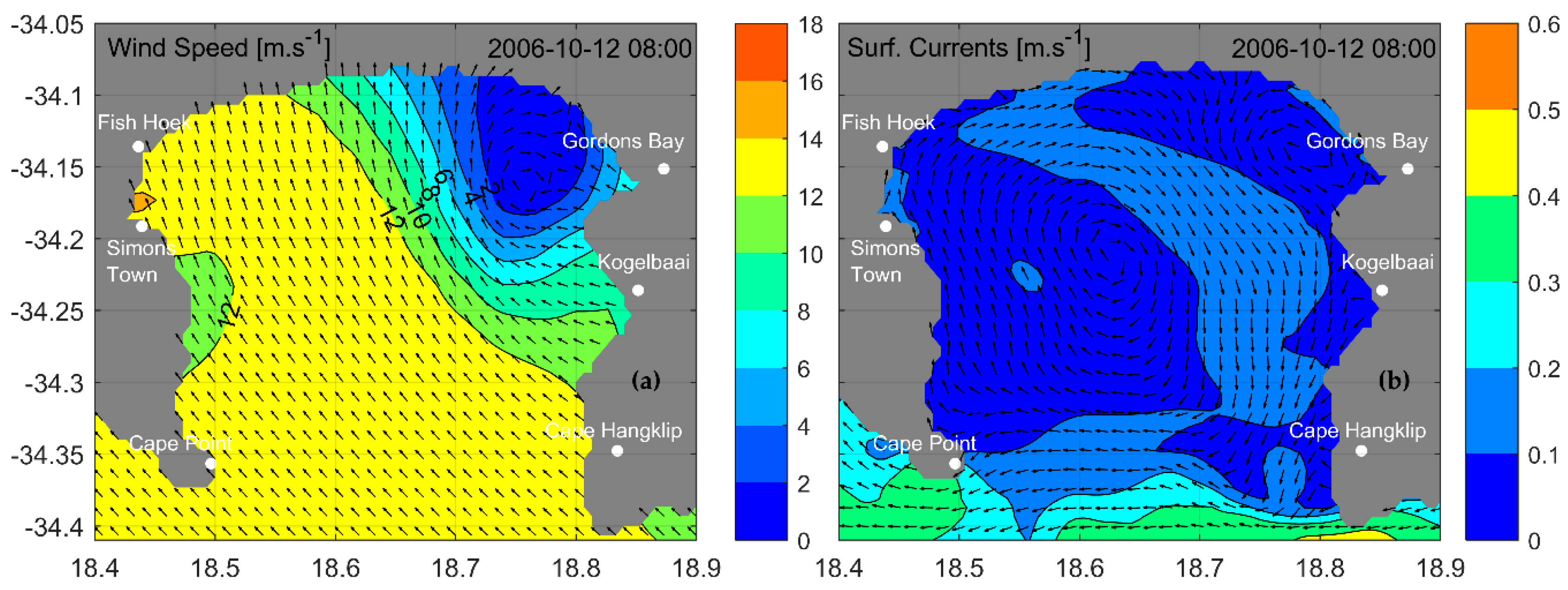
3.5.2. Flow under North-Westerly Wind Events
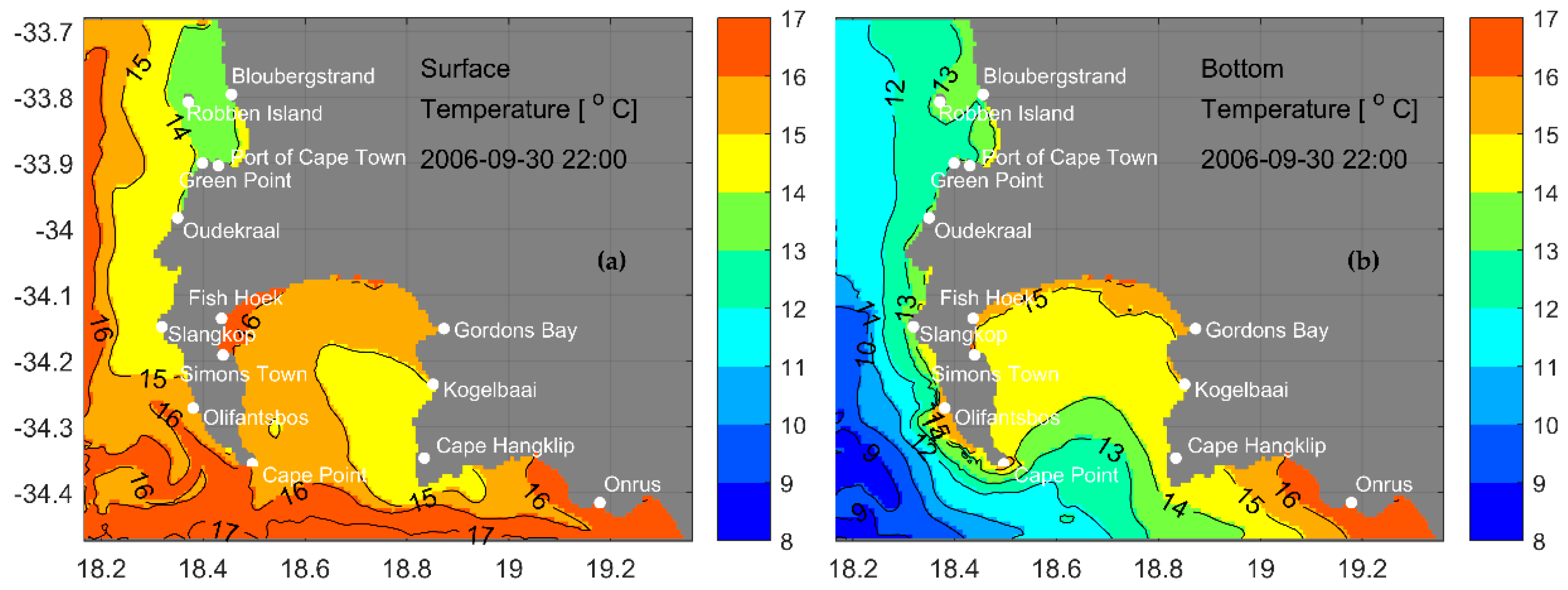
3.5.3. Horizontal Temperature Distributions
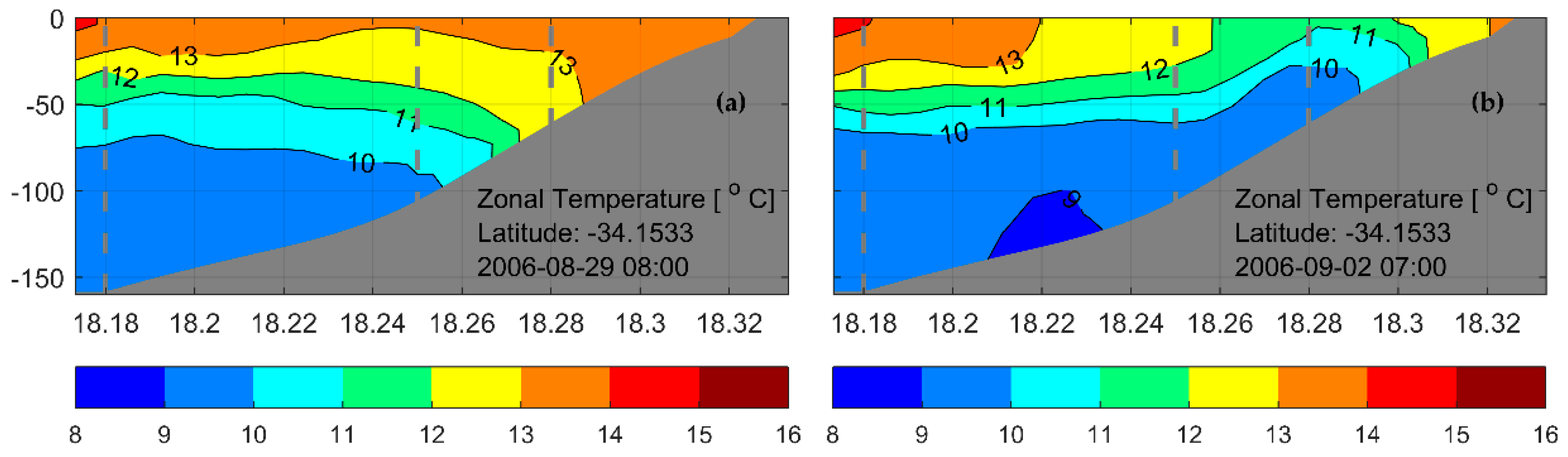
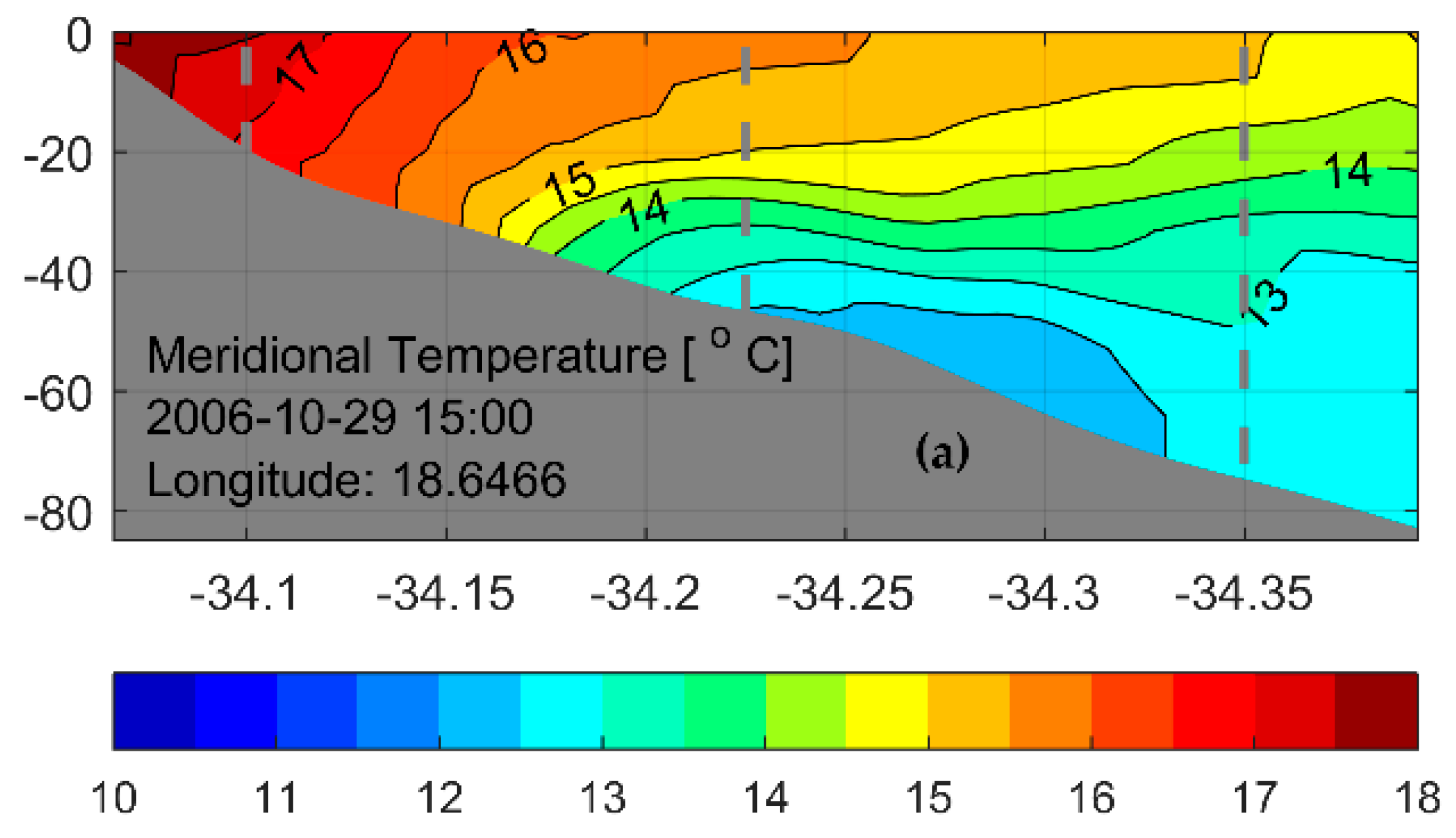
3.5.4. Density Structure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sea Level Pressure | Validation Time Period | Reference Data Description | Location Reference | RMSE (hPa) | |
| 1 August 2006 00:00–30 October 2006 21:00 | RCYC AWS | W1 | 1.5077 | ||
| Robben Island AWS | W2 | 1.0932 | |||
| Strand AWS | W4 | 1.9382 | |||
| 1 August 2010 00:00–30 October 2010 21:00 | RCYC AWS | W1 | 1.6044 | ||
| Robben Island AWS | W2 | 2.1458 | |||
| Strand AWS | W4 | 1.7438 | |||
| Wind | Validation Time Period | Reference Data Description | Location Reference | RMSE | |
| Speed (m s−1) | Direction (°) | ||||
| 1 August 2006 00:00–30 October 2006 21:00 | RCYC AWS | W1 | 2.916 | −21.984 | |
| Robben Island AWS | W2 | 3.403 | 8.230 | ||
| Strand AWS | W4 | 4.086 | −5.699 | ||
| 1 August 2010 00:00–30 October 2010 21:00 | RCYC AWS | W1 | 2.916 | −21.984 | |
| Robben Island AWS | W2 | 3.403 | 8.230 | ||
| Strand AWS | W4 | 4.086 | −5.699 | ||
| Cape Point AWS | W5 | 3.436 | 19.367 | ||
| Slangkop AWS | W6 | 2.740 | 1.040 | ||
| Water Level | Calibration Time Period | Reference Data Description | Location Reference | RMSE (m) | |||
| 1 August 2006 00:00–30 October 2006 21:00 | Cape Town tide gauge | WL1 | 0.205 | ||||
| Simon’s Town tide gauge | WL2 | 0.102 | |||||
| Current Velocity | Calibration Time Period | Reference Data Description | Location Reference | RMSE (m s−1) | |||
| HRM | HYCOM | ||||||
| u | v | u | v | ||||
| 25 August 2006 09:00–27 September 2006 09:00 | Table Bay ADCP | CU1 (near surface) | 0.080 | 0.100 | 0.105 | 0.097 | |
| CU1 (near bottom) | 0.073 | 0.064 | 0.066 | 0.057 | |||
| Site (Type) | Mean Current Parameters for Overlapping Period | HRM | HYCOM | Measured | ||
|---|---|---|---|---|---|---|
| CU1 (calibration) | near surface (m s−1) | 0.088 | 0.074 | 0.128 | 0.04 | 0.05 |
| near bottom (m s−1) | 0.058 | 0.045 | 0.077 | 0.02 | 0.03 | |
| near surface (°) | 74.8 | 218.8 | 96.5 | 21.8 | 121.9 | |
| near bottom (°) | 121.9 | 126.1 | 145.1 | 23.2 | 18.9 | |
| CU2 (validation) | near bottom (m s−1) | 0.077 | 0.016 | 0.106 | 0.03 | 0.09 |
| near bottom (°) | 295.8 | 271.9 | 275.2 | 20.7 | 3.2 | |
| CU3 (validation) | near bottom (m s−1) | 0.047 | 0.010 | 0.070 | 0.02 | 0.06 |
| near bottom (°) | 108.9 | 266.5 | 133.3 | 24.4 | 133.2 | |
| CU4 (validation) | near surface (m s−1) | 0.074 | 0.048 | 0.067 | 0.01 | 0.02 |
| near bottom (m s−1) | 0.046 | 0.033 | 0.045 | 0.00 | 0.01 | |
| near surface (°) | 164.9 | 222.7 | 176.6 | 11.7 | 46.0 | |
| near bottom (°) | 188.0 | 237.3 | 174.2 | 13.8 | 63.1 | |
| CU5 (validation) | near bottom (m s−1) | 0.040 | 0.019 | 0.087 | 0.05 | 0.06 |
| near bottom (°) | 224.1 | 153.8 | 238.0 | 13.9 | 84.2 |
| Water Level | Validation Time Period | Reference Data Description | Location Reference | RMSE (m) | |||
| 1 August 2010 00:00–22 October 2010 21:00 | Cape Town tide gauge | WL1 | 0.039 | ||||
| Simon’s Town tide gauge | WL2 | 0.158 | |||||
| Current Velocity | Validation Time Period | Reference Data Description | Location Reference | RMSE (m s−1) | |||
| HRM | HYCOM | ||||||
| u | v | u | v | ||||
| 27August 2006 11:00–27 September 2006 06:00 | Table Bay SeaPac 1 | CU2 (near bottom) | 0.060 | 0.078 | 0.082 | 0.101 | |
| 27August 2006 11:00–03 October 2006 03:00 | Table Bay SeaPac 2 | CU3 (near bottom) | 0.044 | 0.048 | 0.070 | 0.049 | |
| 20 August 2010 11:00–13 September 2010 09:00 | Gordon’s Bay ADCP | CU4 (near surface) | 0.057 | 0.088 | 0.053 | 0.049 | |
| CU4 (near bottom) | 0.044 | 0.046 | 0.032 | 0.049 | |||
| 29 September 2010 11:00–22 October 2010 08:00 | Simon’s Town SeaPac | CU5 (near bottom) | 0.057 | 0.071 | 0.043 | 0.105 | |
| Temperature (T)/Salinity (S) | Validation Time Period | Reference Data Description | Location Reference | RMSE | |||
| HRM | HYCOM | ||||||
| T (°C) | S (ppt) | T (°C) | S (ppt) | ||||
| 26 October 2006 10:30:59 | WOD Cast ID # 17365255 | TS4 | 0.89 | 0.13 | 2.76 | 2.48 | |
| 26 October 2006 13:57:59 | WOD Cast ID # 17365256 | TS5 | 1.57 | 0.08 | 1.20 | 0.21 | |
| 26 October 2006 17:17:59 | WOD Cast ID # 17365257 | TS6 | 2.08 | 0.15 | 3.40 | 0.30 | |
| 28 October 2006 11:00:59 | WOD Cast ID # 17365268 | TS7 | 1.29 | 0.16 | 1.29 | 0.16 | |
| 29 October 2006 17:32:59 | WOD Cast ID # 17365280 | TS8 | 3.14 | 0.32 | 3.50 | 0.37 | |
| 29 October 2006 18:14:00 | WOD Cast ID # 17365281 | TS9 | 3.57 | 0.34 | 3.57 | 0.35 | |
| 29 October 2006 18:49:00 | WOD Cast ID # 17365282 | TS10 | 3.58 | 0.38 | 4.55 | 0.45 | |
| 1 September 2010 08:19:00 | WOD Cast ID # 13192128 | TS11 | 0.15 | 0.13 | 0.91 | 0.13 | |
| Waves | Validation Time Period | Reference Data Description | Location Reference | RMSE | |||
| Hs (m) | Tp (s) | Dp (°) | |||||
| 1 August 2006 00:00–30 October 2006 21:00 | TNPA Wave Rider Buoy | WV1 | 0.49 | 1.45 | 10.80 | ||
References
- Salonen, N.M. Towards Rogue Wave Characterization in False Bay, South Africa. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2019. [Google Scholar]
- Day, J.H. The biology of false bay, South Africa. Trans. R. Soc. S. Afr. 1970, 39, 211–221. [Google Scholar] [CrossRef]
- de Vos, M.; Rautenbach, C. Investigating the connection between metocean conditions and coastal user safety: An analysis of search and rescue data. Saf. Sci. 2019, 117, 217–228. [Google Scholar] [CrossRef]
- Shannon, L.V.; Nelson, G.; Jury, M.R. Hydrological and Meteorological Aspects of Upwelling in the Southern Benguela Current. In Coastal Upwelling; Richards, F.A., Ed.; American Geophysical Union: Washington, DC, USA, 1981; Volume 1, pp. 39–43. ISBN 9781118665329. [Google Scholar]
- Van Ieperen, M.P. Hydrology of Table Bay; Final Report; Department of Oceanography, University of Cape Town: Cape Town, South Africa, 1971. [Google Scholar]
- Quick, A.J.R.; Roberts, M.J. Table Bay, Cape Town, South Africa: Synthesis of available information and management implications. S. Afr. J. Sci. 1993, 89, 276–287. [Google Scholar]
- Pfaff, M.C.; Logston, R.C.; Raemaekers, S.J.P.N.; Hermes, J.C.; Blamey, L.K.; Cawthra, H.C.; Colenbrander, D.R.; Crawford, R.J.M.; Day, E.; du Plessis, N.; et al. A synthesis of three decades of socio-ecological change in False Bay, South Africa: Setting the scene for multidisciplinary research and management. Elementa 2019, 7, 32. [Google Scholar] [CrossRef]
- Gründlingh, M.L.; Hunter, I.T.; Potgieter, E. Bottom currents at the entrance to False Bay, South Africa. Cont. Shelf Res. 1989, 9, 1029–1048. [Google Scholar] [CrossRef]
- Harris, T.F.W. Review of Coastal Current in Southern African Waters. National Scientific Programmes Unit, CSIR. 1978. Available online: https://researchspace.csir.co.za/dspace/handle/10204/2300 (accessed on 26 June 2020).
- Western Cape Government Provincial Treasury. Provincial Economic Review and Outlook; Western Cape Government Provincial Treasury: Cape Town, South Africa, 2017.
- Celliers, L.; Colenbrander, D.R.; Breetzke, T.; Oelofse, G. Towards increased degrees of integrated coastal management in the city of Cape Town, South Africa. Ocean Coast. Manag. 2015, 105, 138–153. [Google Scholar] [CrossRef]
- Sowman, M.; Sunde, J. Social impacts of marine protected areas in South Africa on coastal fishing communities. Ocean Coast. Manag. 2018, 157, 168–179. [Google Scholar] [CrossRef]
- Ballance, A.; Ryan, P.G.; Turpie, J.K. How much is a clean beach worth? The impact of litter on beach users in the Cape Peninsula, South Africa. S. Afr. J. Sci. 2000, 96, 210–213. [Google Scholar]
- Munien, S.; Gumede, A.; Gounden, R.; Bob, U.; Gounden, D.; Perry, N.S. Profile of visitors to coastal and marine tourism locations in cape town, South Africa. Geoj. Tour. Geosites 2019, 27, 1134–1147. [Google Scholar] [CrossRef]
- Van Ballegooyen, R. Ben Schoeman Dock Berth Deepening Project Integrated Marine Impact Assessment Study; Council for Scientific and Industrial Research: Stellenbosch, South Africa, 2007. [Google Scholar]
- Potgieter, L.; Goedhals-gerber, L.L. Risk Profile of Weather and System-Related Port Congestion for the Cape Town Container Terminal. S. Afr. Bus. Rev. 2020, 24. [Google Scholar] [CrossRef]
- Colenbrander, D.; Sutherland, C. Reducing the pathology of risk: Developing an integrated municipal coastal protection zone for the City of Cape Town. In Climate Change at the City Scale: Impacts, Mitigation and Adaptation in Cape Town; Cartwright, A., Parnell, S., Oelofse, G., Ward, S., Eds.; Routledge: New York, NY, USA, 2012; pp. 182–201. ISBN 9780203112656. [Google Scholar]
- Boyd, A.J.; Tromp, B.B.; Horstman, D.A. The hydrology off the South African south-western coast between Cape Point and Danger Point in 1975. S. Afr. J. Mar. Sci. 1985, 3, 145–168. [Google Scholar] [CrossRef]
- Tyson, P.D.; Garstang, M.; Swap, R.; Kållberg, P.; Edwards, M. An air transport climatology for subtropical Southern Africa. Int. J. Climatol. 1996, 16, 265–291. [Google Scholar] [CrossRef]
- Jury, M.R. Wind shear and Differential Upwelling Along the South Western tip of Africa. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 1984. [Google Scholar]
- Gründlingh, M.L.; Largier, J.L. Fisiese Oseanografie in Valsbaai: ’ n Oorsig. R. Soc. S. Afr. Trans. Trsaac 1988, 47. [Google Scholar]
- Coleman, F. The Development and Validation of a Hydrodynamic Model of False Bay By. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2019. [Google Scholar]
- CSIR. Effects of Proposed Harbour Developments on the Table Bay Coastline. Report Volume I, ME 1086/1, 1972.
- CSIR. Effects of Proposed Harbour Developments on the Table Bay Coastline. Report Volume 2, ME 1086/2, 1972.
- Schumann, E.H.; Perrins, L.A. Tidal and inertial currents around South Africa. Coast. Eng. 1982, 2562–2580. [Google Scholar]
- Gunn, B.W. The Nearshore dynamics of Matroos Bay-Field and Theoretical Investigations. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 1977. [Google Scholar]
- Gunn, B.W. The Dynamics of Two Cape, Coastal Embayments; Unpublished Report; Department of Oceanography, University of Cape Town: Cape Town, South Africa, 1977; Volume 1. [Google Scholar]
- Taunton-Clark, J.; Kamstra, F. Aspects of marine environmental variability near Cape Town, 1960–1985. S. Afr. J. Mar. Sci. 1988, 6, 273–283. [Google Scholar] [CrossRef][Green Version]
- Nelson, G.; Polito, A. Information on currents in the cape Peninsula area, South Africa. S. Afr. J. Mar. Sci. 1987, 5, 287–304. [Google Scholar] [CrossRef]
- Atkins, G.R. Camps Bay Outfall Investigation; Institute of Oceanography, University of Cape Town: Cape Town, South Africa, 1965. [Google Scholar]
- Atkins, G.R. Green Point Outfall Investigation; Institute of Oceanography, University of Cape Town: Cape Town, South Africa, 1965. [Google Scholar]
- Andrews, W.R.H.; Hutchings, L. Upwelling in the Southern Benguela Current. Prog. Oceanogr. 1980, 9, 1–81. [Google Scholar] [CrossRef]
- Atkins, G.R. Winds and current patterns in false bay. Trans. R. Soc. S. Afr. 1970, 39, 139–148. [Google Scholar] [CrossRef]
- Atkins, G.R. Thermal structure and salinity of false bay. Trans. R. Soc. S. Afr. 1970, 39, 117–128. [Google Scholar] [CrossRef]
- Wainman, C.K.; Polito, A.; Nelson, G. Winds and subsurface currents in the false bay region, South Africa. S. Afr. J. Mar. Sci. 1987, 5, 337–346. [Google Scholar] [CrossRef]
- Shipley, A.M. Some aspects of wave refraction in False Bay. S. Afr. J. Sci. 1964, 60, 115–120. [Google Scholar]
- Gründlingh, M.L. Quasi-synoptic survey of the thermohaline properties of False Bay. S. Afr. J. Sci. 1992, 88, 325–334. [Google Scholar]
- Jury, M.R. Coastal gradients in False Bay, south of Cape Town: What insights can be gained from mesoscale reanalysis? Ocean Sci. 2020, 16, 1545–1557. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Small, C. Improved estimates of coastal population and exposure to hazards released. EOS 2002, 83, 301–305. [Google Scholar] [CrossRef]
- de Mey, P.; Craig, P.; Davidson, F.; Edwards, C.A.; Ishikawa, Y.; Kindle, J.C.; Proctor, R.; Thompson, K.R.; Zhu, J. Applications in coastal modeling and forecasting. Oceanography 2009, 22, 198–205. [Google Scholar] [CrossRef][Green Version]
- Fossati, M.; Piedra-Cueva, I. A 3D hydrodynamic numerical model of the Río de la Plata and Montevideo’s coastal zone. Appl. Math. Model. 2013, 37, 1310–1332. [Google Scholar] [CrossRef]
- Sotillo, M.G.; Cailleau, S.; Lorente, P.; Levier, B.; Aznar, R.; Reffray, G.; Amo-Baladrón, A.; Chanut, J.; Benkiran, M.; Alvarez-Fanjul, E. The myocean IBI ocean forecast and reanalysis systems: Operational products and roadmap to the future copernicus service. J. Oper. Oceanogr. 2015, 8, 63–79. [Google Scholar] [CrossRef]
- Zhang, X.; Marta-Almeida, M.; Hetland, R.D. A high-resolution pre-operational forecast model of circulation on the Texas-Louisiana continental shelf and slope. J. Oper. Oceanogr. 2012, 5, 19–34. [Google Scholar] [CrossRef]
- Kiambo, R.; Coley, C.; Francis, J.; Amaral, M.; Hale, L. A Capacity Needs Assessment: Report of the Western Indian Ocean Marine Science Association Coastal Management Capacity Building Needs Assessment; University of Rhode Island: Narragansett, RI, USA, 2001. [Google Scholar]
- Deltares Delft3D FLOW–Simulation of Multi-Dimensional Hydrodynamic Flows and Transport Phenomena, Including Sediments, User Manual; Deltares: Delft, The Netherlands, 2020.
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Rey, A.J.M.; Mulligan, R.P. Influence of Hurricane Wind Field Variability on Real-Time Forecast Simulations of the Coastal Environment. J. Geophys. Res. Ocean. 2021, 126, 1–20. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current system. Part I: Flow structure, eddy flux, and observational tests. J. Phys. Oceanogr. 2008, 38, 29–43. [Google Scholar] [CrossRef]
- Hasan, G.M.J.; van Maren, D.S.; Ooi, S.K. Hydrodynamic modeling of Singapore’s coastal waters: Nesting and model accuracy. Ocean Model. 2016, 97, 141–151. [Google Scholar] [CrossRef]
- Rautenbach, C.; Daniels, T.; de Vos, M.; Barnes, M.A. A coupled wave, tide and storm surge operational forecasting system for South Africa: Validation and physical description. Nat. Hazards 2020, 103, 1407–1439. [Google Scholar] [CrossRef]
- Deltares Delft3D WAVE—Simulation of Short-Crested Waves with SWAN, User Manual; Deltares: Delft, The Netherlands, 2020; ISBN 9290793740.
- Garcia, M.; Ramirez, I.; Verlaan, M.; Castillo, J. Application of a three-dimensional hydrodynamic model for San Quintin Bay, B.C., Mexico. Validation and calibration using OpenDA. J. Comput. Appl. Math. 2015, 273, 428–437. [Google Scholar] [CrossRef]
- Metzger, E.J.; Helber, R.W.; Hogan, P.J.; Posey, P.G.; Thoppil, P.G.; Townsend, T.L.; Wallcraft, A.J. Global Ocean Forecast System 3.1 Validation Testing; US Naval Research Laboratory: Hancock County, MS, USA, 2017. [Google Scholar]
- Bleck, R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Model. 2002, 4, 55–88. [Google Scholar] [CrossRef]
- Putzu, S.; Enrile, F.; Besio, G.; Cucco, A.; Cutroneo, L.; Capello, M.; Stocchino, A. A reasoned comparison between two hydrodynamic models: Delft3D-Flow and ROMS (regional oceanic modelling system). J. Mar. Sci. Eng. 2019, 7, 464. [Google Scholar] [CrossRef]
- Elias, E.P.L.; Walstra, D.J.R.; Roelvink, J.A.; Stive, M.J.F.; Klein, M.D. Hydrodynamic validation of Delft3D with field measurements at Egmond. In Proceedings of the Coastal Engineering 2000—27th International Conference on Coastal Engineering, ICCE 2000, Sydney, Australia, 16–21 July 2000; Volume 276. [Google Scholar]
- Roelvink, J.A.; Van Banning, G.K.F.M. Design and development of DELFT3D and application to coastal morphodynamics. Oceanogr. Lit. Rev. 1995, 11, 925. [Google Scholar]
- Gerritsen, H.; De Goede, E.D.; Platzek, F.W.; van Kester, J.A.T.M.; Genseberger, M.; Uittenbogaard, R.E. Validation Document Delft3D- FLOW, a Software System for 3D Flow Simulations; 1.1.; Deltares: Delft, The Netherlands, 2008. [Google Scholar]
- de Mendoza, F.P.; Bonamano, S.; Martellucci, R.; Melchiorri, C.; Consalvi, N.; Piermattei, V.; Marcelli, M. Circulation during storms and dynamics of suspended matter in a sheltered coastal area. Remote Sens. 2018, 10, 602. [Google Scholar] [CrossRef]
- Peng, Z.; Bradon, J. 3-D Comprehensive Hydrodynamic Modelling in the Arabian Gulf. J. Coast. Res. 2016, 75, 547–551. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: New York, NY, USA, 1993; ISBN 9780521458689. [Google Scholar]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Rogers, W.E.; Kaihatu, J.M.; Hsu, L.; Jensen, R.E.; Dykes, J.D.; Holland, K.T. Forecasting and hindcasting waves with the SWAN model in the Southern California Bight. Coast. Eng. 2007, 54, 1–15. [Google Scholar] [CrossRef]
- Zubier, K.; Panchang, V.; Demirbilek, Z. Simulation of waves at duck (North Carolina) using two numerical models. Coast. Eng. J. 2003, 45, 439–469. [Google Scholar] [CrossRef]
- Thomas, T.J.; Dwarakish, G.S. Numerical Wave Modelling–A Review. Aquat. Procedia 2015, 4, 443–448. [Google Scholar] [CrossRef]
- Ardhuin, F.; Marié, L.; Rascle, N.; Forget, P.; Roland, A. Observation and estimation of lagrangian, stokes, and Eulerian currents induced by wind and waves at the sea surface. J. Phys. Oceanogr. 2009, 39, 2820–2838. [Google Scholar] [CrossRef]
- Perrie, W.; Tang, C.L.; Hu, Y.; DeTracy, B.M. The impact of waves on surface currents. J. Phys. Oceanogr. 2003, 33, 2126–2140. [Google Scholar] [CrossRef]
- Tamtare, M.T.; Dumont, D.; Chavanne, C. The Stokes drift in ocean surface drift prediction. Egu Gen. Assem. Conf. Abstr. 2020, 9752, 1–13. [Google Scholar] [CrossRef]
- List, J.H.; Hanes, D.M.; Ruggiero, P. Predicting longshore gradients in longshore transport: Comparing the CERC formula to Delft3D. In Proceedings of the Coastal Engineering 2006—30th International Conference (In 5 Volumes), San Diego, CA, USA, 3–8 September 2006; Mckee Smith, J., Ed.; World Scientific: Singapore, 2007; pp. 3370–3380. [Google Scholar]
- Reniers, A.J.H.M.; Roelvink, J.A.; Thornton, E.B. Morphodynamic modeling of an embayed beach under wave group forcing. J. Geophys. Res. Ocean. 2004, 109, 1–22. [Google Scholar] [CrossRef]
- Mahadevan, A. Modeling vertical motion at ocean fronts: Are nonhydrostatic effects relevant at submesoscales? Ocean Model. 2006, 14, 222–240. [Google Scholar] [CrossRef]
- Fan, Y.; Yu, Z.; Shi, F. Are Hydrostatic Models Still Capable of Simulating Oceanic Fronts; Naval Research Lab Stennis Detachment Stennis Space Center MS Ocean Dynamics and Prediction Branch: Washington, DC, USA, 2016. [Google Scholar]
- Fringer, O.B.; Dawson, C.N.; He, R.; Ralston, D.K.; Zhang, Y.J. The future of coastal and estuarine modeling: Findings from a workshop. Ocean Model. 2019, 143, 101458. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Rautenbach, C.; Barnes, M.A.; de Vos, M. Tidal characteristics of South Africa. Deep-Sea Res. Part I Oceanogr. Res. Pap. 2019, 150, 103079. [Google Scholar] [CrossRef]
- Battjes, J.A.; Zitman, T.J.; Holthuijsen, L.H. A re-analysis of the spectra observed in JONSWAP. J. Phys. Oceanogr. 1986, 17, 1288–1295. [Google Scholar] [CrossRef][Green Version]
- Gweba, B. Developing a methodology for the assessment of wave energy along the South African Coast. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2018. [Google Scholar]
- Hahmann, A.N.; Lennard, C.; Badger, J.; Vincent, C.L.; Kelly, M.C.; Volker, P.J.H.; Argent, B.; Refslund, J.; Andrea, N.; Louise, C.; et al. Mesoscale modeling for the Wind Atlas of South Africa (WASA) project Department of Wind Energy E Report 2014; DTU Wind Energy: Roskilde, Denmark, 2014. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.B.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Berrisford, P.; Dee, D.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S.; Uppala, S. The ERA-Interim Archive; ECMWF: Reading, UK, 2011. [Google Scholar]
- Lane, A. The Heat Balance of the North Sea; Proudman Oceanographic Laboratory: Birkenhead, UK, 1989. [Google Scholar]
- Gill, A. Atmosphere-Ocean Dynamics, 1st ed.; Academic Press: London, UK, 1982; Volume 30, ISBN 9780080570525. [Google Scholar]
- Williams, J.J.; Esteves, L.S. Guidance on Setup, Calibration, and Validation of Hydrodynamic, Wave, and Sediment Models for Shelf Seas and Estuaries. Adv. Civ. Eng. 2017. [Google Scholar] [CrossRef]
- Peixto, J.P.; Oort, A.H. Physics of Climate, 1st ed.; American Institute of Physics Press: New York, NY, USA, 1984; Volume 56, ISBN 9780883187128. [Google Scholar]
- Manwell, J.; McGowan, J.; Rogers, A. Wind Energy Explained: Theory, Design, and Application, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2009; ISBN 9780470015001. [Google Scholar]
- Sembiring, L.; Van Ormondt, M.; Van Dongeren, A.; Roelvink, D. A validation of an operational wave and surge prediction system for the Dutch coast. Nat. Hazards Earth Syst. Sci. 2015, 15, 1231–1242. [Google Scholar] [CrossRef]
- Madsen, O.S.; Poon, Y.K.; Graber, H.C. Spectral wave attenuation by bottom friction: Theory. In Proceedings of the 21st International Conference on Coastal Engineering, Costa del Sol-Malaga, Spain, 20–25 June 1988; pp. 492–504. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. Coast. Eng. Proc. 1978, 1, 32. [Google Scholar] [CrossRef]
- Van der Westhuysen, A.J. Advances in the Spectral Modelling of Wind Waves in Thenearshore. Doctoral Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Good, S.; Fiedler, E.; Mao, C.; Martin, M.J.; Maycock, A.; Reid, R.; Roberts-Jones, J.; Searle, T.; Waters, J.; While, J.; et al. The current configuration of the OSTIA system for operational production of foundation sea surface temperature and ice concentration analyses. Remote Sens. 2020, 12, 720. [Google Scholar] [CrossRef]
- Backeberg, B.C.; Counillon, F.; Johannessen, J.A.; Pujol, M.I. Assimilating along-track sla data using the EnOI in an eddy resolving model of the agulhas system. Ocean Dyn. 2014, 64, 1121–1136. [Google Scholar] [CrossRef]
- Luyt, H. Quantifying the SST Biases in Data Assimilative Ocean Simulations of the Benguela Upwelling System. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 2018. [Google Scholar]







| Circulation Model (Delft3D FLOW v6.03.00) | ||
| Parameterisation | Model | Coefficient |
| Bottom roughness | Chézy (quadratic friction law) | C2D = 65 (u), C2D = 15 (v) |
| Wind drag breakpoint coefficients | [88] | U10 = 0 m s−1, 100 m s−1 | A = 0.63 × 10−3, 7.23 × 10−3 |
| Background horizontal eddy viscosity | - | 10 m2 s−1 |
| Background vertical eddy viscosity | - | 1 × 10−6 m2 s−1 |
| Background horizontal eddy diffusivity | - | 10 m2 s−1 |
| Background vertical eddy diffusivity | - | 1 × 10−6 m2 s−1 |
| Turbulence closure model | k-L | |
| Secchi depth | Ocean | 2.0 m |
| Stanton number | Ocean | 1.3 × 10−3 |
| Dalton number | Ocean | 1.7 × 10−3 |
| Wave Model (SWAN v40.72) | ||
| Parameterisation | Model | Coefficient |
| Bottom friction | Madsen et al. [89] | Kn = 0.05 |
| Depth-induced breaking | Battjes and Jansen [90] | Alpha (dissipation) = 1 Gamma (breaker) = 0.8 |
| White-capping | Van der Westhuysen [91] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Vos, M.; Vichi, M.; Rautenbach, C. Simulating the Coastal Ocean Circulation Near the Cape Peninsula Using a Coupled Numerical Model. J. Mar. Sci. Eng. 2021, 9, 359. https://doi.org/10.3390/jmse9040359
de Vos M, Vichi M, Rautenbach C. Simulating the Coastal Ocean Circulation Near the Cape Peninsula Using a Coupled Numerical Model. Journal of Marine Science and Engineering. 2021; 9(4):359. https://doi.org/10.3390/jmse9040359
Chicago/Turabian Stylede Vos, Marc, Marcello Vichi, and Christo Rautenbach. 2021. "Simulating the Coastal Ocean Circulation Near the Cape Peninsula Using a Coupled Numerical Model" Journal of Marine Science and Engineering 9, no. 4: 359. https://doi.org/10.3390/jmse9040359
APA Stylede Vos, M., Vichi, M., & Rautenbach, C. (2021). Simulating the Coastal Ocean Circulation Near the Cape Peninsula Using a Coupled Numerical Model. Journal of Marine Science and Engineering, 9(4), 359. https://doi.org/10.3390/jmse9040359







