Spatiotemporal Drought Risk Assessment Considering Resilience and Heterogeneous Vulnerability Factors: Lempa Transboundary River Basin in The Central American Dry Corridor
Abstract
:1. Introduction
2. Materials and Methods
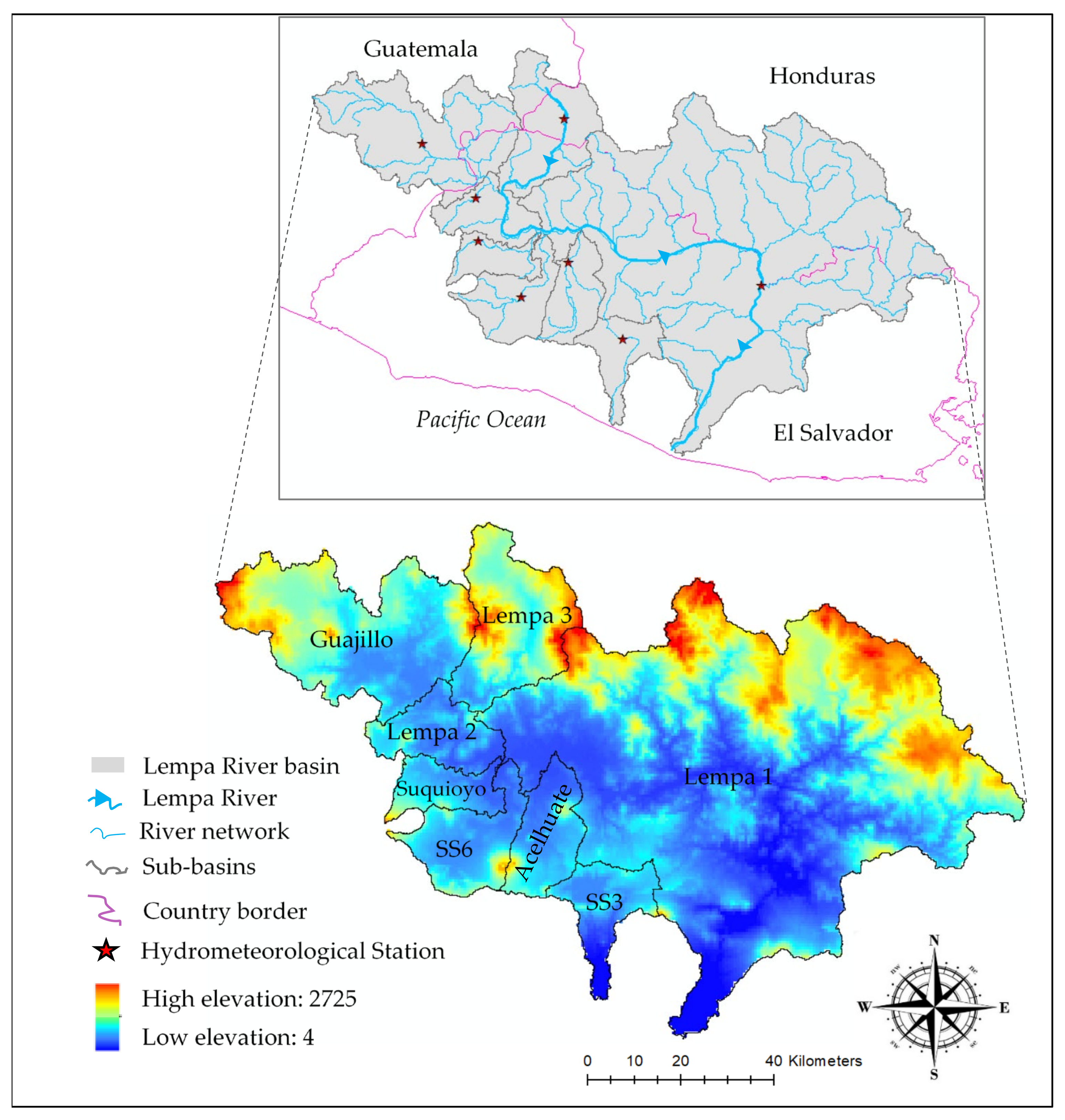
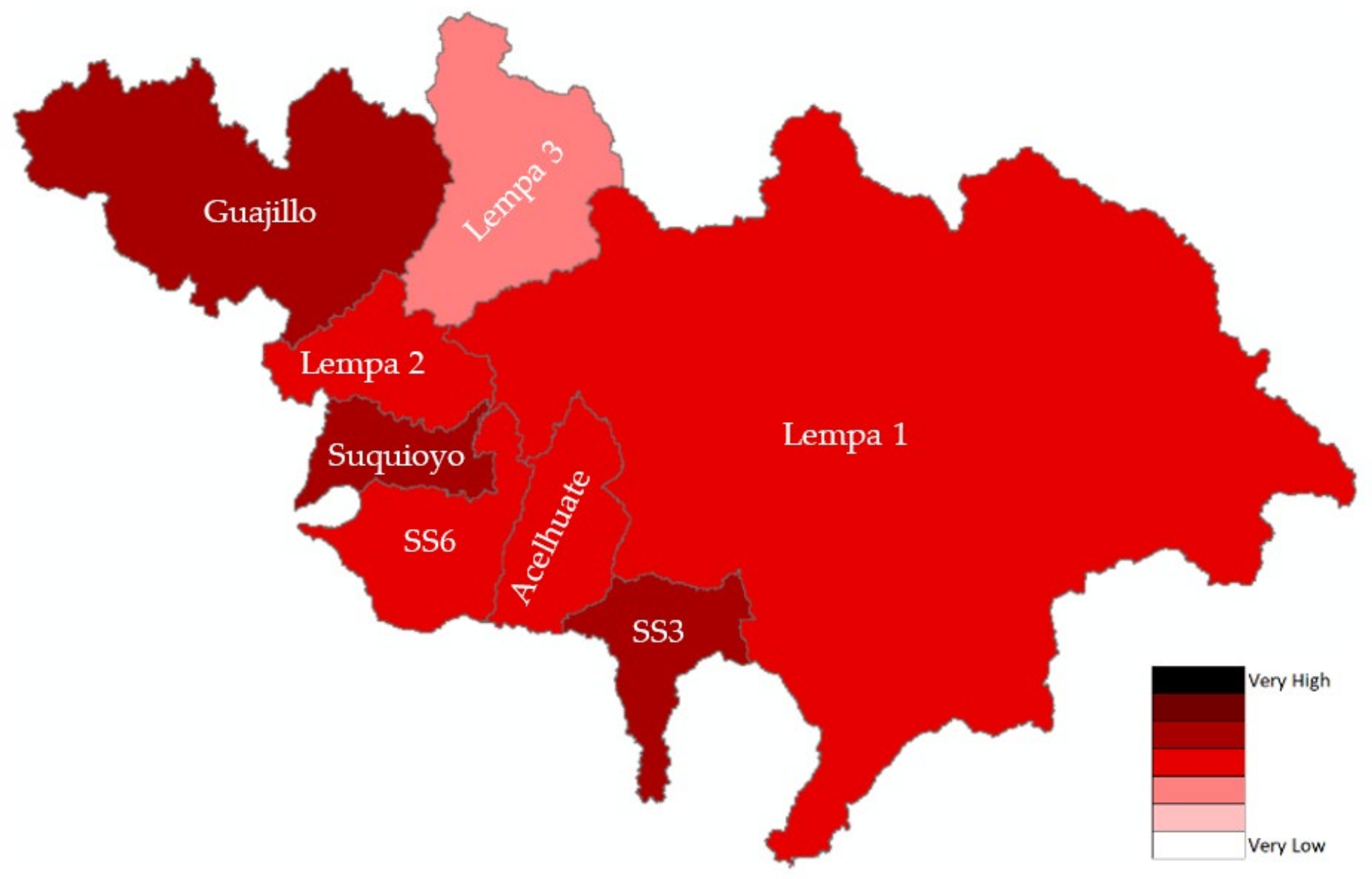
2.1. Case Study
2.2. Data
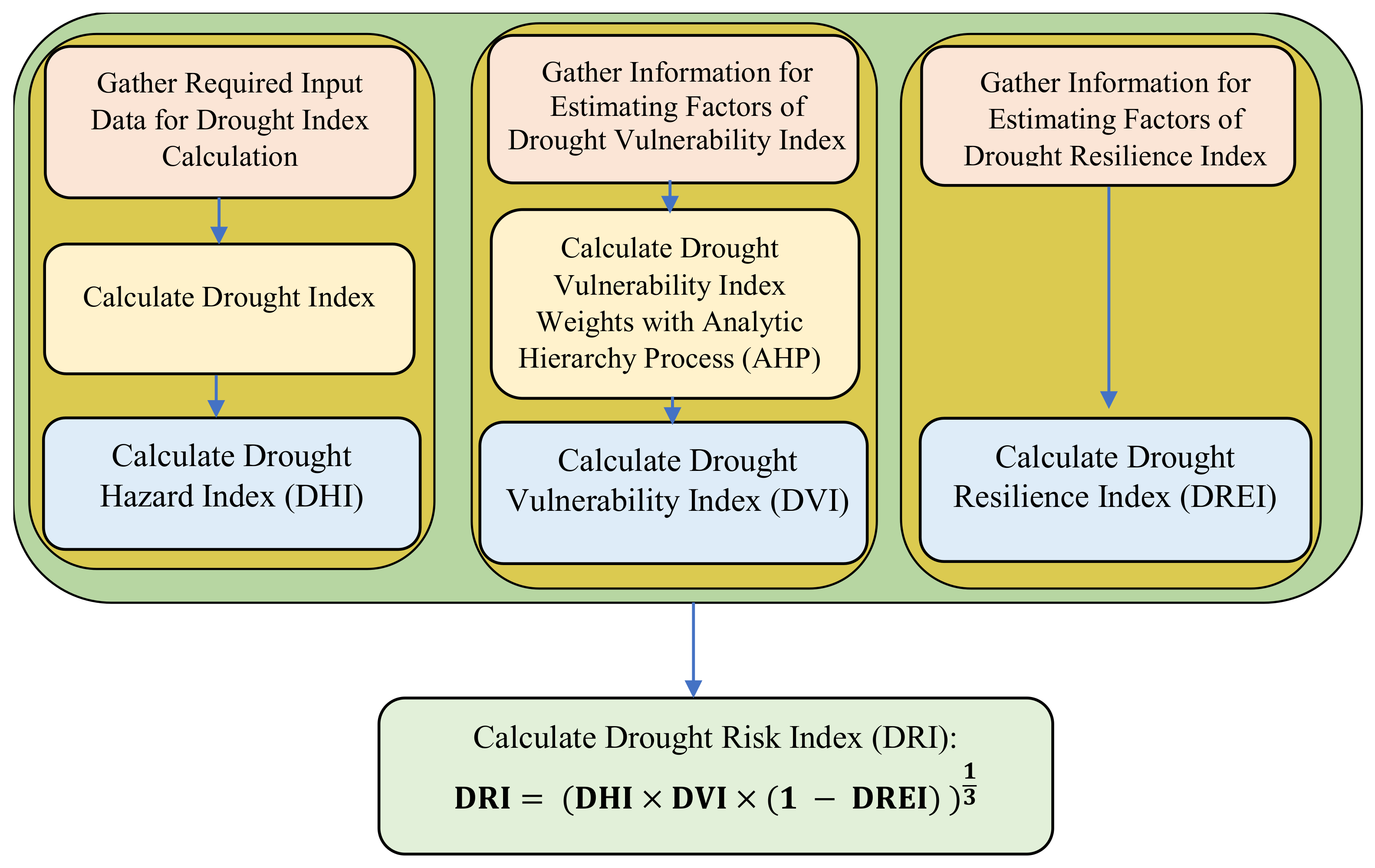
2.3. Drought Risk Assessment
2.3.1. Drought Hazard Index (DHI)
Drought Characteristics
- Drought duration (DD): the number of months between the start and the end of droughts; the start month is considered, and the end month is omitted in calculations [51].
- Drought severity (DS): the integral of the area confined between the horizontal line below the drought index threshold and the start-end points of the drought event. This method of demarcating is based on run theory [53].
- Drought intensity (DI): DS per DD, which suggests that events with less duration and more severity have a greater intensity.
- Drought frequency (DF): the numbers of events per quinquennium, and the numbers of events for the entire period (31 years, from 1980 to 2010).
Standardized Evapotranspiration Deficit Index (SEDI)
2.3.2. Drought Vulnerability Index (DVI)
- Population Density (PD): the number of habitants per km2. Disaster with similar severity will affect more people if they occur in a more populated area.
- Agricultural Occupation (AO): the percentage of people working in the agriculture segment, including farmers and agricultural workers. Farmers fail to plant or get less production due to drought.
- Irrigated Land (IL): the percentage of irrigated land to total land. As the supplied water for irrigated land depends on the surface and groundwater resources, the IL factor is directly related to meteorological drought [2,11,60]. IL involves cash crops that usually are dependent on irrigation. Usually, the presence of irrigation avoids water stress in the crop fields in comparison to rainfed. At the same time, IL still represents the system’s vulnerability to lack of supplied water due to droughts [61]. We employed a systematic approach that considers all parts of the system, not the separate ones.
- Soil Water holding Capacity (SWC): the difference in water content between field capacity and permanent wilting point, which shows soil’s ability to buffer crops during periods of deficit moisture.
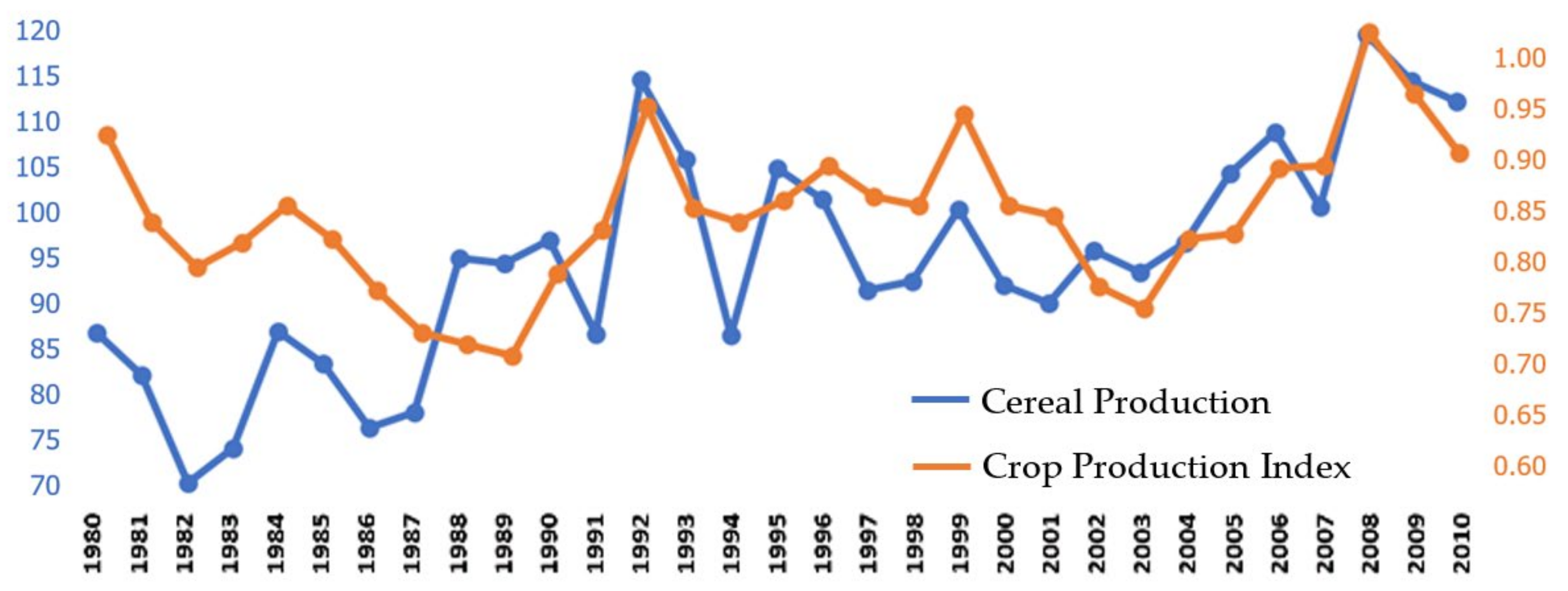
- Food Production (FP): the amount of food, i.e., food crops that are considered edible and contain nutrients, produced in metric tons per square kilometer. Droughts in higher food production areas will have a higher negative impact on the economy.
2.3.3. Drought Resilience Index (DREI)
- Governance (Go): The stability and effectiveness of institutional structures to provide equitable public services, freedom in selecting government, and enforcement of laws to prevent and control crime and violence. The total number of voter participation, violent crimes, extortion, and threats per 10,000 populations, as well as the percentage of householders that receive trash collection, are five components that create the Go factor [28,30].
- Infrastructure (In): The ability to exchange information and physically distribute goods and services (Transportation and Health Care). Three healthcare infrastructure components including the number of physicians, nurses, midwives, and hospital beds per 10,000 population, and two transportation infrastructure components including the length of road and rail lines by total land area and the number of ports and airports per 10,000 km2 land area [27], and two communicational infrastructure components including the percentage of householders with a fixed phone line and percentage of householders with at least one cellular phone [69] are the seven components creating the In factor [30].
- Environmental capacity (EnC): The environment’s ability to recover and maintain species health, biodiversity, and critical ecosystem services after impact. The percentage of total land area that is protected represents this factor [30].
3. Results
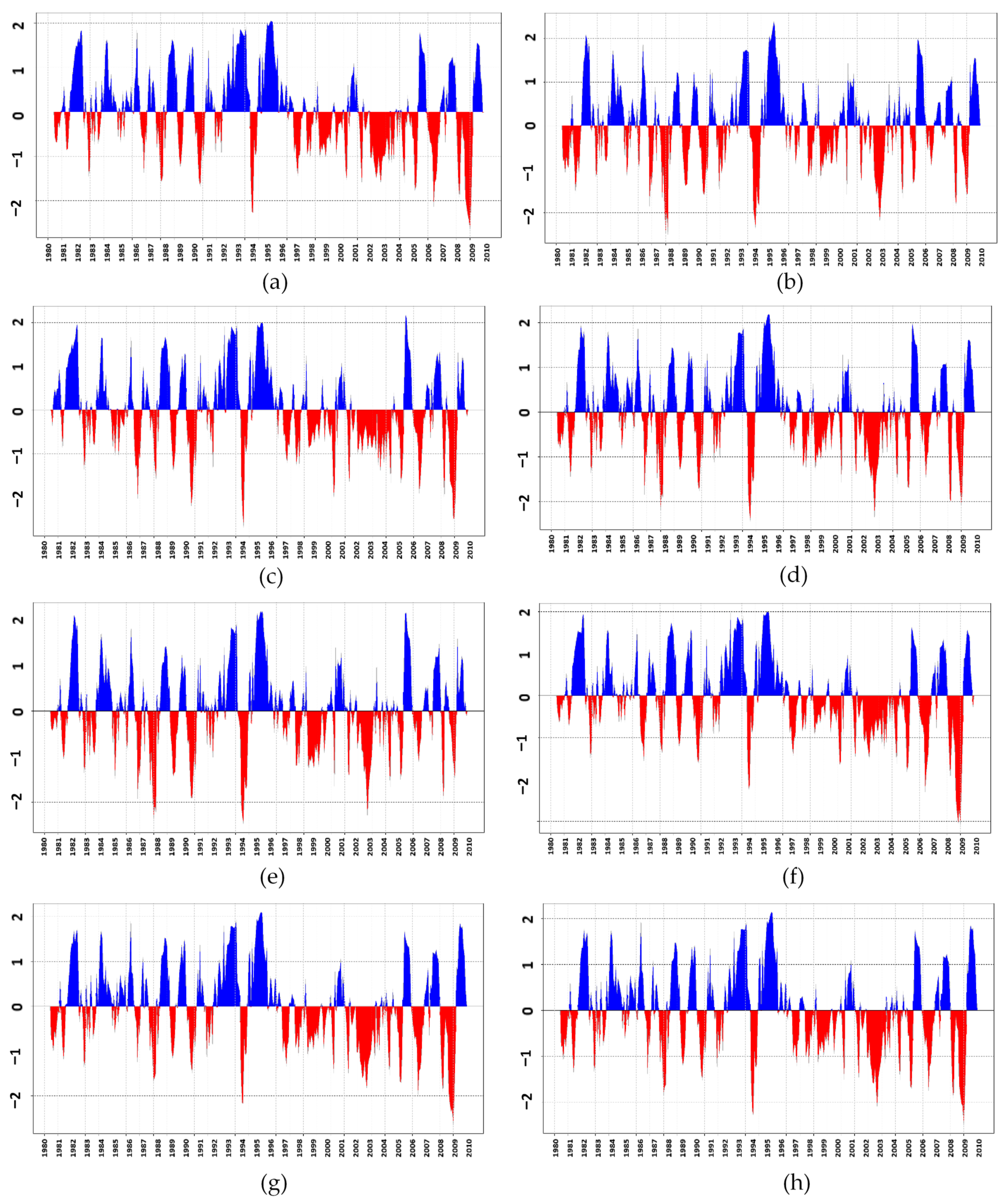
3.1. Drought Index
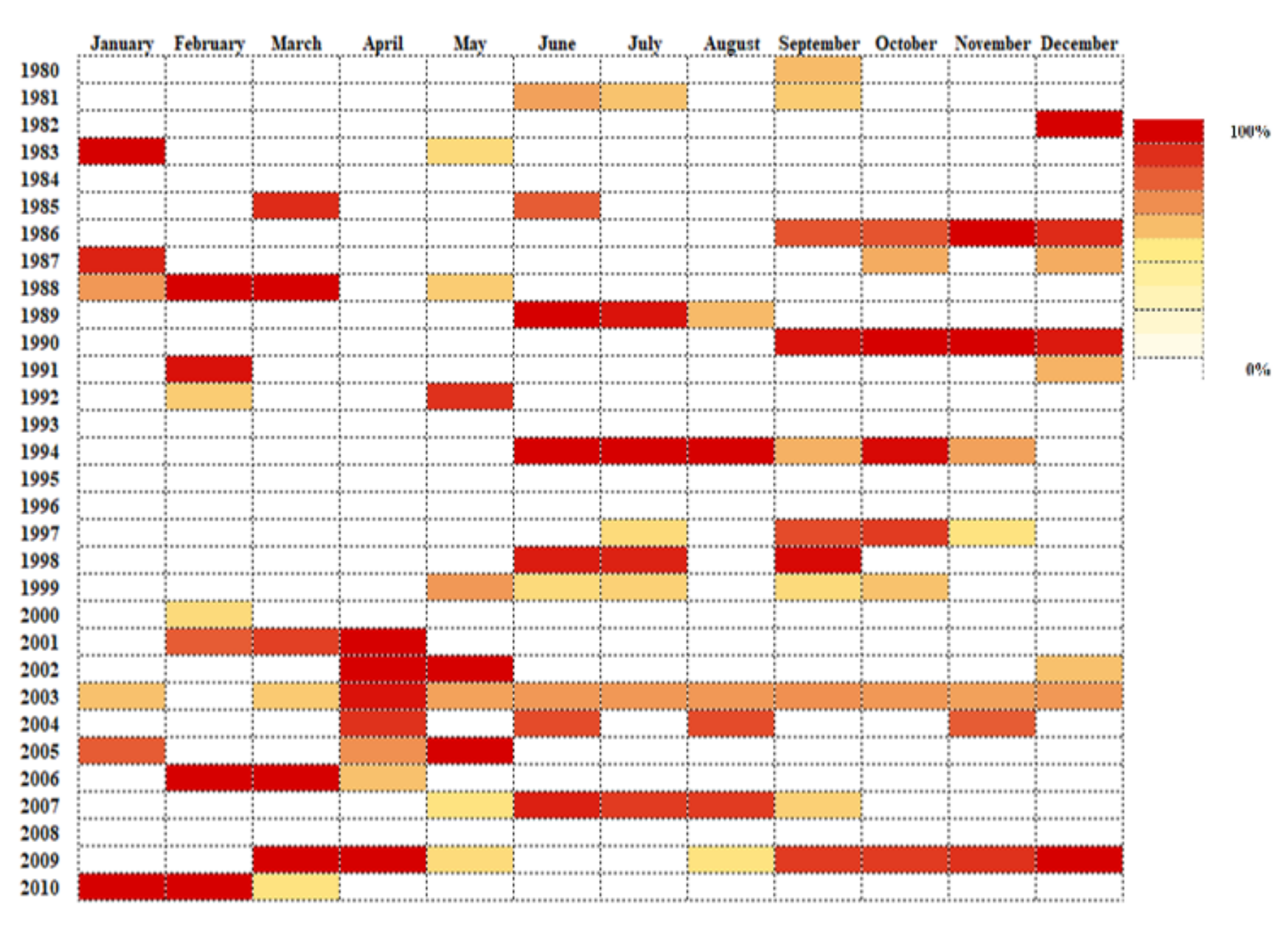
3.2. Drought Characteristics
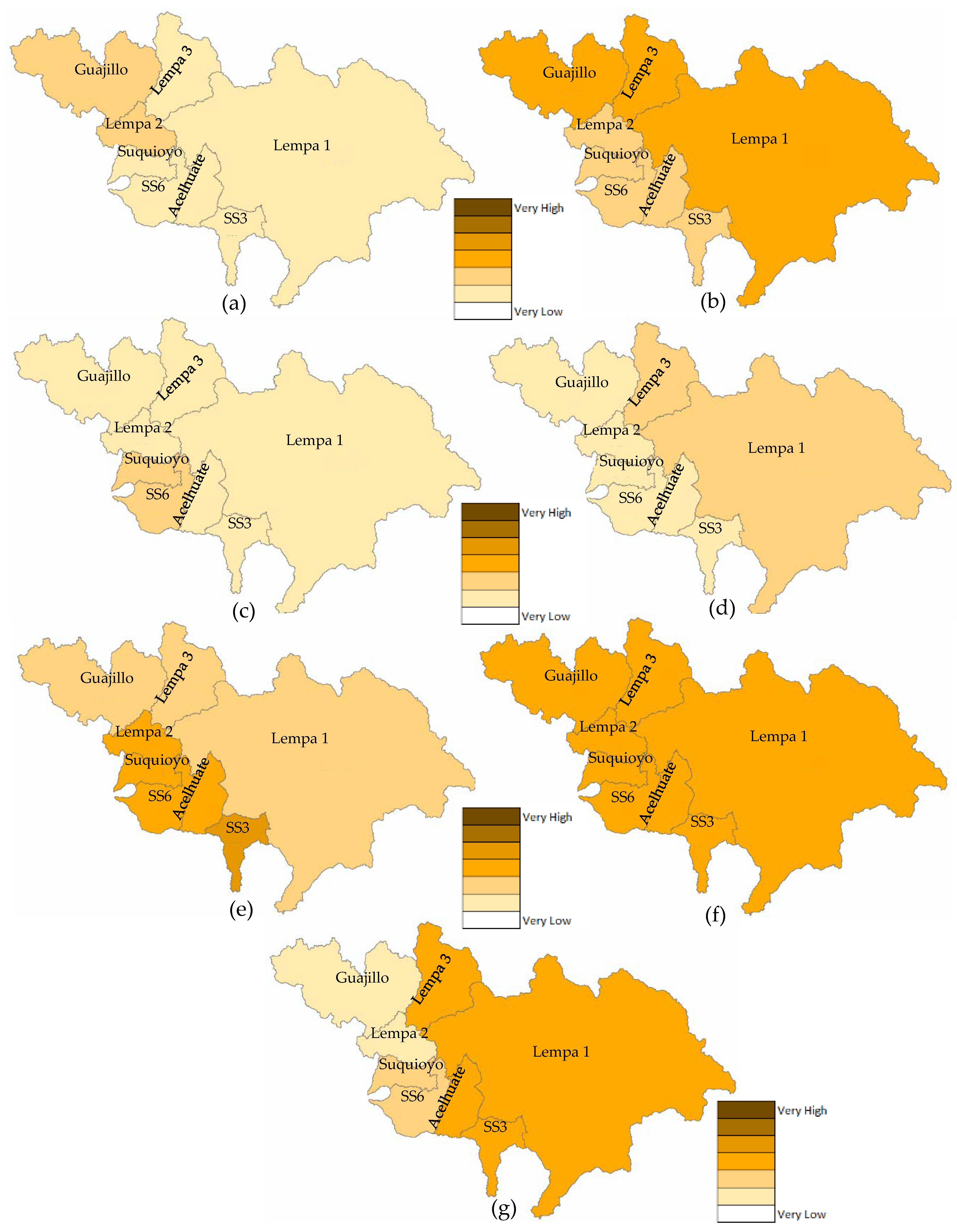
3.3. Percentage of Drought Area
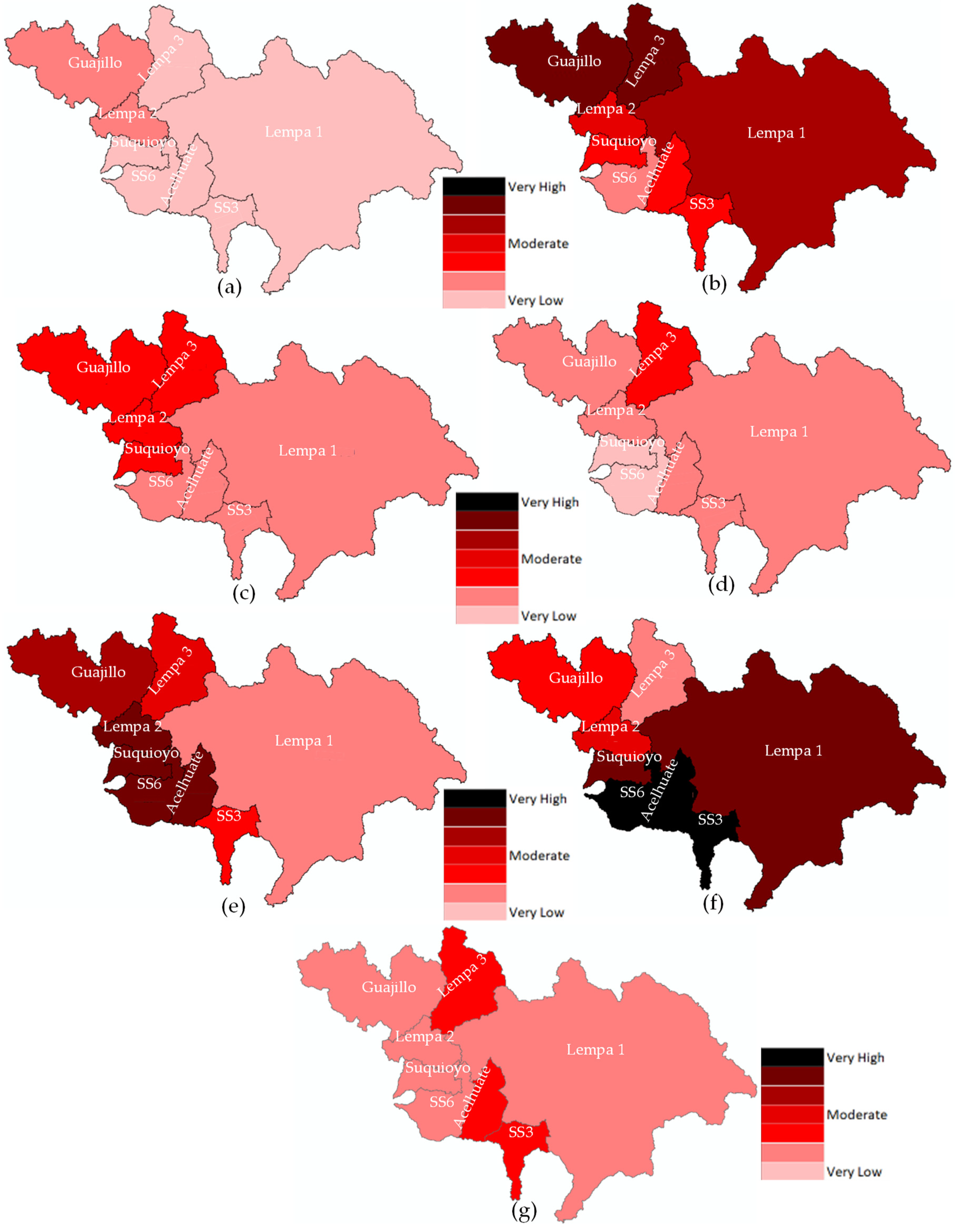
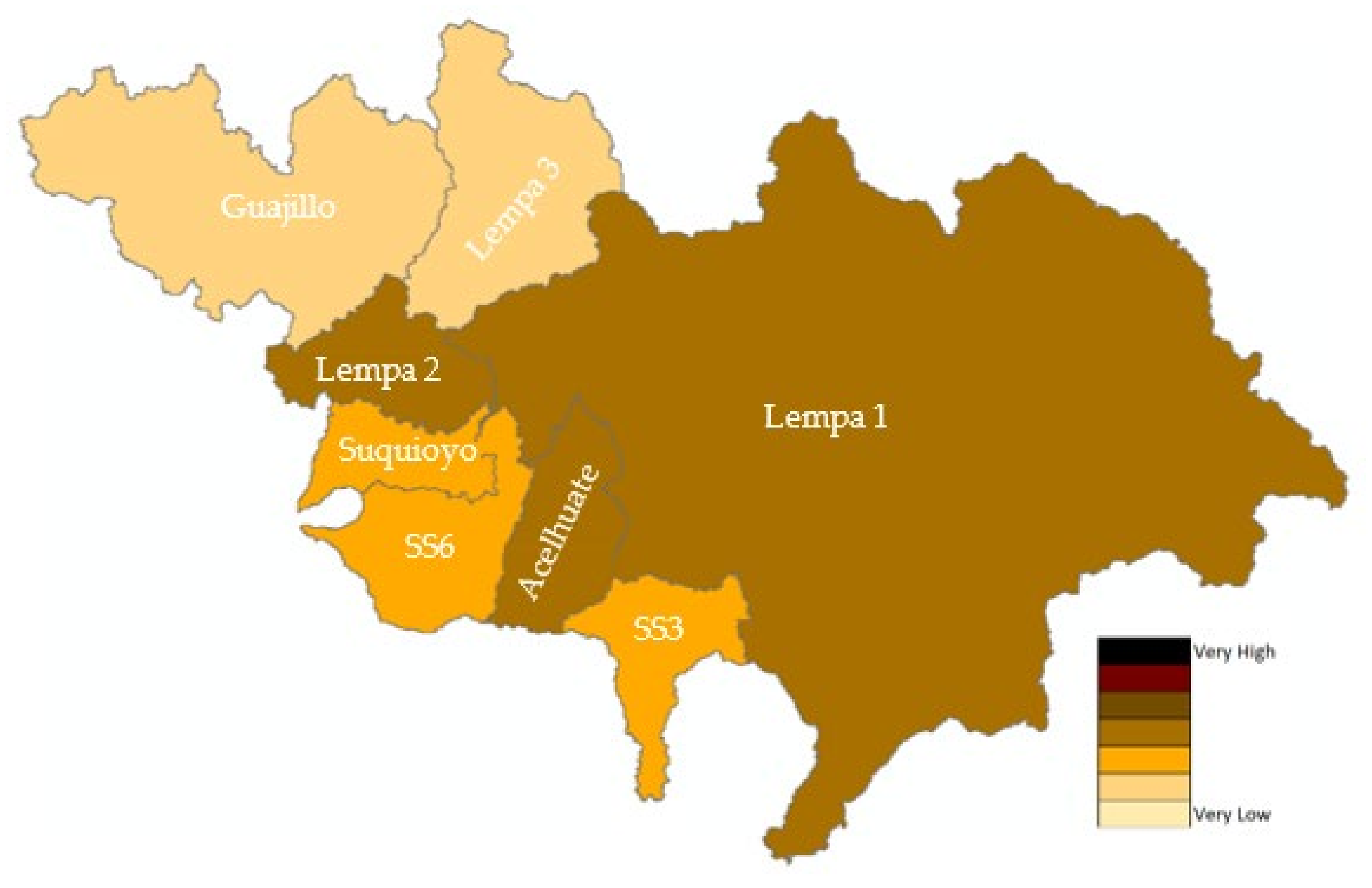
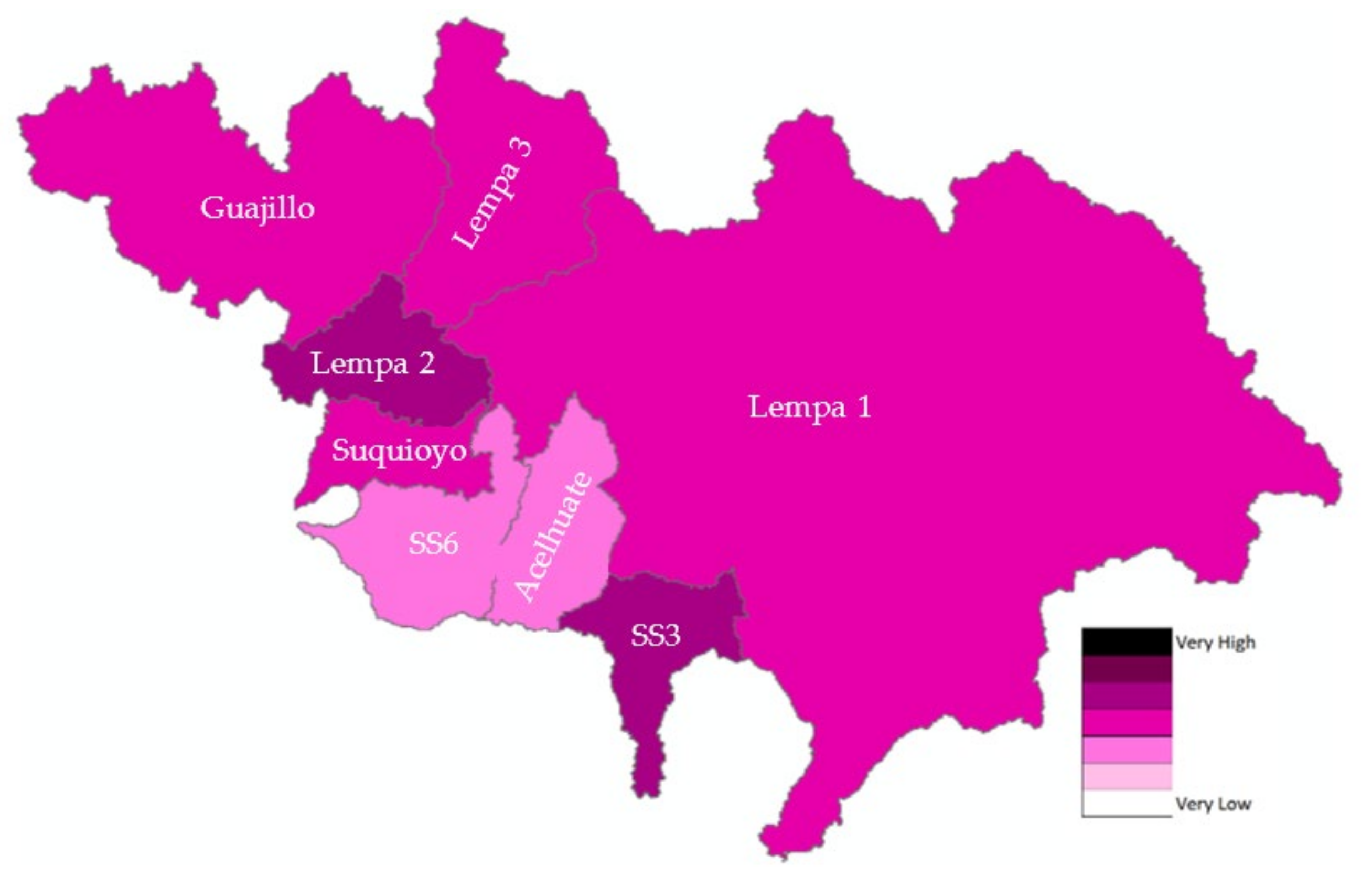
3.4. Drought Risk Assessment
4. Discussion
4.1. Calculation of Droughts and Their Characteristics
4.2. Drought Risk Assessment
4.3. Strengths and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Santos, C.A.G.; Neto, R.M.B.; Nascimento, T.V.M.D.; da Silva, R.M.; Mishra, M.; Frade, T.G. Geospatial drought severity analysis based on PERSIANN-CDR-estimated rainfall data for Odisha state in India (1983–2018). Sci. Total Environ. 2021, 750, 141258. [Google Scholar] [CrossRef] [PubMed]
- García-León, D.; Standardi, G.; Staccione, A. An integrated approach for the estimation of agricultural drought costs. Land Use Policy 2021, 100, 104923. [Google Scholar] [CrossRef]
- Gaitán, E.; Monjo, R.; Pórtoles, J.; Pino-Otín, M.R. Impact of climate change on drought in Aragon (NE Spain). Sci. Total Environ. 2020, 740, 140094. [Google Scholar] [CrossRef] [PubMed]
- Haldar, A.; Alam, A.; Satpati, L. Habitat, Ecology and Ekistics; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Liu, Y.; Chen, J. Future global socioeconomic risk to droughts based on estimates of hazard, exposure, and vulnerability in a changing climate. Sci. Total Environ. 2021, 751, 142159. [Google Scholar] [CrossRef]
- Diaz, V.; Perez, G.A.C.; Van Lanen, H.A.; Solomatine, D.; Varouchakis, E.A. An approach to characterise spatiotemporal drought dynamics. Adv. Water Resour. 2020, 137, 103512. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Miralles, D.G.; Domínguez-Castro, F.; Azorin-Molina, C.; El Kenawy, A.; McVicar, T.R.; Tomás-Burguera, M.; Beguería, S.; Maneta, M.; Peña-Gallardo, M. Global Assessment of the Standardized Evapotranspiration Deficit Index (SEDI) for Drought Analysis and Monitoring. J. Clim. 2018, 31, 5371–5393. [Google Scholar] [CrossRef]
- Shahid, S.; Behrawan, H. Drought risk assessment in the western part of Bangladesh. Nat. Hazards 2008, 46, 391–413. [Google Scholar] [CrossRef]
- Blauhut, V. The triple complexity of drought risk analysis and its visualisation via mapping: A review across scales and sectors. Earth Sci. Rev. 2020, 210, 103345. [Google Scholar] [CrossRef]
- Hagenlocher, M.; Meza, I.; Anderson, C.C.; Min, A.; Renaud, F.G.; Walz, Y.; Siebert, S.; Sebesvari, Z. Drought vulnerability and risk assessments: State of the art, persistent gaps, and research agenda. Environ. Res. Lett. 2019, 14, 083002. [Google Scholar] [CrossRef]
- Guo, H.; Wang, R.; Garfin, G.M.; Zhang, A.; Lin, D.; Liang, Q.; Wang, J. Rice drought risk assessment under climate change: Based on physical vulnerability a quantitative assessment method. Sci. Total Environ. 2021, 751, 141481. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Hua, L.; Yan, Z. Datasets of meteorological drought events and risks for the developing countries in Eurasia. Big Earth Data 2020, 4, 191–223. [Google Scholar] [CrossRef] [Green Version]
- Sena, A.; Ebi, K.L.; Freitas, C.; Corvalan, C.; Barcellos, C. Indicators to measure risk of disaster associated with drought: Implications for the health sector. PLoS ONE 2017, 12, e0181394. [Google Scholar] [CrossRef]
- Dabanli, I.J.N.H.; Discussions, E.S.S. Drought Risk Assessment by Using Drought Hazard and Vulnerability Indexes. Nat. Hazards Earth Syst. Sci. Discuss. 2018, 1–15. [Google Scholar] [CrossRef]
- Zhang, L.; Song, W.; Song, W. Assessment of Agricultural Drought Risk in the Lancang-Mekong Region, South East Asia. Int. J. Environ. Res. Public Health 2020, 17, 6153. [Google Scholar] [CrossRef]
- Adedeji, O.; Olusola, A.; James, G.; Shaba, H.A.; Orimoloye, I.R.; Singh, S.K.; Adelabu, S. Early warning systems development for agricultural drought assessment in Nigeria. Environ. Monit. Assess. 2020, 192, 1–21. [Google Scholar] [CrossRef]
- Rose, M.A.J.; Chithra, N.R. Evaluation of temporal drought variation and projection in a tropical river basin of Kerala. J. Water Clim. Chang. 2020, 11, 115–132. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Kuo, E.-D.; Chi, W.-J. Analysis of Meteorological Drought Resilience and Risk Assessment of Groundwater Using Signal Analysis Method. Water Resour. Manag. 2021, 35, 179–197. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef]
- Chambers, R. Vulnerability, Coping and Policy (Editorial Introduction). IDS Bull. 2006, 37, 33–40. [Google Scholar] [CrossRef] [Green Version]
- Sajjad, M.; Lin, N.; Chan, J.C. Spatial heterogeneities of current and future hurricane flood risk along the U.S. Atlantic and Gulf coasts. Sci. Total Environ. 2020, 713, 136704. [Google Scholar] [CrossRef] [PubMed]
- Marasco, S.; Cardoni, A.; Noori, A.Z.; Kammouh, O.; Domaneschi, M.; Cimellarof, G.P. Integrated platform to assess seismic resilience at the community level. Sustain. Cities Soc. 2021, 64, 102506. [Google Scholar] [CrossRef]
- Sajjad, M.; Chan, J.C.; Chopra, S.S. Rethinking disaster resilience in high-density cities: Towards an urban resilience knowledge system. Sustain. Cities Soc. 2021, 102850. [Google Scholar] [CrossRef]
- Cutter, S.L.; Barnes, L.; Berry, M.; Burton, C.; Evans, E.; Tate, E.; Webb, J. A place-based model for understanding community resilience to natural disasters. Glob. Environ. Chang. 2008, 18, 598–606. [Google Scholar] [CrossRef]
- Cutter, S.L.; Ash, K.D.; Emrich, C.T. The geographies of community disaster resilience. Glob. Environ. Chang. 2014, 29, 65–77. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction. Global Assessment Report (GAR) on Disaster Risk Reduction. Available online: https://gar.undrr.org/ (accessed on 29 September 2020).
- Hughey, E.; Morath, D.; Mielbrecht, S.; Gray, H.; Todd, B.; Stelow, C.; Fernandes, P.; Leuck, R.; Green, J. National Disaster Preparedness Baseline Assessment: El Salvador. Available online: https://www.pdc.org/wp-content/uploads/2018/06/NDPBA_ElSalvador_Final_Report_English.pdf (accessed on 6 August 2020).
- Armenteras, D.; Gibbes, C.; Vivacqua, C.A.; Espinosa, J.S.; Duleba, W.; Goncalves, F.; Castro, C. Interactions between Climate, Land Use and Vegetation Fire Occurrences in El Salvador. Atmosphere 2016, 7, 26. [Google Scholar] [CrossRef] [Green Version]
- Jennewein, J.S.; Jones, K.W. Examining ‘willingness to participate’in community-based water resource management in a transboundary conservation area in Central America. Water Policy 2016, 18, 1334–1352. [Google Scholar] [CrossRef]
- Hernández, W. Nacimiento y Desarrollo del río Lempa; Servicio Nacional de Estudios Territoriales (MARN/SNET): San Salvador, El Salvador, 2005. [Google Scholar]
- Helman, P.; Tomlinson, R. Two Centuries of Climate Change and Climate Variability, East Coast Australia. J. Mar. Sci. Eng. 2018, 6, 3. [Google Scholar] [CrossRef] [Green Version]
- El Salvador’s Ministry of Environment and Natural Resources (MARN). Water Resources Maps. Available online: https://web.archive.org/web/20090422151648/http://snet.gob.sv/cd2/SeccionSIG/map_hi.htm (accessed on 15 March 2019).
- Anticó, E.; Cot, S.; Ribó, A.; Rodríguez-Roda, I.; Fontàs, C. Survey of Heavy Metal Contamination in Water Sources in the Municipality of Torola, El Salvador, through In Situ Sorbent Extraction. Water 2017, 9, 877. [Google Scholar] [CrossRef] [Green Version]
- Seiber, J.; Purkey, D. WEAP—Water Evaluation and Planning System User Guide for WEAP 2015; Stockholm Environmental Institute: Boston, MA, USA, 2015. [Google Scholar]
- El Salvador’s Ministry of Environment and Natural Resources (MARN). Available online: https://www.marn.gob.sv/ (accessed on 19 March 2019).
- Oti, J.O.; Kabo-Bah, A.T.; Ofosu, E. Hydrologic response to climate change in the Densu River Basin in Ghana. Heliyon 2020, 6, e04722. [Google Scholar] [CrossRef] [PubMed]
- Khoshnazar, A.; Nasrabadi, T.; Abbasi Maedeh, P. Evaluating the efficiency of artificial neural network in prediction of Electrical conductivity of Zarrinehroud River. Human Environ. 2012, 10, 1–16. [Google Scholar]
- Sajjad, M.; Chan, J.C.; Lin, N. Incorporating natural habitats into coastal risk assessment frameworks. Environ. Sci. Policy 2020, 106, 99–110. [Google Scholar] [CrossRef]
- MacKenzie, C.A. Summarizing Risk Using Risk Measures and Risk Indices. Risk Anal. 2014, 34, 2143–2162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Commission, J.R.C.-E. Handbook on Constructing Composite Indicators: Methodology and User Guide; OECD Publishing: Paris, France, 2008. [Google Scholar]
- Waldinger, M.D.; Zwinderman, A.H.; Olivier, B.; Schweitzer, D.H. Geometric Mean IELT and Premature Ejaculation: Appropriate Statistics to Avoid Overestimation of Treatment Efficacy. J. Sex. Med. 2008, 5, 492–499. [Google Scholar] [CrossRef]
- Abyani, M.; Asgarian, B.; Zarrin, M. Sample geometric mean versus sample median in closed form framework of seismic reliability evaluation: A case study comparison. Earthq. Eng. Eng. Vib. 2019, 18, 187–201. [Google Scholar] [CrossRef]
- Khalifeh, S.; Khoshnazar, A. Evaluation of Water Quality in Zarrinehrood River Using the Standard Quality Index of Iran’s Surface Water Resources. Water Wastewater Sci. Eng. 2018, 3, 22–34. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Li, M.; Ma, Z.; Yang, Q.; Lv, M.; Clark, R. Assessment of an Evapotranspiration Deficit Drought Index in Relation to Impacts on Ecosystems. Adv. Atmos. Sci. 2019, 36, 1273–1287. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Lai, C. Severe drought events inducing large decrease of net primary productivity in mainland China during 1982–2015. Sci. Total Environ. 2020, 703, 135541. [Google Scholar] [CrossRef] [PubMed]
- Veettil, A.V.; Mishra, A.K. Multiscale hydrological drought analysis: Role of climate, catchment and morphological variables and associated thresholds. J. Hydrol. 2020, 582, 124533. [Google Scholar] [CrossRef]
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, duration and severity of drought in the Semiarid Northeast Brazil region. Int. J. Clim. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Oikonomou, P.D.; Karavitis, C.A.; Tsesmelis, D.E.; Kolokytha, E.; Maia, R. Drought Characteristics Assessment in Europe over the Past 50 Years. Water Resour. Manag. 2020, 34, 4757–4772. [Google Scholar] [CrossRef]
- Yevjevich, V.M. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. Ph.D. Dissertation, Colorado State University, Fort Collins, CO, USA, 1967. [Google Scholar]
- Kim, D.; Rhee, J. A drought index based on actual evapotranspiration from the Bouchet hypothesis. Geophys. Res. Lett. 2016, 43, 10–277. [Google Scholar] [CrossRef]
- Mercado, V.D.; Perez, G.C.; Solomatine, D.; Van Lanen, H.A. Spatio-temporal Analysis of Hydrological Drought at Catchment Scale Using a Spatially-distributed Hydrological Model. Procedia Eng. 2016, 154, 738–744. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate Computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef] [Green Version]
- Le Cozannet, G.; Nicholls, R.J.; Hinkel, J.; Sweet, W.V.; McInnes, K.L.; Van De Wal, R.S.W.; Slangen, A.B.A.; Lowe, J.A.; White, K.D. Sea Level Change and Coastal Climate Services: The Way Forward. J. Mar. Sci. Eng. 2017, 5, 49. [Google Scholar] [CrossRef] [Green Version]
- Vaughan, M. The Story of an African Famine: Gender and Famine in Twentieth-Century Malawi; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Yodmani, S. Disaster Risk Management and Vulnerability Reduction: Protecting the Poor. In Proceedings of the Social Protection Workshop 6: Protecting Communities—Social Funds and Disaster Management, the Asian Development Bank, Manila, Philippines, 5–9 February 2001. [Google Scholar]
- Zhu, X.; Hou, C.; Xu, K.; Liu, Y. Establishment of agricultural drought loss models: A comparison of statistical methods. Ecol. Indic. 2020, 112, 106084. [Google Scholar] [CrossRef]
- Zachariah, M.; Mondal, A.; Das, M.; AchutaRao, K.M.; Ghosh, S. On the role of rainfall deficits and cropping choices in loss of agricultural yield in Marathwada, India. Environ. Res. Lett. 2020, 15, 094029. [Google Scholar] [CrossRef]
- El Salvador’s Department of Statistics and Census. Available online: https://www.digestyc.gob.sv/ (accessed on 20 June 2020).
- National Institute of Statistics Guatemala. Available online: https://www.ine.gob.gt/ine/ (accessed on 27 July 2020).
- Honduras’s National Institute of Statistics. Available online: https://www.ine.gob.hn/V3/ (accessed on 18 August 2020).
- The World Bank Group. Available online: https://www.worldbank.org/en/search?q=data¤tTab=1&label=2473192505 (accessed on 9 January 2021).
- Assessment of Water Holding Capacity of Soils Map. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/use/worldsoils/?cid=nrcs142p2_054022 (accessed on 26 January 2021).
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Pacific Disaster Center. Available online: https://www.pdc.org/ (accessed on 14 January 2021).
- Cutter, S.L.; Burton, C.G.; Emrich, C.T. Disaster Resilience Indicators for Benchmarking Baseline Conditions. J. Homel. Secur. Emerg. Manag. 2010, 7, 1–24. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Differences in Spatial Patterns of Drought on Different Time Scales: An Analysis of the Iberian Peninsula. Water Resour. Manag. 2006, 20, 37–60. [Google Scholar] [CrossRef]
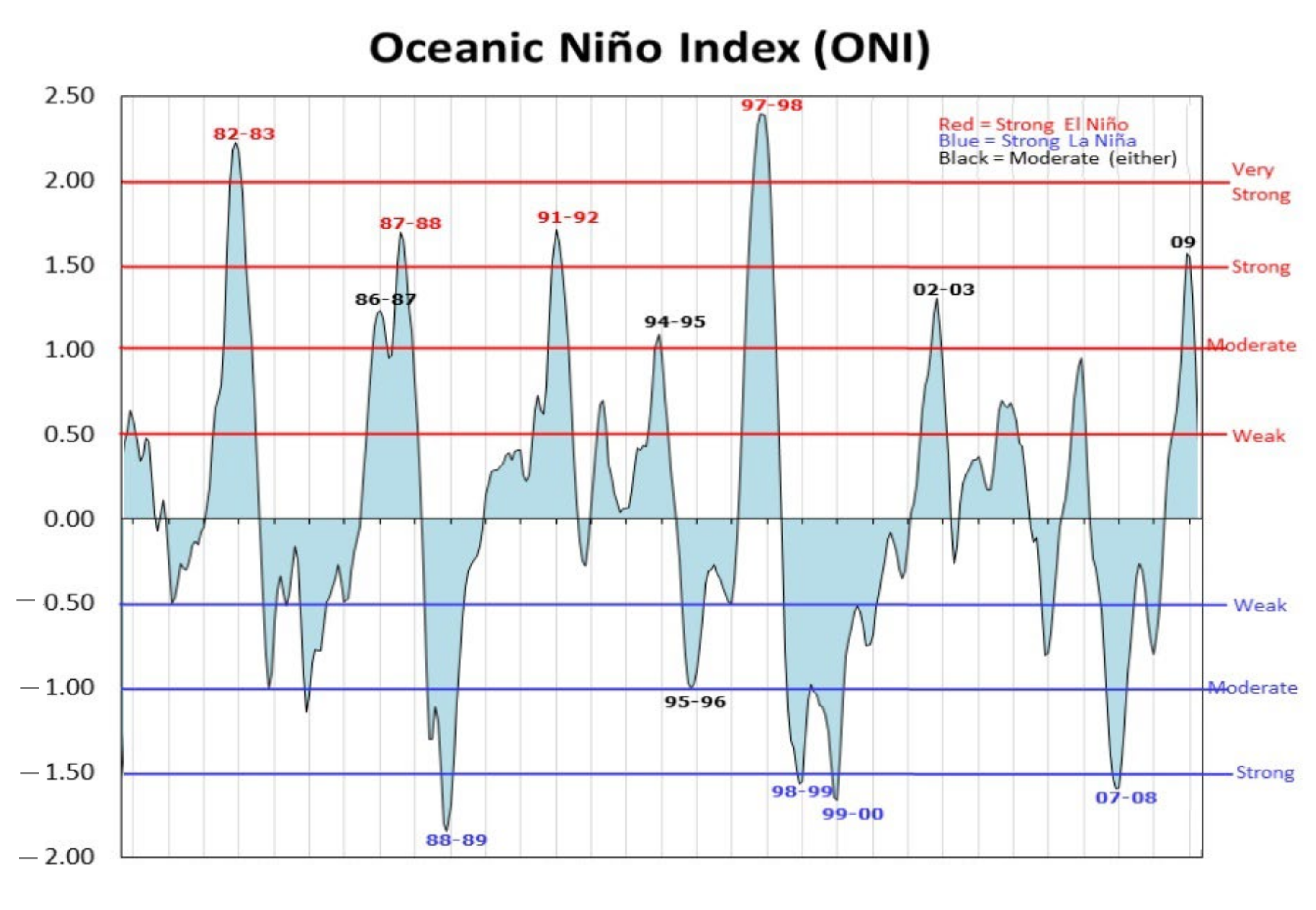
- Golden Gate Weather Services. El Niño and La Niña Years and Intensities Based on Oceanic Niño Index (ONI). Available online: https://ggweather.com/enso/oni.htm (accessed on 22 February 2021).
- Karim, M.R.; Rahman, M.A. Drought risk management for increased cereal production in Asian least developed countries. Weather Clim. Extrem. 2015, 7, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Lewis, J.E.; Rowland, J.; Nadeau, A. Estimating maize production in Kenya using NDVI: Some statistical considerations. Int. J. Remote Sens. 1998, 19, 2609–2617. [Google Scholar] [CrossRef]
- The World Bank Group. Cereal Production (Metric Tons)—El Salvador. Available online: https://data.worldbank.org/indicator/AG.PRD.CREL.MT?locations=SV (accessed on 19 February 2021).
- The World Bank Group. Indicators. Available online: https://data.worldbank.org/indicator (accessed on 20 February 2021).




| DRI, DHI, DVI, and DREI Values | DRI, DHI, and DVI Category | DREI Category |
|---|---|---|
| 0 to 0.15 | Very Low | Very High |
| 0.15 to 0.29 | Low | High |
| 0.29 to 0.43 | Relatively Low | Relatively High |
| 0.43 to 0.57 | Moderate | Moderate |
| 0.57 to 0.71 | Relatively High | Relatively Low |
| 0.71 to 0.85 | High | Low |
| 0.85 to 1 | Very High | Very Low |
| Drought Index Value | Category | Weight (Dw) | Occurrence Probability | Rating (Dr) |
|---|---|---|---|---|
| ≤−0.8 | Extreme (E) | 4 | Very high | 4 |
| High | 3 | |||
| Low | 2 | |||
| Very low | 1 | |||
| −0.8 to −0.63 | Severe (S) | 3 | Very high | 4 |
| High | 3 | |||
| Low | 2 | |||
| Very low | 1 | |||
| −0.63 to −0.42 | Moderate (M) | 2 | Very high | 4 |
| High | 3 | |||
| Low | 2 | |||
| Very low | 1 | |||
| −0.42 to 0 | Low (L) | 1 | Very high | 4 |
| High | 3 | |||
| Low | 2 | |||
| Very low | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoshnazar, A.; Corzo Perez, G.A.; Diaz, V. Spatiotemporal Drought Risk Assessment Considering Resilience and Heterogeneous Vulnerability Factors: Lempa Transboundary River Basin in The Central American Dry Corridor. J. Mar. Sci. Eng. 2021, 9, 386. https://doi.org/10.3390/jmse9040386
Khoshnazar A, Corzo Perez GA, Diaz V. Spatiotemporal Drought Risk Assessment Considering Resilience and Heterogeneous Vulnerability Factors: Lempa Transboundary River Basin in The Central American Dry Corridor. Journal of Marine Science and Engineering. 2021; 9(4):386. https://doi.org/10.3390/jmse9040386
Chicago/Turabian StyleKhoshnazar, Ali, Gerald A. Corzo Perez, and Vitali Diaz. 2021. "Spatiotemporal Drought Risk Assessment Considering Resilience and Heterogeneous Vulnerability Factors: Lempa Transboundary River Basin in The Central American Dry Corridor" Journal of Marine Science and Engineering 9, no. 4: 386. https://doi.org/10.3390/jmse9040386
APA StyleKhoshnazar, A., Corzo Perez, G. A., & Diaz, V. (2021). Spatiotemporal Drought Risk Assessment Considering Resilience and Heterogeneous Vulnerability Factors: Lempa Transboundary River Basin in The Central American Dry Corridor. Journal of Marine Science and Engineering, 9(4), 386. https://doi.org/10.3390/jmse9040386








