A Barotropic Solver for High-Resolution Ocean General Circulation Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. NEMO Model
2.2. Barotropic Solver
2.3. NEMO PCG Solver
2.4. CA-PCG Solver
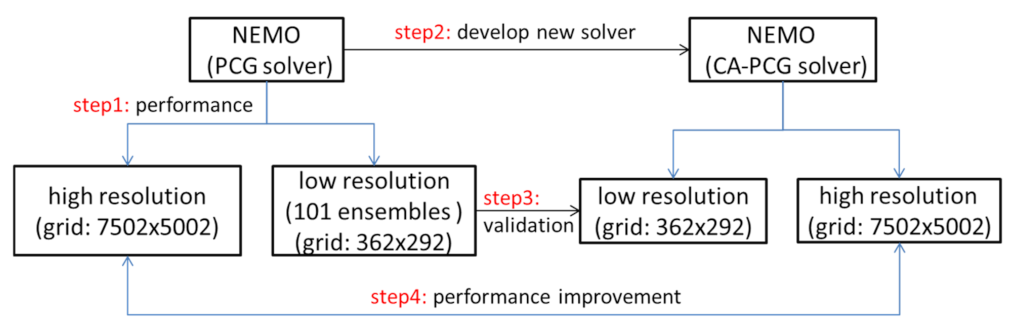
2.5. Experimental Description
2.5.1. Low-Resolution Simulation
2.5.2. High-Resolution Simulation
2.6. Community Earth System Model (CESM) Port-Verification Tool
3. Results
3.1. Validity of the Results Using the CA-PCG Solver
3.2. Performance of the NEMO Model Using the CA-PCG Solver
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Algorithm A1. Preconditioned conjugate gradient (PCG) [22]. |
| Required: Coefficient matrix , which is a definite positive symmetric matrix, preconditioner (diagonal matrix of the diagonal elements of A), initial guess value and vector associated with grid block |
| 1. Initialization: Given initial guess , |
| 2. ,,, /* initial the value */ |
| 3. () /* preconditioner */ |
| 4. For until convergence |
| 5. /* matrix-vector multiplication */ |
| 6. /* inner product, global reduction */ |
| 7. /* inner product, global reduction */ |
| 8. |
| 9. |
| 10. |
| 11. |
| 12. |
| 13. /* update vector */ |
| 14. /* update vector */ |
| 15. Update_Halo() /* boundary communication*/ |
| 16. End for /* the result is */ |
- N × N is the global domain size.
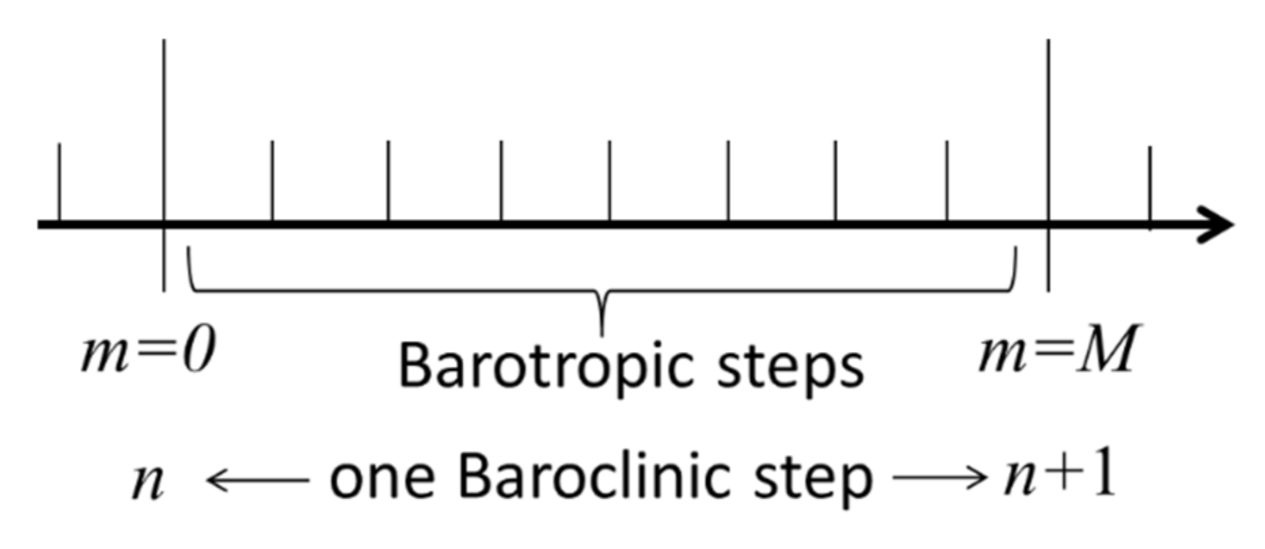
- The global domain is divided into m x m blocks with a size of n x n ().
- The p = m × m processes occur, and each process corresponds to exactly one grid block. Then, the total time of the barotropic mode is the execution time of the PCG solver on each block.
- K is the iteration number.
- Step 5, with a total of 9n operations from one matrix-vector multiplication (MVM).
- Steps 6 and 7, with a total of 6n operations, from two vector–vector multiplication (VVMs) for inner products, two additional inverse operations of the preconditioner, which has the same cost as the preconditioner (for the diagonal preconditioner, its operation number is n), and two masking operations for land point exclusion.
- Steps 10, 11, 13, and 14, with a total of 4n operations, from four vector-scaling operations.
Appendix C
| Algorithm A2. Communication-avoiding Krylov subspace method with a PCG (CA-PCG) |
| CA-PCG consists of a two-level nested loop (k,j), outer loop indexed by k, and inner loop index , given initial PCG vectors , , and : outer loop: prepare the required info for iterations over and , inner loop: update the PCG vectors with their coordinates in the Krylov subspace |
| 1. Initialization: Given initial guess and set residual , , |
| 2. /* preconditioner */ |
| 3. For =, until convergence done |
| 4. /* construct and compute , a polynomial of degree j with and , */ /* matrix-vector multiplication */ |
| 5. /* boundary communication */ |
| 6. Compute Gram matrix /* inner product with global reduction */ |
| 7. Assemble from , which is a change basis matrix, with all 0 in columns s + 1 and 2s + 1 |
| 8. Initial short vector ,, |
| 9. /* in this paper */ |
| 10. /* inner product, is ready, no global reduction */ |
| 11. /* update short vector */ |
| 12. /* update short vector */ |
| 13. /* inner product, is ready, no global reduction */ |
| 14. /* update short vector */ |
| 15. /* inner loop end */ |
| 16. , , /* update long vectors*/ |
| 17. /* boundary communication */ |
| 18. /* outer loop end, the result is */ |
|
Regarding , satisfies the three-term recurrence via , , and . In this paper, the monomial bases were used, so . |
Appendix D
| CPU | 2*Intel Xeon Scalable Cascade Lake 6248 (2.5 GHz, 20 Cores) |
|---|---|
| L3 cache | 27.5 MB |
| Memory | 12 × Samsung 16 GB DDR4 ECC REG 2666 |
| Interconnect (Network) | Intel OmniPath 100 Gbps |
| Storage | Lustre (NVMe) |
| BIOS settings | 4.1.05 |
| OS/kernel | 3.10.0-1062.el7.x86_64 |
References
- Chassignet, E.P.; Xu, X. Impact of Horizontal Resolution (1/12° to 1/50°) on Gulf Stream Separation, Penetration, and Variability. J. Phys. Oceanogr. 2019, 47, 1999–2021. [Google Scholar] [CrossRef]
- Qiao, F.; Zhao, W.; Yin, X.; Huang, X.; Liu, X.; Shu, Q.; Wang, G.; Song, Z.; Li, X.; Liu, H.; et al. A Highly Effective Global Surface Wave Numerical Simulation with Ultra-High Resolution. In Proceedings of the SC16: International Conference for High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 13–18 November 2016; pp. 46–56. [Google Scholar]
- Zhao, W.; Song, Z.Y.; Qiao, F.L.; Yin, X.Q. High efficient parallel numerical surface wave model based on an irregular quasi-rectangular domain decomposition scheme. Sci. China Earth Sci. 2014, 44, 1049–1058. [Google Scholar] [CrossRef]
- Cohn, S.E.; Dee, D.; Marchesin, D.; Isaacson, E.; Zwas, G. A fully implicit scheme for the barotropic primitive equations. Mon. Weather Rev. 1985, 113, 641–646. [Google Scholar] [CrossRef] [Green Version]
- Dukowicz, J.K.; Smith, R.D. Implicit free-surface method for the Bryan-Cox-Semtner ocean model. J. Geophy. Res. Ocean. 1994, 99, 7991–8014. [Google Scholar] [CrossRef]
- Concus, P.; Golub, G.H.; O’Leary, D.P. Numerical solution of nonlinear elliptic partial differential equations by a generalized conjugate gradient method. Computing 1978, 19, 321–339. [Google Scholar] [CrossRef]
- Concus, M. On computingINV block preconditionings for the conjugate gradient method. BIT 1986, 26, 493–504. [Google Scholar] [CrossRef]
- Smith, R.; Jones, P.; Briegleb, B.; Bryan, F.; Danabasoglu, G.; Dennis, J.; Dukowicz, J.; Eden, C.; Fox-Kemper, B.; Gent, P.; et al. The Parallel Ocean Program (POP) Reference Manual; Tech. Rep. LAUR-10-01853; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010; p. 141. [Google Scholar]
- Madec, G. NEMO Ocean Engine. In Note du Pole de Modelisation; Institut Pierre-Simon Laplace: Paris, France, 2008; p. 27. [Google Scholar]
- Xu, S.; Huang, X.; Oey, L.Y.; Xu, F.; Fu, H.; Zhang, Y.; Yang, G. POM.gpu-v1.0: A GPU-based Princeton Ocean Model. Geosci. Model. Dev. 2015, 8, 2815–2827. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Huang, X.; Baker, A.; Tseng, Y.; Bryan, F.; Dennis, J.; Yang, G. Improving the scalability of the ocean barotropic solver in the community earth system model. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Austin, TX, USA, 15 November 2015; pp. 1–12. [Google Scholar]
- Madec, G.; Delecluse, P.; Imbard, M.; Levy, C. Opa 8 ocean general circulation model reference manual. Tech. Rep. 1998, 11, 91. [Google Scholar]
- Carson, E. Communication-Avoiding Krylov Subspace Methods in Theory and Practice. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2015. [Google Scholar]
- Antonov, J.I.; Seidov, D.; Boyer, T.P.; Locarnini, R.A.; Johnson, D.R. World Ocean. Atlas 2009 Volume 2: Salinity; Levitus, S., Ed.; NOAA Atlas NESDIS 69; U.S. Government Printing Office: Washington, DC, USA, 2010; p. 184.
- Locarnini, R.; Mishonov, A.; Antonov, J.; Boyer, T.; Garcia, H.; Baranova, O.; Zweng, M.; Johnson, D. World Ocean. Atlas 2009, Volume 1: Temperature; NOAA Atlas NESDIS 61; U.S. Government Printing Office: Washington, DC, USA, 2010; p. 182.
- Steele, M.; Morley, R.; Ermold, W. PHC: A global ocean hydrography with a high quality Arctic Ocean. J. Clim. 2001, 14, 2079–2087. [Google Scholar] [CrossRef]
- Griffies, S.M.; Biastoch, A.; Böning, C.; Bryan, F.; Jianjun, Y. Coordinated ocean-ice reference experiments (COREs). Ocean. Modell. 2009, 26, 1–46. [Google Scholar] [CrossRef]
- Large, W.G.; Yeager, S.G. The global climatology of an interannually varying air–sea flux data set. Clim. Dyn. 2009, 33, 341–364. [Google Scholar] [CrossRef]
- Baker, A.; Xu, H.; Dennis, J.; Levy, M.; Nychka, D.; Mickelson, S.; Edwards, J.; Vertenstein, M.; Wegener, A. A methodology for evaluating the impact of data compression on climate simulation data. In Proceedings of the 23rd International Symposium on High-Performance Parallel and Distributed Computing, Vancouver, BC, Canada, 23–27 June 2014; pp. 203–214. [Google Scholar]
- Wang, Y.; Hao, H.; Zhang, J.; Jiang, J.; He, J.; Ma, Y. Performance optimization and evaluation for parallel processing of big data in earth system models. Cluster Comput. 2017, 22, 2371–2381. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (roms)—a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean. Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Eisenstat, S.C. Efficient Implementation of a Class of Preconditioned Conjugate Gradient Methods. Siam J. Sci. Comput. 1981, 2, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Huang, X.; Wang, X.; Fu, H.; Xu, S.; Ruan, H.; Xue, W.; Yang, G. A scalable barotropic mode solver for the parallel ocean program. In Proceedings of the Euro-Par 2013 Parallel Processing, Aachen, Germany, 26–30 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 739–750. [Google Scholar]
- Hoemmen, M. Communication-Avoiding Krylov Subspace Methods. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2010. [Google Scholar]
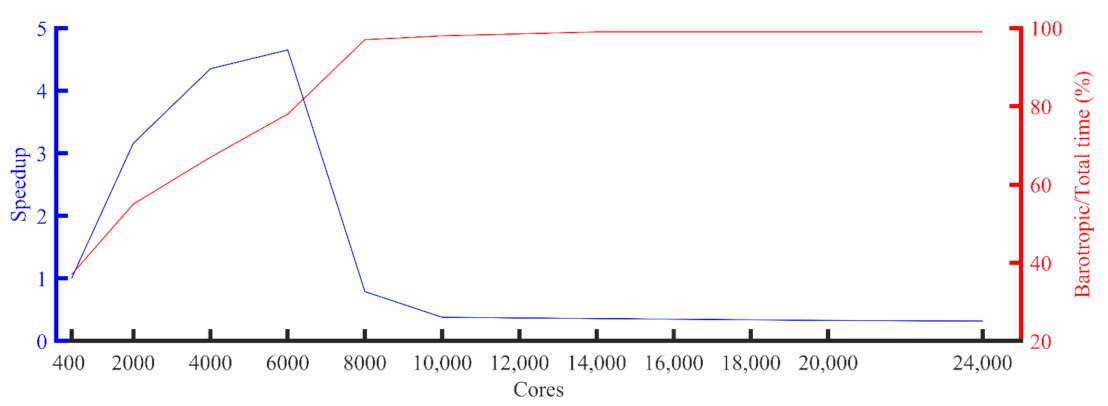
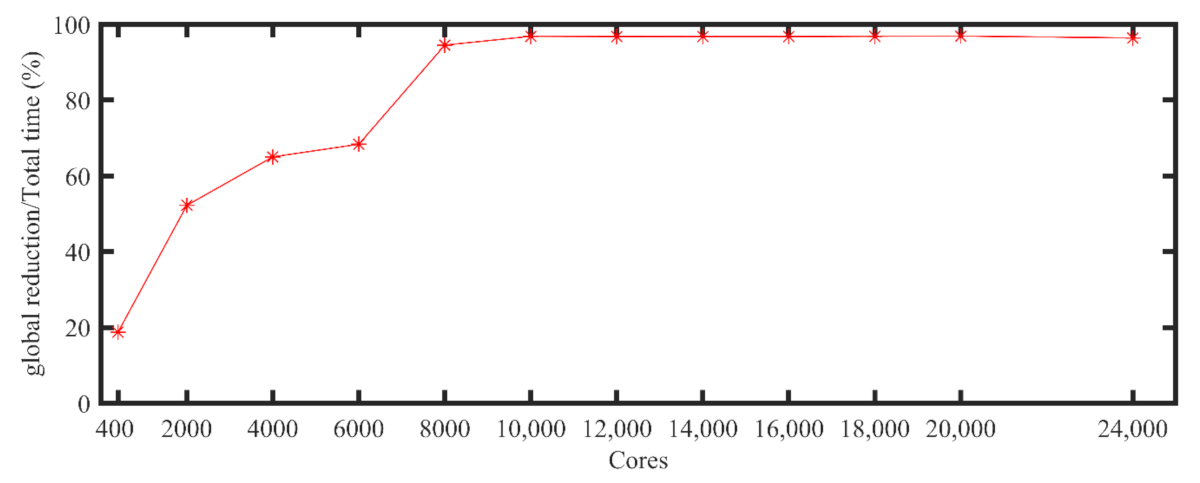

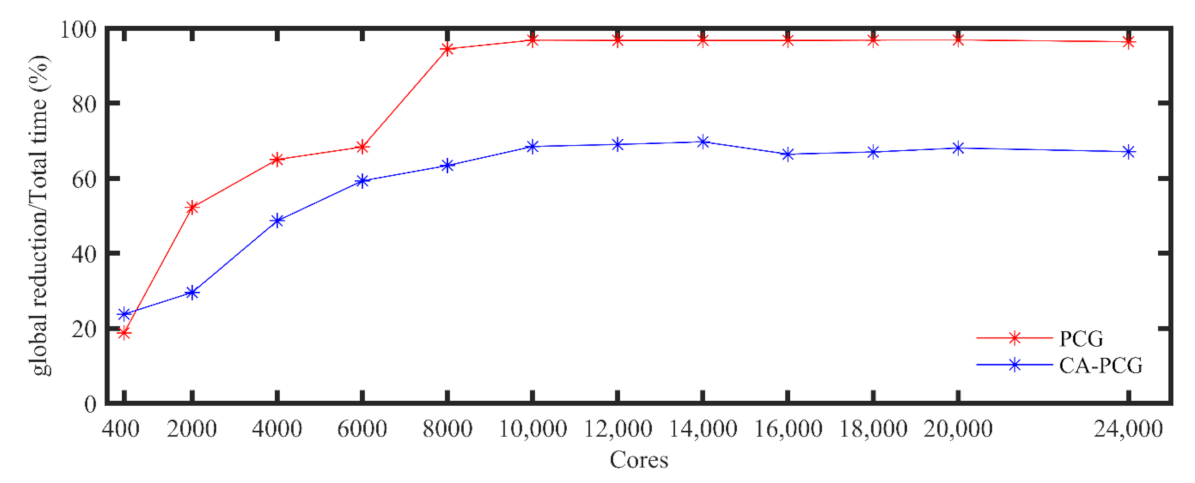

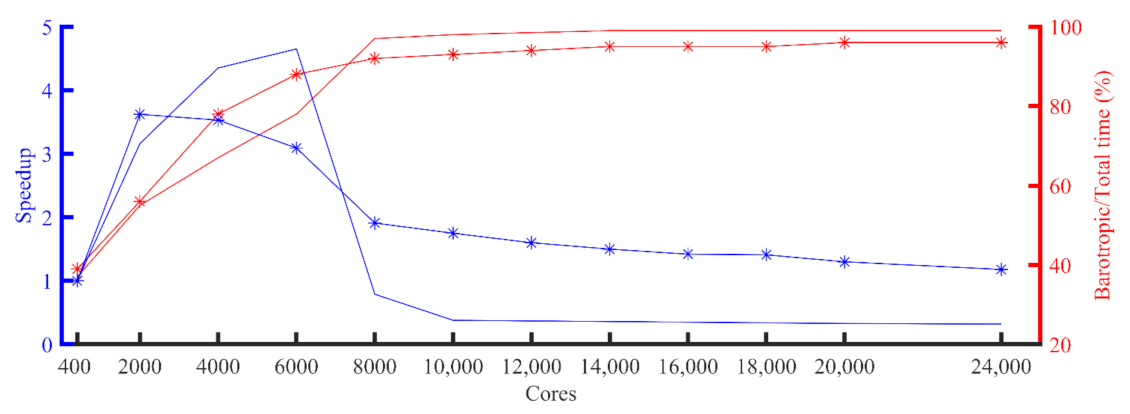
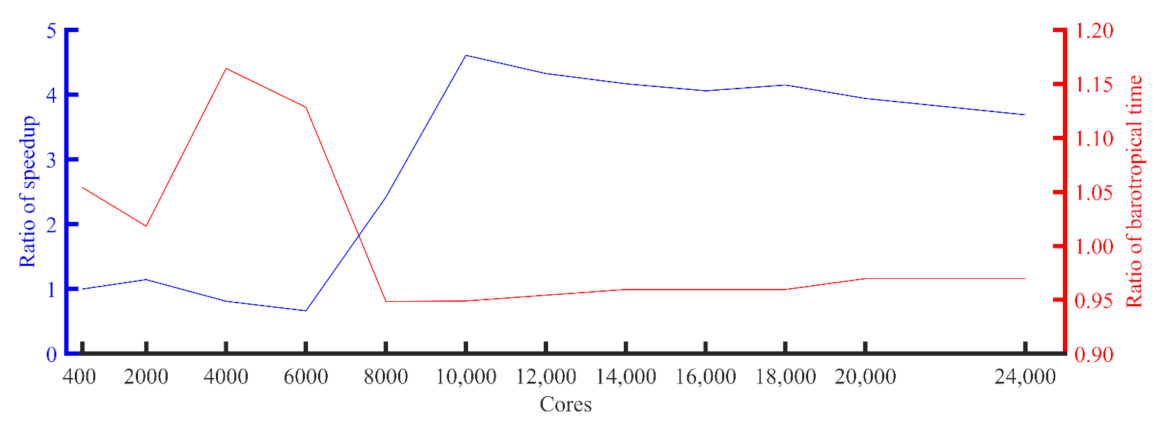
| Number of Processes | GYRE_PCG (s) | Speedup | GYRE_CAPCG (s) | Speedup |
|---|---|---|---|---|
| 400 | 7025 | 1.00 | 7196 | 1.00 |
| 2000 | 2221 | 3.16 | 1987 | 3.62 |
| 4000 | 1614 | 4.35 | 2035 | 3.53 |
| 6000 | 1510 | 4.65 | 2329 | 3.09 |
| 8000 | 8841 | 0.79 | 3762 | 1.91 |
| 10,000 | 18,076 | 0.38 | 4109 | 1.75 |
| 12,000 | 18,784 | 0.37 | 4499 | 1.60 |
| 14,000 | 19,493 | 0.36 | 4789 | 1.50 |
| 16,000 | 20,005 | 0.35 | 5067 | 1.42 |
| 18,000 | 20,470 | 0.34 | 5114 | 1.41 |
| 20,000 | 20,936 | 0.33 | 5539 | 1.30 |
| 24,000 | 21,737 | 0.32 | 6104 | 1.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhou, S.; Zhou, S.; Song, Z.; Liu, W. A Barotropic Solver for High-Resolution Ocean General Circulation Models. J. Mar. Sci. Eng. 2021, 9, 421. https://doi.org/10.3390/jmse9040421
Yang X, Zhou S, Zhou S, Song Z, Liu W. A Barotropic Solver for High-Resolution Ocean General Circulation Models. Journal of Marine Science and Engineering. 2021; 9(4):421. https://doi.org/10.3390/jmse9040421
Chicago/Turabian StyleYang, Xiaodan, Shan Zhou, Shengchang Zhou, Zhenya Song, and Weiguo Liu. 2021. "A Barotropic Solver for High-Resolution Ocean General Circulation Models" Journal of Marine Science and Engineering 9, no. 4: 421. https://doi.org/10.3390/jmse9040421
APA StyleYang, X., Zhou, S., Zhou, S., Song, Z., & Liu, W. (2021). A Barotropic Solver for High-Resolution Ocean General Circulation Models. Journal of Marine Science and Engineering, 9(4), 421. https://doi.org/10.3390/jmse9040421







