Innovation Concept Model and Prototype Validation of Robotic Fish with a Spatial Oscillating Rigid Caudal Fin
Abstract
1. Introduction
2. Background
3. Conceptual Design and Prototype
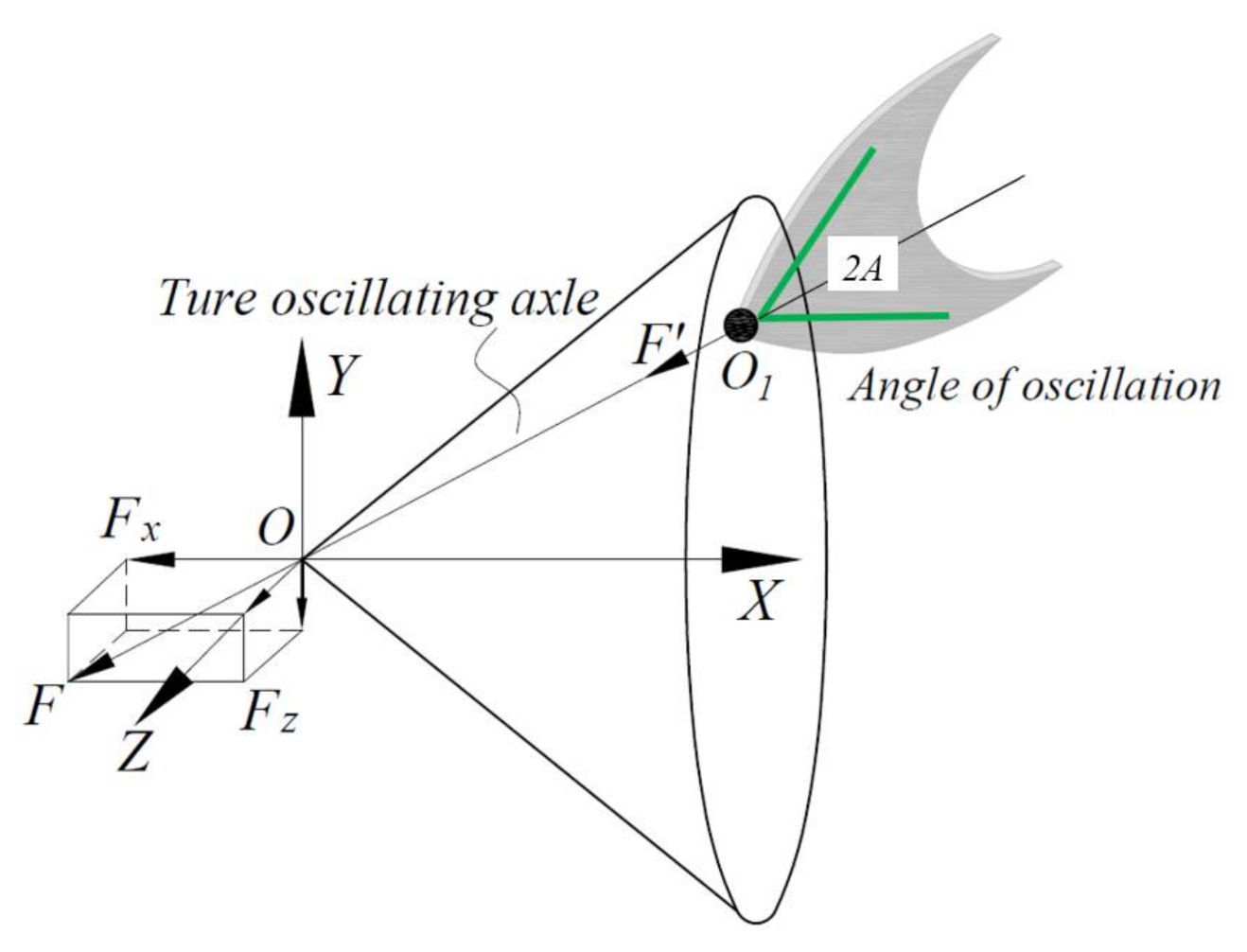
3.1. Conceptual Design of Mechanism
3.2. Conceptual Prototype Design
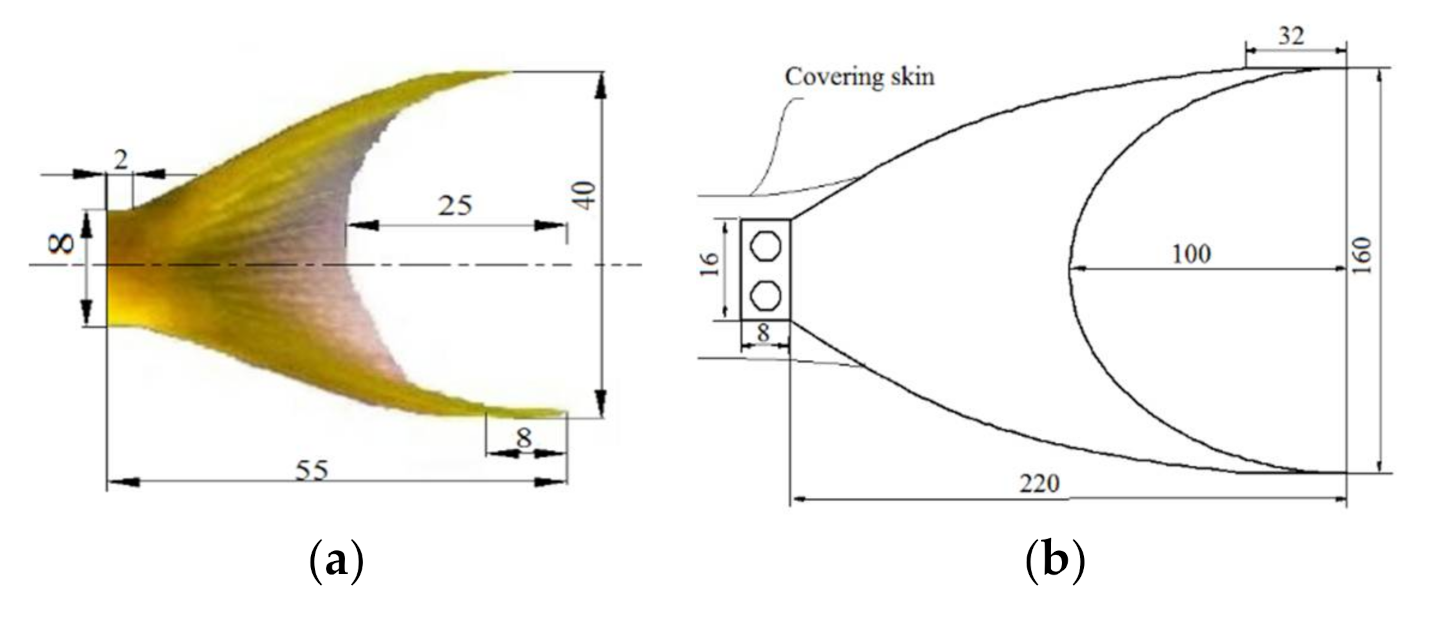
3.3. Design of the Rigid Caudal Fin
4. Experimental Results
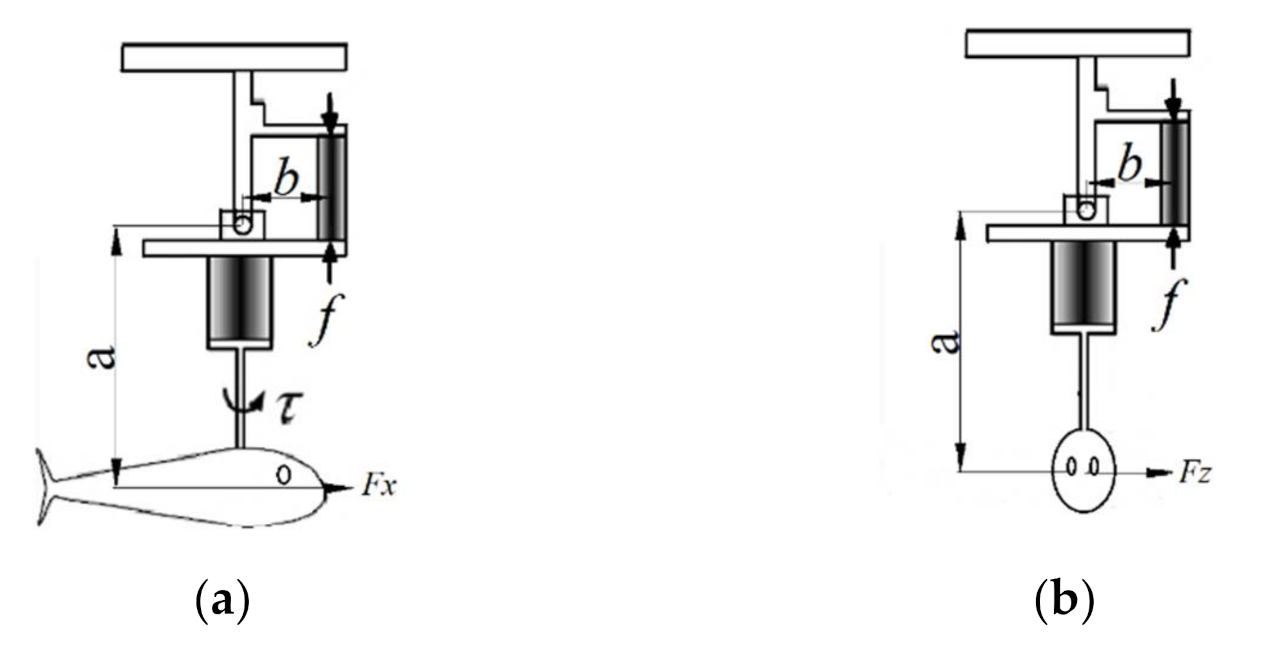
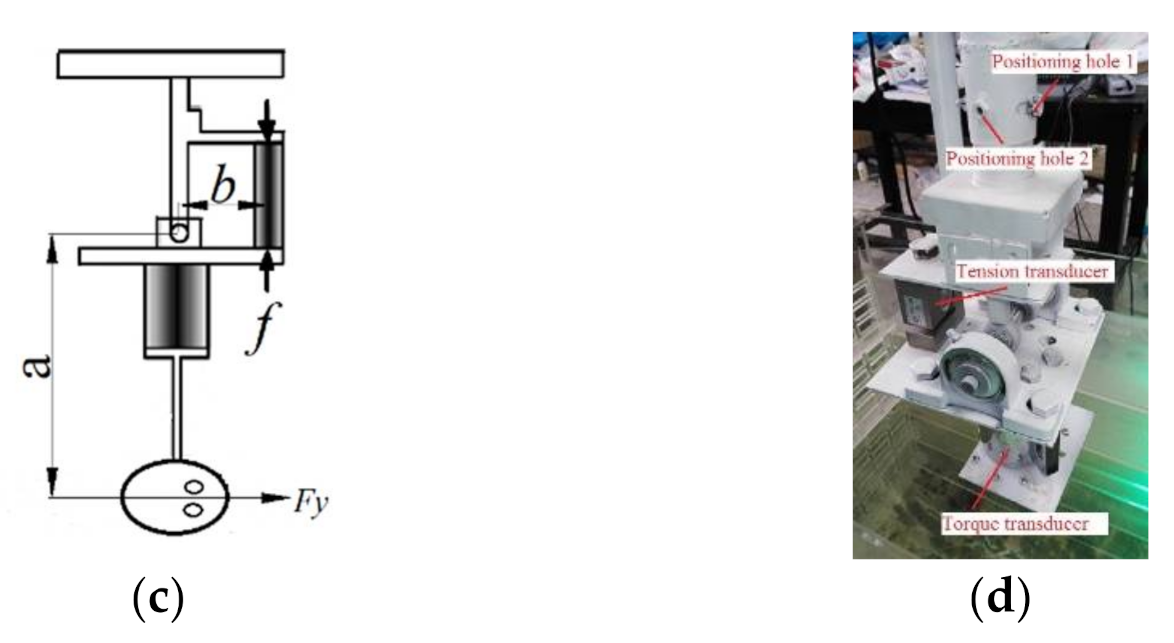
4.1. Experimental Apparatus Design
4.2. Experiments
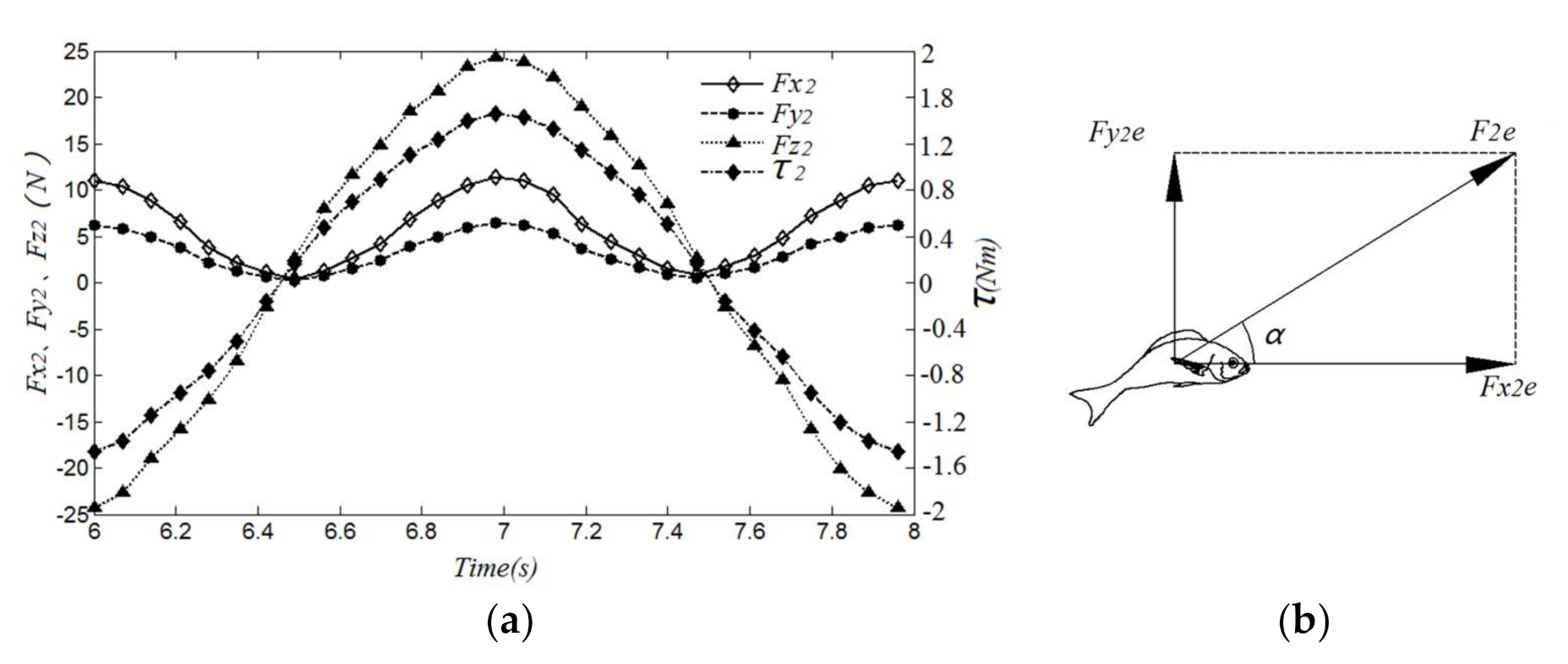
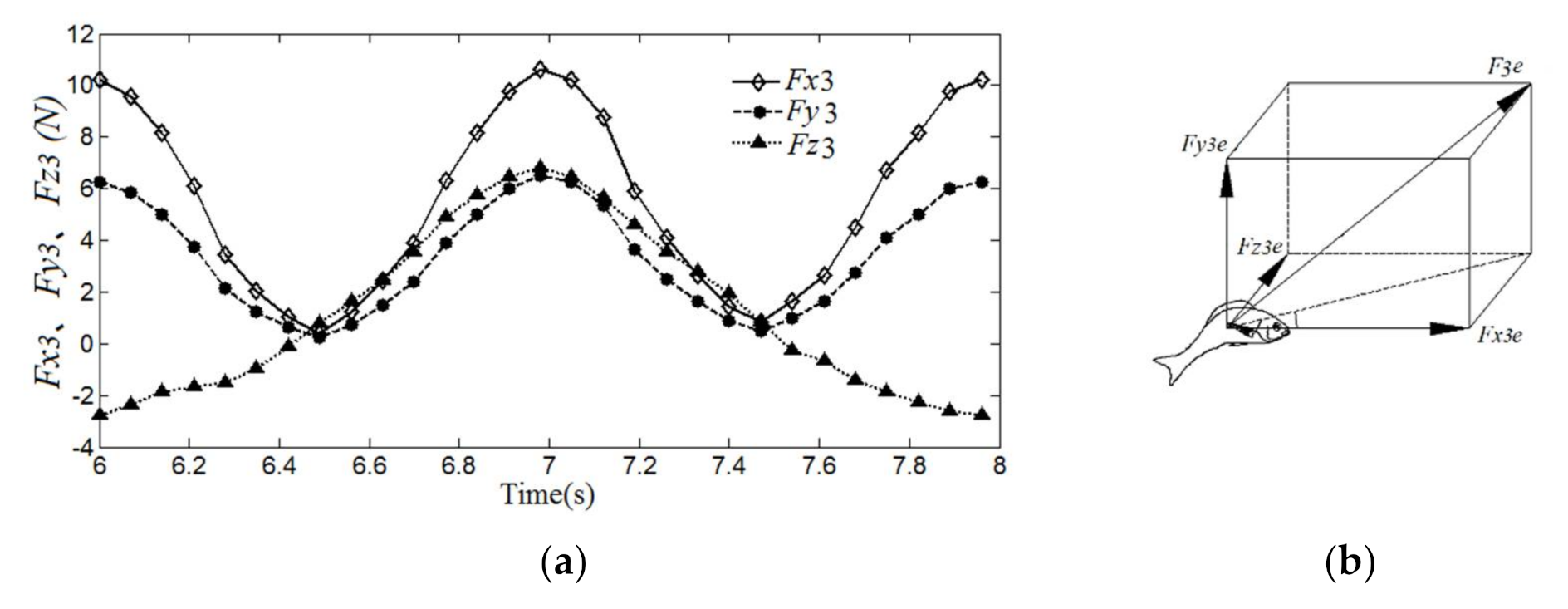
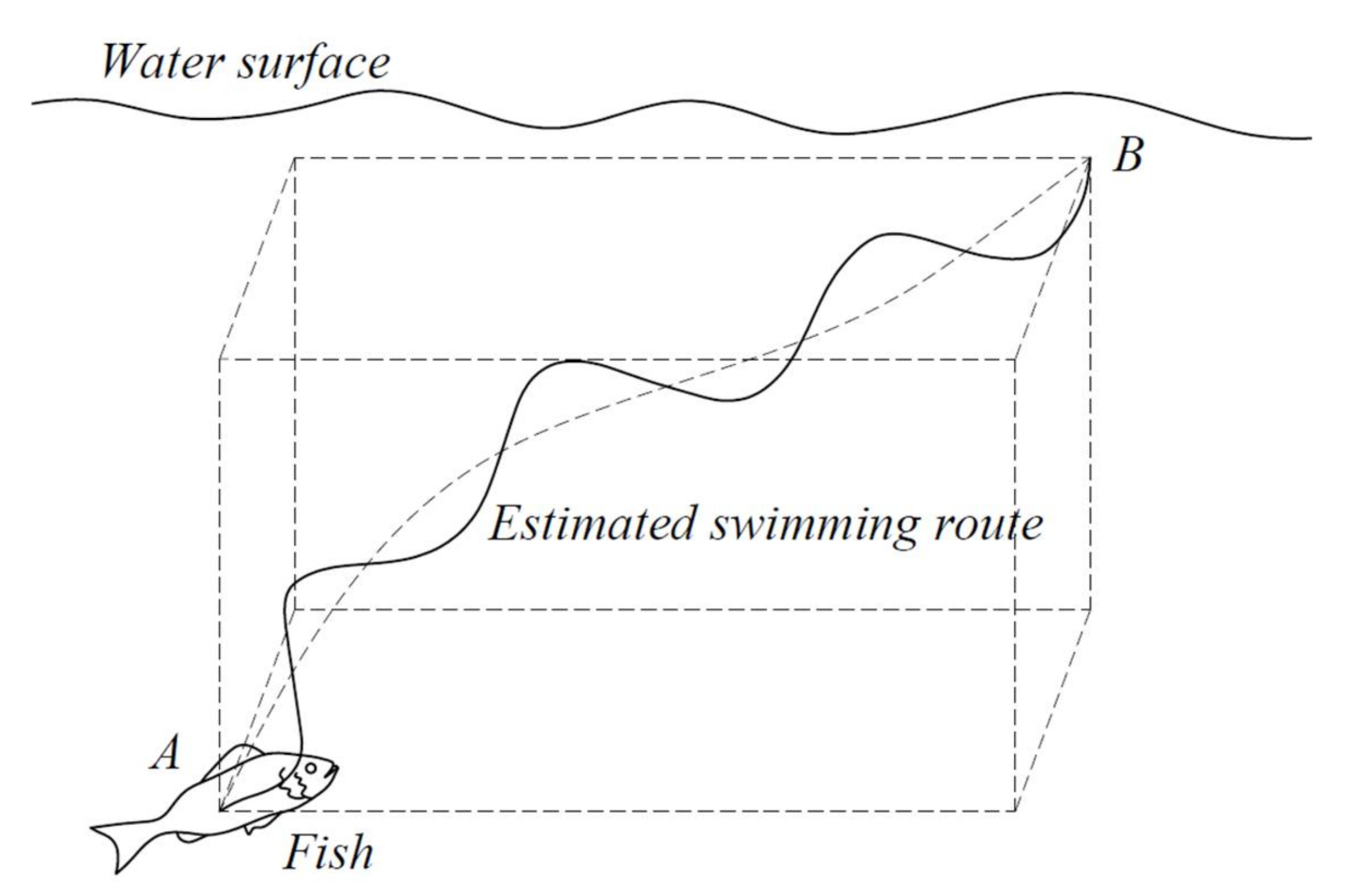
4.3. Results and Discussion
5. Results
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, Y.; Bi, S.; Li, G.; Hildre, H.P.; Zhang, H. From Natural Complexity to Biomimetic Simplification: The Realization of Bionic Fish Inspired by the Cownose Ray. IEEE Robot. Autom. Mag. 2019, 26, 27–38. [Google Scholar] [CrossRef]
- Zhang, C. Simulation Analysis of Bionic Robot Fish Based on MFC Materials. Math. Probl. Eng. 2019, 66, 1226–1234. [Google Scholar] [CrossRef]
- Heathcote, S.; Wang, Z. Effect of spanwise flexibility on flapping wing propulsion. Fluids Struct. 2008, 24, 183–199. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.Z.; Hu, Y.H. Dolphin-like propulsive mechanism based on an adjustable Scotch yoke. Mech. Mach. Theory 2009, 44, 603–614. [Google Scholar] [CrossRef]
- Apalkov, A.; Fernandez, R. Mechanical actuator for biomimetic propulsion and the effect of the caudal fin elasticity on the swimming performance. Sens. Actuators A 2012, 178, 164–174. [Google Scholar] [CrossRef]
- Nguyen, P.L. Dynamic Modeling and Experiment of a Fish Robot with a Flexible Tail Fin. Bionic Eng. 2013, 10, 39–45. [Google Scholar] [CrossRef]
- Mason, R.; Joel, W.B. Experiments in carangiform robotic fish locomotion. Robotics and Automation Proceedings. In Proceedings of the IEEE International Conference, San Francisco, CA, USA, 24–28 April 2000; pp. 428–435. [Google Scholar]
- Liang, C.Q. Research on Fish-Liked Propulsion Technology and SPC-Ⅱ Propulsion System Design; Harbin Engineering University: Harbin, China, 2004. [Google Scholar]
- Conte, J.; Hover, F.S. A fast-starting mechanical fish that accelerates at 40 m s−2. Bioinspir. Biomim. 2010, 5, 1–9. [Google Scholar] [CrossRef]
- Morgansen, K.A.; Triplett, B.I.; Klein, D.J. Geometric Methods for Modeling and Control of Free-Swimming Fin-Actuated Underwater Vehicles. IEEE Trans. Robot. 2007, 23, 1184–1199. [Google Scholar] [CrossRef]
- Castaño, M.L.; Tan, X.B. Model Predictive Control-Based Path-Following for Tail-Actuated Robotic Fish. Dyn. Syst. Meas. Control 2019, 1, 141. [Google Scholar] [CrossRef]
- Yu, J.Z.; Tan, M. Development of a biomimetic robotic fish and its control algorithm. IEEE Trans. Cybern. 2004, 34, 1798–1810. [Google Scholar] [CrossRef]
- Yu, J.Z.; Wen, L. A survey on fabrication, control, and hydrodynamic function of biomimetic robotic fish. Sci. China Technol. Sci. 2017, 60, 1365–1380. [Google Scholar] [CrossRef]
- Yu, J.Z.; Wang, M. Motion Control and Motion Coordination of Bionic Robotic Fish: A Review. Bionic Eng. 2018, 15, 579–598. [Google Scholar] [CrossRef]
- Zhao, S.Q. Experimental Research of A Tail-Fin Propulsive System; Harbin Engineering University: Harbin, China, 2008. [Google Scholar]
- Nguyen, Q.S.; Heo, S. Performance evaluation of an improved fish robot actuated by piezoceramic actuators. Smart Mater. Struct. 2010, 19, 1–8. [Google Scholar] [CrossRef]
- George, V.; Lauder, E.J.; Anderson, J.T. Fish biorobotics: Kinematics and hydrodynamics of self-propulsion. Exp. Biol. 2007, 210, 2767–2780. [Google Scholar]
- Salumäe, T.; Kruusmaa, M. A Flexible Fin with Bio-Inspired Stiffness Profile and Geometry. Bionic Eng. 2011, 8, 418–428. [Google Scholar] [CrossRef]
- Hadi, E.D.; Taavi, S. Modelling of a biologically inspired robotic fish driven by compliant parts. Bioinspir. Biomim. 2014, 9, 1–11. [Google Scholar]
- Barrett, D.S.; Triantafyllou, M.S.; Yue, D.P. Drag reduction in fish-like locomotion. Fluid Mech. 1999, 392, 183–212. [Google Scholar] [CrossRef]
- Mwaffo, V. Zebrafish swimming in the flow: A particle image velocimetry study. PEER J. 2017, 5, 4041. [Google Scholar] [CrossRef]
- Chan, W.L.; Kang, T.; Lee, Y.J. Experiments and identification of an ostraciiform fish robot. In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 15–18 December 2008. [Google Scholar]
- Costa, D.; Franciolini, M.; Palmieri, G.; Crivellini, A.; Scaradozzi, D. Computational fluid dynamics analysis and design of an ostraciiform swimming robot. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 135–140. [Google Scholar]
- Costa, D.; Callegari, M.; Palmieri, G.; Scaradozzi, D.; Brocchini, M.; Zitti, G. Experimental Setup for the Validation of the Bio-Inspired Thruster of an Ostraciiform Swimming Robot. In Proceedings of the 2018 14th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Oulu, Finland, 2–4 July 2018; pp. 1–6. [Google Scholar]
- Wen, L.; Wang, T.M. Hydrodynamic investigation of a self-propelled robotic fish based on a force-feedback control method. Bioinspir. Biomim. 2012, 7, 1–17. [Google Scholar] [CrossRef]
- Beal, D.N.; Bandyopadhyay, P.R. A harmonic model ofhydrodynamic forces produced by a flapping fin. Exp. Fluids 2007, 6, 75–82. [Google Scholar]
- Wang, S.Y.; Zhu, J.; Wang, X.G.; Li, Q.F.; Zhu, H.Y.; Zhou, R. Optimization and simulation of a bionic fish tail driving system based on linear hypocycloid with hydrodynamics. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Wang, S.Y.; Wang, X.G.; Li, Q. A Bionic Fish Propulsive Mechanism with Caudal Fin Oscillating in Variable Direction Based on Linear Hypocycloid. In Proceedings of the 14th IFToMM World Congress, Taipei, Taiwan, 25–30 October 2015; pp. 28–32. [Google Scholar]
- Ren, Q.Y.; Xu, J.X. A GIM-based biomimetic learning approach for motion generation of a multi-joint robotic fish. Bionic Eng. 2013, 10, 423–433. [Google Scholar] [CrossRef]
- Li, Z.C. The Software and Hard Hardware Design and Dynamic Research on the Robot Fish; Harbin Institute of Technology: Harbin, China, 2009. [Google Scholar]





| Variable | Experiment 1 | Experiment 2 | Experiment 3 |
|---|---|---|---|
| 0° | −30° | −30° | |
| 0° | 0 | −30° | |
| [60°,120°] | [60°,120°] | [75°,135°] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Han, Y.; Mao, S. Innovation Concept Model and Prototype Validation of Robotic Fish with a Spatial Oscillating Rigid Caudal Fin. J. Mar. Sci. Eng. 2021, 9, 435. https://doi.org/10.3390/jmse9040435
Wang S, Han Y, Mao S. Innovation Concept Model and Prototype Validation of Robotic Fish with a Spatial Oscillating Rigid Caudal Fin. Journal of Marine Science and Engineering. 2021; 9(4):435. https://doi.org/10.3390/jmse9040435
Chicago/Turabian StyleWang, Shuyan, Yu Han, and Shiteng Mao. 2021. "Innovation Concept Model and Prototype Validation of Robotic Fish with a Spatial Oscillating Rigid Caudal Fin" Journal of Marine Science and Engineering 9, no. 4: 435. https://doi.org/10.3390/jmse9040435
APA StyleWang, S., Han, Y., & Mao, S. (2021). Innovation Concept Model and Prototype Validation of Robotic Fish with a Spatial Oscillating Rigid Caudal Fin. Journal of Marine Science and Engineering, 9(4), 435. https://doi.org/10.3390/jmse9040435






