Lateral Deflection Behavior of Perforated Steel Plates: Experimental and Numerical Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Specimen and Scenario
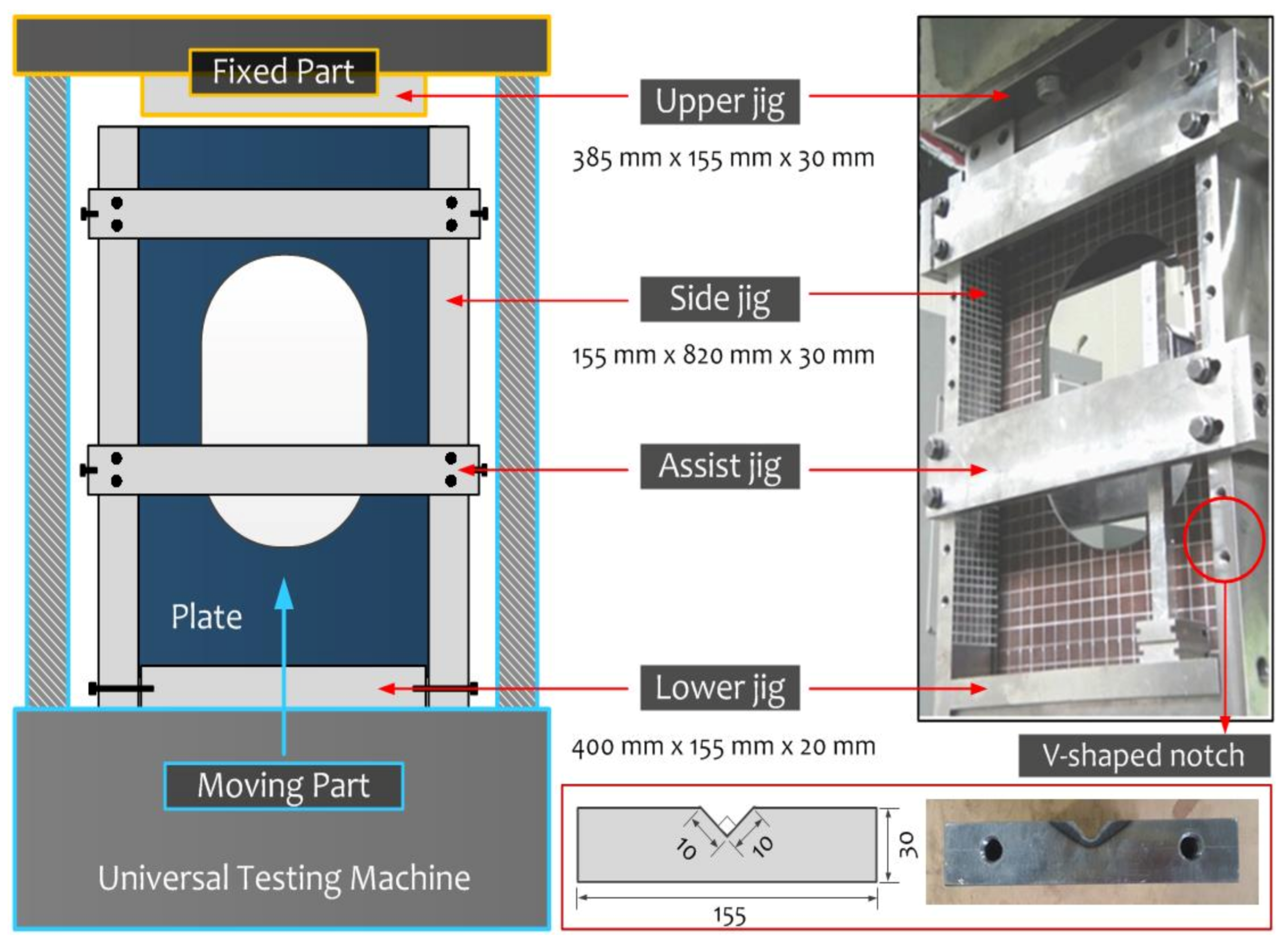
2.2. Experimental Apparatus
2.3. Finite Element Analysis
3. Results and Discussion
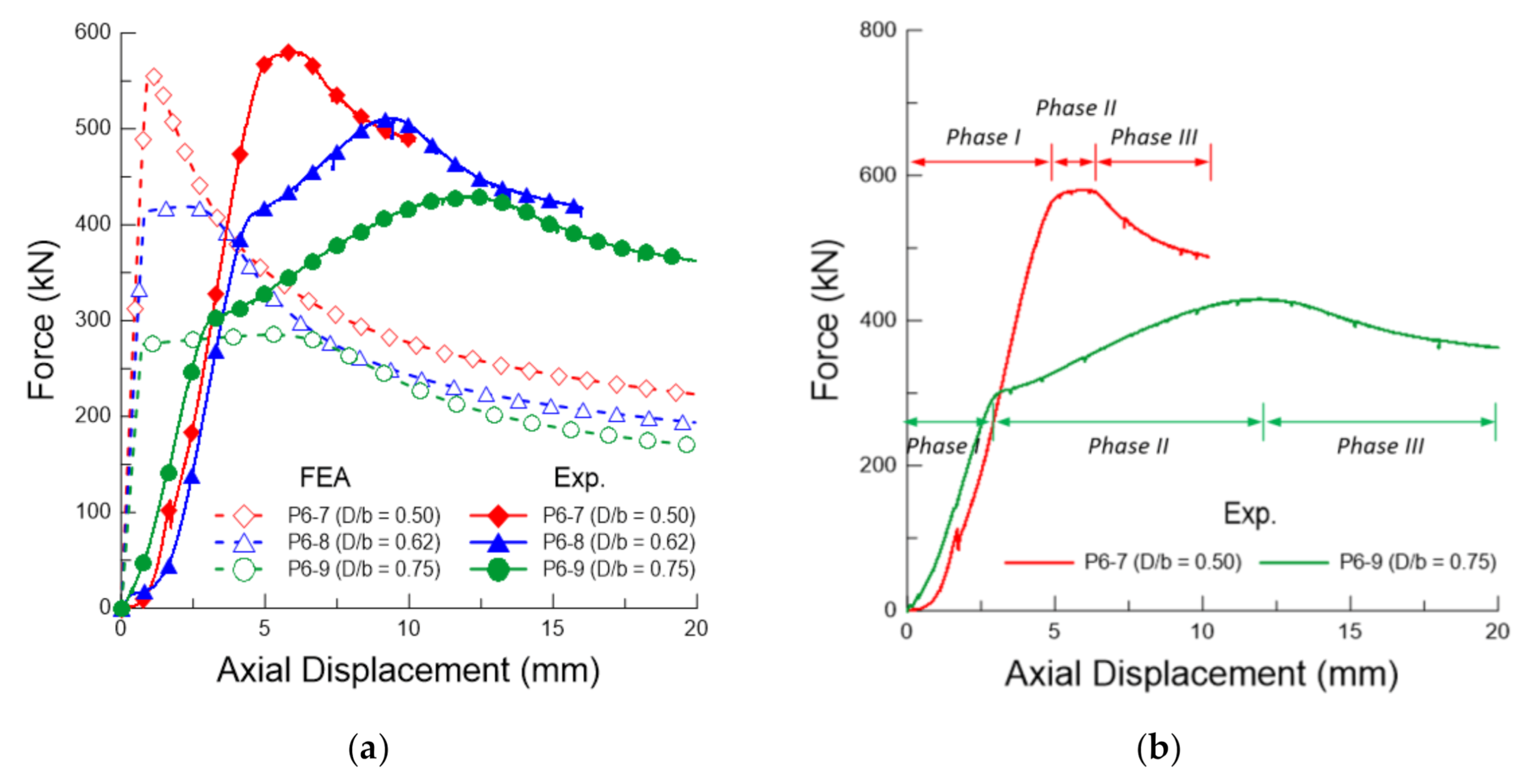
3.1. Axial Displacement
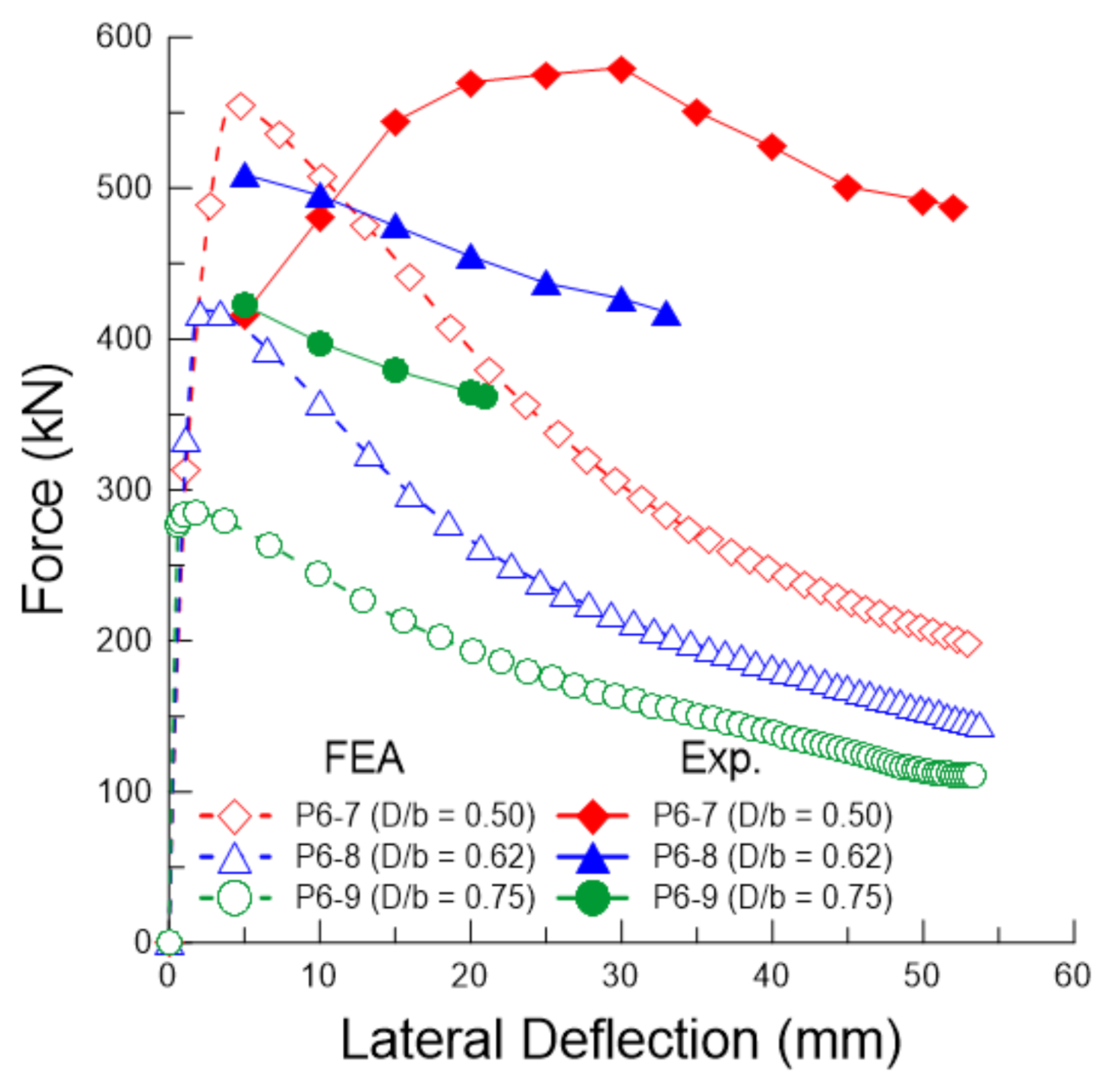
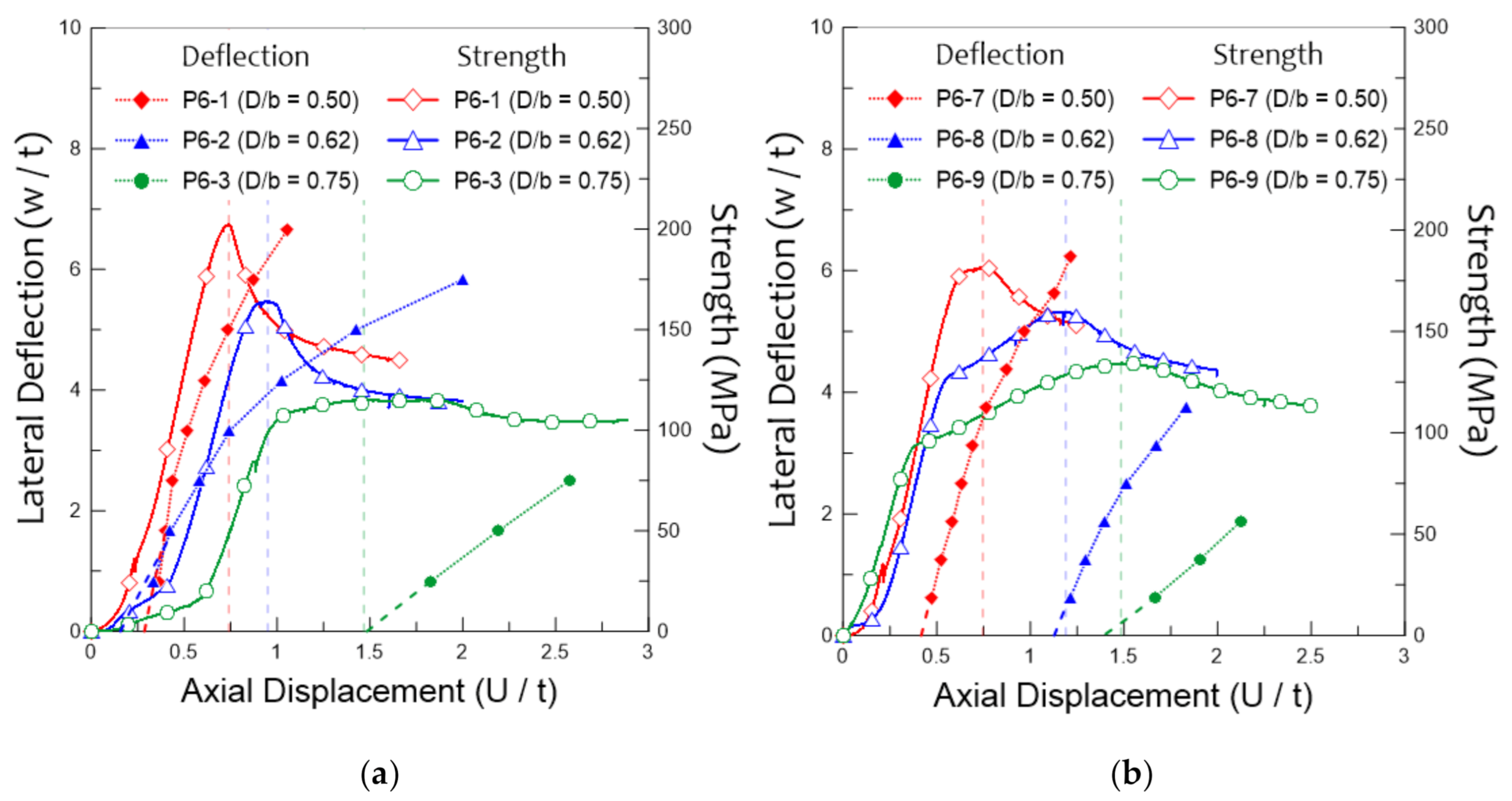
3.2. Lateral Deflection
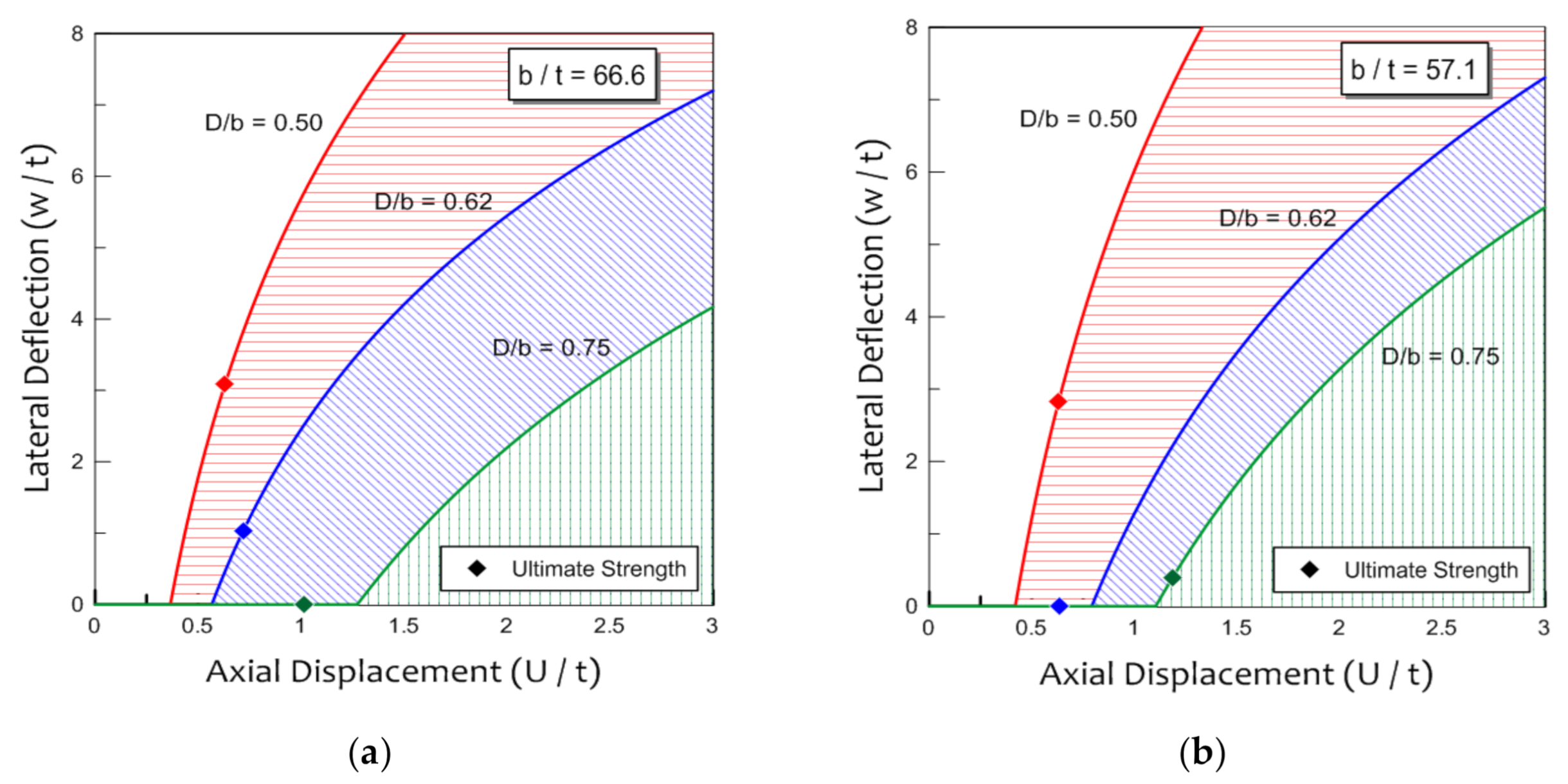
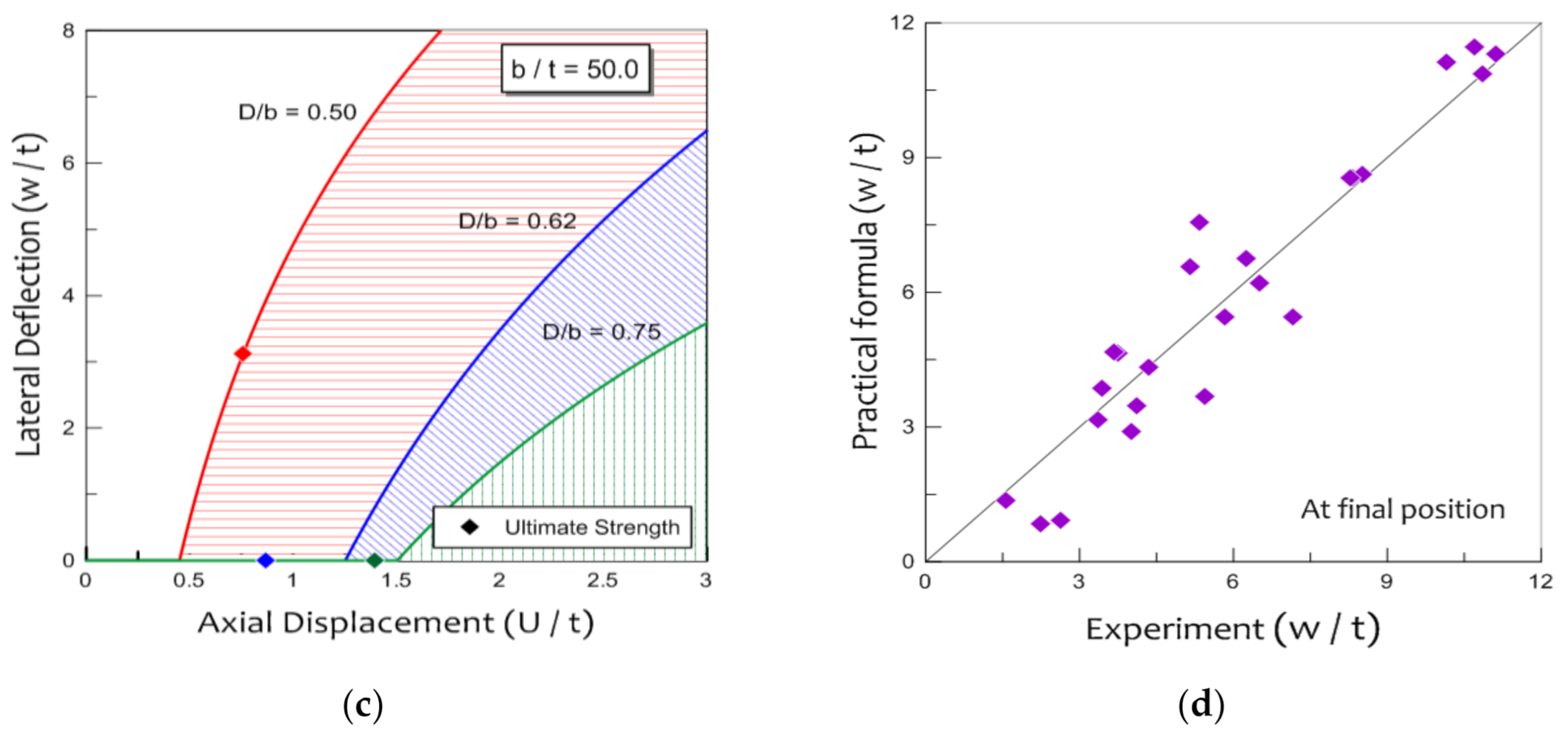
3.3. Practical Curve
4. Conclusions
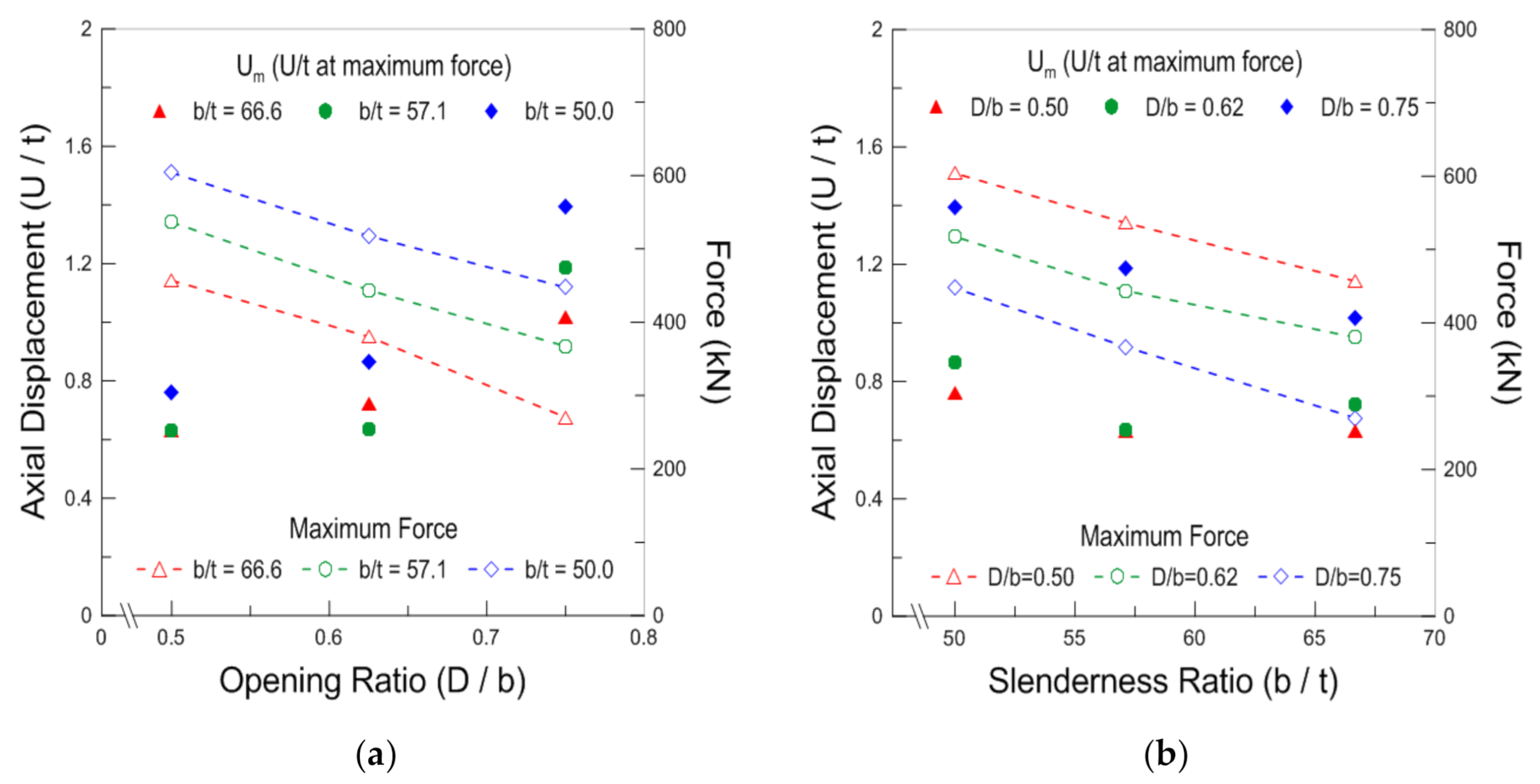
- The axial displacement of the perforated plate at its ultimate strength increased with an increase in the opening ratio and thickness of the perforated plate. In other words, a thick perforated plate with a large opening size must be axially displaced higher in to reach its ultimate strength. Therefore, within the allowable stress ranges, it is recommended that one install a perforated plate with a large opening size and thickness to a certain part, which is expected to result in a large axial displacement.
- The perforated plate experiences two major changes: global and local buckling; the stiffness of the plate changes materially in each process. Local buckling occurred mainly around the opening and was more dominant with an increase in the opening ratio. In addition, the ultimate strength of the perforated plate was determined at the end of the local buckling phase.
- There was a distinct difference in the behavior of lateral deflection between perforated plates with different opening ratios. The lateral deflection of the perforated plate with a small opening ratio showed a rapid increase in the buckling strength of the plate. In contrast, the lateral deflection of the perforated plate with a large opening ratio was maintained at a constant level before the ultimate strength, and then it gradually increased after the ultimate strength of the plate.
- The occurrence point of lateral deflection delayed as the opening ratio increased, and the slenderness ratio decreased. However, in the cases of perforated plates with large opening ratios (more than 0.75) and small slenderness ratios (less than 57.1), the occurrence of lateral deflection indicated that the perforated plate had already reached its ultimate strength.
- The practical curves are suggested on the basis of the buckling experimental results, which showed the amount of lateral deflection with the increase in axial displacement as well as the occurrence point of ultimate strength dependent on the opening and slenderness ratio.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.H.; Park, J.S.; Lee, K.H.; Kim, J.H.; Kim, M.H.; Lee, J.M. Computational analysis and design formula development for the design of curved plates for ships and offshore structures. Struct. Eng. Mech. 2014, 49, 705–726. [Google Scholar]
- El-Sawy, K.M.; Nazmy, A.S.; Martini, M.I. Elasto-plastic buckling of perforated plates under uniaxial compression. Thin Walled Struct. 2004, 42, 1083–1101. [Google Scholar]
- Kumar, M.S.; Alagusundaramoorthy, P.; Sundaravadivelu, R. Ultimate strength of ship plating under axial compression. Ocean Eng. 2006, 33, 1249–1259. [Google Scholar] [CrossRef]
- Ghavami, K.; Khedmati, M.R. Numerical and experimental investigations on the compression behaviour of stiffened plates. J. Constr. Steel Res. 2006, 62, 1087–1100. [Google Scholar]
- Silva, C.C.C.; Helbig, D.; Cunha, M.; Santos, E.D.; Rocha, L.A.O.; Real, M.V.; Isoldi, L.A. Numerical buckling analysis of thin steel plates with centered hexagonal perforation through constructal design method. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 309. [Google Scholar] [CrossRef]
- Seifi, R.; Chahardoli, S.; Attar, A.A. Axial buckling of perforated plates reinforced with strips and middle tubes. Mech. Res. Commun. 2017, 85, 21–32. [Google Scholar]
- Cheng, B.; Zhao, J. Strengthening of perforated plates under uniaxial compression: Buckling analysis. Thin Walled Struct. 2010, 48, 905–914. [Google Scholar]
- Mateus, A.F.; Witz, J.A. A parametric study of the post-buckling behavior of steel plates. Eng. Struct. 2001, 23, 172–185. [Google Scholar] [CrossRef]
- Han, D.S.; Han, G.J. The deflection coefficient of a rectangular plate reinforced in the middle. Int. J. Precis. Eng. Manuf. 2009, 10, 73–78. [Google Scholar] [CrossRef]
- Gong, Y.; Gao, Y.; Xie, D.; Liu, J. Deflection and fracture of a clamped plate under lateral indentation by a sphere. Ocean Eng. 2015, 103, 21–30. [Google Scholar]
- Kwon, Y.B.; Park, H.S. Compression tests of longitudinally stiffened plates undergoing distortional buckling. J. Constr. Steel Res. 2011, 67, 1212–1224. [Google Scholar] [CrossRef]
- Seifi, R.; Khoda-yari, N. Experimental and numerical studies on buckling of cracked thin-plates under full and partial compression edge loading. Thin Walled Struct. 2011, 49, 1504–1516. [Google Scholar] [CrossRef]
- Gordo, J.M.; Soares, C.G. Compressive tests on stiffened panels of intermediate slenderness. Thin Walled Struct. 2011, 49, 782–794. [Google Scholar] [CrossRef]
- Kim, J.H.; Park, D.H.; Kim, S.K.; Kim, M.S.; Lee, J.M. Experimental study and development of design formula for estimating the ultimate strength of curved plates. Appl. Sci. 2021, 11, 2379. [Google Scholar] [CrossRef]
- Memon, B.A.; Su, X.Z. Arc-length technique for nonlinear finite element analysis. J. Zhejiang Univ. Sci. A 2004, 5, 618–628. [Google Scholar] [CrossRef]
- Kim, J.H.; Jeon, J.H.; Park, J.S.; Seo, H.D.; Ahn, H.J.; Lee, J.M. Effect of reinforcement on buckling and ultimate strength of perforated plates. Int. J. Mech. Sci. 2015, 92, 194–205. [Google Scholar] [CrossRef]
- Smith, C.S.; Davidson, P.C.; Chapman, J.C.; Dowling, P.J. Strength and stiffness of ships’ plating under in-plane compression and tension. Trans. R. Inst. Nav. Archit. 1988, 130, 227–296. [Google Scholar]
- Ueda, Y.; Yao, T. The influence of complex initial deflection modes on the behavior and ultimate strength of rectangular plates in compression. J. Constr. Steel Res. 1985, 5, 265–302. [Google Scholar] [CrossRef]
- Mert, M. Linear and Nonlinear Buckling Analyses of Plates Using the Finite Element Method. Master’s Thesis, Linkoping University, Linkoping, Sweden, June 2014. [Google Scholar]
- Xu, S.; Liu, B.; Wu, Y.G.W.; Soares, C.G. Experimental and numerical analysis of ultimate strength of inland catamaran subjected to vertical bending moment. Ocean Eng. 2019, 188, 106320. [Google Scholar] [CrossRef]
- Cui, J.; Wang, D. An experimental and numerical investigation on ultimate strength of stiffened plates with opening and perforation corrosion. Ocean Eng. 2020, 205, 107282. [Google Scholar] [CrossRef]
- Kim, U.N.; Choe, I.H.; Paik, J.K. Buckling and ultimate strength of perforated plate panels subject to axial compression: Experimental and numerical investigations with design formulations. Ships Offshore Struct. 2009, 4, 337–361. [Google Scholar] [CrossRef]







| Material | Chemical Composition | ||||||
|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Ni | Cr | |
| Mild steel | 0.150 | 0.220 | 0.900 | 0.010 | 0.004 | 0.010 | 0.020 |
| Test Model | Plate | Opening Size | ||
|---|---|---|---|---|
| a/b | t (mm) | D (mm) | L (mm) | |
| P8-1 | 2.0 | 6 | 200 | 300 |
| P8-2 | 250 | 350 | ||
| P8-3 | 300 | 400 | ||
| P8-4 | 7 | 200 | 300 | |
| P8-5 | 250 | 350 | ||
| P8-6 | 300 | 400 | ||
| P8-7 | 8 | 200 | 300 | |
| P8-8 | 250 | 350 | ||
| P8-9 | 300 | 400 | ||
| P6-1 | 1.5 | 6 | 200 | 300 |
| P6-2 | 250 | 350 | ||
| P6-3 | 300 | 400 | ||
| P6-4 | 7 | 200 | 300 | |
| P6-5 | 250 | 350 | ||
| P6-6 | 300 | 400 | ||
| P6-7 | 8 | 200 | 300 | |
| P6-8 | 250 | 350 | ||
| P6-9 | 300 | 400 | ||
| P4-1 | 1.0 | 6 | 200 | 300 |
| P4-2 | 250 | 350 | ||
| P4-3 | 7 | 200 | 300 | |
| P4-4 | 250 | 350 | ||
| P4-5 | 8 | 200 | 300 | |
| P4-6 | 250 | 350 | ||
| Material | Elastic Modulus | Poisson Ratio | Yield Stress |
|---|---|---|---|
| Mild steel | 210 GPa | 0.3 | 343 MPa |
| Test Model | At Maximum Force | At Final Position | ||
|---|---|---|---|---|
| U/t | σu/σy | U/t | w/t | |
| P8-1 | 0.653 | 0.615 | 2.504 | 10.85 |
| P8-2 | 0.613 | 0.460 | 3.258 | 5.333 |
| P8-3 | 0.568 | 0.322 | 2.309 | 4.000 |
| P8-4 | 0.654 | 0.627 | 2.146 | 11.12 |
| P8-5 | 0.507 | 0.526 | 2.627 | 5.143 |
| P8-6 | 1.051 | 0.413 | 1.957 | 3.357 |
| P8-7 | 0.905 | 0.591 | 1.880 | 8.322 |
| P8-8 | 0.788 | 0.512 | 2.344 | 3.750 |
| P8-9 | 1.305 | 0.424 | 2.335 | 2.250 |
| P6-1 | 0.740 | 0.590 | 1.678 | 8.500 |
| P6-2 | 0.950 | 0.478 | 2.001 | 5.833 |
| P6-3 | 1.467 | 0.335 | 3.334 | 3.667 |
| P6-4 | 0.654 | 0.542 | 1.439 | 8.286 |
| P6-5 | 0.801 | 0.391 | 1.740 | 4.355 |
| P6-6 | 1.321 | 0.352 | 2.226 | 3.429 |
| P6-7 | 0.745 | 0.529 | 1.273 | 6.500 |
| P6-8 | 1.189 | 0.465 | 2.001 | 4.125 |
| P6-9 | 1.484 | 0.391 | 2.500 | 2.625 |
| P4-1 | 0.500 | 0.461 | 2.615 | 10.16 |
| P4-2 | 0.598 | 0.448 | 2.003 | 7.167 |
| P4-3 | 0.583 | 0.507 | 2.193 | 10.71 |
| P4-4 | 0.596 | 0.469 | 1.549 | 5.431 |
| P4-5 | 0.626 | 0.531 | 1.391 | 6.250 |
| P4-6 | 0.620 | 0.437 | 1.503 | 1.556 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-H.; Park, D.-H.; Kim, S.-K.; Kim, J.-D.; Lee, J.-M. Lateral Deflection Behavior of Perforated Steel Plates: Experimental and Numerical Approaches. J. Mar. Sci. Eng. 2021, 9, 498. https://doi.org/10.3390/jmse9050498
Kim J-H, Park D-H, Kim S-K, Kim J-D, Lee J-M. Lateral Deflection Behavior of Perforated Steel Plates: Experimental and Numerical Approaches. Journal of Marine Science and Engineering. 2021; 9(5):498. https://doi.org/10.3390/jmse9050498
Chicago/Turabian StyleKim, Jeong-Hyeon, Doo-Hwan Park, Seul-Kee Kim, Jeong-Dae Kim, and Jae-Myung Lee. 2021. "Lateral Deflection Behavior of Perforated Steel Plates: Experimental and Numerical Approaches" Journal of Marine Science and Engineering 9, no. 5: 498. https://doi.org/10.3390/jmse9050498
APA StyleKim, J.-H., Park, D.-H., Kim, S.-K., Kim, J.-D., & Lee, J.-M. (2021). Lateral Deflection Behavior of Perforated Steel Plates: Experimental and Numerical Approaches. Journal of Marine Science and Engineering, 9(5), 498. https://doi.org/10.3390/jmse9050498






