Optimum Curvature Characteristics of Body/Caudal Fin Locomotion
Abstract
1. Introduction
2. Materials and Methods
2.1. Optimization Problem Definition
2.2. Optimization Algorithm
3. Results
3.1. Reference Case
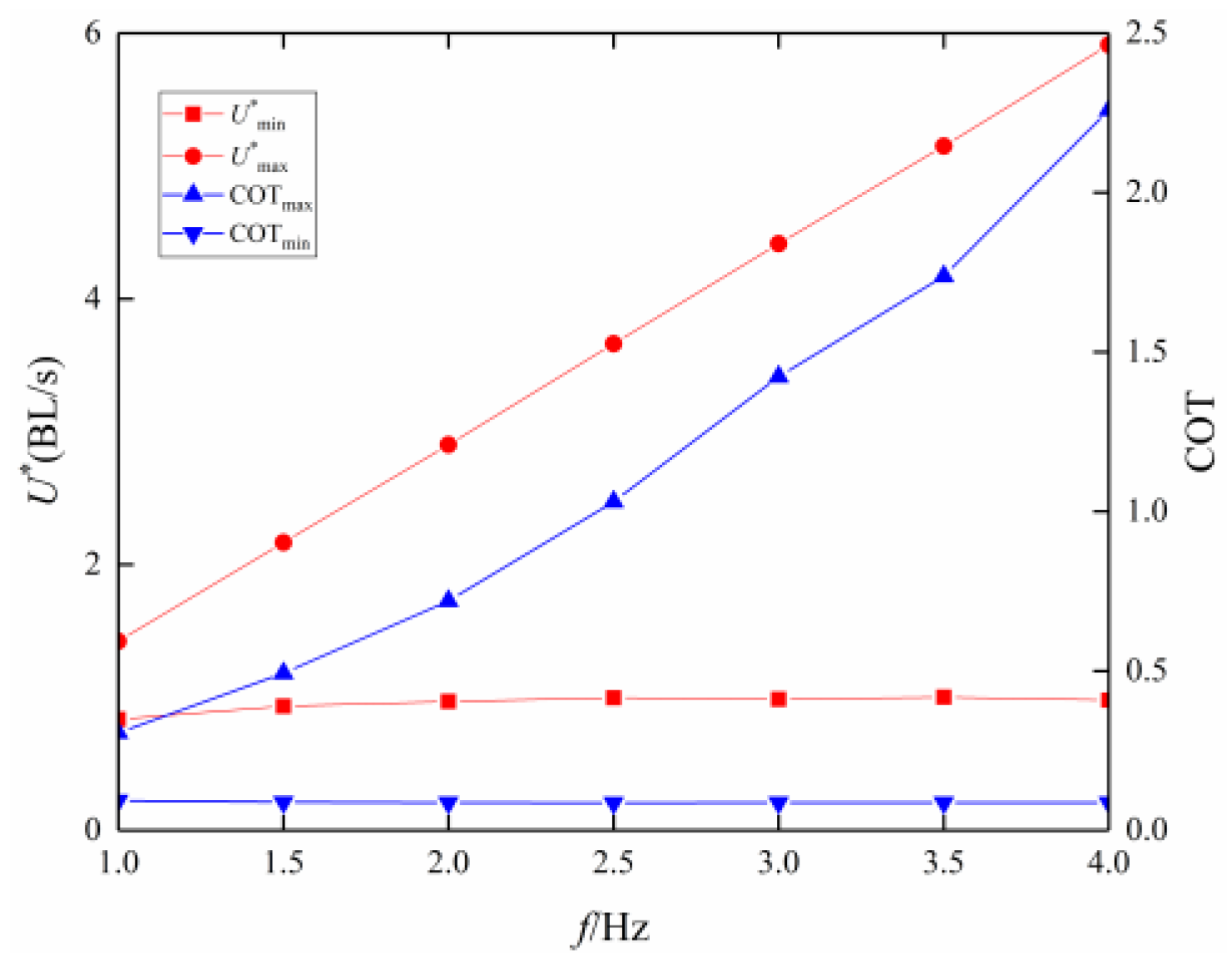
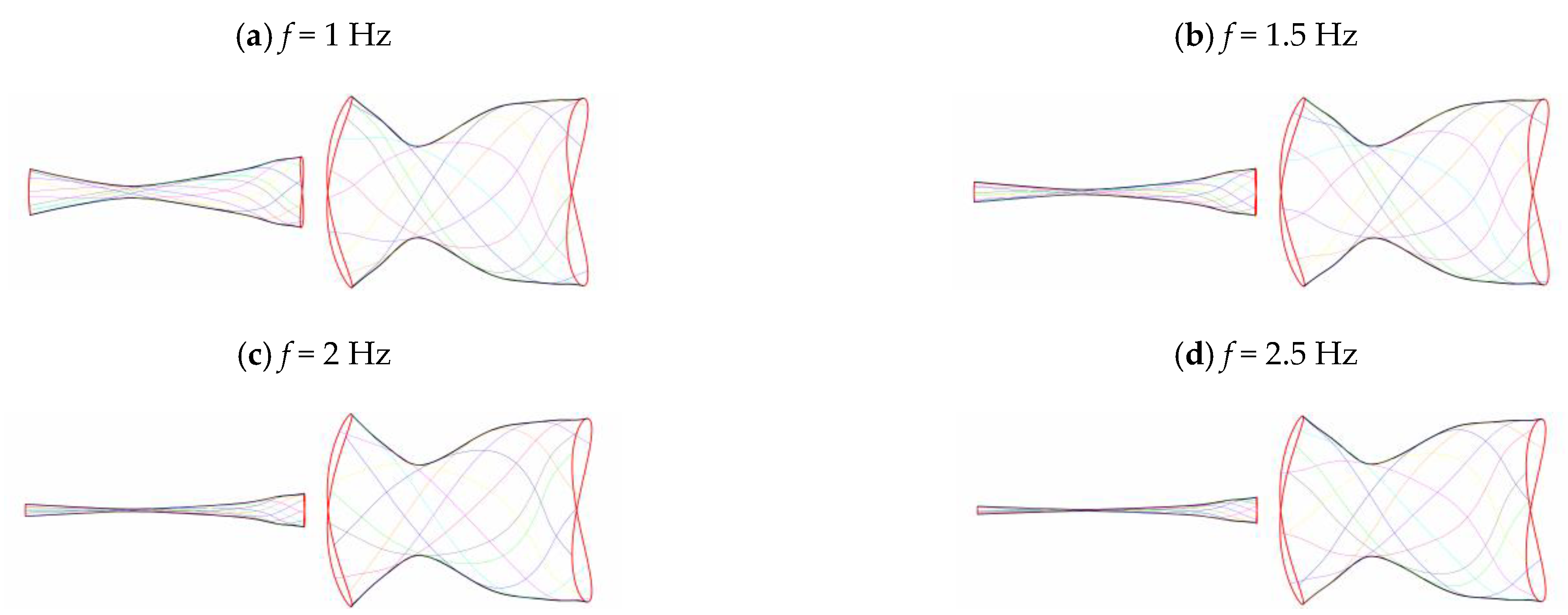
3.2. Frequency Effect
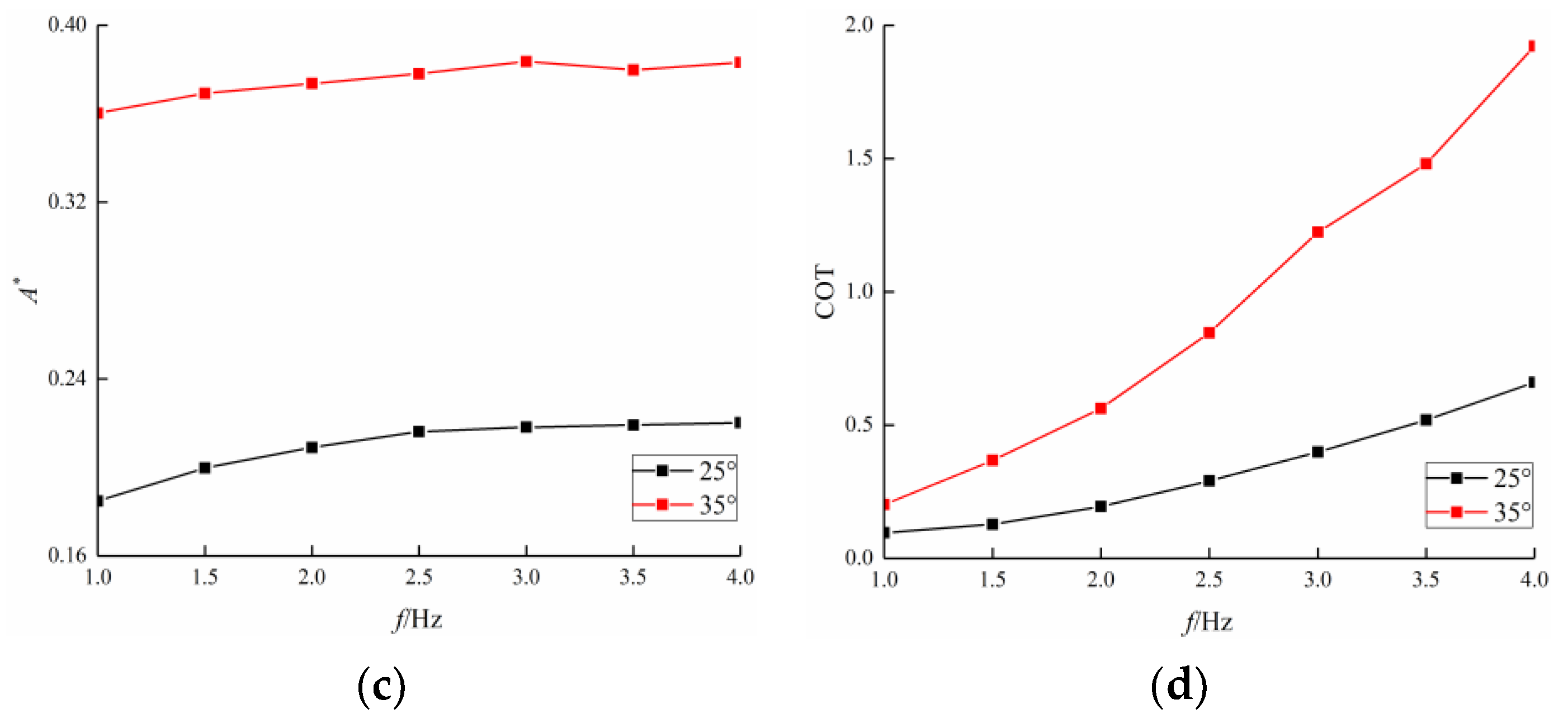
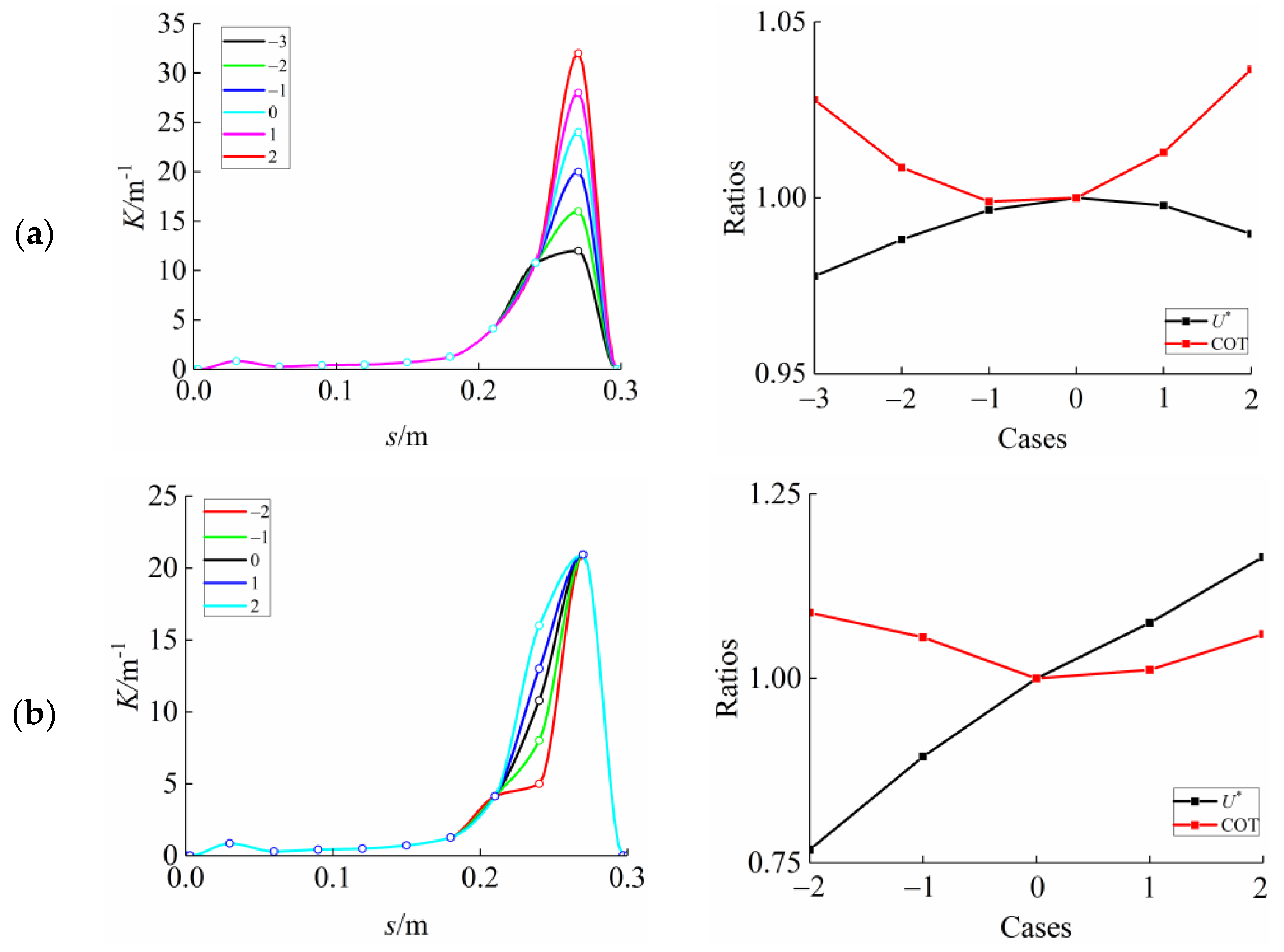
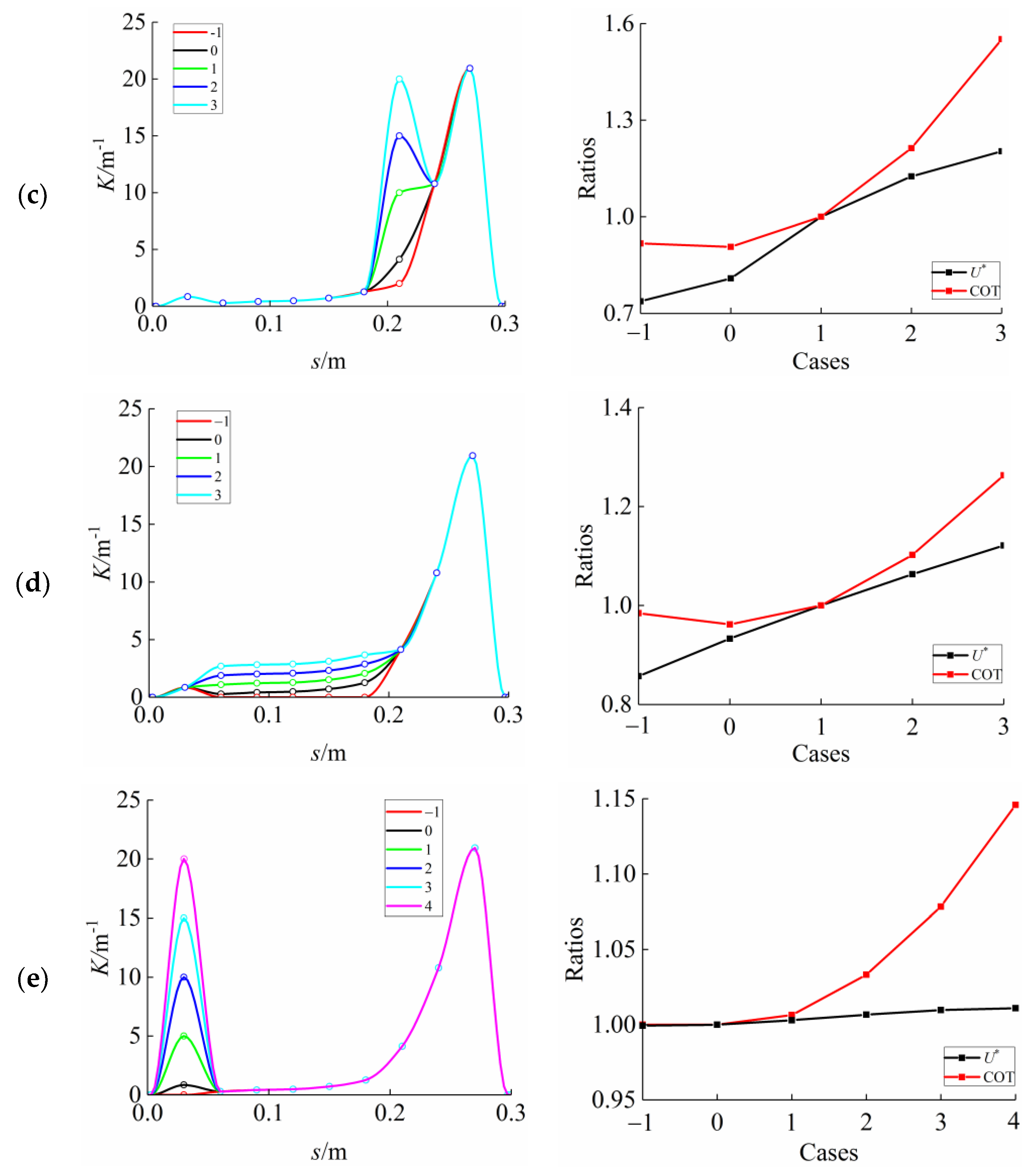
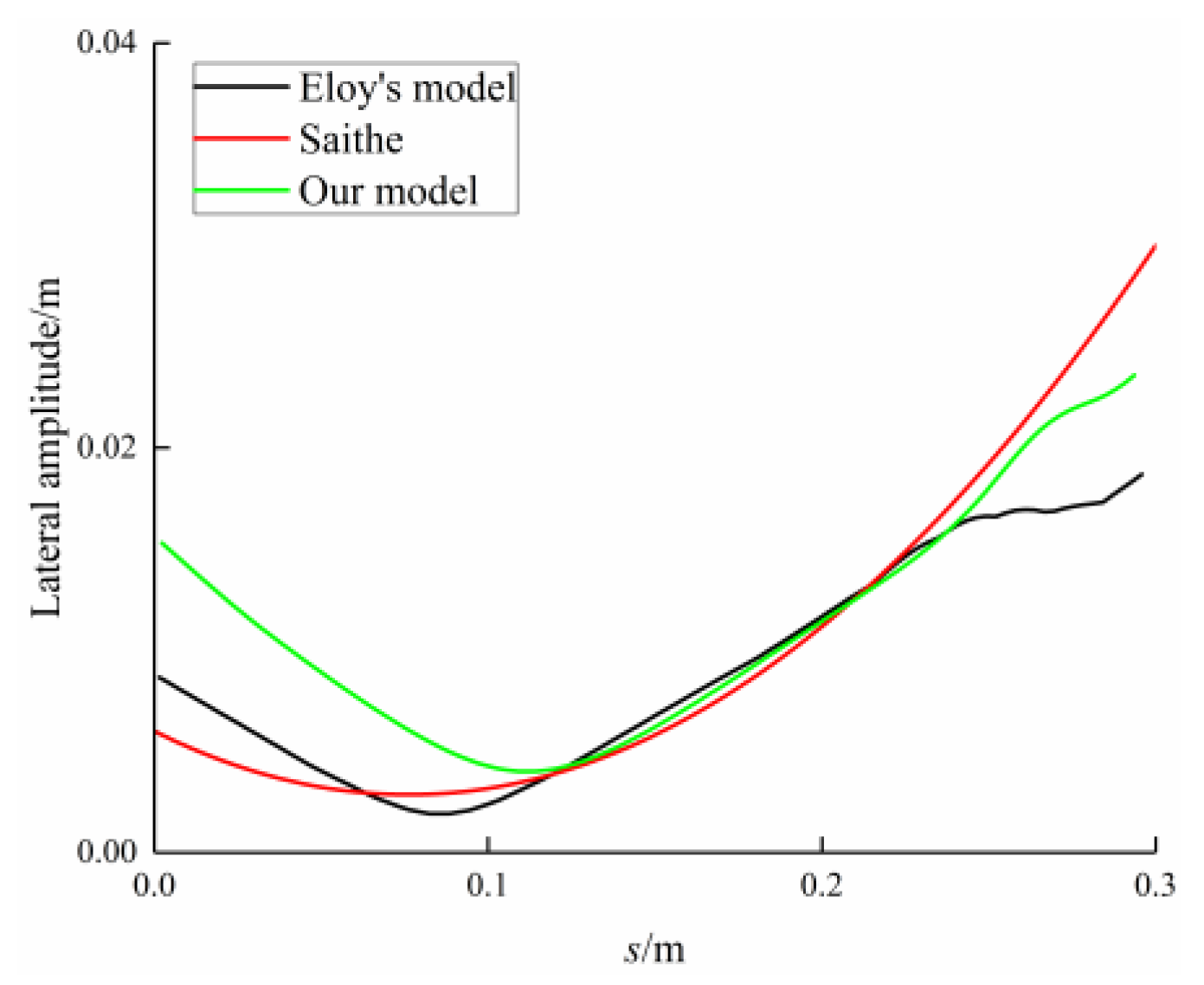
3.3. Curvature Amplitude
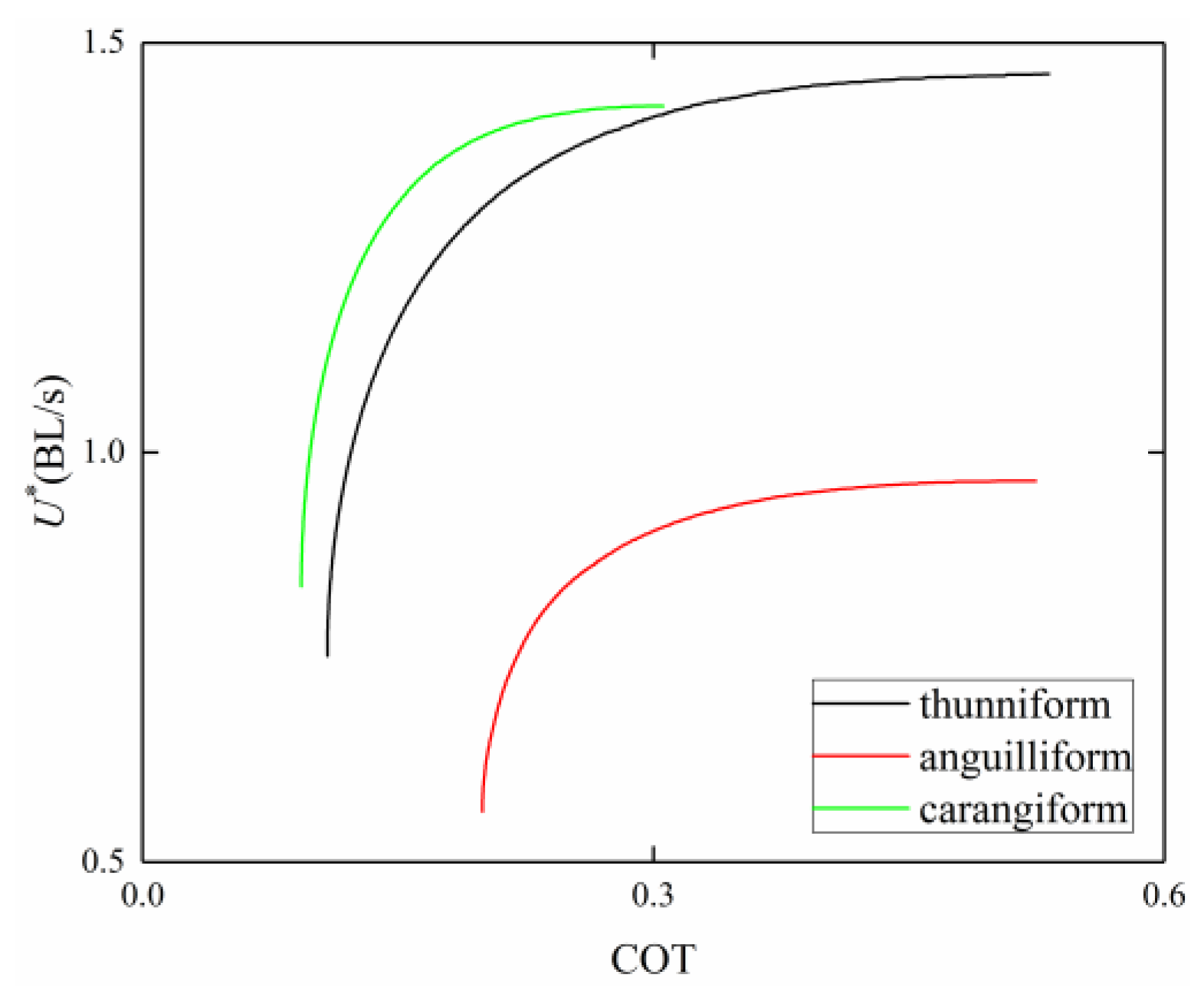
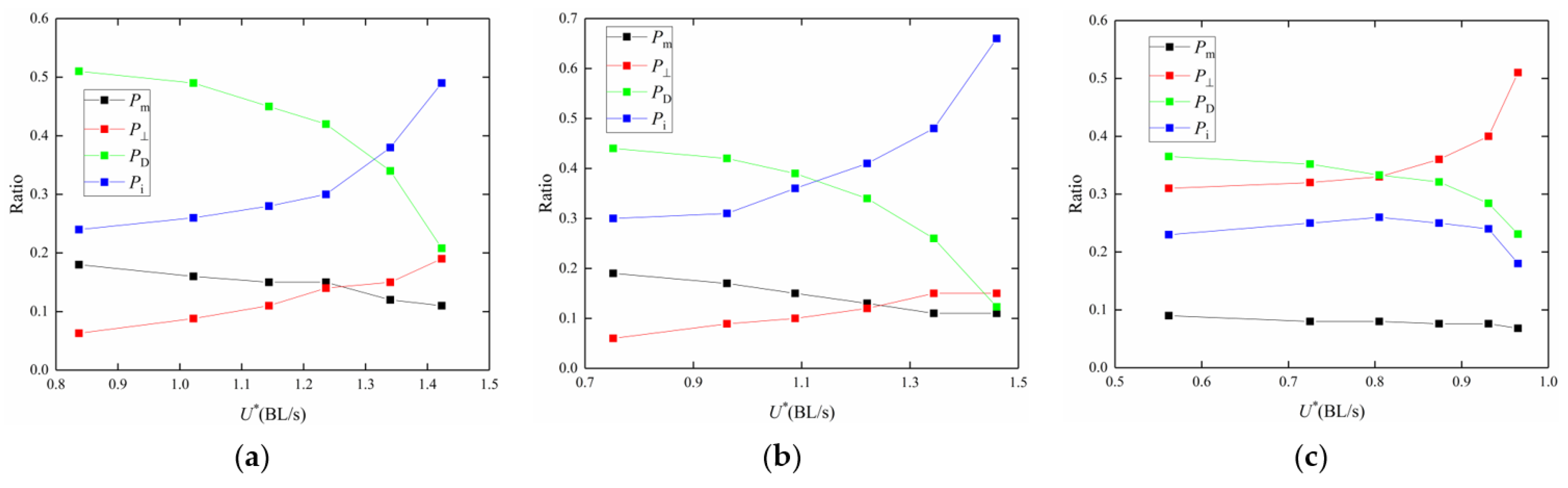
3.4. Comparison among BCF Fish
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sfakiotakis, M.; Lane, D.M.; Davies, J.B.C. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 1999, 24, 237–252. [Google Scholar] [CrossRef]
- Lindsey, C. Form, function and locomotory habits in fish. Locomotion 1978. [Google Scholar] [CrossRef]
- Wolf, Z.; Jusufi, A.; Vogt, D.; Lauder, G.V. Fish-like aquatic propulsion studied using a pneumatically-actuated soft-robotic model. Bioinspiration Biomim. 2020, 15, 046008. [Google Scholar] [CrossRef]
- Bhalla, A.P.S.; Griffith, B.E.; Patankar, N.A. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 2013, 9, e1003097. [Google Scholar] [CrossRef] [PubMed]
- Lauder, G.V. Fish locomotion: Recent advances and new directions. Annu. Rev. Mar. Sci. 2015, 7, 521–545. [Google Scholar] [CrossRef] [PubMed]
- Gray, J. Studies in animal locomotion: I. The movement of fish with special reference to the eel. J. Exp. Biol. 1933, 10, 88–104. [Google Scholar] [CrossRef]
- Videler, J.J.; Hess, F. Fast continuous swimming of two pelagic predators, saithe (Pollachius virens) and mackerel (Scomber scombrus): A kinematic analysis. J. Exp. Biol. 1984, 109, 209–228. [Google Scholar] [CrossRef]
- Gillis, G.B. Environmental effects on undulatory locomotion in the American eel Anguilla rostrata: Kinematics in water and on land. J. Exp. Biol. 1998, 201, 949–961. [Google Scholar] [CrossRef]
- Long, J.H.; Koob-Emunds, M.; Sinwell, B.; Koob, T.J. The notochord of hagfish Myxine glutinosa: Visco-elastic properties and mechanical functions during steady swimming. J. Exp. Biol. 2002, 205, 3819–3831. [Google Scholar] [CrossRef]
- Wardle, C.; Videler, J.; Altringham, J. Tuning in to fish swimming waves: Body form, swimming mode and muscle function. J. Exp. Biol. 1995, 198, 1629–1636. [Google Scholar] [CrossRef]
- Cheng, J.Y.; Blickhan, R. Bending moment distribution along swimming fish. J. Theor. Biol. 1994, 168, 337–348. [Google Scholar] [CrossRef]
- Hamlet, C.L.; Hoffman, K.A.; Tytell, E.D.; Fauci, L.J. The role of curvature feedback in the energetics and dynamics of lamprey swimming: A closed-loop model. PLoS Comput. Biol. 2018, 14, e1006324. [Google Scholar] [CrossRef] [PubMed]
- Gross, D.; Roux, Y.; Argentina, M. Curvature-based, time delayed feedback as a means for self-propelled swimming. J. Fluids Struct. 2019, 86, 124–134. [Google Scholar] [CrossRef]
- Williams, T.L.; McMillen, T. Strategies for swimming: Explorations of the behaviour of a neuro-musculo-mechanical model of the lamprey. Biol. Open 2015, 4, 253–258. [Google Scholar] [CrossRef]
- Johnson, T.P.; Syme, D.A.; Jayne, B.C.; Lauder, G.V.; Bennett, A.F. Modeling red muscle power output during steady and unsteady swimming in largemouth bass. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1994, 267, R481–R488. [Google Scholar] [CrossRef]
- Curtin, N.; Woledge, R. Efficiency of energy conversion during sinusoidal movement of white muscle fibres from the dogfish Scyliorhinus canicula. J. Exp. Biol. 1993, 183, 137–147. [Google Scholar] [CrossRef]
- Jayne, B.; Lauder, G. Red muscle motor patterns during steady swimming in largemouth bass: Effects of speed and correlations with axial kinematics. J. Exp. Biol. 1995, 198, 1575–1587. [Google Scholar] [CrossRef]
- Altringham, J.D.; Wardle, C.S.; Smith, C.I. Myotomal muscle function at different locations in the body of a swimming fish. J. Exp. Biol. 1993, 182, 191–206. [Google Scholar] [CrossRef]
- Bowtell, G.; Williams, T. Anguilliform body dynamics: Modelling the interaction between muscle activation and body curvature. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1991, 334, 385–390. [Google Scholar] [CrossRef]
- Bowtell, G.; Williams, T.L. Anguilliform body dynamics: A continuum model for the interaction between muscle activation and body curvature. J. Math. Biol. 1994, 32, 83–91. [Google Scholar] [CrossRef]
- McMillen, T.; Williams, T.; Holmes, P. Nonlinear muscles, passive viscoelasticity and body taper conspire to create neuromechanical phase lags in anguilliform swimmers. PLoS Comput. Biol. 2008, 4, e1000157. [Google Scholar] [CrossRef]
- McMillen, T.; Holmes, P. An elastic rod model for anguilliform swimming. J. Math. Biol. 2006, 53, 843–886. [Google Scholar] [CrossRef]
- Van Rees, W.M.; Gazzola, M.; Koumoutsakos, P. Optimal morphokinematics for undulatory swimmers at intermediate Reynolds numbers. J. Fluid Mech. 2015, 775, 178–188. [Google Scholar] [CrossRef]
- Eloy, C. On the best design for undulatory swimming. J. Fluid Mech. 2013, 717, 48–89. [Google Scholar] [CrossRef]
- Babu, S.P.M.; Sadeghi, A.; Mondini, A.; Mazzolai, B. Antagonistic pneumatic actuators with variable stiffness for soft robotic applications. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Korea, 14–18 April 2019; pp. 283–288. [Google Scholar]
- Li, Y.; Zhou, W.; Cao, Y.; Jia, F. Design of Embedded Structure Variable Stiffness Pneumatic Actuator. In Proceedings of the 2019 International Conference on Intelligent Robotics and Applications (ICIRA), Shenyang, China, 8–11 August 2019; pp. 234–239. [Google Scholar]
- Wright, B.; Vogt, D.M.; Wood, R.J.; Jusufi, A. Soft sensors for curvature estimation under water in a soft robotic fish. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Korea, 14–18 April 2019; pp. 367–371. [Google Scholar]
- White, C.; Lauder, G.V.; Bart-Smith, H. Tunabot Flex: A tuna-inspired robot with body flexibility improves high-performance swimming. Bioinspiration Biomim. 2020, 16, 026019. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; White, C.; Wainwright, D.K.; Di Santo, V.; Lauder, G.V.; Bart-Smith, H. Tuna robotics: A high-frequency experimental platform exploring the performance space of swimming fishes. Sci. Robot. 2019, 4. [Google Scholar] [CrossRef]
- Mahl, T.; Hildebrandt, A.; Sawodny, O. A variable curvature continuum kinematics for kinematic control of the bionic handling assistant. IEEE Trans. Robot. 2014, 30, 935–949. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, H.; Wang, X.; Liang, B. Approximate Piecewise Constant Curvature Equivalent Model and Their Application to Continuum Robot Configuration Estimation. In Proceedings of the 2020 IEEE International Conference on Systems, Man and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 1929–1936. [Google Scholar]
- Faulkner, J.; Dirven, S. A generalised, modular, approach for the forward kinematics of continuum soft robots with sections of constant curvature. In Proceedings of the 2017 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; pp. 1–6. [Google Scholar]
- Valdivia y Alvarado, P.P.A. Design of Biomimetic Compliant Devices for Locomotion in Liquid Environments. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Cui, Z.; Yang, Z.; Shen, L.; Jiang, H.Z. Complex modal analysis of the movements of swimming fish propelled by body and/or caudal fin. Wave Motion 2018, 78, 83–97. [Google Scholar] [CrossRef]
- Lighthill, M.J. Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1971, 179, 125–138. [Google Scholar]
- Taylor, G.I. Analysis of the swimming of long and narrow animals. Proc. the R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 214, 158–183. [Google Scholar]
- Hoerner, S.F. Fluid-Dynamic Drag. Theoretical, Experimental and Statistical Information; SF Hoerner Fluid Dynamics: Vancouver, WA, USA, 1965; pp. 108–112. [Google Scholar]
- Clarke, A.; Johnston, N.M. Scaling of metabolic rate with body mass and temperature in teleost fish. J. Anim. Ecol. 1999, 68, 893–905. [Google Scholar] [CrossRef]
- Webb, P.W. Hydrodynamics and energetics of fish propulsion. Bull. Fish. Res. Board Can. 1975, 190, 1–159. [Google Scholar]
- Videler, J.J. Fish Swimming; Springer: Berlin/Heidelberg, Germany, 1993; Volume 10. [Google Scholar]
- Gazzola, M.; Van Rees, W.M.; Koumoutsakos, P. C-start: Optimal start of larval fish. J. Fluid Mech. 2012, 698, 5–18. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Verma, S.; Hadjidoukas, P.; Wirth, P.; Rossinelli, D.; Koumoutsakos, P. Pareto optimal swimmers. In Proceedings of the 2017 the Platform for Advanced Scientific Computing Conference, Lugano, Switzerland, 26–28 June 2017; pp. 1–11. [Google Scholar]
- Tokić, G.; Yue, D.K.P. Optimal shape and motion of undulatory swimming organisms. Proc. R. Soc. B Biol. Sci. 2012, 279, 3065–3074. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, H.; Huang, Q.; Chen, W. Investigation of the Resonant Effect in Carangiform Locomotion. In Proceedings of the 2020 6th International Conference on Mechatronics and Robotics Engineering (ICMRE), Barcelona, Spain, 12–15 February 2020; pp. 58–62. [Google Scholar]
- Patel, N.K.; Singh Bhalla, A.P.; Patankar, N.A. A new constraint-based formulation for hydrodynamically resolved computational neuromechanics of swimming animals. J. Comput. Phys. 2018, 375, 684–716. [Google Scholar] [CrossRef]
- Boyer, F.; Porez, M.; Leroyer, A. Poincaré–Cosserat equations for the Lighthill three-dimensional large amplitude elongated body theory: Application to robotics. J. Nonlinear Sci. 2010, 20, 47–79. [Google Scholar] [CrossRef]
- Candelier, F.; Boyer, F.; Leroyer, A. Three-dimensional extension of Lighthill’s large-amplitude elongated-body theory of fish locomotion. J. Fluid Mech. 2011, 674, 196–226. [Google Scholar] [CrossRef]
- Triantafyllou, G.S.; Triantafyllou, M.; Grosenbaugh, M. Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Kern, S.; Koumoutsakos, P. Simulations of optimized anguilliform swimming. J. Exp. Biol. 2006, 209, 4841–4857. [Google Scholar] [CrossRef]
- Wiens, A.; Hosoi, A. Self-similar kinematics among efficient slender swimmers. J. Fluid Mech. 2018, 840, 106–130. [Google Scholar] [CrossRef]
- Eloy, C. Optimal Strouhal number for swimming animals. J. Fluids Struct. 2012, 30, 205–218. [Google Scholar] [CrossRef]
- Maertens, A.P.; Gao, A.; Triantafyllou, M.S. Optimal undulatory swimming for a single fish-like body and for a pair of interacting swimmers. J. Fluid Mech. 2017, 813, 301–345. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, H. Optimum Curvature Characteristics of Body/Caudal Fin Locomotion. J. Mar. Sci. Eng. 2021, 9, 537. https://doi.org/10.3390/jmse9050537
Liu Y, Jiang H. Optimum Curvature Characteristics of Body/Caudal Fin Locomotion. Journal of Marine Science and Engineering. 2021; 9(5):537. https://doi.org/10.3390/jmse9050537
Chicago/Turabian StyleLiu, Yanwen, and Hongzhou Jiang. 2021. "Optimum Curvature Characteristics of Body/Caudal Fin Locomotion" Journal of Marine Science and Engineering 9, no. 5: 537. https://doi.org/10.3390/jmse9050537
APA StyleLiu, Y., & Jiang, H. (2021). Optimum Curvature Characteristics of Body/Caudal Fin Locomotion. Journal of Marine Science and Engineering, 9(5), 537. https://doi.org/10.3390/jmse9050537





