1D–3D Coupling for Gas Flow Analysis of the Air-Intake System in a Compression Ignition Engine

Abstract

Devices for reducing environmental pollutant emissions are being installed in ship compression ignition (CI) engines; alternatively, the designs of intake and exhaust pipes and ports are being modified to tune the performance according to the user’s needs. In both cases, substantial computation time and cost are required to simulate the gas flow of the CI engine with an air-intake system. In order to simulate the air-intake system of the CI engine, which changes according to the user’s needs, at a low cost and in a short time, we aimed to analyze the gas flow using a 1D–3D coupled method. The 1D zone was analyzed using the method of characteristics, and the 3D zone was analyzed using the commercial computational fluid dynamics (CFD) code Ansys Fluent R15.0, whereas their coupling was achieved by applying the developed 1D–3D coupling algorithm to Ansys Fluent R15.0 using user-defined functions (UDFs). In the comparison of the pressure of the intake pipe with the experimental result, the average error was 0.58%, thereby validating the approach. In addition, when analyzing the intake pipe and port in a 3D zone, the results of the velocity and pressure were expressed as contours, allowing them to be visualized. It is expected that the 1D–3D coupling algorithm of the air-intake system can be used to reflect the user’s needs and can be used as a method to quickly and accurately calculate the gas flow within tens of minutes.

1. Introduction

It is important for ship engines to reduce emissions of environmental pollutants, while maintaining performance, efficiency, and stability. The International Maritime Organization (IMO) has implemented regulations to reduce emissions of air pollutants such as CO₂, SOx, and NOx from ships. The energy efficiency design index (EEDI) related to CO₂ emissions requires a minimum energy efficiency level per capacity mile (e.g., tonne mile) for different ship type and size segments. Since the level is to be tightened incrementally every five years, and so the EEDI demands continuous innovation and technical development of all the components influencing the fuel efficiency of a ship from its design phase [1]. Regulations related to emissions of SOx and NOx have increased the number of ships installing environmental pollutant emissions reduction devices such as scrubbers, exhaust gas recirculation (EGR) [2], and selective catalytic reduction (SCR) [3]; alternatively, they use liquefied natural gas (LNG) as fuel [4]. Since the use of LNG as fuel must be considered during the ship’s construction phase, existing ships are using low sulfur fuel oils (LSFOs) to reduce SOx emission. LSFOs are now replacing the traditional intermediate bunker fuels and heavy fuel oils with ultra-low sulfur fuel oils (ULSFO) (sulfur < 0.1% m/m) for use in the sulfur emission control area (SECA) in Europe and North America from 2015, and a global sulfur cap regulation was implemented from 2020 with very low sulfur oils (VLSFO) (sulfur < 0.5%m/m) [5]. When the fuel is changed to LSFO, etc., the intake and exhaust gas flows will be different, and the application of an environmental pollutant emission reduction system to a ship’s compression ignition (CI) engine requires analysis of the gas flow in the intake system to predict performance. In CI engines, the gas flow in the intake and exhaust system is pulsating flow with periodic pressure vibrations [6], and it has the characteristics of a variable wavelength depending on the shape of the manifold and pipe, resulting in pressure waves, reflective waves, overlapping waves, interference, resonance, etc. [7]. In the intake system, these various characteristics work in combination, so it is necessary to design the shape of the intake pipe and port considering the results of the gas flow analysis.

Experimental studies and numerical analysis studies are being conducted on ways to analyze the performance characteristics of the engine and reduce emissions, and as an experimental method, studies on the fuel system are being conducted. Beatrice et al. evaluated the power density sensitivity to the engine operating parameters by conducting an experimental study on the functional requirements for the diesel engine. The advantage of using a very high fuel injection pressure was confirmed, and a compromise that combines high performance and fuel economy was proposed [8]. Blasio et al. conducted research on the diesel engine’s CO₂ emission and fuel injection system, and analyzed the effect of the decrease in peak firing pressure on fuel economy, emissions, etc., and confirmed the advantage of using a high injection pressure [9]. An experimental study on the fuel used in the engine was carried out by Puškár et al., who studied the effect of reducing gaseous emissions by mixing biodiesel with marine diesel engines [10]. In order to reduce the emission of environmental pollutants as well as experimental studies, parallel numerical analysis is being conducted, and Lamas et al. characterized the pre-injection pattern suitable for Wärtsilä 6L 46, a marine diesel engine, using a computational fluid dynamics (CFD) model verified by the experimental results [11].

Methods for predicting intake flow using a numerical analysis of intake systems in CI engines and for reducing fuel consumption or improving volume efficiency have been proposed in previous research. Battista et al. studied how to manage intake flow and temperature to reduce fuel consumption and environmental pollutants, and they confirmed the impact of low-temperature intake on internal combustion (IC) engines using EGR and others [12]. Furthermore, studies by Pelić et al. related to the effect of the intake system of ship engines on NOx emissions and a reduction in fuel consumption found that the fuel consumption and cylinder pressure and temperature are affected by the valve timing of the intake system and pressure in the intake manifold [13]. Gas flow analysis was also used to study the design, performance, and knocking of natural gas (NG)-fueled engines, and Xiang et al. used the commercial CFD code GT-Power to provide basic parameters and necessary numerical tools and frameworks that affect the knocking behavior of NG fuel engine operations [14]. To predict the 1D unsteady compressible flow of engine air path systems, Stockar et al. compared two different models and presented a compromise in terms of computational time, accuracy, and stability in simulating the engine in real time [15].

If 3D modeling and commercial CFD codes are used to simulate gas flow in the intake system, various analysis models such as chemical reactions and multiphase flow can be applied, and it is possible to model real motion using a dynamic mesh. However, the fact that high-end workstations are needed for calculation, in addition to extensive computation time, presents a problem; thus, it is not suitable to analyze gas flow by modeling the entire engine system in 3D [16].

Among the 1D gas flow analysis methods, the method of characteristics (MOC) has a fast calculation time, and the accuracy of the calculation results in a straight pipe has been proven; however, the accuracy of the calculation results is poor in complex shapes such as bent pipes, tapered pipes, and junctions [17]. In addition, it is difficult to visualize the gas flow because it is impossible to express calculation results such as pressure and velocity as contours, and there is a disadvantage in that there is a limitation in applying various analysis models. Therefore, a method of coupling 1D and 3D has been used to analyze the gas flow of the cylinder and the intake and exhaust systems of the CI engine.

The numerical analysis method using 1D–3D coupling can cope with changes in shape and achieve rapid calculation, allowing results to be efficiently obtained for various models. For this reason, advanced research is being conducted on numerical analysis for engines using 1D–3D coupling. Torre et al. simulated fluid dynamics using a coupled 1D–quasi-3D approach for IC engine intake and exhaust systems [18]. An automatic quasi-3D grid generator was developed, and the fully 3D and quasi-3D OpenFOAM models were coupled with the 1D code GASDYN to simulate the entire engine system. Onorati et al. performed a 1D–3D fluid dynamic simulation for intake and exhaust systems of a turbocharged diesel engine [19]. In addition to analyzing the flow field of the manifold, which is the main advantage of the 1D–3D simulation, it was confirmed that the predicted wave motion in the intake and exhaust system showed better results compared to the measured data. Millo et al. analyzed the gas flow inside the cylinder of a diesel engine by coupling the 1D commercial code GT-SUITE and the 3D commercial code CONVERGE CFD [20]. A 1D–3D coupling function built in a commercial code was used, and a method of predicting the performance of a diesel engine was proposed using the results of gas flow analysis. Dimitriou et al. analyzed gas flow for the exhaust gas recirculation system by coupling the 1D commercial code GT-POWER and the 3D commercial code STAR-CCM [21]. It was found that the 1D–3D coupling function built in the commercial code could obtain accurate results only when analyzing the gas flow for an analysis model that can be accurately calculated using only the 1D code without coupling it with the 3D code.

The above-described studies performed numerical analyses for non-ship engines, and there is a limitation in that the calculation formulas cannot be modified because a 1D–3D coupling function built in a commercial CFD code was used. If there is a limitation that the expression used for calculation cannot be modified according to the user’s request, it then cannot be used to study the physical correlation with the calculation result by analyzing the calculation process. Furthermore, because the built-in 1D–3D coupling method of commercial codes is a method of applying the calculation result of a 1D code to the boundary conditions of a 3D code, there is a functional limitation whereby coupled 1D–3D approaches are only applicable for analysis models that can be used in 1D code. Because of these functional limitations and the disadvantage of not being able to freely modify the calculation formula, the previous methods are not suitable for the simulation of the intake system of a ship CI engine tailored to the needs of various users.

In order to install additional environmental pollutant emission reduction devices in ship engines or to design CI engines to meet the needs of users who want to perform performance tuning and to calculate the kinetic energy of the exhaust gas acting on the turbine for turbocharger matching [22], the design of the intake and exhaust pipes and ports is being revised, necessitating substantial computation time and cost to perform simulations to predict the performance of custom-designed CI engines [23]. The purpose of this study was to develop a 1D–3D coupling algorithm that can analyze the gas flow of a CI engine at a low cost and in a short time, as well as to propose a 1D–3D coupled gas flow analysis method for the air-intake system. In order to reduce the time required for calculation, only the part that needs to be visualized is modeled as a 3D zone. The 1D–3D coupling algorithm was written in user-defined functions (UDFs) based on the MOC, and the 1D and 3D zones were simultaneously calculated using the commercial CFD code Ansys Fluent R15.0. Compared with the experimental results, the results of the gas flow analysis were verified, and we propose a simulation method capable of actively responding to changes in various intake systems and capable of rapid calculations at low cost. We intend to use the 1D–3D coupling gas flow analysis method of the air-intake system proposed in this study to predict the flow state and performance according to the shape of the intake system in the development stage of ship CI engines. In addition, by reducing the computational time required for numerical analysis of the gas flow of the entire engine system to a level of several minutes, we intend to use it to develop a simulation model that can respond quickly to changes in the intake and exhaust systems. In the following section, we will discuss the theory used in the calculation of the 1D zone, the 1D–3D coupling method, and the verification compared with the experimental results.

2. Theoretical Interpretation

In order to analyze the gas flow of the engine in the 1D zone of the cylinder, it is necessary to calculate the cylinder pressure and the mass flow rate into or out of the cylinder [24]. In the calculation using the MOC, the boundary conditions of the cylinder are calculated by including the timing profile of the valve in the logic, and the calculation sequence involves calculating the mass flow rate and then the cylinder pressure.

2.1. Mass Flow Rate into or out of the Cylinder

In order to use the MOC, the mass flow rate ($m)$ is expressed as a nondimensional form ($\xi )$ as follows [25]:

$$\xi =\frac{m\times a_{01}}{p_{01}\times F}\times {\left[\left(\frac{2\times {\kappa }^2}{\kappa -1}\right)\times {\left(\frac{p_2}{p_{01}}\right)}^{\frac{2}{\kappa }}\times \left\{1-{\left(\frac{p_2}{p_{01}}\right)}^{\frac{\kappa -1}{\kappa }}\right\}\right]}^{\frac{1}{2}},$$

(1)

where $a$ is the speed of sound, $p$ is the pressure, $F$ is the opening area of the intake valve, $\kappa$ is the specific heat ratio (1.4 for air), subscript 0 represents stagnation conditions, subscript 1 represents upstream conditions, and subscript 2 represents downstream conditions. $\left(p_2/p_{01}\right)$ denotes the pressure ratio of the flow before and after passing through the valve; on the other hand, when the flow is choked, Equation (1) becomes:

$$\xi =\frac{m\times a_0}{p_0\times F}=\kappa \times {\left(\frac{2}{\kappa +1}\right)}^{\frac{\kappa +1}{2\left(\kappa -1\right)}}.$$

(2)

Using the pressure ratio $\left(p_2/p_{01}\right)$ of the cylinder and the intake port, the mass flow rate ($m)$ of the intake air into the cylinder over time is as follows:

$$\frac{dm}{dt}=\frac{p_{01}F}{a_{01}}f\left(\frac{p_2}{p_{01}}\right)\times {10}^5\mathrm{kg}/\mathrm{s}.$$

(3)

The mass flow ($m)$ is a positive value when the flow is into the cylinder; $p_{01}$ is the intake air pressure, $p_2$ is the cylinder pressure, and $a_{01}$ is the air stagnation speed of sound. Conversely, when flow is out of the cylinder, $m$ is represented by a negative value; $p_{01}$ is the cylinder pressure, $p_2$ is the intake pressure, and $a_{01}$ is the cylinder stagnation speed of sound.

2.2. Cylinder Pressure

The cylinder pressure $(p_c)$ can be calculated using the mass flow rate ($m)$ into or out of the cylinder [25].

$$\frac{d{p}_c}{dt}=\frac{1}{V_c}\left\{a_{0a}^2{\left(\frac{dm}{dt}\right)}_a-a_c^2{\left(\frac{dm}{dt}\right)}_e-\kappa p_c\frac{d{V}_c}{dt}\right\},$$

(4)

where $V_c$ is the volume of the cylinder, the subscript $a$ represents the air-intake conditions, and the subscript $e$ represents the exhaust conditions. The mass flow rate ${\left(dm/dt\right)}_e$ of the exhaust gas denotes the value passing through the exhaust valve, whereas the mass flow rate ${\left(dm/dt\right)}_a$ of the intake air is obtained using Equation (3). The mass balance of the cylinder can be expressed as Equation (5), which can be applied to the calculation for a single-cylinder engine.

$$\frac{d{m}_c}{dt}={\left(\frac{dm}{dt}\right)}_a-{\left(\frac{dm}{dt}\right)}_e.$$

(5)

3. 1D–3D Coupling Methodology

3.1. Modeling

Figure 1 shows a schematic diagram of the CI engine, which is the target of gas flow analysis using the 1D–3D coupling method and the pressure measurement location for validation, while the engine components are modeled by dividing it into 1D and 3D zones. In order to shorten the time required for calculation, only the intake pipe and the intake port of the intake system, which are the targets for which the results should be visualized, were modeled in 3D, and areas such as the cylinder, exhaust pipe, and reservoir were modeled in 1D. The 1D–3D coupling faces were created at two positions, i.e., the positions of the intake valve and the intake pipe. The coupling method in the intake pipe used the 1D–3D coupling algorithm of the pipe systems developed in the author’s previous work. This is a method that coupled 1D and 3D zones using characteristics that meet at the coupling face, and is a suitable method for use in straight pipes [26].

The 1D–3D coupling algorithm code was written in UDFs using the C language, and Figure 2 shows the location where the 1D–3D coupling algorithm UDFs were applied. The structure of the 1D code for analyzing the gas flow of the CI engine consists of the main program, as well as the cylinder, intake, and exhaust subroutines, whereby the cylinder subroutine calculates the mass balance, volume, and pressure of the cylinder [27].

1D–3D Coupling Algorithm for the Air-Intake System

In the gas flow analysis using the 1D–3D coupling algorithm, the 1D zones were calculated using the MOC and the code was written in C language, while the 3D zones were calculated using the commercial CFD code Ansys Fluent R15.0 using the finite volume method. The 1D–3D coupling algorithm was developed as a method of obtaining characteristics or physical quantities that meet at the coupling face, where the calculation results of each zone are applied to the calculation of 1D and 3D zones.

Figure 3 shows the data exchange process of the 1D–3D coupling algorithm code [28]. The data exchange process starts by setting the initial value in the 1D zone and compiling the UDFs in the 3D zone. In the 3D zone, the 1D–3D coupling face is the boundary condition, and the boundary condition of the 3D zone applies the result calculated in UDF using the PROFILE function. The 3D zone to which the boundary condition is applied is calculated according to the analysis conditions set in the commercial CFD code Ansys Fluent R15.0, and the calculation is repeated until the calculation results converge. When the calculation converges, the calculation result of the 3D zone is transmitted to the UDF using the ADJUST function. At this time, the 1D–3D coupling algorithm is performed using the calculation result of the transmitted 3D zone; in the subsequent step, the calculation is repeated using the calculation result from the previous time step instead of the initial value.

The 1D–3D coupling algorithm of the intake gas flow, which couples the intake port in the 1D zone and the cylinder in the 3D zone at the position of the intake valve, is a method of coupling that uses the pressure and speed of sound of the coupling face; a flow chart is shown in Figure 4. The pressure and speed of sound at the 1D–3D coupling face of the intake port are applied to the intake subroutine, and the intake air mass flow rate is calculated using the pressure in the 3D zone, while the gas flow state is determined using the stagnation speed of sound of the intake gas flow in the 3D zone.

Depending on the direction of the gas flow, the method of calculating the mass balance of the cylinder varies. The gas flow into the cylinder is calculated using the pressure and speed of sound in the 3D zone, whereas the gas flow out of the cylinder is calculated using the pressure and speed of sound in the 1D zone. The pressure of the intake gas flow can be calculated using the mass flow rate obtained by the intake subroutine, the mass balance of the cylinder, and the opening area of the intake valve. The gas flow of the intake port and cylinder is calculated by applying the pressure result of the intake gas flow to each zone according to the calculation order on the 1D–3D coupling face.

3.2. Time Step Size

Since the time step size of the 1D zone is calculated using the MOC, and the time step size of the 3D zone is calculated using the Courant number, the time step sizes of the 1D zone and the 3D zone are different [29]. In addition, since the time step size is proportional to the size of the mesh, the time step size is smaller in the 3D zone, where the size of the mesh is small compared to the 1D zone.

Figure 5 shows the process of synchronizing time steps in 1D–3D coupling. The nondimensional distance n of the X-axis represents the position of the mesh, whereas 1D and 3D are coupled at n + 1. When the initial time step is 0, the slope of the characteristics is the same because it is calculated by the initial value. Thereafter, the time step size of the 3D zone is calculated according to the Courant number; when the current time exceeds the 1D zone, the time step size is synchronized using linear interpolation.

4. Validation

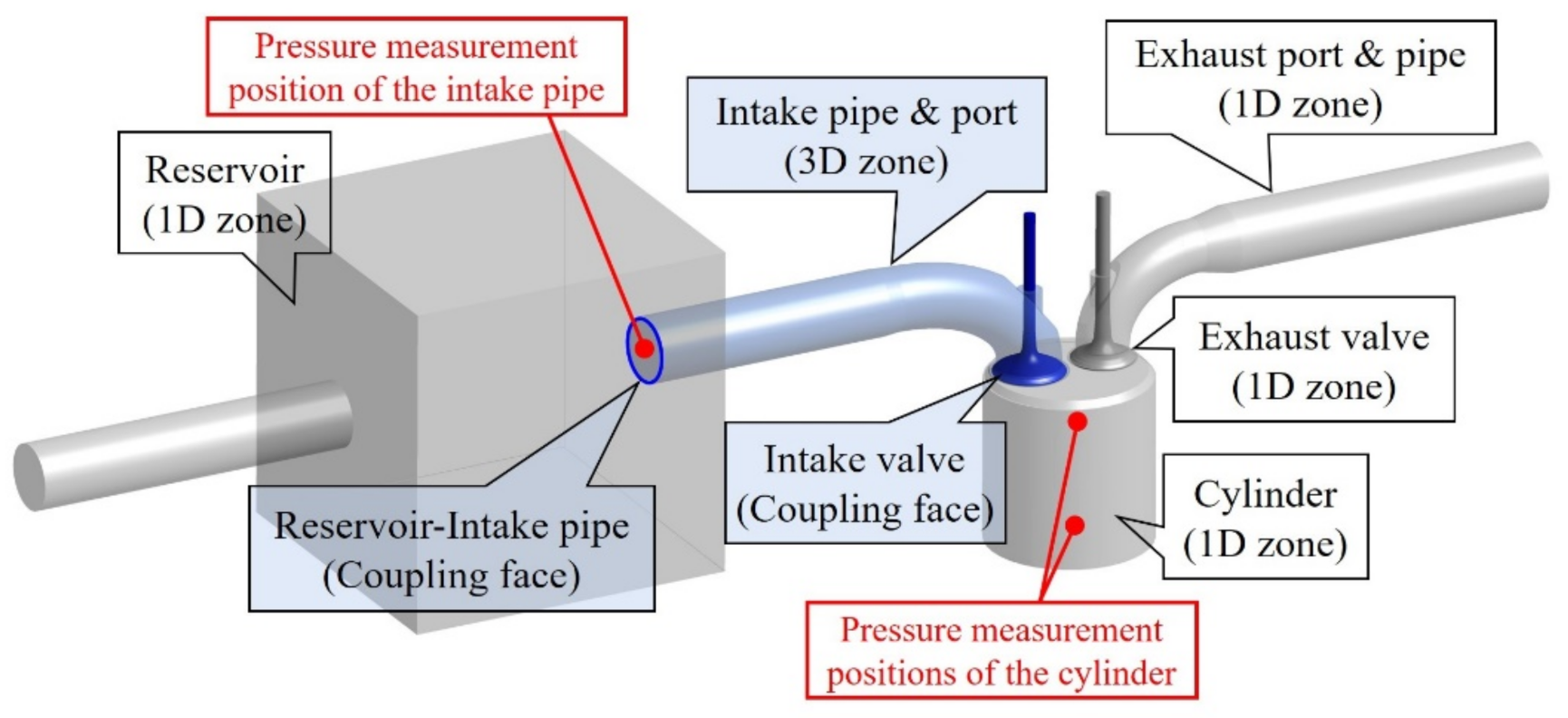
In order to verify the results of analyzing the gas flow using the 1D–3D coupling algorithm for the air-intake system of the CI engine, the results were compared with the results measured through experiments. In order to develop an experiment with the same characteristics as the gas flow analysis conditions, the intake pipe and cylinder pressures were measured in cold flow by connecting an electric motor to the flywheel of the experimental apparatus engine, comparing the results at engine speeds of 700, 900, and 1100 RPM.

Figure 6 shows a comparison of the cylinder pressure results measured through the experiment and the cylinder pressure results of the 1D–3D coupling gas flow analysis. When the cylinder pressure increased and decreased, the results of the experiment and analysis were the same; furthermore, since the valve profile of the experimental apparatus engine was applied to the gas flow analysis, the timing of the increase and decrease in the pressure result was considered to be the same.

Table 1. Peak cylinder pressure results of the 1D–3D gas flow analysis and experiment.

Engine Speed (RPM)	Peak Cylinder Pressure (Bar)		Error (%)
	Experimental	1D–3D Coupling
700	36.39	36.96	1.57
900	38.00	38.90	2.37
1100	38.35	39.30	2.48

presents a comparison of the analysis results based on the results of measuring the peak cylinder pressure through an experiment, whereby the peak cylinder pressure was found at the TDC (0 CA°) of the compression stroke. Compared with the experimental results, the result of gas flow analysis was considered to be valid because there was an average pressure error of 2.14%. It is expected that the results of the gas flow analysis will appear higher than the experimental results because of the difference between the theoretical calculation and the actual phenomenon, but the error is expected to decrease in the future if the exhaust system is modeled on the shape of the experimental device and calculated in a 3D zone.

Figure 7 shows a comparison of the cylinder pressure results for the process of closing the intake valve (482–598 CA°) during the gas exchange process of the cylinder. At this time, the piston moves downward to the BDC (540 CA°); however, since the intake valve is open, there is little change in the cylinder pressure. After the BDC (540 CA°), the piston moves upward, and the cylinder pressure increases. After the AVC (580 CA°), the intake valve is closed, and the cylinder pressure increases significantly. In the results of the 1D–3D coupling gas flow analysis, the phase during which the cylinder pressure increased was similar to that found experimentally.

Table 2. Cylinder pressure results of the 1D–3D gas flow analysis and experiment when the air-intake valve was closed (580 CA°).

Engine Speed (RPM)	Cylinder Pressure at AVC (Bar)		Error (%)
	Experimental	1D–3D Coupling
700	1.92	1.84	4.17
900	1.95	1.86	4.62
1100	2.03	1.96	3.45

presents a comparison of the results of cylinder pressure at the AVC (580 CA°), which is the moment when the intake valve is closed. In a study by Tadros et al. comparing simulated data and measured data of in-cylinder pressure at three different loads, the error was found to be less than 5.7% [30]. In this study, when comparing the cylinder pressure measured through the experiment as a standard, the pressure error occurring in the result of the 1D–3D coupling gas flow analysis was, on average, 4.08%, which can be considered a valid result.

Figure 8 shows a comparison of the result of 1D–3D coupling gas flow analysis based on the result of measuring the pressure of the intake pipe through the experiment, highlighting the pressure of the intake pipe at 342–580 CA° when the intake valve was opened. Since the intake air entered the cylinder from the time the intake valve was opened, negative pressure appeared in the intake pipe, and the time at which the maximum negative pressure appeared slowed as the engine speed increased. As for the phase of pressure change, the results of the experiment and the 1D–3D coupling gas flow analysis were similar, whereby the pressure of the intake pipe increased after the TDC (360 CA°). After the valve overlapping period, the pressure in the intake pipe increased to atmospheric pressure, and a phase in which the pressure decreased to near the BDC (540 CA°) appeared.

Table 3. Maximum negative pressure results of the 1D–3D gas flow analysis, experiment, and 1D gas flow analysis (author’s previous study) in the intake pipe when the air-intake valve was open.

Engine Speed (RPM)	Maximum Negative Pressure (bar)			Error (%)
	Experimental	1D–3D Coupling	1D Analysis (Author’s Previous Study)	1D–3D	1D
700	0.9687	0.9636	0.9550	0.53	1.41
900	0.9582	0.9518	0.9391	0.67	1.99
1100	0.9414	0.9363	0.9209	0.54	2.18

presents a comparison of the maximum negative pressure results of the 1D–3D coupling gas flow analysis based on the maximum negative pressure of the intake pipe measured through the experiment. The maximum negative pressure results of the 1D–3D gas flow analysis was 0.58% on average, and the error was reduced by 1.28% compared to the average of 1.86% in the author’s previous study, which analyzed the gas flow by modeling the entire CI engine in 1D. The reason for the reduction in error compared to the results of the 1D gas flow analysis is that it is possible to calculate the influence of the reflected wave generated when the flow passes through a complex shape by calculating the intake ports that are bent or tapered in a 3D zone, thus facilitating an accurate calculation of the influence of pressure and reflected waves.

5. Conclusions

A 1D–3D coupling algorithm was developed for the air-intake system of a CI engine, and the result of analyzing gas flow through its application was verified by comparing it with an experimental study. In terms of the peak pressure of the cylinder, the magnitude and phase of the pressure were similar to the experimental results, and the pressure result of the cylinder during the intake gas exchange process was also similar to the experimental results, thereby verifying the results.

In addition, valid results were obtained by comparing the results of the 1D–3D combined gas flow analysis of the intake pipe pressure with the experimental results; moreover, using the 1D–3D coupling algorithm to analyze the gas flow, it was possible to reduce the error in magnitude and phase of the pressure that occurred in the 1D gas flow analysis. In order to accurately calculate the influence of the pressure wave and the reflected wave of the gas flow passing through the intake port, which is a complex shape, it was considered necessary to model this in a 3D zone.

In the gas flow analysis using the 1D–3D coupling algorithm, results such as the velocity and pressure of the intake port and pipe, which are 3D zones, can be expressed as contours. Therefore, they can be used to observe detailed gas flow, design the shape of the intake port, and predict the performance of the CI engine according to the shape. Figure 9 shows the result of the velocity of gas flow passing through the intake port at the moment when the intake valve was fully open. This is a state in which gas flow enters the cylinder through the intake port. As the gas flow passed through the bend, the speed increased, whereby a faster engine speed led to greater differences in speed distribution. Figure 10 shows the pressure result as a contour at the same moment, showing the area where the pressure increased or decreased while passing through the bend area of the intake port. In this way, it was possible to analyze the contours of the analysis results by modeling the shape of bent and tapered pipes in 3D, which would be simplified to straight pipes in a 1D gas flow analysis.

The time required to analyze the gas flow of the CI engine using the 1D–3D coupling in this study was about 20 minutes using a computer with an 8-core central processing unit (CPU) for the 700 RPM model. It is expected that this can be used as a numerical analysis method that can quickly obtain calculation results without using a high-resolution workstation.

A 1D–3D coupling algorithm was developed to analyze gas flow by modeling the cylinder and exhaust system in 1D and the intake system in 3D for CI engines, and the results were verified through comparison with an experiment, as summarized below:

(1)

Using the MOC and a commercial CFD code, a 1D–3D coupling algorithm was developed that can analyze the gas flow of the air-intake system of a CI engine in 3D.

(2)

The 1D–3D coupling algorithm of the intake system was able to calculate the influence of the reflected waves on bent and tapered pipes, and its validity was verified upon obtaining an error of 0.58% as a result of comparing the calculation with the pressure of the intake pipe achieved through an experiment.

(3)

The calculation could be completed within tens of minutes using the 1D–3D coupling algorithm of the air-intake system, and it is expected to be used as a method to accurately and quickly calculate the unsteady gas flow of various ship CI engines.

If it is used in conjunction with the 1D–3D coupling gas flow analysis of exhaust systems in the future, it is expected that it can be used to analyze the effect of the environmental pollutant emissions reduction devices installed in the intakes and exhaust systems of CI engines.