Effect of Depth-Induced Breaking on Wind Wave Simulations in Shallow Nearshore Waters off Northern Taiwan during the Passage of Two Super Typhoons
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Cases
2.2. Information on Offshore Wave Buoys
2.3. Direct Modification of Typhoon Winds from ERA5
2.4. Configuration of the Wave-Circulation Modeling System
2.5. Parameterization of Depth-Induced Wave Breaking
2.5.1. BJ78 Model
2.5.2. TG83 Model
2.5.3. CT93 Model
2.6. Parameterization of the Wave-Breaking Index
2.6.1. Constant Wave Breaking Criterion (γ)
2.6.2. Wave Breaking Criterion Based on Local Steepness or Peak Steepness
3. Results
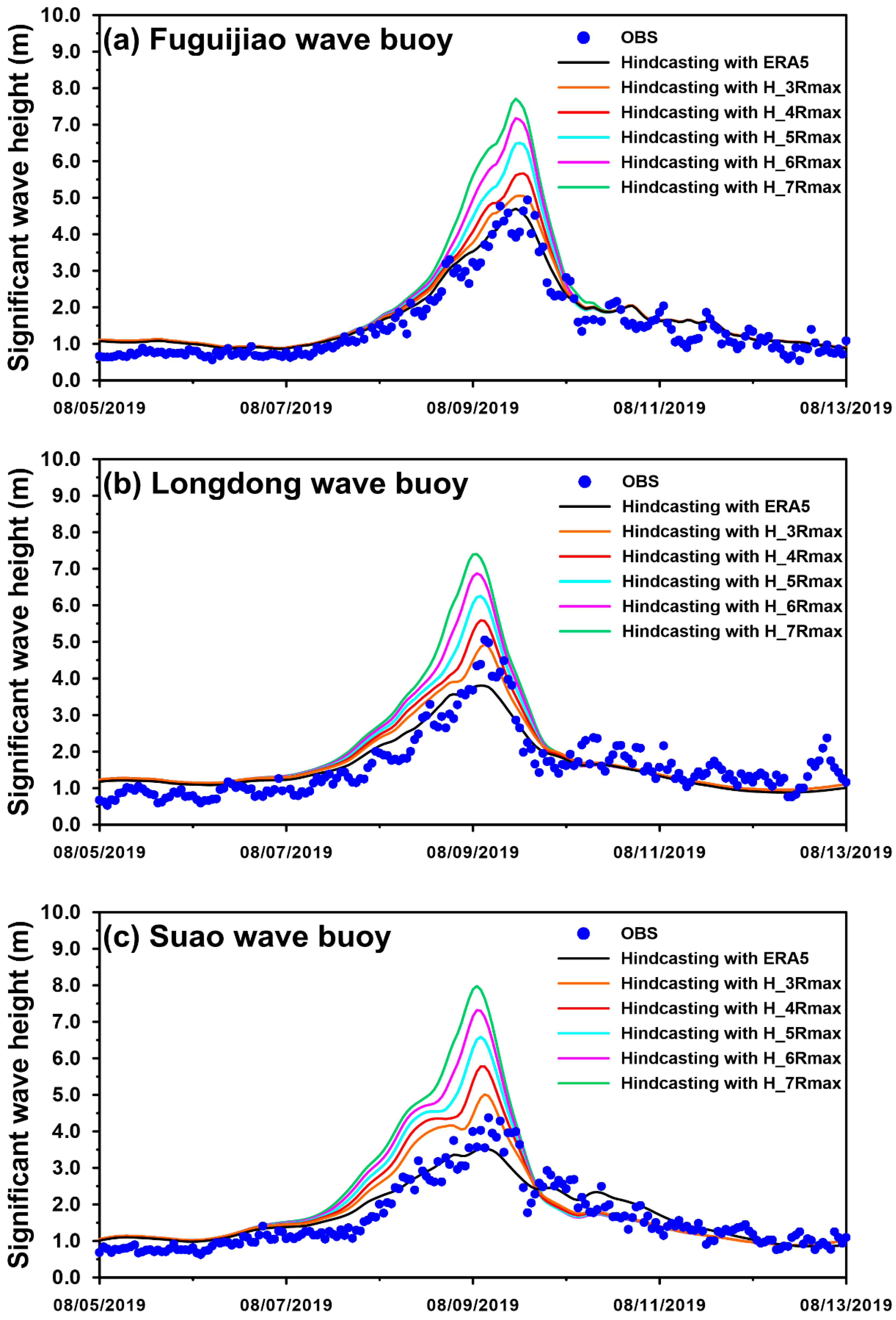
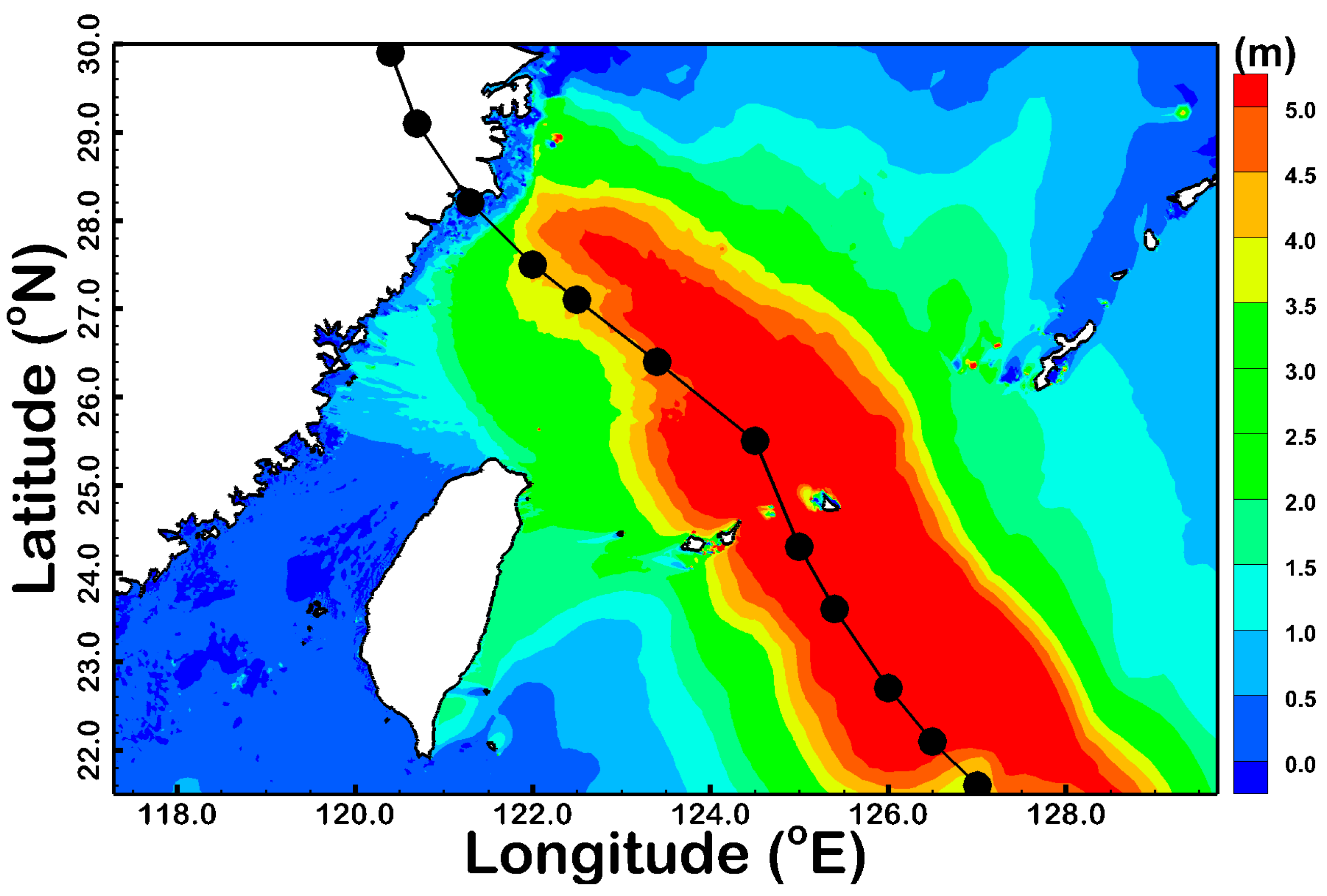
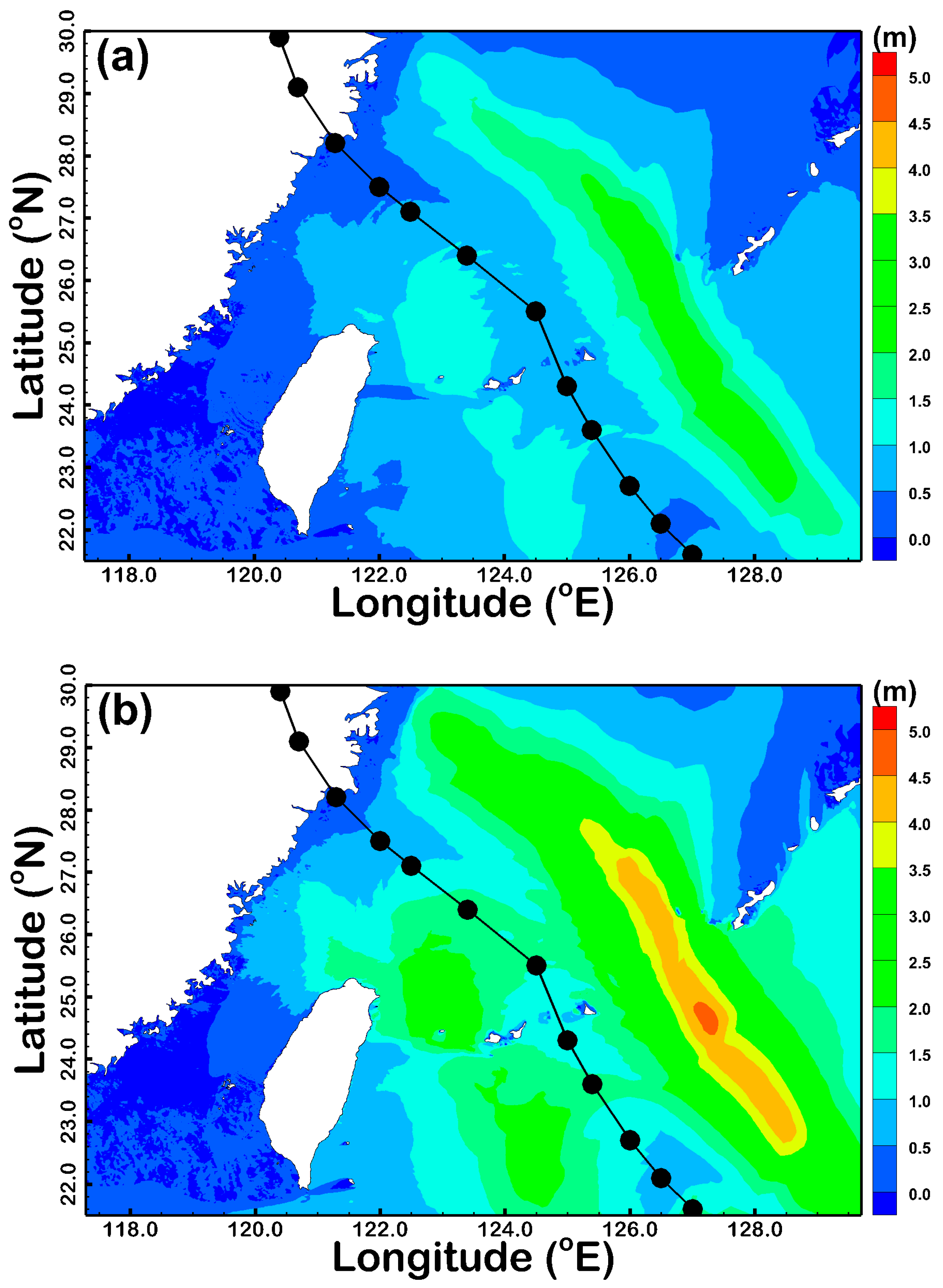
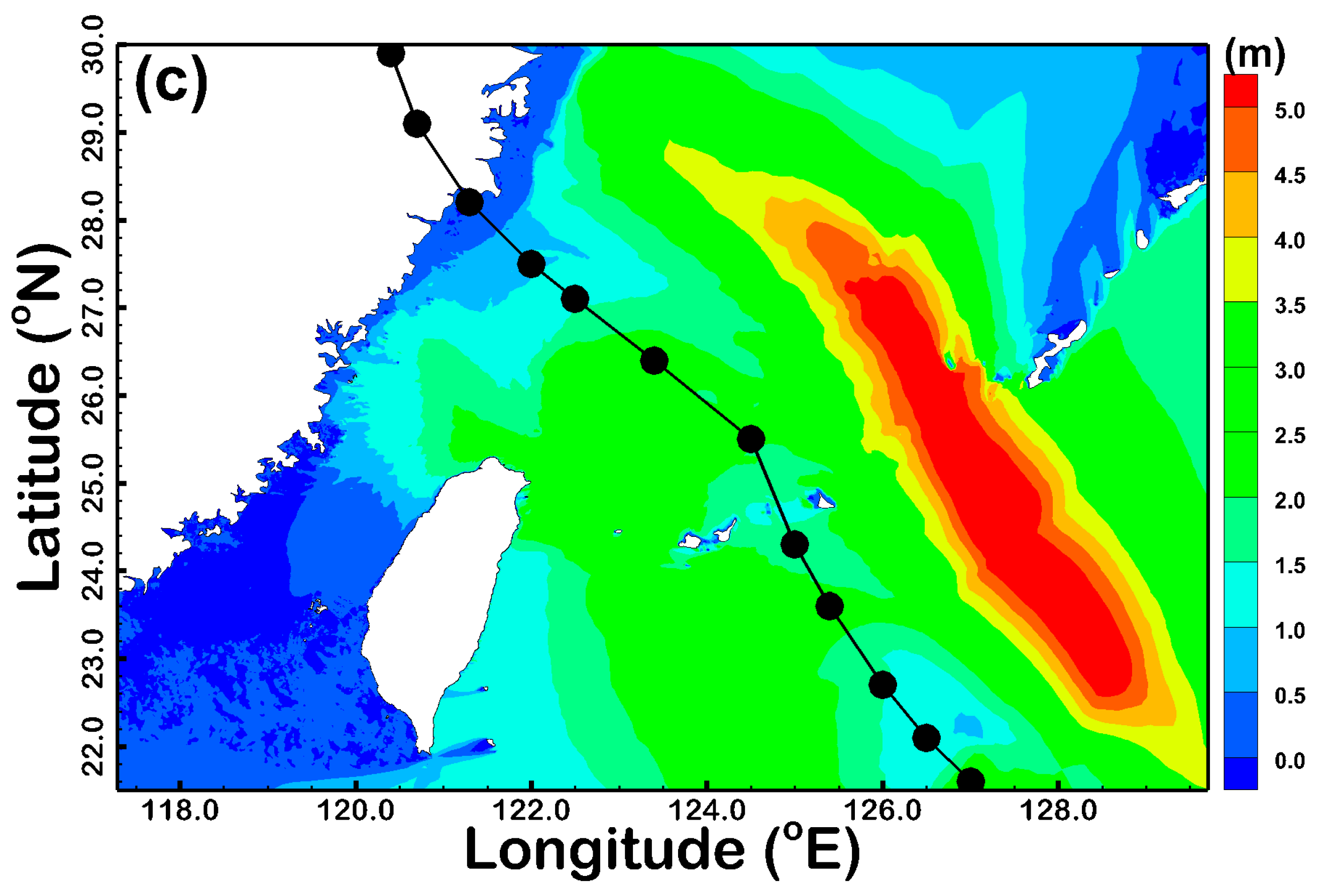
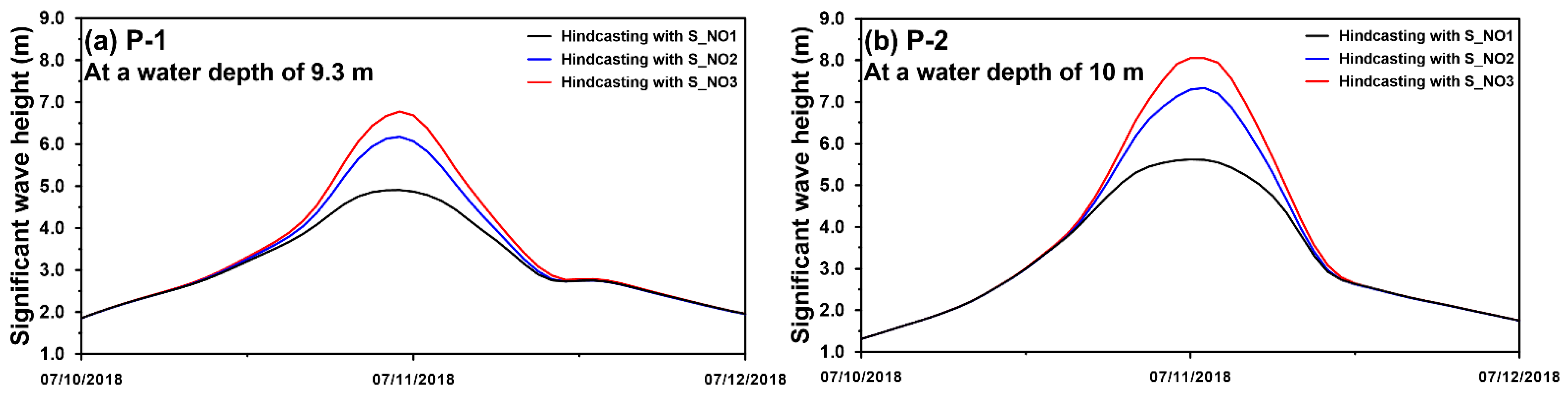
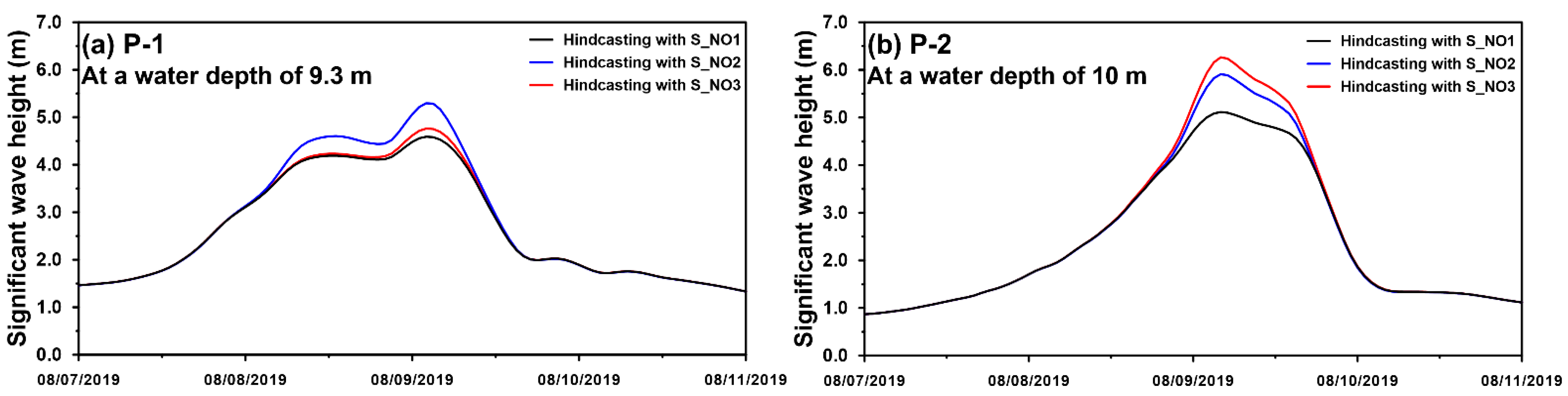
3.1. Validation for Typhoon-Driven SWHs with Various Rtrs
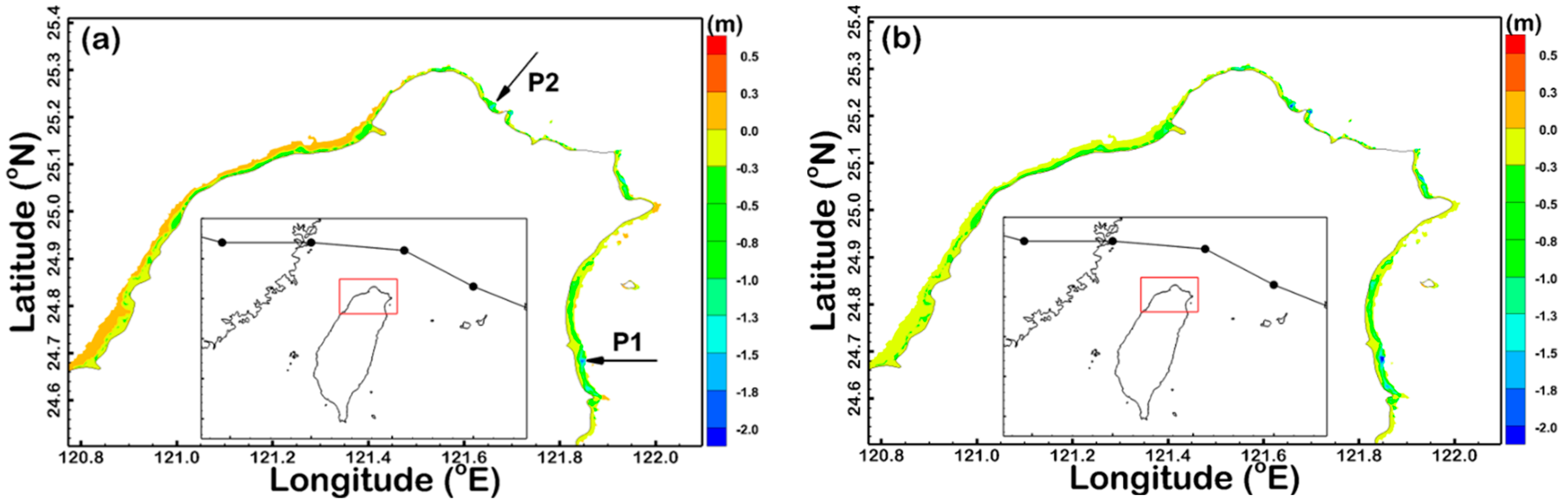
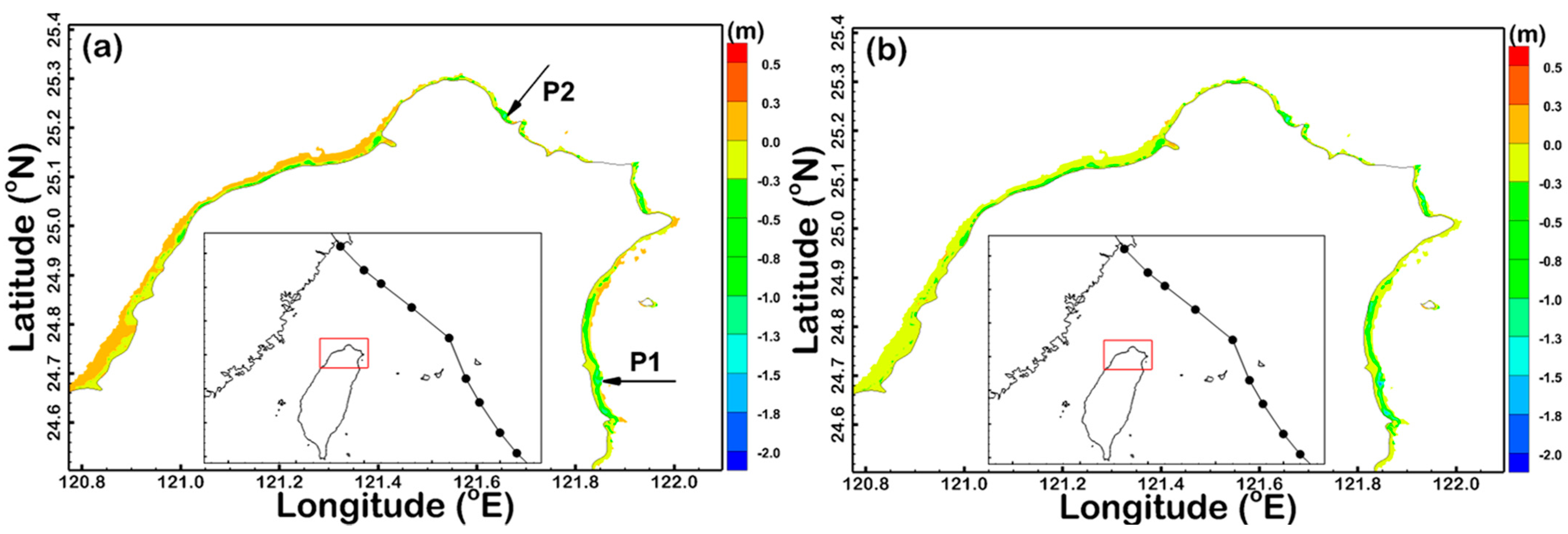
3.2. Effect of the Wave-Breaking Formulation on the Typhoon-Driven SWH Simulation in the Surf Zone
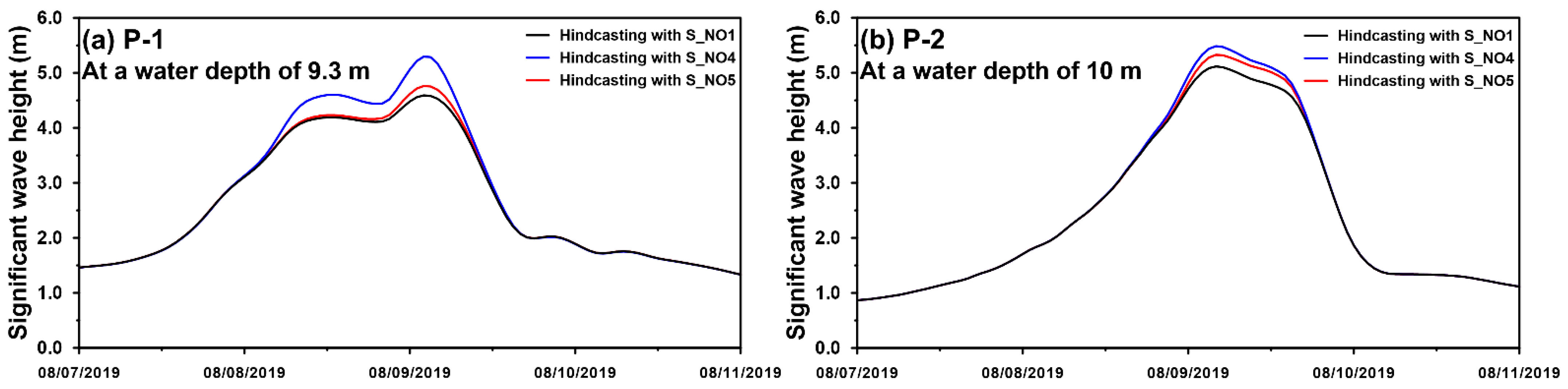
3.3. Effect of the Wave-Breaking Criterion on the Typhoon-Driven SWH Simulation in the Surf Zone
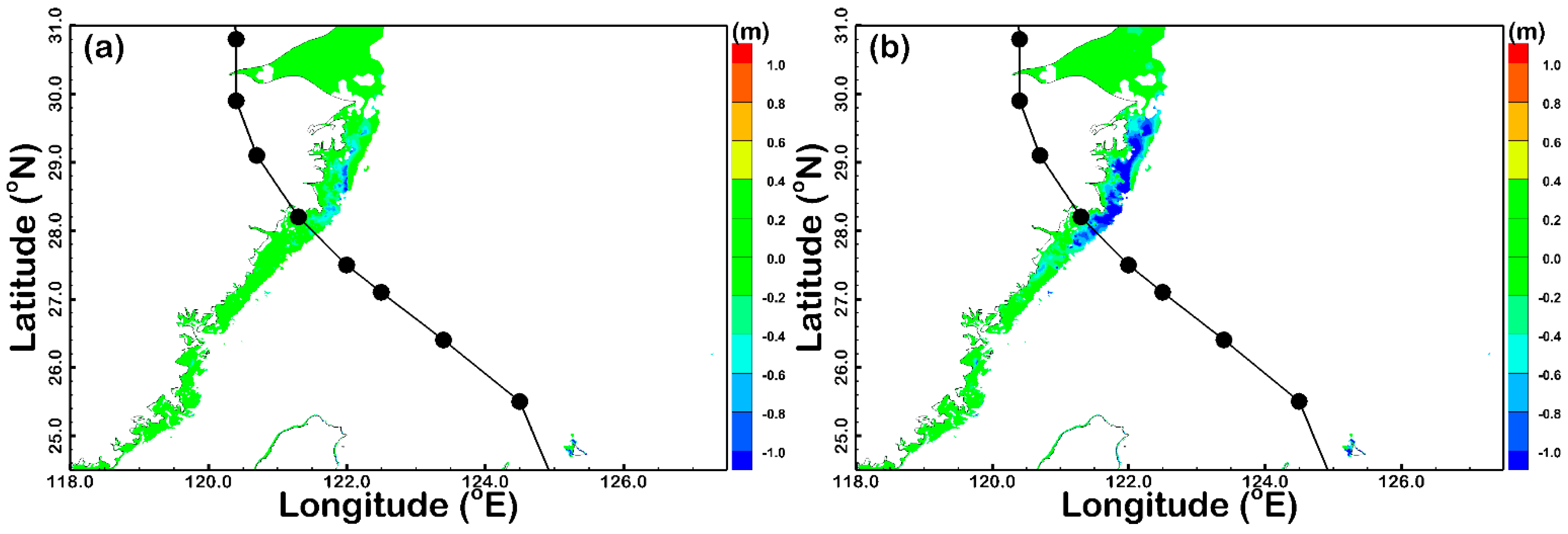
4. Discussion and Uncertainty
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 10, 205. [Google Scholar] [CrossRef] [Green Version]
- Stockdon, H.F.; Sallenger, A.H.; Holman, R.A.; Howd, P.A. A simple model for the spatially-variable coastal response to hurricanes. Mar. Geol. 2007, 238, 1–20. [Google Scholar] [CrossRef]
- Hoeke, R.K.; McInnes, K.L.; Kruger, J.C.; McNaught, R.J.; Hunter, J.R.; Smithers, S.G. Widespread inundation of Pacific islands triggered by distant-source wind-waves. Glob. Planet. Chang. 2013, 108, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Wadey, M.; Brown, S.; Nicholls, R.J.; Haigh, I. Coastal flooding in the Maldives: An assessment of historic events and their implications. Nat. Hazards 2017, 89, 131–159. [Google Scholar] [CrossRef] [Green Version]
- Melet, A.; Almar, R.; Hemer, M.; le Cozannet, G.; Meyssignac, B.; Ruggiero, P. Contribution of wave setup to projected coastal sea level changes. J. Geophys. Res. Ocean. 2020, 125, e2020JC016078. [Google Scholar] [CrossRef]
- Hoefel, F.; Elgar, S. Wave-induced sediment transport and sandbar migration. Science 2003, 299, 1885–1887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feddersen, F. Scaling surf zone turbulence. Geophys. Res. Lett. 2012, 39, L18613. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Battjes, J.A.; Stive, M.J.F. Calibration and verification of a dissipation model for random breaking waves. J. Geophys. Res. 1985, 90, 9159–9167. [Google Scholar] [CrossRef]
- Nairn, R.B. Prediction of Cross-Shore Sediment Transport and Beach Profile Evolution. Ph.D. Thesis, Imperial College London, London, UK, 1990. [Google Scholar]
- Holthuijsen, L.H.; Booij, N. Experimental Wave Breaking in SWAN. In Coastal Engineering 2006; McKee Smith, J., Ed.; American Society of Civil Engineers: New York, NY, USA, 2006; pp. 392–402. [Google Scholar]
- Apotsos, A.; Raubenheimer, B.; Elgar, S.; Guza, R.T. Testing and calibrating parametric wave transformation models on natural beaches. Coast. Eng. 2008, 55, 224–235. [Google Scholar] [CrossRef] [Green Version]
- Ruessink, B.G.; Walstra, D.J.R.; Southgate, H.N. Calibration and verification of a parametric wave model on barred beaches. Coast. Eng. 2003, 48, 139–149. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. A numerical calculation of storm tides induced by a tropical storm impinging on a continental shelf. Mon. Weather Rev. 1965, 93, 343–358. [Google Scholar] [CrossRef] [Green Version]
- Jelesnianski, C.P. Numerical computations of storm surges without bottom stress. Mon. Weather Rev. 1996, 94, 379–394. [Google Scholar] [CrossRef]
- Dube, S.K.; Sinha, P.C.; Roy, G.D. The numerical simulation of storm surges along the Bangladesh coast. Dyn. Atmos. Ocean. 1985, 9, 121–133. [Google Scholar] [CrossRef]
- Ginis, I.; Sutyrin, G. Hurricane-generated depth-averaged currents and sea surface elevation. J. Phys. Oceanogr. 1995, 25, 1218–1242. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.L. Back-propagation neural network for the prediction of the short-term storm surge in Taichung harbor, Taiwan. Eng. Appl. Artif. Intell. 2008, 21, 63–72. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C.; Hsu, M.H. Computational investigation of typhoon-induced storm surges along the coast of Taiwan. Nat. Hazards 2012, 64, 1161–1185. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, Y.P.; Li, J.X.; Ding, X.L. Improvement of wind field hindcasts for tropical cyclones. Water Sci. Eng. 2016, 9, 58–66. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-B.; Chen, H.; Hsiao, S.-C.; Chang, C.-H.; Lin, L.-Y. Wind forcing effect on hindcasting of typhoon-driven extreme waves. Ocean Eng. 2019, 188, 106260. [Google Scholar] [CrossRef]
- Hsiao, S.-C.; Chen, H.; Chen, W.-B.; Chang, C.-H.; Lin, L.-Y. Quantifying the contribution of nonlinear interactions to storm tide simulations during a super typhoon event. Ocean Eng. 2019, 194, 106661. [Google Scholar] [CrossRef]
- Hsiao, S.-C.; Chen, H.; Wu, H.-L.; Chen, W.-B.; Chang, C.-H.; Guo, W.-D.; Chen, Y.-M.; Lin, L.-Y. Numerical Simulation of Large Wave Heights from Super Typhoon Nepartak (2016) in the Eastern Waters of Taiwan. J. Mar. Sci. Eng. 2020, 8, 217. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, S.-C.; Wu, H.-L.; Chen, W.-B.; Chang, C.-H.; Lin, L.-Y. On the Sensitivity of Typhoon Wave Simulations to Tidal Elevation and Current. J. Mar. Sci. Eng. 2020, 8, 731. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R.; Demaria, M.; Marchok, T.P.; Gross, J.M.; Mcadie, C.J. Statistical Tropical Cyclone Wind Radii Prediction Using Climatology and Persistence. Weather Forecast. 2007, 22, 781–791. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modelling with SCHISM. Ocean Modell. 2016, 102, 64–81. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.J.; Baptista, A.M. SELFE: A semi-implicit Eulerian-Lagrangian finite-element model for cross-scale ocean circulation. Ocean Modell. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ye, F.; Yu, H.; Sun, W.; Moghimi, S.; Myers, E.; Nunez, K.; Zhang, R.; Wang, H.; Roland, A.; et al. Simulating compound flooding events in a hurricane. Ocean Dyn. 2020, 70, 621–640. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate, oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C. Modeling flood inundation induced by river flow and storm surges over a river basin. Water 2014, 6, 3182–3199. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-B.; Liu, W.-C. Assessment of storm surge inundation and potential hazard maps for the southern coast of Taiwan. Nat. Hazards 2016, 82, 591–616. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C.; Hsu, M.-H. Modeling evaluation of tidal stream energy and the impacts of energy extraction on hydrodynamics in the Taiwan strait. Energies 2013, 6, 2191–2203. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-B.; Chen, H.; Lin, L.-Y.; Yu, Y.-C. Tidal Current Power Resource and Influence of Sea-Level Rise in the Coastal Waters of Kinmen Island, Taiwan. Energies 2017, 10, 652. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-B.; Liu, W.-C.; Hsu, M.-H.; Hwang, C.-C. Modeling investigation of suspended sediment transport in a tidal estuary using a three-dimensional model. Appl. Math. Model. 2015, 39, 2570–2586. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C. Investigating the fate and transport of fecal coliform contamination in a tidal estuarine system using a three-dimensional model. Mar. Pollut. Bull. 2017, 116, 365–384. [Google Scholar] [CrossRef]
- Roland, A. Development of WWM II: Spectral Wave Modeling on Unstructured Meshes. Ph.D. Thesis, Technology University Darmstadt, Darmstadt, Germany, 2009. [Google Scholar]
- Komen, G.J.; Cavaleri, M.; Donelan, K.; Hasselmann, S.; Hasselmann, P.A.E.; Janssen, M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1994; p. 532. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Deutsches Hydrographisches Institut: Berlin, Germany; Hamburg, Germany, 1973. [Google Scholar]
- Chen, W.-B.; Lin, L.-Y.; Jang, J.-H.; Chang, C.-H. Simulation of typhoon-induced storm tides and wind waves for the northeastern coast of Taiwan using a tide-surge-wave coupled model. Water 2017, 9, 549. [Google Scholar] [CrossRef]
- Su, W.-R.; Chen, H.; Chen, W.-B.; Chang, C.-H.; Lin, L.-Y.; Jang, J.-H.; Yu, Y.-C. Numerical investigation of wave energy resources and hotspots in the surrounding waters of Taiwan. Renew. Energy 2018, 118, 814–824. [Google Scholar] [CrossRef]
- Shih, H.-J.; Chang, C.-H.; Chen, W.-B.; Lin, L.-Y. Identifying the Optimal Offshore Areas for Wave Energy Converter Deployments in Taiwanese Waters Based on 12-Year Model Hindcasts. Energies 2018, 11, 499. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, S.-C.; Cheng, C.-T.; Chang, T.-Y.; Chen, W.B.; Wu, H.-L.; Jang, J.-H.; Lin, L.-Y. Assessment of Offshore Wave Energy Resources in Taiwan Using Long-Term Dynamically Downscaled Winds from a Third-Generation Reanalysis Product. Energies 2021, 14, 653. [Google Scholar] [CrossRef]
- Orton, P.; Georgas, N.; Blumberg, A.; Pullen, J. Detailed modeling of recent severe storm tides in estuaries of the New York City region. J. Geophys. Res. Ocean. 2012, 117, C09030. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Weisberg, R.H.; Huang, Y.; Luettich, R.A.; Westerink, J.J.; Kerr, P.C.; Donahue, A.S.; Grane, G.; Akli, L. Implications from the comparisons between two- and three-dimensional model simulations of the Hurricane Ike storm surge. J. Geophys. Res. Ocean. 2013, 118, 3350–3369. [Google Scholar] [CrossRef] [Green Version]
- Zu, T.; Gana, J.; Erofeevac, S.Y. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Res. Part I 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Zhang, Y.J.; Magnusson, L.; Loftis, J.D. Cross-scale Modeling of Storm Surge, Tide and inundation in Mid-Atlantic Bight and New York City during Hurricane Sandy, 2012. Estuar. Coast. Shelf Sci. 2020, 233, 106544. [Google Scholar] [CrossRef]
- Battjes, J.A.; Beji, S. Breaking Waves Propagating over a Shoal. In Coastal Engineering 1992, Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; ASCE: Reston, VA, USA, 1992; pp. 42–50. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due to Breaking of Random Waves. In Coastal Engineering 1978, Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; ASCE: Reston, VA, USA, 1978; pp. 569–587. [Google Scholar]
- Thornton, E.B.; Guza, R.T. Transformation of wave height distribution. J. Geophys. Res. 1983, 88, 5925–5938. [Google Scholar] [CrossRef] [Green Version]
- Thornton, E.B.; Guza, R.T. Energy saturation and phase speeds measured on a natural beach. J. Geophys. Res. 1982, 87, 9499–9508. [Google Scholar] [CrossRef]
- Church, J.C.; Thornton, E.B. Effects of breaking wave induced turbulence within a longshore current model. Coast. Eng. 1993, 20, 1–28. [Google Scholar] [CrossRef]
- Miche, R. Mouvements ondulatoires des mers en profondeur constante ou décroissante. Annales des Ponts Chaussees 1944, 369–406. [Google Scholar]
- Calisir, E.; Soran, M.B.; Akpinar, A. Quality of the ERA5 and CFSR winds and their contribution to wave modelling performance in a semi-closed sea. J. Oper. Oceanogr. 2021. [Google Scholar] [CrossRef]
- Van der Westhuysen, A.J. Modeling of depth-induced wave breaking under finite depth wave growth conditions. J. Geophys. Res. Ocean 2009, 115, C01008. [Google Scholar] [CrossRef]
- Salmon, J.E.; Holthuijsen, L.H. Modeling depth-induced wave breaking over complex coastal bathymetries. Coast. Eng. 2015, 105, 21–35. [Google Scholar] [CrossRef]
- Lin, S.; Sheng, J. Assessing the performance of wave breaking parameterizations in shallow waters in spectral wave models. Ocean Modell. 2017, 120, 41–59. [Google Scholar] [CrossRef]
- Pezerat, M.; Bertin, X.; Martins, K.; Mengual, B.; Hamm, L. Simulating storm waves in the nearshore area using spectral model: Current issues and a pragmatic solution. Ocean Modell. 2021, 158, 101737. [Google Scholar] [CrossRef]

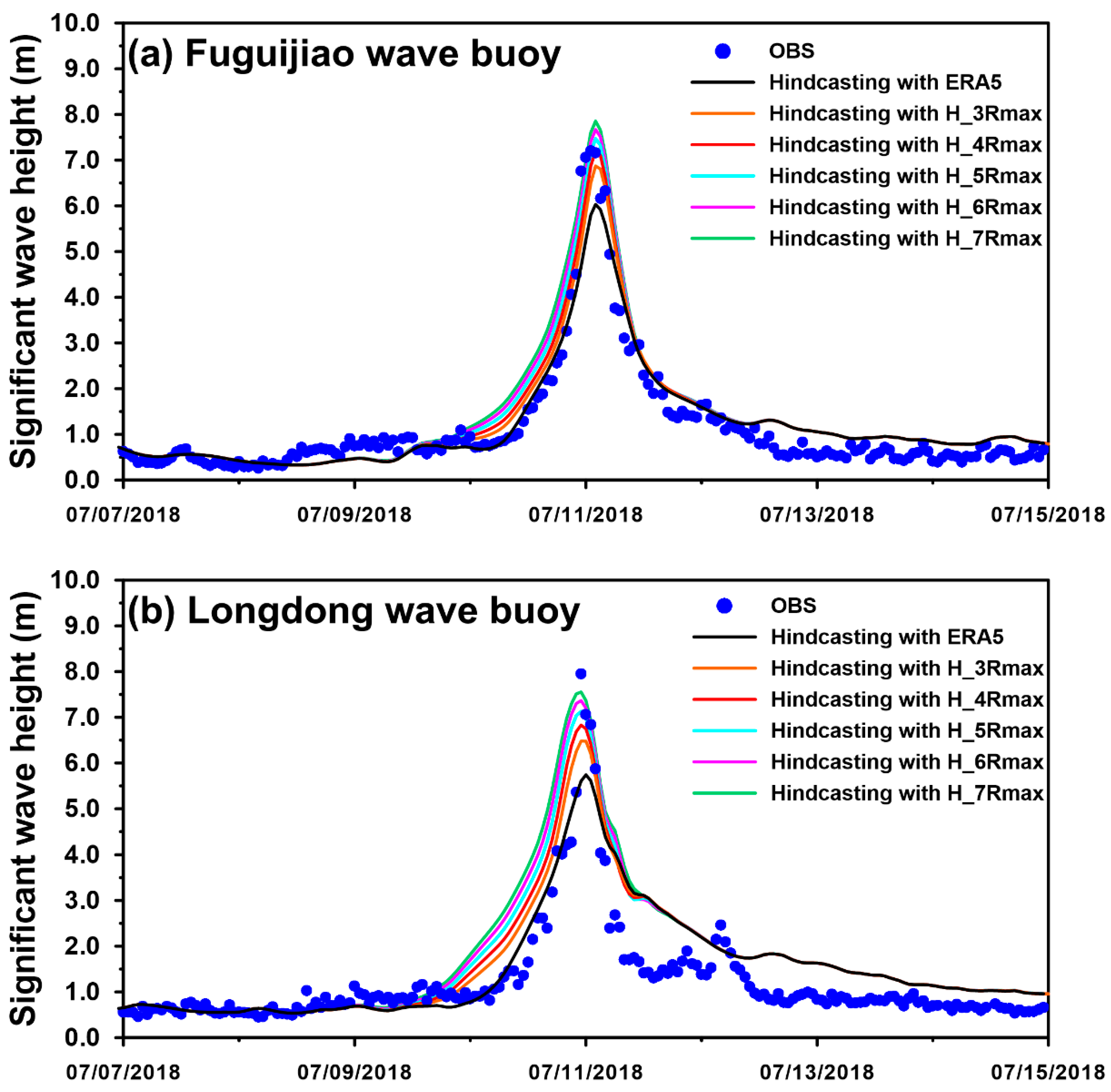

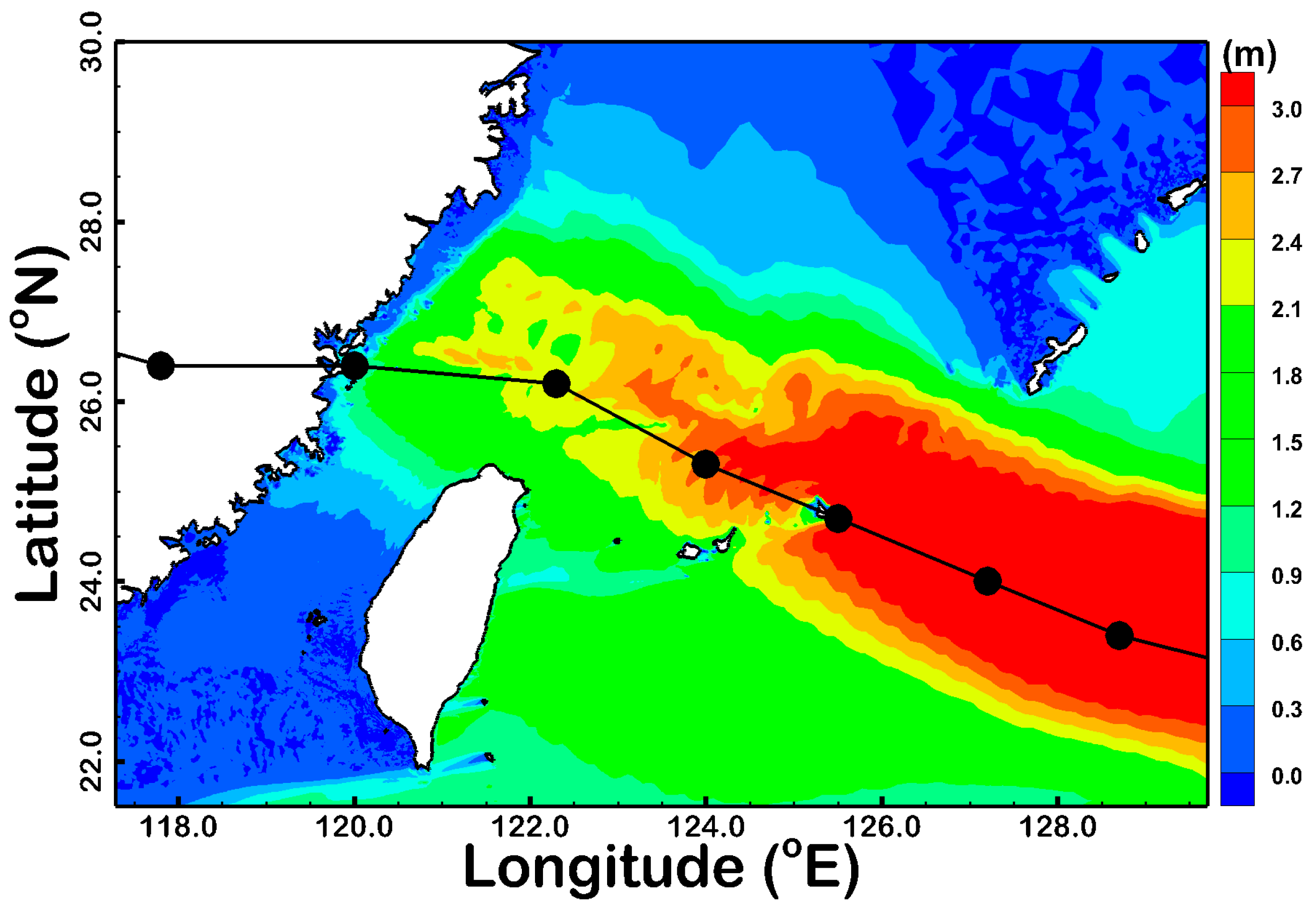
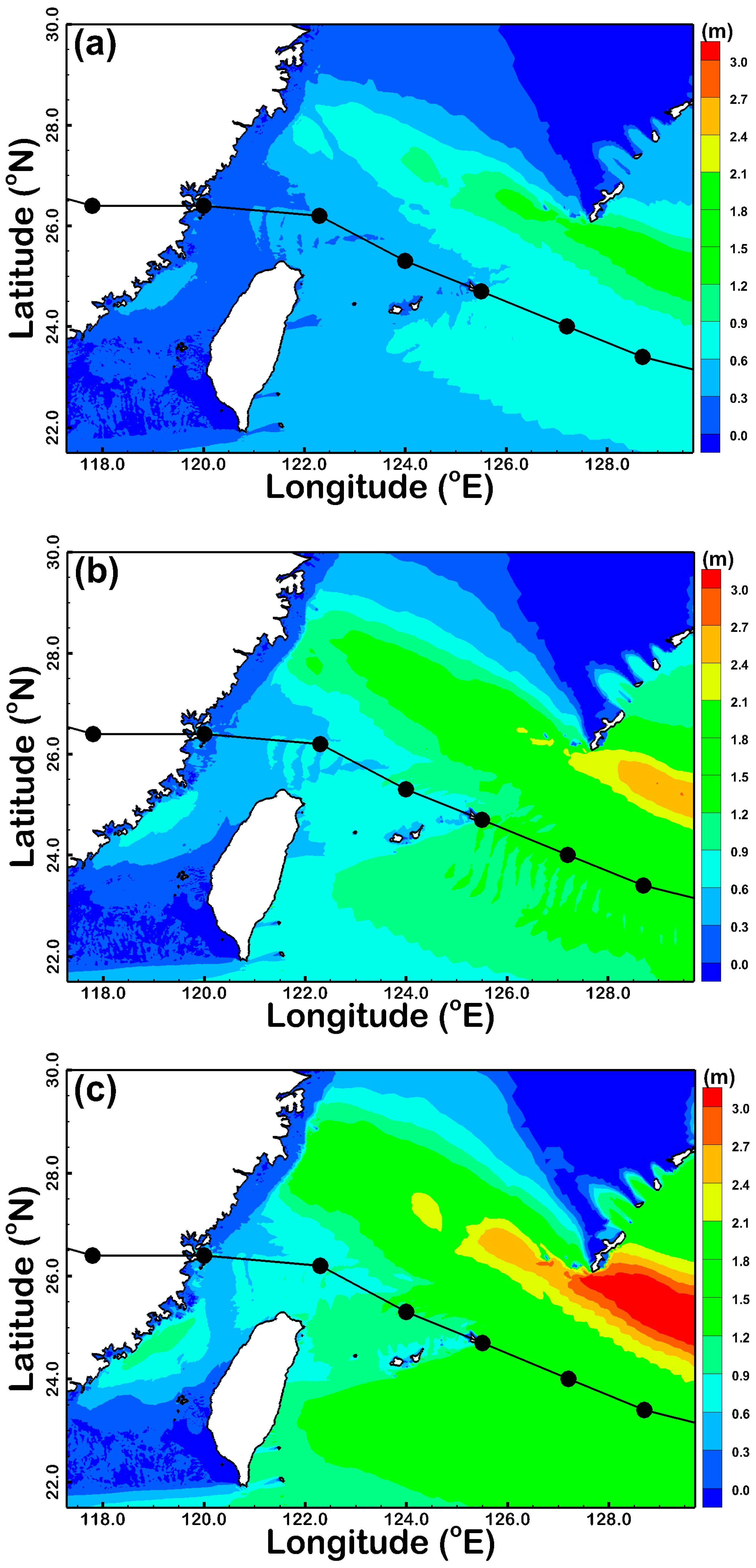




| Buoy Name | Longitude (°E) | Latitude (°N) | Water Depth (m) |
|---|---|---|---|
| Fuguijiao | 121.5336 | 25.3036 | 30 |
| Longdong | 121.9225 | 25.0978 | 27 |
| Suao | 121.8758 | 24.6247 | 23 |
| Scenario | Wave-Breaking Formulation | Wave-Breaking Criterion | Rtrs |
|---|---|---|---|
| S_NO1 | BJ87 | 0.78 | 4Rmax |
| S_NO2 | TG83 | 0.42 | 4Rmax |
| S_NO3 | CT93 | 0.78 | 4Rmax |
| S_NO4 | BJ87 | Based on Local Steepness | 4Rmax |
| S_NO5 | BJ87 | Based on Peak Steepness | 4Rmax |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, S.-C.; Wu, H.-L.; Chen, W.-B.; Guo, W.-D.; Chang, C.-H.; Su, W.-R. Effect of Depth-Induced Breaking on Wind Wave Simulations in Shallow Nearshore Waters off Northern Taiwan during the Passage of Two Super Typhoons. J. Mar. Sci. Eng. 2021, 9, 706. https://doi.org/10.3390/jmse9070706
Hsiao S-C, Wu H-L, Chen W-B, Guo W-D, Chang C-H, Su W-R. Effect of Depth-Induced Breaking on Wind Wave Simulations in Shallow Nearshore Waters off Northern Taiwan during the Passage of Two Super Typhoons. Journal of Marine Science and Engineering. 2021; 9(7):706. https://doi.org/10.3390/jmse9070706
Chicago/Turabian StyleHsiao, Shih-Chun, Han-Lun Wu, Wei-Bo Chen, Wen-Dar Guo, Chih-Hsin Chang, and Wen-Ray Su. 2021. "Effect of Depth-Induced Breaking on Wind Wave Simulations in Shallow Nearshore Waters off Northern Taiwan during the Passage of Two Super Typhoons" Journal of Marine Science and Engineering 9, no. 7: 706. https://doi.org/10.3390/jmse9070706
APA StyleHsiao, S.-C., Wu, H.-L., Chen, W.-B., Guo, W.-D., Chang, C.-H., & Su, W.-R. (2021). Effect of Depth-Induced Breaking on Wind Wave Simulations in Shallow Nearshore Waters off Northern Taiwan during the Passage of Two Super Typhoons. Journal of Marine Science and Engineering, 9(7), 706. https://doi.org/10.3390/jmse9070706








