Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools
Abstract
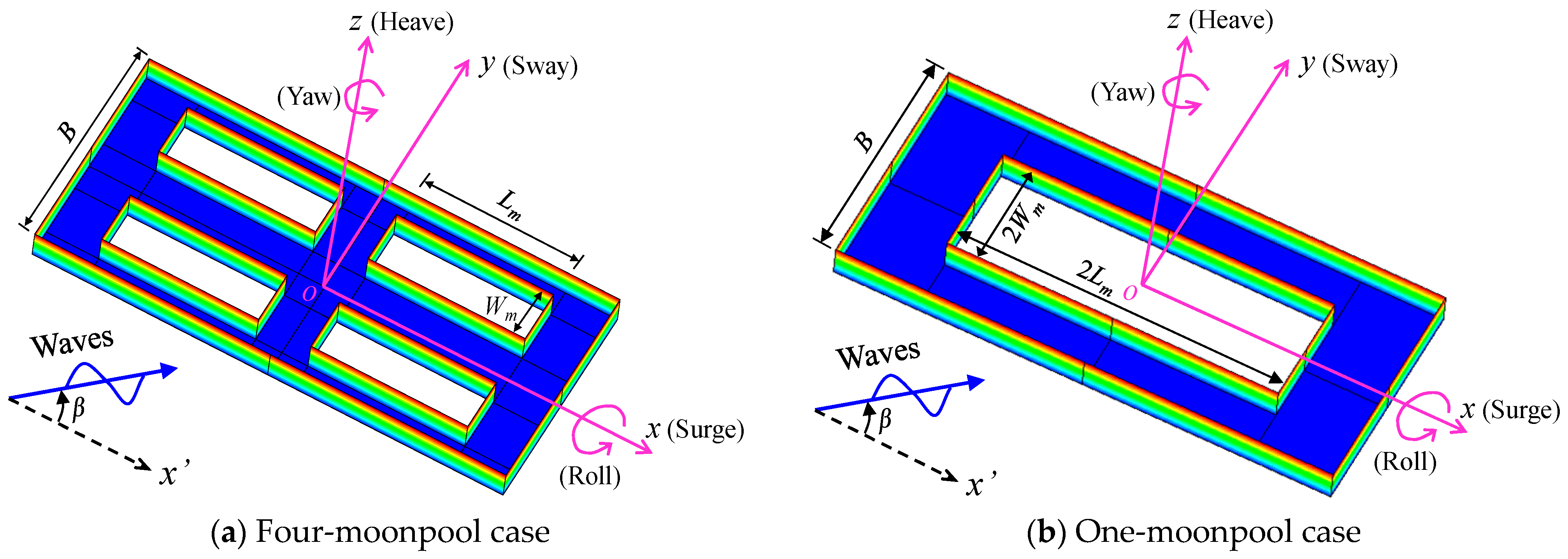
:1. Introduction
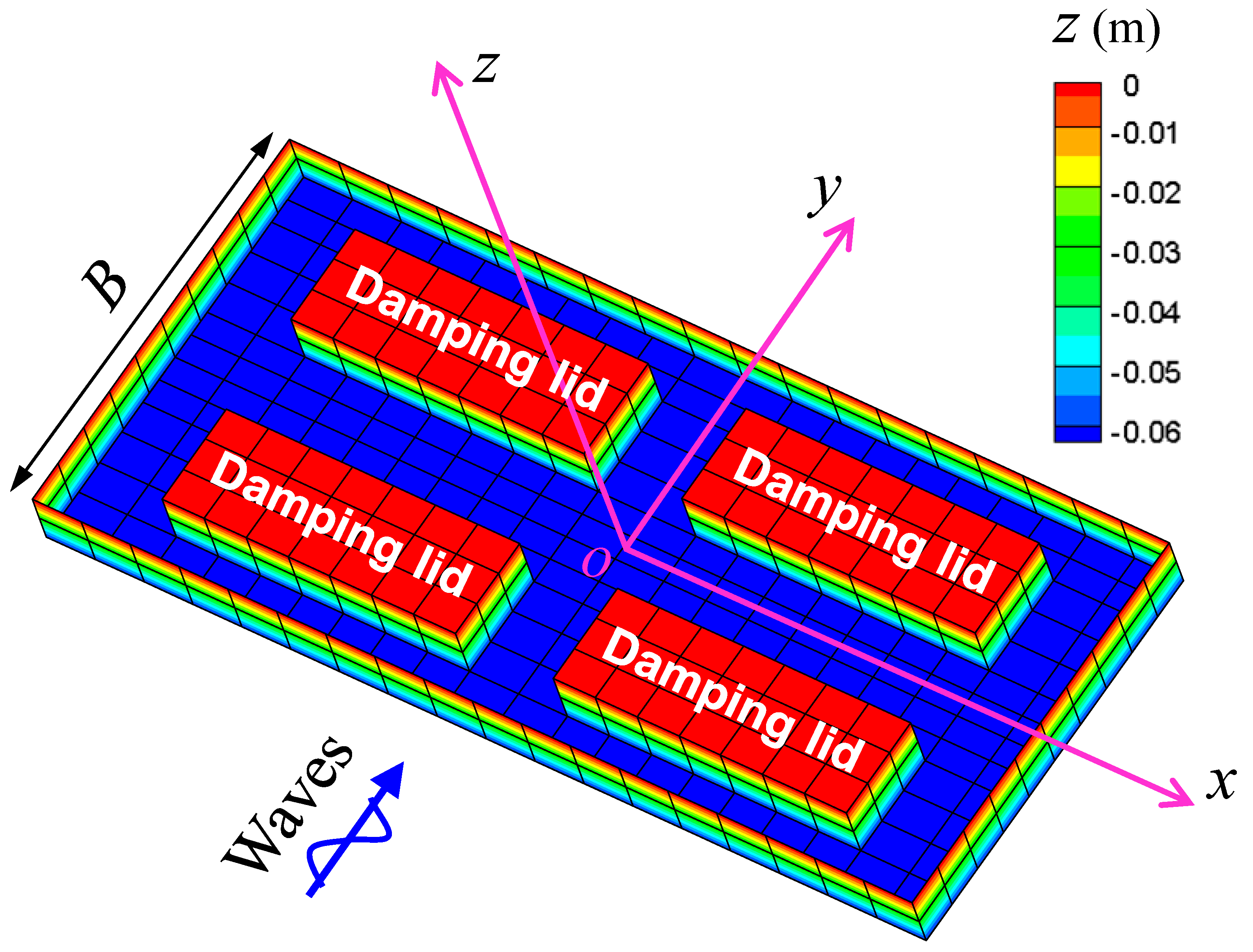
2. Numerical Analysis Method
3. Physical Experiments
4. Results and Discussion
4.1. Mesh Convergence
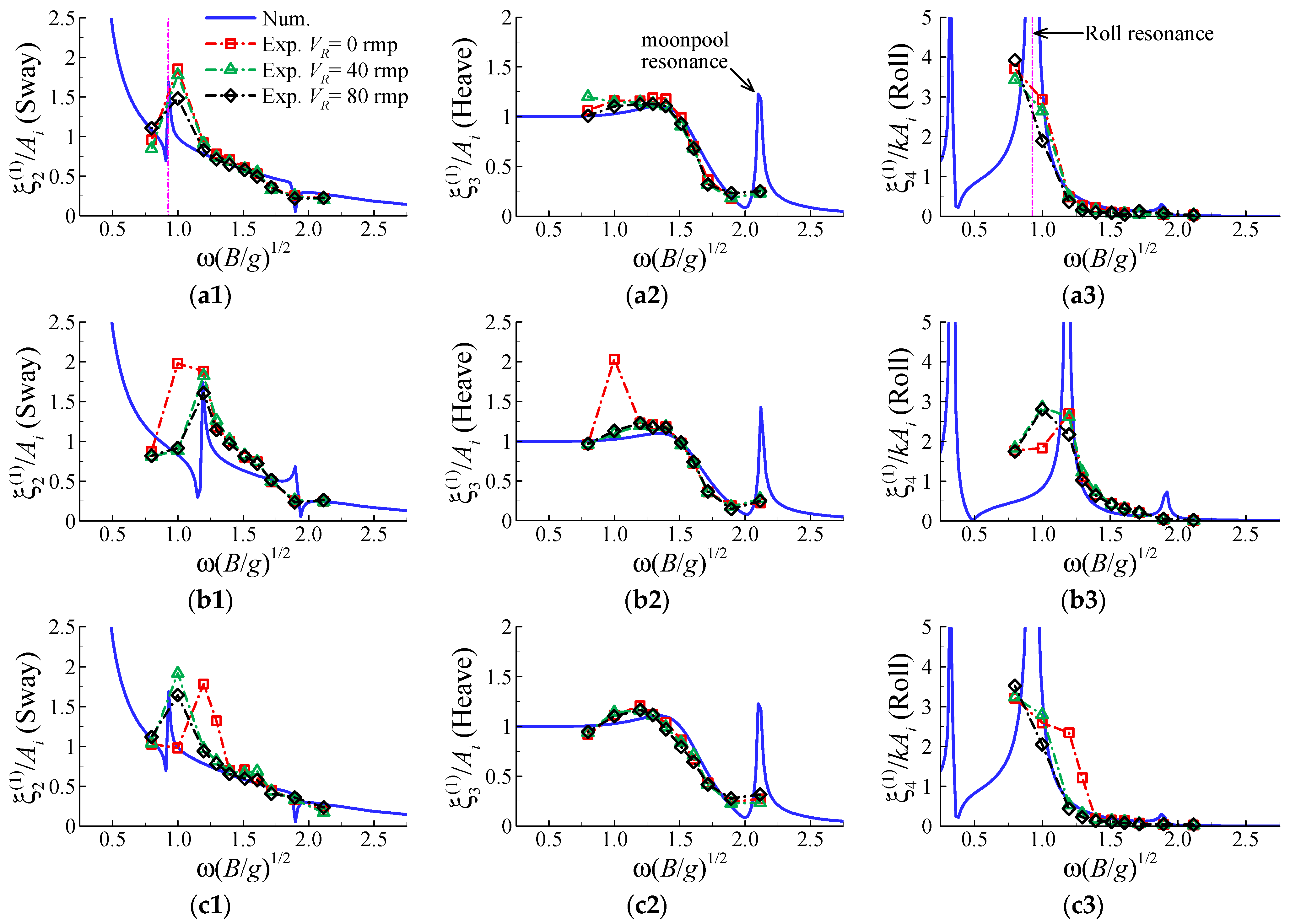
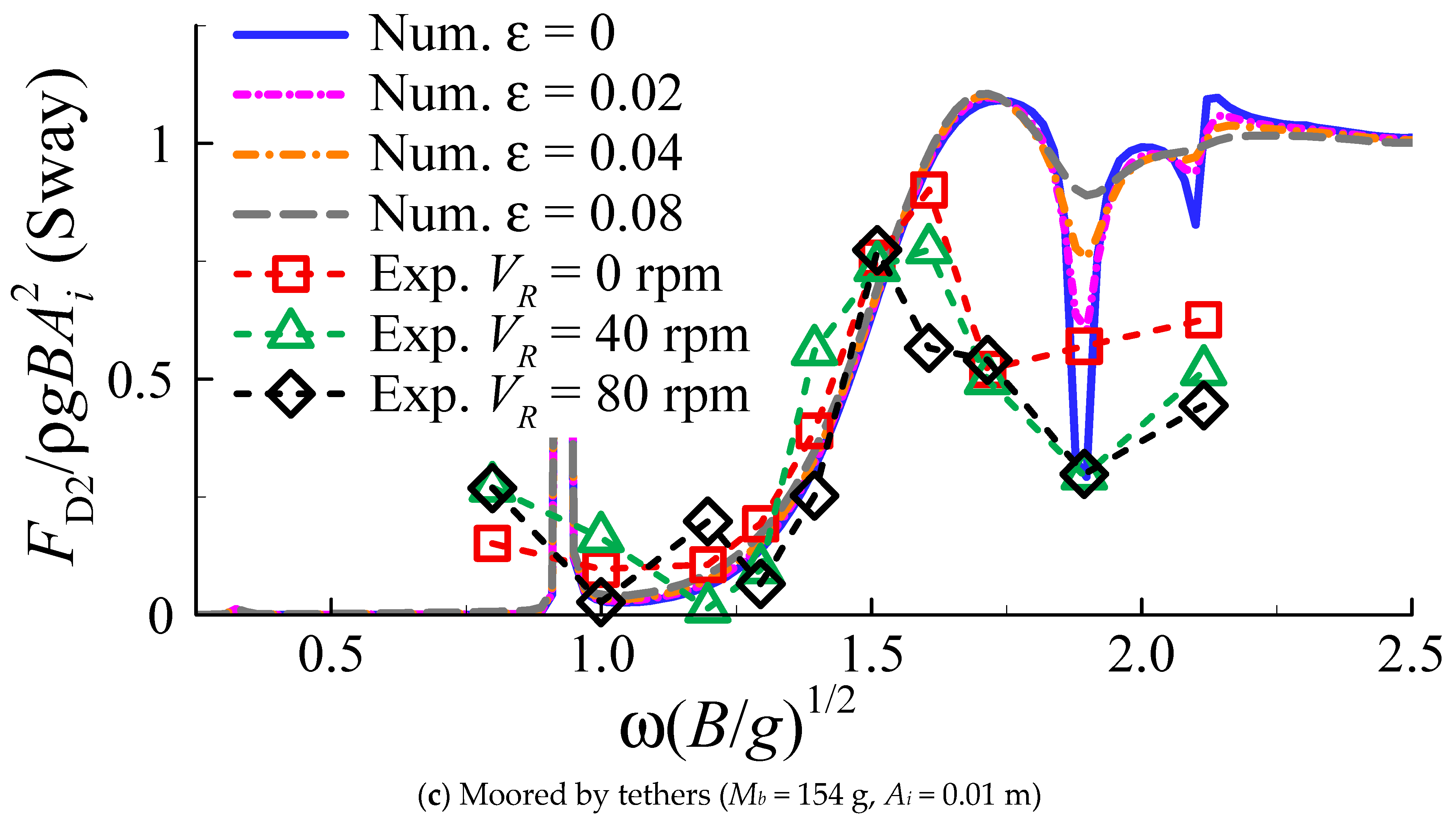
4.2. First-Order Motion Responses
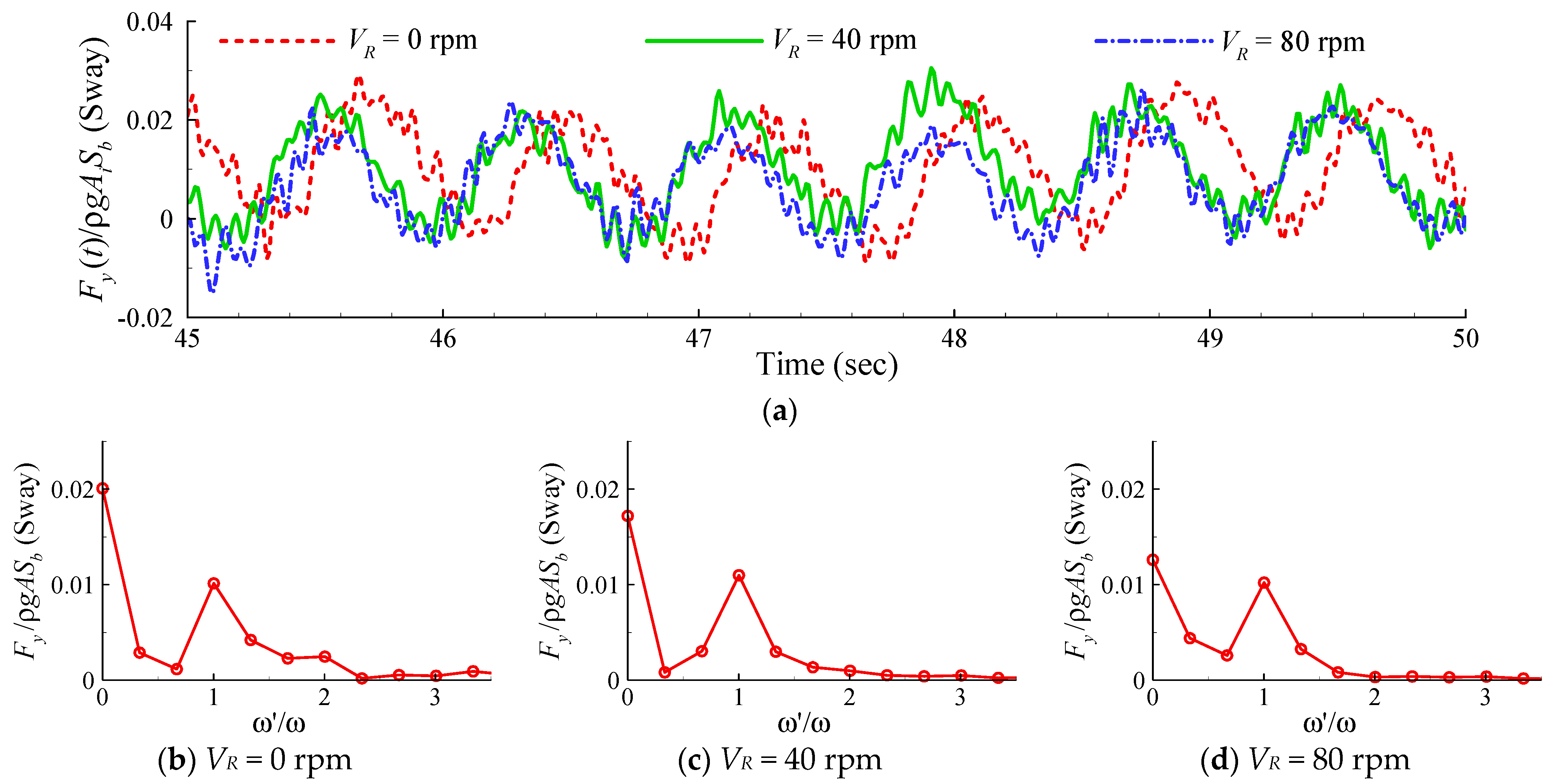
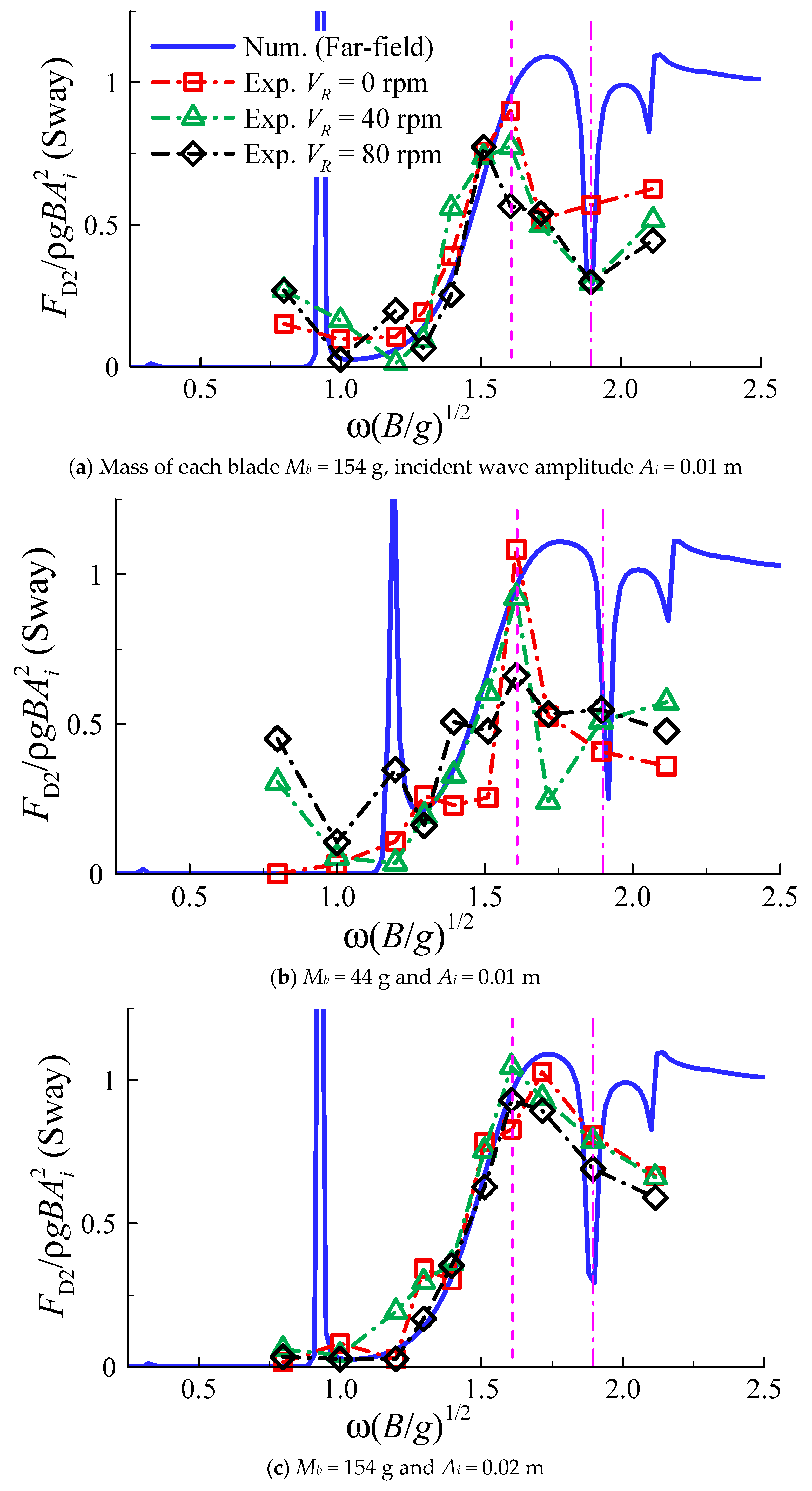
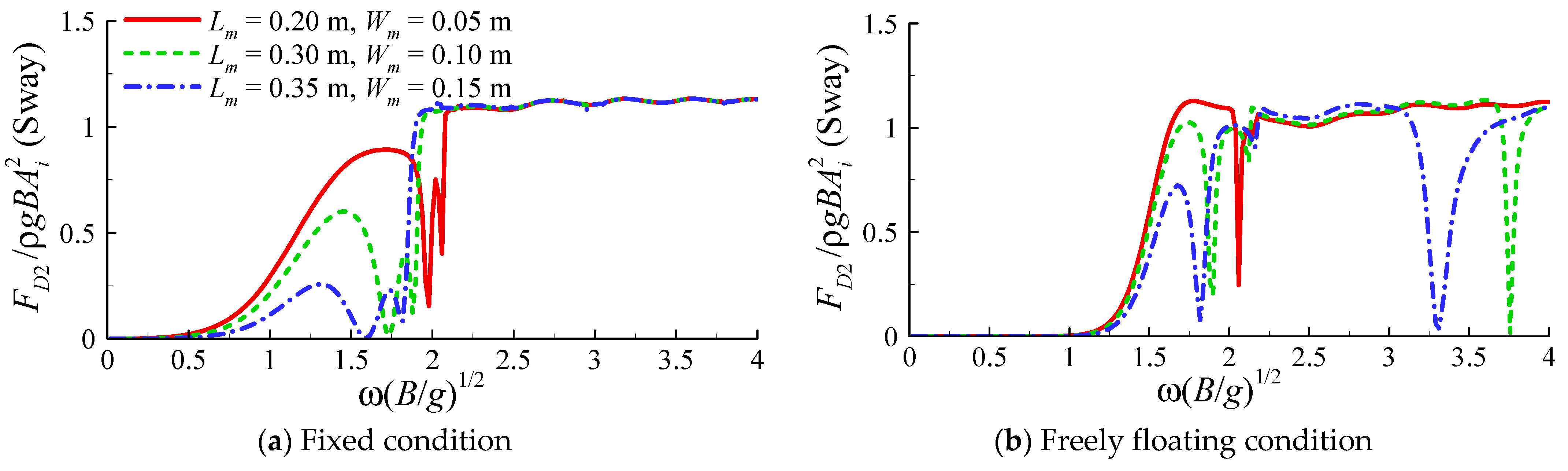
4.3. Influence of Turbine Rotations
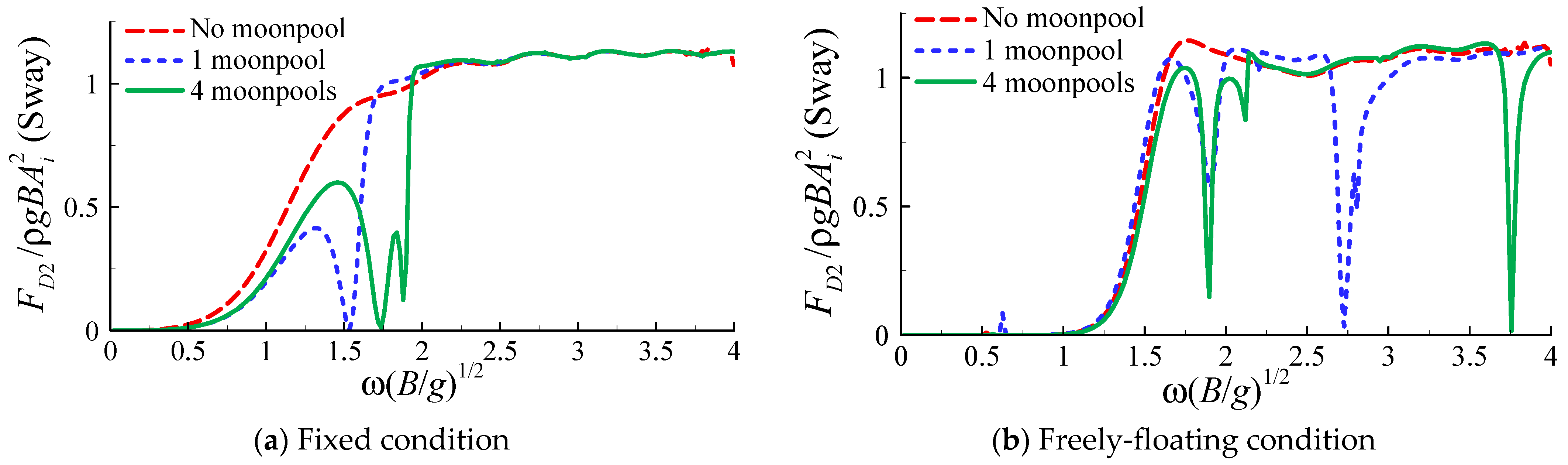
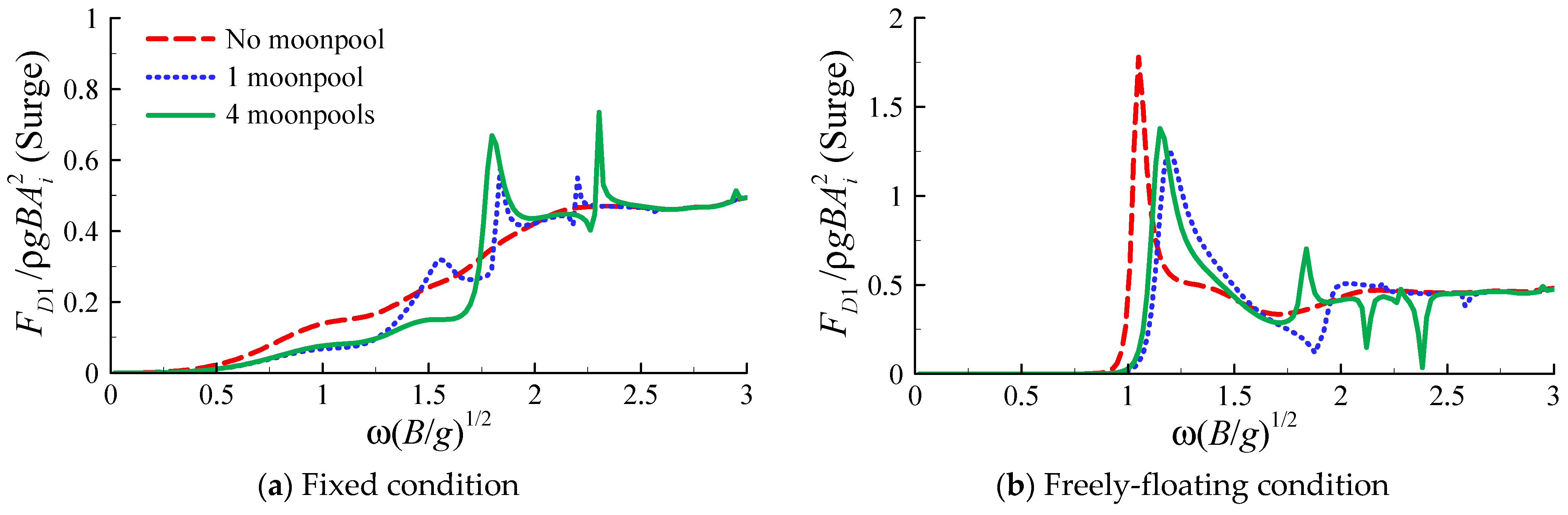
4.4. Influence of Moonpool(s)
4.5. Influence of Wave Heading
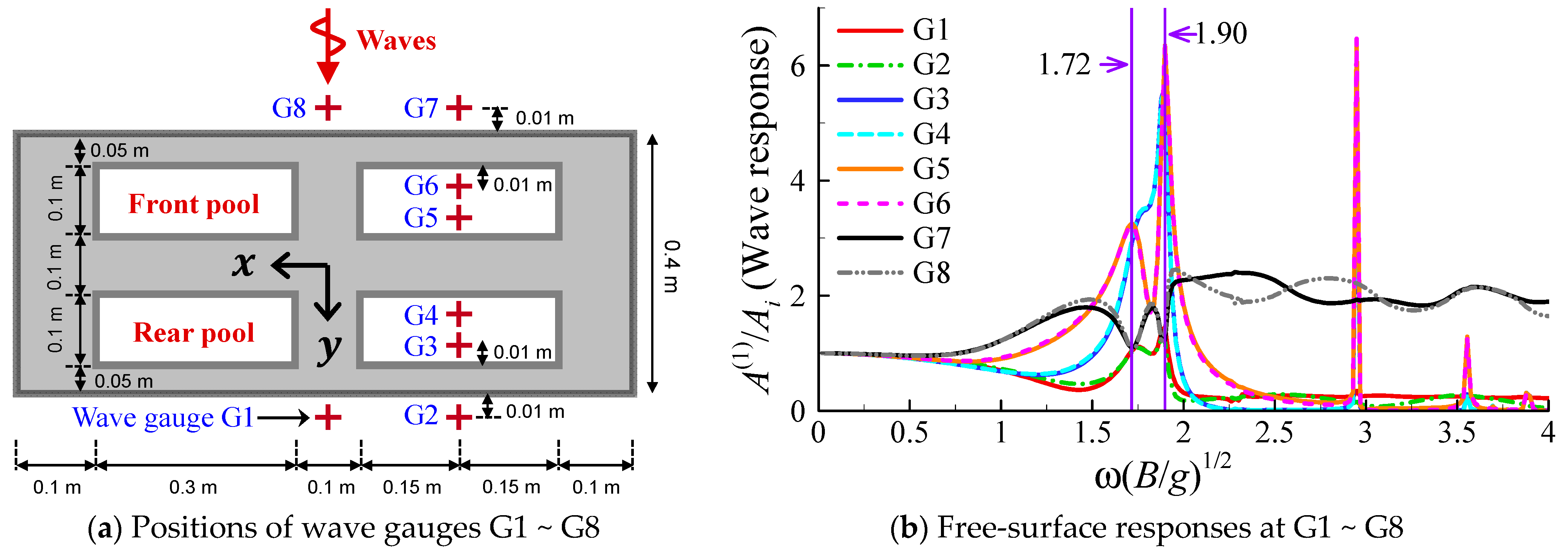
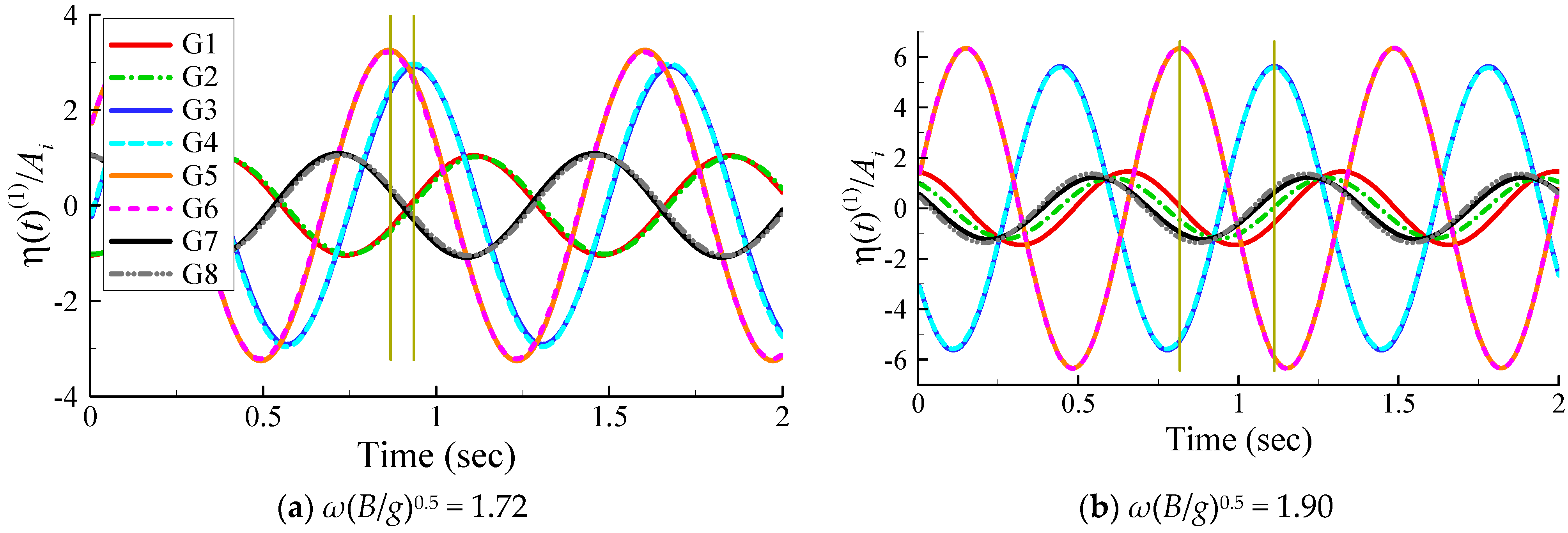
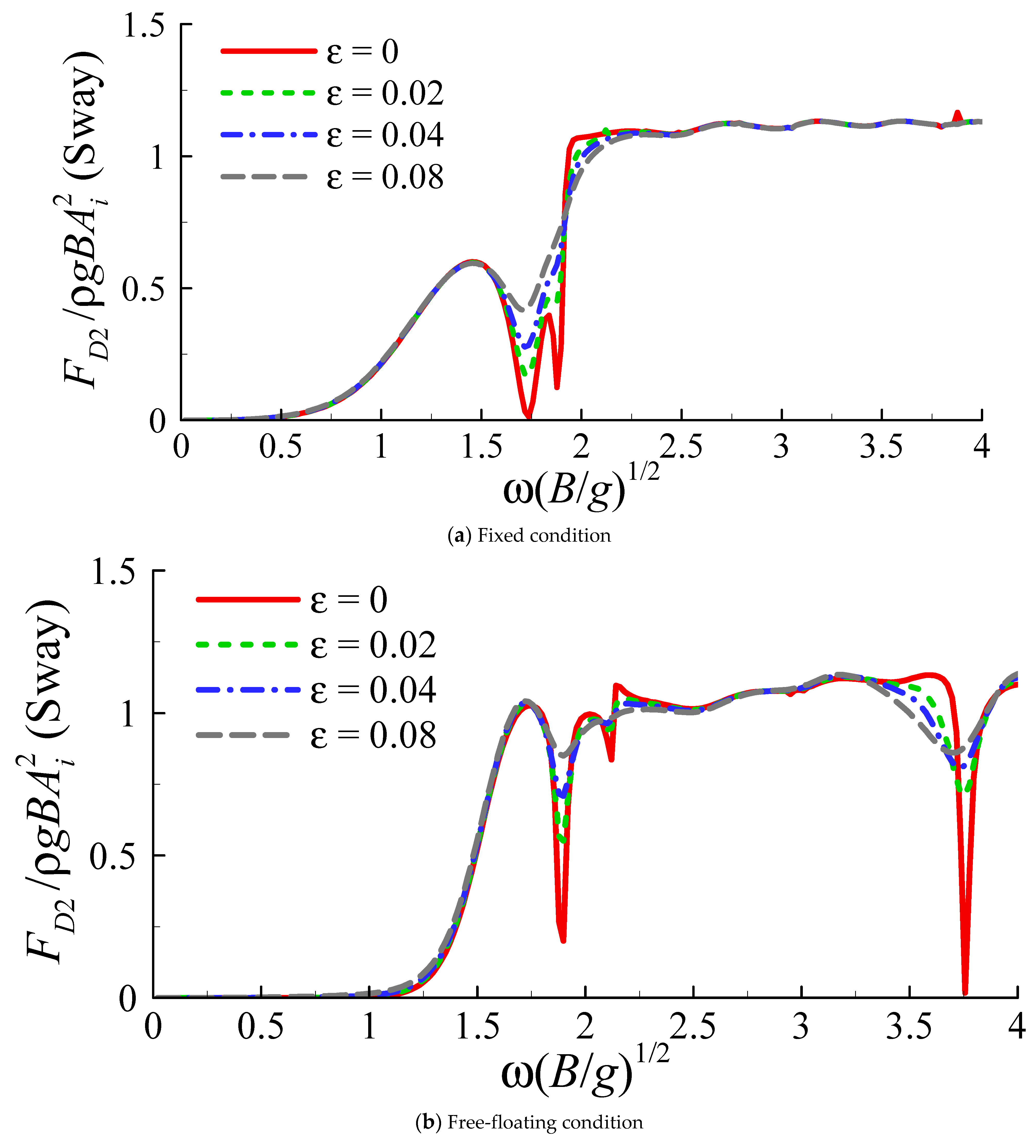
4.6. Influence of Viscous Damping of Moonpool Resonance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jonkman, J.M.; Buhl, M.L. Loads analysis of a floating offshore wind turbine using fully coupled simulation. In Proceedings of the Wind Power, Los Angeles, CA, USA, 3–6 June 2007; pp. 1–32. [Google Scholar]
- Robertson, A.N.; Jonkman, J.M. Loads analysis of several offshore floating wind turbine concepts. In Proceedings of the International Society of Offshore and Polar Engineers Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Hu, Y.; He, E. Active structural control of a floating wind turbine with a stroke-limited hybrid mass damper. J. Sound Vib. 2017, 410, 447–472. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Chen, M.Z.Q.; Li, Z.; Sun, Y. Load mitigation for a barge-type floating offshore wind turbine via inerter-based passive structural control. Eng. Struct. 2018, 177, 198–209. [Google Scholar] [CrossRef]
- Yang, J.; He, E.M.; Hu, Y.Q. Dynamic modeling and vibration suppression for an offshore wind turbine with a tuned mass damper in floating platform. Appl. Ocean Res. 2019, 83, 21–29. [Google Scholar] [CrossRef]
- Palraj, M.; Rajamanickam, P. Motion control of a barge for offshore wind turbine (OWT) using gyrostabilizer. Ocean Eng. 2020, 209, 107500. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Li, C.; Wang, J. Investigation on mooring breakage effects of a 5 MW barge-type floating offshore wind turbine using F2A. Ocean Eng. 2021, 233, 108887. [Google Scholar] [CrossRef]
- Li, L.; Ruzzo, C.; Collu, M.; Gao, Y.; Failla, G.; Arena, F. Analysis of the coupled dynamic response of an offshore floating multi-purpose platform for the Blue Economy. Ocean Eng. 2020, 217, 107943. [Google Scholar] [CrossRef]
- Choisnet, T.; Favre, M.; Lyubimova, M.; Rogier, E. A robust concrete floating wind turbine foundation for worldwide applications. In Proceedings of the Grand Renewable Energy Proceedings, Tokyo, Japan, 27 July–1 August 2014. [Google Scholar]
- Maisondieu, C.; Ferrant, P. Evaluation of the 3D flow dynamics in a moonpool. In Proceedings of the 13th International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003. [Google Scholar]
- Zhang, X.; Bandyk, P. On two-dimensional moonpool resonance for twin bodies in a two-layer fluid. Appl. Ocean Res. 2013, 40, 1–13. [Google Scholar] [CrossRef]
- Fredriksen, A.G.; Kristiansen, T.; Faltinsen, O.M. Wave-induced response of a floating two-dimensional body with a moonpool. Philos. Trans. R. Soc. A 2015, 373, 20140109. [Google Scholar] [CrossRef]
- Ravinthrakumar, S.; Kristiansen, T.; Molin, B.; Ommani, B. A two-dimensional numerical and experimental study of piston and sloshing resonance in moonpools with recess. J. Fluid Mech. 2019, 877, 142–166. [Google Scholar] [CrossRef]
- Molin, B. On the piston and sloshing modes in moonpools. J. Fluid Mech. 2001, 430, 27–50. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Rognebakke, O.F.; Timokha, A.N. Two-dimensional resonant piston-like sloshing in a moonpool. J. Fluid Mech. 2007, 575, 359–397. [Google Scholar] [CrossRef] [Green Version]
- Kristiansen, T.; Faltinsen, O.M. Application of a vortex tracking method to the piston-like behaviour in a semi-entrained vertical gap. Appl. Ocean Res. 2008, 30, 1–16. [Google Scholar] [CrossRef]
- Kristiansen, T.; Faltinsen, O.M. Gap resonance analyzed by a new domain—Decomposition method combining potential and viscous flow. Appl. Ocean Res. 2012, 34, 198–220. [Google Scholar] [CrossRef]
- Kristiansen, T.; Sauder, T.; Firoozkoohi, R. Validation of a hybrid code combining potential and viscous flow with application to 3D moonpool. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Jiang, S.C.; Sun, Z.; Feng, A.C.; Zhang, G.Y. On hydrodynamic behavior of fluid resonance in moonpool and its suppression by using various convex appendages. Ocean Eng. 2019, 192, 106552. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. On damping of two-dimensional piston-mode sloshing in a rectangular moonpool under forced heave motions. J. Fluid Mech. 2015, 772, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Tan, L.; Lu, L.; Tang, G.Q.; Cheng, L.; Chen, X.B. A viscous damping model for piston mode resonance. J. Fluid Mech. 2019, 871, 510–533. [Google Scholar] [CrossRef]
- Beyer, F.; Choisnet, T.; Kretschmer, M.; Cheng, P.W. Coupled MBS-CFD simulation of the IDEOL floating offshore wind turbine foundation compared to wave tank model test data. In Proceedings of the 25th International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015; pp. 367–374. [Google Scholar]
- Borisade, F.; Choisnet, T.; Cheng, P.W. Design study and full scale MBS-CFD simulation of the IDEOL floating offshore wind turbine foundation. J. Phys. Conf. Ser. 2016, 753, 092002. [Google Scholar] [CrossRef] [Green Version]
- Kosasih, K.M.A.; Niizato, H.; Okubo, S.; Mitani, S.; Suzuki, H. Wave tank experiment and coupled simulation analysis of barge-type offshore wind turbine. In Proceedings of the 29th International Offshore Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Ikoma, T.; Nakamura, M.; Moritsu, S.; Aida, Y.; Masuda, K.; Eto, H. Effects of four moon pools on a floating system installed with twin-VAWTs. In Proceedings of the ASME 2019 2nd International Offshore Wind Technical Conference, St. Julian’s, Malta, 3–6 November 2019. IOWTC2019-7598. [Google Scholar]
- Ikoma, T.; Tan, L.; Moritsu, S.; Aida, Y.; Masuda, K. Motion characteristics of a barge-type floating vertical-axis wind turbine with moonpools. Ocean Eng. 2021, 230, 109006. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, S. Mean drift forces on vertical cylindrical bodies placed in front of a breakwater. Fluids 2020, 5, 148. [Google Scholar] [CrossRef]
- He, G.H.; Zhang, Z.G.; Wang, W.; Wang, Z.K.; Jing, P.L. Near-trapping on a four-column structure and the reduction of wave drift forces using optimized method. J. Mar. Sci. Eng. 2020, 8, 174. [Google Scholar] [CrossRef] [Green Version]
- Cong, P.W.; Liu, Y.Y. Local Enhancements of the mean drift wave force on a vertical column shielded by an exterior thin porous shell. J. Mar. Sci. Eng. 2020, 8, 349. [Google Scholar] [CrossRef]
- Seo, M.G.; Ha, Y.J.; Nam, B.W.; Kim, Y. Experimental and numerical analysis of wave drift force on KVLCC2 moving in oblique waves. J. Mar. Sci. Eng. 2021, 9, 136. [Google Scholar] [CrossRef]
- Ikoma, T.; Maeda, H.; Rheem, C.K. Slowly varying wave drifting force on a very large floating structure in short crested waves. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; Volume 1, pp. 533–539. [Google Scholar]
- Newman, J.N. Progress in wave load computations on offshore structures. In Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004. [Google Scholar]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Pinkster, J.A.; Oortmerssen, G. Computation of the first- and second- order wave forces on oscillating bodies in regular waves. In Proceedings of the International Conference on Numerical Ship Hydrodynamics, Berkeley, CA, USA, 19–21 September 1977. [Google Scholar]
- Maruo, H. The drift of a body floating in waves. J. Ship Res. 1960, 4, 1–10. [Google Scholar]
- Newman, J.N. The drift force and moment on ships in waves. J. Ship Res. 1967, 11, 51–60. [Google Scholar] [CrossRef]
- Chen, X.B. Middle-field formulation for the computation of wave-drift loads. J. Eng. Math. 2007, 59, 61–82. [Google Scholar] [CrossRef]
- Choi, Y.R.; Hong, S.Y.; Choi, H.S. An analysis of second-order wave forces on floating bodies by using a higher-order boundary element method. Ocean Eng. 2000, 28, 117–138. [Google Scholar] [CrossRef]
- Park, D.M.; Kim, J.H.; Kim, Y. Numerical study of mean drift force on stationary flexible barge. J. Fluids Struct. 2017, 74, 445–468. [Google Scholar] [CrossRef]
- Kashiwagi, M.; Endo, K.; Yamaguchi, H. Wave drift forces and moments on two ships arranged side by side in waves. Ocean Eng. 2005, 32, 529–555. [Google Scholar] [CrossRef]
- Chen, X.B.; Liu, H.X.; Duan, W.Y. Semi-analytical solutions to wave diffraction of cylindrical structures with a moonpool with a restricted entrance. J. Eng. Math. 2015, 90, 51–66. [Google Scholar] [CrossRef]
- Collu, M.; Brennan, F.P.; Patel, M.H. Conceptual design of a floating support structure for an offshore vertical axis wind turbine: The lessons learnt. Ships Offshore Struct. 2014, 9, 3–21. [Google Scholar] [CrossRef]
- Borg, M.; Shires, A.; Collu, M. Offshore floating vertical axis wind turbines, dynamics modelling state of the art. part I: Aerodynamics. Renew. Sustain. Energy Rev. 2014, 39, 1214–1225. [Google Scholar] [CrossRef] [Green Version]
- Paulsen, U.S.; Borg, M.; Madsen, H.A.; Pedersen, T.F.; Hattel, J.; Ritchie, E.; Ferreira, C.S.; Svendsen, H.G.; Berthelsen, P.A.; Smadja, C. Outcomes of the DeepWind conceptual design. Energy Procedia 2015, 80, 329–341. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Hu, C.; Sueyoshi, M.; Yoshida, S.; Iwashita, H.; Kashiwagi, M. Motion response characteristics of a Kyushu-University semi-submersible Floating Wind Turbine with trussed slender structures: Experiment vs. numerical simulation. Ocean Eng. 2021, 232, 109078. [Google Scholar] [CrossRef]
- Blusseau, P.; Patel, M.H. Gyroscopic effects on a large vertical axis wind turbine mounted on a floating structure. Renew. Energy 2012, 46, 31–42. [Google Scholar] [CrossRef]
- Mostafa, N.; Murai, M.; Nishimura, R.; Fujita, O.; Nihei, Y. Study of motion of spar-type floating wind turbines in waves with effect of gyro moment at inclination. J. Nav. Archit. Mar. Eng. 2012, 9, 67–79. [Google Scholar] [CrossRef] [Green Version]
- Murai, M.; Nishimura, R. A study on an experiment of behavior of a SPAR type offshore wind turbine considering rotation of wind turbine blades. In Proceedings of the OCEANS’10 IEEE Sydney, Sydney, Australia, 24–27 May 2010; pp. 1–8. [Google Scholar]
- Nihei, Y.; Matsuura, M.; Fujioka, H.; Suzuki, H. An approach for the optimum design of TLP type offshore wind turbines. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. OMAE2011-50258. [Google Scholar]
- Lee, C.; Newman, J. Wamit User Manual, Version 7.4; Wamit, Inc.: Chestnut Hill, MA, USA, 2021. [Google Scholar]
- Tan, L.; Ikoma, T.; Fujishima, K.; Aida, Y.; Masuda, K. Investigation of motions of a floating wind turbine foundation with multiple moonpools. In Proceedings of the Fourteenth (2020) ISOPE Pacific-Asia Offshore Mechanics Symposium, Dalian, China, 22–25 November 2020. [Google Scholar]
- Michima, P.; Kawabe, H. Preliminary chart of drill ship operability considering moon-pool sloshing effects. In Proceedings of the 24th International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Vada, T.; Pan, Z.Y. On the handling of moonpool resonances by Green’s function methods. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]

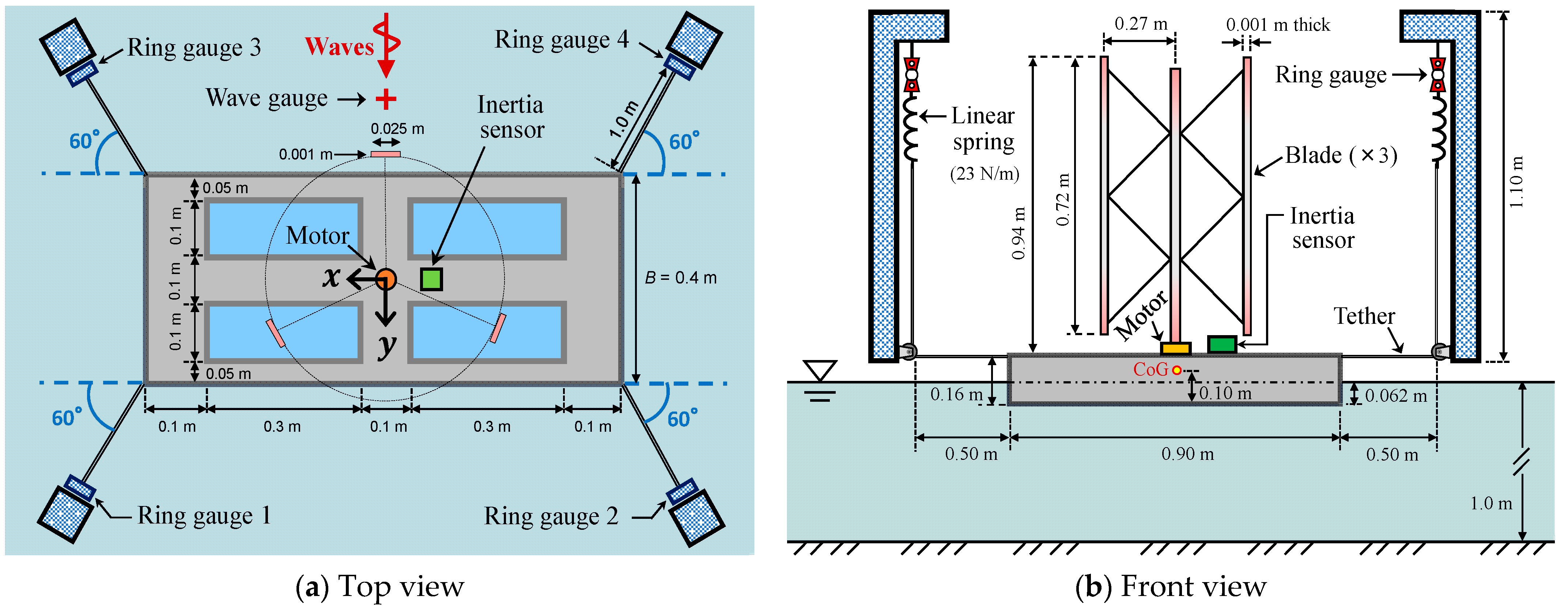



| Parameter | Value |
|---|---|
| Incident wave period (T) | 0.6 s ~ 1.6 s |
| Incident wave amplitude (Ai) | 0.01 m or 0.02 m |
| Mass of each blade (Mb) | 44 g or 154 g |
| Rotating velocity of turbine (VR) | 0, 40 rpm or 80 rpm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, L.; Ikoma, T.; Aida, Y.; Masuda, K. Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools. J. Mar. Sci. Eng. 2021, 9, 709. https://doi.org/10.3390/jmse9070709
Tan L, Ikoma T, Aida Y, Masuda K. Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools. Journal of Marine Science and Engineering. 2021; 9(7):709. https://doi.org/10.3390/jmse9070709
Chicago/Turabian StyleTan, Lei, Tomoki Ikoma, Yasuhiro Aida, and Koichi Masuda. 2021. "Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools" Journal of Marine Science and Engineering 9, no. 7: 709. https://doi.org/10.3390/jmse9070709
APA StyleTan, L., Ikoma, T., Aida, Y., & Masuda, K. (2021). Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools. Journal of Marine Science and Engineering, 9(7), 709. https://doi.org/10.3390/jmse9070709







