Passive Heave Compensator Design and Numerical Simulation for Strand Jack during Lift Operation in Deep Water
Abstract
:1. Introduction
2. Configuration of the Lifting System and Dynamic Model
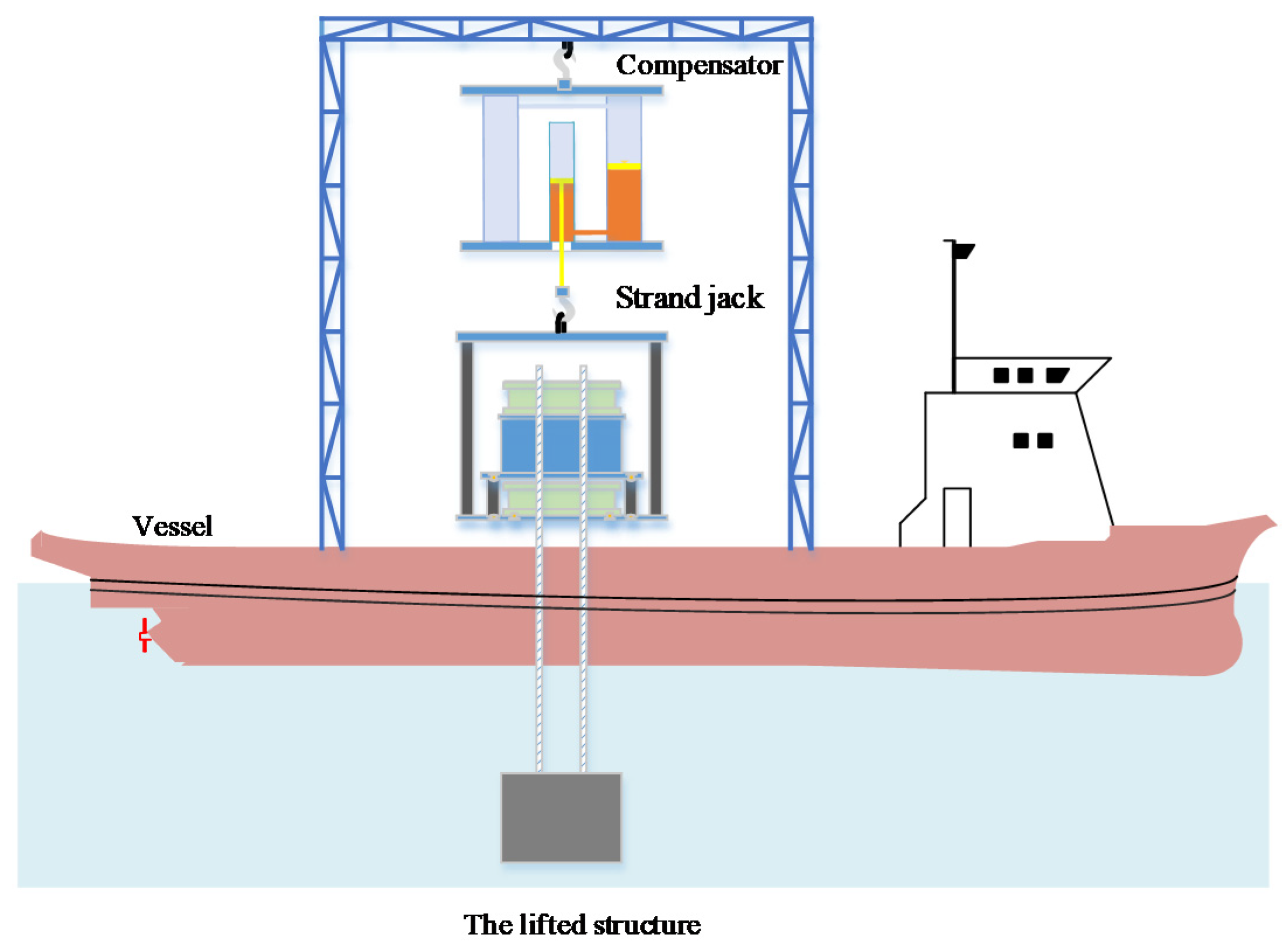
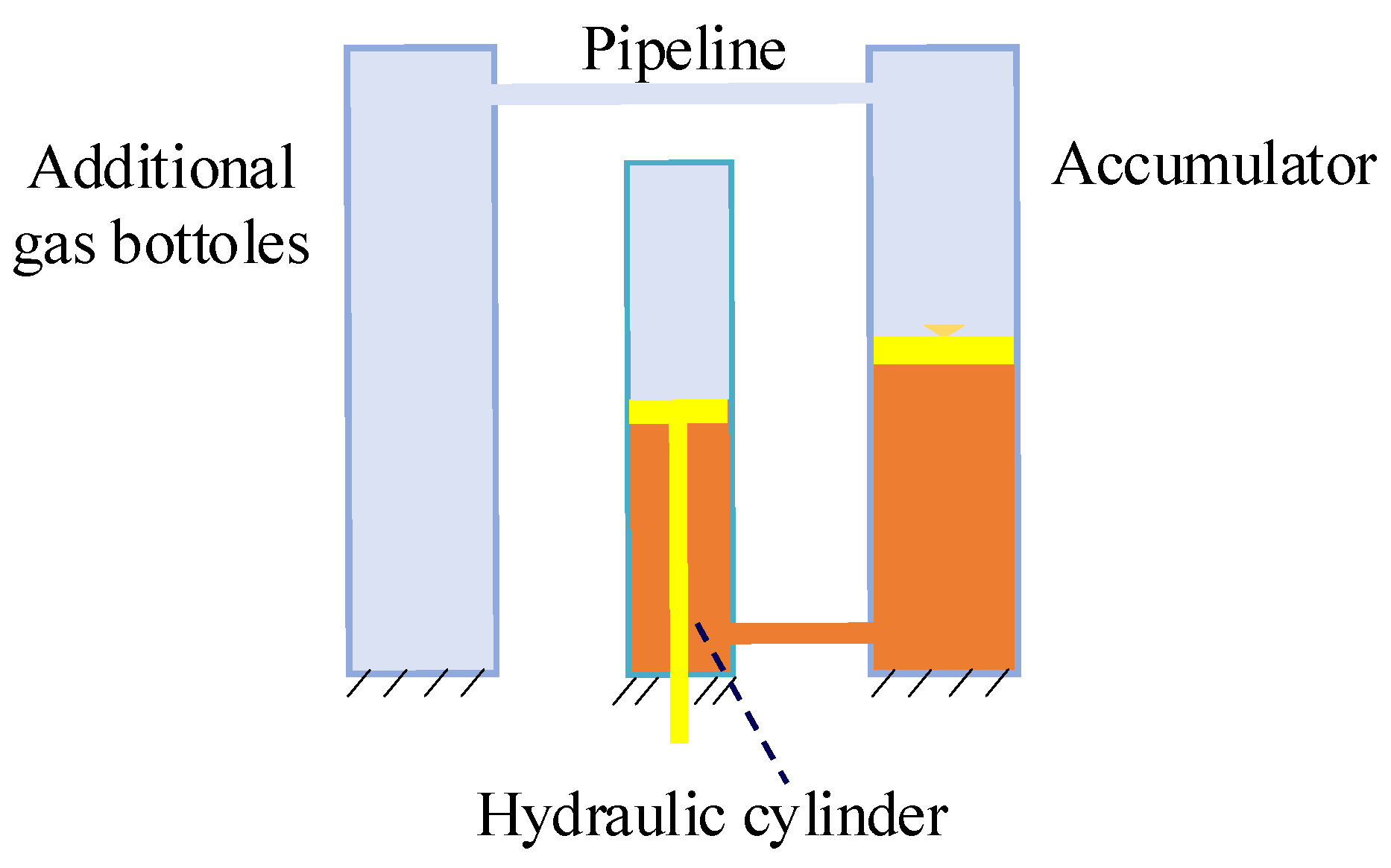
2.1. Configuration of the Lifting System and Working Principle of the Compensator
2.2. Dynamic Model of the Strand Jack Lifting System
- The hydraulic oil is uncompressible.
- Neglecting leakage flows and seal friction forces of the hydraulic cylinder of the compensator.
- All the strands have the same dimensions and mechanical properties.
- Neglecting damping effect in the strands.
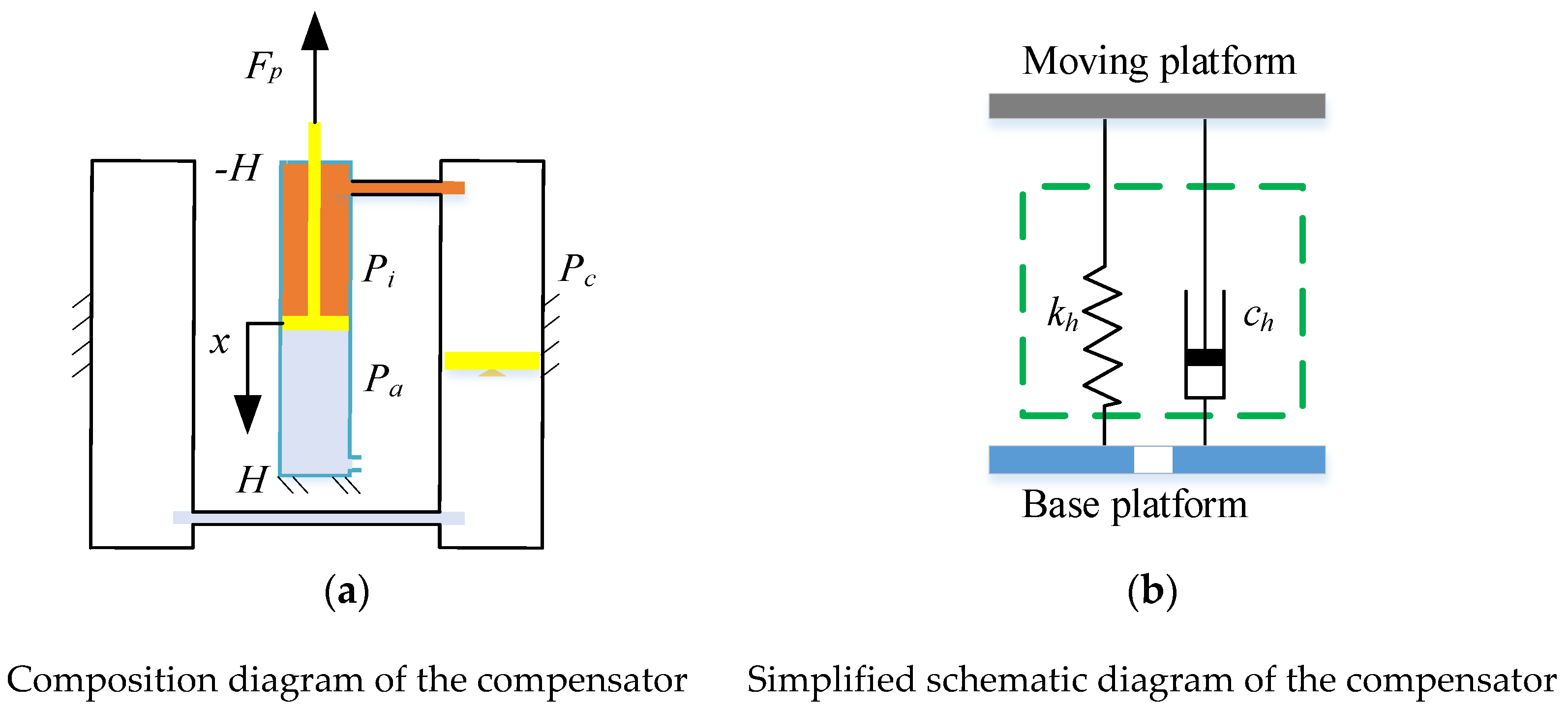
2.3. Mathematical Modeling of the Compensator
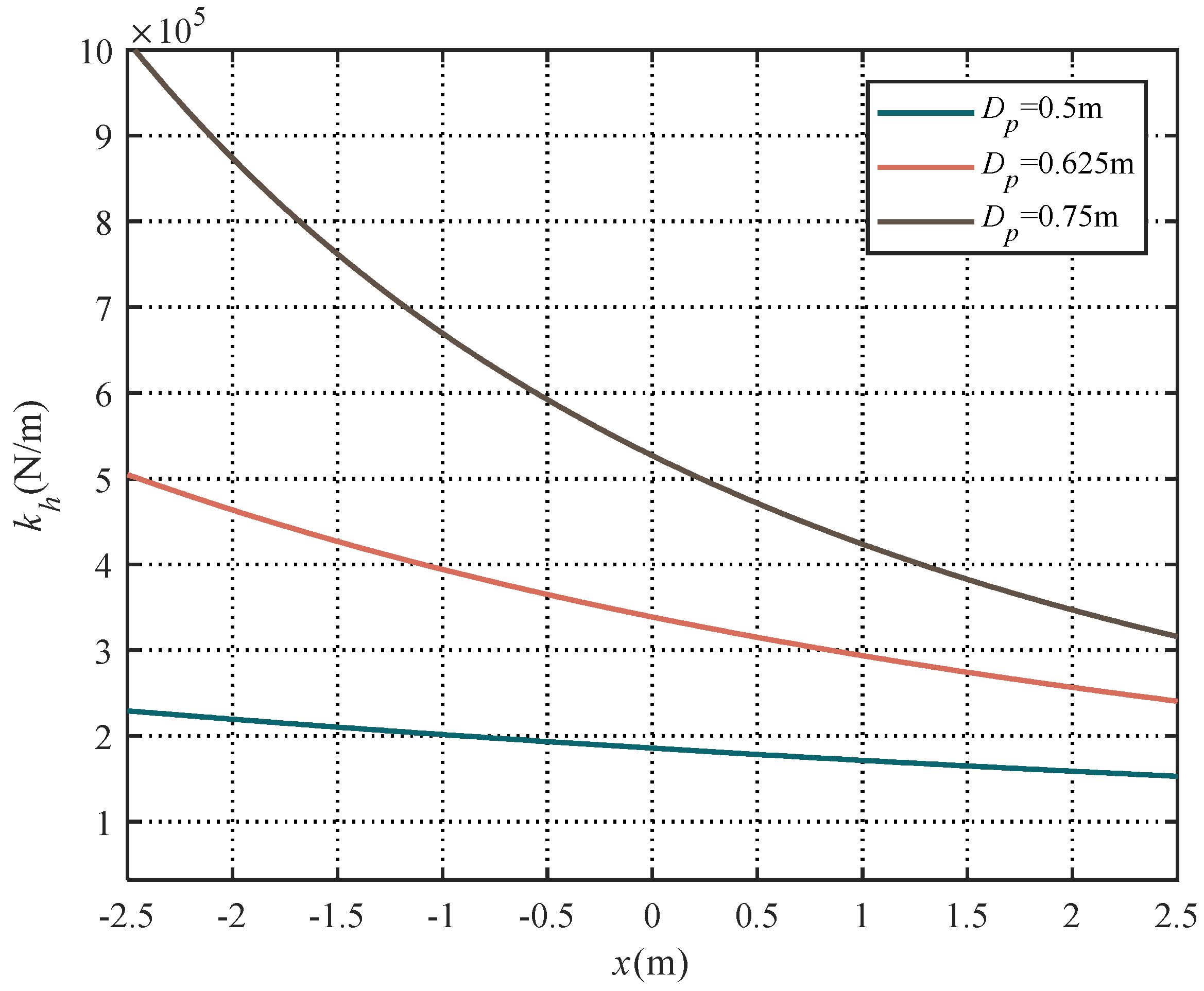
2.3.1. Stiffness of the Compensator
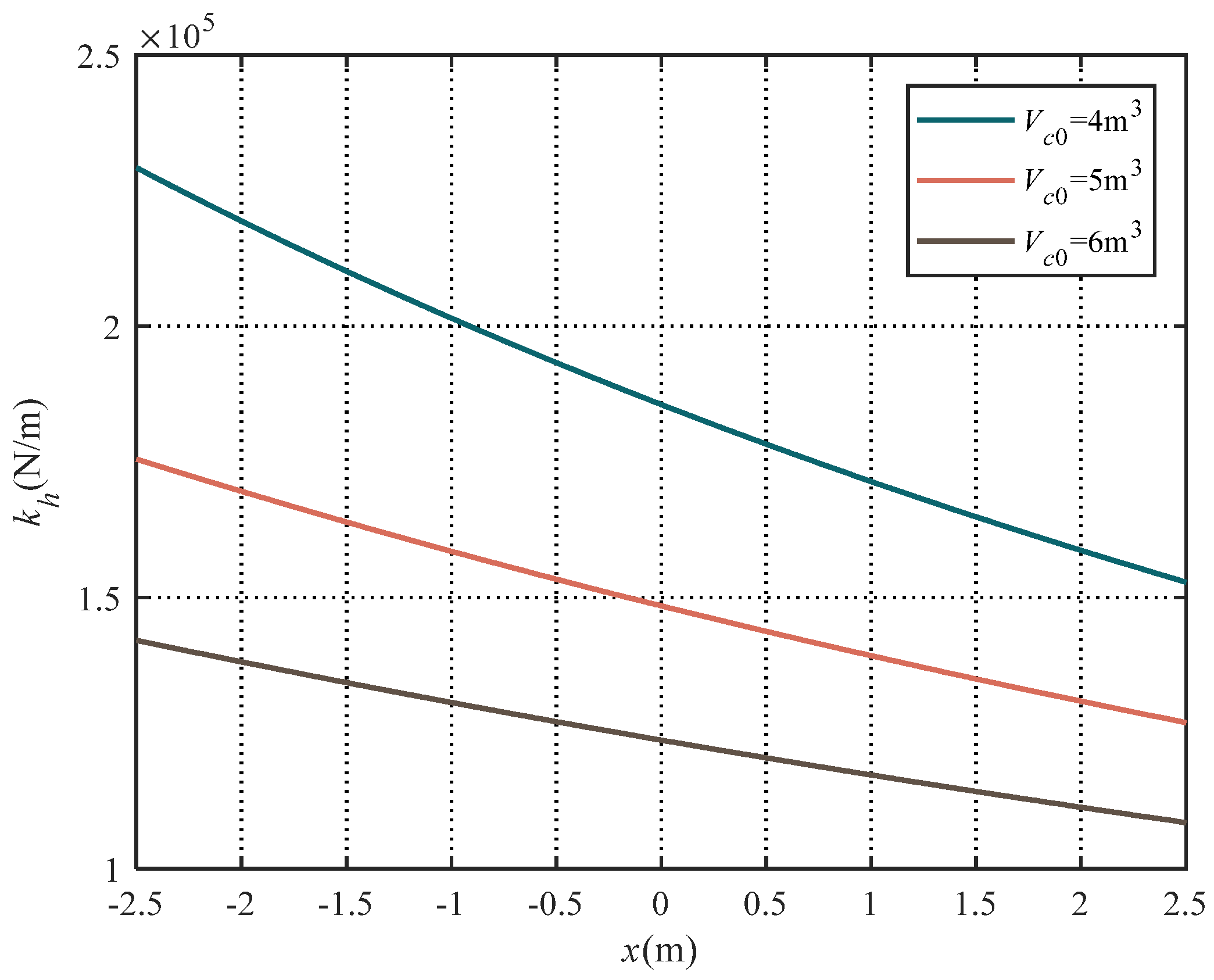
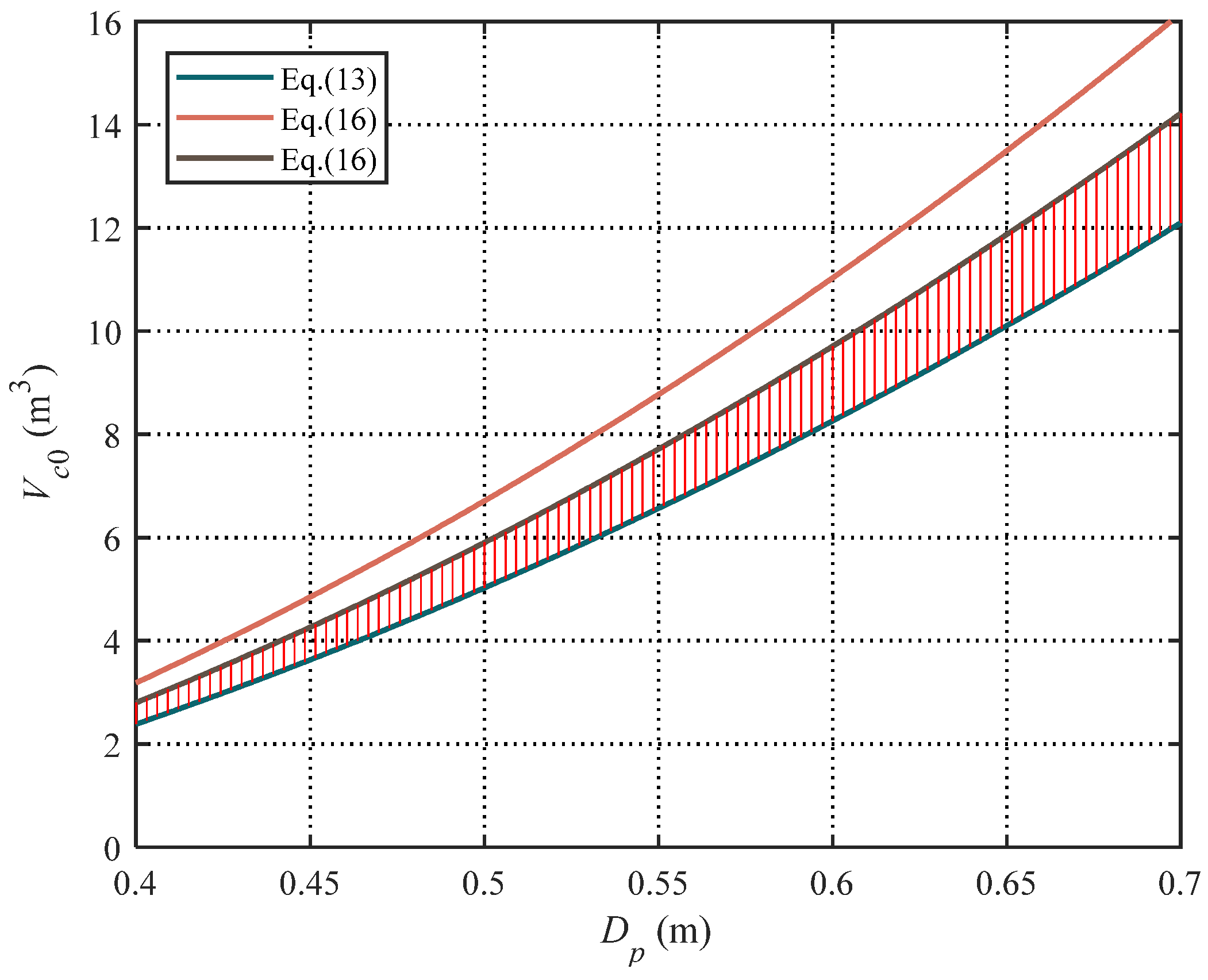
2.3.2. Optimization of the Gas Volume
2.4. Dynamic Model of the Strand Jack with the Passive Compensator
2.4.1. Damping Model of the Compensator
2.4.2. Strand Model
2.4.3. Hydrodynamic Damping Coefficient
3. Numerical Simulation
3.1. Numerical Setting
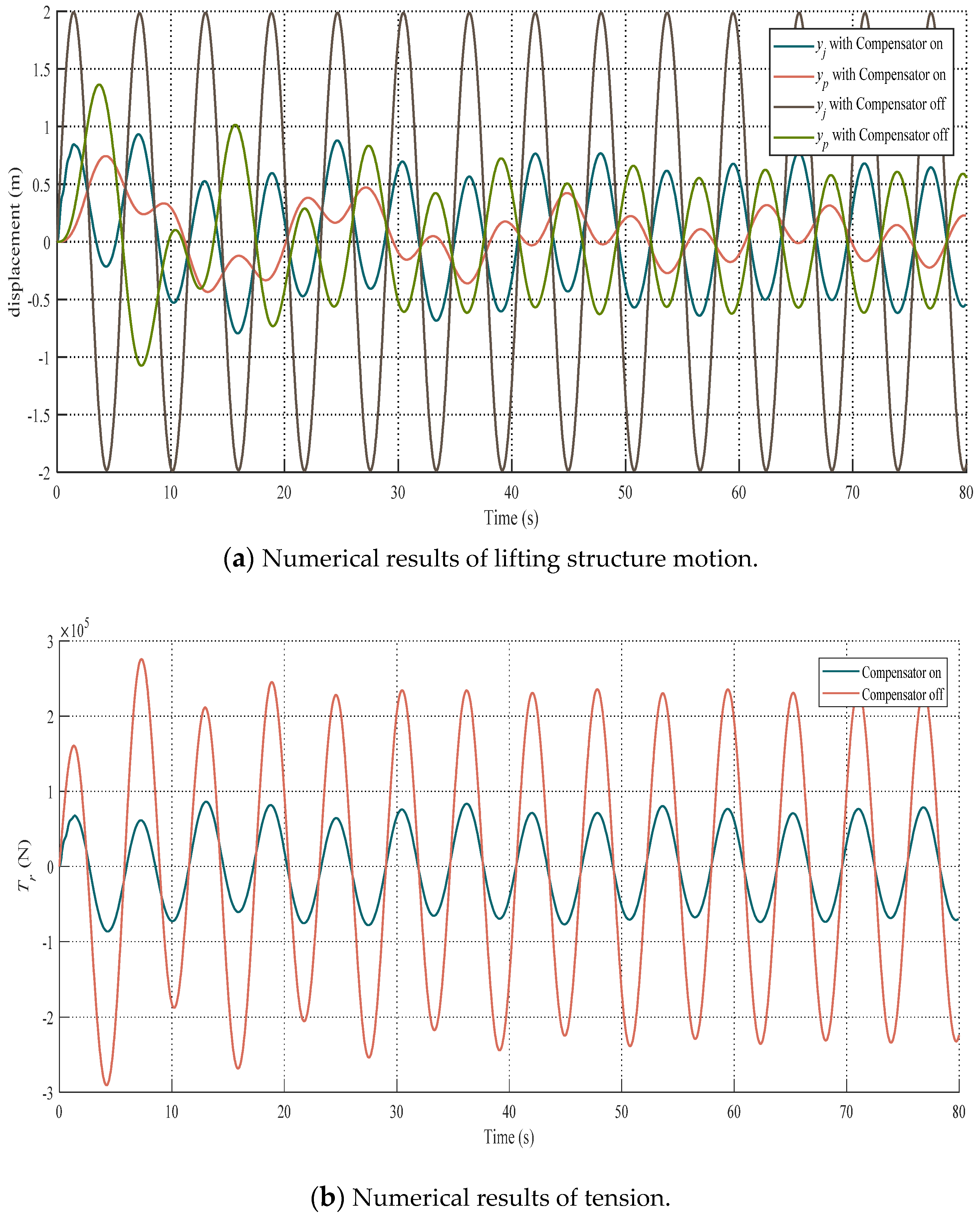
3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, A.M.; Jin, X.; Liu, Y.; Tao, F.; He, C.; He, M. A Low-Deck Floatover Installation Technology with Strand Jack Lifting Scheme. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Wang, W.; Yang, M.; Bian, Y.; Yan, S.; Yang, J.; Qin, L. Study of hydraulic synchronous lifting system for shipwreck salvage with cushion compensation. Chin. J. Constr. Mach. 2017, 15, 400–405. [Google Scholar]
- Mi, Z.; Pan, L.; Chen, J.; Chen, L.; Wu, R. Consecutive lifting and lowering electrohydraulic system for large size and heavy structure. Autom. Constr. 2013, 30, 1–8. [Google Scholar] [CrossRef]
- Woodacre, J.K.; Bauer, R.J.; Irani, R.A. A review of vertical motion heave compensation systems. Ocean Eng. 2015, 104, 140–154. [Google Scholar] [CrossRef]
- Quan, W.; Liu, Y.; Zhang, Z.; Li, X.; Liu, C. Scale model test of a semi-active heave compensation system for deep-sea tethered ROVs. Ocean Eng. 2016, 126, 353–363. [Google Scholar] [CrossRef]
- Nam, B.W.; Kim, N.W.; Hong, S.Y. Experimental and numerical study on coupled motion responses of a floating crane vessel and a lifted subsea manifold in deep water. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 552–567. [Google Scholar] [CrossRef]
- Collins, M.D. Applications of a Motion Compensation Stabilized Vertical Array of Hydrophones. IEEE Access 2019, 7, 79433–79437. [Google Scholar] [CrossRef]
- Lee, H.-W.; Roh, M.-I.; Ham, S.-H.; Ha, S. Dynamic simulation of the wireline riser tensioner system for a mobile offshore drilling unit based on multibody system dynamics. Ocean Eng. 2015, 106, 485–495. [Google Scholar] [CrossRef]
- Kang, H.-S.; Kim, M.-H.; Aramanadka, S.S.B. Tension variations of hydro-pneumatic riser tensioner and implications for dry-tree interface in semisubmersible. Ocean Syst. Eng. 2017, 23, 21–38. [Google Scholar] [CrossRef]
- Chen, B.; Yu, J.; Yu, Y.; Xu, L.; Hao, S.; Wu, C.; Wu, H. Study on key performance parameters of hydro-pneumatic tensioner for top tensioned riser. Appl. Ocean Res. 2019, 84, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Duc, L.V.; Trong, N.K. Combination of input shaping and radial spring-damper to reduce tridirectional vibration of crane payload. Mech. Syst. Signal Process. 2019, 116, 310–321. [Google Scholar]
- Quan, W.; Liu, Y.; Zhang, A.; Li, X. The nonlinear finite element modeling and performance analysis of the passive heave compensation system for the deep-sea tethered ROVs. Ocean Eng. 2016, 127, 246–257. [Google Scholar] [CrossRef]
- InterMoore Inc. Depth Compensated Subsea Passive Heave Compensator. U.S. Patent US7934561B2, 3 May 2011.
- Cannell, D.; Labbe, C.; Odigie, E.; Riddell, S. Passive Heave Compensator. U.S. Patent US9718652B2, 1 August 2017. [Google Scholar]
- Peter, A. Motion Control in Offshore and Dredging Industry; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Veritas, D.N. Dnv-rp-h103 Modelling and Analysis of Marine Operations; Det Norske Veritas: Bærum, Norway, 2011. [Google Scholar]


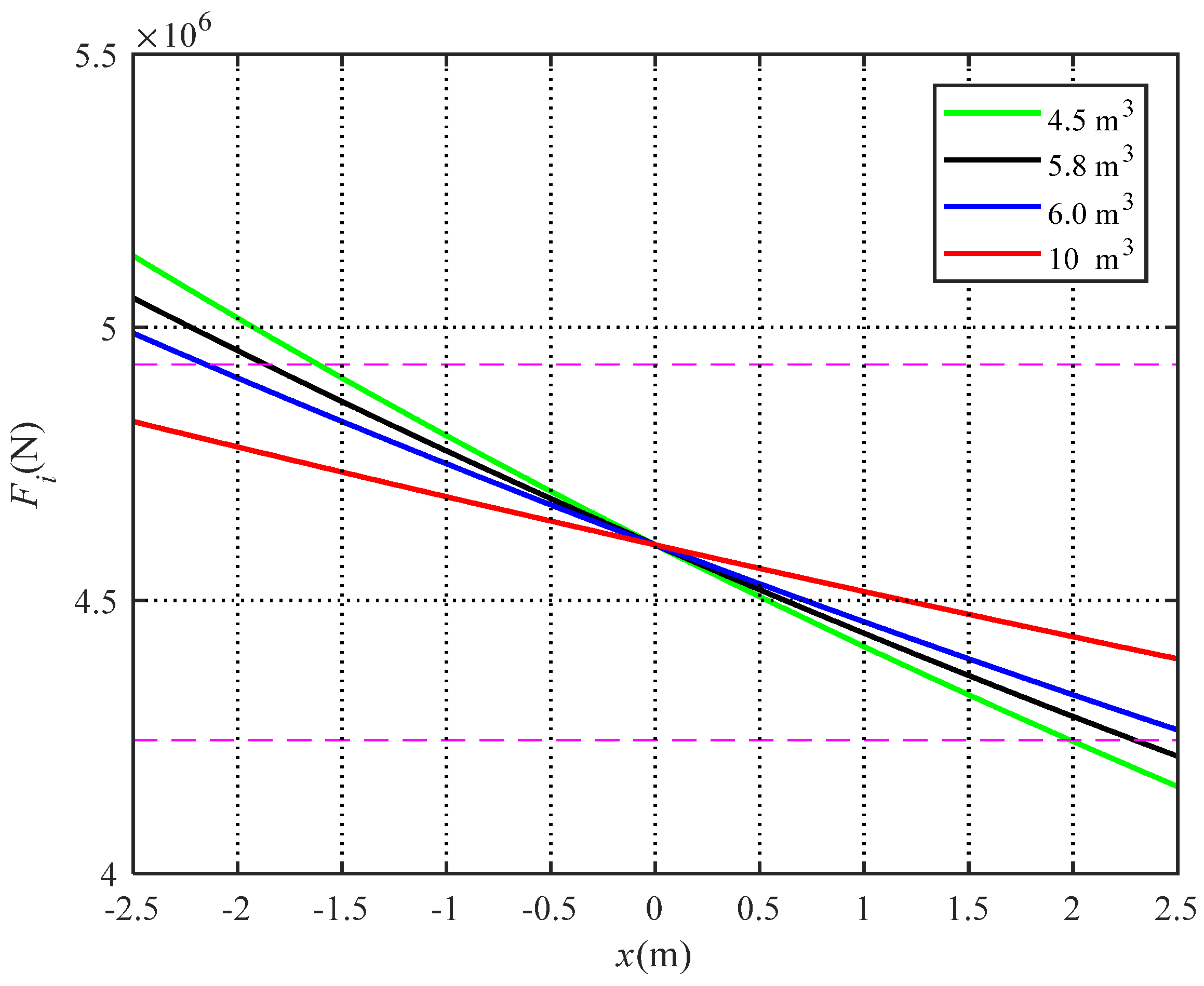

| Vc0 = 4.5 | Vc0 = 5.8 | Vc0 = 6 | Vc0 = 10 | |
|---|---|---|---|---|
| Spring force at x = −2.5 (N) | 5.14 × 106 | 5.06 × 106 | 4.99 × 106 | 4.83 × 106 |
| Spring force at x = 2.5 (N) | 4.15 × 106 | 4.21 × 106 | 4.27 × 106 | 4.39 × 106 |
| Diameter (mm) | Cross-Section Area (mm2) | Young’s Modulus (GPa) | Mass per Unit Length (kg/m) |
|---|---|---|---|
| 15.2 | 139 | 195 | 1.19 |
| List of Items | Value |
|---|---|
| Mj, ton | 1 |
| Ml, ton | 400 |
| L, m | 300 |
| ρ, g/cm3 | 1.02 |
| List of Items | Value |
|---|---|
| Vd0, m3 | 5.8 |
| dp, mm | 500 |
| dr, mm | 280 |
| dt, mm | 50 |
| lt, m | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Y.; Yi, B.; Wu, S.; Xu, J. Passive Heave Compensator Design and Numerical Simulation for Strand Jack during Lift Operation in Deep Water. J. Mar. Sci. Eng. 2021, 9, 714. https://doi.org/10.3390/jmse9070714
Zhan Y, Yi B, Wu S, Xu J. Passive Heave Compensator Design and Numerical Simulation for Strand Jack during Lift Operation in Deep Water. Journal of Marine Science and Engineering. 2021; 9(7):714. https://doi.org/10.3390/jmse9070714
Chicago/Turabian StyleZhan, Yong, Bailin Yi, Shaofei Wu, and Jianan Xu. 2021. "Passive Heave Compensator Design and Numerical Simulation for Strand Jack during Lift Operation in Deep Water" Journal of Marine Science and Engineering 9, no. 7: 714. https://doi.org/10.3390/jmse9070714
APA StyleZhan, Y., Yi, B., Wu, S., & Xu, J. (2021). Passive Heave Compensator Design and Numerical Simulation for Strand Jack during Lift Operation in Deep Water. Journal of Marine Science and Engineering, 9(7), 714. https://doi.org/10.3390/jmse9070714





