Nature-Inspired Modified Bat Algorithm for the High-Efficiency Optimization of a Multistage Centrifugal Pump for a Reverse Osmosis Desalination System
Abstract
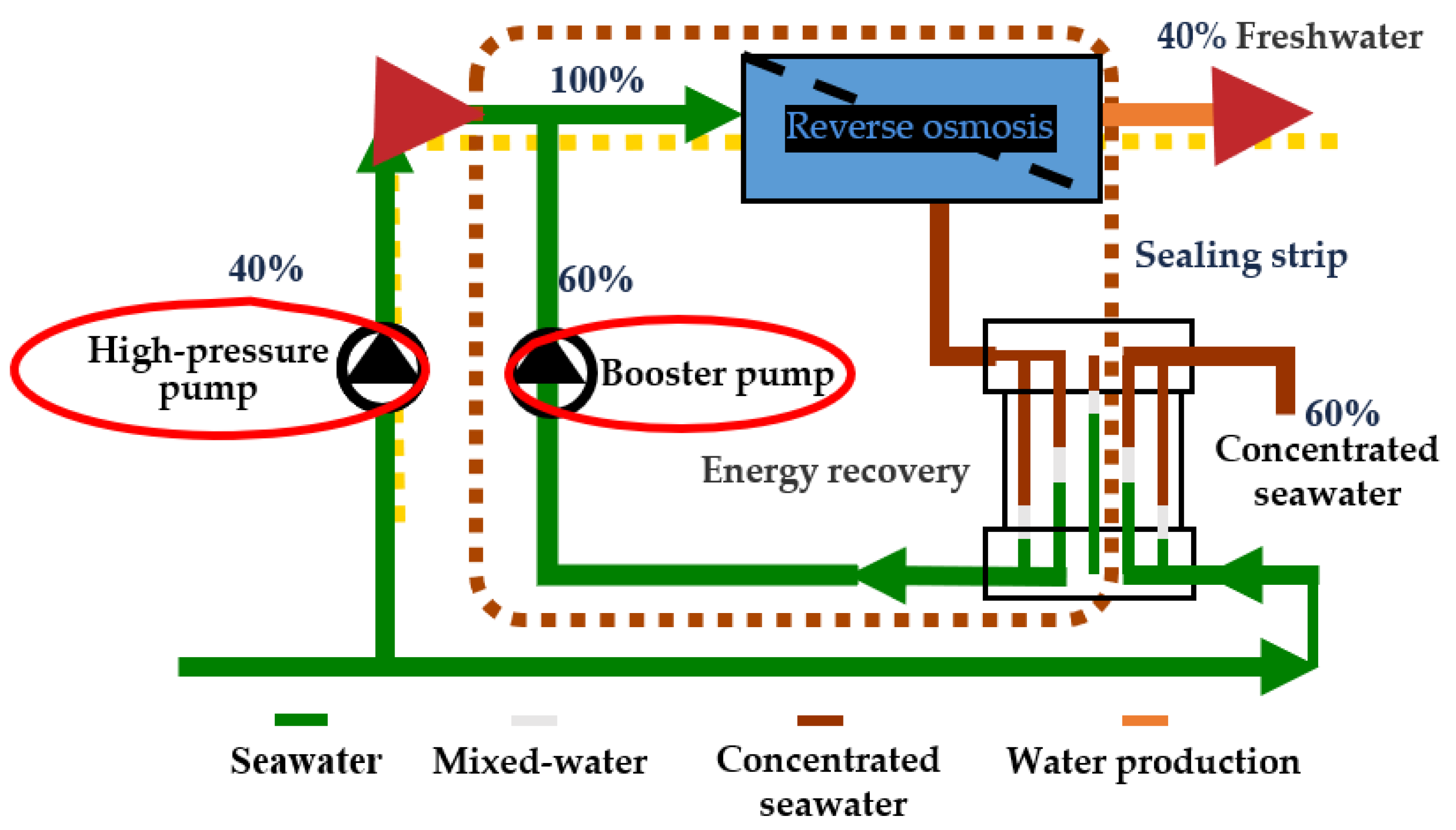
:1. Introduction
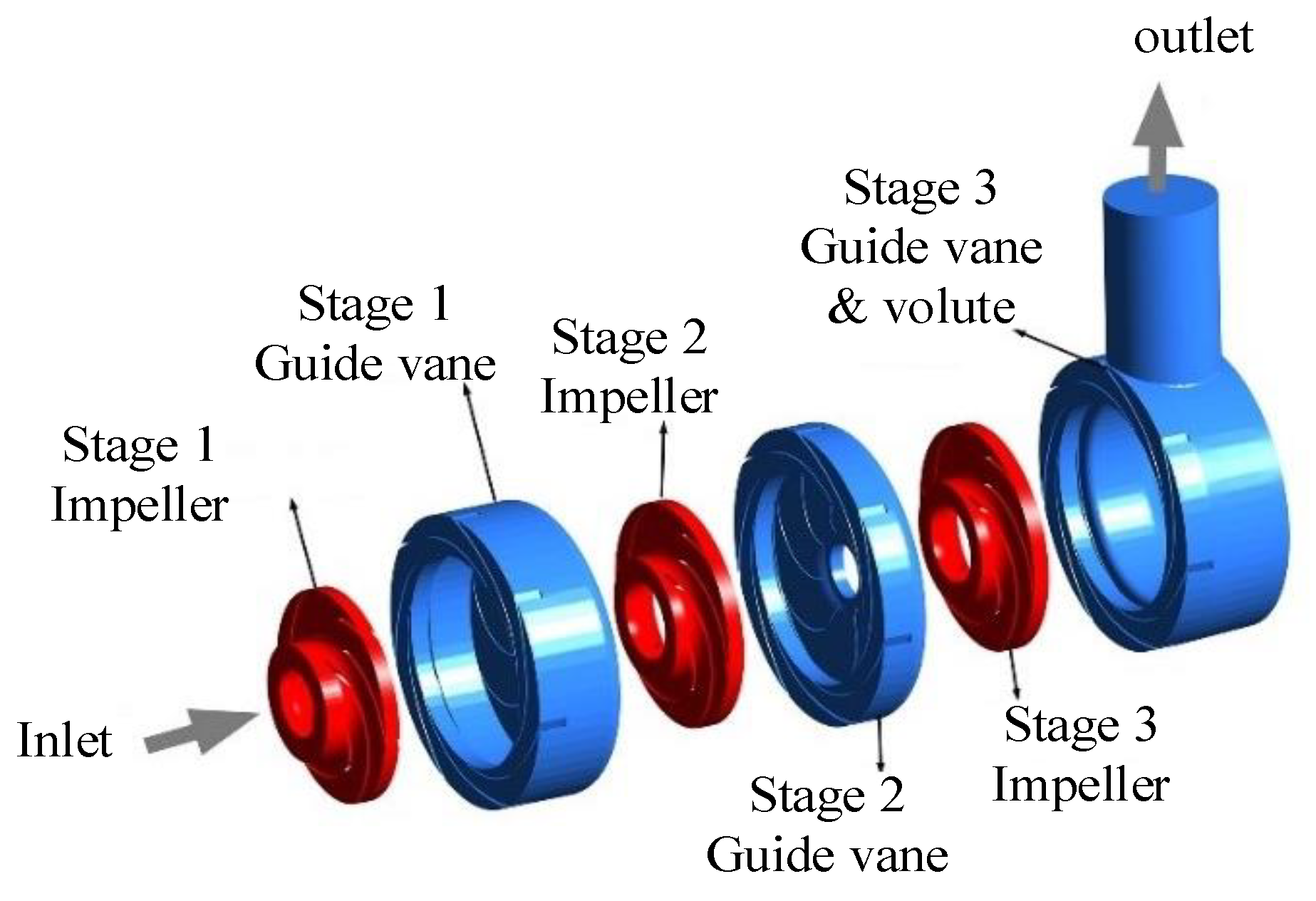
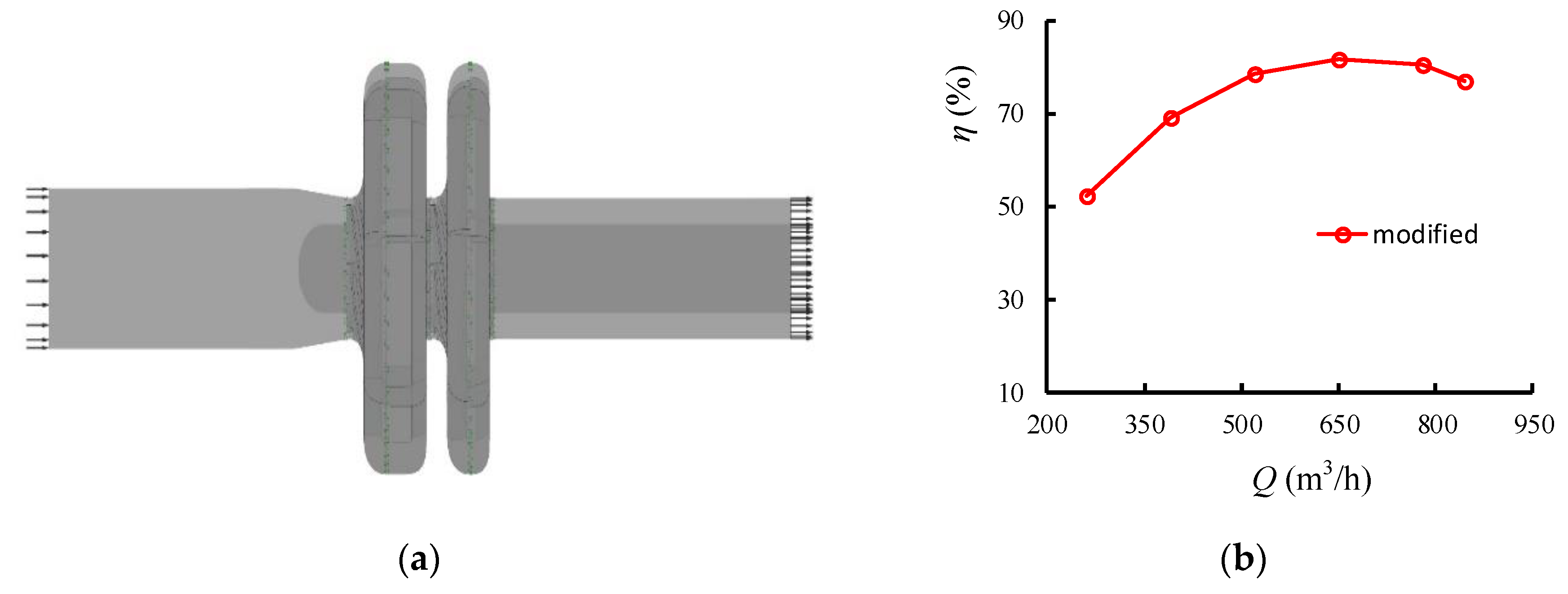
2. Research Object and Computational Domain
2.1. Research Object
2.2. Governing Equations
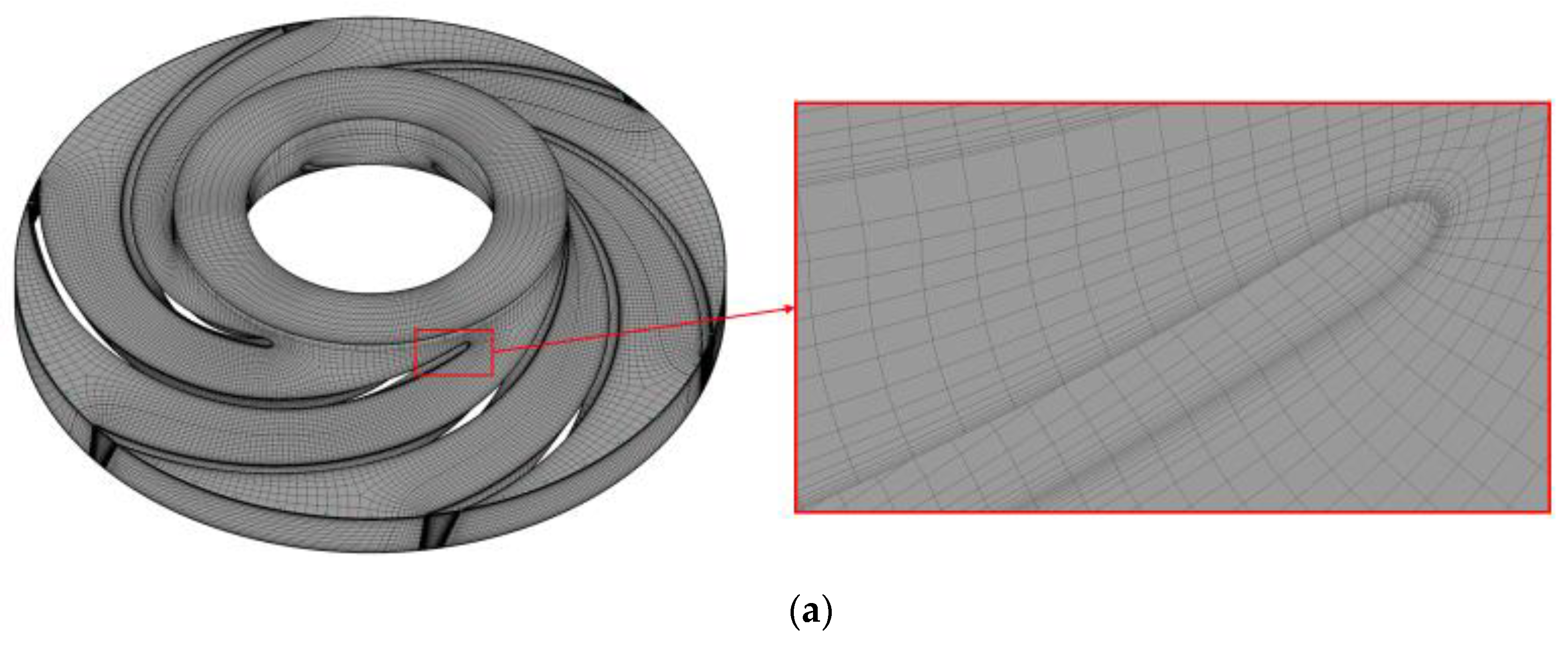
2.3. Test of Grid Sensitivity
2.4. Calculation (CFX) Setup
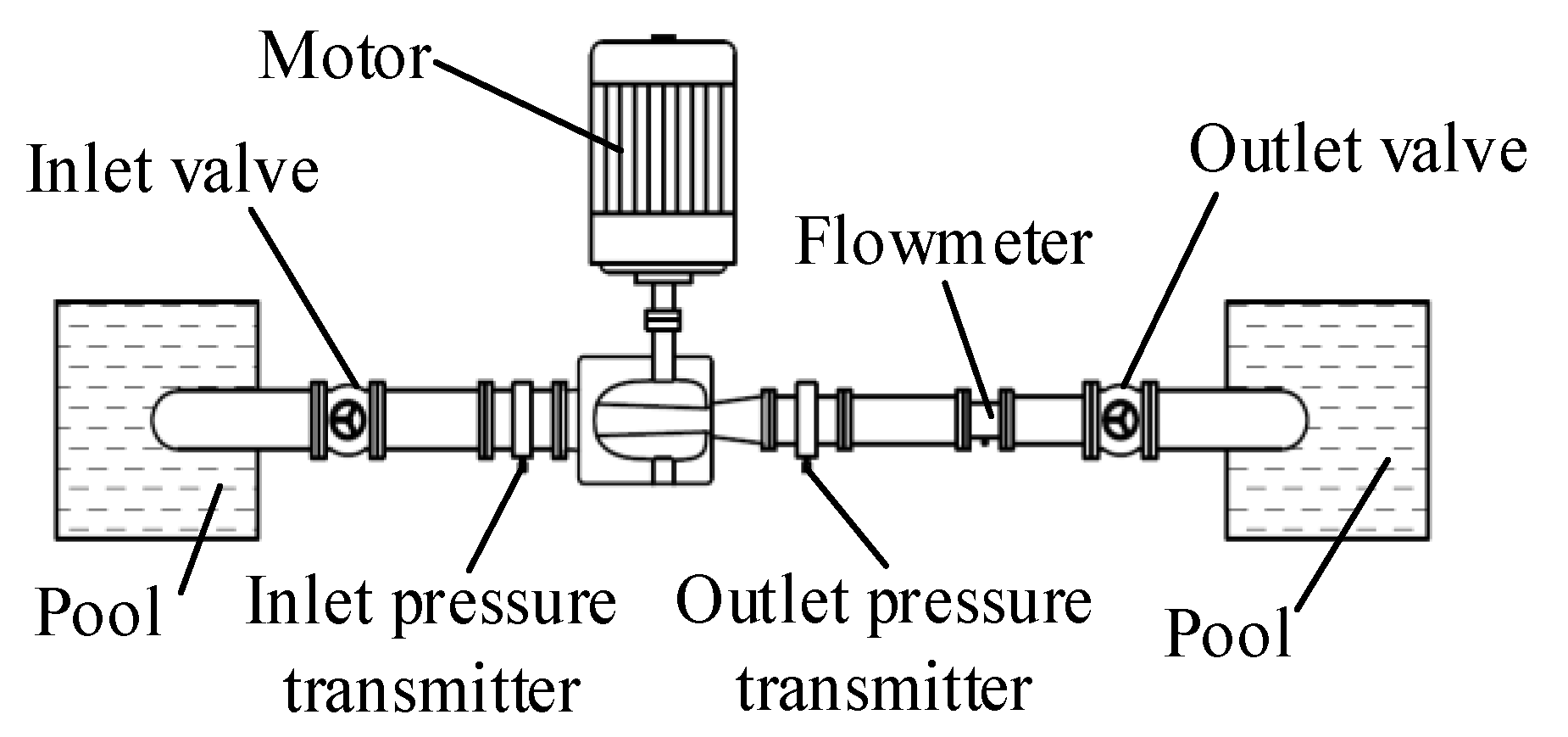
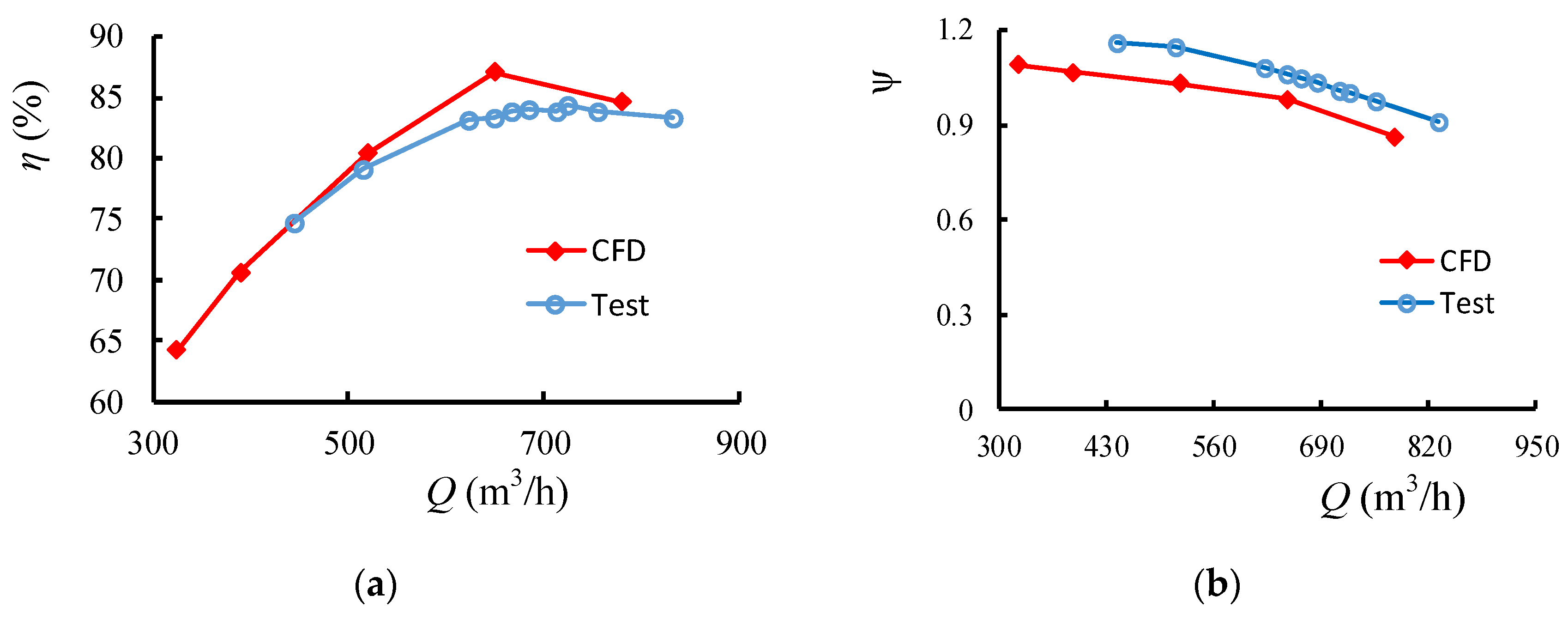
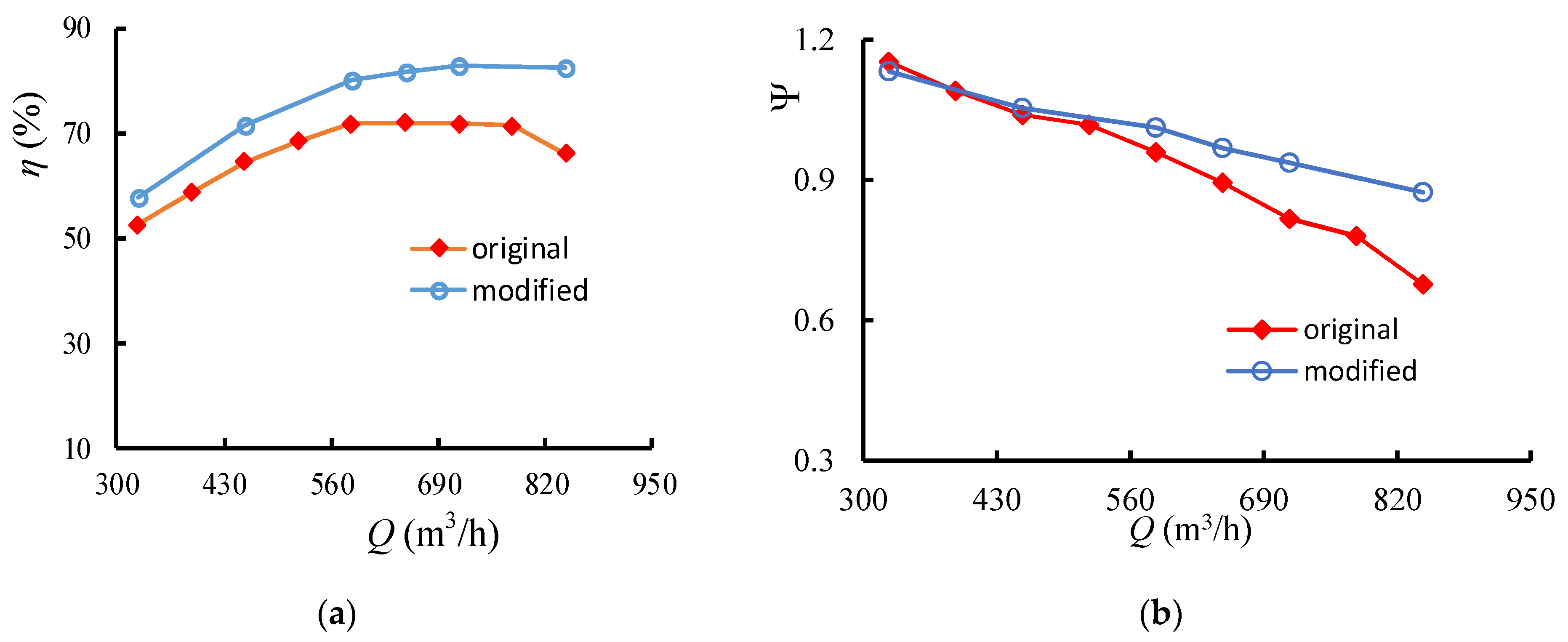
2.5. External Characteristic Test
3. Strategy for Optimization
3.1. Structure Improvement of the Multi-Stage Pump Guide Vane
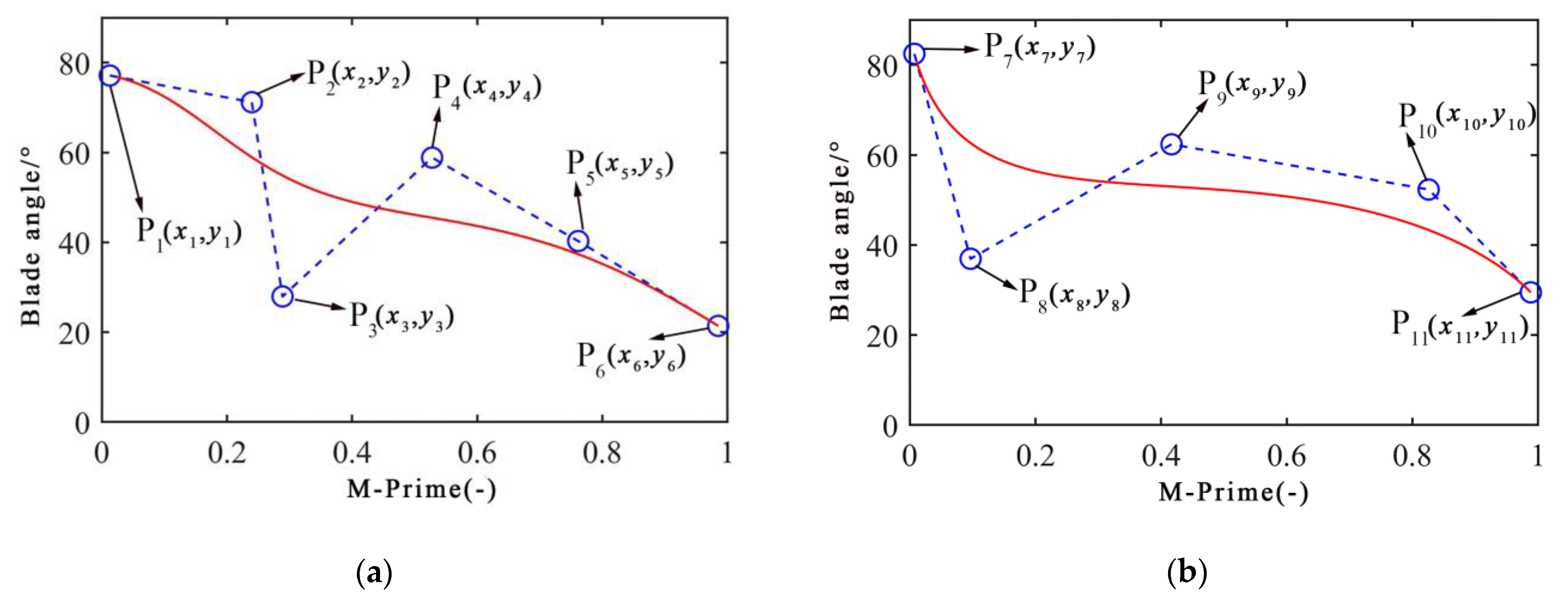
3.2. Impeller and Guide Vane Parameterization
3.3. Numerical Calculation Process Control
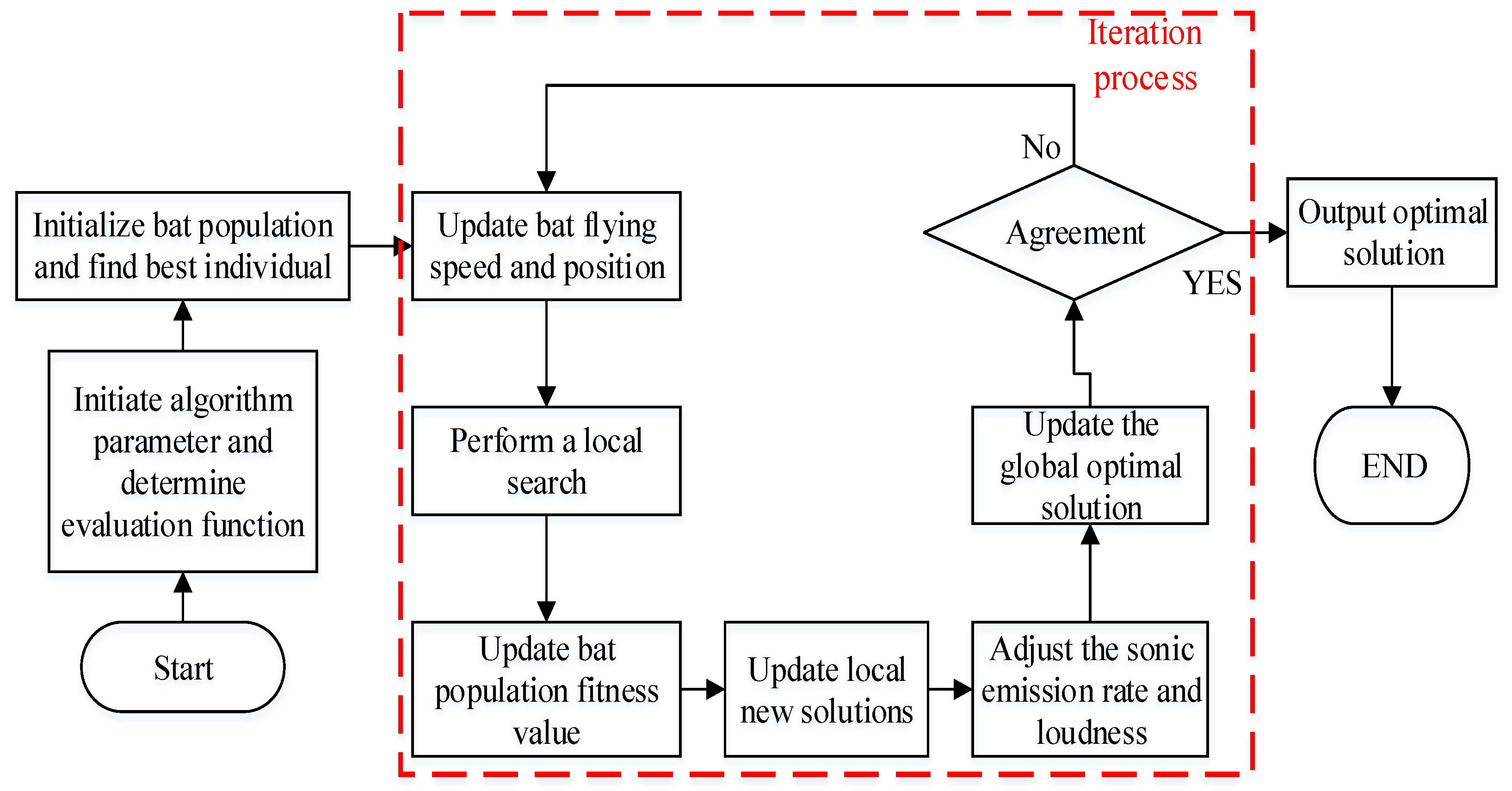
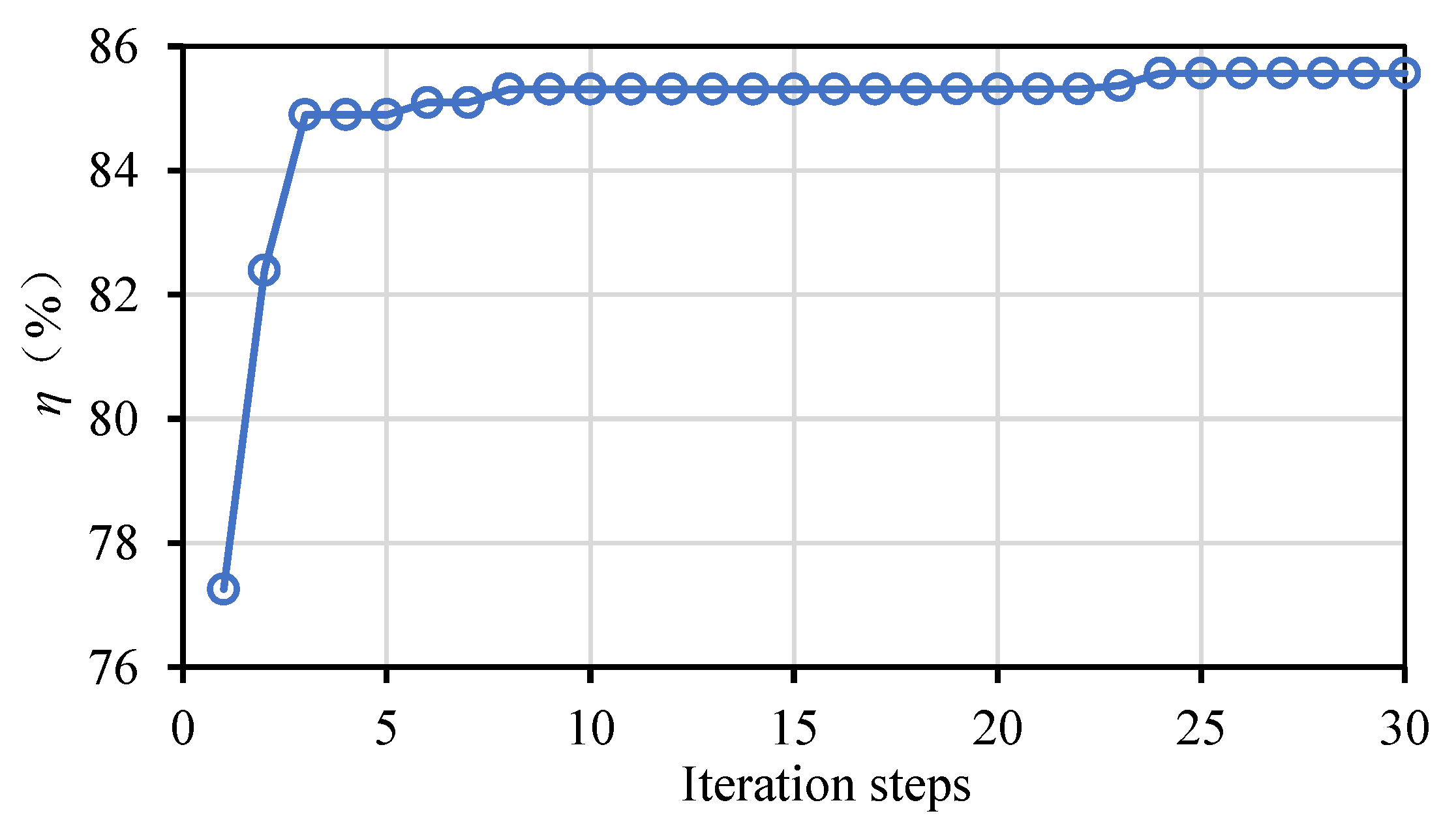
3.4. Improved Bat Algorithm Settings
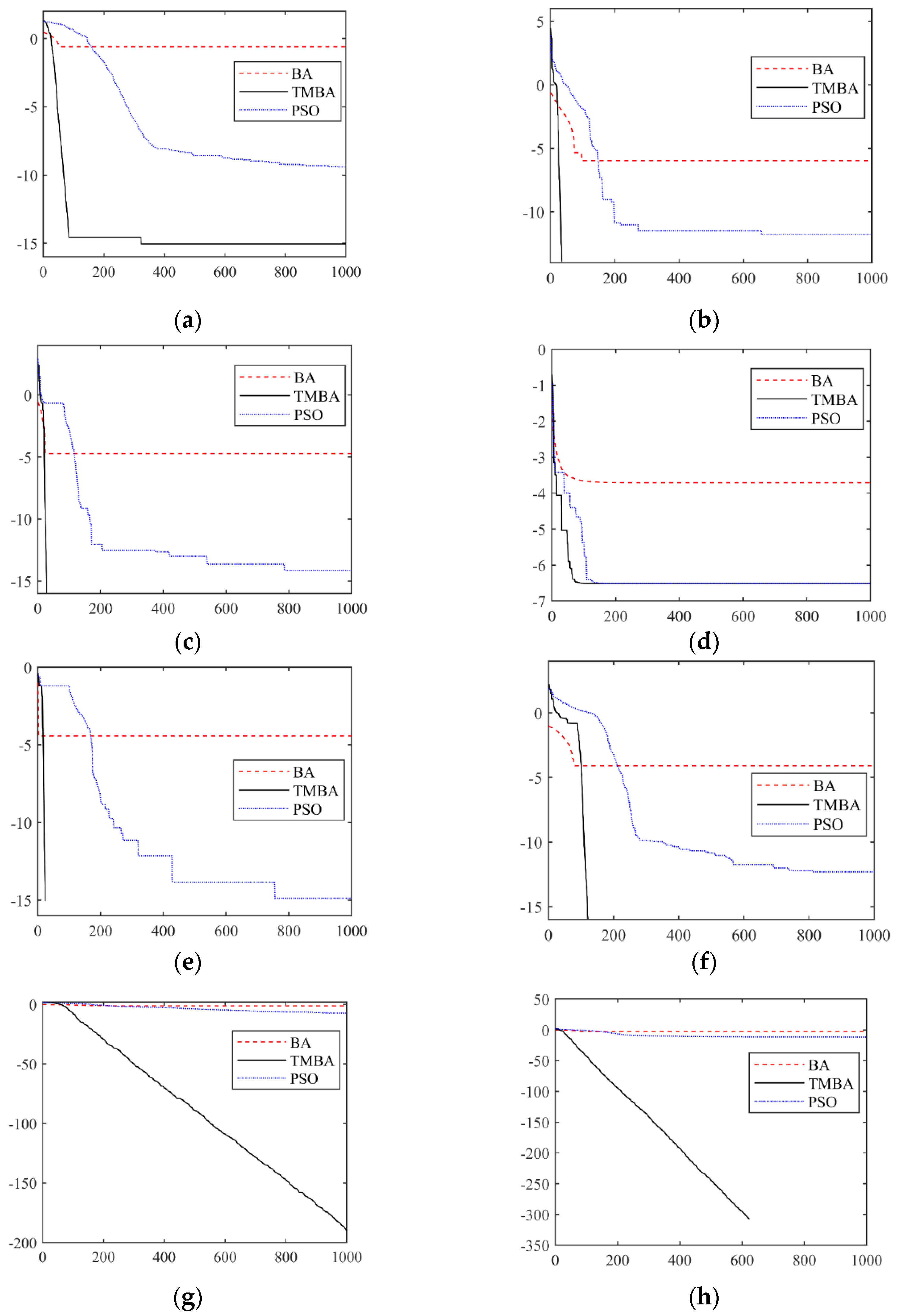
3.5. Verification of Modified BA
4. Results
4.1. Structure Improvement of the Positive Guide Vane
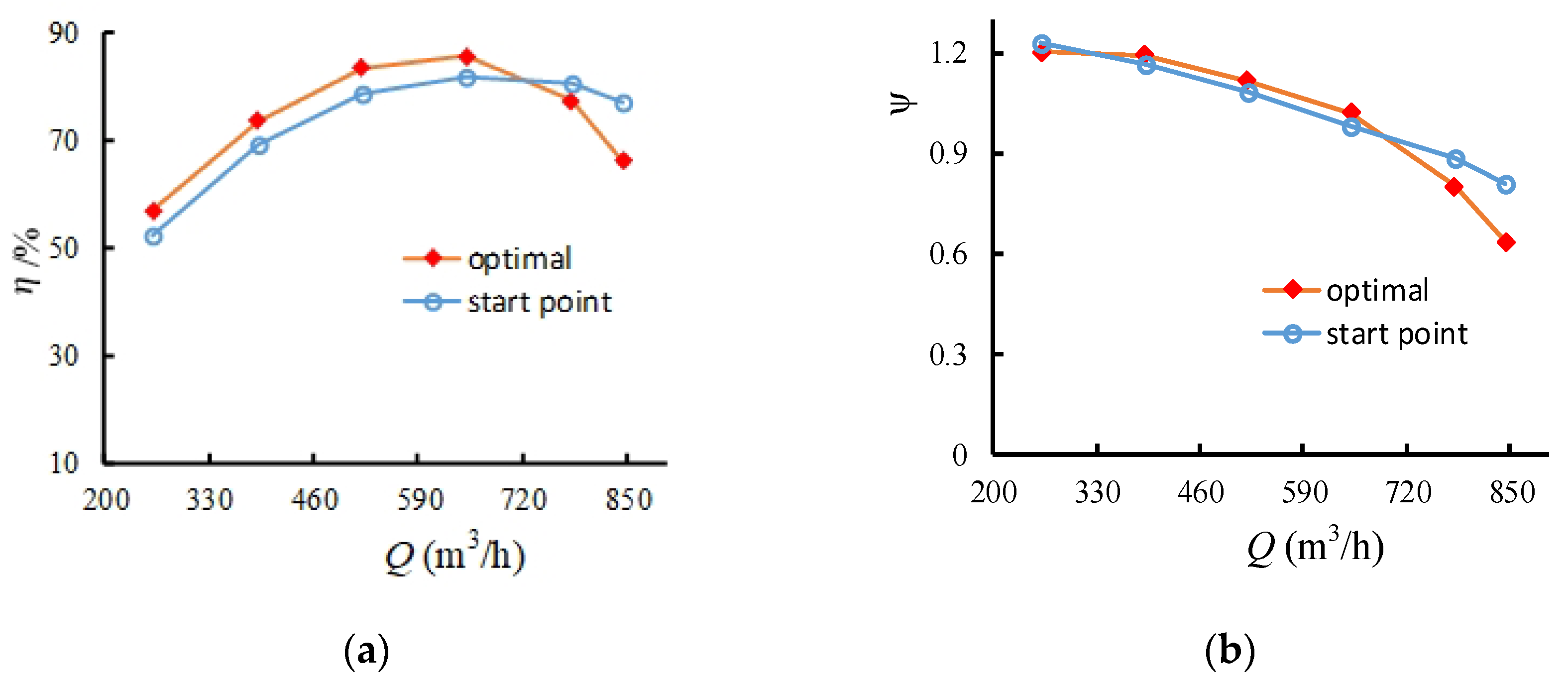
4.2. Matching Optimization of the Improved Structure
4.3. Analysis of the External Characteristics
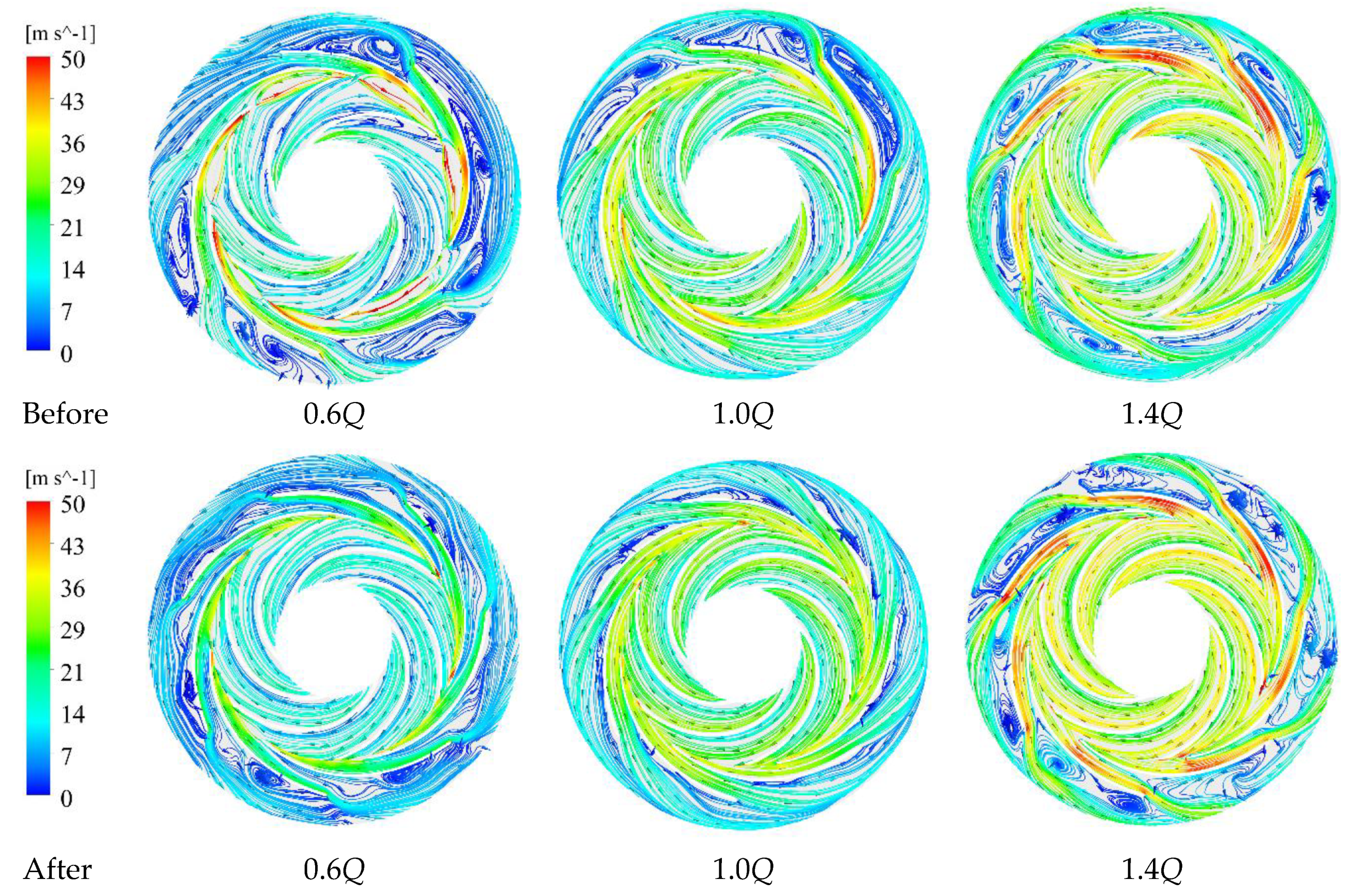
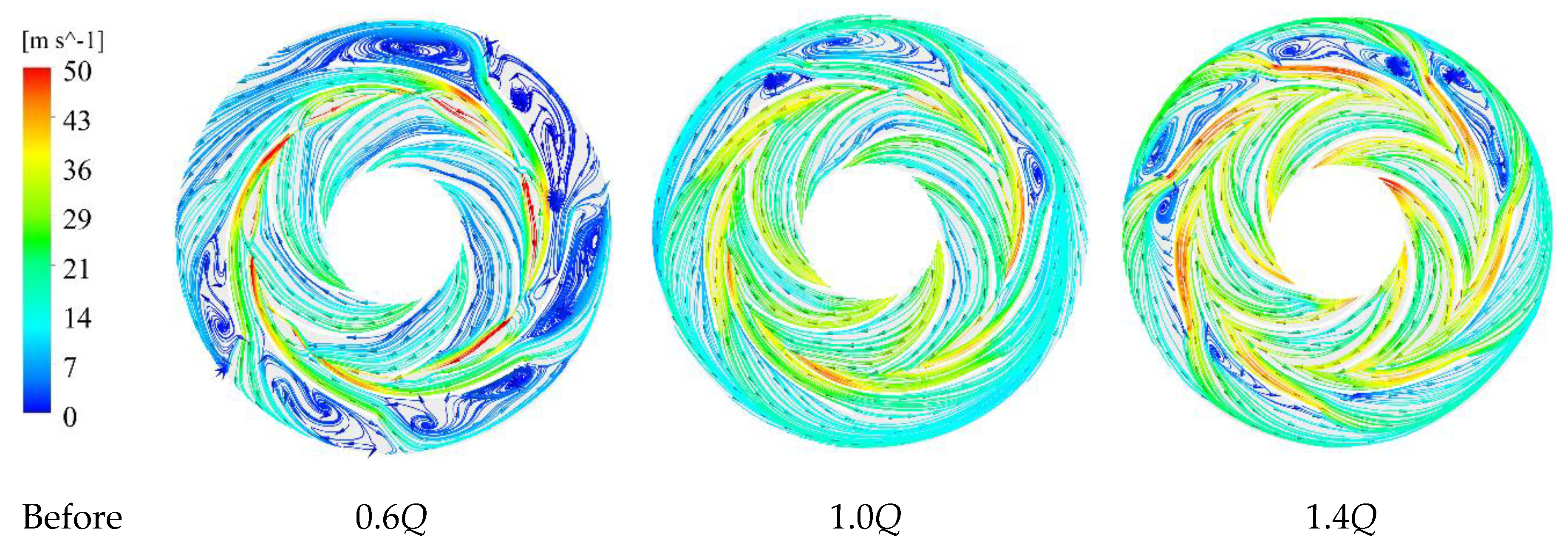
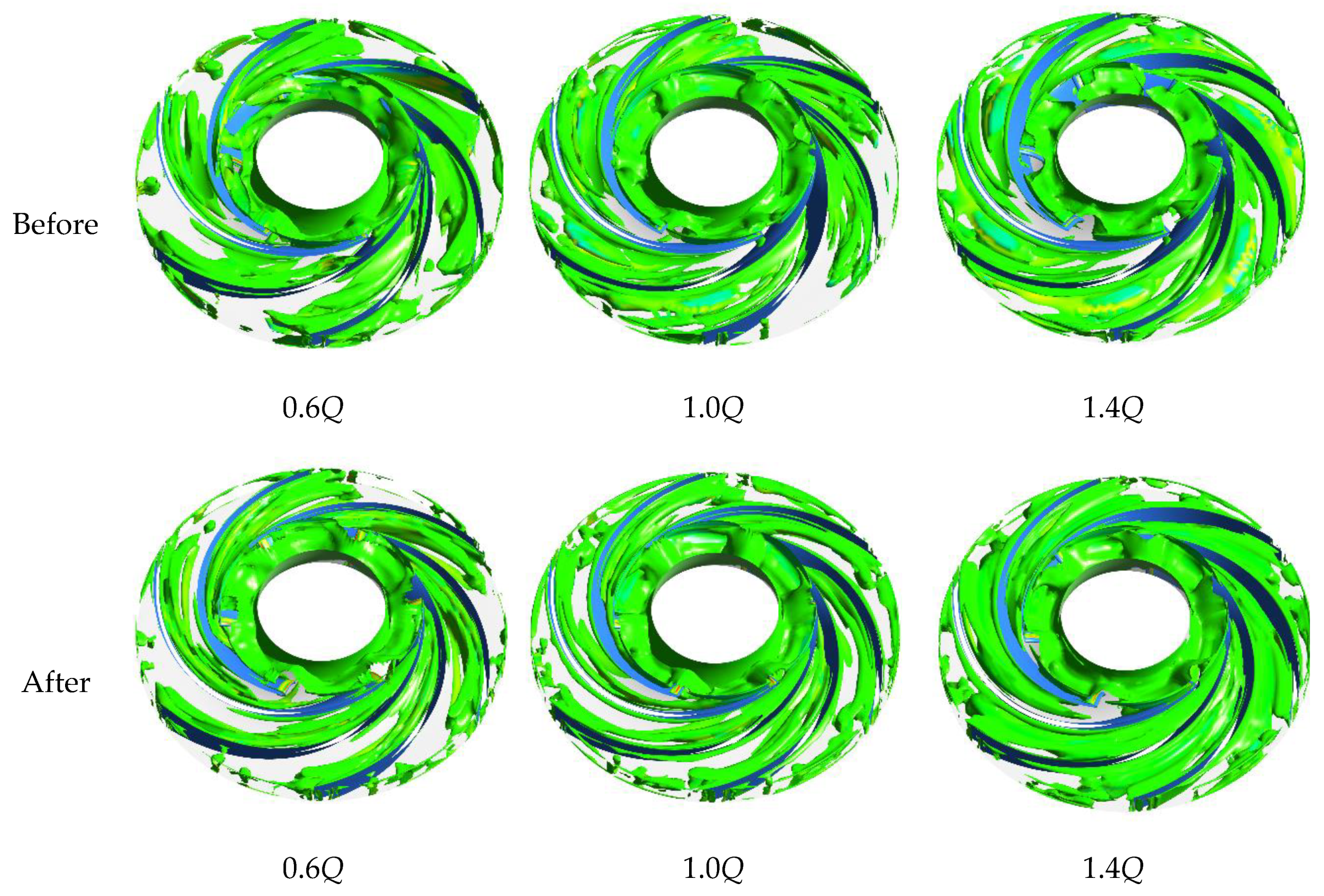
4.4. Internal Flow Analysis
5. Conclusions
- After the modification of the positive guide vane structure, the efficiency was improved in both the rated design and non-design flow conditions without obvious separation and backflow.
- With the improved bat algorithm, there was a 3.98% increase in the design point efficiency after the final optimization. At 0.8Q, the efficiency rose by 4.75%, and the head still met its demands.
- At 0.6Q, the backflow and flow separation in some part of the impeller-guide vane was reduced significantly after the optimization. The vortex at the exit of the improved guide vane channel was significantly smaller and the number was reduced.
- Under the design conditions, all of the large-size vortices disappeared after optimization. In the overload conditions, the flow situation of the optimized model deteriorated. The reason may be that the wrap angle of the guide vane was reduced after the optimization, which made the liquid leave the blade prematurely, and generated more and larger vortices under the action of the pressure difference and shear stress.
- The study provides a reference for the optimization design of the impeller–guide vane matching effect in a multistage pump using an improved bat algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, T.; Pei, J.; Yuan, S.; Osman, M.K.; Wang, J.; Wang, W. Fluid-structure interaction analysis of an impeller for a high-pressure booster pump for seawater desalination. J. Mech. Sci. Technol. 2017, 31, 5319–5328. [Google Scholar] [CrossRef]
- Jones, E.; Qadir, M.; van Vliet, M.T.; Smakhtin, V.; Kang, S.M. The state of desalination and brine production: A global outlook. Sci. Total. Environ. 2019, 657, 1343–1356. [Google Scholar] [CrossRef]
- Wang, W.; Osman, M.K.; Pei, J.; Yuan, S.; Cao, J.; Osman, F.K. Efficiency-House Optimization to Widen the Operation Range of the Double-Suction Centrifugal Pump. Complexity 2020, 2020, 9737049. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, X. Review of design optimization methods for turbomachinery aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Simpson, T.W.; Mauery, T.M.; Korte, J.J.; Mistree, F. Kriging models for global approximation in simulation-based multidisciplinary design optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef] [Green Version]
- An, Z.; Zhounian, L.; Peng, W.; Linlin, C.; Dazhuan, W. Multi-objective optimization of a low specific speed centrifugal pump using an evolutionary algorithm. Eng. Optim. 2015, 48, 1251–1274. [Google Scholar] [CrossRef]
- Pei, J.; Yin, T.; Yuan, S.; Wang, W.; Wang, J. Cavitation optimization for a centrifugal pump impeller by using orthogonal design of experiment. Chin. J. Mech. Eng. 2017, 30, 103–109. [Google Scholar] [CrossRef]
- Gan, X.; Wang, W.; Pei, J.; Yuan, S.; Tang, Y.; Osman, M.K. Direct Shape Optimization and Parametric Analysis of a Vertical Inline Pump via Multi-Objective Particle Swarm Optimization. Energies 2020, 13, 425. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Li, Y.; Yuan, S.; Wang, W.; Zheng, Y.; Osman, M.K. Multiobjective Combination Optimization of an Impeller and Diffuser in a Reversible Axial-Flow Pump Based on a Two-Layer Artificial Neural Network. Processes 2020, 8, 309. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Li, Y.; Osman, M.K.; Yuan, S.; Zhang, B.; Liu, J. Multi-Condition Optimization of Cavitation Performance on a Double-Suction Centrifugal Pump Based on ANN and NSGA-II. Processes 2020, 8, 1124. [Google Scholar] [CrossRef]
- Si, Q.; Yuan, S.; Wang, C.; Hu, B. Optimal design of submersible multistage pumps with low specific speed. Trans. Chin. Soc. Agric. Eng. 2012, 28, 122–127. [Google Scholar]
- Kim, J.-H.; Lee, H.-C.; Kim, J.-H.; Choi, Y.-S.; Yoon, J.-Y.; Yoo, I.-S.; Choi, W.-C. Improvement of Hydrodynamic Performance of a Multiphase Pump Using Design of Experiment Techniques. J. Fluids Eng. 2015, 137, 081301. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Design Method of Controllable Blade Angle and Orthogonal Optimization of Pressure Rise for a Multiphase Pump. Energies 2018, 11, 1048. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Shi, W.; Wang, X.; Jiang, X.; Yang, Y.; Li, W.; Zhou, L. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics. Appl. Energy 2017, 187, 10–26. [Google Scholar] [CrossRef]
- Kawashima, D.; Kanemoto, T.; Sakoda, K.; Wada, A.; Hara, T. Matching Diffuser Vane with Return Vane Installed in Multistage Centrifugal Pump. Int. J. Fluid Mach. Syst. 2008, 1, 86–91. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Yang, X.-S. Bat algorithm for multi-objective optimisation. Int. J. Bio-Inspired Comput. 2011, 3, 267. [Google Scholar] [CrossRef]
- Yang, X.-S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141. [Google Scholar] [CrossRef] [Green Version]
- Medvitz, R.B.; Kunz, R.F.; Boger, D.A.; Lindau, J.W.; Yocum, A.M.; Pauley, L. Performance Analysis of Cavitating Flow in Centrifugal Pumps Using Multiphase CFD. J. Fluids Eng. 2002, 124, 377–383. [Google Scholar] [CrossRef]
- Bardina, J.; Huang, P.; Coakley, T. Turbulence modeling validation. In Proceedings of the 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997; p. 21. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Osman, M.K.; Wang, W.; Yuan, J.; Zhao, J.; Wang, Y.; Liu, J. Flow loss analysis of a two-stage axially split centrifugal pump with double inlet under different channel designs. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5316–5328. [Google Scholar] [CrossRef]
- Wang, W.; Osman, M.K.; Pei, J.; Gan, X.; Yin, T. Artificial Neural Networks Approach for a Multi-Objective Cavitation Optimization Design in a Double-Suction Centrifugal Pump. Processes 2019, 7, 246. [Google Scholar] [CrossRef] [Green Version]
- Gülich, J.F. Centrifugal Pumps; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Wang, Y.; Wang, P.; Zhang, J.; Cui, Z.; Cai, X.; Zhang, W.; Chen, J. A Novel Bat Algorithm with Multiple Strategies Coupling for Numerical Optimization. Mathematics 2019, 7, 135. [Google Scholar] [CrossRef] [Green Version]
- Arellano-Valle, R.B.; Bolfarine, H. On some characterizations of the t-distribution. Stat. Probab. Lett. 1995, 25, 79–85. [Google Scholar] [CrossRef]
- Ramli, M.; Abas, Z.A.; Desa, M.; Abidin, Z.Z.; Alazzam, M. Enhanced convergence of Bat Algorithm based on dimensional and inertia weight factor. J. King Saud Univ. Comput. Inf. Sci. 2019, 31, 452–458. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.-S.; Dong, X.-R.; Wang, Y.-Q.; Liu, J.-M.; Zhang, Y.-N.; Cai, X.-S.; Gui, N. Third generation of vortex identification methods: Omega and Liutex/Rortex based systems. J. Hydrodyn. 2019, 31, 205–223. [Google Scholar] [CrossRef]
- Liu, J.; Liu, C. Modified normalized Rortex/vortex identification method. Phys. Fluids 2019, 31, 061704. [Google Scholar] [CrossRef] [Green Version]








| Parameter | Value |
|---|---|
| Impeller inlet diameter | 222 |
| Impeller outlet diameter | 400 |
| Impeller outlet width | 27 |
| Impeller blade wrap angle | 140 |
| Impeller blade inlet angle | 10 |
| Impeller blade exit angle | 27 |
| Number of impeller blades | 6 |
| Diameter of guide vane base circle | 404 |
| Outlet diameter of guide vane | 552 |
| Guide vane outlet width | 33 |
| Wrap angle of guide vane | 84 |
| Guide vane blade inlet placement angle | 8.5 |
| Guide vane blade exit placement angle | 21 |
| Number of guide vanes | 7 |
| Item | Mesh I | Mesh II | Mesh III | Mesh IV | Mesh V |
|---|---|---|---|---|---|
| Total Mesh (×106) | 9.128 | 9.861 | 10.987 | 12.250 | 13.034 |
| GCI (%) | 5.027 | 4.132 | 2.816 | 2.015 | 1.980 |
| ψ | 0.86 | 0.91 | 0.96 | 0.98 | 0.98 |
| Control Point | Optimization Variable | Upper Limit | Lower Limit |
|---|---|---|---|
| P1 | x1 | 0 | 0 |
| y1 | 0 | 1 | |
| P2 | x2 | 0.07 | 0.14 |
| y2 | 26 | 39 | |
| P3 | x3 | 0.27 | 0.39 |
| y3 | 55 | 68 | |
| P4 | x4 | 0.51 | 0.59 |
| y4 | 86 | 98 | |
| P5 | x5 | 0.72 | 0.80 |
| y5 | 117 | 128 | |
| P6 | x6 | 0.9832 | 0.9832 |
| y6 | 141 | 159 | |
| P7 | x7 | 0 | 0 |
| y7 | 0 | 1 | |
| P8 | x8 | 0.04 | 0.07 |
| y8 | 18 | 24 | |
| P9 | x9 | 0.09 | 0.15 |
| y9 | 36 | 45 | |
| P10 | x10 | 0.13 | 0.21 |
| y10 | 67 | 75 | |
| P11 | x11 | 0.2510 | 0.2510 |
| y11 | 80 | 89 |
| Parameter | Value |
|---|---|
| Bat population size np | 16 |
| Maximum iteration steps Nit | 30 |
| Acoustic frequency range [fmin, fmax] | [0, 2] |
| Initial sonic loudness | 1.2 |
| Initial sonic emission rate | 0.5 |
| t distribution step adjust coefficient | 0.8 |
| Gauss distribution adjust coefficient | 0.08 |
| Maximum number of stalls | 3 |
| Stagnation threshold | 10−2 |
| y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | y6 | y7 |
| 0.51 | 0.14 | 27.29 | 0.39 | 67.98 | 0.59 | 89.29 | 0.80 | 127.96 | 158.98 | 0.02 |
| x8 | y8 | x9 | y9 | x10 | y10 | y11 | H (m) | η (%) | P (kw) | |
| 0.05 | 23.99 | 0.11 | 44.94 | 0.18 | 74.99 | 88.99 | 388.84 | 85.57 | 802.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Pei, J.; Wang, W.; Osman, M.K.; Jiang, W.; Zhao, J.; Deng, Q. Nature-Inspired Modified Bat Algorithm for the High-Efficiency Optimization of a Multistage Centrifugal Pump for a Reverse Osmosis Desalination System. J. Mar. Sci. Eng. 2021, 9, 771. https://doi.org/10.3390/jmse9070771
Gong X, Pei J, Wang W, Osman MK, Jiang W, Zhao J, Deng Q. Nature-Inspired Modified Bat Algorithm for the High-Efficiency Optimization of a Multistage Centrifugal Pump for a Reverse Osmosis Desalination System. Journal of Marine Science and Engineering. 2021; 9(7):771. https://doi.org/10.3390/jmse9070771
Chicago/Turabian StyleGong, Xiaobo, Ji Pei, Wenjie Wang, Majeed Koranteng Osman, Wei Jiang, Jiantao Zhao, and Qifan Deng. 2021. "Nature-Inspired Modified Bat Algorithm for the High-Efficiency Optimization of a Multistage Centrifugal Pump for a Reverse Osmosis Desalination System" Journal of Marine Science and Engineering 9, no. 7: 771. https://doi.org/10.3390/jmse9070771
APA StyleGong, X., Pei, J., Wang, W., Osman, M. K., Jiang, W., Zhao, J., & Deng, Q. (2021). Nature-Inspired Modified Bat Algorithm for the High-Efficiency Optimization of a Multistage Centrifugal Pump for a Reverse Osmosis Desalination System. Journal of Marine Science and Engineering, 9(7), 771. https://doi.org/10.3390/jmse9070771







