Diffraction and Radiation of Water Waves by a Heaving Absorber in Front of a Bottom-Mounted, V-shaped Breakwater of Infinite Length
Abstract
:1. Introduction
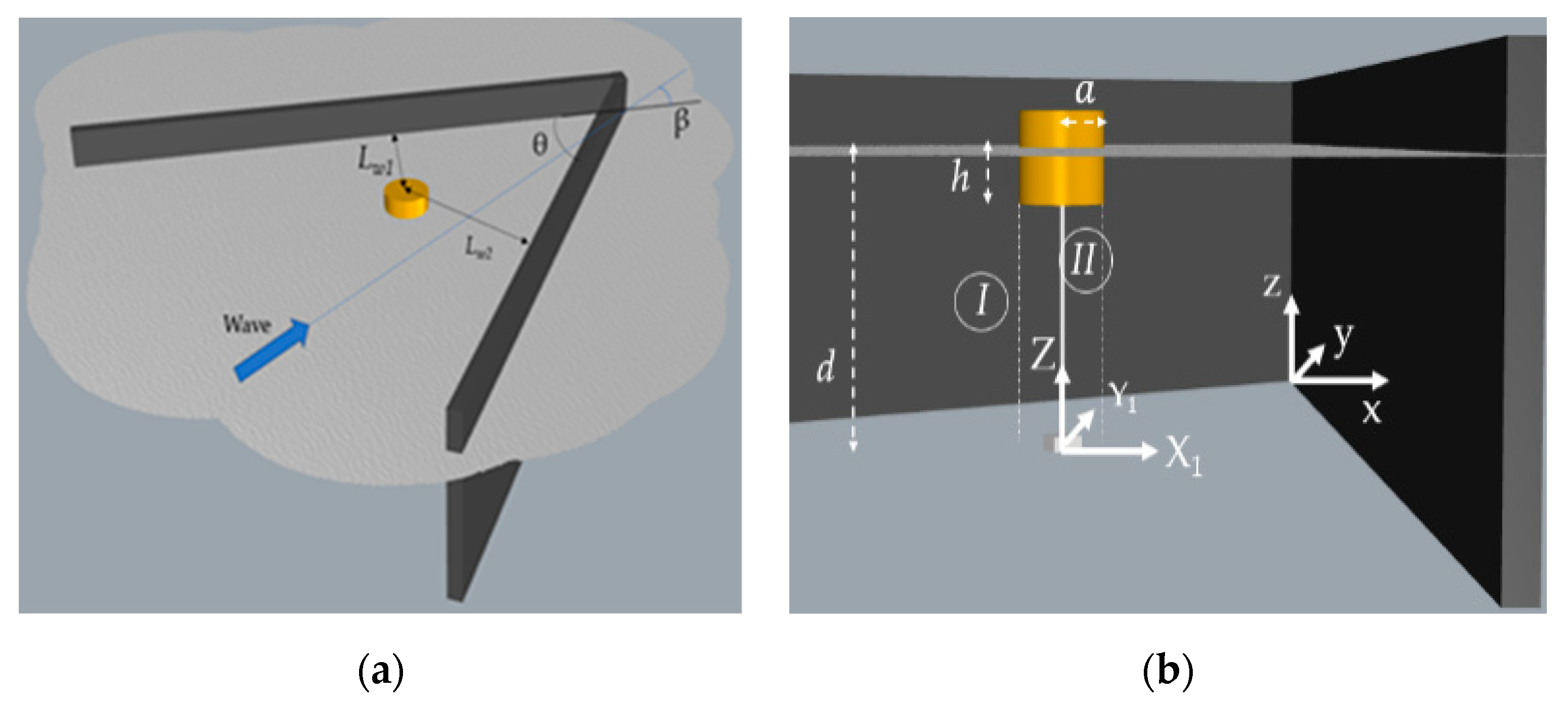
2. Diffraction and Motion Problem Formulation
3. Hydrodynamic Forces
4. Wave Power Absorption
5. Numerical Results
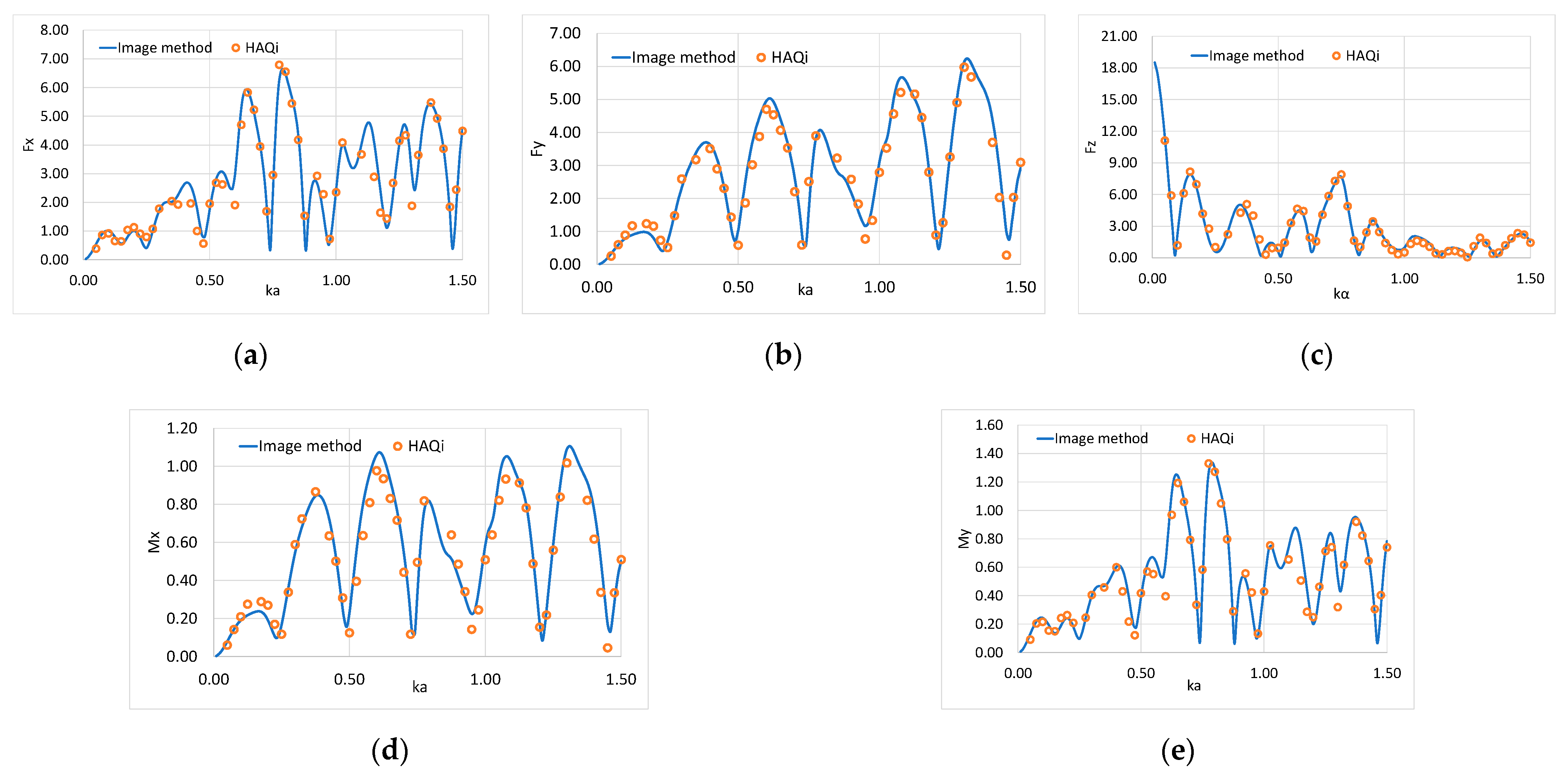
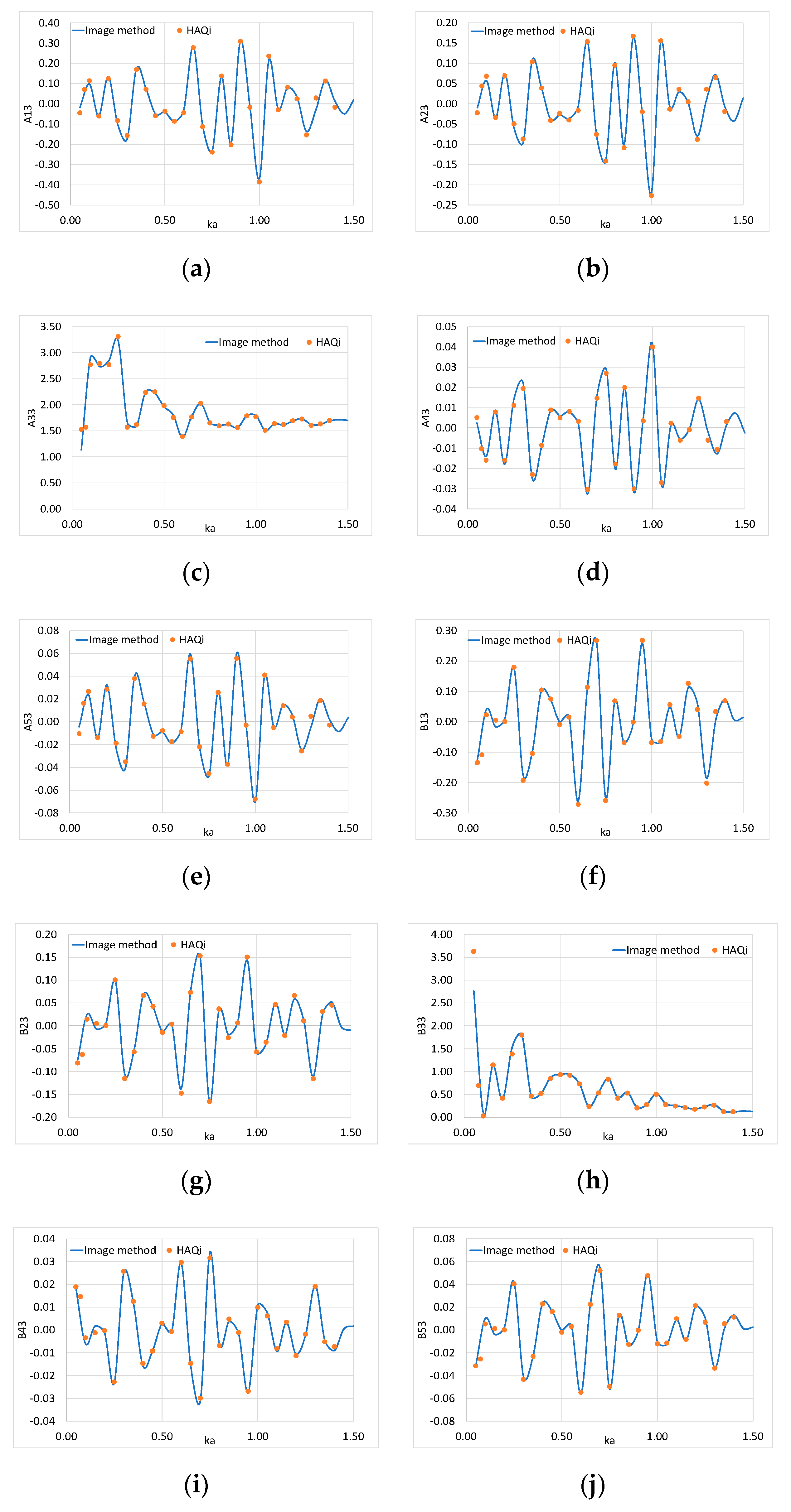
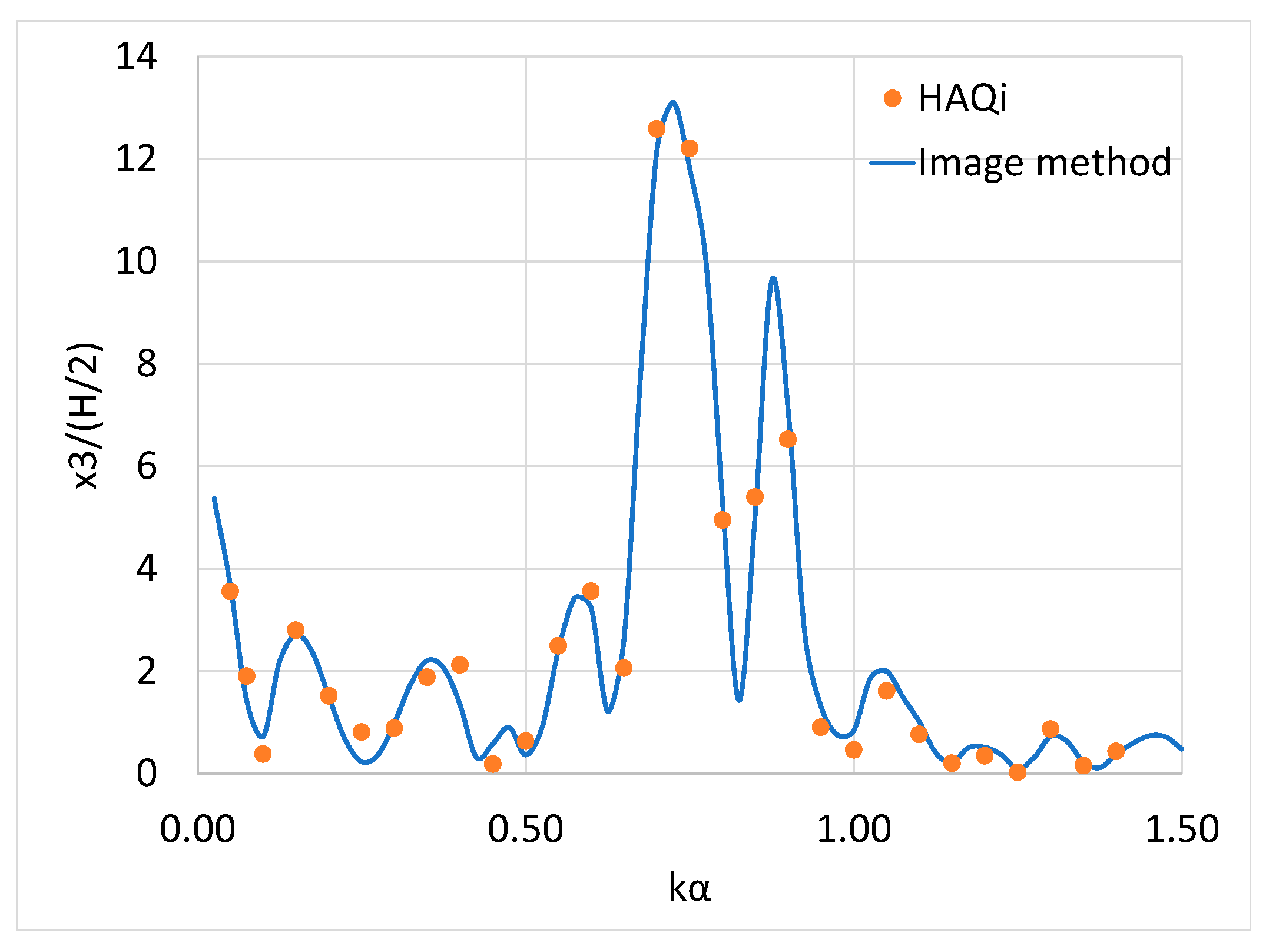
5.1. Result Validation
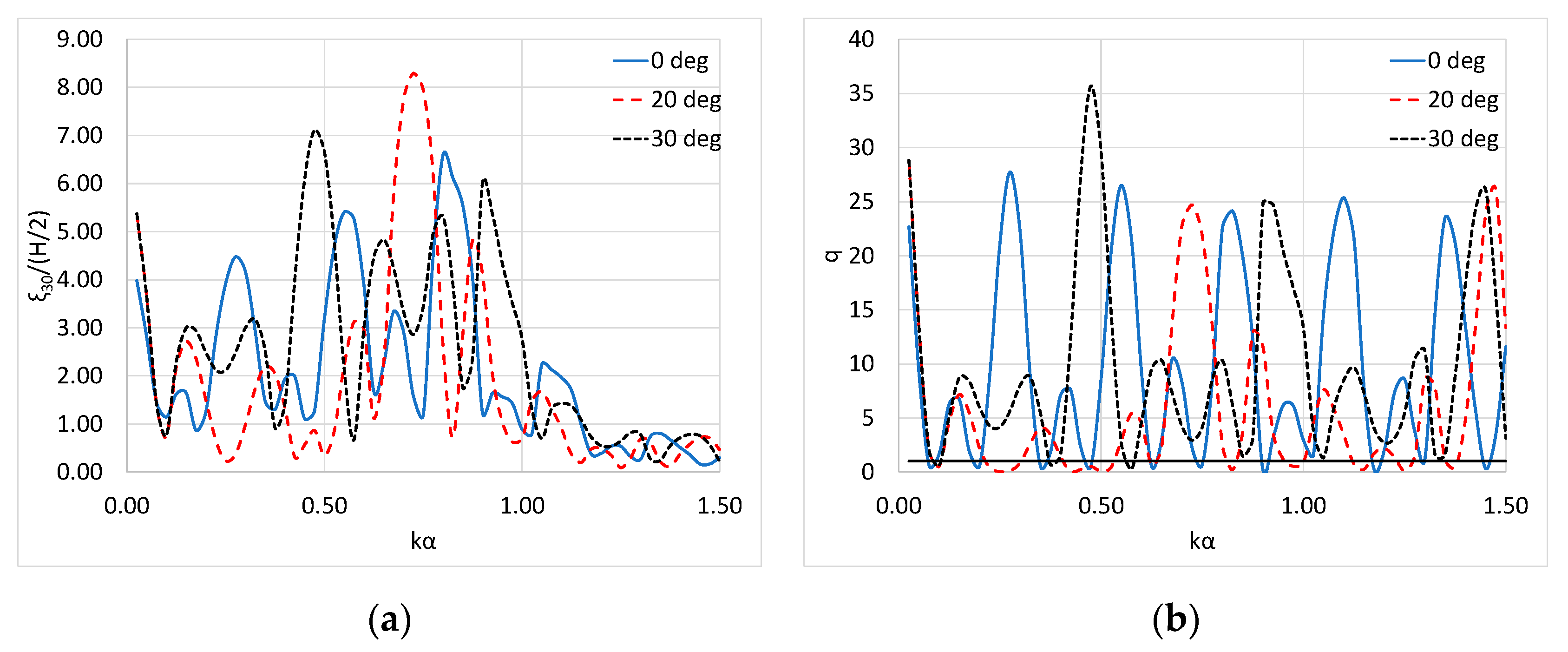
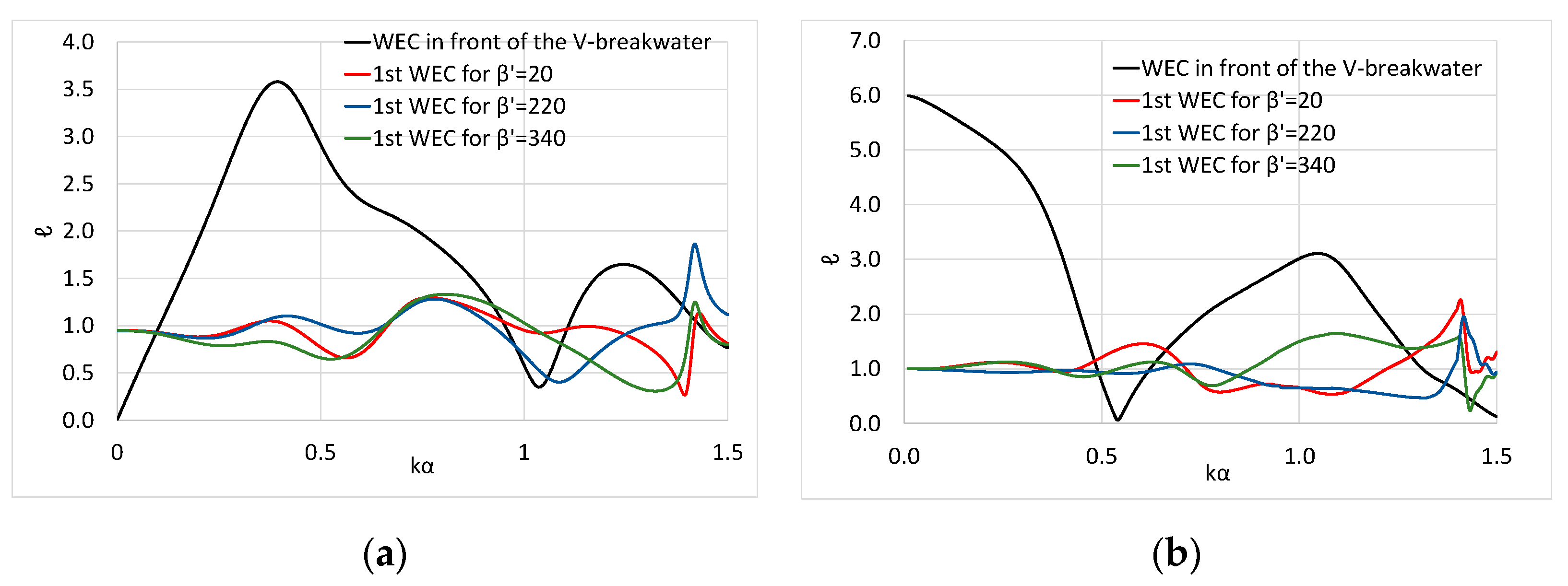
5.2. Effect of the Incoming Wave Train Angle
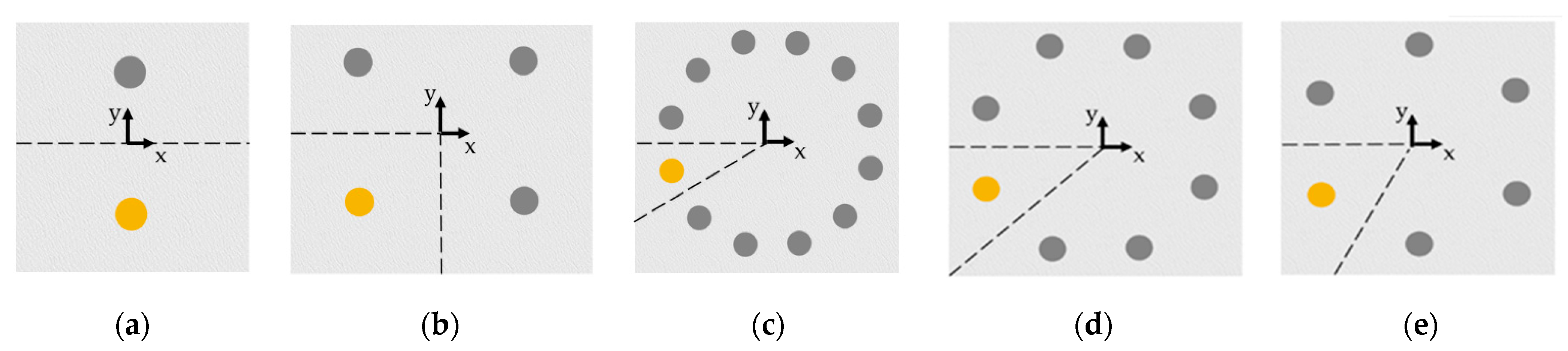
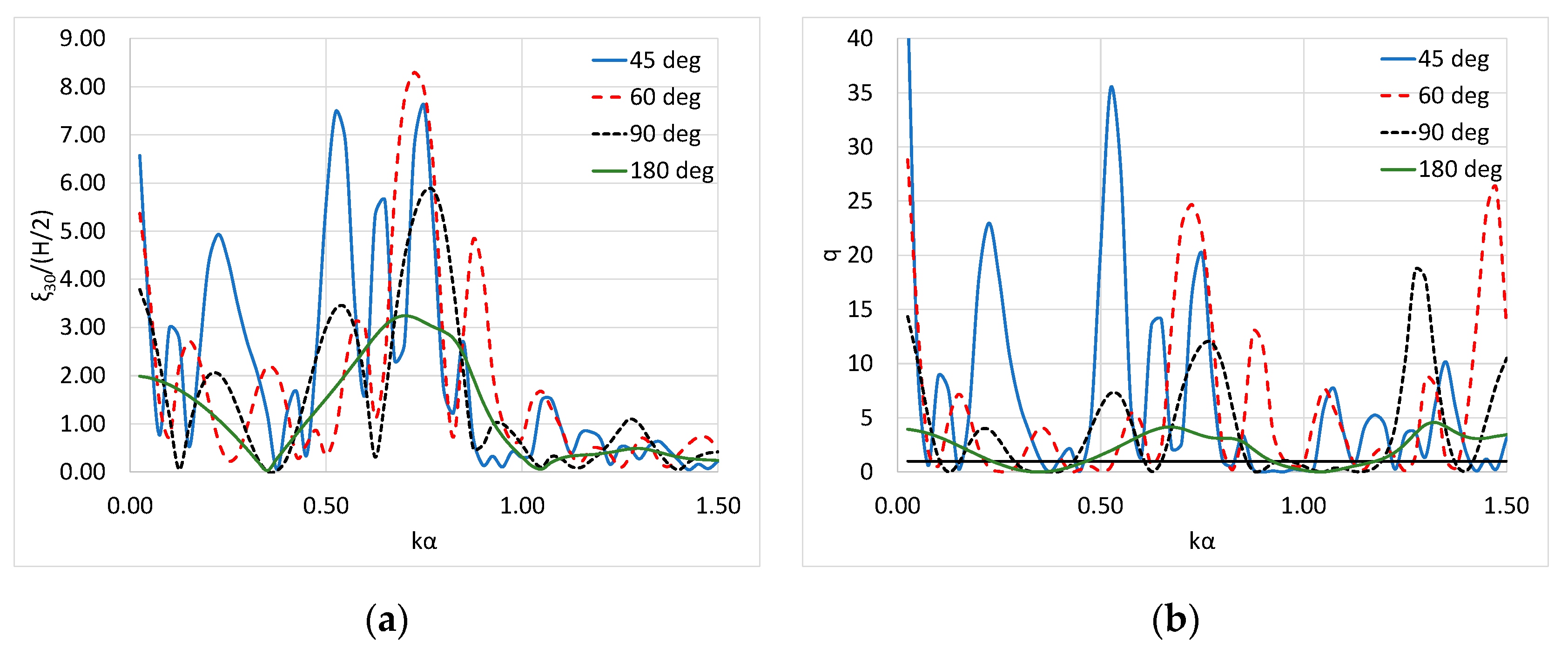
5.3. Effect of the Formed Angle by the Breakwater
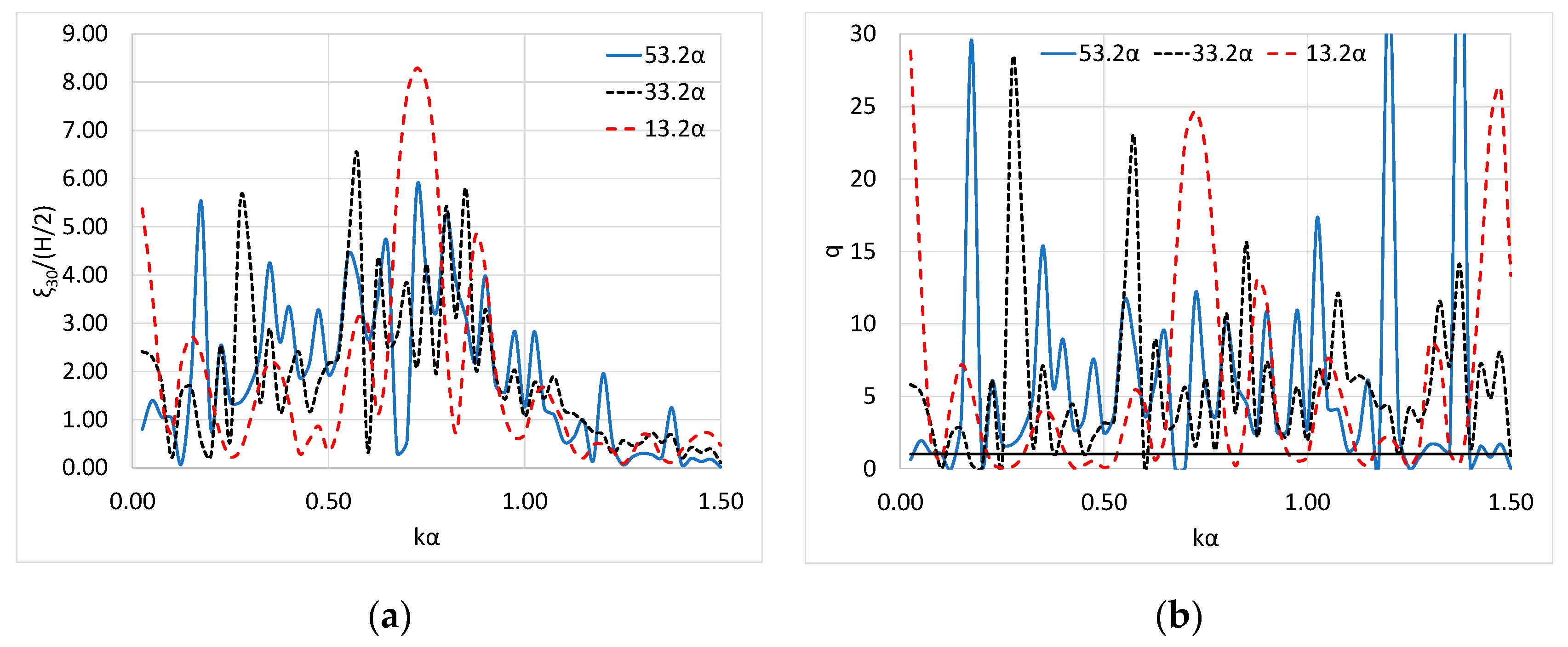
5.4. Effect of the WEC (Wave Energy Converter)’s Distance from the Breakwater’s Walls
6. Conclusions
- Compared to a WEC in unbounded waters (i.e., no presence of a breakwater), the deployment of a converter at the formed angle’s inner area of a V-shaped vertical wall amplifies the power absorption. This power efficiency amplification is strongly dependent on: (a) the wave heading angle, (b) the formed by the vertical walls angle and (c) the distance between the WEC and the breakwater.
- The heave motion of the converter and its power efficiency are increased for values of wave heading angle, β, in the range of (0, θ). On the other hand, for β = 0, or β = θ, i.e., for incident wave directions parallel to either of the breakwater’s walls, the absorbed wave power reduces. From a physical point of view, the efficiency amplification can be related to the enhanced wave interaction phenomena due to the presence of the converters of the array, whereas the reduction in the absorbed power at specific values of β, corresponding to incident wave directions parallel to either of the breakwater’s walls, can be traced back to the fact that in such cases the incident wave train is not primarily reflected on the breakwater’s wall, which is parallel to the incident wave direction.
- The decrease in the formed by the breakwater angle, θ, enhances the converter’s power absorption ability compared to higher values of θ. However, the effect of the smallest examined breakwater angle (i.e., 45 degrees) on the WEC’s performance is not always constructive, since at specific wave frequencies the θ = 180 degrees, i.e., linear breakwater, seems to operate more efficiently.
- The installation of the converter at successively larger distances from the breakwater induces enhanced hydrodynamic interactions between the wall and the converter that consecutively increase the WEC’s power absorption ability. However, this is not always true since the wave interaction phenomena are not always constructive at every examined wave frequency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wave Energy Market by Technology, Location, Application and Region—Global Forecast to 2025. Available online: https://www.marketsandmarkets.com/ (accessed on 30 June 2021).
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.M.; Rheem, C.K.; Koh, K.K.; Faizul, A.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Zou, Q.P.; Qiao, D.S.; Cai, S.Q. Hybrid floating breakwater-WEC system: A review. Ocean Eng. 2019, 186, 106126. [Google Scholar] [CrossRef]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.; Losada, I. Review of innovative harbor breakwaters for wave-energy conversion. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 03119001. [Google Scholar] [CrossRef]
- Renewable Technology. Available online: https://reneable-technology.com/projects/mutriku-wave-energy-plant/ (accessed on 30 June 2021).
- SINNPower. Available online: https://sinnpower.com (accessed on 30 June 2021).
- Mccartney, B.L. Floating breakwater design. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 304–318. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Angelides, D. Performance of moored floating breakwaters. Int. J. Offshore Polar Eng. 2005, 15, 264–273. [Google Scholar]
- Mavrakos, S.A.; Katsaounis, G.M.; Nielsen, K.; Lemonis, G. Numerical performance investigation of an array of heaving wave power converters in front of a vertical breakwater. In Proceedings of the 14th International Offshore and Polar Engineering Conference (ISOPE 2004), Toulon, France, 23–28 May 2004. [Google Scholar]
- Mavrakos, S.A.; Katsaounis, G.M.; Kladas, A.; Kimoulakis, N. Numerical and experimental investigation of performance of heaving WECs coupled with DC generators. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- Teng, B.; Ning, D.Z. Wave diffraction from a uniform cylinder in front of a vertical wall. Ocean Eng. 2003, 21, 48–52. [Google Scholar]
- Teng, B.; Ning, D.Z.; Zhang, X.T. Wave radiation by a uniform cylinder in front of a vertical wall. Ocean Eng. 2004, 31, 201–224. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave diffraction from a truncated cylinder in front of a vertical wall. Ocean Eng. 2015, 104, 329–343. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave radiation from a truncated cylinder in front of a vertical wall. Ocean Eng. 2016, 111, 602–614. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A.; Katsaounis, G.M. Theoretical evaluation of the hydrodynamic characteristics of arrays of vertical axisymmetric floater of arbitrary shape in front of a vertical breakwater. J. Mar. Sci. Eng. 2020, 8, 62. [Google Scholar] [CrossRef] [Green Version]
- Konispoliatis, D.N.; Mavrakos, S.A. Wave power absorption by arrays of wave energy converters in front of a vertical breakwater: A theoretical study. Energies 2020, 13, 1985. [Google Scholar] [CrossRef] [Green Version]
- Cong, P.W.; Chen, L.F.; Gou, Y. Hydrodynamic interaction among multiple columns in front of a vertical wall. Ocean Eng. 2020, 197, 106877. [Google Scholar] [CrossRef]
- Li, A.J.; Liu, Y. Water wave diffraction and radiation by a submerged horizontal circular cylinder in front of a vertical wall. In Proceedings of the 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual Conference, 3–7 August 2020. [Google Scholar]
- Loukogeorgaki, E.; Chatjigeorgiou, I. Hydrodynamic performance of an array of wave energy converters in front of a vertical wall. In Proceedings of the 13th European Wave and Tidal Energy Conference (EWTEC, 2019), Naples, Italy, 1–6 September 2019. [Google Scholar]
- Loukogeorgaki, E.; Chatjigeorgiou, I. Hydrodynamic performance of an array of truncated cylinders in front of a vertical wall. Ocean Eng. 2019, 189, 106407. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Boufidi, I.; Chatjigeorgiou, I. Performance of an array of oblate spheroidal heaving wave energy converters in front of a wall. Water 2020, 12, 188. [Google Scholar] [CrossRef] [Green Version]
- Ning, D.; Teng, B.; Song, X. Analytical study on wave diffraction from a vertical circular cylinder in front of orthogonal vertical walls. Mar. Sci. Bull. 2005, 7, 1–9. [Google Scholar]
- Ning, D.; Teng, B. Study on the oscillation of a uniform cylinder in front of two vertical walls intersecting normally. Chin. Eng. Sci. 2003, 5, 84–91. [Google Scholar]
- Konispoliatis, D.; Mavrakos, S. Theoretical analysis of a vertical cylindrical floater in front of an orthogonal breakwater. Fluids 2020, 5, 135. [Google Scholar] [CrossRef]
- Konispoliatis, D.; Mavrakos, S. Hydrodynamic efficiency of a wave energy converter in front of an orthogonal breakwater. J. Mar. Sci. Eng. 2021, 9, 94. [Google Scholar] [CrossRef]
- Masuda, Y. Apparatus for Generating Electrical Power by Wave Energy and Dissipating Waves. Patent No. GB1492427, 16 November 1977. [Google Scholar]
- Reslo, D.T.; Briggs, M.J.; Fowler, J.E.; Markle, D.G. Floating “V” Shaped Breakwater. Patent No. US005702203A, 30 December 1997. [Google Scholar]
- Briggs, M. Performance Characteristics of a Rapidly Installed Breakwater System; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2001; p. 248, ERDC/CHL TR-01-13.
- Briggs, M.; Ye, W.; Demirbilek, Z.; Zhang, J. Field and numerical comparisons of the RIBS floating breakwater. J. Hydraul. Res. 2002, 40, 289–301. [Google Scholar] [CrossRef]
- Miao, G.P.; Cheng, J.S.; You, Y.X.; Wang, J.Q. Wave defending effects of V-type bottom-mounted breakwaters. China Ocean Eng. 2005, 19, 195–204. [Google Scholar]
- Chang, K.H.; Tsaur, D.H.; Huang, L.H. Accurate solution to diffraction around a modified V-shaped breakwater. Coast. Eng. 2012, 68, 56–66. [Google Scholar] [CrossRef]
- Ding, N.; Yu, J.; Hou, J. Characteristics of dynamic pressure on floating V-shaped breakwater. J. Drain. Irrig. Mach. Eng. 2014, 32, 29–32. [Google Scholar]
- Yu, Y.; Ding, N.; Lin, J.; Hou, J. Wave pressure acting on V-shaped floating breakwater in random seas. J. Ocean Univ. China 2015, 14, 975–981. [Google Scholar] [CrossRef]
- Yeung, R.W.; Sphaier, S.H. Wave-interference effects on a truncated cylinder in a channel. J. Eng. Math. 1989, 23, 95–117. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 9th ed.; Dover Publications: Mineola, NY, USA, 1970. [Google Scholar]
- Mavrakos, S.A.; Koumoutsakos, P. Hydrodynamic interaction among vertical axisymmetric bodies restrained in waves. Appl. Ocean Res. 1987, 9, 128–140. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients for groups of interacting vertical axisymmetric bodies. Ocean Eng. 1991, 18, 485–515. [Google Scholar] [CrossRef]
- Mavrakos, S.A.; McIver, P. Comparison of methods for computing hydrodynamic characteristics of arrays of wave power devices. Appl. Ocean Res. 1997, 19, 283–291. [Google Scholar] [CrossRef]
- Mavrakos, S.A. User’s Manual for the Software HAMVAB; School of Naval Architecture and Marine Engineering, Laboratory for Floating Structures and Mooring Systems: Athens, Greece, 1995. [Google Scholar]
- Bardis, L.; Mavrakos, S.A. User’s Manual for the Computer Code HAQ; Laboratory for Floating Bodies and Mooring Systems, National Technical University of Athens: Athens, Greece, 1988. [Google Scholar]
- Garisson, C.J. Hydrodynamics of a large objects on the sea. Part I: Hydrodynamic analysis. J. Hydronautics 1974, 8, 5–12. [Google Scholar] [CrossRef]
- Garisson, C.J. Hydrodynamics of a large objects on the sea. Part II: Motion of free floating bodies. J. Hydronautics 1975, 9, 58–63. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Near-trapping of waves by circular arrays of vertical cylinders. Appl. Ocean Res. 1997, 19, 83–99. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Trapping and near-trapping by arrays of cylinders in waves. J. Eng. Math. 1999, 35, 149–179. [Google Scholar] [CrossRef]
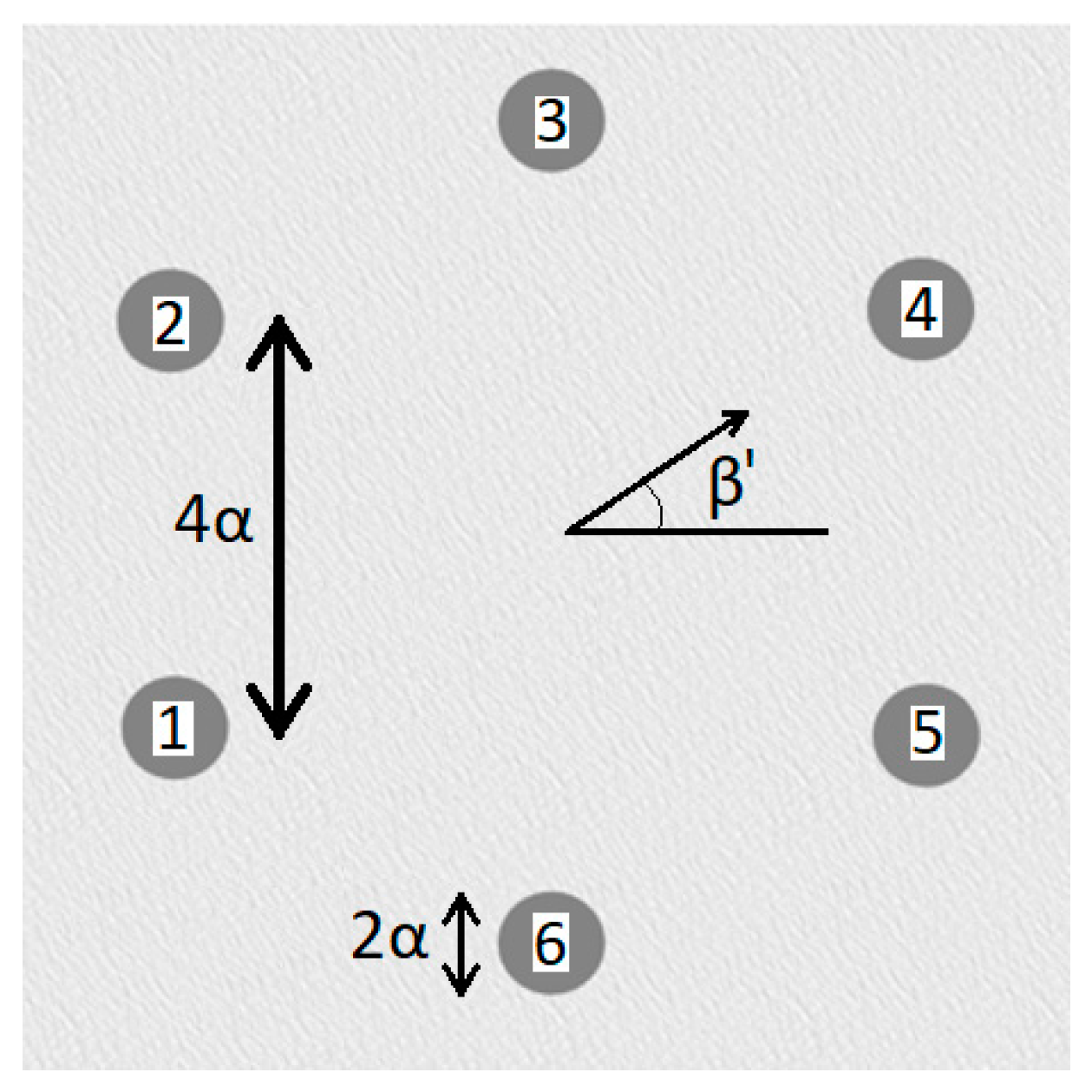
| θ/N | θ = 180 | θ = 90 | θ = 60 | θ = 45 | θ = 36 | θ = 30 | θ = 25.71 | θ = 22.5 | θ = 20 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | β | β | β | β | β | β | β | β | β |
| 2 | 360 − β | 360 − β | 360 − β | 360 − β | 360 − β | 360 − β | 360 − β | 360 − β | 360 − β |
| 3 | 2θ + β | 2θ + β | 2θ + β | 2θ + β | 2θ + β | 2θ + β | 2θ + β | 2θ + β | |
| 4 | 2θ − β | 2θ − β | 2θ − β | 2θ − β | 2θ − β | 2θ − β | 2θ − β | 2θ − β | |
| 5 | 360 − (2θ + β) | 360 − (2θ + β) | 360 − (2θ + β) | 360 − (2θ + β) | 360 − (2θ + β) | 360 − (2θ + β) | 360 − (2θ + β) | ||
| 6 | 360 − (2θ − β) | 360 − (2θ − β) | 360 − (2θ − β) | 360 − (2θ − β) | 360 − (2θ − β) | 360 − (2θ − β) | 360 − (2θ − β) | ||
| 7 | 4θ + β | 4θ + β | 4θ + β | 4θ + β | 4θ + β | 4θ + β | |||
| 8 | 4θ − β | 4θ − β | 4θ − β | 4θ − β | 4θ − β | 4θ − β | |||
| 9 | 360 − (4θ + β) | 360 − (4θ + β) | 360 − (4θ + β) | 360 − (4θ + β) | 360 − (4θ + β) | ||||
| 10 | 360 − (4θ − β) | 360 − (4θ − β) | 360 − (4θ − β) | 360 − (4θ − β) | 360 − (4θ − β) | ||||
| 11 | 6θ + β | 6θ + β | 6θ + β | 6θ + β | |||||
| 12 | 6θ − β | 6θ − β | 6θ − β | 6θ − β | |||||
| 13 | 360 − (6θ + β) | 360 − (6θ + β) | 360 − (6θ + β) | ||||||
| 14 | 360 − (6θ − β) | 360 − (6θ − β) | 360 − (6θ − β) | ||||||
| 15 | 8θ + β | 8θ + β | |||||||
| 16 | 8θ − β | 8θ − β | |||||||
| 17 | 360 − (8θ + β) | ||||||||
| 18 | 360 − (8θ − β) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konispoliatis, D.N.; Mavrakos, S.A. Diffraction and Radiation of Water Waves by a Heaving Absorber in Front of a Bottom-Mounted, V-shaped Breakwater of Infinite Length. J. Mar. Sci. Eng. 2021, 9, 833. https://doi.org/10.3390/jmse9080833
Konispoliatis DN, Mavrakos SA. Diffraction and Radiation of Water Waves by a Heaving Absorber in Front of a Bottom-Mounted, V-shaped Breakwater of Infinite Length. Journal of Marine Science and Engineering. 2021; 9(8):833. https://doi.org/10.3390/jmse9080833
Chicago/Turabian StyleKonispoliatis, Dimitrios N., and Spyridon A. Mavrakos. 2021. "Diffraction and Radiation of Water Waves by a Heaving Absorber in Front of a Bottom-Mounted, V-shaped Breakwater of Infinite Length" Journal of Marine Science and Engineering 9, no. 8: 833. https://doi.org/10.3390/jmse9080833






