Comparative Analysis of Two Approaches for Correcting the Systematic Ocean Temperature Bias of CAS-ESM-C
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model
2.2. Data
2.3. Assimilation Approach
2.4. Bias Correction Scheme
- The observed climatological temperature field from the WOA data is interpolated in a three-dimensional direction according to the ocean model grid point, and the resulting value is Twoa.
- The statistics of the model error Rm are established by the 108 model ensembles used in the EnOI approach, and the observation error Ro is calculated according to an empirical function (exponential function) related to the ocean model depth; with an increase in depth, Ro will decrease gradually. It is shown that the model error Rm and the observation error Ro in the EnOI approach and the bias correction approach are identical.
- The bias correction weight coefficient WK is calculated monthly as
- The bias of the sea temperature is corrected:where Tmod represents the temperature integrated from the previous model step, and Tcor is the temperature field after bias correction.Hence, WK represents the weight of the model error Rm relative to the observation error Ro. Since Ro is determined by the empirical function, if Rm is large, then WK ≈ 1; thus, Tcor ≈ Twoa, and the influence of the bias correction is readily observable, whereas if Rm is small, then WK ≈ 0, Tcor ≈ Tmod, and the bias correction has almost no effect.
- Tcor is then restored into the model, and the integration operation is continued until the next correction step.
3. Results
3.1. Differences between the Two Schemes Are Due to the Correction of Sea Temperature Bias
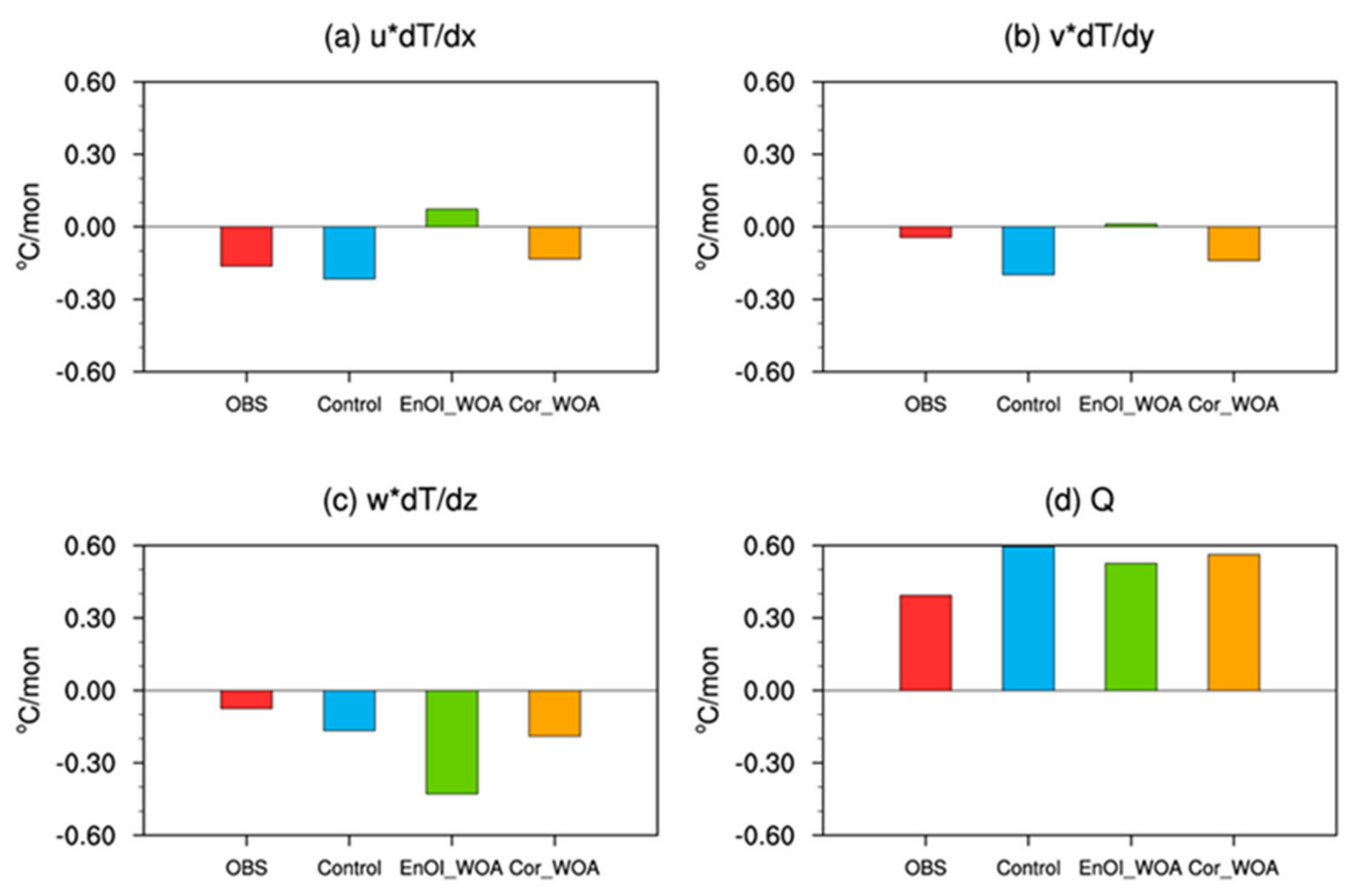
3.2. Analysis of the Causes of the Inconsistent Current Field
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V. Evaluation of climate models. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marq, M., Eds.; Cambridge University Press: Cambridge, UK, 2014; pp. 741–866. [Google Scholar]
- Karl, T.R.; Trenberth, K.E. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef] [Green Version]
- Behringer, D.W.; Ji, M.; Leetmaa, A. An improved coupled model for ENSO prediction and implications for ocean initialization. Part I: The Ocean Data Assimilation System. Mon. Weather Rev. 1998, 126, 1013–1021. [Google Scholar] [CrossRef]
- Brune, S.; Nerger, L.; Baehr, J. Assimilation of oceanic observations in a global coupled Earth system model with the SEIK filter. Ocean Model. 2015, 96, 254–264. [Google Scholar] [CrossRef] [Green Version]
- Fujii, Y.; Nakaegawa, T.; Matsumoto, S.; Yasuda, T.; Yamanaka, G.; Kamachi, M. Coupled climate simulation by constraining ocean fields in a coupled model with ocean data. J. Clim. 2009, 22, 5541–5557. [Google Scholar] [CrossRef]
- Oke, P.R.; Brassington, G.B.; Griffin, D.A.; Schiller, A. The Bluelink ocean data assimilation system (BODAS). Ocean Model. 2008, 21, 46–70. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.P.; Zhu, J.; Xu, L.; Guo, P.W. Evaluation of mid-depth currents of NCEP reanalysis data in the tropical Pacific using ARGO float position information. Adv. Atmos. Sci. 2005, 22, 677–684. [Google Scholar]
- Xue, Y.; Wen, C.; Yang, X.; Behringer, D.; Kumar, A.; Vecchi, G.; Rosati, A.; Gudgel, R. Evaluation of tropical Pacific observing systems using NCEP and GFDL ocean data assimilation systems. Clim. Dyn. 2017, 49, 843–868. [Google Scholar] [CrossRef]
- Karspeck, A.R.; Yeager, S.; Danabasoglu, G.; Hoar, T.; Tribbia, J. An ensemble adjustment Kalman Filter for the CCSM4 ocean component. J. Clim. 2013, 26, 7392–7413. [Google Scholar] [CrossRef] [Green Version]
- Dai, A. Precipitation characteristics in eighteen coupled climate models. J. Clim. 2006, 19, 4605–4630. [Google Scholar] [CrossRef] [Green Version]
- Tian, B.J. Spread of model climate sensitivity linked to double-Intertropical Convergence Zone bias. Geophys. Res. Lett. 2015, 42, 4133–4141. [Google Scholar] [CrossRef]
- Lin, J.L. The double-ITCZ problem in IPCC AR4 coupled GCMs: Ocean-atmosphere feedback analysis. J. Clim. 2007, 20, 4497–4525. [Google Scholar] [CrossRef]
- Kug, J.-S.; Ham, Y.-G.; Lee, J.-Y.; Jin, F.-F. Improved simulation of two types of El Niño in CMIP5 models. Environ. Res. Lett. 2012, 7, 034002. [Google Scholar] [CrossRef]
- Latif, M.; Sperber, K.; Arblaster, J.; Braconnot, P.; Chen, D.; Colman, A.; Cubasch, U.; Cooper, C.; Delecluse, P.; DeWitt, D.; et al. ENSIP: The El Nino simulation intercomparison project. Clim. Dyn. 2001, 18, 255–276. [Google Scholar] [CrossRef] [Green Version]
- Delworth, T.L.; Broccoli, A.J.; Rosati, A.; Stouffer, R.J.; Balaji, V.; Beesley, J.A.; Cooke, W.F.; Dixon, K.W.; Dunne, J.; Dunne, K.A.; et al. GFDL’s CM2 global coupled climate models. Part I: Formulation and simulation characteristics. J. Clim. 2006, 19, 643–674. [Google Scholar] [CrossRef]
- Gainusa-Bogdan, A.; Hourdin, F.; Traore, A.K.; Braconnot, P. Omens of coupled model biases in the CMIP5 AMIP simulations. Clim. Dyn. 2018, 51, 2927–2941. [Google Scholar] [CrossRef]
- Meehl, G.A.; Covey, C.; McAvaney, B.; Latif, M.; Stouffer, R.J. Overview of the coupled model intercomparison project. Bull. Am. Meteorol. Soc. 2005, 86, 89–93. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Rosati, A. An inflated ensemble filter for ocean data assimilation with a biased coupled GCM. Mon. Weather Rev. 2010, 138, 3905–3931. [Google Scholar] [CrossRef]
- Zhang, S.; Chang, Y.S.; Yang, X.; Rosati, A. Balanced and coherent climate estimation by combining data with a biased coupled model. J. Clim. 2014, 27, 1302–1314. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, S.; Liu, Z.; Wu, X.; Han, G. Correction of biased climate simulated by biased physics through parameter estimation in an intermediate coupled model. Clim. Dyn. 2016, 47, 1899–1912. [Google Scholar] [CrossRef]
- Chen, D.; Cane, C.M.; Zebiak, S.E.; Canizares, R.; Kaplan, A. Bias correction of an ocean-atmosphere coupled model. Geophys. Res. Lett. 2000, 27, 2585–2588. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.-S.; Zhang, S.; Rosati, A.; Delworth, T.L.; Stern, W.F. An assessment of oceanic variability for 1960–2010 from the GFDL ensemble coupled data assimilation. Clim. Dyn. 2013, 40, 775–803. [Google Scholar] [CrossRef]
- Han, G.J.; Zhang, X.F.; Zhang, S.; Wu, X.R.; Liu, Z. Mitigation of coupled model biases induced by dynamical core misfitting through parameter optimization: Simulation with a simple pycnocline prediction model. Nonlinear Process. Geophys. 2014, 21, 357–366. [Google Scholar] [CrossRef] [Green Version]
- Lu, F.; Liu, Z.; Zhang, S.; Jacob, R. Assessing extratropical impact on the tropical bias in coupled climate model with regional coupled data assimilation. Geophys. Res. Lett. 2017, 44, 3384–3392. [Google Scholar] [CrossRef]
- Dawson, A.; Matthews, A.J.; Stevens, D.P.; Roberts, M.J.; Vidale, P.L. Importance of oceanic resolution and mean state on the extra-tropical response to El Nio in a matrix of coupled models. Clim. Dyn. 2013, 41, 1439–1452. [Google Scholar] [CrossRef]
- Fang, X.H.; Zheng, F.; Zhu, J. The cloud-radiative effect when simulating strength asymmetry in two types of El Nino events using CMIP5 models. J. Geophys. Res. Ocean. 2015, 120, 4357–4369. [Google Scholar] [CrossRef]
- Zheng, F.; Zhu, J. Improved ensemble-mean forecasting of ENSO events by a zero-mean stochastic error model of an intermediate coupled model. Clim. Dyn. 2016, 47, 3901–3915. [Google Scholar] [CrossRef]
- Zheng, F.; Zhang, R.H. Interannually varying salinity effects on ENSO in the tropical pacific: A diagnostic analysis from Argo. Ocean Dyn. 2015, 65, 691–705. [Google Scholar] [CrossRef]
- Zheng, F.; Yu, J.-Y. Contrasting the skills and biases of deterministic predictions for the two types of El Nino. Adv. Atmos. Sci. 2017, 34, 1395–1403. [Google Scholar] [CrossRef]
- Cooper, M.; Haines, K. Altimetric assimilation with water property conservation. J. Geophys. Res. Ocean. 1996, 101, 1059–1077. [Google Scholar] [CrossRef]
- Fujii, Y.; Matsumoto, S.; Kamachi, M.; Ishizaki, S. Estimation of the Equatorial Pacific Salinity Field Using Ocean Data Assimilation Systems. Adv. Geosci. 2010, 18, 197–212. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Zhang, X.; Wu, X.; Han, G.; Zhao, Y.; Yu, X.; Liu, C.; Liu, Y.; Wu, S.; et al. Coupled data assimilation and parameter estimation in coupled ocean-atmosphere models: A review. Clim. Dyn. 2020, 54, 5127–5144. [Google Scholar] [CrossRef]
- Yan, C.X.; Zhu, J.; Li, R.F.; Zhou, G.Q. Roles of vertical correlations of background error and T-S relations in estimation of temperature and salinity profiles from sea surface dynamic height. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Derber, J.; Bouttier, F. A reformulation of the background error covariance in the ECMWF global data assimilation system. Tellus A Dyn. Meteorol. Oceanogr. 1999, 51, 195–221. [Google Scholar] [CrossRef]
- Ji, M.; Leetmaa, A.; Derber, J. An ocean analysis system for seasonal to interannual climate studies. Mon. Weather Rev. 1995, 123, 460–481. [Google Scholar] [CrossRef] [Green Version]
- Kimoto, M.; Yoshikawa, I.; Ishii, M. An ocean data assimilation system for climate monitoring. J. Meteorol. Soc. Jpn. 1997, 75, 471–487. [Google Scholar] [CrossRef]
- Counillon, F.; Keenlyside, N.; Bethke, I.; Wang, Y.; Billeau, S.; Shen, M.L.; Bentsen, M. Flow-dependent assimilation of sea surface temperature in isopycnal coordinates with the Norwegian Climate Prediction Model. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 32437. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.R.; Wang, H.; Zheng, F.; Cai, Q. An ensemble-based SST nudging method proposed for correcting the subsurface temperature field in climate model. Acta Oceanol. Sin. 2020, 39, 73–80. [Google Scholar] [CrossRef]
- Carton, J.A.; Giese, B.S.; Cao, X.H.; Miller, L. Impact of altimeter, thermistor, and expendable bathythermograph data on retrospective analyses of the tropical Pacific Ocean. J. Geophys. Res. Ocean. 1996, 101, 14147–14159. [Google Scholar] [CrossRef]
- Luo, H.; Zheng, F.; Zhu, J. Evaluation of oceanic surface observation for reproducing the upper ocean structure in ECHAM5/MPI-OM. J. Geophys. Res. Ocean. 2017, 122, 9695–9711. [Google Scholar] [CrossRef] [Green Version]
- Bjerknes, J. A possible response of atmospheric Hadley circulation to equatorial anomalies of ocean temperature. Tellus 1966, 18, 820–829. [Google Scholar] [CrossRef] [Green Version]
- Bjerknes, J. Atmospheric teleconnections from equatorial pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Gill, A.E. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar] [CrossRef]
- Horel, J.D.; Wallace, J.M. Planetary-scale atmospheric phenomena associated with the southern oscillation. Mon. Weather Rev. 1981, 109, 813–829. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Keenlyside, N.; Botzet, M.; Haak, H.; Luo, J.J.; Latif, M.; Marotzke, J.; Mikolajewicz, U.; Roeckner, E. Ocean circulation and tropical variability in the coupled model ECHAM5/MPI-OM. J. Clim. 2006, 19, 3952–3972. [Google Scholar] [CrossRef] [Green Version]
- Alexander, M.A.; Blade, I.; Newman, M.; Lanzante, J.R.; Lau, N.C.; Scott, J.D. The atmospheric bridge: The influence of ENSO teleconnections on air-sea interaction over the global oceans. J. Clim. 2002, 15, 2205–2231. [Google Scholar] [CrossRef]
- Jin, F.F. An equatorial ocean recharge paradigm for ENSO. Part I: Conceptual model. J. Atmos. Sci. 1995, 54, 811–829. [Google Scholar] [CrossRef]
- Zheng, F.; Zhu, J.; Zhang, R.-H. Impact of altimetry data on ENSO ensemble initializations and predictions. Geophys. Res. Lett. 2007, 34, L13611. [Google Scholar] [CrossRef]
- Zheng, F.; Fang, X.H.; Zhu, J.; Yu, J.Y.; Li, X.C. Modulation of Bjerknes feedback on the decadal variations in ENSO predictability. Geophys. Res. Lett. 2016, 43, 12560–12568. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, C.; Zhu, J. Assimilation of sea surface temperature in a global hybrid coordinate ocean model. Adv. Atmos. Sci. 2018, 35, 1291–1304. [Google Scholar] [CrossRef]
- Su, T.; Xue, F.; Sun, H.; Zhou, G. The El Nino-Southern Oscillation cycle simulated by the climate system model of Chinese Academy of Sciences. Acta Oceanol. Sin. 2015, 34, 55–65. [Google Scholar] [CrossRef]
- Dong, X.; Su, T.H.; Wang, J.; Lin, R.P. Decadal variation of the Aleutian Low-Icelandic Low seesaw simulated by a climate system model (CAS-ESM-C). Atmos. Ocean. Sci. Lett. 2014, 7, 110–114. [Google Scholar]
- Dong, X.; Lin, R.P.; Zhu, J.; Lu, Z.T. Evaluation of ocean data assimilation in CAS-ESM-C: Constraining the SST field. Adv. Atmos. Sci. 2016, 33, 795–807. [Google Scholar] [CrossRef]
- Du, M.J.; Zheng, F.; Zhu, J.; Lin, R.P.; Yang, H.-P. A new ensemble-based approach to correct the systematic ocean temperature bias of CAS-ESM-C to improve its simulation and data assimilation abilities. J. Geophys. Res. Ocean. 2020, 125. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, G.; Zeng, Q. Assessments of the climate system model (CAS-ESM-C) using IAP AGCM4 as its atmospheric component. Chin. J. Atmos. Sci. 2012, 36, 215–233. [Google Scholar]
- Zhang, H. Development of IAP Atmospheric General Circulation Model Version 4.0 and Its Climate Simulations; Chinese Academy of Sciences: Beijing, China, 2009. [Google Scholar]
- Liu, H.; Zhang, X.; Wei, L.I.; Yongqiang, Y.U.; Rucong, Y.U. An eddy-permitting oceanic general circulation model and its preliminary evaluation. Adv. Atmos. Sci. 2004, 21, 675–690. [Google Scholar]
- Dickinson, R.E.; Oleson, K.W.; Bonan, G.; Hoffman, F.; Thornton, P.; Vertenstein, M.; Yang, Z.-L.; Zeng, X. The Community Land Model and its climate statistics as a component of the Community Climate System Model. J. Clim. 2006, 19, 2302–2324. [Google Scholar] [CrossRef]
- Boyer, T.P.; Antonov, J.I.; Baranova, O.K.; Garcia, H.E.; Johnson, D.R.; Mishonov, A.V.; O’Brien, T.D.; Seidov, D.; Smolyar, I.; Zweng, M.M.; et al. World ocean database 2013. NOAA atlas NESDIS 2013. [Google Scholar] [CrossRef]
- Behringer, D.; Xue, Y. Evaluation of the global ocean data assimilation system at NCEP: The Pacific Ocean. In Proceedings of the Eighth Symposium on Integrated Observing and Assimilation Systems for Atmosphere, Oceans, and Land Surface, NOAA/NWS/NCEP/EMC, Camp Springs, MD, USA, 11–15 January 2004. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Cohn, S.E. An introduction to estimation theory. J. Meteorol. Soc. Jpn. 1997, 75, 257–288. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte-Carlo methods to forecast error statistics. J. Geophys. Res.-Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Fu, W.; Zhu, J.; Yan, C.; Liu, H. Toward a global ocean data assimilation system based on ensemble optimum interpolation: Altimetry data assimilation experiment. Ocean Dyn. 2009, 59, 587–602. [Google Scholar] [CrossRef]
- Yan, C.; Zhu, J.; Xie, J. An ocean data assimilation system in the Indian Ocean and west Pacific Ocean. Adv. Atmos. Sci. 2015, 32, 1460–1472. [Google Scholar] [CrossRef]
- Carnes, M.R.; Mitchell, J.L.; de Witt, P.W. Synthetic temperature profiles derived from Geosat altimetry: Comparison with air-dropped expendable bathythermograph profiles. J. Geophys. Res.Ocean. 1990, 95, 17979–17992. [Google Scholar] [CrossRef]









| Data Type | Description | Temporal Coverage | Source | Application |
|---|---|---|---|---|
| Sea temperature climatological | World Ocean Atlas 2013 | 12 months | Boyer et al., 2013 | Assimilation |
| Ocean reanalysis | GODAS | 1980–2018 | D. Behringer and Xue, 2004 | Validation |
| Atmospheric reanalysis | ERA-Interim | 1980–2018 | Dee et al., 2011 | Validation |
| Experiment | Description | Test Time |
|---|---|---|
| OBS | Ocean reanalysis data | 30 years |
| Control | No correction | 30 years |
| EnOI_WOA | Assimilated WOA by EnOI approach | 30 years |
| Cor_WOA | Ensemble-based correction approach | 30 years |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, M.; Zheng, F.; Zhu, J.; Lin, R.; Yi, K. Comparative Analysis of Two Approaches for Correcting the Systematic Ocean Temperature Bias of CAS-ESM-C. J. Mar. Sci. Eng. 2021, 9, 925. https://doi.org/10.3390/jmse9090925
Du M, Zheng F, Zhu J, Lin R, Yi K. Comparative Analysis of Two Approaches for Correcting the Systematic Ocean Temperature Bias of CAS-ESM-C. Journal of Marine Science and Engineering. 2021; 9(9):925. https://doi.org/10.3390/jmse9090925
Chicago/Turabian StyleDu, Mengjiao, Fei Zheng, Jiang Zhu, Renping Lin, and Kan Yi. 2021. "Comparative Analysis of Two Approaches for Correcting the Systematic Ocean Temperature Bias of CAS-ESM-C" Journal of Marine Science and Engineering 9, no. 9: 925. https://doi.org/10.3390/jmse9090925
APA StyleDu, M., Zheng, F., Zhu, J., Lin, R., & Yi, K. (2021). Comparative Analysis of Two Approaches for Correcting the Systematic Ocean Temperature Bias of CAS-ESM-C. Journal of Marine Science and Engineering, 9(9), 925. https://doi.org/10.3390/jmse9090925







