A Cost-Effective Approach to the Risk Reduction of Cable Fault Triggered by Laying Repeaters of Fiber-Optic Submarine Cable Systems in Deep-Sea
Abstract
:1. Introduction
2. The Mechanical Construction of Repeaters and Cables and Their Sinking Speeds
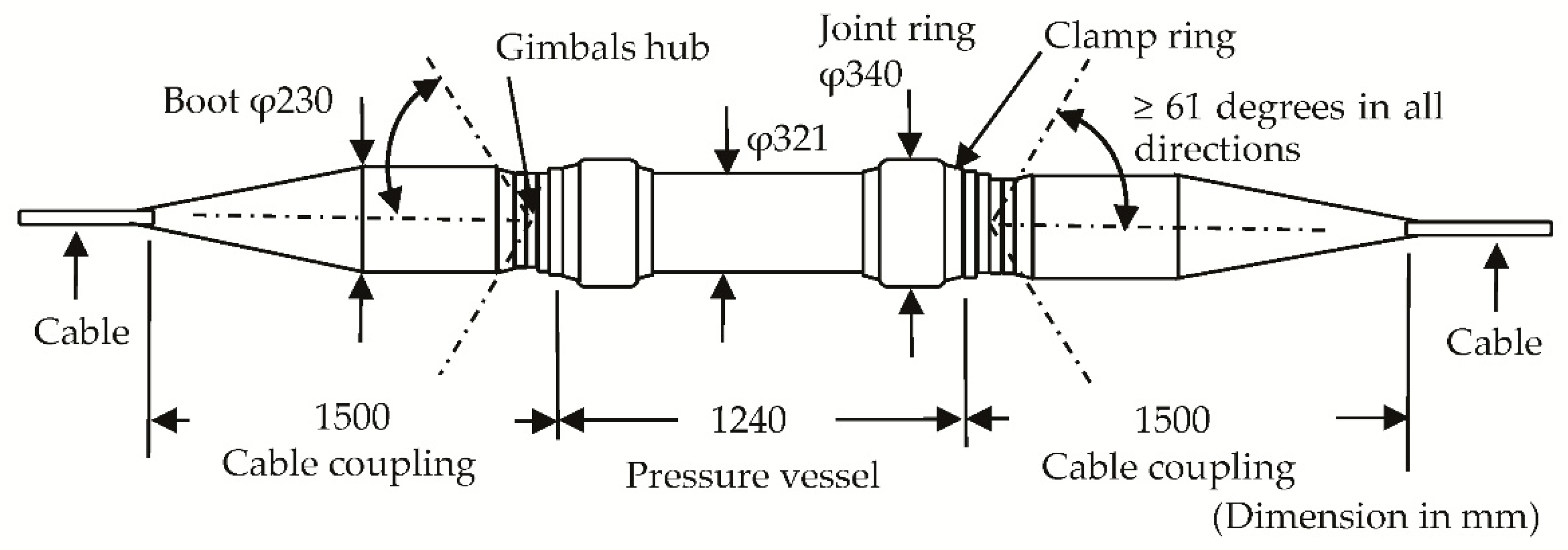
2.1. Repeater
2.2. Cables
2.3. Comparison of Sinking Speeds of Repeater and Cables
2.3.1. Method for a Physical Experiment to Confirm the Sinking Speed of the Repeater with Cables
- Step 1: Record the position of the laying ship and the time at the beginning of the repeater laying process.
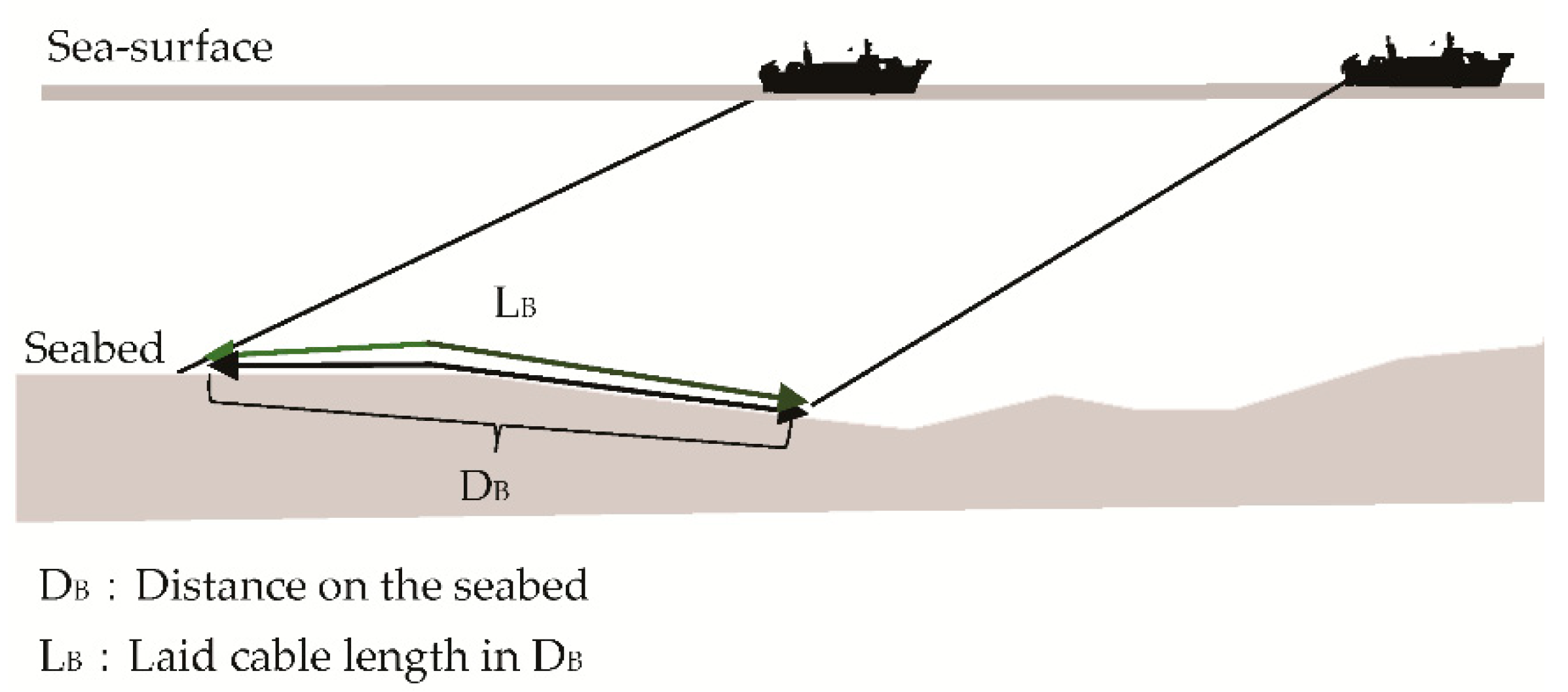
- Step 2: Based on the change in the cable tension on the ship (details are explained in Section 3), record the time when the repeater reaches the seabed, the estimated seabed position, and the water depth from the bathymetry data (obtained by the route survey before the system design).
- Step 3: Calculate the sinking speed from the time difference between Steps 1 and 2.
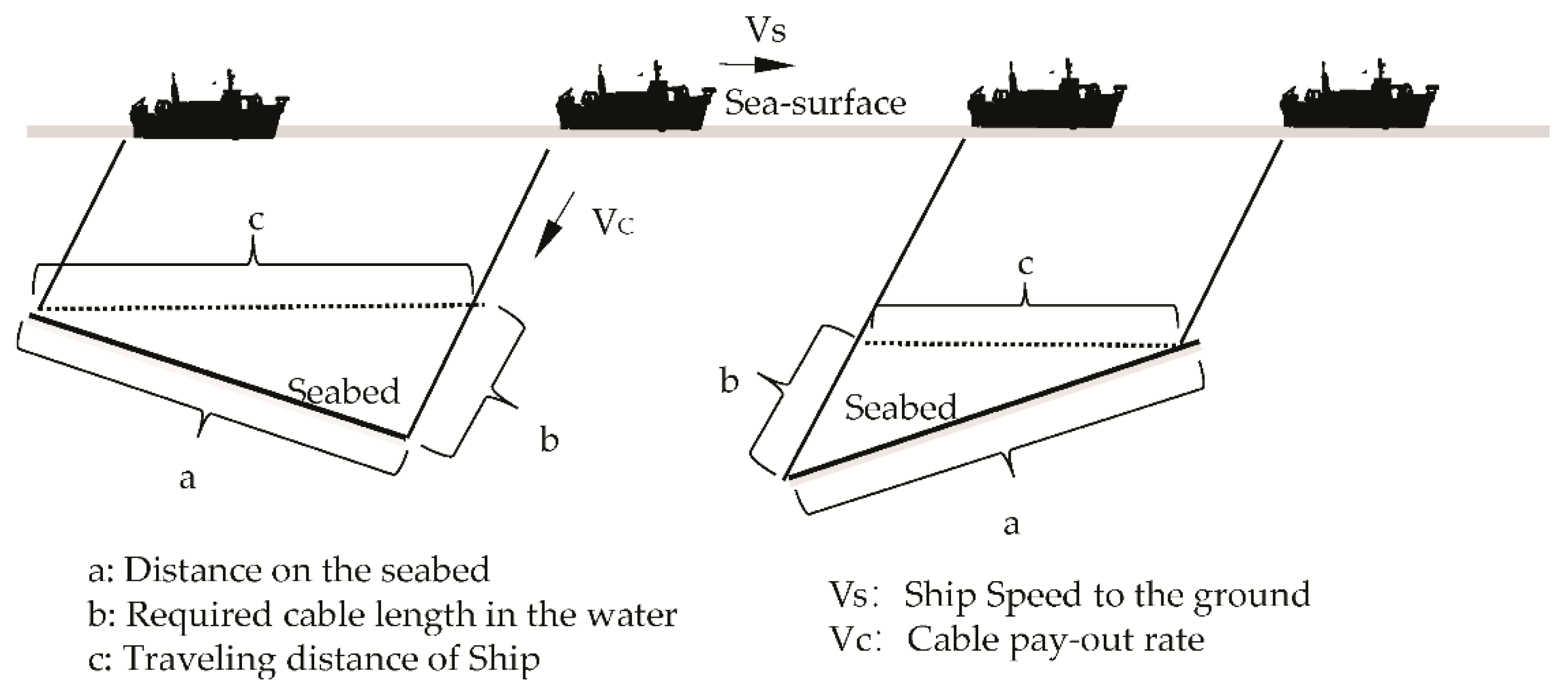
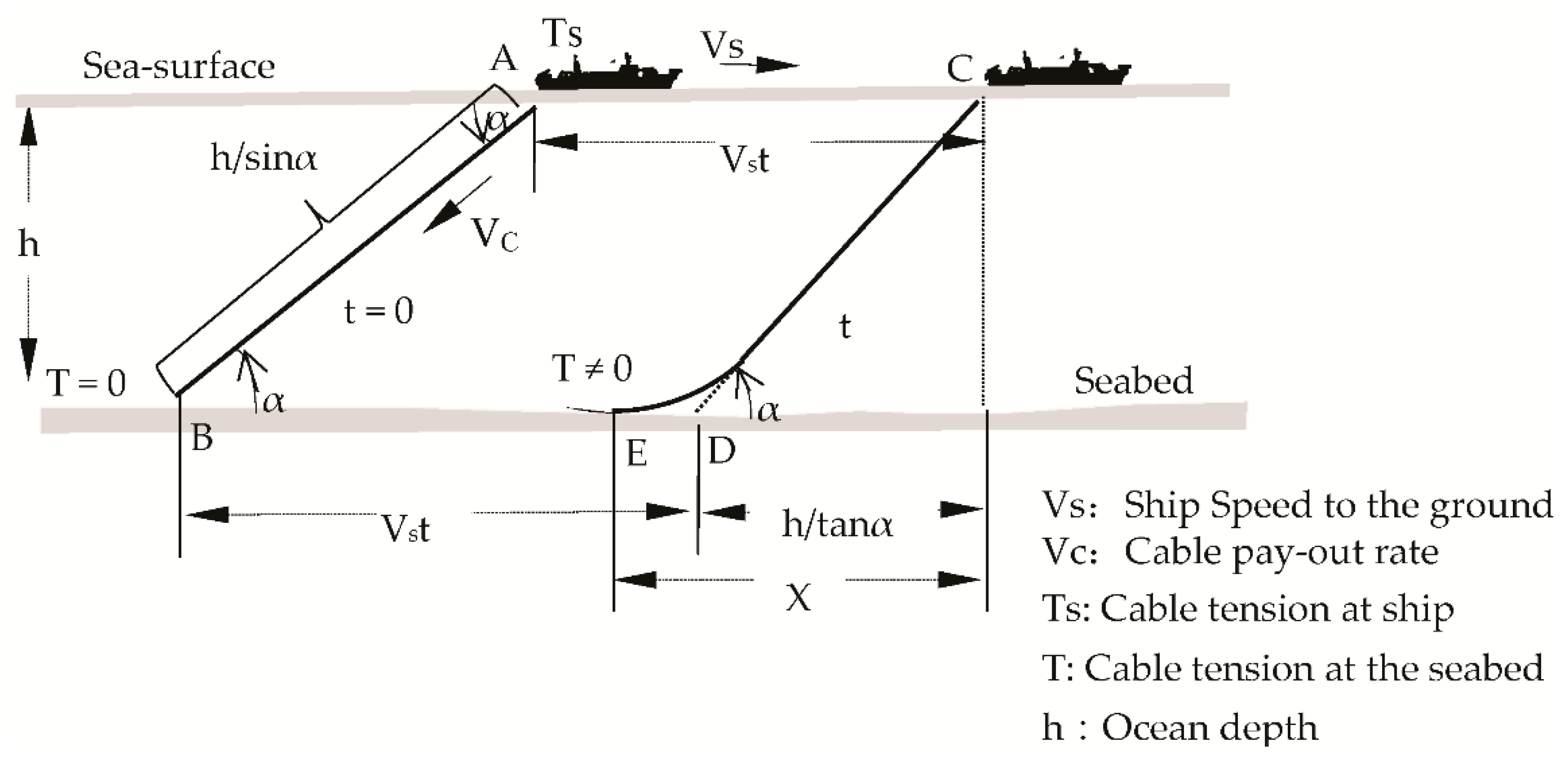
2.3.2. Calculation of Transversal Sinking Speed of Cables
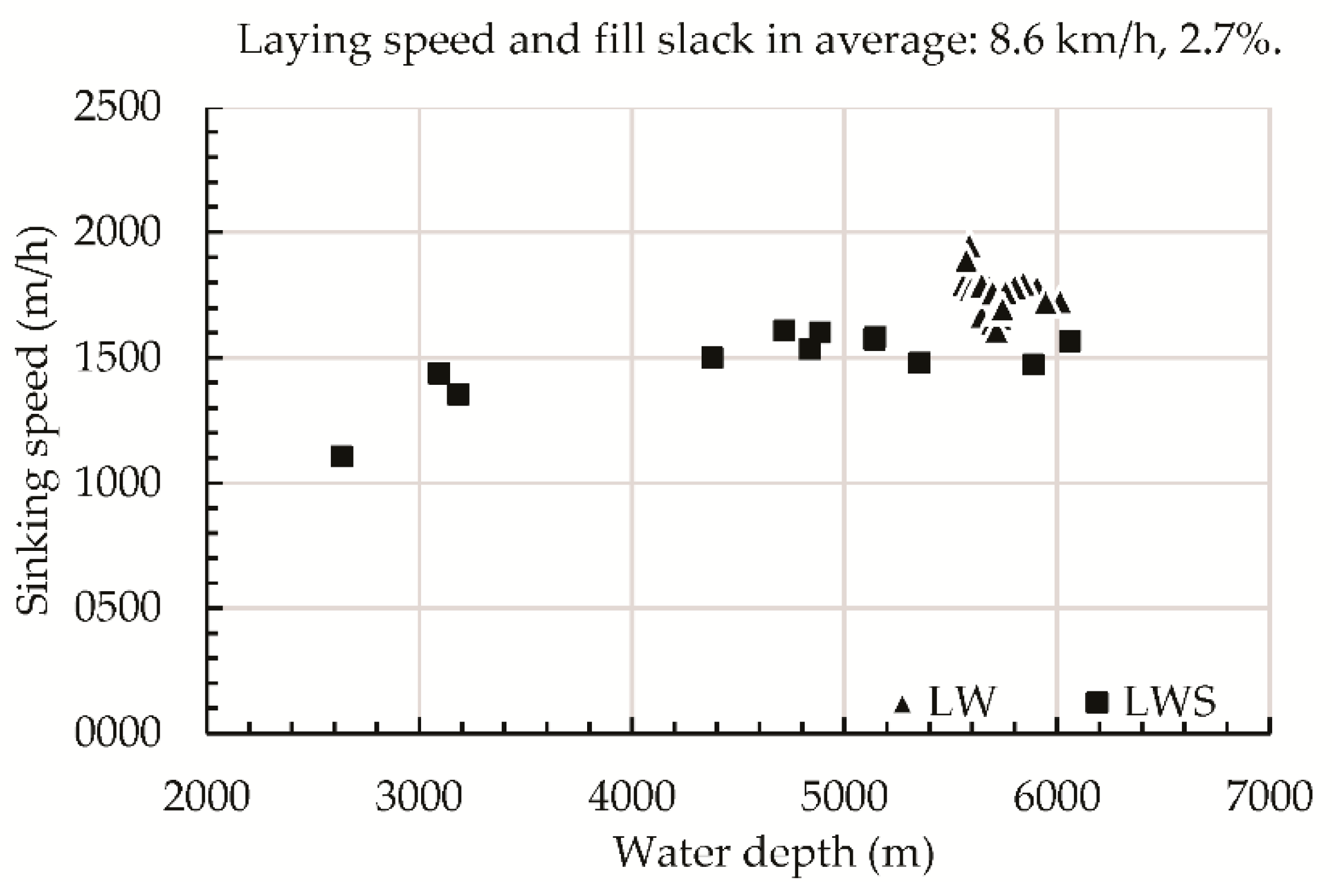
2.3.3. Comparative Sinking Speeds between Repeater and Cables
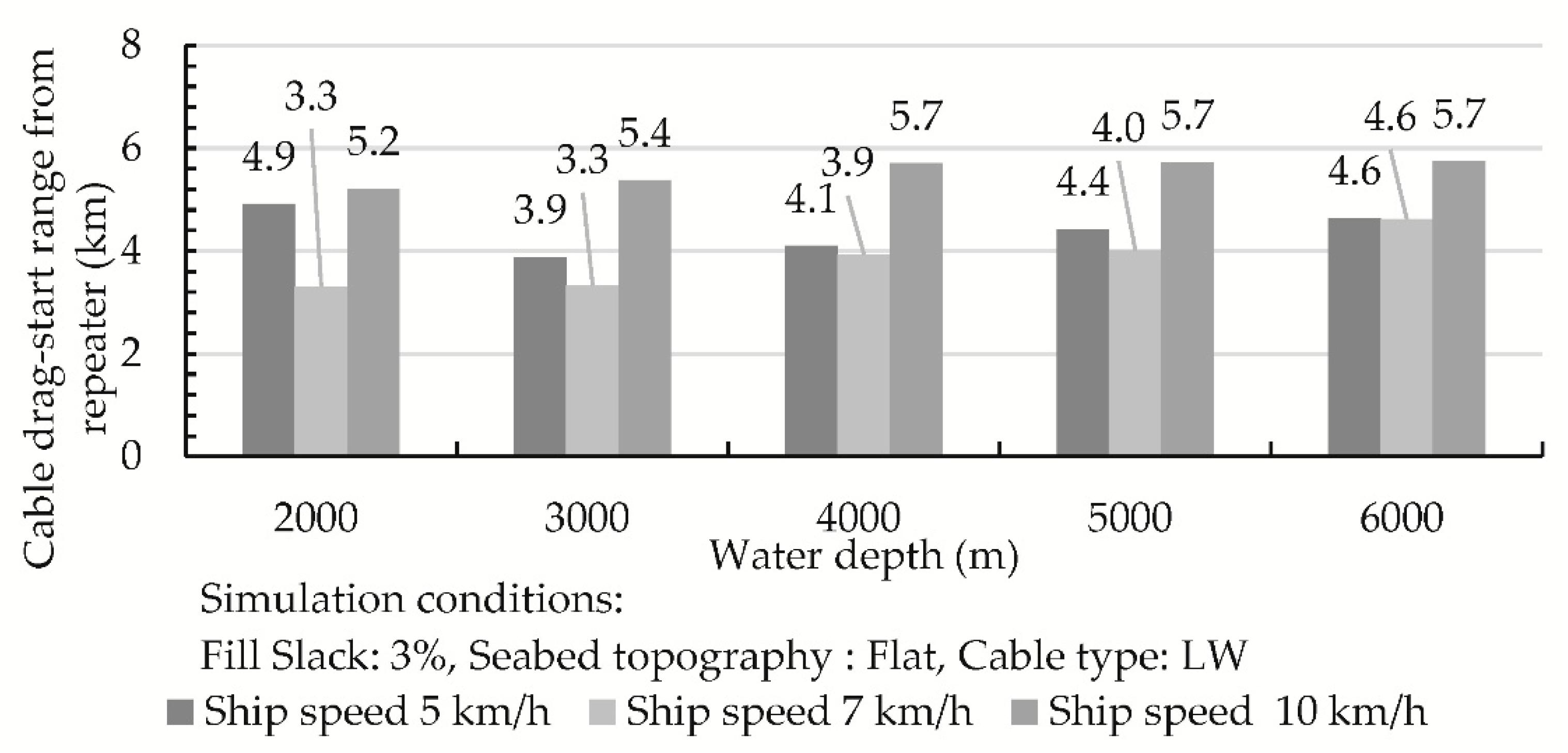
2.4. Repeater Spacing
3. Numerical Simulation of Cable Behavior in the Water
3.1. Definition of Slack
- (1)
- Fill slack
- (2)
- Seabed slack
- (3)
- Meaning of a Negative slack value
3.2. Reason for Simulation
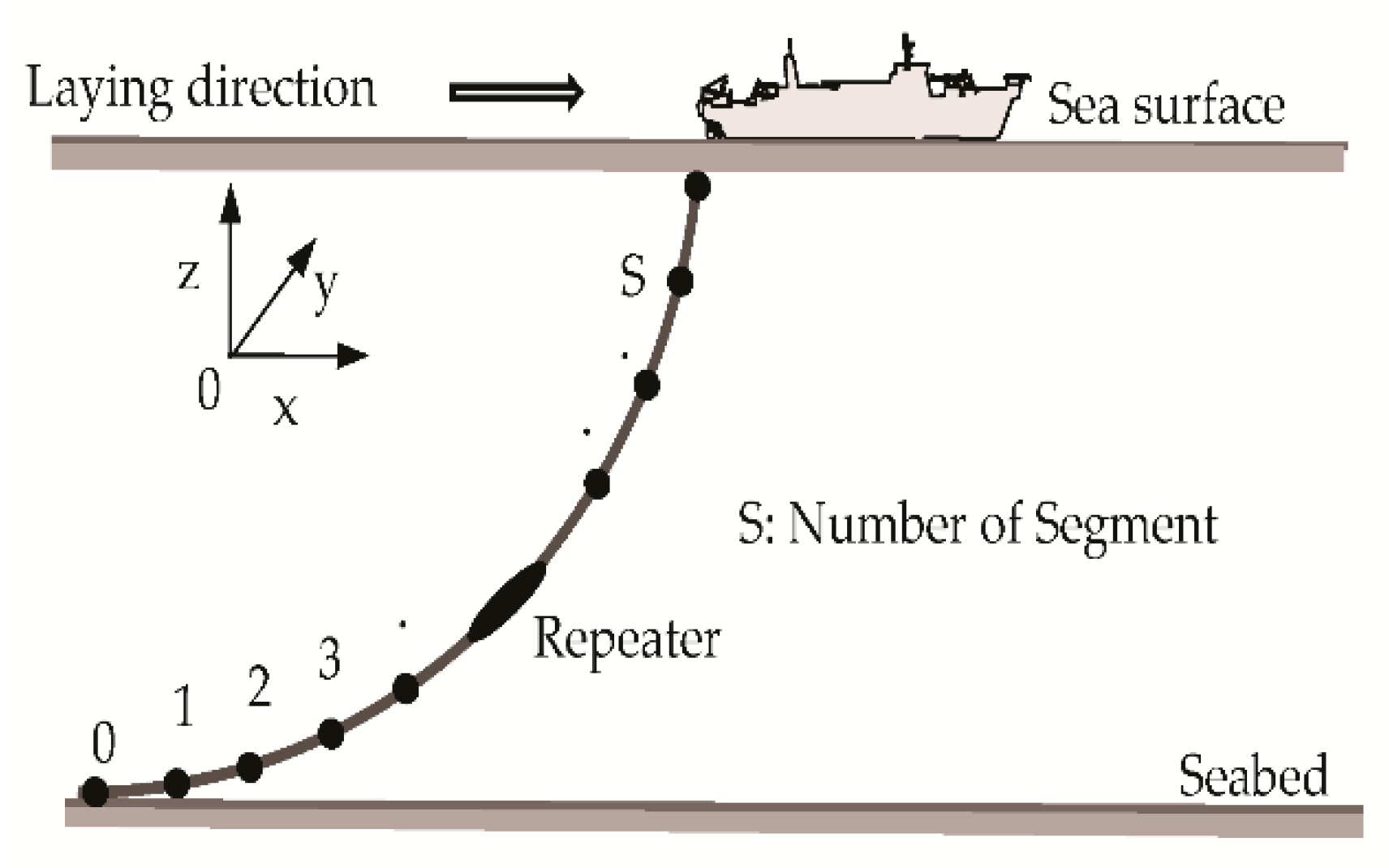
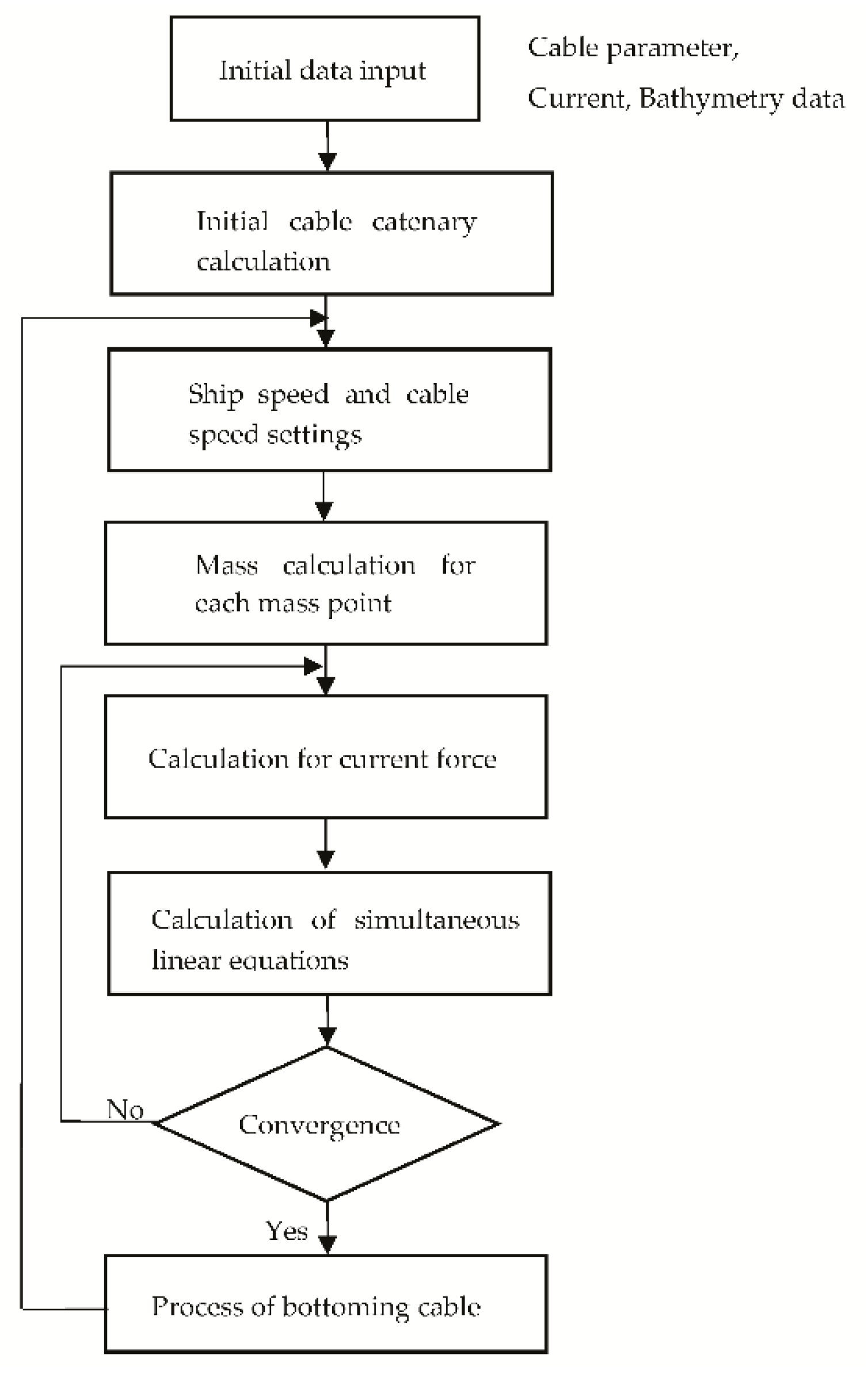
3.3. Calculation Procedure
3.4. Simulation Analysis of Cable Behavior, including Repeaters
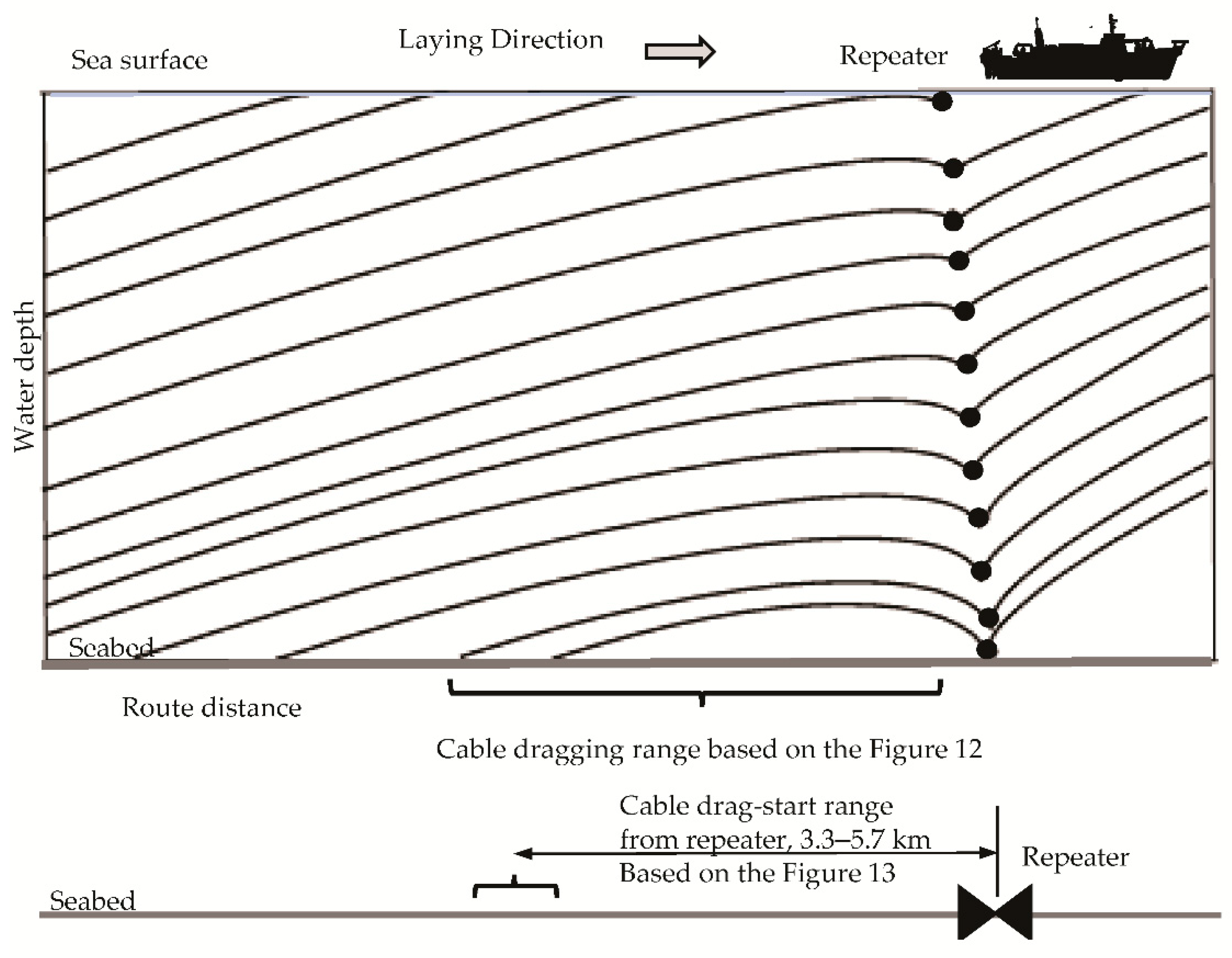
3.4.1. Typical Behavior of Cable Catenary in the Water
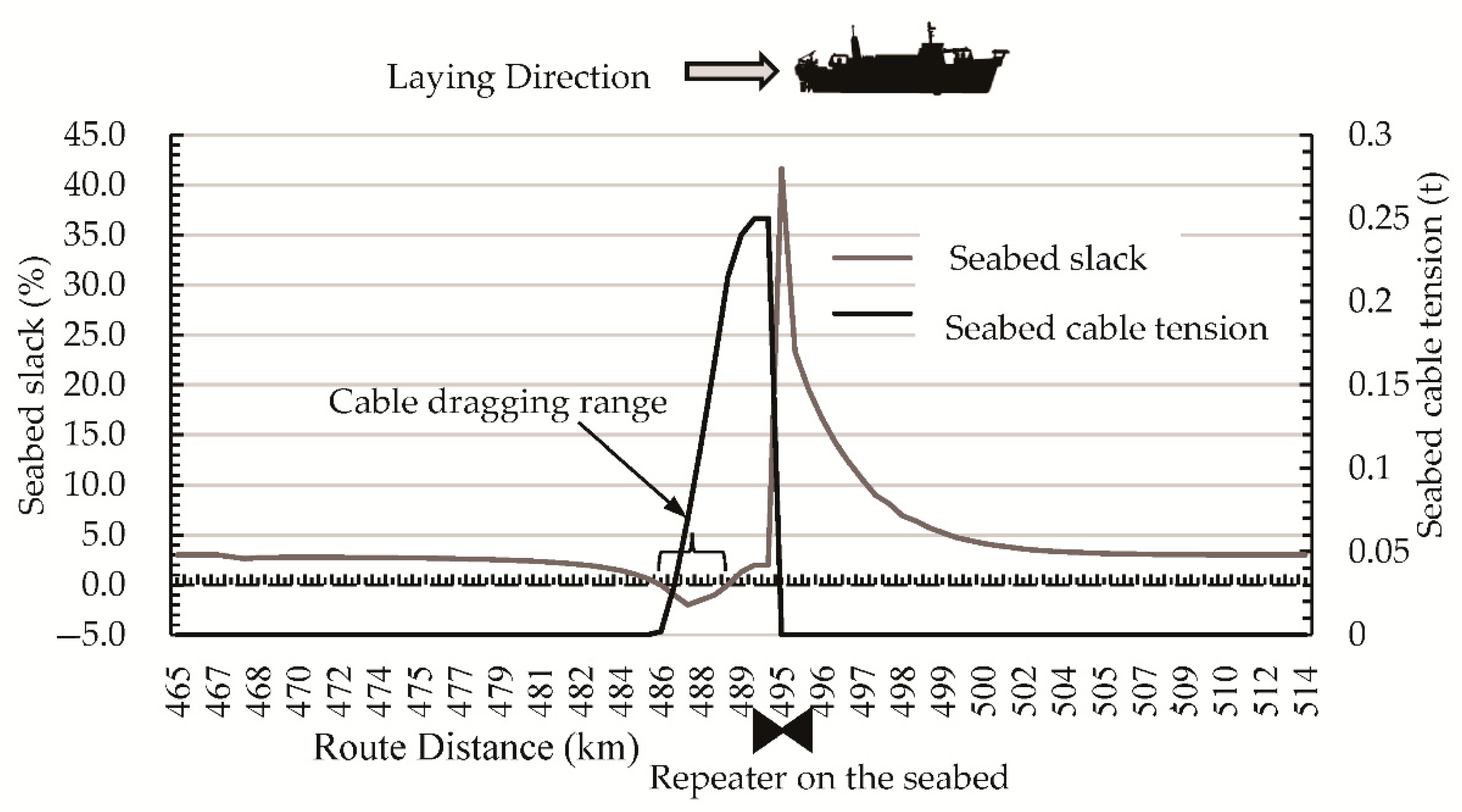
3.4.2. Simulation Analysis of Seabed Slack and Seabed Cable Tension, before and after the Repeater Reaches the Seabed
- (1)
- In the 465–484 km range, the seabed slack is 3%, which is the same as the fill slack, and the seabed tension is constant at 0 t.
- (2)
- At 484 km, the seabed slack begins to decrease.
- (3)
- In the 485–488.5 km range, the seabed slack decreases from zero to negative 2% and then gradually returns to zero. The increase in the seabed cable tension is inversely proportional to the change in the seabed slack, and when the seabed slack becomes positive, the seabed cable tension changes at a slower rate. As a result, the cable behind the repeater will be dragged by the increased seabed cable tension, due to negative slack.
- (4)
- At 489 km, the seabed slack increases to positive 2%, and the curve of the seabed cable tension change becomes flat. As a result, the drag force acting on the cable will be gradually reduced.
- (5)
- At 495 km, the repeater reaches the seabed, and the seabed cable tension suddenly drops from about 0.27 t to zero. The seabed slack rises sharply to about 43% and then slowly declines. The seabed slack rises rapidly because the cable is pulled while it sinks, due to the weight of the repeater; for that reason, when the repeater reaches the seabed, the cable length is longer than the distance on the seabed.
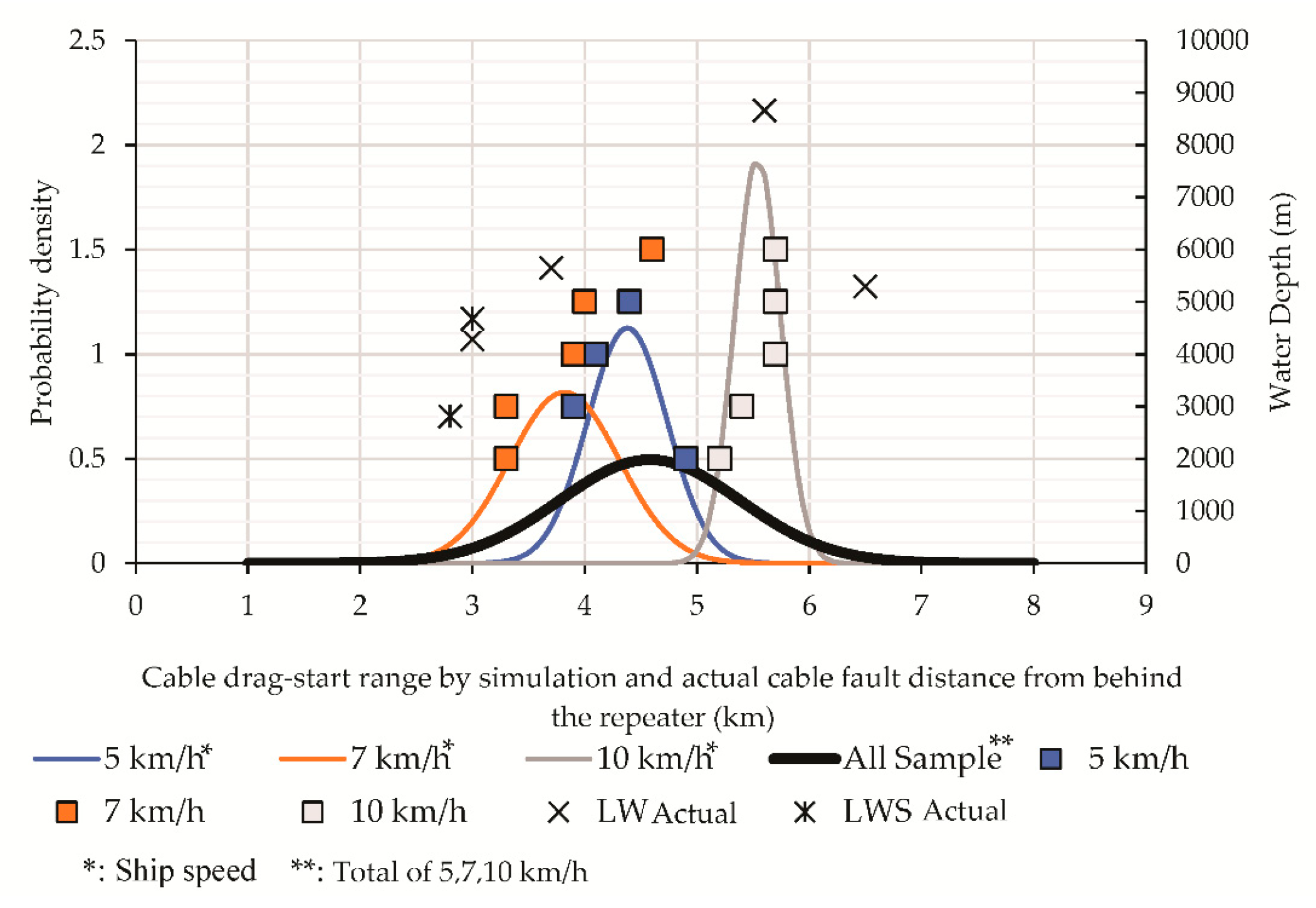
3.4.3. Analysis of Cable Drag-Start Range from Repeater
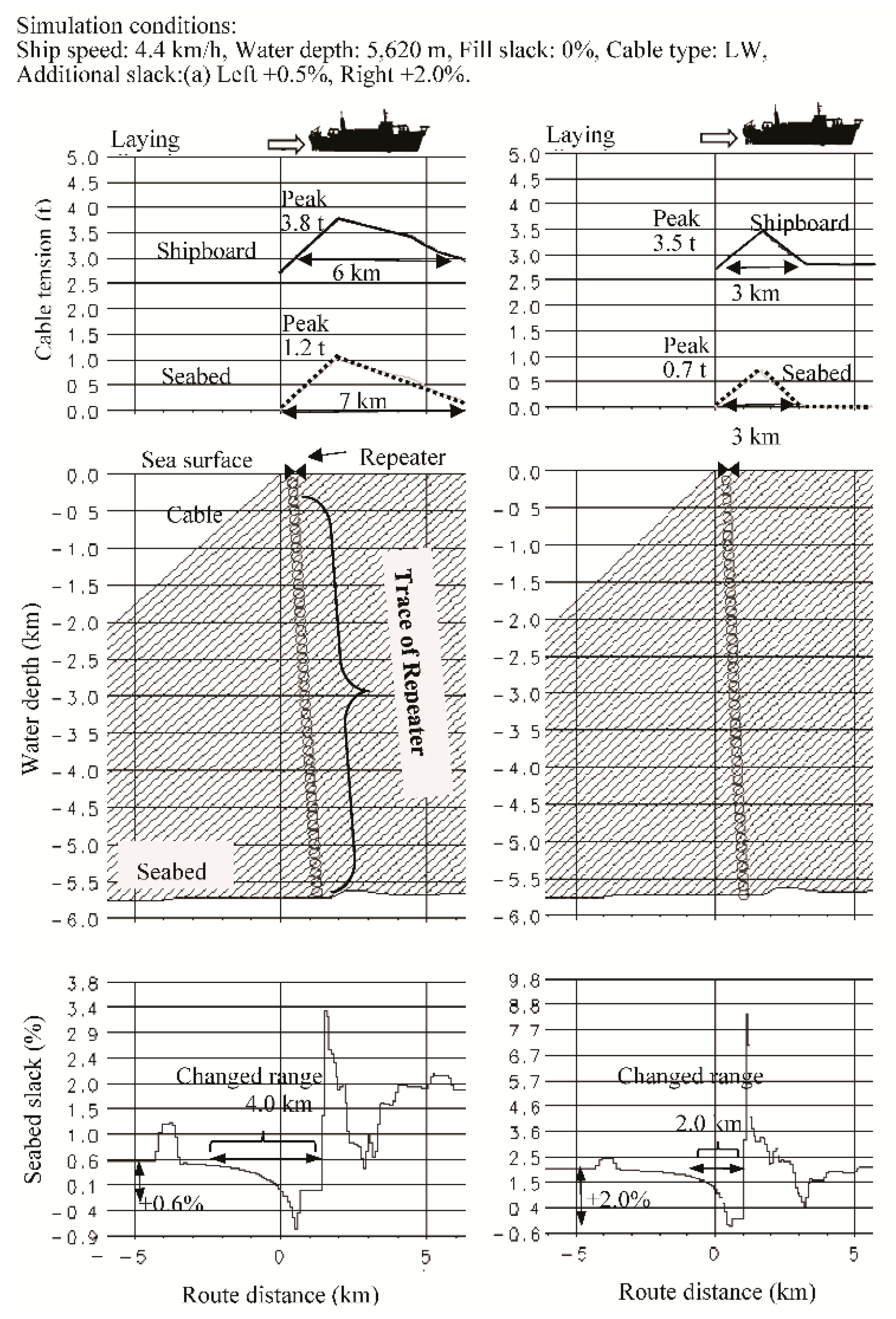
3.5. Comparative Verification of Cable Behavior in Different Repeater Laying Conditions
4. Study of Cable Faults Triggered by Laying Repeater at Great Water Depths
4.1. Collection and Classification of Cable Faults behind the Repeater
- (1)
- period: years 1999–2016;
- (2)
- time and date of the occurrence of a fault;
- (3)
- laying direction of the system in the installation stage;
- (4)
- fault category;
- (5)
- cable types;
- (6)
- water depth;
- (7)
- cable fault within 7 km behind the repeater, determined by the maximum cable drag-start distance from the repeater (5.7 km) in the simulation in Section 3.4.3 and an uncertainty factor of about 1.2 times;
- (8)
- the topographic gradient of the seabed was obtained by calculations, based on the distance between two points, changes in the water depth, and the water depth at the fault point;
- (9)
- time from system deployment to the occurrence of a fault.
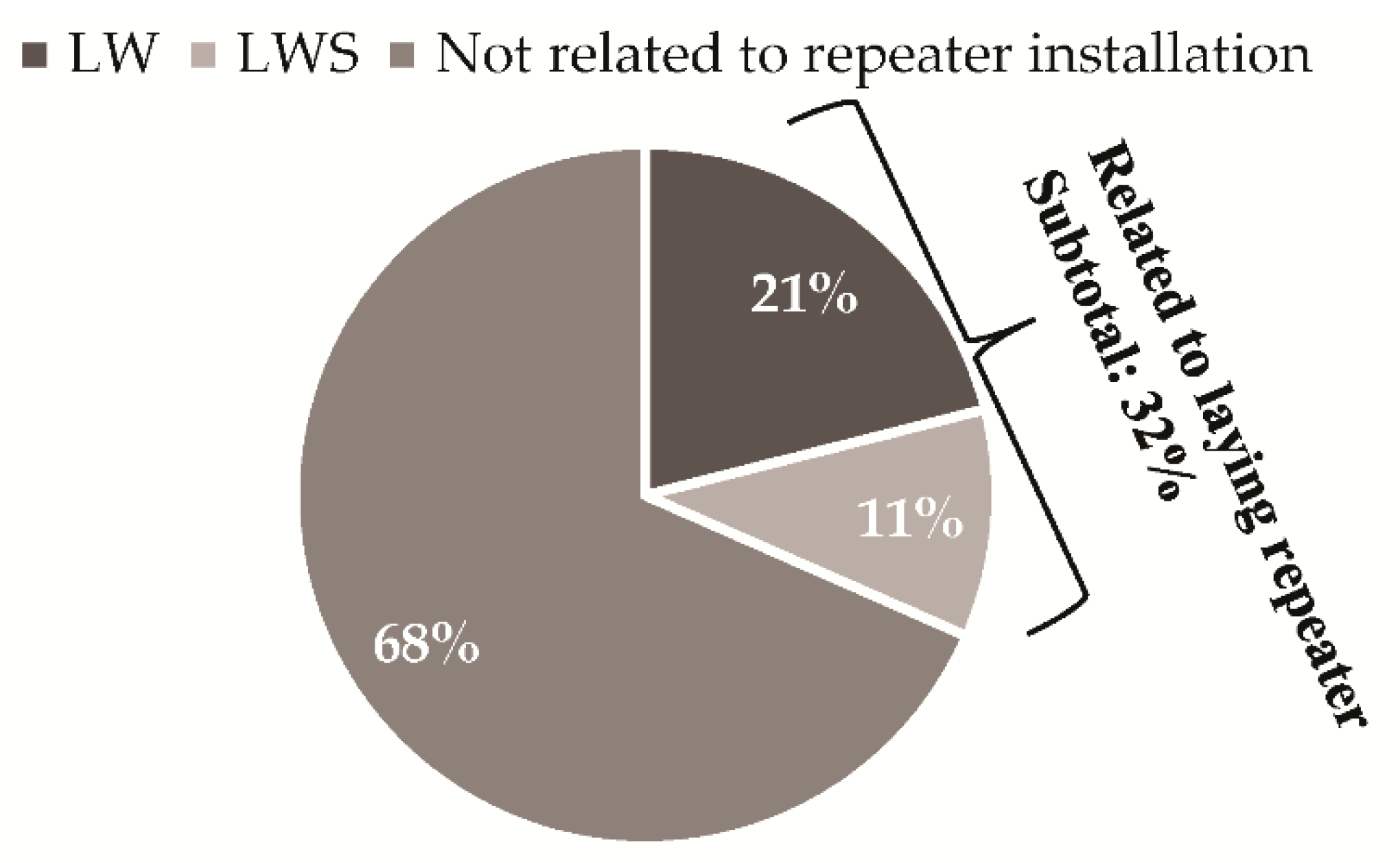
4.2. Results of Cable Fault Analysis
- (1)
- Fault category: all shunt (insulation fault) for LW and LWS types.
- (2)
- The proportion and distribution of cable faults.
- (3)
- Details of the fault.
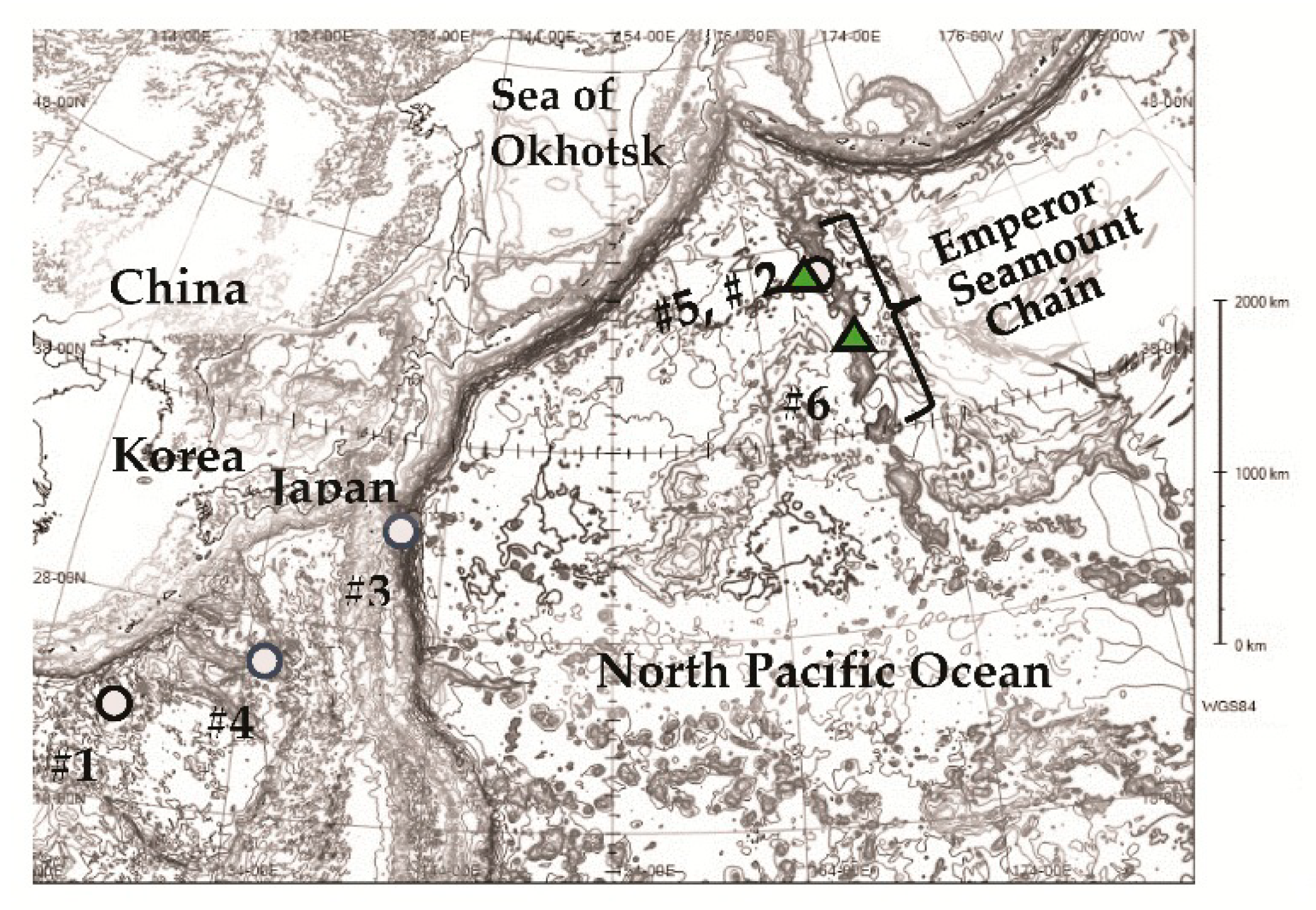
4.3. Summary of the Fault Analysis in the Northwest Pacific
- (1)
- Overall trend.
- (2)
- Geographical distribution of fault locations.
- (3)
- Fault distance behind the repeater.
- (4)
- Topographic gradient of the seabed.
- (5)
- Time to fault after system deployment and total fault number.
- (6)
- Season of fault occurrence.
- (7)
- Fault-free area.
4.4. Consideration of Geographical Locations Where Cable Faults Tend to Occur
4.4.1. Cable Faults in Trenches
- (1)
- Review of the literature on cabled submarine seismic observation system
- (2)
- Features of the deep seafloor surface, based on physical evidence of submarine cable system.
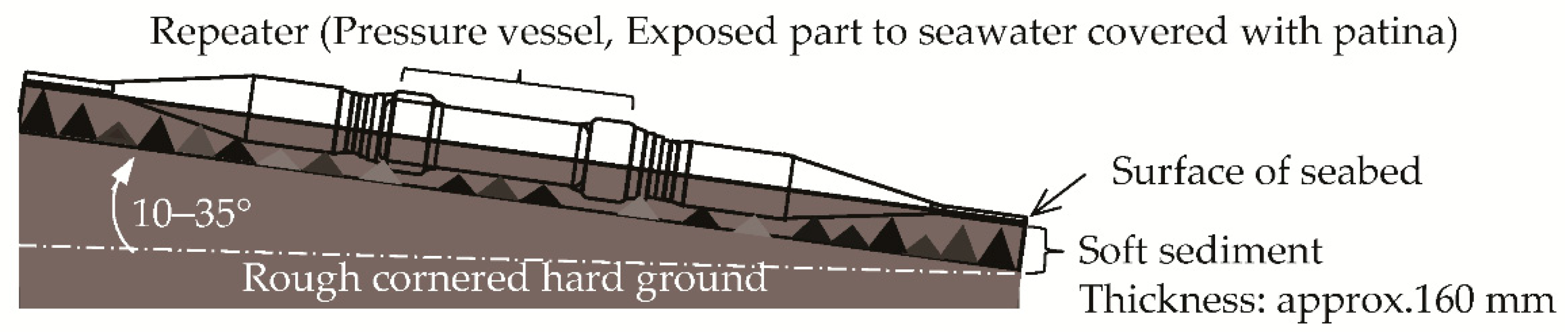
4.4.2. A Factor of Unarmored Cable Damage by the Deep Seafloor
5. Discussion on the Mitigation of Cable Faults Associated with Laying Repeater
5.1. Best Approach to Protecting Submarine Cable Systems from Natural Hazards
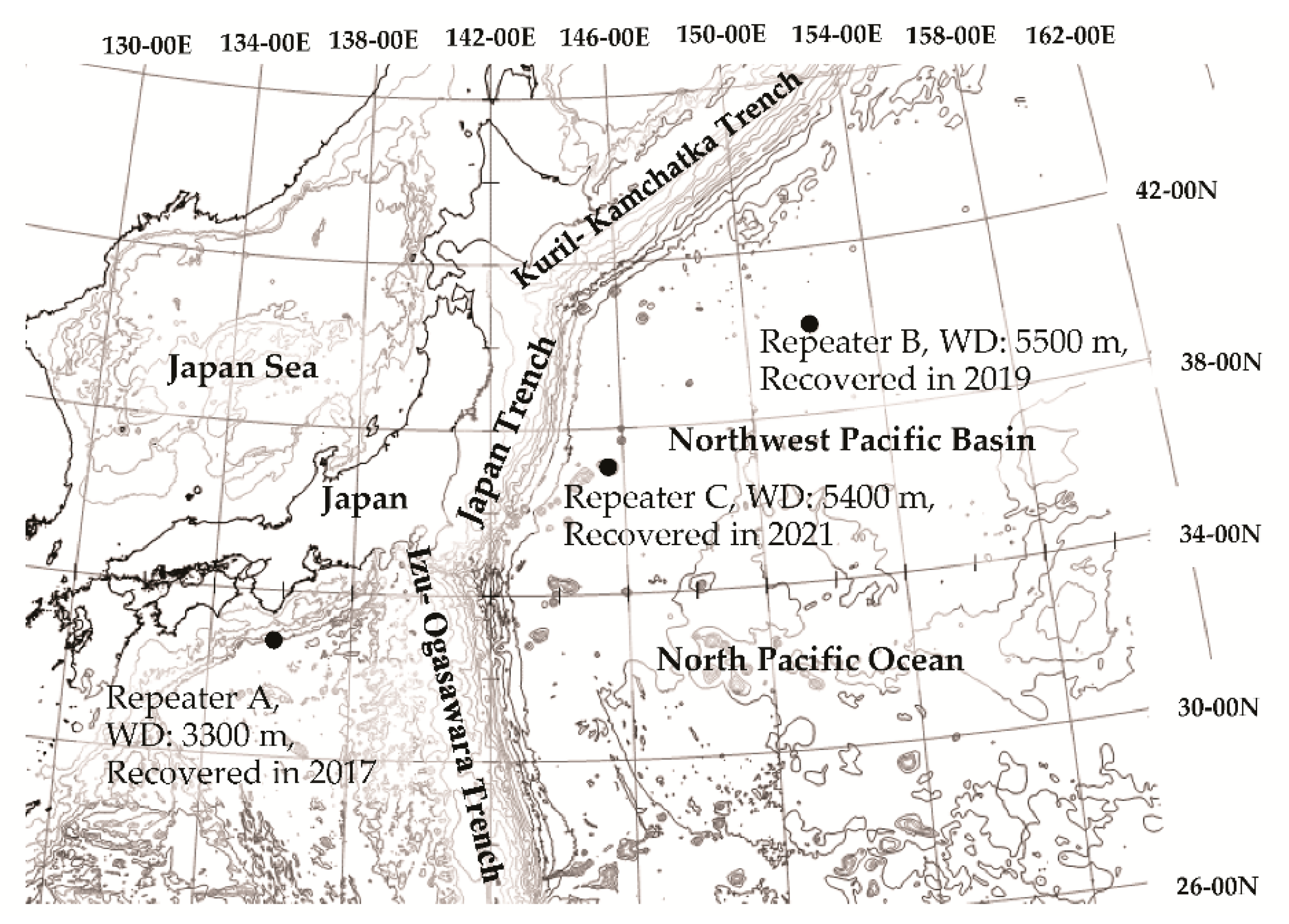
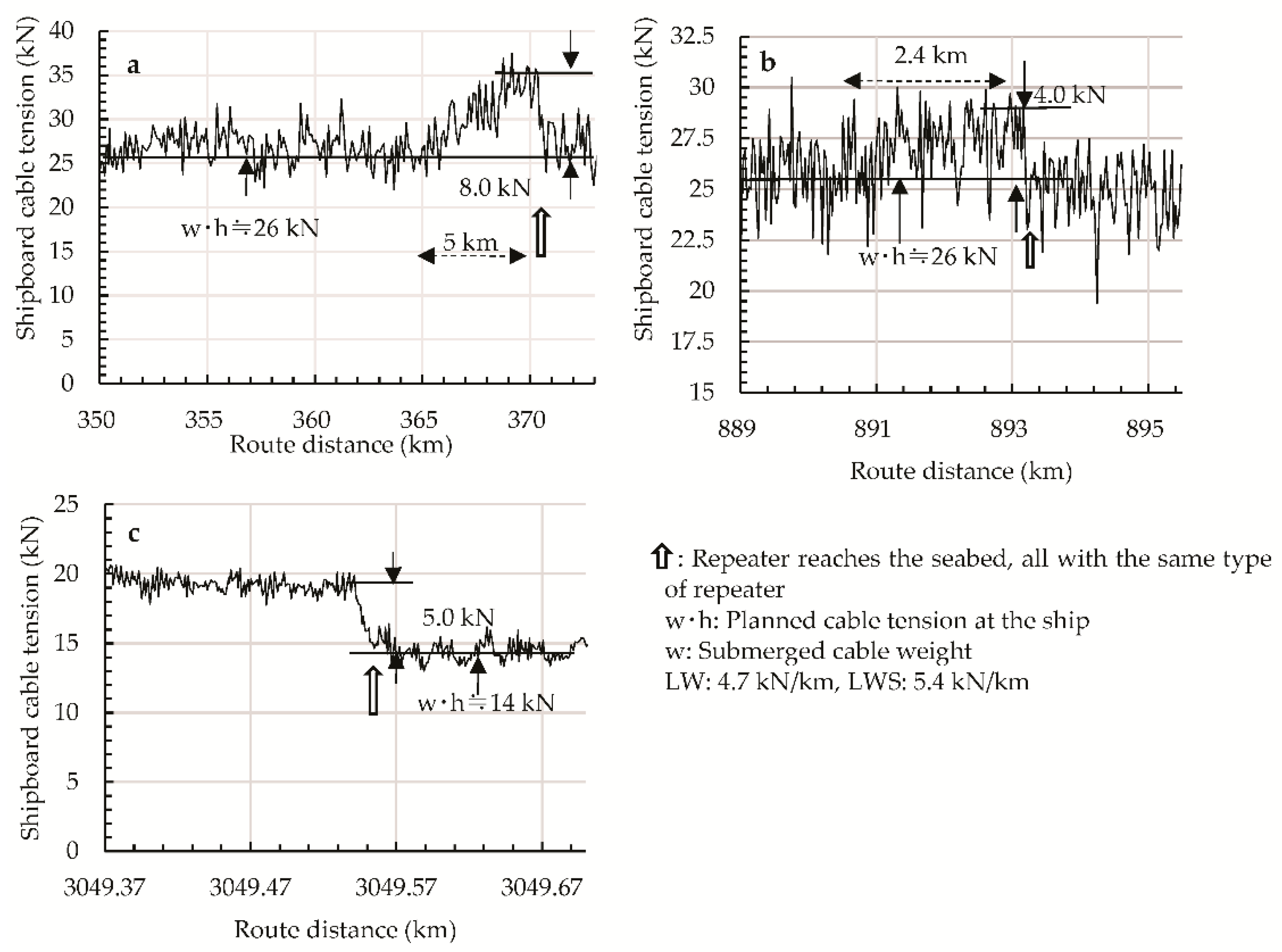
5.2. Shipboard Cable Tension Measurement When Repeater Reaches the Seabed
5.3. Proposal to Minimize the Impact of Cable Faults Relating to Laying Repeaters
- Step 1: marine route survey;
- Step 2: route design;
- Step 3: submarine plant design;
- Step 4: submergible equipment manufacturing;
- Step 5: system assembly and test;
- Step 6: marine installation, including laying design;
- Step 7: land cable and terminal equipment manufacturing, installation, and test;
- Step 8: system test.
Comparative Verification of Each Process to Reduce Cable Faults
- a: increase the extra slack to +3–4.5% [5], which requires a cable length of about 150 m;
- b: reduce the laying speed by half.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ash, S.; Godwin, M.; Green, M.; Morgan, N. From Elektron to “e” Commerce: 150 Years of Laying Submarine Cables; Global Marine Systems: Chelmsford, UK, 2000; pp. 13, 17, 51. ISBN 0953907805. [Google Scholar]
- Wildman Whitehouse Patent 2027 of 1860, Specification in Pursuance of the Conditions of the Letters Patent, Filed by the said Edward Orange Wildman Whitehouse in the Great Seal Patent Office on the 23 February 1861. Available online: https://atlantic-cable.com/Books/Whitehouse/Patents/2027.htm (accessed on 30 June 2020).
- NEC Press Release; June 2016. Faster Cable System Is Ready for Service, Boosts Trans-Pacific Capacity, and Connectivity. Available online: https://www.nec.com/en/press/201606/global_20160629_02.html (accessed on 30 July 2021).
- Gavey, R.; Carter, L.; Liu, J.T.; Talling, P.J.; Hsu, R.; Pope, E.; Evans, G. Frequent Sediment Density Flows from 2006 to 2015, Triggered by Competing Seismic and Weather Events: Observations from subsea Cable Breaks Off Southern Taiwan. Mar. Geol. 2017, 384, 147–158. [Google Scholar] [CrossRef]
- Ogasawara, Y.; Natsu, W. Proposal for reducing the failure rate of fiber-optic submarine cables in deep-sea based on fault analysis and experiments. J. Adv. Mar. Sci. Technol. Soc. 2020, 25, 1–12. [Google Scholar] [CrossRef]
- Burnett, R.; Beckman, R.C.; Davenport, T.M. Submarine Cables: The Handbook of Low and Policy; Martinus Nijhoff Publishers: Boston, MA, USA, 2014; p. 31. ISBN 978-90-04-26033-7. [Google Scholar]
- Zajac, E.E. Dynamics and kinematics of the laying and recovery of submarine cable. Bell Syst. Tech. J. 1957, 36, 1129–1207. [Google Scholar] [CrossRef]
- Kishimoto, R.; Kitazawa, I. Dynamic Behavior of a Submarine Cable in a Uniform Sea Flow. Bull. JSME 1982, 25, 204–212. [Google Scholar] [CrossRef]
- Kojima, J. Three-Dimensional Dynamic Analysis for Laying and Recovery of Optical Submarine Cables. J. Soc. Nav. Archit. Jpn. 1990, 1990, 309–318. (In Japanese) [Google Scholar] [CrossRef]
- Niiro, Y.; Ejiri, Y.; Yamamoto, H. The first Transpacific optical fiber submarine cable system. In Proceedings of the IEEE International Conference on Communications, World Prosperity Through Communications, Boston, MA, USA, 11–14 June 1989; pp. 1520–1524. [Google Scholar] [CrossRef]
- Maurice, E.K.; Ron, J.R.; Robert, K.S.; Sheridan, S.; Irish, O.B.; Wall, D.; Waterworth, G.; Perratt, B.; Wilson, S.; Holden, S. Global Trends in Submarine Cable System Faults 2019 UPDATE. Presented at Oral Session OP 8-1, Suboptic 2019 New Orleans, USA. 2019. Available online: https://suboptic2019.com/suboptic-2019-papers-archive/ (accessed on 25 June 2020).
- Matthew, P. Wood and Lionel Carter. Whale Entanglements with Submarine Telecommunication Cables. IEEE J. Ocean. Eng. Soc. 2008, 33, 445–450. [Google Scholar] [CrossRef]
- Norimatsu, N.; Marugome, I.; Noguchi, Y.; Yamazaki, Y.; Yamamoto, H. Design and Test result of os-560M optical submarine cable, repeater housing, and coupling. ITE ITEJ Tech. Rep. 1991, 17, 17–23. ISSN 0386-4227(In Japanese) [Google Scholar] [CrossRef]
- Davis, J.R. Copper and Copper Alloys, ASM International c2001 ASM Specialty Handbook; Prepared under the Direction of the ASM International Handbook Committee: Materials Park, OH, USA, 2001; ISBN 9780871707268. [Google Scholar]
- Nishida, T.; Nagatomi, O. Latest Technologies and the OCC-SC300 Optical Submarine Cable. NEC Tech. J. 2010, 5, 18–22. [Google Scholar]
- Akiba, S.; Nishi, S. Submarine Cable Network Systems; NTT Quality Printing Service Co.: Tokyo, Japan, 2001; pp. 15–17, 262–264. [Google Scholar]
- Takagi, R.; Uchida, N.; Nakayama, T.; Azuma, R.; Ishigami, A.; Okada, T.; Nakamura, T.; Shiomi, K. Estimation of the Orientations of the S-net Cabled Ocean-Bottom Sensors. Seismol. Res. Lett. 2019, 90, 2175–2187. [Google Scholar] [CrossRef]
- Nakamura, T.; Hashimoto, N. Rotation motions of cabled ocean-bottom seismic stations during the 2011 Tohoku earthquake and their effects on magnitude estimation for early warnings. Geophys. J. Int. 2019, 216, 1413–1427. [Google Scholar] [CrossRef] [Green Version]
- Ohta, T.; Nishiyama, T. Route Design/Cable Laying Technologies for Optical Submarine Cables. NEC Tech. J. 2010, 5, 46–50. [Google Scholar]
- Yoneyama, K.; Sakuyama, H.; Hagisawa, A. Construction Technology for Use in Repeated Transoceanic Optical Submarine Cable Systems. NEC Tech. J. 2010, 5, 41–45. [Google Scholar]

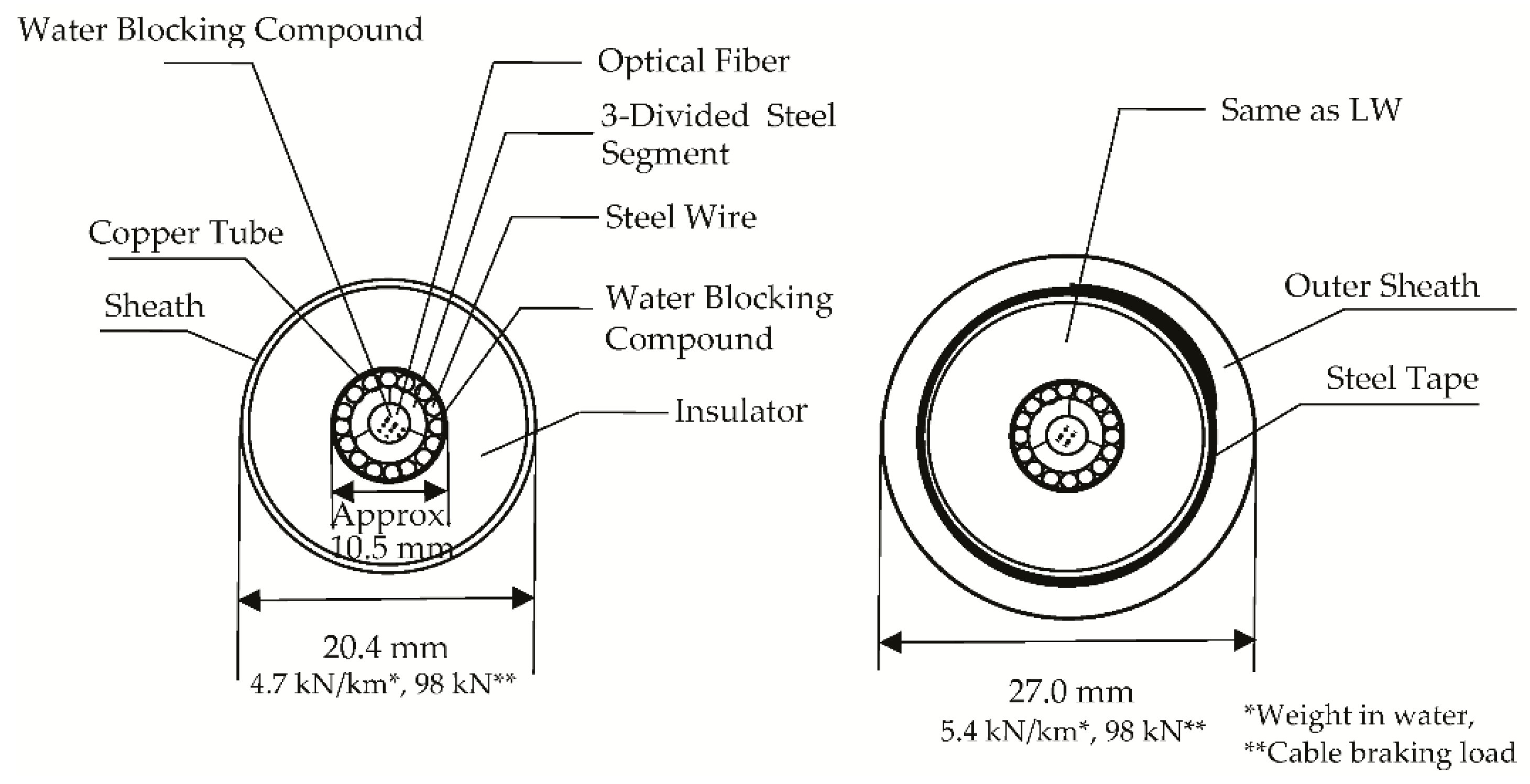




| Cable Parameter and Physical Constants Required for Calculation | LW | LWS |
|---|---|---|
| d: Diameter (mm) | 20.4 | 27.0 |
| w: Weight in water (kN/km) | 4.7 | 5.4 |
| CD: Hydrodynamics coefficient of the cable drag [16] | 2.5 | |
| ρ: Density of seawater (kg·sec2/m4) [16] | 102 | |
| Calculation result | ||
| H: Hydrodynamic constant (degree·knot) | 47.8 | 44.6 |
| Us: Transverse sinking velocity (m/h) | 1544 | 1441 |
| Targets | Sinking Speed (m/h) | Ratio of Repeater Sinking Speed to Cable (%) |
|---|---|---|
| Repeater with LW | 1750 | +13.34 |
| LW (Calculation) | 1544 | --- |
| Repeater with LWS | 1500 | +4.09 |
| LWS (Calculation) | 1441 | --- |
| Items/Figure 23 | a | b | c |
|---|---|---|---|
| Ship speed (km/h) | 6.0 | 10.0 | 1.3 |
| Water depth (m) | 5400 | 5423 | 2620 |
| Fill slack (%) | 0.0 | 0.0 | −1.7 |
| Additional slack (%) | +1.6 | +2.5 | 0.0 |
| Cable type | LW | LW | LWS |
| Steps | Measures | Cost Impact | |
|---|---|---|---|
| Step 3 | If the planned repeater location on the seabed cannot avoid the hazardous terrain, place the repeater outside the range. | High | |
| If the planned repeater location on the seabed cannot avoid the hazardous terrain, use the LWS cable within the allowable water depth range. | Middle | ||
| Step 6 | Method 1 | Apply “a” or “b” at cable lengths to repeaters 2.8-6.5 km after laying the repeater, not applied. | Low |
| |||
| |||
| Method 2 | Keep laying cable at a low speed less than 2 km/h | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogasawara, Y.; Natsu, W. A Cost-Effective Approach to the Risk Reduction of Cable Fault Triggered by Laying Repeaters of Fiber-Optic Submarine Cable Systems in Deep-Sea. J. Mar. Sci. Eng. 2021, 9, 939. https://doi.org/10.3390/jmse9090939
Ogasawara Y, Natsu W. A Cost-Effective Approach to the Risk Reduction of Cable Fault Triggered by Laying Repeaters of Fiber-Optic Submarine Cable Systems in Deep-Sea. Journal of Marine Science and Engineering. 2021; 9(9):939. https://doi.org/10.3390/jmse9090939
Chicago/Turabian StyleOgasawara, Yukitoshi, and Wataru Natsu. 2021. "A Cost-Effective Approach to the Risk Reduction of Cable Fault Triggered by Laying Repeaters of Fiber-Optic Submarine Cable Systems in Deep-Sea" Journal of Marine Science and Engineering 9, no. 9: 939. https://doi.org/10.3390/jmse9090939
APA StyleOgasawara, Y., & Natsu, W. (2021). A Cost-Effective Approach to the Risk Reduction of Cable Fault Triggered by Laying Repeaters of Fiber-Optic Submarine Cable Systems in Deep-Sea. Journal of Marine Science and Engineering, 9(9), 939. https://doi.org/10.3390/jmse9090939






