The Quasi-Static Response of Moored Floating Structures Based on Minimization of Mechanical Energy
Abstract
:1. Introduction
2. Theoretical Backgrounds of the Proposed Method
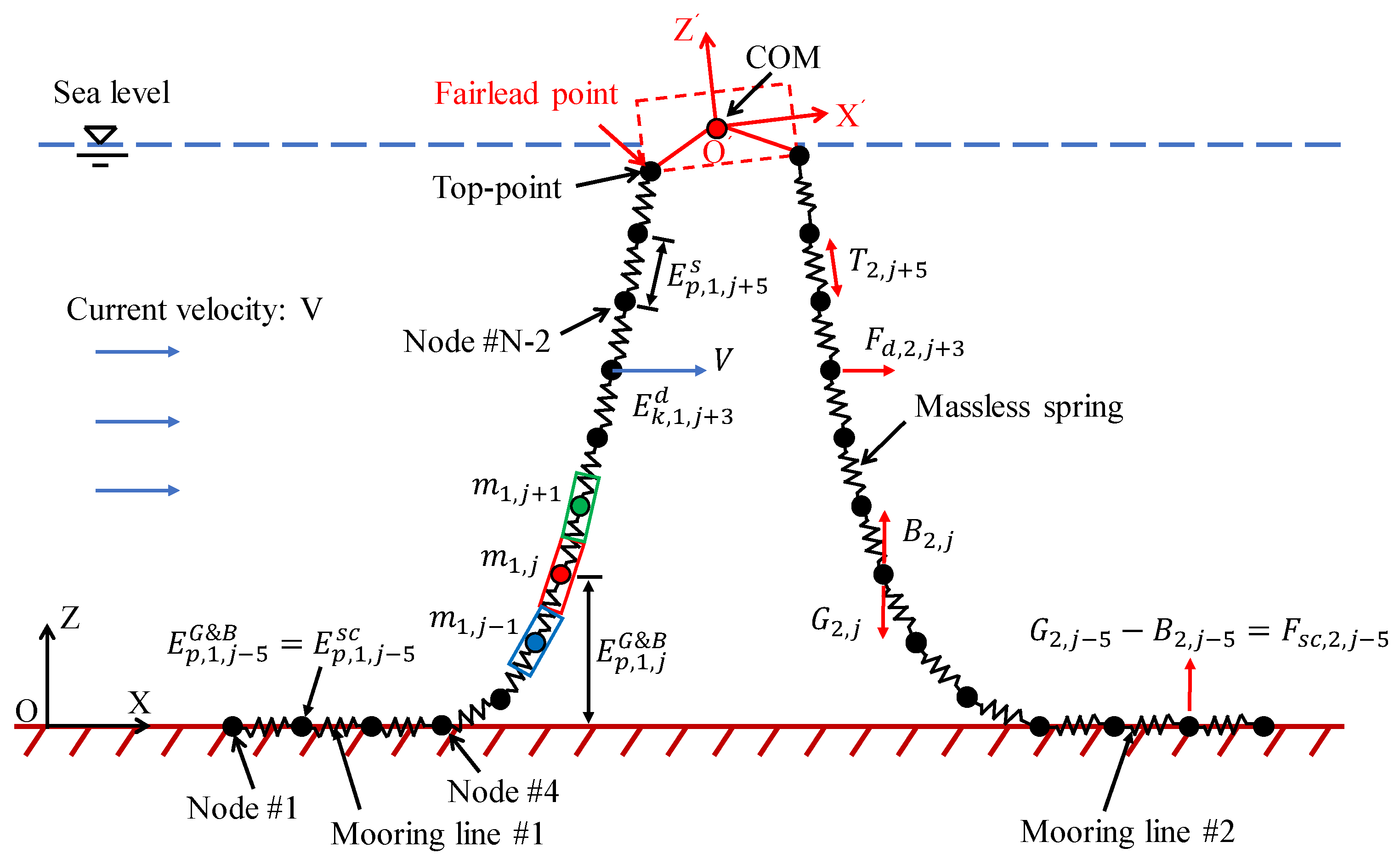
2.1. Moored Floating Structure Architecture
2.2. Mechanical Energy Induced by Quasi-Static Forces
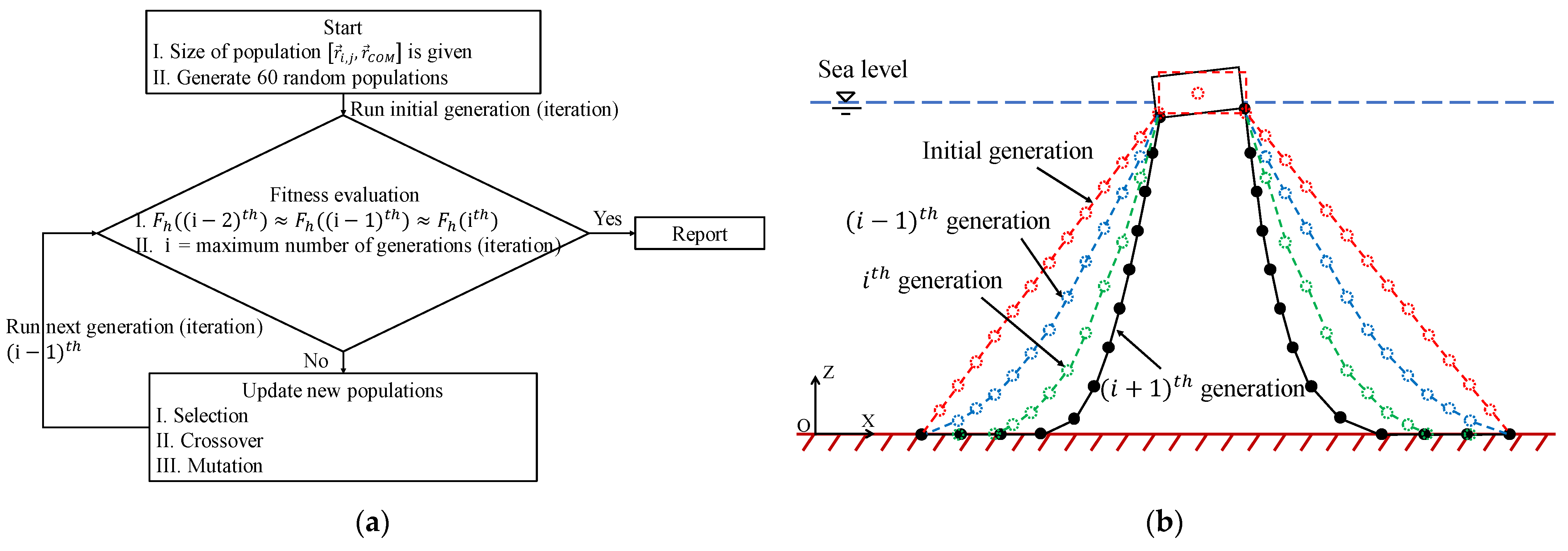
2.3. Minimization of Mechanical Energy
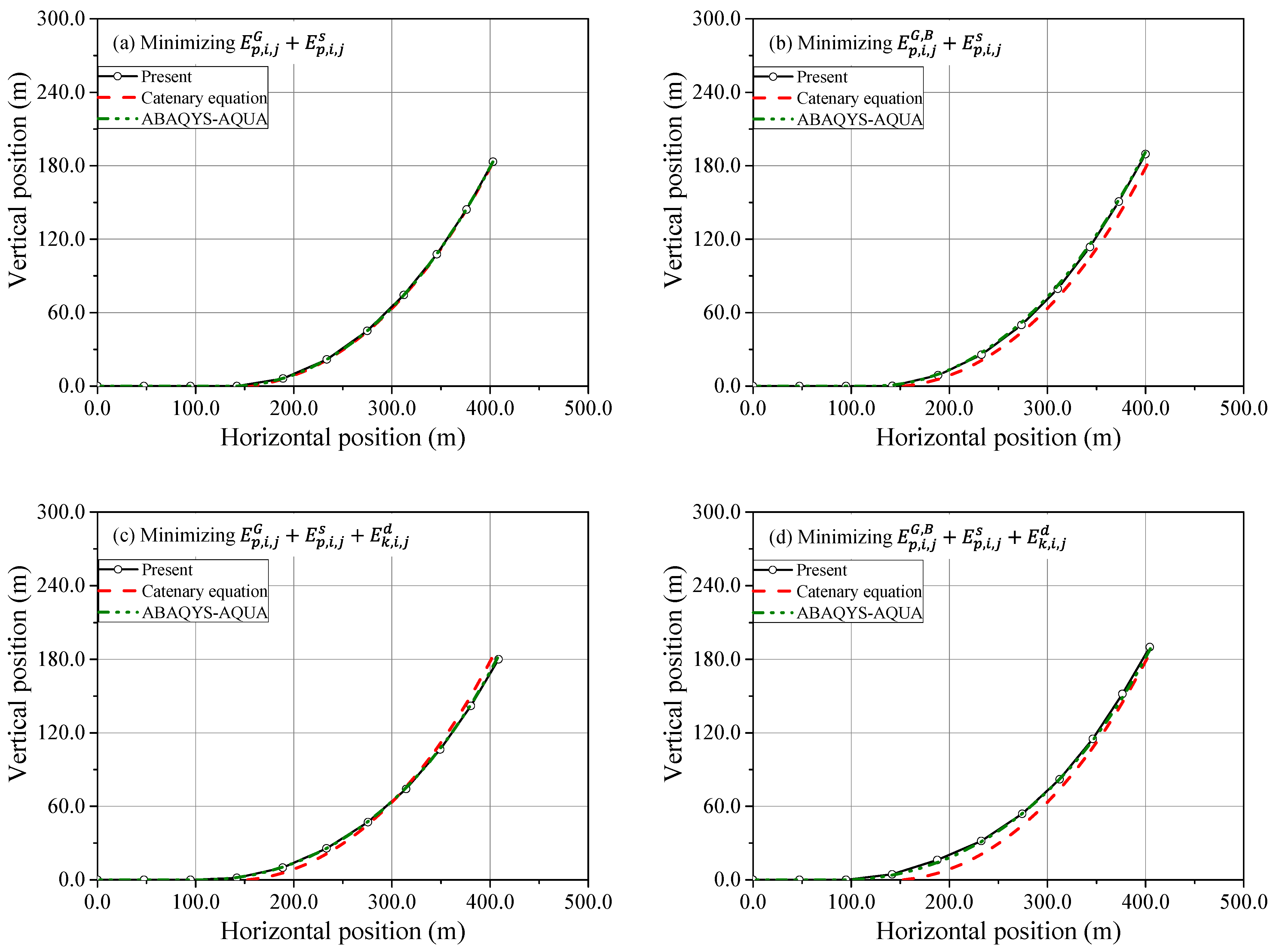
3. Validation and Case Studies
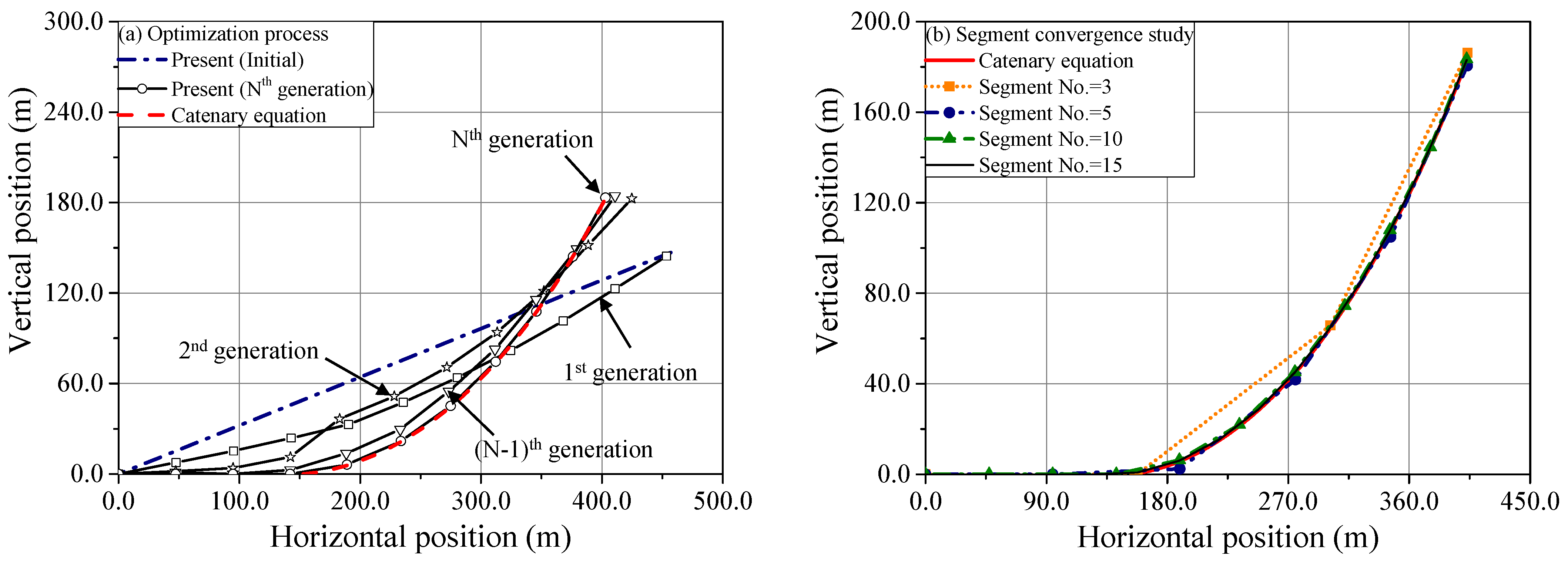
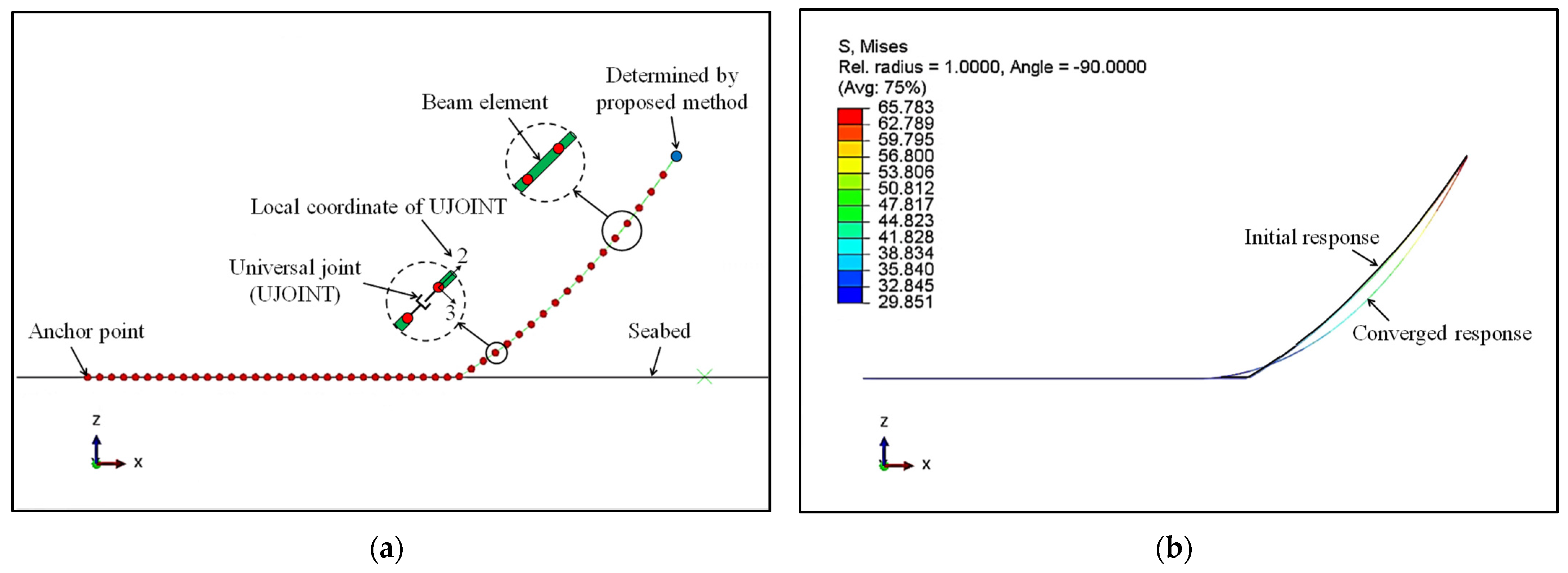
3.1. The Suspended Mooring Line
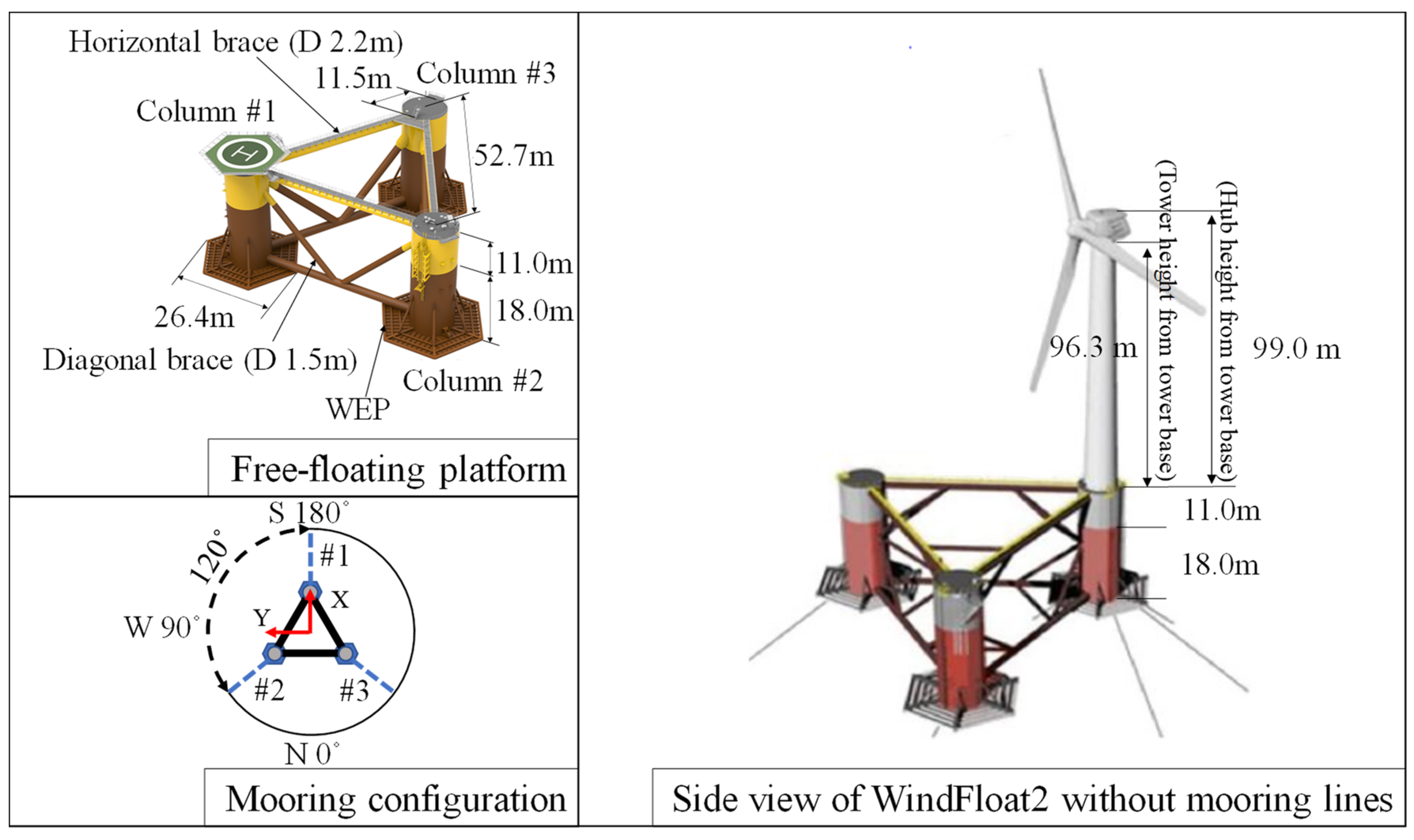
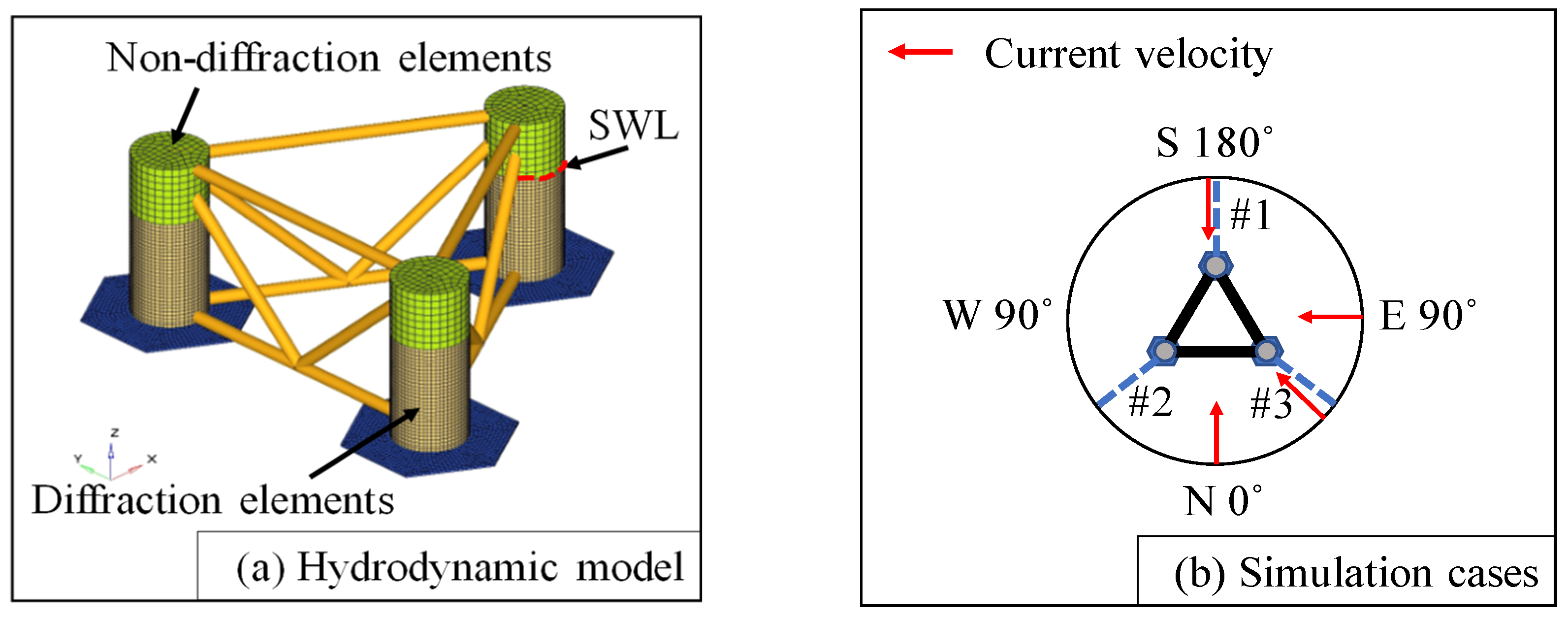
3.2. The WindFloat 2 Floating Platform
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maffra, S.A.R.D.S.; Pacheco, M.A.C.; de Menezes, I.F.M. Genetic Algorithm Optimization for Mooring Systems; Tecgraf PUC-Rio Publications: Rio, Brazil, 2001. [Google Scholar]
- Fitzgerald, J. Position Mooring of Wave Energy Converters. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, November 2009. [Google Scholar]
- Mavrakos, S.A.; Papazoglou, V.J.; Trintafyllou, M.S.; Hatjigeorgiou, J. Deep water mooring dynamics. J. Mar. Struct. 1996, 9, 181–209. [Google Scholar] [CrossRef]
- Pascoal, R.; Huang, S.; Barltrop, N.; Guedes Soares, C. Equivalent force model for the effect of mooring systems on the horizontal motions. J. Appl. Ocean Res. 2005, 27, 165–172. [Google Scholar] [CrossRef]
- Pascoal, R.; Huang, S.; Barltrop, N.; Guedes Soares, C. Assessment of the effect of mooring systems on the horizontal motions with an equivalent force to model. Ocean Eng. 2006, 33, 1644–1668. [Google Scholar] [CrossRef]
- Jain, R. A simple method of calculating the equivalent stiffnesses in mooring cables. J. Appl. Ocean Res. 1980, 2, 139–142. [Google Scholar] [CrossRef]
- Agarwal, A.K.; Jain, A.K. Dynamic behaviour of offshore spar platforms under regular sea waves. Ocean Eng. 2003, 30, 487–516. [Google Scholar] [CrossRef]
- Vicente, P.C.; Falcão, A.F.O.; Justino, P.A.P. Optimization of mooring configuration parameters of floating wave energy converters. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Montasir, O.A.; Yenduri, A.; Kurian, V.J. Effect of mooring line configurations on the dynamic responses of truss spar platforms. Ocean Eng. 2015, 96, 161–172. [Google Scholar] [CrossRef]
- Masciola, M. Instructional and Theory Guide to the Mooring Analysis Program. NREL. Available online: https://nwtc.nrel.gov/system/files/MAP_v0.87.06a-mdm.pdf (accessed on 2 January 2021).
- Jonkman, J.M.; Buhl, M.L., Jr. Development and verification of a fully coupled simulator for offshore wind turbines. Renewable Energy Laboratory. In Proceedings of the 5th AIAA Aerospace Sciences Meeting and Exhibit, Wind Energy Symposium, Reno, NV, USA, 8–11 January 2007. NREL/TP-500-40979. [Google Scholar]
- Masciola, M.; Jonkman, J.; Robertson, A. Implementation of a multisegmented, quasi-static cable model. In Proceeding of the 23rd International Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- ANSYS/AQWA. AQWA-Theory Manual; Inc. Southpointe 275 Technology Drive Canonsburg: Canonsburg, PA, USA, 2013. [Google Scholar]
- Li, C.B.; Choung, J.; Kim, B.I. Prediction of stress spectra under low period sea states. Ships Offshore Struct. 2018, 13, 56–67. [Google Scholar] [CrossRef]
- Bhinder, M.A.; Karimirad, M.; Weller, S.; Debruyne, Y.; Guérinel, M.; Sheng, W. Modelling mooring line non-linearities (material and geometric effects) for a wave energy converter using AQWA, SIMA and Orcaflex. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Angelelli, E.; Zanuttigh, B.; Martinelli, L.; Ferri, F. Physical and numerical modelling of mooring forces and displacements of a wave activated body energy converter. In Proceeding of the ASME 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Murphy, S.; Bhinder, M.A.; Casaubieilh, P.; Sheng, W. Effects of tidal range on mooring systems of wave energy converters. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Chen, D.; Wang, C.M.; Zhang, H. Examination of net volume reduction of gravity-type open-net fish cages under sea currents. Aquac. Eng. 2021, 92, 102–128. [Google Scholar] [CrossRef]
- Knight, R.D. Physics for Scientists and Engineers, 3rd ed.; Pearson: San Francisco, CA, USA, 2016. [Google Scholar]
- Mathworks. Matlab User Manual; Mathworks: Natick, MA, USA, 2020. [Google Scholar]
- ABAQUS/AQUA. ABAQUS-Theory Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2016. [Google Scholar]
- Li, C.B.; Seo, J.K.; Paik, J.K. Proposed formulas for evaluation of the equivalent material properties of a multiholed structures. Ocean. Eng. 2016, 121, 312–322. [Google Scholar] [CrossRef]
- Li, C.B.; Kim, S.J.; Lee, J.C.; Paik, J.K.; Sohn, J.M. Dynamic structural response characteristics of perforated blast walls under hydrocarbon explosion. In Proceeding of the 7th International Conference on Thin-Walled Structures, Busan, Korea, 28 September–2 October 2014. [Google Scholar]
- Li, C.B.; Choung, J. A new method of predicting hotspot stresses for longitudinal attachments with reduced element sensitivities. Int. J. Nav. Archit. Ocean. Eng. 2021, 13, 379–395. [Google Scholar] [CrossRef]
- Kim, C.S.; Li, C.B.; Choung, J.; Kim, Y.H. Prediction of crack growth of an aged coast guard patrol ship based on various approaches. In Proceeding of the 6th International Conference on Marine Structures, Lisbon, Portugal, 8–10 May 2017. [Google Scholar]
- Kim, C.S.; Li, C.B.; Kim, Y.H.; Choung, J. Prediction of crack growth lives of an aged Korean coast guard patrol ship based on extended finite element method (XFEM) J-Integral. J. Soc. Nav. Archit. 2017, 54, 335–343. [Google Scholar]
- Bureau Veritas. Fatigue of Top Chain of Mooring Lines Due to In-Plane and Out-Of-Plane Bendings; Guidance Note NI 604; Bureau Veritas: Neuilly-sur-Seine, France, 2014. [Google Scholar]
- Li, C.B.; Choung, J. Fatigue damage analysis for a floating offshore wind turbine mooring line using the artificial neural network approach. Ships Offshore Struct. 2016, 12, 288–295. [Google Scholar] [CrossRef]
- Li, C.B.; Choung, J.; Noh, M.H. Wide-banded fatigue damage evaluation of Catenary mooring lines using artificial neural networks models. Mar. Struct. 2018, 60, 186–200. [Google Scholar] [CrossRef]
- Marbus, G.D. Verification of the Water Forces on Stringer of Allseas’ Solitaire. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]


| Parameters | Value |
|---|---|
| Size of the population | 60 |
| Number of generations | 200 |
| Crossover type | Multi-point |
| Crossover probability | 0.5 |
| Mutation probability | 0.5 |
| Elite count | 2 |
| Tolerance | 1 × 10−6 |
| Items | Unit | Value |
|---|---|---|
| Unstretched length | m | 473.30 |
| Line diameter | m | 0.0809 |
| Line density | kg/m | 130.40 |
| Cross-sectional area (A) | m2 | 0.0051 |
| Young’s modulus (E) | Pa | 1.15 × 1011 |
| Line stiffness (EA) | N/m | 1.25 × 106 |
| Drag tangent coefficient | -/- | 1.00 |
| Drag normal coefficient | -/- | 0.03 |
| Items | Quasi-Static Forces | Mechanical Energy |
|---|---|---|
| Case I | and | |
| Case II | , and | |
| Case III | , and (1.7 m/s) | |
| Case IV | , , and (1.7 m/s) |
| Items | Unit | Value | Items | Unit | Value |
|---|---|---|---|---|---|
| Mass | kg | 6.927 × 106 | Drag tangent coefficient | -/- | 1.000 |
| Displacement | m3 | 6951.8 | Drag normal coefficient | -/- | 0.025 |
| Coord. for COM | m | (0.0, 0.0, −9.0) | Coord. for fairlead point #1 | m | (30.43, 0.0, −18.0) |
| Roll inertia for COM | kg-m2 | 4.747 × 109 | Coord. for fairlead point #2 | m | (−15.21, 26.35, −18.0) |
| Pitch inertia for COM | kg-m2 | 4.747 × 109 | Coord. for fairlead point #3 | m | (−15.21, −26.35, −18.0) |
| Yaw inertia for COM | kg-m2 | 6.722 × 109 | Coord. for anchor point #1 | m | (680.43, 0.0, 0.0) |
| Unstretched length | m | 650.0 | Coord. for anchor point #2 | m | (−340.21, 589.27, 0.0) |
| Line diameter | m | 0.14142 | Coord. for anchor point #3 | m | (−340.21, −589.27, 0.0) |
| Line density | kg/m | 199.0 | |||
| Axial stiffness | N | 8.54 × 108 |
| Items | Current Direction (°) | |||
|---|---|---|---|---|
| Case I | 55 | 1025 | None | None |
| Case II | 1.7 | 0.0 | ||
| Case III | 45.0 | |||
| Case IV | 90.0 | |||
| Case V | 180.0 |
| Translation along Axial () | Translation along Axial () | Translation along Axial () | |||||||
| AQWA | Proposed | Error (%) | AQWA | Proposed | Error (%) | AQWA | Proposed | Error (%) | |
| Case I | 0.000 | 0.000 | 0.00 | 0.000 | 0.000 | 0.00 | −9.580 | −9.601 | 0.22 |
| Case II | 0.320 | 0.342 | 6.88 | 0.000 | 0.000 | 0.00 | −9.590 | −9.594 | 0.04 |
| Case III | 0.230 | 0.211 | −8.26 | 0.250 | 0.232 | −7.20 | −9.590 | −9.584 | 0.10 |
| Case IV | 0.030 | 0.034 | 6.67 | 0.330 | 0.345 | 4.55 | −9.590 | −9.600 | −0.06 |
| Case V | −0.340 | −0.352 | 3.53 | 0.000 | 0.000 | 0.00 | −9.590 | −9.599 | −0.01 |
| Rotation about Axial (o) | Rotation about Axial (o) | Rotation about Axial (o) | |||||||
| AQWA | Proposed | Error (%) | AQWA | Proposed | Error (%) | AQWA | Proposed | Error (%) | |
| Case I | 0.000 | 0.000 | 0.00 | 0.000 | 0.000 | 0.00 | 0.000 | 0.000 | 0.00 |
| Case II | 0.000 | 0.000 | 0.00 | 0.050 | 0.053 | 6.00 | 0.000 | 0.000 | 0.00 |
| Case III | −0.030 | −0.021 | −30.00 | 0.030 | 0.026 | −13.33 | −0.150 | −0.132 | −12.00 |
| Case IV | −0.050 | −0.058 | 16.00 | 0.000 | 0.000 | 0.00 | 0.210 | 0.254 | 11.43 |
| Case V | 0.000 | 0.000 | 0.00 | −0.050 | −0.054 | 8.00 | 0.000 | 0.000 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.B.; Chen, M.; Choung, J. The Quasi-Static Response of Moored Floating Structures Based on Minimization of Mechanical Energy. J. Mar. Sci. Eng. 2021, 9, 960. https://doi.org/10.3390/jmse9090960
Li CB, Chen M, Choung J. The Quasi-Static Response of Moored Floating Structures Based on Minimization of Mechanical Energy. Journal of Marine Science and Engineering. 2021; 9(9):960. https://doi.org/10.3390/jmse9090960
Chicago/Turabian StyleLi, Chun Bao, Mingsheng Chen, and Joonmo Choung. 2021. "The Quasi-Static Response of Moored Floating Structures Based on Minimization of Mechanical Energy" Journal of Marine Science and Engineering 9, no. 9: 960. https://doi.org/10.3390/jmse9090960
APA StyleLi, C. B., Chen, M., & Choung, J. (2021). The Quasi-Static Response of Moored Floating Structures Based on Minimization of Mechanical Energy. Journal of Marine Science and Engineering, 9(9), 960. https://doi.org/10.3390/jmse9090960








