Cohesive Zone Model Modification Techniques According to the Mesh Size in Finite Element Models of Stiffened Panels with Debonding
Abstract
:1. Introduction
2. Theoretical Background
3. Reference Benchmark Study and Finite Element Modeling
3.1. Benchmark Study
3.2. Development of Finite Element Model
4. FE Model Results and Validation
4.1. Validation of the FE model
4.2. Additional Numerical Results for the SSCS
5. Application of Modified CZM to Multi-Stiffened Plate
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Zhao, Q.; Qiao, P. A critical review on buckling and post-buckling analysis of composite structures. Front. Aerosp. Eng. 2013, 2, 157–168. [Google Scholar]
- Milazzo, A.; Oliveri, V. Post-buckling analysis of cracked multilayered composite plates by pb-2 Rayleigh–Ritz method. Compos. Struct. 2015, 132, 75–78. [Google Scholar] [CrossRef]
- Groh, R.; Avitabile, D.; Pirrera, A. Generalised path-following for well-behaved nonlinear structures. Comput. Methods Appl. Mech. Eng. 2018, 331, 394–426. [Google Scholar] [CrossRef]
- Liguori, F.S.; Zucco, G.; Madeo, A.; Garcea, G.; Leonetti, L.; Weaver, P.M. An isogeometric framework for the optimal design of variable stiffness shells undergoing large deformations. Int. J. Solids Struct. 2021, 210–211, 18–34. [Google Scholar] [CrossRef]
- Lanzi, L. A numerical and experimental investigation on composite stiffened panels into post-buckling. Thin-Walled Struct. 2004, 42, 1645–1664. [Google Scholar] [CrossRef]
- Bisagni, C. Numerical analysis and experimental correlation of composite shell buckling and post-buckling. Compos. Part B Eng. 2000, 31, 655–667. [Google Scholar] [CrossRef]
- Dębski, H.; Teter, A.; Kubiak, T.; Samborski, S. Local buckling, post-buckling and collapse of thin-walled channel section composite columns subjected to quasi-static compression. Compos. Struct. 2016, 136, 593–601. [Google Scholar] [CrossRef]
- ANSYS© Mechanical APDL. Release 19.2, Help System; Fracture Analysis Guide; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Orifici, A.; Alberdi, I.O.D.Z.; Thomson, R.S.; Bayandor, J. Compression and post-buckling damage growth and collapse analysis of flat composite stiffened panels. Compos. Sci. Technol. 2008, 68, 3150–3160. [Google Scholar] [CrossRef] [Green Version]
- Bisagni, C. Progressive delamination analysis of stiffened composite panels in post-buckling. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Newport, RI, USA, 1–4 May 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar] [CrossRef]
- Riccio, A.; Raimondo, A.; Scaramuzzino, F. A robust numerical approach for the simulation of skin–stringer debonding growth in stiffened composite panels under compression. Compos. Part B Eng. 2015, 71, 131–142. [Google Scholar] [CrossRef]
- Zou, D.; Bisagni, C. Skin-stiffener separation in T-stiffened composite specimens in postbuckling condition. J. Aerosp. Eng. 2018, 31, 04018027. [Google Scholar] [CrossRef] [Green Version]
- Raimondo, A.; Doesburg, S.; Bisagni, C. Numerical study of quasi-static and fatigue delamination growth in a post-buckled composite stiffened panel. Compos. Part B Eng. 2020, 182, 107589. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, K.; Ding, F.; Qin, T.; Xu, J.; Liu, F.; Zhang, J. A post-buckling compressive failure analysis framework for composite stiffened panels considering intra-, inter-laminar damage and stiffener debonding. Results Phys. 2019, 13, 102205. [Google Scholar] [CrossRef]
- Bisagni, C.; Vescovini, R.; Davila, C.G. Single-stringer compression specimen for the assessment of damage tolerance of postbuckled structures. J. Aircr. 2011, 48, 495–502. [Google Scholar] [CrossRef]
- Vescovini, R.; Dávila, C.; Bisagni, C. Failure analysis of composite multi-stringer panels using simplified models. Compos. Part B Eng. 2013, 45, 939–951. [Google Scholar] [CrossRef]
- Yetman, J.E.; Sobey, A.J.; Blake, J.I.R.; Shenoi, R.A. Investigation into skin stiffener debonding of top-hat stiffened composite structures. Compos. Struct. 2015, 132, 1168–1181. [Google Scholar] [CrossRef] [Green Version]
- Álvarez, D.; Blackman, B.; Guild, F.; Kinloch, A. Mode I fracture in adhesively-bonded joints: A mesh-size independent modelling approach using cohesive elements. Eng. Fract. Mech. 2014, 115, 73–95. [Google Scholar] [CrossRef] [Green Version]
- Gliszczynski, A.; Samborski, S.; Wiacek, N.; Rzeczkowski, J. Mode I interlaminar fracture of glass/epoxy unidirectional laminates. Part II: Numerical analysis. Materials 2019, 12, 1604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef] [Green Version]
- Turon, A.; Dávila, C.; Camanho, P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.; Costa, J.; Renart, J. Accurate simulation of delamination growth under mixed-mode loading using cohesive elements: Definition of interlaminar strengths and elastic stiffness. Compos. Struct. 2010, 92, 1857–1864. [Google Scholar] [CrossRef]
- Mantzaroudis, V.K.; Stamatelos, D.G. Development of an efficient finite element model for the analysis of buckling, debonding and collapse characteristics of composite stiffened panels under compressive loading. In Proceedings of the International Symposium on Aircraft Technology, MRO & Operations 2021, Budapest, Hungary, 28–30 June 2021; Springer Nature: Cham, Switzerland, 2021. (under publication). [Google Scholar]
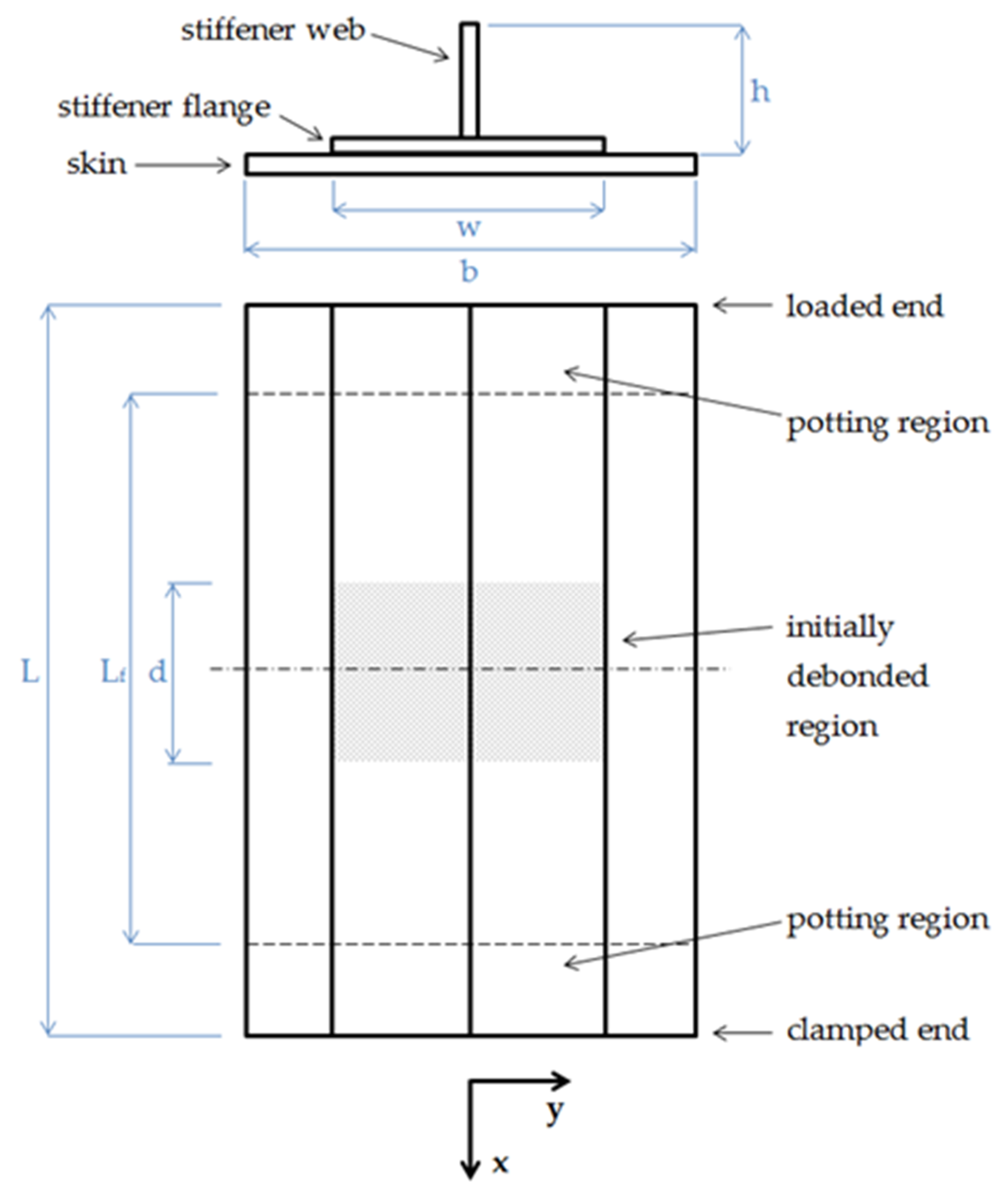









| Geometric Characteristic | Value | Material Property | Value |
|---|---|---|---|
| Total length, L (mm) | 400 | E11 (GPa) | 147.8 |
| Free length, Lf (mm) | 300 | E22 = E33 (GPa) | 11.8 |
| Width, b (mm) | 64 | G12 = G13 (GPa) | 6 |
| Skin lay-up | [90/±45/0]s | G23 (GPa) | 4 |
| Stiffener flange lay-up | [06/±453] | v12 = v13 | 0.3 |
| Stiffener web lay-up | [±453/06]s | v23 | 0.45 |
| Ply thickness, t (mm) | 0.125 | Max normal traction (mode I) (MPa) | 50 |
| Total stiffener height, h (mm) | 14 | Max shear traction (mode II) (MPa) | 100 |
| Stiffener flange width, w (mm) | 32 | GIc (J/m2) | 243 |
| Debonded length (mm) | 80 | GIIc = GIIIc (J/m2) | 514 |
| Element Type | Element Length | CZM Modification | CZM Max Normal Traction (MPa) | CZM Max Shear Traction (MPa) |
|---|---|---|---|---|
| SOLID185 SOLSH190 | 1.25 mm (17,280 elements) | No CZM Modification | 50 | 100 |
| CZM Modification (Ne = 3) | 26 | 37.8 | ||
| CZM Modification (Ne = 5) | 20.1 | 29.3 | ||
| SOLID185 SOLSH190 | 2.5 mm (8640 elements) | No CZM Modification | 50 | 100 |
| CZM Modification (Ne = 3) | 18.4 | 26.7 | ||
| CZM Modification (Ne = 5) | 14.2 | 20.7 | ||
| SOLID185 SOLSH190 | 5 mm (4320 elements) | No CZM Modification | 50 | 100 |
| CZM Modification (Ne = 3) | 13 | 18.9 | ||
| CZM Modification (Ne = 5) | 10.1 | 14.6 | ||
| SOLID185 SOLSH190 | 10 mm (2160 elements) | No CZM Modification | 50 | 100 |
| CZM Modification (Ne = 3) | 9.2 | 13.4 | ||
| CZM Modification (Ne = 5) | 7.1 | 10.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mantzaroudis, V.K.; Stamatelos, D.G. Cohesive Zone Model Modification Techniques According to the Mesh Size in Finite Element Models of Stiffened Panels with Debonding. Computation 2022, 10, 5. https://doi.org/10.3390/computation10010005
Mantzaroudis VK, Stamatelos DG. Cohesive Zone Model Modification Techniques According to the Mesh Size in Finite Element Models of Stiffened Panels with Debonding. Computation. 2022; 10(1):5. https://doi.org/10.3390/computation10010005
Chicago/Turabian StyleMantzaroudis, Vasileios K., and Dimitrios G. Stamatelos. 2022. "Cohesive Zone Model Modification Techniques According to the Mesh Size in Finite Element Models of Stiffened Panels with Debonding" Computation 10, no. 1: 5. https://doi.org/10.3390/computation10010005
APA StyleMantzaroudis, V. K., & Stamatelos, D. G. (2022). Cohesive Zone Model Modification Techniques According to the Mesh Size in Finite Element Models of Stiffened Panels with Debonding. Computation, 10(1), 5. https://doi.org/10.3390/computation10010005






