On the High-Resolution Discretization of the Maxwell Equations in a Composite Tape and the Heating Effects Induced by the Dielectric Losses

Abstract

Electromagnetic field propagation inside composite materials represents a challenge where fiber-scale simulation remains intractable using classical simulation methods. The present work proposes an original 3D simulation with a mesh resolution fine enough to resolve the fiber scale, thanks to the use of Proper Generalized Decomposition (PGD)-based space decomposition, which avoids the necessity of considering homogenized properties and considers the richest description of the involved physics from the solution of the Maxwell equations. This high-resolution simulation enables comparing the electromagnetic field propagation in a composite part, depending on the considered frequency and the fiber’s/wave polarization’s relative orientation. The electromagnetic fields are then post-processed to identify the heat generation terms and- the resulting induced thermal field. The results prove the ability of the PGD-based discretization to attain extremely high levels of resolution, the equivalent of ${10}^{10}$ finite-element degrees of freedom. The obtained results show an enhanced wave penetration when the electric field polarization coincides with the fiber orientation. On the contrary, when the electric field is polarized along the normal to the fiber orientation, both the penetration and the associated heating reduce significantly, compromising the use of homogenized models, rendering them unable to reproduce the observed behaviors.

1. Introduction

Electromagnetic wave propagation has always been tricky to model using the classical numerical methods, motivating new numerical schema proposals, as in [1], and used, for instance, in [2]. Microwave heating of composites adds a layer of complexity on top of the classical problems of electromagnetic wave propagation. Having a multi-layered component with a heterogeneous composition in each layer induces multiple issues in the simulation. Moreover, high-performance composite materials are a heterogeneous combination of electrical conductors (the carbon fibers) with a dielectric material (the resin), as considered in [3] when addressing composite materials and in [4] in the case of multi-layered composite materials.

The simulation of the composite materials subjected to microwave heating is, therefore, a challenging issue, addressed in several works by using the so-called Nedelec functions. For instance, Nedelec functions are used in [2] for wave guides and then in [5] for antenna propagation, or used coupled to hexahedral 3D elements in [6]. However, until now, the technology is not fully mastered. In fact, the simulation must take into consideration the discontinuity of the wave across elements of the mesh. From this fact, classical simulations require the use of Nedelec discontinuous/continuous shape functions, as introduced in [1], with some applications addressed in [7,8]. Such elements are cumbersome in some cases. Therefore, continuous approximations with regularization are widely employed. The regularized formulation is introduced in [9], and then employed in [10] for describing the skin effect and in [11] in the case of microwave propagation. The interested reader can also refer to the quite recent work, [12]. The present work is based on the regularization method detailed in [13], and it considers the penalized boundary conditions introduced in [14].

Regularization solves one fold of the problem. However, the second fold—the rich physics appearing in one section of the composite part—has not yet been addressed. In fact, the thickness direction of a composite tape is degenerated with respect to the other dimensions, being several orders of magnitude lower than the length, for example [15]. The need to avoid excessively degenerated elements in classical simulation techniques will require the use of an extremely fine mesh in the simulated tape. Aiming to alleviate this issue, separated representations were proposed in [16], and then applied to plates and shells in [17,18], respectively.

Most developments mainly address spherical inclusions, instead of continuous fiber-reinforced composites, by using statistical [19] or deterministic [20] approaches, while other developments rely on the use of homogenized properties to treat continuous fiber composites in commercial software [21] and customized simulations [22].

In [23], the electromagnetic wave penetration and absorption were computed using the electromagnetic wave theory, while in [24], the authors experimentally determined the homogenized composite material conductivity without considering the anisotropic effect of the laminate. A recent simulation attempt considered a continuous fiber-reinforced composite as a conductive cylinder [25], or the equivalent circuits method and digital wave implementation [26]. The experimental homogenization of composite material absorption was studied in [27]. However, classical methods homogenizing the composite dielectric matrix along with the fiber inclusions fail as soon as the inclusions volume fraction increases. A 10% volume fraction of spherical inclusion led to erroneous results when using classical homogenization [19]. In real composite materials, the fiber volume fraction is often much larger than 10%.

From this fact, the space-separated representation technique appears as an appealing approach to circumvent the problem and tackle the composite using a representation of the material without homogenization as considered in [28], with a more detailed description in [29]. The Proper Generalized Decomposition—PGD—is an “a priori” model order reduction technique based on the use of separated representations, which allows one to solve a 3D model as a sequence of lower-dimensional problems. The so-called in-plane–out-of-plane decomposition was employed in a composite manufacturing simulation [30], as well as in the domain of computational rheology in [31]. The reader can refer to the review [32], and the numerous references therein. The PGD was successfully used in several applications involving composite materials while using in-plane homogenized properties of composite laminates in [33,34]. In the simulation of microwave heating, PGD was used to simulate the behavior of the composite laminate while considering homogenized properties at the ply level in [35]. Then, the numerical approach was validated in [12]. Such a simulation would still homogenize the material properties in each ply; despite being a better approach than a complete homogenization of the part in 3D, it does not address the real 3D behavior of a tow. A direct (non-homogenized) approach was tackled in [36,37], where the simulations addressed solid conductive bars immersed into a dielectric domain. To the best knowledge of the authors, there is no simulation of the microwave heating of composite materials that resolves the fiber-scale using a macro formulation without any homogenization.

The present work leverages PGD’s capabilities to attain the fiber-scale resolution during the heating of a composite tape using microwaves. The work starts with a brief review of the regularized modeling of the Maxwell equations. Then, the thermal modeling is reviewed. In Section 3, the PGD algorithm and its application for the current problem is illustrated. The results of the electric and thermal fields are addressed in Section 4 and Section 5. The results also emphasize the effect of fiber alignment with respect to the incident electromagnetic field, as well as the effect of the wave frequency on the heating process.

The considered simulations discussed later attain a level of resolution equivalent to ${10}^{10}$ finite-element degrees of freedom, and the solutions are computed in about one hour on a standard laptop, proving, therefore, the ability of PGD to solve high-fidelity problems with low computational resources. The results also prove, from a more physical viewpoint, the effect of the frequency on the wave penetration, as well as the effect of the relative orientation between the incident electric field polarization and the orientation of the continuous fibers constituting the composite reinforcement. Field polarization is proved to be of utmost importance with respect to the penetration depth and the associated heating, an effect unseen in materials simulated by considering homogenized properties.

2. Modeling of the Composite-Materials Heating Process

This part reviews the thermal modeling of composite materials when using an electromagnetic heat source. The current work focuses on the use of microwave heating while considering the potential influence of changing the electromagnetic frequency $\omega$.

2.1. Electromagnetic Formulation

Classical modeling and a simulation of electromagnetic problems using a finite-elements method used discontinuous edge elements to approximate the double-curl formulation that exists to discretize the Maxwell equations [1]. While efficient to circumvent the main complexity of such a formulation by ensuring the continuity of the tangential components and the discontinuity of the normal components [38], such a formulation creates an ill-conditioned discrete system for a large number of degrees of freedom [8]. Therefore, a nodal-regularized formulation is derived with a penalty ad hoc solution that accounts for discontinuity across media interfaces as discussed in [9,39], with a recent comprehensive regularization method described in [14]. Such a formulation was successfully used and coupled with Proper Generalized Decomposition to alleviate the computation time in composite-laminates processing in [35], and was experimentally validated in [12]. In fact, composite laminates exhibit a rich physical behavior in the thickness dimension that is several orders of magnitude lower than the in-plane dimensions. Therefore, composite laminates require an extremely fine mesh in the thickness dimension.

In the absence of the current density, the Maxwell equations’ double-curl formulation in the frequency domain reads, for the electric field:

$$\nabla \times \left(\frac{1}{\mu }\nabla \times \mathbf{E}\right)-{\omega }^2ϵ\mathbf{E}=0,\mathrm{in}\Omega \subset {\mathbb{R}}^3,$$

(1)

with $ϵ$ being the complex permitivity, written as:

$$ϵ={ϵ}_r-i\frac{\sigma }{\omega },$$

(2)

and where $\mu$, ${ϵ}_r$, and $\sigma$ represent, respectively, the magnetic permeability, the electric permitivity, and the electric conductivity.

The previous equation is complemented with adequate boundary conditions. In our examples below, each one will be applied with its corresponding boundary conditions. Without loss of generality, only Dirichlet boundary conditions and/or homogeneous Neumann ones will be used. The weighted residual weak form is obtained by multiplying (1) by a test function ${\mathbf{E}}^{\ast }$ (in fact, by the conjugate of the test function, ${\overline{\mathbf{E}}}^{\ast }$, to define properly a scalar product while taking into consideration that the electric field is a complex field, i.e., $\mathbf{E}={\mathbf{E}}_r+i{\mathbf{E}}_i$), and then integrating by parts. The final weak form is written as:

$$\begin{array}{c}{\int }_{\Omega }\frac{1}{\mu }(\nabla \times \mathbf{E})·(\nabla \times {\overline{\mathbf{E}}}^{\ast })d\mathbf{x}-{\omega }^2{\int }_{\Omega }ϵ\mathbf{E}·{\overline{\mathbf{E}}}^{\ast }d\mathbf{x}-\\ {\int }_{\partial \Omega }\frac{1}{\mu }(\nabla \times \mathbf{E})·(\mathbf{n}\times {\overline{\mathbf{E}}}^{\ast })d\mathbf{x}=0,\end{array}$$

(3)

for all regular-enough test functions ${\overline{\mathbf{E}}}^{\ast }$.

In Equation (3), the boundary integral vanishes if the test function verifies $\mathbf{n}\times {\overline{\mathbf{E}}}^{\ast }=0$ where Dirichet boundary conditions are enforced, i.e., $\mathbf{n}\times \mathbf{E}$. This will be the case for the rest of this work, as it considers only Dirichlet or homogeneous Neumann boundary conditions. Thus, the weak form reduces to the following expression:

$${\int }_{\Omega }\frac{1}{\mu }(\nabla \times \mathbf{E})·(\nabla \times {\overline{\mathbf{E}}}^{\ast })d\mathbf{x}-{\omega }^2{\int }_{\Omega }ϵ\mathbf{E}·{\overline{\mathbf{E}}}^{\ast }d\mathbf{x}=0.$$

(4)

Despite that Equation (4) satisfies the Gauss equation $\nabla ·\left(ϵ\mathbf{E}\right)=0$, it produces spurious solutions, as its discrete counterpart after approximating the different fields does not ensure the fulfillment of the Gauss equation. Thus, to avoid the spurious solutions generated by the discretization effect, a regularization should be added to the strong form of the problem (1). This work adopts the regularization considered in [14]:

$$\nabla \times \left(\frac{1}{\mu }\nabla \times \mathbf{E}\right)-\overline{ϵ}\nabla \left(\frac{1}{\overline{ϵ}ϵ\mu }\nabla ·\left(ϵ\mathbf{E}\right)\right)-{\omega }^2ϵ\mathbf{E}=0,$$

(5)

whose regularized weak form, with Dirichlet boundary conditions applied on the domain boundary, becomes:

$$\begin{array}{c}{\int }_{\Omega }\frac{1}{\mu }(\nabla \times \mathbf{E})·(\nabla \times {\overline{\mathbf{E}}}^{\ast })d\mathbf{x}-{\omega }^2{\int }_{\Omega }ϵ\mathbf{E}·{\overline{\mathbf{E}}}^{\ast }d\mathbf{x}+\\ {\int }_{\Omega }\frac{\tau }{\overline{ϵ}ϵ\mu }\left(\nabla ·\left(ϵ\mathbf{E}\right)\right)(\nabla ·(\overline{ϵ}{\overline{\mathbf{E}}}^{\ast }))d\mathbf{x}-{\int }_{\partial \Omega }\frac{\tau }{\overline{ϵ}ϵ\mu }(\nabla ·\left(ϵ\mathbf{E}\right)(\mathbf{n}·(\overline{ϵ}{\overline{\mathbf{E}}}^{\ast })))d\mathbf{x}=0,\end{array}$$

(6)

where $\tau$ is a regularization coefficient, as proposed in [13]. According to [13], $\tau$ may take a unit value everywhere in the domain, except on domain or material interfaces, where it should vanish.

2.2. Thermal Modeling

This part leverages the electric field simulation into a thermal model by defining a heat-generation model from the simulation of the electric field in the domain. Once the electric field $\mathbf{E}$ is available, one can define a heat-generation term per unit of volume Q as:

$$Q=\pi \omega {ϵ}_0{ϵ}_r{\mathbf{E}}^T·\overline{\mathbf{E}}+\frac{1}{2}{\mathbf{E}}^T·\sigma ·\overline{\mathbf{E}}.$$

(7)

Once the heat-generation term is defined, one can solve the transient heat equation to estimate the thermal field inside the composite part. The heat equation is given by [25]:

$$\rho C_p\frac{\partial T}{\partial t}-\nabla \left(\mathbf{K}·\nabla T\right)=Q,$$

(8)

with T being the temperature field, $\rho$ the material density, $C_p$ the heat capacitance at constant pressure, and $\mathbf{K}$ the orthotropic conductivity tensor. The weak form of the heat transfer problem writes:

$${\int }_{\Omega }{T}^{\ast }\rho C_p\frac{\partial T}{\partial t}+{\int }_{\Omega }\nabla T^{\ast }·\mathbf{K}·\nabla Td\Omega ={\int }_{\Omega }{T}^{\ast }Qd\Omega +{\int }_{\Gamma }{T}^{\ast }\left(\mathbf{K}·\nabla T\right)·\mathbf{n}d\Gamma ,$$

(9)

with $T^{\ast }$ being any test function with the appropriate regularity, $\Gamma$ the external boundary of the simulated domain, and $\mathbf{n}$ the outward unit vector normal to $\Gamma$. For a defined prismatic plate domain $\Omega =(x,y,z)$ such as $x\in [0,L_x]$, $y\in [0,L_y]$, and $z\in [0,L_z]$, the weak form defined in Equation (9) is complemented with the following boundary conditions:

$$\left\{\begin{array}{c}\left(\mathbf{K}·\nabla T\right){·\mathbf{n}|}_{y=L_y}=h(T(x,y=L_y,z,t)-T_{\infty })\hfill \\ \left(\mathbf{K}·\nabla T\right){·\mathbf{n}|}_{\Gamma -\left(y=L_y\right)}=0\hfill \\ T(x,y,z,t=0)=T_0\hfill \end{array}\right..$$

(10)

In the sequel, the following values are considered: $T_0=25$ °C and $T_{\infty }=25$ °C.

3. PGD Applied to Space Decomposition

This part aims to simulate the electromagnetic heating of the composite part by using a mesh that solves the fiber scale, that is, a mesh fine enough to allow the correct representation of the heating of each fiber, with several elements included in a single fiber. Therefore, since such a mesh is prohibitive of using classical simulation methods, Proper Generalized Decomposition (PGD) is used to alleviate computation costs and make the simulation possible [28]. PGD alleviates the computational complexity of the problem’s solution by using a separated representation and solving a high-dimensional problem as a sequence of lower-dimensionality problems. For instance, the electric field $\mathbf{E}$ is computed as a sequence of $1D\times 1D\times 1D$ problems by considering the separated representation:

$$\mathbf{E}(x,y,z)=\left(\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right)=\left(\begin{array}{c}{\displaystyle \sum _{i=1}^k}{X}_i^x\left(x\right)Y_i^x\left(y\right)Z_i^x\left(z\right)\\ {\displaystyle \sum _{i=1}^k}{X}_i^y\left(x\right)Y_i^y\left(y\right)Z_i^y\left(z\right)\\ {\displaystyle \sum _{i=1}^k}{X}_i^z\left(x\right)Y_i^z\left(y\right)Z_i^z\left(z\right)\end{array}\right),$$

(11)

while, for the heat problem, a non-incremental domain decomposition approach is performed by solving the thermal problem in a separated form by considering the temperature field T, approximated in the following separated form:

$$T(x,y,z,t)=\sum _{i=1}^{k_T}{X}_i^T\left(x\right)Y_i^T\left(y\right)Z_i^T\left(z\right)U_i\left(t\right).$$

(12)

The PGD solution is computed using a rank-one update greedy algorithm. Readers not familiar with the PGD technique can refer to [29] or to [40] for composite-materials heating applications, and the numerous references therein.

Nonlinear models are addressed with the PGD after performing an affine representation of the nonlinear fields by using, for example, the singular value decomposition (SVD) of the problem parameters—in our case, the nonlinear material properties, as described in [41] for cement paste and in [42] for hardly separable composite laminates. Thus, when considering a $1D\times 1D\times 1D$ decomposition, any nonlinear material property $\beta$ involved in the differential equation can be written at a given iteration p of the considered linearization algorithm as:

$${\beta }_p=\sum _{i=1}^{n_p}{\mathcal{A}}_i^p\left(x\right){\mathcal{B}}_i^p\left(y\right){\mathcal{C}}_i^p\left(z\right).$$

(13)

Then, the problem can be solved using the PGD as any linear problem to obtain the quantity of interest (the unknown field) at that iteration. From the obtained solution, the material properties can be updated everywhere in the domain, and then the SVD can be applied again to ensure the affine decomposition of the nonlinear material properties.

Thus, simulating nonlinear problems is not a real difficulty. However, the simulations addressed later have been performed with an effective value of the material properties because no data exists for the thermal dependence of the properties involved in the electromagnetic model.

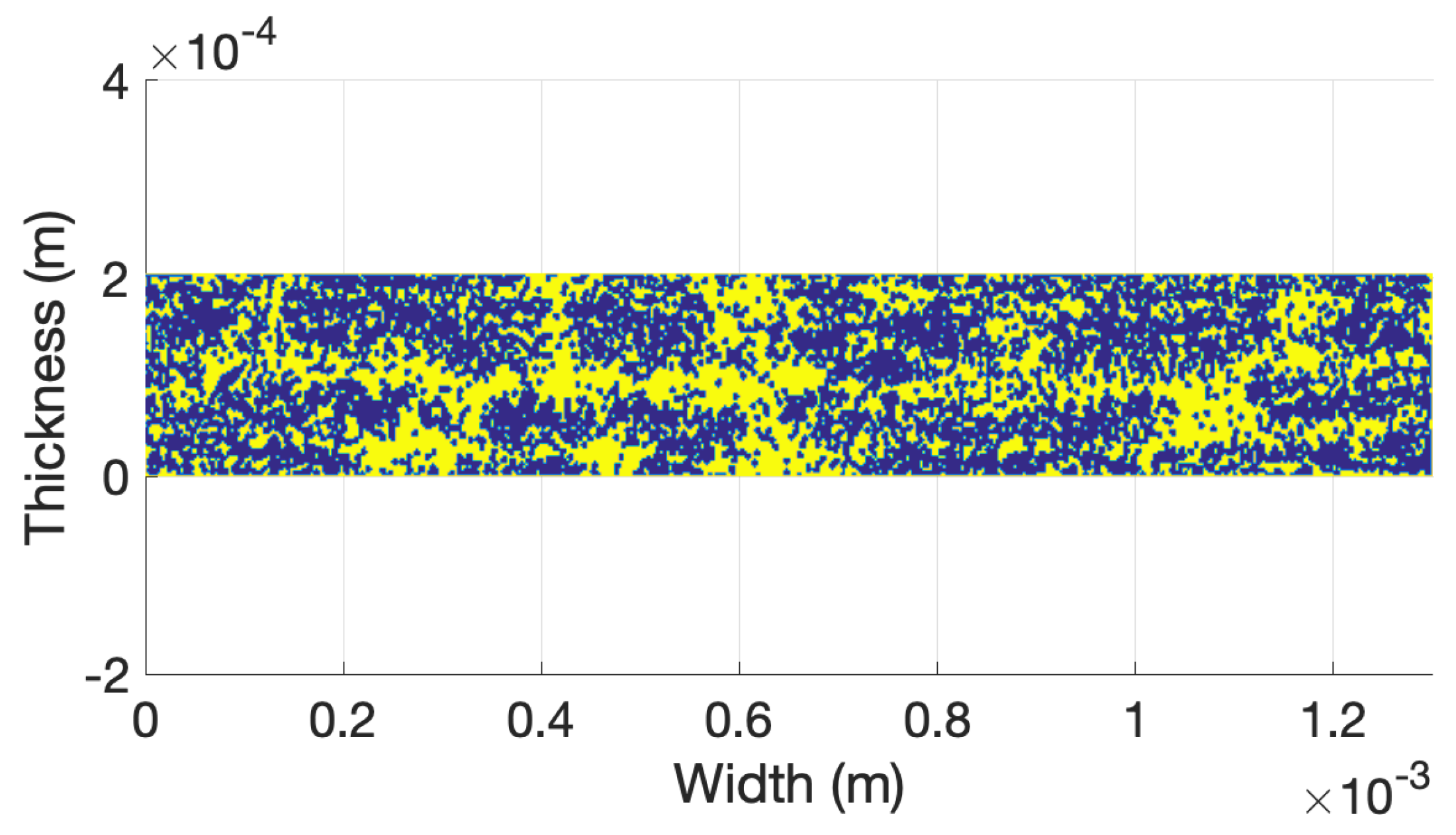
4. High-Resolution Electromagnetic Simulation and Process Parameters

This section addresses the simulation of the electric field in the composite tow at the fiber-scale level using two approaches: (i) an extruded 2D section and (ii) a full 3D-scanned part obtained by using micro-tomography.

4.1. Simulation of a Composite Part with Extruded In-Plane Section

In this section, the considered material cross-section is shown in Figure 1. The depicted cross-section has a height of $L_y=0.2$ mm and a width of $L_x=1.25$ mm. The simulated part is an extrusion of this $2D$ cross-section, with a depth of $L_z=50$ mm.

The in-plane material properties are separated using a singular value decomposition. Therefore, for any material property p, one can write:

$$p=\sum X_i^p\left(x\right){\alpha }_i{Y}_i^p\left(y\right)$$

(14)

with $X_i^p$ being the normalized x components of the singular value decomposition, $Y_i^p$ the normalized y components, and ${\alpha }_i$ the singular values. The truncation is performed for ${\alpha }_i/{\alpha }_1<{10}^{-6}$.

To identify the fiber orientation effect on the electric field propagation in the part, an extremely fine mesh consisting of 7000 nodes along the x direction, 4000 nodes along the y direction, and 4000 nodes along the z direction is used, representing the equivalent of $342\times {10}^9$ degrees of freedom. Two sets of boundary conditions are used. Set one writes:

$$\left\{\begin{array}{c}{E}_y(x=0,x=L_x)=0\hfill \\ E_z(x=0,x=L_x)=0\hfill \\ E_x(y=L_y)=cos\left(2\pi {\mathcal{L}}_x\left(\frac{x}{L_x}\right)\right)\hfill \\ E_z(y=L_y)=0\hfill \\ E_x(z=0,z=L_z)=0\hfill \\ E_y(z=0,z=L_z)=0\hfill \\ \left(\nabla \times \mathbf{E}\right)·\left(\mathbf{n}\times \overline{{\mathbf{E}}^{\ast }}\right){|}_{{\Gamma }^{\ast }}=0\hfill \end{array}\right.$$

(15)

where ${\Gamma }^{\ast }$ is the part of $\Gamma$ where no Dirichlet boundary conditions are prescribed. On the other hand, set two writes:

$$\left\{\begin{array}{c}{E}_y(x=0,x=L_x)=0\hfill \\ E_z(x=0,x=L_x)=0\hfill \\ E_x(y=L_y)=0\hfill \\ E_z(y=L_y)=cos\left(2\pi {\mathcal{L}}_z\left(\frac{z}{L_z}\right)\right)\hfill \\ E_x(z=0,z=L_z)=0\hfill \\ E_y(z=0,z=L_z)=0\hfill \\ \left(\nabla \times \mathbf{E}\right)·\left(\mathbf{n}\times \overline{{\mathbf{E}}^{\ast }}\right){|}_{{\Gamma }^{\ast }}=0\hfill \end{array}\right.$$

(16)

In Equations (15) and (16), ${\mathcal{L}}_x$ and ${\mathcal{L}}_z$ are, respectively, the length scale along x and z computed using the wave frequency $\omega$ and its wave length $\lambda =\frac{c}{\omega }$, using:

$$\begin{array}{c}{\mathcal{L}}_x=\frac{L_x}{\lambda }\hfill \\ {\mathcal{L}}_z=\frac{L_z}{\lambda }\hfill \end{array},$$

(17)

with c being the light speed. Therefore, the application of the real wave propagating along a unidirectional axis at the top surface of the part $y=L_y$ is simulated. To identify the dependence on the frequency, two frequencies are selected for illustrative purposes: ${\omega }_1=2.45$ GHz and ${\omega }_2=24.5$ GHz. The material properties are given in

Table 1. Properties of the fiber and matrix phases in the parallel and perpendicular direction to the fibers. The notation // is used to refer to the direction parallel to the fibres, whereas ⊥ refers to the direction normal to the fibers.

Parameter	Value // to the Fibers	Value ⊥ to the Fibers	Value in the Matrix
${ϵ}_r$	$20+i$	$20+i$	1
${\mu }_r$	1	1	1
$\sigma$	${10}^3$	${10}^2$	${10}^{-4}$

as taken from [12,43] (properties identified in the framework of Simultool, AGE2020 European Research Project).

With the values indicated in Table 1, the set 1 of boundary conditions, considering a field polarization along the x direction and, thus, perpendicular to the fibers, we illustrate the results in four consecutive figures. These figures correspond first to the two 3D views for the selected frequencies, ${\omega }_1$ and ${\omega }_2$, to show the difference in the propagation of the electric field on the domain’s outer surface. Later, we show two figures corresponding to the through-the-thickness section, and compare the results for ${\omega }_1$ and ${\omega }_2$. The simulation outputs are illustrated in Figure 2 for ${\omega }_1$ and Figure 3 for ${\omega }_2$ using 3D views, showing a better wave propagation for lower incident wave frequencies. The through-the-thickness sections are illustrated in Figure 4 for ${\omega }_1$ and Figure 5 for ${\omega }_2$. The through-the thickness propagation results illustrate the penetration depth in the composite thickness, with a clear difference in the wave magnitude when changing the frequency of the incident wave, concluding with a higher penetration at lower frequencies.

The results for the second set of boundary conditions are given using 3D views in Figure 6 for ${\omega }_1$ and Figure 7 for ${\omega }_2$. The through-the-thickness penetrations are illustrated in Figure 8 for ${\omega }_1$ and in Figure 9 for ${\omega }_2$. Again, these results show the penetration depth in the composite part, with a clear difference in the wave magnitude when changing the frequency of the incident wave, with a higher penetration depth for lower frequencies.

Then, for the same frequency, the effect of considering different polarization is analyzed. Concerning the results for the frequency ${\omega }_1$, Figure 4 illustrates the through-the-thickness penetration of a wave polarized in the normal direction to the fibers ($E_x$), while Figure 8 illustrates the penetration of an incident wave polarized parallel to the fibers ($E_z$). By comparing Figure 4 and Figure 8, it can be noticed that the penetration is higher when the wave polarization coincides with the fibers’ orientation. Similar results and conclusions are found when considering the second frequency ${\omega }_2$, by comparing Figure 5 (incident wave normally polarized) and Figure 9 (incident wave polarized along the fiber orientation).

As a review of the results discussed above, one can clearly state two main conclusions:

• The electric field penetration inside the part is deeper for lower frequencies, and the electric field exhibits, therefore, a higher intensity for lower frequencies;
• The electric field penetration inside the part is higher when the wave polarization is parallel to the fiber orientation.

The first conclusion is quite intuitive, as the higher the frequency, the lower the penetration depth, while the second conclusion seems more related to the possibility of the electric field penetrating when its polarization is parallel to the fibers.

4.2. Simulation of a Real 3D-Scanned Composite Part

This section considers a 3D micro-tomography scan of a composite part and identifies the different phases using a k-means algorithm. After selecting three phases, the results are shown in Figure 10. The k-means algorithm identified three phases illustrated in red, dark blue, and light blue. The red is the carbon fibers phase, the dark blue is the matrix phase, and the light blue represents the air-bubble entrapment. The air is considered to have ${ϵ}_r^{air}=1$, ${\mu }_r^{air}=1$, and ${\sigma }_r^{air}=0$. With these assigned properties, one can use an in-plane–out-of-plane decomposition and the PGD method.

First of all, the material properties in the 3D domain are separated using singular value decomposition. Again, for any property p, one may write:

$$p(x,y,z)=\sum _{i=1}^{n_p}{U}_i^T{\alpha }_i{V}_i,$$

(18)

with $U_i(x,y)$ being the normalized singular vectors decomposition in the in-plane domain $(x,y)$, and $V_i\left(z\right)$ the normalized singular vectors of the out-of-plane domain z. The values ${\alpha }_i$ are the singular values or the weights of the i-vectors. The method truncates the material properties’ representation at i for ${\alpha }_i/{\alpha }_1<{10}^{-6}$. When having the material properties in the in-plane–out-of-plane separated form, one can easily apply the proper generalized decomposition for the considered domain, as explained in [15] for thermal models and [17] for mechanical deformation.

The considered specimen has the dimensions $L_x=1.6$ mm, $L_y=0.512$ mm, and $L_z=2.1$ mm. The results depicted in Figure 11 are associated with the boundary conditions given by Equation (15), while the results related to the boundary conditions given in Equation (16) are shown in Figure 12.

The comparison of Figure 11 (wave polarization perpendicular to the fibers) with Figure 12 (polarization along the fiber direction) reinforces the conclusions drawn in Section 4.1: the propagation inside the plate is higher when the polarization coincides with the fiber orientation, even when the fibers are not fully aligned. Another conclusion can also be inferred: when the fibers are not aligned, the in-depth propagation is smaller than the one seen in the case of fully aligned fibers.

5. Thermal Simulation

The electric field is leveraged to compute the volumetric heat source Q, as described in Equation (7). Without loss of generality, the simulation in this section is performed on $L_z=50$ mm, the extruded fibers’ domain.

The propagation of the electric field operates differently in the domain, and consequently, the heat generation will also depend strongly on it and on the material parameters. For example, consider the second term of Equation (7), such as:

$$\begin{array}{ll}\frac{1}{2}{\mathbf{E}}^T·\sigma ·\overline{\mathbf{E}}& =\frac{1}{2}{\left(\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right)}^T·\left(\begin{array}{ccc}{\sigma }_{\perp }& 0& 0\\ 0& {\sigma }_{\perp }& 0\\ 0& 0& {\sigma }_{//}\end{array}\right)·\left(\begin{array}{c}\overline{E_x}\\ \overline{E_y}\\ \overline{E_z}\end{array}\right)\\ & =\frac{1}{2}\left(E_x.{\sigma }_{\perp }.\overline{E_x}+E_y.{\sigma }_{\perp }.\overline{E_y}+E_z.{\sigma }_{//}.\overline{E_z}\right)\end{array}$$

(19)

Equation (19) clearly reflects the difference between the results expected from the set 1 of boundary conditions where only $E_x$ is imposed, and those related to the set 2 where only $E_z$ is imposed, especially in view of the difference between ${\sigma }_{//}$ and ${\sigma }_{\perp }$. The heat-source distribution is illustrated in Figure 13 for set 1 and in Figure 14 for set 2 of the boundary conditions for the part with aligned fibres. One can clearly identify the regions where the fibers concentrate, with high heat generation, while the regions where the matrix concentrates exhibit a smaller heat generation.

Concerning the heat generation, the temperature field is computed using the heat equation and the PGD-based discretization method. The results are illustrated in Figure 15 for an incident wave polarized in the direction normal to the fibers, and in Figure 16 for a wave polarized in the direction parallel to the fibers. The results are presented for $t=50$ s, a time frame at which we can clearly identify a high heating efficiency when polarizing the incident wave parallel to the composite tow fibers’ orientation. The choice of $t=50$ s is motivated to ensure a large-enough time frame, allowing one to show a relevant heating difference depending on the field polarization, while keeping the associated computing time reasonable. The time discretization consists of 500 nodes within the considered 50-s time frame. The convergence of the numerical results with respect to further refinements was checked. The heat generation terms Q are multiplied by $380\times {10}^3$ V in both cases, to consider a more realistic heat source.

6. Conclusions

This work uses the PGD method to simulate the microwave heating of composite parts with a fiber-length resolution. The simulation clearly proves the ability of the PGD to solve high-fidelity problems with the equivalent of more than ${10}^{10}$ degrees of freedom, within about an hour, on a standard laptop.

The results also prove the effect of the frequency on the wave penetration, as well as the effect of the relative orientation between the external imposed field polarization and the fibers. A field polarized in the fiber direction can penetrate deeper into the material, while when polarized in the normal direction with respect to the fiber orientation, the field penetration is much smaller, being absorbed at the surface neighborhood, with the associated impact in the heating process—a behavior that could become profitable for optimizing processes, increasing efficiency, or/and guaranteeing the part quality.

These results are of major relevance and emphasize the limits of homogenized models that fail to address localized behaviors. In fact, homogenized materials rarely address the anisotropic behavior of the composites or the effect of the field polarization.